Abstract
Let G be a graph embedded in the plane and let \(\mathcal {A} \) be an arrangement of pseudolines intersecting the drawing of G. An aligned drawing of G and \(\mathcal {A} \) is a planar polyline drawing \(\varGamma \) of G with an arrangement \(A \) of lines so that \(\varGamma \) and \(A \) are homeomorphic to G and \(\mathcal {A} \). We show that if \(\mathcal {A} \) is stretchable and every edge e either entirely lies on a pseudoline or intersects at most one pseudoline, then G and \(\mathcal {A} \) have a straight-line aligned drawing. In order to prove these results, we strengthen the result of Da Lozzo et al. [5], and prove that a planar graph G and a single pseudoline \(\mathcal {L}\) have an aligned drawing with a prescribed convex drawing of the outer face. We also study the more general version of the problem where only a set of vertices is given and we need to determine whether they can be collinear. We show that the problem is \(\mathcal {NP} \)-hard but fixed-parameter tractable.
Work was partially supported by grant WA 654/21-1 of the German Research Foundation (DFG).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Two fundamental primitives for highlighting structural properties of a graph in a drawing are alignment of vertices such that they are collinear and geometrically separating unrelated graph parts, e.g., separating them by a straight line. Not surprisingly, both these techniques have been previously considered from a theoretical point of view in the case of planar straight-line drawings.
Da Lozzo et al. [5] study the problem of producing a planar straight-line drawing of a given embedded graph \(G=(V,E)\), i.e., G has a fixed combinatorial embedding and a fixed outer face, such that a given set \(S \subseteq V\) of vertices is collinear. It is clear that if such a drawing exists, then the line containing the vertices in S is a simple curve starting and ending at infinity that for each edge e of G either fully contains e or intersects e in at most one point, which may be an endpoint. We call such a curve a pseudoline with respect to G. Da Lozzo et al. [5] show that this is a full characterization of the alignment problem, i.e., a straight-line drawing where the vertices in S are collinear exists if and only if there exists a pseudoline \(\mathcal L\) with respect to G that contains the vertices in S. However testing whether such a pseudoline exists is an open problem, which we consider in this paper.
Likewise, for the problem of separation, Biedl et al. [1] considered so-called HH-drawings, where given an embedded graph \(G=(V,E)\) and a partition \(V = A \dot{\cup }B\), one seeks a planar drawing of G in which A and B can be separated by a line. Again, it turns out that such a drawing exists if and only if there exists a pseudoline \(\mathcal L\) with respect to G such that the vertices in A and B are separated by \(\mathcal L\) in the sense that they are in different halfplanes. Cano et al. [2] extend the result to planar straight-line drawings with a given star-shaped outer face.
In particular, the results of Da Lozzo et al. [5] show that given a pseudoline \(\mathcal L\) with respect to G one can always find a planar straight-line drawing of G such that the vertices on \(\mathcal L\) are collinear and the vertices contained in the halfplanes defined by \(\mathcal L\) are separated by a line L. In other words, a topological configuration consisting of a planar graph G and a pseudoline with respect to G can always be stretched. In this paper we initiate the study of this stretchability problem with more than one given pseudoline.
Aligned Drawing (b) of a 2-aligned planar graph (a). The pseudolines \(\mathcal {R}\) and \(\mathcal {B}\) and the corresponding lines in the drawing are drawn red and blue, respectively. (c) A non-stretchable arrangement of 9 pseudolines, which can be seen as a stretchable arrangement of 8 pseudolines (grey) and an edge (black solid).
More formally, a pair \((G, \mathcal {A})\) is a k-aligned graph if \(G=(V,E)\) is a planar embedded graph and \(\mathcal {A} = \{\mathcal {L}_1, \dots , \mathcal {L}_k\}\) is an arrangement of (pairwise intersecting) pseudolines with respect to G. If the number k of curves is clear from the context, we drop it from the notation and simply speak of aligned graphs. For 1-aligned graphs we write \((G, \mathcal {L})\) instead of \((G,\{\mathcal {L}\})\). Let \(A = \{L_1, \dots , L_k\}\) be a line arrangement and \(\varGamma \) be planar drawing of G. A tuple \((\varGamma ,A)\) is an aligned drawing of \((G, \mathcal {A})\) if and only if the following properties hold; refer to Fig. 1(a-b). (i) The arrangement of A is homeomorphic to the arrangement of \(\mathcal {A} \) (i.e., \(\mathcal {A} \) is stretchable), (ii) \(\varGamma \) is homeomorphic to the planar embedding of G, (iii) each line \(L_i\) intersects in \(\varGamma \) the same vertices and edges as \(\mathcal {L}_i\) in G, and it does so in the same order. We focus on straight-line aligned drawings. For brevity, unless stated otherwise, the term aligned drawing refers to a straight-line drawing throughout this paper.
Note that the stretchability of \(\mathcal {A} \) is a necessary condition for the existence of an aligned drawing. Since testing stretchability is \(\mathcal {NP} \)-hard [14, 15], we assume that a geometric realization A of \(\mathcal {A} \) is provided. However, line arrangements of size up to 8 are always stretchable [10] and only starting from 9 lines non-stretchable arrangements exist; see the Pappus configuration [11] in Fig. 1(c). It is conceivable that in practical applications, e.g., stemming from user interactions, the number of lines to stretch is small. The same configuration illustrates an example of an 8-aligned graph with a single edge that does not have an aligned drawing.
The aligned drawing convention generalizes the problems studied by Da Lozzo et al. and Biedl et al. who concentrated on the case of a single line. We study a natural extension of their setting and ask for alignment on general line arrangements.
In addition to the strongly related work mentioned above, there are several other works that are related to the alignment of vertices in drawings. Dujmović [6] shows that every n-vertex planar graph \(G=(V, E)\) has a planar straight-line drawing such that \(\varOmega (\sqrt{n})\) vertices are aligned, and Da Lozzo et al. [5] show that in planar treewidth-3 graphs, one can align \(\varTheta (n)\) vertices and that in treewidth-k graphs one can align \(\varOmega (k^{2})\) vertices. Chaplik et al. [3] study the problem of drawing planar graphs such that all edges can be covered by k lines. They show that it is \(\mathcal {NP} \)-hard to decide whether such a drawing exists. Deciding whether there exists a drawing where all vertices lie on k lines is open [4]. Drawings of graphs on n lines where a mapping between the vertices and the lines is provided have been studied by Dujmović et al. [7, 8].
Contribution & Outline. First we study the topological setting where we are given a planar graph G and set S of vertices to align in Sect. 3. We show that the problem is \(\mathcal {NP} \)-hard but fixed-parameter tractable (FPT) with respect to |S|. Afterwards in Sect. 4 we consider the geometric setting where we seek an aligned drawing of an aligned graph. In Sect. 4.2, we strengthen the result of Da Lozzo et al. and Biedl et al. and show that there exists a 1-aligned drawing of G with a given convex drawing of the outer face. In Sect. 4.3 we consider k-aligned graphs with a stretchable pseudoline arrangement, where every edge e either entirely lies on a pseudoline or intersects with at most one pseudoline, which can either be in the interior or an endpoint of e. We utilize the previous result to prove that every such k-aligned graph has an aligned drawing, for any value of k. The proofs of statements marked with  can be found in the full version on arXiv [12].
can be found in the full version on arXiv [12].
2 Preliminaries
Let \(\mathcal {A} \) be a pseudoline arrangement of a set of k pseudolines \(\mathcal {L}_1, \dots , \mathcal {L}_k\) and \((G, \mathcal {A})\) be an aligned graph. The set of cells in \(\mathcal {A} \) is denoted by \(\mathrm {cells}(\mathcal {A})\). A cell is empty if it does not contain a vertex of G. Removing from a pseudoline its intersections with other pseudolines gives a set of its pseudosegments.
Let \(G=(V, E)\) be a planar embedded graph with a vertex set V and an edge set E. We call \(v \in V\) interior if v does not lie on the boundary of the outer face of G. An edge \(e\in E\) is interior if e does not lie entirely on the boundary of the outer face of G. An interior edge is a chord if it connects two vertices on the outer face. A point p of an edge e is an interior point of e if p is not an endpoint of e. A triangulation is a planar embedded graph whose inner faces are all triangles and whose outer face is bounded by a simple cycle. A triangulation of a graph G is a triangulation that contains G as a subgraph. For a graph G and an edge e of G, not being an edge of a separating triangle, the graph G/e is obtained from G by contracting e and merging the resulting multiple edges and removing self-loops. A k-wheel is a wheel graph \(W_k\) with k vertices on the outer face and one interior vertex. Let \(\varGamma \) be a drawing of G and let C be a cycle in G. We denote with \(\varGamma [C]\) the drawing of C in \(\varGamma \). A k-aligned triangulation of \((G, \mathcal {A})\) is a k-aligned graph \((G_T, \mathcal {A})\) with \(G_T\) being a triangulation of G.
A vertex is \(\mathcal {L}_i\)-aligned (or simply aligned to \(\mathcal {L}_i\)) if it lies on the pseudoline \(\mathcal {L}_i\). A vertex that is not aligned is free. An edge e is \(\mathcal {L}_i\)-aligned (or simply aligned) if it completely lies on \(\mathcal {L}_i\). Let \(E_{\mathrm {aligned}}\) be the set of all aligned edges. An intersection vertex lies on the intersection of two pseudolines \(\mathcal {L}_i\) and \(\mathcal {L}_j\). An edge is i-anchored (\(i=0,1,2\)) if i of its endpoints are aligned to distinct curves. Let \(E_i\) be the set of i-anchored edges; note that, the set of edges is the disjoint union  . A 0-anchored, 0-crossed, non-aligned edge is also called free. An edge e is (at most) l-crossed if (at most) l distinct pseudolines intersect e in its interior. A non-empty edge set \(A \subset E\) is l-crossed if l is the smallest number such that every edge in A is at most l-crossed.
. A 0-anchored, 0-crossed, non-aligned edge is also called free. An edge e is (at most) l-crossed if (at most) l distinct pseudolines intersect e in its interior. A non-empty edge set \(A \subset E\) is l-crossed if l is the smallest number such that every edge in A is at most l-crossed.
The alignment complexity of an aligned graph \(\mathcal G\) in a way describes how “complex” the relationship between the graph G and the line arrangement \( \mathcal {L}_1, \dots , \mathcal {L}_k\) is and formally is defined as a triple \((l_0, l_1, l_2)\) , where \(l_i\), \(i=0,1,2\), describes the “complexity of i-anchored edges”, i.e. it indicates that \(E_i\) is at most \(l_i\)-crossed or has to be empty, if \(l_i = \bot \). For example, an aligned graph where every vertex is aligned and every edge has at most l interior intersections has the alignment complexity \((\bot , \bot , l)\). For further examples, see Fig. 2.
3 Complexity and Fixed-Parameter Tractability
In this section we deal with the topological setting where we are given a planar embedded graph \(G=(V, E)\) and a subset \(S \subset V\) to be collinear. According to Da Lozzo et al. [5], this is equivalent to the existence of a pseudoline \(\mathcal {L}(S)\) with respect to G passing exactly through the vertices in S. We refer to this problem as pseudoline existence problem. Using techniques similar to Fößmeier and Kaufmann [9], we can show that the pseudoline existence problem is \(\mathcal {NP} \)-hard; see full version [12]. In the following, we show that the pseudoline existence problem is FPT with respect to |S|. In the first step deal with biconnected planar embedded graphs only. Additionally to the set of vertices S we require the pseudoline to pass through a set of faces F. This trick allows us to combine two independent pseudolines of two biconnected components of a planar embedded graph. Thus, let additionally G be biconnected and F be a subset of faces of G. Notice that in case that the vertices of S are not independent, they can only form a linear forest, i.e., a set of paths, as otherwise there is no pseudoline through the vertices S with respect to G. Let \({G}^{\star }\) be the dual graph of G (see Fig. 3.a) and let \(S' \subseteq S\) be the subset of vertices that form end-points of the paths induced by S. We denote by f a face of G and by  its dual vertex. An extended dual \({G}^{\star }_{\mathrm {e}}(S,F)\) is the graph obtained from \({G}^{\star }\) by the following steps. We omit the parameters (S, F) if they are clear from the context.
its dual vertex. An extended dual \({G}^{\star }_{\mathrm {e}}(S,F)\) is the graph obtained from \({G}^{\star }\) by the following steps. We omit the parameters (S, F) if they are clear from the context.
- Step 1: :
-
For each path induced by S that contains exactly one edge, subdivide the edge by a vertex and add it to S,
- Step 2: :
-
Place the vertices of S into the corresponding faces of \({G}^{\star }\) and the edges induced by them (red vertices and edges in Fig. 3(a)).
- Step 3: :
-
Connect the vertices of \(S'\) to all vertices of the dual face they lie in (red dashed edges in Fig. 3(a)).
- Step 4: :
-
For each vertex \(v \in S\) remove the edges dual to the primal edges incident to v.
- Step 5: :
-
Remove all the dual vertices that have in degree zero or one; see Fig. 3(b).
- Step 6: :
-
Replace each vertex
 of \({G}^{\star }\) with a clique of the size equal the degree of
of \({G}^{\star }\) with a clique of the size equal the degree of 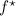 , each vertex v of this clique corresponds to an edge \(e^*\) incident to a vertex
, each vertex v of this clique corresponds to an edge \(e^*\) incident to a vertex  , thus we call it a clique vertex corresponding to
, thus we call it a clique vertex corresponding to 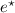 and denote by
and denote by  . For each edge of \({G}^{\star }_e\) that has survived, we connect the two corresponding to it clique vertices.
. For each edge of \({G}^{\star }_e\) that has survived, we connect the two corresponding to it clique vertices. - Step 7: :
-
Recall that F is a set of faces of G. Assume we would like our pseudoline to pass through the faces of F. To check for existence of such a pseudoline we further augment the graph \({G}^{\star }_{\mathrm {e}}\) as follows. For each \(f\in F\), additionally to the clique that is built on face vertices
 , corresponding to the edges incident to the dual vertex f, we add a star with a new center vertex \(\mathrm {cent}(f)\) that has
, corresponding to the edges incident to the dual vertex f, we add a star with a new center vertex \(\mathrm {cent}(f)\) that has  as leaves. Finally, we set \(\mathrm {cent}(F)=\{\mathrm {cent}(f) \mid f\in F\}\).
as leaves. Finally, we set \(\mathrm {cent}(F)=\{\mathrm {cent}(f) \mid f\in F\}\).
Lemma 1
(
 ). Let \(G=(V,E)\) be a biconnected planar embedded graph, let \(S\subset V\) be a set of vertices that induce a linear forest and let F be a set of faces of G. There exist an aligned graph \((G,\mathcal {L})\), where \(\mathcal {L}\) passes through all vertices of S and faces F if and only if there exists a simple cycle C in the extended dual \({G}^{\star }_{\mathrm {e}}(S,F)\) through the vertices of \(S\cup \mathrm {cent}(F)\).
). Let \(G=(V,E)\) be a biconnected planar embedded graph, let \(S\subset V\) be a set of vertices that induce a linear forest and let F be a set of faces of G. There exist an aligned graph \((G,\mathcal {L})\), where \(\mathcal {L}\) passes through all vertices of S and faces F if and only if there exists a simple cycle C in the extended dual \({G}^{\star }_{\mathrm {e}}(S,F)\) through the vertices of \(S\cup \mathrm {cent}(F)\).
We utilize the following theorem.
Theorem 1
(Wahlström [16]). Given a graph \(G=(V,E)\) and a subset \(S\subset ~V\), it can be tested in \(O(2^{|S|}\mathrm {poly}(n))\) time whether a simple cycle through the vertices in S exists. In affirmative the cycle can be reported within the same asymptotic time.
Theorem 1 together with Lemma 1 gives a \(O(2^{|S|}\mathrm {poly}(n))\) time algorithm to solve the pseudoline construction problem for the case of biconnected graphs. We next sketch how this can be extended to general planar graphs.
Lemma 2
(
 ). Let \(G=(V,E)\) be a planar embedded graph, \(S\subset V\) and c be a cut vertex of G separating G into subgraphs \(G_1=(V_1,E_1)\) and \(G_2=(V_2,E_2)\). Let \(S_1=S \cap V_1 \ne \emptyset \) and \(S_2 = S \cap V_2 \setminus \{c\} \ne \emptyset \). Let f be the face of \(G_1\) where \(G_2\) lies. There exists an aligned graph \((G,\mathcal {L}(S))\) if and only if there exist aligned graphs \((G_1,\mathcal {L}(S_1))\) and \((G_2,\mathcal {L}(S_2))\), such that \(\mathcal {L}(S_1)\) passes through face f.
). Let \(G=(V,E)\) be a planar embedded graph, \(S\subset V\) and c be a cut vertex of G separating G into subgraphs \(G_1=(V_1,E_1)\) and \(G_2=(V_2,E_2)\). Let \(S_1=S \cap V_1 \ne \emptyset \) and \(S_2 = S \cap V_2 \setminus \{c\} \ne \emptyset \). Let f be the face of \(G_1\) where \(G_2\) lies. There exists an aligned graph \((G,\mathcal {L}(S))\) if and only if there exist aligned graphs \((G_1,\mathcal {L}(S_1))\) and \((G_2,\mathcal {L}(S_2))\), such that \(\mathcal {L}(S_1)\) passes through face f.
Utilizing Lemma 2, we can recursively decompose a graph into biconnected components, check for the pseudoline existence by applying Lemma 1 and Theorem 1 and glue the pseudolines if they exist. This implies the following:
Theorem 2
(
 ). Given a planar embedded graph \(G=(V,E)\) and a subset \(S\subset V\), it can be tested in \(O(4^{|S|}\mathrm {poly}(n))\) time whether an aligned graph \((G,\mathcal {L}(S))\) exists.
). Given a planar embedded graph \(G=(V,E)\) and a subset \(S\subset V\), it can be tested in \(O(4^{|S|}\mathrm {poly}(n))\) time whether an aligned graph \((G,\mathcal {L}(S))\) exists.
4 Drawing Aligned Graphs
We show that every aligned graph where each edge either entirely lies on a pseudoline or is intersected by at most one pseudoline, i.e., alignment complexity \((1, 0, \bot )\), has an aligned drawing. For 1-aligned graphs we show the stronger statement that every 1-aligned graph has an aligned drawing with a given aligned convex drawing of the outer face. We first present our proof strategy and then deal with 1- and k-aligned graphs.
4.1 Proof Strategy
Our general strategy for proving the existence of aligned drawings of an aligned graph \((G, \mathcal {A})\) is as follows. First, we show that we can triangulate \((G, \mathcal {A})\) by adding vertices and edges without invalidating its properties. We can thus assume that our aligned graph \((G, \mathcal {A})\) is an aligned triangulation. Second we show that, unless G is a specific graph (e.g., a k-wheel or a triangle), it contains a specific type of edge, namely an edge that is contained in a pseudoline, or an edge that is not intersected by any of the pseudolines. Third, we exploit the existence of such an edge to inductively prove the existence of an aligned drawing of \((G, \mathcal {A})\). Depending on whether the edge is contained in a separating triangle or not, we either decompose along that triangle or contract the edge. In both cases the problem reduces to smaller instances that are almost independent. In order to combine solutions, it is, however, crucial to use the same arrangement of lines \(A \) for both of them.
In the following we introduce the necessary tools used for all three steps on k-aligned graphs of alignment complexity \((1, 0, \bot )\). Recall, that for this class (i) every free edge is at most 1-crossed, (ii) every 1-anchored edge has no intersections, and (iii) there is no edge with its endpoints on two pseudolines. Lemma 3 shows that every aligned graph has an aligned triangulation with almost the same alignment complexity. If G contains a separating triangle, Lemma 4 shows that \((G, \mathcal {A})\) admits an aligned drawing if both split components have an aligned drawing. Finally, with Lemma 5 we obtain a drawing of \((G, \mathcal {A})\) from a drawing of the aligned graph \((G/e, \mathcal {A})\) where one special edge e is contracted. For simplicity we assume the input graph to be 2-connected, general graphs allow similar techniques.
Lemma 3
(
 ). Let \((G, \mathcal {A})\) be a biconnected k-aligned graph of alignment complexity (2, 0, 0). There exists a k-aligned triangulation \((G_T=(V_T, E_T), \mathcal {A})\) of \((G,\mathcal {A})\) whose size is \(O(k^4n)\). Each edge in \(E_T \setminus E(G)\) is at most 1-crossed and 0-anchored, or 0-crossed and 1-anchored.
). Let \((G, \mathcal {A})\) be a biconnected k-aligned graph of alignment complexity (2, 0, 0). There exists a k-aligned triangulation \((G_T=(V_T, E_T), \mathcal {A})\) of \((G,\mathcal {A})\) whose size is \(O(k^4n)\). Each edge in \(E_T \setminus E(G)\) is at most 1-crossed and 0-anchored, or 0-crossed and 1-anchored.
Proof sketch
To triangulate \((G, \mathcal {A})\), we exhaustively apply each of the following steps.
-
1.
If f is a non-triangular face whose boundary contains a 2-crossed edge uv, we build a triangle by inserting a vertex x in the intermediate cell, as shown in Fig. 4(a). This step ensures that every edge of a non-triangular face is at most 1-crossed.
-
2.
If f is a non-triangular face whose interior contains the intersection I of a set of pseudolines, we place a vertex v on I and connect v to two disjoint vertices on f with two simple paths, where every vertex of the path, which is not an endpoint, is free; compare Fig. 4(b).
-
3.
If f is a non-triangular face with an aligned edge \(e=uv\) we can split f into two faces \(f'\) and \(f''\) (as shown in Fig. 4(c)) such that \(f'\) contains e on its boundary. Then we can triangulate \(f'\) with 1-crossed edges. A similar approach works for aligned vertices; see Fig. 4(d).
-
4.
If f is a non-triangular face whose interior contains a pseudosegment \(\mathcal {S}\), then we find two edges vw, xy as shown in Fig. 4(e) and we can triangulate by inserting a vertex on \(\mathcal {S}\) and 1-crossed edges.
-
5.
If none of the cases above applies, then no non-triangular face contains a pseudosegment. Thus all remaining non-triangular faces can be triangulated with free edges. \(\square \)
In order to simplify the constructions we augment the input graph with an additional cycle in the outer face, so that no two pseudolines intersect in the outer face. More formally, let \(\mathcal {A} \) be an arrangement of pseudolines \(\mathcal {L}_1, \mathcal {L}_2, \dots , \mathcal {L}_k\). Let \(U_1, U_2, \dots , U_t \in \mathrm {cells}(\mathcal {A})\) be the set of unbounded cells in the arrangement of \(\mathcal {A} \) such that \(U_i, U_{i + 1}\) are adjacent cells with \(U_{t+1} = U_1\). For \(k > 1\), a k-aligned graph is proper (i) if the boundary of the outer face is a 0-anchored 1-crossed cycle of length t such that every unbounded region \(U_i\) contains exactly one vertex of the cycle, and (ii) every aligned edge in \((G, \mathcal {A})\) is 0-crossed. Observe that for every k-aligned graph \((G, \mathcal {A})\) there is proper k-aligned triangulation \((G', \mathcal {A})\) containing G as a minor.
The following two lemmas show that we can reduce the size of the aligned graph and obtain a drawing by merging two drawings or by unpacking an edge.
Lemma 4
(
 ). Let \((G, \mathcal {A})\) be a k-aligned triangulation. Let T be a separating triangle splitting G into subgraphs \(G_{\mathrm {in}}, G_{\mathrm {out}} \) so that \(G_{\mathrm {in}} \cap G_{\mathrm {out}} =T\) and \(G_{\mathrm {out}} \) contains the outer face of G. Then, (i) \((G_{\mathrm {out}}, \mathcal {A})\) and \((G_{\mathrm {in}}, \mathcal {A})\) are k-aligned triangulations, and (ii) \((G, \mathcal {A})\) has an aligned drawing if and only if there exists a common line arrangement A such that \((G_{\mathrm {out}}, \mathcal {A})\) has an aligned drawing \((\varGamma _{\mathrm {out}}, A)\) and \((G_{\mathrm {in}}, \mathcal {A})\) has an aligned drawing \((\varGamma _{\mathrm {in}}, A)\) with the outer face drawn as \(\varGamma _{\mathrm {out}} [T]\).
). Let \((G, \mathcal {A})\) be a k-aligned triangulation. Let T be a separating triangle splitting G into subgraphs \(G_{\mathrm {in}}, G_{\mathrm {out}} \) so that \(G_{\mathrm {in}} \cap G_{\mathrm {out}} =T\) and \(G_{\mathrm {out}} \) contains the outer face of G. Then, (i) \((G_{\mathrm {out}}, \mathcal {A})\) and \((G_{\mathrm {in}}, \mathcal {A})\) are k-aligned triangulations, and (ii) \((G, \mathcal {A})\) has an aligned drawing if and only if there exists a common line arrangement A such that \((G_{\mathrm {out}}, \mathcal {A})\) has an aligned drawing \((\varGamma _{\mathrm {out}}, A)\) and \((G_{\mathrm {in}}, \mathcal {A})\) has an aligned drawing \((\varGamma _{\mathrm {in}}, A)\) with the outer face drawn as \(\varGamma _{\mathrm {out}} [T]\).
Lemma 5
(
 ). Let \((G, \mathcal {A})\) be a k-aligned triangulation of alignment complexity \((1,0,\bot )\) and let e be a 0-anchored aligned edge or a free edge of G that is not an edge of a separating triangle. Then \((G/e, \mathcal {A})\) is a k-aligned triangulation of alignment complexity \((1,0,\bot )\). Further, \((G, \mathcal {A})\) has an aligned drawing if \((G/e, \mathcal {A})\) has an aligned drawing.
). Let \((G, \mathcal {A})\) be a k-aligned triangulation of alignment complexity \((1,0,\bot )\) and let e be a 0-anchored aligned edge or a free edge of G that is not an edge of a separating triangle. Then \((G/e, \mathcal {A})\) is a k-aligned triangulation of alignment complexity \((1,0,\bot )\). Further, \((G, \mathcal {A})\) has an aligned drawing if \((G/e, \mathcal {A})\) has an aligned drawing.
Proof sketch
Since u and v either both lie in the same cell or both in the interior of a pseudosegment, \((G/e, \mathcal {A})\) is an aligned triangulation.
Let c be the vertex in G / e obtained by contracting \(e=uv\) and let f be the face obtained by removing the vertex c from the aligned drawing \((\varGamma ', A)\) of \((G/e, \mathcal {A})\). We place u at the position of c. This leaves a unique face \(f'\) to place v in. Since G / e is a triangulation, \(f'\) is star-shaped. Thus we can either place v close to u within its cell or on its line. \(\square \)
4.2 One Pseudoline
We show that every 1-aligned graph \((G, \mathcal {R})\) has an aligned drawing \((\varGamma , R)\), where \(\mathcal {R}\) is a single pseudoline and R the corresponding straight-line.
Lemma 6
Let \((G,\mathcal {R})\) be a 1-aligned triangulation with k vertices on the outer face without a chord. If G is neither a triangle nor a k-wheel, then \((G, \mathcal {R})\) contains an interior aligned or an interior free edge.
All possible variations of vertices and edges in Lemma 7.
Proof
We first prove two useful claims.
Claim 1. Consider the order in which \(\mathcal {R}\) intersects the vertices and edges of G. If vertices u and v are consecutive on \(\mathcal {R}\), then the edge uv is aligned.
Observe that the edge uv can be inserted into G without creating crossings. Since G is a triangulation, it therefore contains uv, and, further, since no 1-crossed edge can have both its endpoints on \(\mathcal {R}\), it follows that indeed uv is aligned. This proves the claim.
Claim 2. Let \((G,\mathcal {R})\) be an aligned triangulation without aligned edges and let x be an interior free vertex of G, then x is incident to a free edge.
Assume for a contradiction that all neighbors of x lie either on \(\mathcal {R}\) or on the other side of \(\mathcal {R}\). First, we slightly modify \(\mathcal {R}\) to a curve \(\mathcal {R}'\) that does not contain any vertices. Assume v is an aligned vertex; see Fig. 5. Since there are no aligned edges, \(\mathcal {R}\) enters v from a face f incident to v and leaves it to a different face \(f'\) incident to v. We then reroute \(\mathcal {R}\) from f to \(f'\) locally around v. If v is incident to x, we choose the rerouting such that it crosses the edge vx.
Notice that if e is intersected by \(\mathcal {R}\) in its endpoints, then \(\mathcal {R}'\) either does not intersect it, or intersects it in an interior point. Moreover, e cannot be intersected by \(\mathcal {R}'\) twice as in such case \(\mathcal {R}\) would pass through both its endpoints. Therefore \((G, \mathcal {R}')\) is an aligned graph without any aligned vertices. Now, since G is a triangulation, \(\mathcal {R}'\) is a simple cycle in the dual \({G}^{\star }\) of G, and hence corresponds to a cut C of G. Let H denote the connected component of \(G-C\) that contains x and note that all edges of H are free. By the assumption and the construction of \(\mathcal {R}'\), x is the only vertex in H. Thus, \(\mathcal {R}'\) intersects only the faces incident to x which are interior. This contradicts the assumption that \(\mathcal {R}'\) passes through the outer face of G. This finishes the proof of the claim.
We now prove the lemma. Assume that G is neither a triangle nor a k-wheel. Thus, G contains at least two interior vertices. If one of both vertices is free, we find a free edge by Claim 2. Otherwise, there is no free internal vertex, therefore the only edge which can intersect \(\mathcal {R}\) is a chord of G. Since G does not contain any chord, there is a pair of aligned vertices consecutive along \(\mathcal {R}\). Thus by Claim 1 the instance \((G, \mathcal {R})\) has an aligned edge. \(\square \)
Theorem 3
(
 ). Let \((G, \mathcal {R})\) be an aligned graph and let \((\varGamma _O, R)\) be a convex aligned drawing of the aligned outer face \((O, \mathcal {R})\) of G. There exists an aligned drawing \((\varGamma , R)\) of \((G, \mathcal {R})\) with the same line R and the outer face drawn as \(\varGamma _O\).
). Let \((G, \mathcal {R})\) be an aligned graph and let \((\varGamma _O, R)\) be a convex aligned drawing of the aligned outer face \((O, \mathcal {R})\) of G. There exists an aligned drawing \((\varGamma , R)\) of \((G, \mathcal {R})\) with the same line R and the outer face drawn as \(\varGamma _O\).
Proof sketch. Given an arbitrary aligned graph \((G, \mathcal {R})\), we first triangulate it using Lemma 3. As long as it has a free or an aligned edge e we do the following. If e is contained in a separating triangle, we decompose the graph using Lemma 4. Otherwise we simply contract e (Lemma 5). If no such edge exists, \((G, \mathcal {R})\) is either a triangle or a k-wheel (Lemma 6) and has an obvious straight-line aligned drawing. We obtain an aligned drawing of (G, R) by reversing the sequence contraction (Lemma 5) and decompositions along the separating triangles (Lemma 4). \(\square \)
4.3 Alignment Complexity \((1, 0, \bot )\)
Let \((G, \mathcal {A})\) be a k-aligned graph of alignment complexity \((1, 0, \bot )\), i.e., every edge has at most one interior intersection and 2-anchored edges are forbidden. In this section, we prove that every such k-aligned graph has an aligned drawing. Figure 6 illustrates the statement of the following lemma.
Lemma 7
Let \((G, \mathcal {A})\) be a proper k-aligned triangulation of alignment complexity \((1, 0, \bot )\) that does neither contain an interior free edge, nor a 0-anchored aligned edge, nor a separating triangle. Then (i) every intersection contains a vertex, (ii) every cell of the pseudoline arrangement contains exactly one free vertex, (iii) every pseudosegment is either covered by two aligned edges or intersected by an edge.
Illustrations for the proof Lemma 7
Proof
The statement follows trivially from the following sequence of claims. We refer to an aligned vertex that is not an intersection vertex as a flexible aligned vertex.
Claim 1. Every pseudosegment alternately intersects flexible aligned vertices and edges.
Let \(\mathcal {S}\) be a pseudosegment in the pseudoline arrangement \(A \). As in the proof of Lemma 6 one can argue that if two vertices occur consecutively along \(\mathcal {S}\), then we find an aligned edge. Assume that \(\mathcal {S}\) intersects two edges \(e_1,e_2\) consecutively as depicted in Fig. 7(a). Since G is a triangulation, it follows that \(e_1\) and \(e_2\) share an endpoint v. Every 1-crossed edge in G is 0-anchored, thus all endpoints of \(e_1\) and \(e_2\) must be free. Further \(e_1\) and \(e_2\) are consecutive in the circular order of edges around v as otherwise we would either find an intersection with \(\mathcal {S}\) between \(e_1\) and \(e_2\) or a free edge. Thus, \(e_1\) and \(e_2\) bound a face and are 1-crossed, hence their endpoints distinct from v are in the same cell and connected by an edge e, which is thus free. In a proper graph, the edges on the outer face are 1-crossed, thus, e is an interior edge, contradicting our assumptions.
Claim 2. Every cell contains at least one free vertex.
Observe that every triangle T containing the intersection of two pseudolines has at least one l-crossed edge, with \(l\ge 2\). Since by definition \((G, \mathcal {A})\) does not contain 2-anchored aligned edges, T cannot contain an empty cell in its interior. Further, since G is proper, the outer face of G contains the intersection of every pair of pseudolines in its interior. Thus, since G is triangulated every cell contains at least one vertex.
Claim 3. Every cell contains at most one free vertex.
The following proof is similar to Claim 2 in the proof of Lemma 6. Let \(\mathcal {C}\) be a cell and assume for the sake of a contradiction that \(\mathcal {C}\) contains more than one vertex in the interior; see Fig. 7(b). These vertices are connected by edges to adjacent cells. If \(\mathcal {C}\) contains a vertex v on its boundary, we reroute the corresponding pseudolines close to v such that v is now outside of \(\mathcal {C}\); refer to Fig. 7(c). Let \(\mathcal {C}'\) be the resulting cell, it represents a cut in the graph with two components A and B, where \(\mathcal {C}'\) contains B in its interior. It is not difficult to see that the modified pseudolines are still pseudolines with respect to G. Since \((G, \mathcal {A})\) neither contains l-anchored edges nor l-crossed edges, \(l \ge 2\), every edge of \((G, \mathcal {A} ')\) intersects the boundary of \(\mathcal {C}'\) at most once. Hence, B is connected and since it contains at least two vertices it also contains at least one free edge, contradicting our initial assumption.
Claim 4. Every flexible aligned vertex is incident to two 1-anchored aligned edges.
Let v be a vertex lying in the interior of a pseudosegment \(\mathcal {S}\). Let u and w be the anchored vertices incident to \(\mathcal {S}\). Further, let x and y be the vertices in the interior of the two cells incident to \(\mathcal {S}\). Our instance \((G, \mathcal {A})\) is triangulated and every edge is at most 1-crossed. Thus, the vertices u, x, w, y build a quadrangle containing v in its interior. Since G does not contain a separating triangles, it cannot contain the edge xy. Moreover, \(\mathcal {S}\) contains exactly v in its interior, otherwise we would find a free aligned edge. Finally, since \((G, \mathcal {A})\) is an aligned triangulation, the vertex v is connected to all four vertices and, thus incident to two 1-anchored aligned edges.
Since \((G, \mathcal {A})\) is an aligned triangulation, Property (iii) immediately follows from Claims 3 and 4. \(\square \)
Lemma 8
Let \((G, \mathcal {A})\) be a proper k-aligned triangulation of alignment complexity \((1, 0, \bot )\) that does neither contain an interior free edge, nor a 0-anchored aligned edge, nor a separating triangle. Let \(A \) be a line arrangement homeomorphic to the pseudoline arrangement \(\mathcal {A} \). Then \((G, \mathcal {A})\) has an aligned drawing \((\varGamma , A)\).
Proof
We obtain a drawing \((\varGamma , A)\) by placing a free vertex in its cell, an aligned vertex on its pseudosegment and an intersection vertex on its intersection. According to Lemma 7 every cell and every intersection contains exactly one vertex and each pseudosegment is either crossed by an edge or it is covered by two aligned edges. Observe that the union of two adjacent cells of the arrangement \(A \) is convex. Thus, this drawing of G has an homeomorphic embedding to \((G, \mathcal {A})\) and every edge intersects in \((\varGamma , A)\) the line \(L \in A \) corresponding to the pseudoline \(\mathcal {L}\in \mathcal {A} \) in \((G, \mathcal {A})\) \(\square \)
The following theorem can be proven along the same lines as Theorem 3.
Theorem 4
(
 ). Every k-aligned graph \((G, \mathcal {A})\) of alignment complexity \((1, 0,\bot )\) with a stretchable pseudoline arrangement \(\mathcal {A} \) has an aligned drawing.
). Every k-aligned graph \((G, \mathcal {A})\) of alignment complexity \((1, 0,\bot )\) with a stretchable pseudoline arrangement \(\mathcal {A} \) has an aligned drawing.
5 Conclusion
In this paper we showed that if \(\mathcal {A} \) is stretchable, then every k-aligned graph \((G, \mathcal {A})\) of alignment complexity \((1, 0,\bot )\) has a straight-line aligned drawing. As an intermediate result we showed that a 1-aligned graph \((G, \mathcal {R})\) has an aligned drawing with a fixed convex drawing of the outer face. We showed that the less restricted version of this problem, where we are only given a set of vertices to be aligned, is \(\mathcal {NP} \)-hard but fixed-parameter tractable.
The case of more general alignment complexities is widely open. Our techniques imply the existence of one-bend aligned drawings of general 2-aligned graphs [13]. However, the existence of straight-line aligned drawings is unknown even if in addition to 1-crossed edges, we only allow 2-anchored edges, i.e., in the case of alignment complexity (1, 0, 0). In particular, there exist 2-aligned graphs that neither contain a free edge nor an aligned edge but their size is unbounded in the size of the arrangement; see full version [12]. It seems that further reductions are necessary to arrive at a base case that can easily be drawn. This motivates the following questions.
-
(1)
What are all the combinations of line numbers k and alignment complexities C such that for every k-aligned graph \((G,\mathcal {A})\) of alignment complexity C there exists a straight-line aligned drawing provided \(\mathcal {A} \) is stretchable?
-
(2)
Given a k-aligned graph \((G,\mathcal {A})\) and a line arrangement A homeomorphic to \(\mathcal {A} \), what is the complexity of deciding whether \((G,\mathcal {A})\) admits a straight-line aligned drawing \((\varGamma ,A)\)?
References
Biedl, T., Kaufmann, M., Mutzel, P.: Drawing planar partitions II: HH-drawings. In: Hromkovič, J., Sýkora, O. (eds.) WG 1998. LNCS, vol. 1517, pp. 124–136. Springer, Heidelberg (1998). https://doi.org/10.1007/10692760_11
Cano, J., Tóth, C.D., Urrutia, J.: Upper bound constructions for untangling planar geometric graphs. SIAM J. Discrete Math. 28(4), 1935–1943 (2014)
Chaplick, S., Fleszar, K., Lipp, F., Ravsky, A., Verbitsky, O., Wolff, A.: Drawing graphs on few lines and few planes. In: Hu, Y., Nöllenburg, M. (eds.) GD 2016. LNCS, vol. 9801, pp. 166–180. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-50106-2_14
Chaplick, S., Fleszar, K., Lipp, F., Ravsky, A., Verbitsky, O., Wolff, A.: The complexity of drawing graphs on few lines and few planes. Algorithms and Data Structures. LNCS, vol. 10389, pp. 265–276. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-62127-2_23
Da Lozzo, G., Dujmović, V., Frati, F., Mchedlidze, T., Roselli, V.: Drawing planar graphs with many collinear vertices. In: Hu, Y., Nöllenburg, M. (eds.) GD 2016. LNCS, vol. 9801, pp. 152–165. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-50106-2_13
Dujmović, V.: The utility of untangling. In: Di Giacomo, E., Lubiw, A. (eds.) GD 2015. LNCS, vol. 9411, pp. 321–332. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-27261-0_27
Dujmović, V., Evans, W., Kobourov, S., Liotta, G., Weibel, C., Wismath, S.: On graphs supported by line sets. In: Brandes, U., Cornelsen, S. (eds.) GD 2010. LNCS, vol. 6502, pp. 177–182. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18469-7_16
Dujmović, V., Langerman, S.: A center transversal theorem for hyperplanes and applications to graph drawing. Discrete Comput. Geom. 49(1), 74–88 (2013)
Fößmeier, U., Kaufmann, M.: Nice drawings for planar bipartite graphs. In: Bongiovanni, G., Bovet, D.P., Di Battista, G. (eds.) CIAC 1997. LNCS, vol. 1203, pp. 122–134. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62592-5_66
Goodman, J.E., Pollack, R.: Proof of Grünbaum’s conjecture on the stretchability of certain arrangements of pseudolines. J. Comb. Theory Ser. A 29(3), 385–390 (1980)
Levi, F.: Die Teilung der projektiven Ebene durch Gerade oder Pseudogerade. Ber. Math.-Phys. Kl. Sächs. Akad. Wiss 78, 256–267 (1926)
Mchedlidze, T., Radermacher, M., Rutter, I.: Aligned Drawings of Planar Graphs (2017). https://arxiv.org/abs/1708.08778v2
Mchedlidze, T., Radermacher, M., Rutter, I.: Aligned drawings of planar graphs. In: Proceedings of the 33rd European Workshop on Computational Geometry (EuroCG 2017) (2017)
Mnev, N.E.: The universality theorems on the classification problem of configuration varieties and convex polytopes varieties. In: Viro, O.Y., Vershik, A.M. (eds.) Topology and Geometry — Rohlin Seminar. LNM, vol. 1346, pp. 527–543. Springer, Heidelberg (1988). https://doi.org/10.1007/BFb0082792
Shor, P.: Stretchability of pseudolines is NP-hard. In: Applied Geometry and Discrete Mathematics-The Victor Klee Festschrift, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 4, pp. 531–554. American Mathematical Society (1991)
Wahlström, M.: Abusing the Tutte matrix: an algebraic instance compression for the K-set-cycle problem. In: 30th International Symposium on Theoretical Aspects of Computer Science, STACS 2013, pp. 341–352 (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Mchedlidze, T., Radermacher, M., Rutter, I. (2018). Aligned Drawings of Planar Graphs. In: Frati, F., Ma, KL. (eds) Graph Drawing and Network Visualization. GD 2017. Lecture Notes in Computer Science(), vol 10692. Springer, Cham. https://doi.org/10.1007/978-3-319-73915-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-73915-1_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-73914-4
Online ISBN: 978-3-319-73915-1
eBook Packages: Computer ScienceComputer Science (R0)






 of
of 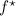 , each vertex v of this clique corresponds to an edge
, each vertex v of this clique corresponds to an edge  , thus we call it a clique vertex corresponding to
, thus we call it a clique vertex corresponding to 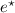 and denote by
and denote by  . For each edge of
. For each edge of  , corresponding to the edges incident to the dual vertex f, we add a star with a new center vertex
, corresponding to the edges incident to the dual vertex f, we add a star with a new center vertex  as leaves. Finally, we set
as leaves. Finally, we set 



