Abstract
In Dafny, the program text is used to both specify and implement programs in the same language [24]. It then uses a fully automated theorem prover to verify that the implementation satisfies the specification. However, the prover often needs further guidance from the user, and another role of the language is to provide such necessary hints and guidance. In this paper, we present a set of verification patterns to support this process. In previous work, we have developed a tactic language for Dafny, where users can encode their verification patterns and re-apply them for several proof tasks [16]. We extend this language with new features, implement our patterns in this tactic language and show, through experiments, generality of the patterns, and applicability of the tactic language.
This work has been supported by EPSRC grants EP/M018407/1 and EP/N014758/1. Special thanks to Rustan Leino and his colleagues at MSR.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The requirement that a tactic has to find a proof is a result of user feedback, and is not required in the semantics described in [16].
- 2.
The generation of this function happens to be the inverse of the well-known tail-recursion to loop compiler optimisation [8].
- 3.
All the statements, including the atomic tactics (modular some name changes) were introduced in [16].
- 4.
Meaning, code such as
 cannot be generated.
cannot be generated. - 5.
This naming convention is used for ghost variables in Dafny, which in certain cases needs to be declared as
 .
. - 6.
If a sequence is given as argument for a method that does not expect a sequence, then Tacny will automatically unroll the sequence into multiple arguments.
- 7.
In [16],
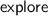 was called
was called 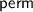 and
and  called
called 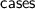 .
. - 8.
If this is a nested tactic call, then it refers to the name of the method/lemma/function that called the parent tactic.
- 9.
For example,
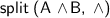 will return
will return 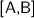 .
. - 10.
This syntax is inspired by the syntax for
 used in Dafny.
used in Dafny. - 11.
The supported tool syntax has some minor limitations and thus deviates slightly.
- 12.
Klein’s FM 2014 keynote also addressed this limitations and its importance.
- 13.
- 14.
For example, Event-B has an operator \(x :\in P\) to express this.
References
Dafny Website. research.microsoft.com/dafny
The Tacny project: FM 2016 information. https://sites.google.com/site/tacnyproject/fm-2016. Accessed 29 May 2016
Autexier, S., Dietrich, D.: A tactic language for declarative proofs. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 99–114. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14052-5_9
Barnett, M., Chang, B.-Y.E., DeLine, R., Jacobs, B., Leino, K.R.M.: Boogie: a modular reusable verifier for object-oriented programs. In: Boer, F.S., Bonsangue, M.M., Graf, S., Roever, W.-P. (eds.) FMCO 2005. LNCS, vol. 4111, pp. 364–387. Springer, Heidelberg (2006). doi:10.1007/11804192_17
Bundy, A.: A science of reasoning. In: Lassez, J.L., Plotkin, G. (eds.) Computational Logic - Essays in Honor of Alan Robinson, pp. 178–198. MIT Press, Cambridge (1991)
Bundy, A., Basin, D., Hutter, D., Ireland, A.: Rippling: Meta-level Guidance for Mathematical Reasoning. Cambridge Tracts in Theoretical Computer Science, vol. 56. Cambridge University Press, Cambridge (2005)
Rod, M.: Burstall: proving properties of programs by structural induction. Comput. J. 12(1), 41–48 (1969)
Burstall, R.M., Darlington, J.: A transformation system for developing recursive programs. J. ACM (JACM) 24(1), 44–67 (1977)
Claessen, K., Johansson, M., Rosén, D., Smallbone, N.: Automating inductive proofs using theory exploration. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 392–406. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38574-2_27
Colón, M.A., Sankaranarayanan, S., Sipma, H.B.: Linear invariant generation using non-linear constraint solving. In: Hunt, W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 420–432. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45069-6_39
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: Proceedings of the 5th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, pp. 84–96. ACM (1978)
Delahaye, D.: A tactic language for the system Coq. In: Parigot, M., Voronkov, A. (eds.) LPAR 2000. LNAI, vol. 1955, pp. 85–95. Springer, Heidelberg (2000). doi:10.1007/3-540-44404-1_7
Ernst, M.D., Perkins, J.H., Guo, P.J., McCamant, S., Pacheco, C., Tschantz, A.S., Xiao, C.: The Daikon system for dynamic detection of likely invariants. Sci. Comput. Program. 69(1), 35–45 (2007)
Freitas, L., Whiteside, I.: Proof patterns for formal methods. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 279–295. Springer, Heidelberg (2014). doi:10.1007/978-3-319-06410-9_20
Gries, D.: The Science of Programming, 1st edn. Springer, New York (1987)
Grov, G., Tumas, V.: Tactics for the dafny program verifier. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 36–53. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49674-9_3
Gupta, A., Rybalchenko, A.: InvGen: an efficient invariant generator. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 634–640. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02658-4_48
Hawblitzel, C., Howell, J., Kapritsos, M., Lorch, J.R., Parno, B., Roberts, M.L., Setty, S., Zill, B.: Ironfleet: proving practical distributed systems correct. In: Proceedings of the 25th Symposium on Operating Systems Principles, pp. 1–17. ACM (2015)
Hawblitzel, C., Lorch, J., Parno, B.: Personal discussions, December 2015
Hoder, K., Kovács, L., Voronkov, A.: Invariant generation in vampire. In: Abdulla, P.A., Leino, K.R.M. (eds.) TACAS 2011. LNCS, vol. 6605, pp. 60–64. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19835-9_7
Joshi, M.: Proof Patterns. Springer, New York (2015)
Jason Koenig, K., Leino, R.M.: Programming language features for refinement (2015)
Leino, K.R.M.: Types in Dafny, 27 February 2015. http://research.microsoft.com/en-us/um/people/leino/papers/krml243.html. (Manuscript KRML 243)
Leino, K.R.M.: Dafny: an automatic program verifier for functional correctness. In: Clarke, E.M., Voronkov, A. (eds.) LPAR 2010. LNCS (LNAI), vol. 6355, pp. 348–370. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17511-4_20
Leino, K.R.M.: Automating induction with an SMT solver. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 315–331. Springer, Heidelberg (2012). doi:10.1007/978-3-642-27940-9_21
Leino, K.R.M., Moskal, M.: Co-induction simply. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 382–398. Springer, Heidelberg (2014). doi:10.1007/978-3-319-06410-9_27
Matichuk, D., Wenzel, M., Murray, T.: An isabelle proof method language. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 390–405. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08970-6_25
Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Srivastava, S., Gulwani, S.: Program verification using templates over predicate abstraction. In: ACM Sigplan Notices, vol. 44, pp. 223–234. ACM (2009)
Sterling, L., Bundy, A., Byrd, L., O’Keefe, R., Silver, B.: Solving symbolic equations with press. In: Calmet, J. (ed.) EUROCAM 1982. LNCS, vol. 144, pp. 109–116. Springer, Heidelberg (1982). doi:10.1007/3-540-11607-9_13
Tumas, V.: Search space reduction for Tacny tactics. Honours thesis, Heriot-Watt University (2016). https://sites.google.com/site/tacnyproject/
van de Snepscheut, J.L.A.: What Computing is All About. Springer, New York (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Summary of New Tacny Features
A Summary of New Tacny Features
This paper has extended and improved Tacny from the version presented in [16] as follows:
-
A new type
 that makes a tactic a first class value is introduced.
that makes a tactic a first class value is introduced. -
 and tactic applications within expressions are now supported.
and tactic applications within expressions are now supported. -
Contracts for tactics, and tactic-level assertions have been added.
-
Several new atomic tactics and lookup functions are supported, including:
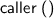 ;
; 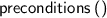 ;
; 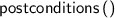 ;
;  ;
;  ;
; 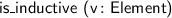 ;
; 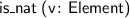 ;
; 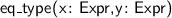 ;
;  ;
; 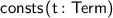 ;
;  ;
;  ;
; 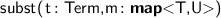 ; and
; and  as an expression.
as an expression. -
Considerable runtime improvements have been achieved.
-
The syntax is improved to align with Dafny conventions and declarative tactics. For example:
 has become
has become  (or
(or 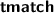 ); tactic-level variable declarations have changed from
); tactic-level variable declarations have changed from 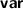 to
to  (or
(or 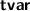 ); Dafny-level variable declarations have changed from
); Dafny-level variable declarations have changed from 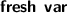 to
to 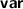 .
.
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Grov, G., Lin, Y., Tumas, V. (2016). Mechanised Verification Patterns for Dafny. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds) FM 2016: Formal Methods. FM 2016. Lecture Notes in Computer Science(), vol 9995. Springer, Cham. https://doi.org/10.1007/978-3-319-48989-6_20
Download citation
DOI: https://doi.org/10.1007/978-3-319-48989-6_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48988-9
Online ISBN: 978-3-319-48989-6
eBook Packages: Computer ScienceComputer Science (R0)


 cannot be generated.
cannot be generated. .
.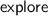 was called
was called 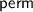 and
and  called
called 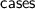 .
.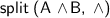 will return
will return 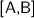 .
. used in Dafny.
used in Dafny. that makes a tactic a first class value is introduced.
that makes a tactic a first class value is introduced. and tactic applications within expressions are now supported.
and tactic applications within expressions are now supported.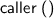 ;
; 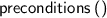 ;
; 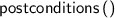 ;
;  ;
;  ;
; 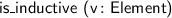 ;
; 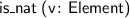 ;
; 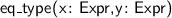 ;
;  ;
; 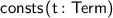 ;
;  ;
;  ;
; 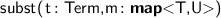 ; and
; and  as an expression.
as an expression. has become
has become  (or
(or 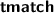 ); tactic-level variable declarations have changed from
); tactic-level variable declarations have changed from 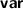 to
to  (or
(or 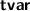 ); Dafny-level variable declarations have changed from
); Dafny-level variable declarations have changed from 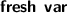 to
to 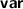 .
.