Abstract
Matrix factorisation is a widely used tool with applications in collaborative filtering, image analysis and in genomics. Several extensions of the classical model have been proposed, such as modelling of multiple related “data views” or accounting for side information on the latent factors. However, as the complexity of these models increases even subtle mismatches of the distributional assumptions on the input data can severely affect model performance. Here, we propose a simple yet effective solution to address this problem by modelling the observed data in a transformed or warped space. We derive a joint model of a multi-view matrix factorisation model that infers view-specific data transformations and provide a computationally efficient variational approximation for parameter inference. We first validate the model on synthetic data before applying it to a matrix completion problem in genomics. We show that our model improves the imputation of missing values in gene-disease association analysis and allows for discovering enhanced consensus structures across multiple data views The data and software related to this paper are available at https://github.com/PMBio/WarpedMF.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Probabilistic matrix factorisation is a widely used tool to impute missing values in dyadic data [16, 19, 26]. Using these models, the unobserved entries in the data matrix can be recovered by the inner product of a (typically low-rank) representation of factors and loadings, which can be inferred from the observed entries in the data matrix. Several extensions of the classical matrix factorisation model (MF) have been considered, including multi-view approaches to combine multiple related matrix factorisation tasks as well as methods to integrate prior (side) information. Intuitively, multi-view models use a set of common latent variables to explain shared structure in multiple complementary views, thereby borrowing statistical strength across datasets. A number of alternative implementations of multi-view models have been proposed, assuming different extents of sharing using a common loading matrix [3, 7], or using a shared subset of the latent factors [27]. A second widely considered extension is modelling additional side information, either on the inferred factors and/or the loadings. The inclusion of such additional data can improve the recovery of the latent variables, in particular if the input matrices are spares or if the number of latent factors is large compared to the dimensionality of the observed data matrix. Existing methods use linear regression on the latent factors [12, 15, 21] or employ multivariate normal priors on the latent factors [1, 28].
However, while in principle powerful, multi-view methods are challenging to apply in practice. This is because the underlying representation of the raw data frequently differs between views and in particular the assumption of marginal Gaussian residuals is hardly met.
To address this limitation, we here show that a simple parametric transformation of the observed data can substantially improve the performance of matrix factorisation models that span multiple views. We fit one parametric transformation for each view, assuming a common latent space representation, such that a common set of factors and loadings explain the observed data across all views. We derive an efficient variational inference scheme that scales to tens of views, each consisting of thousands of rows and columns, where view-specific transformations are estimated as part of the inference. Additionally, our model allows incorporating side information in the form of a covariance prior on either factors and/or loadings.
We first validate our model using synthetic data before applying it to a biomedical problem. We use our model to impute gene-disease associations that have been acquired from multiple complementary data sources. Our results show that learning warping functions within the matrix factorisation framework in conjunction with low-rank side information substantially outperforms previous methods.
2 Related Work
Multi-view formulations differ in the assumptions how specific latent variables are coupled between views [3, 7, 9, 23]. In this work, we assume that all views are consistent and related to the same entities (e.g. diseases and genes), however reflect complementary sources of evidence. We require both latent factor matrices from MF to be shared, of which the inner product represents the consensus across all data sets. The ability to require such consensus structures is strongly dependent on appropriate data pre-processing steps. Several parametric and non-parametric transformations have been considered for this purpose. One objective is to decouple mean and variance relationships [8, 13], for example using the BoxCox transformation [5]. Within the class of transformations, the BoxCox transformation can recover natural logarithmic, square root, and reciprocal functions. In the context of Gaussian processes (GP) regression, more general parametric transformations have been considered, for example a sum of (a small number of) step functions [25]. The parameters of these transformations can be learned jointly with the remaining GP hyper-parameters. Similar principles have also been considered for linear mixed models in statistical genetics [11], as well as for collective link prediction [6]. Moreover, there is some albeit limited work on using warping transformations in conjunction with GP-based function factorisation [22]. However, to the best of our knowledge, there are no methods that consider warping for multi-view matrix factorisation.
There are also a number of existing methods to incorporate side information within the matrix factorisation, where it is available. One approach is to place a regression-based prior that relates the side information in the form of covariates for rows and columns of the data matrix [2, 12, 15, 21]. Scalable inference within the regression-based matrix factorisation models (RBMF-SI) can be achieved through variational approximations that assume a fully-factorised form [15]. Alternatively, side information can also be encoded as row and column covariance priors on the latent factors and loadings [28]. Inference in such models can be prohibitively expensive, mainly since naive implementations require the inversion of matrices with the same dimension as the number of rows or columns of the observed data matrix. We here show how this bottleneck can be addressed using low-rank approximations, which is similar to approaches that have been used for parameter inference in linear mixed models [17].
3 RBMF-SI
We start by briefly reviewing the standard matrix factorisation model that incorporates side information via linear regression [2, 15]. In the RBMF-SI model, each entry (i, j) of the observed data matrix \(\varvec{Y} \in \text {I}\!\text {R}^{I \times J}\) is modelled as the inner product of two factor matrices of rank \(K \ll I,J\) which are \(\varvec{U} \in \text {I}\!\text {R}^{I \times K}\) and \(\varvec{V} \in \text {I}\!\text {R}^{J \times K}\), with Gaussian distributed residuals with variance \(\tau ^{-1}\). The corresponding likelihood is then:
where \(\mathcal {O}\) denotes the set of observed indices in \(\varvec{Y}\) and \(\mathcal {N}(\cdot )\) denotes a normal distribution.
Side information \(\varvec{F} \in \text {I}\!\text {R}^{I \times N_F} \) and \(\varvec{G} \in \text {I}\!\text {R}^{J \times N_G}\) for the factors \(\varvec{U}\) and the loadings \(\varvec{V}\) respectively is incorporated as a multivariate normal prior on factors and loadings using a regression model in the prior mean:
where \(\varvec{I}\) denotes the identity matrix. Here, the regression coefficient matrices \(\varvec{A} \in \text {I}\!\text {R}^{N_F \times K}\) and \(\varvec{B} \in \text {I}\!\text {R}^{N_G \times K}\) are shrunk using an \(L_2\) prior with variances specific for each factor k:
We will show later that by marginalising out the weights \(\varvec{A}\) and \(\varvec{B}\), these regression-priors can be cast as linear covariance matrices derived from the side information \(\varvec{F}\) and \(\varvec{G}\), which results in low rank covariances in case of \(N_F < I\) and \(N_G < J\) (see Sect. 4.1).
4 MV-WarpedMF-SI
In this section, we derive MV-WarpedMF-SI, a multi-view warped matrix factorisation model that accounts for side information (MV-WarpedMF-SI). The model unifies the inference of data transformations and matrix factorisation, performing joint inference for the model parameters of both components.
4.1 Model Description
Let \(\varvec{Y}^{n} \in \text {I}\!\text {R}^{I \times J}\) be an observed data matrix for a data view n where \(n = 1, \ldots , N\). An entry (i, j) from each view could for example represent an association score between a row i and a column j (e.g. gene-disease associations). Rather than modelling the observed data directly, we introduce a deterministic function that maps (warps) the observation space \(\varvec{Y}^{n}\) into a latent space \(\varvec{Z}^{n} \in \text {I}\!\text {R}^{I \times J}\). In principle, any monotonic function could be used. Here, we follow [25] and consider a superposition of a (typically small) set of \(\tanh \) functions (we used \(T=3\) in the experiments):
In this parametrization, \({\alpha }^n_t, {\beta }^n_t \ge 0\) adjust the step size and the steepness respectively, and \({\gamma }^n_t\) adjusts the relative position of each \(\tanh \) factor. We use distinct warping functions for each data view.
In the transformed data space, we assume that the data in all views can be explained by the same lower dimensional factor representation \(\varvec{U} \in \text {I}\!\text {R}^{I \times K}\) and \(\varvec{V} \in \text {I}\!\text {R}^{J \times K}\), where \(K \ll I,J\) denotes the number of latent factors. Consequently, the latent variables capture common structure across views. Additionally, we incorporate individual row \(\varvec{b}^{r^n}\) and column \(\varvec{b}^{c^n}\) bias vectors for each view. Finally, residual variation in the latent space is modelled as multivariate normal \({\varepsilon }^{n}_{ij} \sim \mathcal {N}(0,1/ \tau ^{n})\), assuming view-specific residual variances \(1/\tau ^{n}\). The conditional likelihood of the transformed data \(\varvec{Z}\) follows as:
where \({\mu }^{n}_{ij} = \varvec{U}_{i:} {\varvec{V}_{j:}}^{\scriptscriptstyle \top }+ b^{r^n}_i + b^{c^n}_{j}\) and \(\mathcal {O}^n\) denotes the set of the observed indices (i, j) in view n.
Suppose that side information is available in the form of similarity matrices, \(\varvec{\varSigma }^u \in \text {I}\!\text {R}^{I \times I}\) and \(\varvec{\varSigma }^v \in \text {I}\!\text {R}^{J \times J}\), that indicate the relatedness over rows and columns of \(\varvec{Y}\) respectively. If the side information is given as a feature matrix, the similarity matrix can also be computed from these features using a suitable kernel function e.g. a linear kernel or a Gaussian kernel for real-valued features, or a Jaccard kernel for binary features.
We assume that the factor matrix and the loadings have multivariate normal priors whose covariance matrices correspond to \(\varvec{\varSigma }^u\) and \(\varvec{\varSigma }^v\) respectively:
The additional variance parameters \({\sigma }_{uk}^2\) and \({\sigma }_{vk}^2\) control the prior strength for each factor k of \(\varvec{U}\) and \(\varvec{V}\) respectively.
We note that there is a close relationship between employing a covariance matrix to encode side information and the use of a regression-based model on factors and their coefficients. In fact, the marginal likelihood of a regression model is a special case of our approach with a linear kernel:
Finally, in order to avoid overfitting, we regularise the bias parameters for row and column bias terms by a zero mean and a variance prior over each element:
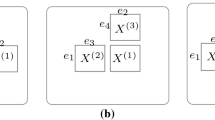
Figure 1 shows a graphical model of MV-WarpedMF-SI, representing the relationships of all variables in the model.
4.2 Training the MV-WarpedMF-SI
We need to make inference of the joint posterior distribution \(p(\varvec{U},\varvec{V},\varvec{b}^r,\varvec{b}^c |\varvec{Y},\theta )\), where \(\theta \) denotes the set of all model parameters (\(\varvec{\alpha ,\beta ,\gamma },\varvec{\tau },\varvec{\tau }^r,\varvec{\tau }^c, \varvec{\sigma }_{u}^2, \varvec{\sigma }_{v}^2\)). Closed-form inference in this matrix factorization model is not tractable. For efficient parameter inference, we here revert to a variational approach to approximate the true posterior over the latent variables with a factorised form. An iterative inference scheme can then be derived by minimising the Kullback-Leibler (KL) divergence between the true posterior and the factorised approximation; see for example [4] for a comprehensive overview. The parameters of the warping functions (\(\varvec{\alpha ,\beta ,\gamma }\)) and the variances (1/\(\varvec{\tau },1/\varvec{\tau }^r,1/\varvec{\tau }^c,\varvec{\sigma }_u^2,\varvec{\sigma }_v^2\)) are inferred using maximum likelihood type II, i.e. by maximising the variational lower bound.
Using a standard change of variable, we first derive the marginal log-likelihood in the observation space. This results in an additional Jacobian term evaluated at each observed data point which appears additively in the marginal log-likelihood of the latent space, leading to:
where \(\phi _n^\prime (Y^{n}_{ij}) = \displaystyle \frac{\partial \phi _n(y)}{\partial y} \Bigr |_{\begin{array}{c} Y_{ij}^{n} \end{array}}\) is a Jacobian term.
Equivalent to minimising the KL divergence, we maximise the variational lower bound of the marginal log-likelihood conditioned on the model parameters, which is:
where \(\mathbb {E}_q[\cdot ]\) denotes the statistical expectation with respect to \(q(\varvec{U},\varvec{V},\varvec{b}^r,\varvec{b}^c)\) as defined below.
To achieve scalable inference, we assume a fully factorise variational distribution q for all latent variables except the factors \(\varvec{U}\) and the loadings \(\varvec{V}\), for which the prior factorisation is maintained. Thus, we choose a multivariate normal distribution parameterised by a mean and a covariance matrix for each latent factor, which enables automatic relevance determination, i.e. the number of effective factors within the model can be pruned by shrinking unused factors to zero [20]. The resulting variational distribution is:
Training of the model is done by optimising the variation lower bound and the Jacobian term with respect to each of the unknown variables including the warping parameters in turn until convergence.
4.3 Efficient Inference of Low-Rank Side Information
The computational limitation for imposing a Gaussian process prior on each latent factor is inverting the covariance matrix. The naive update equations for the covariance matrices of the variational distributions \(q(\varvec{U})\) and \(q(\varvec{V})\) are given by:
The matrix inversions entail cubic time complexity per iteration in the variational EM algorithm, which renders applications to larger datasets intractable. If the side information is low rank, the matrix inversion lemma can be exploited to invert the matrix efficiently, reducing the complexity to cubical scaling in the rank of the prior matrix.
We start by exploiting a standard spectral decomposition of the full covariance matrix:
where  and \(\varvec{P}\varvec{P}^{\scriptscriptstyle \top }= \varvec{P}^{\scriptscriptstyle \top }\varvec{P} = \varvec{I}\).
and \(\varvec{P}\varvec{P}^{\scriptscriptstyle \top }= \varvec{P}^{\scriptscriptstyle \top }\varvec{P} = \varvec{I}\).
More specifically, we apply single value decomposition (SVD) on the covariance to obtain a rank H approximation by forcing all remaining eigenvalues to zero, resulting in \(\varvec{PXP}^{\scriptscriptstyle \top }\). Using the matrix inversion lemma, the updating rule is reformed to:
where \(\varvec{W} = \varvec{X} + \varvec{P}^{\scriptscriptstyle \top }( \varvec{D}^{-1} + \sigma ^2\varvec{I}) \varvec{P} \) and \(\varvec{D}\) is the diagonal matrix from the first part of the updating rule in Eqs. (14) and (15).
Since the eigen decomposition needs only to be performed once at initialisation, the effective computational cost per iteration is therefore dominated by calculating the inverse \(\varvec{W} \in \text {I}\!\text {R}^{H \times H}\), which is cubic in \(H \ll I,J\).
4.4 Missing-Value Imputation with the MV-WarpedMF-SI
The trained model can be used to make predictions of missing values in the transformed space. A consensus prediction using evidence across views can be obtained by calculating \(\tilde{\varvec{U}}\tilde{\varvec{V}}^{\scriptscriptstyle \top }\), where \(\tilde{\varvec{U}}\) and \(\tilde{\varvec{V}}\) correspond to the expected latent factors and loadings under the variational posterior respectively. For each data view, the predictive distribution for any entry in the transformed space \({Z}^n_{ij}\) is a univariate normal distribution with the learned mean and variance:
where \(\mathcal {M}\) is the set of learned variables, \(\tilde{\mu }^{n}_{ij} = \tilde{\varvec{U}}_{i:} {\tilde{\varvec{V}}_{j:}}^{\scriptscriptstyle \top }+ \tilde{b}^{r^n}_{i} + \tilde{b}^{c^n}_{j}\), and \(\tilde{\xi }^n_{ij} = \sum \limits _k^K ( \tilde{U}_{ik}^2 {C^v_k}_{jj} + \tilde{V}_{jk}^2 {C^u_k}_{ii} + {C^u_k}_{ii} {C^v_k}_{jj} ) + {s}^{r^n}_{i} + {s}^{c^n}_{j} + 1/ \tilde{\tau }^{n}\).
The predictive distribution in the observation space can then be obtained by reversing the warping transformation. This is done by squashing the predictive normal distribution in the latent space through the learned warping function, parameterised by \(\varvec{\tilde{\alpha },\tilde{\beta },\tilde{\gamma }}\), leading to:
To compute a point estimate of a missing value, we use the predictive expectation of the warped Gaussian distribution in Eq. (19). Effectively, this operation marginalises over the latent space, integrating over all possible values through the inverse warping function \(\phi ^{-1}\) under its predictive distribution:
Since we parameterise the function in the observation space, its inverse \( \phi _n^{-1}( {Z}^{n}_{ij})\) cannot be analytically computed in a closed form. However, computing the inverse function \(\phi _n^{-1}({Z}^{n}_{ij})\) is similar to finding the root of \(\phi _n( {Y}^{n}_{ij}) - {Z}^{n}_{ij} = 0\). This problem can be solved using the Newton-Raphson method, which typically converges within a few iterations. Although convergence of this method in principle depends on the initialisation, we observed that a random initialisation yields robust results in practice. Finally, we estimate the integral in Eq. (20) by reformulating the one dimensional Gaussian distribution into the form of a Hermite polynomial. This approach allows to approximate the integral using a Gauss-Hermite quadrature, estimating the integral with a weighted sum of a relatively small number of the function evaluated at appropriate points (we used ten evaluations in the experiments).
The implementation of MV-WarpedMF-SI is available at https://github.com/PMBio/WarpedMF.
5 Results
We first applied the MV-WarpedMF-SI model on synthetic datasets to investigate its transformation capability in a multi-view setting. Subsequently we used the model for a genomic imputation task to fill in missing values and recover the consensus structure in a gene-disease prioritisation study.
5.1 Simulation Studies
We simulated synthetic data drawn from the generative model of MV-WarpedMF-SI. Firstly, we simulated covariance matrices from an inverse Wishart distribution and used them to generate latent factors \(\varvec{U}\) and loadings \(\varvec{V}\) by assuming \(K=5\) hidden factors. We then created two 1,000 \(\times \) 1,000 data matrices with \(90\,\%\) missing values from the inner product of the same latent factors, \(\varvec{U}\varvec{V}^{\scriptscriptstyle \top }\), corrupted with Gaussian noise, resulting in \(\varvec{Z}^{1}\) and \(\varvec{Z}^{2}\). To investigate to what extent the model is able to recover a data transformation, we finally created \(\varvec{Y}^{1}\) and \(\varvec{Y}^{2}\) by using a linear superposition of the untransformed data and a non-linear transformation, \(\varvec{Y}^n = (1-\lambda ) \cdot \varvec{Z}^n + \lambda \cdot \phi _n(\varvec{Z}^n)\), where the parameter \(\lambda \) determines the intensity of the transformation and \(\phi \) denotes an exponential and a logarithmic data transformation for the view \(n=1\) and 2 respectively. In total, we generated six datasets with a variable degree of non-linear warping. We also simulated side information regarding row and column similarities using rank \(H=10\) approximations to the true simulated covariances of \(\varvec{U}\) and \(\varvec{V}\).
Impact of the inference of warping functions in multi-view learning. Considered are the proposed MV-WarpedMF and MV-WarpedMF-SI as well as a standard multi-view matrix factorisation model (MV-MF) applied to the raw untransformed data. Box plots show the out of sample prediction accuracy (shown is variation in \(R^2\) across the five folds in each of six datasets) for increasing degrees of non-linear distortion (a). The true generative warping functions and the parametric fits recovered by the model are shown in (b). The predictive distributions in the observed space for each view are depicted in (c).
The proposed models, MV-WarpedMF and MV-WarpedMF-SI were trained on each dataset. For comparison, we also considered a standard (non-warping) multi-view matrix factorisation model (MV-MF) applied to the same data. Both \(\varvec{Y}^{1}\) and \(\varvec{Y}^{2}\) were modelled simultaneously by each model. For each simulated dataset, we evaluated the model performance using five-fold cross validation, calculating the correlation coefficient (\(R^2\)) between observed and predicted matrix values on the hold-out test set.
The prediction results in Fig. 2(a) show that the warped models performed markedly better than the un-warped MV-MF, where the differences were largest for strong non-linearities and the best model was the combination of learning warping function and incorporating side information (MV-WarpedMF-SI). Figure 2(b) shows a comparison of the true transformations and the warping functions inferred using MV-WarpedMF-SI. Representative examples of the predictive density for one entry of the data matrix are shown in Fig. 2(c). The warping model employed in MV-WarpedMF-SI can capture complex and asymmetric distributions, providing a substantially better approximation to the true density than a normal distribution as used in a standard MV-MF.
5.2 Analysis of Therapeutic Gene-Disease Associations
Data. Next, we applied the MV-WarpedMF-SI to a gene-disease association task. The dataset consisted of disease \(\times \) gene matrices. We considered six evidence sources of therapeutic gene-disease relationships as well as the additional validation set of gene-disease associations derived from drugs in clinical trials. These data are freely available via the Open Targets platformFootnote 1:
-
ANIM, \(\varvec{Y}^1\): drug effects on animal models where scores were calculated using the phenodigm similarity to human diseases [24].
-
EXPR, \(\varvec{Y}^2\): differential gene expression profiles of control-disease experiments from Expression AtlasFootnote 2 where scores were calculated from the p-value and \(\log _2\) fold change.
-
GEAS, \(\varvec{Y}^3\): gene association studies in GWAS CatalogFootnote 3 which were scored by the p-value, sample size, and severity effect.
-
LITR, \(\varvec{Y}^4\): literature mining of scientific articles on Pubmed databaseFootnote 4, scoring gene-disease associations by the co-occurrence of the gene and disease terms in the same sentence.
-
PATH, \(\varvec{Y}^5\): evidences of pathway analysis from REACTOMEFootnote 5.
-
SOMU, \(\varvec{Y}^6\): evidences of somatic mutation studies from COSMICFootnote 6.
-
An independent validation set of 22,138 known associations covering 372 diseases and 614 therapeutic genes, derived from ChEMBLFootnote 7, scored by drug development pipeline progression. This dataset was not included for training the models.
We also considered side information of a disease similarity matrix (\(\varvec{\varSigma ^u}\)) derived from disease ontology trees [18] and a gene similarity matrix (\(\varvec{\varSigma ^v}\)), which was estimated from gene expression networks [10]. To define the disease similarity covariance, we considered the inverse of the shortest path distance between diseases through the lowest common ancestor. For the gene similarity network we used the pre-computed 1,000 eigenvectors and eigenvalues of the gene-gene correlation matrix derived from 33,427 gene expression profiles [10].
In total, we constructed six matrices of 426 diseases and 10,721 gene targets, with an average of \(95\,\%\) missing values. These datasets represent typical examples of evidences that differ in scale and distributional properties.
Considered Methods. We compared the following models in single-view learning, where each data view was trained and validated independently, as well as multi-view learning, where all the data views were considered simultaneously. We applied a standard matrix factorisation (MF) [14] and a regression-based MF model with side information (RBMF-SI) [15] to each view separately, both of which were trained on the raw (un-warped) data as baselines. As an additional comparison partner, we also considered preprocessing the raw data using the Box-Cox transformation before applying an MF and an RBMF-SI. We denote these methods as BoxCoxMF and BoxCoxRBMF-SI respectively. The Box-Cox transformation was fit for each data view independently.Footnote 8 Moreover, we applied all the models in multi-view learning, denoting them with the prefix ‘MV’. Finally, the proposed model of learning warping functions during matrix factorisation was used either without (WarpedMF) or with the inclusion of side information (WarpedMF-SI), and in its multi-view form either without (MV-WarpedMF) or with side information (MV-WarpedMF-SI). Table 1 summarises the methods considered in this analysis.
Evaluation of Prediction Accuracy Using Cross Validations. We first assessed the predictive accuracy of the considered methods in terms of their ability to impute held-out values. We trained each model using a five-fold cross validation experiment, and compared the predicted scores to the true values in the hold-out test predictions using the Spearman rank correlation coefficients (Rs). Predictions from all models were assessed on the raw data scale.
While we assessed each method in terms of the imputation task by using both the latent factors and the bias terms (\(\tilde{\varvec{U}} \tilde{\varvec{V}}^{\scriptscriptstyle \top }+ \tilde{\varvec{b}}^r + \tilde{\varvec{b}}^c\)), we also explored the alternative ability to impute gene-disease scores when considering only the inferred latent factors (\(\tilde{\varvec{U}} \tilde{\varvec{V}}^{\scriptscriptstyle \top }\)) without the learned bias terms. Table 2 shows the average test Rs under these two prediction schemes.
For imputation performance, it is not surprising that modelling each view independently can yield better results, where the best performing model combined learning warping function within matrix factorisation with low-rank side information (WarpedMF-SI). The inclusion of side information via low-rank covariance priors (WarpedMF-SI) consistently increased prediction accuracy for all data views, whereas other methods, i.e. the linear regression based MF models (RBMF-SI and BoxCoxRBMF-SI) yielded variable performance.
When considering the inferred latent representations without the bias terms, the WarpedMF-SI model had the highest predictive performance. The proposed warped matrix factorisation models without side information (WarpedMF) was substantially more accurate than un-wapred factorisation models (MF) or the Box-Cox preprocessing models (BoxCoxMF). This is more evident in multi-view learning where the un-warped factorisation (MV-MF) and the Box-Cox preprocessing (MV-BoxCoxMF) failed to capture the consensus across views; very little structure was remained for the shared latent factors to discover. In contrast, learning warping functions in multi-view learning of the MV-WarpedMF model as well as the MV-WarpedMF-SI model maximised the mutual latent structures across views, promoting our confidence in true associations (see the next section).
Evaluation of Consensus Discovery Using Known Associations. To further explore the benefit of the consensus discovery captured by the shared latent factors, we assessed each model using the independent out-of-sample association scores of 22,138 known gene-disease associations. Figure 3(left) shows the test correlation coefficient (Rs) obtained from each model, where the minimum, average and maximum of Rs across views are shown for single-view models. These results show that single-view learning did fail to identify true gene-disease associations, despite the strong predictive performance. Multi-view learning consistently resulted in improved performance, where the best models were the combination of warping and multi-view modelling with or without side information (MV-WarpedMF and MV-WarpedMF-SI), followed by the un-warped factorisation (MV-MF). This confirms that learning warping functions in conjunction with the parameters of matrix factorisation modelling rather than the Box-Cox preprocessing or the un-warped factorisation can capture complex transformations and in particular is an effective approach to adjust for differences in scale between views, leading to significantly improved imputation accuracies. Figure 3(right) depicts the six warping functions inferred by MV-WarpedMF-SI.
6 Conclusion
We have proposed a method to jointly infer a parametric data transformation function while performing inference in matrix factorisation models. Our approach unifies previous efforts, including models that combine data across views and the incorporation of side information. In experiments on real data, we demonstrate that learning warping functions within the matrix factorisation framework and incorporating low-rank side information yield increased accuracy for imputing missing values in single-view learning, and in multi-view learning where joint inference was made across all views. Flexible data transformations will be particularly useful if distant data types are integrated. Our experiments illustrate an example application of such a setting, where we consider gene-disease associations obtained using complementary sources of evidence. We show that learning warping functions in multi-view matrix factorisation can enhance the discovery of the shared latent structures (consensus) underlying across views.
The proposed variational inference scheme is computationally efficient and allows to incorporate side information in the form of multivariate normal (covariance) priors. Combined with suitable low-rank approximations, the proposed strategy is directly applicable to thousands of rows and columns with robust performance.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
This was done by using a SciPy library.
References
Adams, R., Dahl, G., Murray, I.: Incorporating side information in probabilistic matrix factorization with gaussian processes. In: Proceedings of the 26th Conference Annual Conference on Uncertainty in Artificial Intelligence (UAI), pp. 1–9. AUAI Press, Corvallis (2010)
Agarwal, D., Chen, B.C.: Regression-based latent factor models. In: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 19–28. ACM (2009)
Akata, Z., Thurau, C., Bauckhage, C.: Non-negative matrix factorization in multimodality data for segmentation and label prediction. In: 16th Computer Vision Winter Workshop (2011)
Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, New York (2006)
Box, G.E., Cox, D.R.: An analysis of transformations. J. Roy. Stat. Soc. Ser. B (Methodol.) 26(2), 211–252 (1964)
Cao, B., Liu, N.N., Yang, Q.: Transfer learning for collective link prediction in multiple heterogenous domains. In: Proceedings of the 27th International Conference on Machine Learning (2010)
Damianou, A., Ek, C., Titsias, M., Lawrence, N.: Manifold relevance determination. In: Proceedings of the 27th International Conference on Machine Learning (2012)
Durbin, B.P., Hardin, J.S., Hawkins, D.M., Rocke, D.M.: A variance-stabilizing transformation for gene-expression microarray data. Bioinformatics 18(Suppl. 1), S105–S110 (2002)
Fang, Y., Si, L.: Matrix co-factorization for recommendation with rich side information and implicit feedback. In: Proceedings of the 2nd International Workshop on Information Heterogeneity and Fusion in Recommender Systems, pp. 65–69. ACM (2011)
Fehrmann, R.S., Karjalainen, J.M., Krajewska, M., Westra, H.J., Maloney, D., Simeonov, A., Pers, T.H., Hirschhorn, J.N., Jansen, R.C., Schultes, E.A., et al.: Gene expression analysis identifies global gene dosage sensitivity in Cancer. Nat. Genet. 47(2), 115–125 (2015)
Fusi, N., Lippert, C., Lawrence, N.D., Stegle, O.: Warped linear mixed models for the genetic analysis of transformed phenotypes. Nat. Commun. 5 (2014)
Gonen, M., Kaski, S.: Kernelized bayesian matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 36(10), 2047–2060 (2014)
Kelmansky, D.M., Martínez, E.J., Leiva, V.: A new variance stabilizing transformation for gene expression data analysis. Stat. Appl. Genet. Mol. Biol. 12(6), 653–666 (2013)
Kim, Y.D., Choi, S.: Scalable variational bayesian matrix factorization. In: Proceedings of the First Workshop on Large-Scale Recommender Systems (LSRS) (2013)
Kim, Y.D., Choi, S.: Scalable variational bayesian matrix factorization with side information. In: Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Reykjavik, Iceland (2014)
Lim, Y.J., Teh, Y.W.: Variational Bayesian approach to movie rating prediction. In: Proceedings of KDD Cup and Workshop (2007)
Lippert, C., Listgarten, J., Liu, Y., Kadie, C.M., Davidson, R.I., Heckerman, D.: Fast linear mixed models for genome-wide association studies. Nat. Methods 8(10), 833–835 (2011)
Malone, J., Holloway, E., Adamusiak, T., Kapushesky, M., Zheng, J., Kolesnikov, N., Zhukova, A., Brazma, A., Parkinson, H.: Modeling sample variables with an experimental factor ontology. Bioinformatics 26(8), 1112–1118 (2010)
Mnih, A., Salakhutdinov, R.: Probabilistic matrix factorization. In: Advances in Neural Information Processing Systems, pp. 1257–1264 (2007)
Neal, R.M.: Bayesian Learning for Neural Networks, vol. 118. Springer Science & Business Media, New York (2012)
Porteous, I., Asuncion, A.U., Welling, M.: Bayesian matrix factorization with side information and dirichlet process mixtures. In: AAAI (2010)
Schmidt, M.N.: Function factorization using warped gaussian processes. In: Proceedings of the 26th Annual International Conference on Machine Learning, pp. 921–928. ACM (2009)
Singh, A.P., Gordon, G.J.: Relational learning via collective matrix factorization. In: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 650–658. ACM (2008)
Smedley, D., Oellrich, A., Köhler, S., Ruef, B., Westerfield, M., Robinson, P., Lewis, S., Mungall, C., et al.: Phenodigm: analyzing curated annotations to associate animal models with human diseases. Database 2013, bat025 (2013)
Snelson, E., Rasmussen, C.E., Ghahramani, Z.: Warped gaussian processes. Adv. Neural Inf. Process. Syst. 16, 337–344 (2004)
Takács, G., Pilászy, I., Németh, B., Tikk, D.: Scalable collaborative filtering approaches for large recommender systems. J. Mach. Learn. Res. 10, 623–656 (2009)
Virtanen, S., Klami, A., Khan, S.A., Kaski, S.: Bayesian group factor analysis. In: Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics (2012)
Zhou, T., Shan, H., Banerjee, A., Sapiro, G.: Kernelized probabilistic matrix factorization: exploiting graphs and side information. In: SDM, vol. 12, pp. 403–414. SIAM (2012)
Acknowledgement
This work was supported by Open Targets. We are thankful to Dr. Ian Dunham, Dr. Gautier Koscielny, Dr. Samiul Hasan, and Dr. Andrea Pierleoni for their helpful discussion and contributions in curating and managing the data we have used for the described experiments. NP has received support from the Royal Thai Government Scholarship.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Pratanwanich, N., Lió, P., Stegle, O. (2016). Warped Matrix Factorisation for Multi-view Data Integration. In: Frasconi, P., Landwehr, N., Manco, G., Vreeken, J. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2016. Lecture Notes in Computer Science(), vol 9852. Springer, Cham. https://doi.org/10.1007/978-3-319-46227-1_49
Download citation
DOI: https://doi.org/10.1007/978-3-319-46227-1_49
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46226-4
Online ISBN: 978-3-319-46227-1
eBook Packages: Computer ScienceComputer Science (R0)