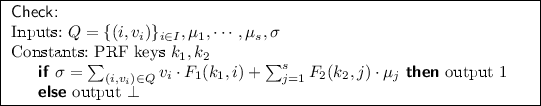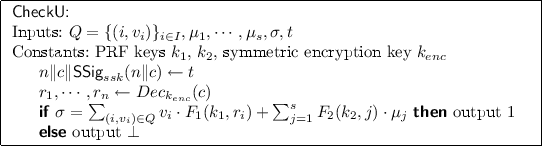Symmetric-Key Based Proofs of Retrievability Supporting Public Verification

Abstract

Proofs-of-Retrievability enables a client to store his data on a cloud server so that he executes an efficient auditing protocol to check that the server possesses all of his data in the future. During an audit, the server must maintain full knowledge of the client’s data to pass, even though only a few blocks of the data need to be accessed. Since the first work by Juels and Kaliski, many PoR schemes have been proposed and some of them can support dynamic updates. However, all the existing works that achieve public verifiability are built upon traditional public-key cryptosystems which imposes a relatively high computational burden on low-power clients (e.g., mobile devices).

In this work we explore indistinguishability obfuscation for building a Proof-of-Retrievability scheme that provides public verification while the encryption is based on symmetric key primitives. The resulting scheme offers light-weight storing and proving at the expense of longer verification. This could be useful in apations where outsourcing files is usually done by low-power client and verifications can be done by well equipped machines (e.g., a third party server). We also show that the proposed scheme can support dynamic updates. At last, for better assessing our proposed scheme, we give a performance analysis of our scheme and a comparison with several other existing schemes which demonstrates that our scheme achieves better performance on the data owner side and the server side.

1 Introduction

Nowadays, storage outsourcing (e.g., Google Drive, Dropbox, etc.) is becoming increasingly popular as one of the applications of cloud computing. It enables clients to access the outsourced data flexibly from any location. However, the storage provider (i.e., server) is not necessarily trusted. This situation gives rise to a need that a data owner (i.e., client) can efficiently verify that the server indeed stores the entire data. More precisely, a client can run an efficient audit protocol with the untrusted server where the server can pass the audit only if it maintains knowledge of the client’s entire outsourced data. Formally, this implies two guarantees that the client wants from the server: Authenticity and Retrievability. Authenticity ensures that the client can verify the correctness of the data fetched from the server. On the other hand, Retrievability provides assurance that the client’s data on the server is intact and no data loss has occurred. Apparently, the client should not need to download the entire data from server to verify the data’s integrity, since this may be prohibitive in terms of bandwidth and time. Also, it is undesirable for the server to read all of the client’s outsourced data during an audit protocol.

One method that achieves the above is called Proofs of Retrievability (PoR) which was initially defined and constructed by Juels and Kaliski [1]. Mainly, PoR schemes can be categorized into two classes: privately verifiable ones and publicly verifiable ones. Note that privately verifiable PoR systems normally only involve symmetric key primitives, which are cheap for the data owner in encrypting and uploading its files. However, in such systems the guarantees of the data’s authenticity and retrievability largely depend on the data owners themselves due to the fact that they need to regularly perform verifications (e.g., auditing) in order to react as early as possible in case of a data loss. Nowadays, users create and upload data everywhere using low power devices, such as mobile phones. Obviously, such privately verifiable PoR system would inevitably impose expensive burdens on low power data owners in the long run. On the other hand, in this scenario with low power users, it is reasonable to have a well equipped server (trusted or semi-trusted) perform auditing on behalf of data owner which requires publicly verifiable PoR systems. However, all of the existing PoR schemes that achieve public verifiability are constructed based on traditional public key cryptography which implies more complex and expensive computations compared to simple and symmetric key cryptographic primitives. (This observation can also be spotted in outsourced computing schemes that support public verification [34–36].) That means a PoR scheme using public key cryptographic primitives incurs relatively expensive overheads on low-capability clients. One might want to construct a public verifiable PoR scheme without relying on traditional public key cryptographic primitives. One cryptographic primitive that can help to overcome this constraint is indistinguishability obfuscation ($i \mathcal {O}$) which achieves that obfuscations of any two distinct (equal-size) programs that implement the same functionality are computationally indistinguishable from each other. $i \mathcal {O}$ has become so important since the recent breakthrough result of Garg et al. in [2]. Garg et al. proposed the first candidate construction of an efficient indistinguishability obfuscator for general programs which are written as boolean circuits. Subsequently, Sahai and Waters [3] showed the power of $i \mathcal {O}$ as a cryptographic primitive: they used $i \mathcal {O}$ to construct denial encryption, public-key encryption, and much more from pseudorandom functions. Most recently, by exploiting $i \mathcal {O}$, Ramchen et al. [4] built a fully secure signature scheme with fast signing and Boneh et al. [5] proposed a multiparty key exchange protocol, an efficient traitor tracing system and more.

Our work. In this paper, we explore this new primitive, $i \mathcal {O}$, for building PoR. In particular, we modify Shacham and Waters’ privately verifiable PoR scheme [6] and apply $i \mathcal {O}$ to construct a publicly verifiable PoR scheme. Our results share a similar property with Ramchen et al.’s signing scheme [4], that is, storing and proving are fast at the expense of longer public verification. Such “imbalance” could be useful in applications where outsourcing files is usually done by low-power client and verifications can be done by well equipped machines (a semi-trusted third party). Our contributions are summarized as follows:

• 1. We explore building proof-of-retrievability systems from obfuscation. The resulting PoR scheme offers light-weight outsourcing, because it requires only symmetric key operations for the data owner to upload files to the cloud server. Likewise, the server also requires less workload during an auditing compared to existing publicly verifiable PoR schemes.

• 2. We show that the proposed PoR scheme can support dynamic updates by applying the Merkle hash tree technique. We first build a modified B+ tree over the file blocks and the corresponding block verification messages $\sigma$. Then we apply the Merkle hash tree to this tree for ensuring authenticity and freshness.

• 3. Note that the current $i \mathcal {O}$ construction candidate will incur a large amount of overhead for generating obfuscation, but it is only a one-time cost during the preprocessing stage of our system. Therefore its cost can be amortized over plenty of future operations. Except for this one-time cost, we show that our proposed scheme achieves good performance on the data owner side and the cloud server side by analysis and comparisons with other recent existing PoR schemes.

Indistinguishability obfuscation indeed provides attractive and interesting features, but the current $i \mathcal {O}$ candidate construction offers impractical generation and evaluation. Given the fact that the development of $i \mathcal {O}$ is still in its nascent stages, in Appendix, we discuss several possible future directions in works on obfuscation in addition to those discussed in [2].

1.1 Related Work

Proof of Retrievability and Provable Data Possession. The first PoR scheme was defined and constructed by Juels and Kaliski [1], and the first Provable Data Possession (PDP) was concurrently defined by Ateniese et al. [7]. The main difference between PoR and PDP is the notion of security that they achieve. Concretely, PoR provides stronger security guarantees than PDP does. A successful PoR audit guarantees that the server maintains knowledge of all of the client’s outsourced data, while a successful PDP audit only ensures that the server is retaining most of the data. That means, in a PDP system a server that lost a small amount of data can still pass an audit with significant probability. Some PDP schemes [8] indeed provide full security. However, those schemes requires the server to read the client’s entire data during an audit. If the data is large, this becomes totally impractical. A detailed comparison can be found in [9]. Since the introduction of PoR and PDP they have received much research attention. On the one hand, subsequent works [6, 10–12] for static data focused on the improvement of communication efficiency and exact security. On the other hand, the works of [13–15] showed how to construct dynamic PDP scheme supporting efficient updates. Although many efficient PoR schemes have been proposed since the work of Juels et al., only a few of them supports efficient dynamic update [16–18].

Observe that in publicly verifiable PoR systems, an external verifier (called auditor) is able to perform an auditing protocol with the cloud server on behalf of the data owner. However, public PoR systems do not provide any security guarantees when the user and/or the external verifier are dishonest. To address this problem Armknecht et al. recently introduced the notion of outsourced proofs of retrievability (OPoR) [19]. In particular, OPoR protects against the collusion of any two parties among the malicious auditor, malicious users and the malicious cloud server. Armknecht et al. proposed a concrete OPoR scheme, named Fortress, which is mainly built upon the private PoR scheme in [6]. In order to be secure in the OPoR security model, Fortress also employs a mechanism that enables the user and the auditor to extract common pseudorandom bits using a time-dependent source without any interaction.

Indistinguishability Obfuscation. Program obfuscation aims to make computer programs “unintelligible” while preserving their functionality. The formal study of obfuscation was started by Barak et al. [20] in 2001. In their work, they first suggested a quite intuitive notion called virtual black-box obfuscation, for which they also showed impossibility. Motivated by this impossibility, they proposed another important notion of obfuscation called indistinguishability obfuscation $(i \mathcal {O})$, which asks that obfuscations of any two distinct (equal-size) programs that implement the same functionalities are computationally indistinguishable from each other. A recent breakthrough result by Garg et al. [2] presented the first candidate construction of an efficient indistinguishability obfuscator for general programs that are written as boolean circuits. The proposed construction was build on the multilinear map candidates [21, 22].

The works of Garg et al. [2] also showed how to apply indistinguishability obfuscation to the construction of functional encryption schemes for general circuits. In subsequent work, Sahai and Waters [3] formally investigated what can be built from indistinguishability obfuscation and showed the power of indistinguishability obfuscation as a cryptographic primitive. Since then, many new applications of general-purpose obfuscation have been explored [24–28]. Most recently, the works of Boneh et al. [5] and Ramchen et al. [4] re-explore the constructions of some existing cryptographic primitives through the lens of obfuscation, including broadcast encryption, traitor tracing and signing. Those proposed constructions indeed obtain some attractive features, although current obfuscation candidates incur prohibitive overheads. Precisely, Boneh et al.’s broadcast encryption achieves that ciphertext size is independent of the number of users, and their traitor tracing system achieves full collusion resistance with short ciphertexts, secret keys and public keys. On the other hand, Ramchen et al. [4] proposed an imbalanced signing algorithm, which is ideally significantly faster than comparable signatures that are not built upon obfuscation. Here “imbalanced” means the signing is fast at the expense of longer verification.

2 Preliminaries

In this section we define proof-of-retrievability, indistinguishability obfuscation, and variants of pseudorandom functions (PRFs) that we will make use of. All the variants of PRFs that we consider will be constructed from one-way functions.

2.1 Proofs of Retrievability

Below, we give the definition of publicly verifiable PoR scheme in a way similar to that in [6]. A proof of retrievability scheme defines four algorithms, KeyGen, Store, Prove and Verify, which are specified as follows:

• $(pk,sk) \leftarrow$ KeyGen $(1^\lambda )$. On input the security parameter $\lambda$, this randomized algorithm generates a public-private keypair (pk, sk).

• $(M^*, t) \leftarrow$ Store(sk, M). On input a secret key sk and a file $M \in \{0, 1\}^*$, this algorithm processes M to produce $M^*$, which will be stored on the server, and a tag t. The tag t contains information associated with the file $M^*$.

• $(0,1) \leftarrow \mathbf {Audit}(\mathbf {Prove},\mathbf {Verify})$. The randomized proving and verifying algorithms together define an Audit-protocol for proving file retrievability. During protocol execution, both algorithms take as input the public key pk and the file tag t output by Store. Prove algorithm also takes as input the processed file description $M^*$ that is output by Store, and Verify algorithm takes as input public verification key VK. At the end of the protocol, Verify outputs 0 or 1, with 1 indicating that the file is being stored on the server. We denote a run of two parties executing such protocol as:

  $$\begin{aligned} \{0,1\} \leftarrow (\mathbf {Verify}(pk, VK, t) \rightleftharpoons \mathbf {Prove}(pk, t, M^*)). \end{aligned}$$

Correctness. For all keypairs (pk, sk) output by KeyGen, for all files $M \in \{0, 1\}^*$, and for all $(M^*, t)$ output by Store(sk, M), the verification algorithm accepts when interacting with the valid prover:

$$\begin{aligned} ({\mathbf {Verify}}(pk, VK, t) \rightleftharpoons {\mathbf {Prove}}(pk, t, M^*)) = 1. \end{aligned}$$

2.2 Obfuscation Preliminaries

We recall the definition of indistinguishability obfuscation from [2, 3].

Definition 1

Indistinguishability Obfuscation ($i \mathcal {O}$). A uniform PPT machine $i \mathcal {O}$ is called an indistinguishability obfuscator for a circuit class $\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}$ if the following conditions are satisfied:

• For all security parameters $\lambda \in \mathbb {N}$, for all $C \in \mathcal {C}_\lambda$, for all inputs x, we have that $\mathsf {Pr}[C'(x) = C(x) : C' \leftarrow i\mathcal {O}(\lambda , C)] = 1$.

• For any (not necessarily uniform) PPT distinguisher (Samp, D), there exists a negligible function $negl(\cdot )$ such that the following holds: if for all security parameters $\lambda \in \mathbb {N}$, $\mathrm {Pr}[\forall x, C_0(x) = C_1(x) : (C_0; C_1; \tau ) \leftarrow Samp(1^\lambda )] > 1 - negl(\lambda ),$ then we have

  $$\begin{aligned} | \mathrm {Pr}[D(\tau , i\mathcal {O}(\lambda , C_0))&= 1 : (C_0;C_1;\tau ) \leftarrow Samp(1^\lambda )]- \\ \mathrm {Pr}[D(\tau , i\mathcal {O}(\lambda , C_1))&= 1 : (C_0;C_1;\tau ) \leftarrow Samp(1^\lambda )] | \le negl(\lambda ). \end{aligned}$$

2.3 Puncturable PRFs

A pseudorandom function (PRF) is a function $F: \mathcal {K} \times \mathcal {M} \rightarrow \mathcal {Y}$ with $K \mathop {\leftarrow }\limits ^{\$} \mathcal {K}$ such that the function $F(K, \cdot )$ is indistinguishable from random. A constrained PRF [29] is a PRF $F(K, \cdot )$ that is able to evaluate at certain portions of the input space and nowhere else. A puncturable PRF [3, 29] is a type of constrained PRF that enables the evaluation at all bit strings of a certain length, except for any polynomial-size set of inputs. Concretely, it is defined with two PPT algorithms $(\mathsf {Eval}_F, \mathsf {Puncture}_F)$ such that the following two properties hold:

• Functionality Preserved under Puncturing. For every PPT algorithm $\mathcal {A}$ with input $1^\lambda$ outputs a set $S \subseteq \{0, 1\}^n$, for all $x \in \{0,1\}^n \backslash S$, we have

  $$\begin{aligned} \mathrm {Pr}[\mathsf {Eval}_F (K\{S\},x) = F(K,x) : K \mathop {\leftarrow }\limits ^{\$} \mathcal {K}, K\{S\} \leftarrow \mathsf {Puncture}_F(K,S)] = 1 \end{aligned}$$

• Pseudorandom at Punctured Points. For every pair of PPT algorithms $(\mathcal {A}_1, \mathcal {A}_2)$ such that $\mathcal {A}_1(1^\lambda )$ outputs a set $S \subseteq \{0,1\}^n$ and a state $\sigma$, consider an experiment where $K \mathop {\leftarrow }\limits ^{\$} \mathcal {K}, K\{S\} \leftarrow \mathsf {Puncture}_F(K,S)$. It holds that

  $$ |\mathrm {Pr}[\mathcal {A}_2(\sigma , K\{S\}, S, F(K,S)) = 1)] - \\ \mathrm {Pr}[\mathcal {A}_2(\sigma , K\{S\}, S, U_{m(\lambda )\cdot |S|}) = 1 ]| \le negl(\lambda ) $$

3 Security Definitions

The security definitions of Authenticity and Retrievability in [17, 18] are essentially equivalent to the security definition of Soundness in [6]. Note that the security definitions in [17, 18] are for dynamic PoR systems, while the one in [6] considers only static PoR systems. The only difference between a static PoR scheme and a dynamic PoR scheme is that the latter one supports secure dynamic updates, including modification, deletion and insertion. This affects the access to oracles in the security game. Below we present the security definitions for static PoR systems in the same way as [17, 18] and then point out how to obtain the security definitions for dynamic PoR systems based on the static one.

3.1 Security Definitions on Static PoR

Authenticity. Authenticity requires that the client can always detect if any message sent by the server deviates from honest behavior. More precisely, consider the following game between a challenger $\mathcal {C}$, a malicious server $\widetilde{\mathcal {S}}$ and an honest server $\mathcal {S}$ for the adaptive version of authenticity:

• The challenger initializes the environment and provides $\widetilde{\mathcal {S}}$ with public parameters.

• The malicious sever $\widetilde{\mathcal {S}}$ specifies a valid protocol sequence $P = (op_1, op_2, \cdots ,$ $op_{\mathrm {poly}(\lambda )})$ of polynomial size in the security parameter $\lambda$. The specified operations $op_t$ can be either Store or Audit. $\mathcal {C}$ executes the protocol with both $\widetilde{\mathcal {S}}$ and an honest server $\mathcal {S}$.

If at execution of any $op_j$, the message sent by $\widetilde{\mathcal {S}}$ differs from that of the honest server $\mathcal {S}$ and $\mathcal {C}$ does not output reject, the adversary $\widetilde{\mathcal {S}}$ wins and the game results in 1, else 0.

Definition 2

A static PoR scheme is said to satisfy adaptive Authenticity, if any polynomial-time adversary $\widetilde{\mathcal {S}}$ wins the above security game with probability no more than $\mathsf {negl}(\lambda )$.

Retrievability. Retrievability guarantees that whenever a malicious server can pass the audit test with non-negligible probability, the server must know the entire content of $\mathcal {M}$; and moreover, $\mathcal {M}$ can be recovered by repeatedly running the Audit-protocol between the challenger $\mathcal {C}$ and the server $\widetilde{\mathcal {S}}$. More precisely, consider the following security game:

• The challenger initializes the environment and provides $\widetilde{\mathcal {S}}$ with public parameters.

• The malicious server $\widetilde{\mathcal {S}}$ specifies a protocol sequence $P = (op_1, op_2, \cdots ,$ $op_{\mathrm {poly}(\lambda )})$ of polynomial size in terms of the security parameter $\lambda$. The specified operations $op_t$ can be either Store or Audit. Let $\mathcal {M}$ be the correct content value.

• The challenger $\mathcal {C}$ sequentially executes the respective protocols with $\widetilde{\mathcal {S}}$. At the end of executing P, let $st_\mathcal {C}$ and $st_{\widetilde{\mathcal {S}}}$ be the final configurations (states) of the challenger and the malicious server, respectively.

• The challenger now gets black-box rewinding access to the malicious server in its final configuration $st_{\widetilde{\mathcal {S}}}$. Starting from the configurations $(st_\mathcal {C},st_{\widetilde{\mathcal {S}}})$, the challenger runs the Audit-protocol repeatedly for a polynomial number of times with the server $\widetilde{\mathcal {S}}$ and attempts to extract out the content value as $\mathcal {M}'$.

If the malicious server $\widetilde{\mathcal {S}}$ passes the Audit-protocol with non-negligible probability and the extracted content value $\mathcal {M}' \ne \mathcal {M}$, then this game outputs 1, else 0.

Definition 3

A static PoR scheme is said to satisfy Retrievability, if there exists an efficient extractor $\mathcal {E}$ such that for any polynomial-time $\widetilde{\mathcal {S}}$, if $\widetilde{\mathcal {S}}$ passes the Audit-protocol with non-negligible probability, and then after executing the Audit-protocol with $\widetilde{\mathcal {S}}$ for a polynomial number of times, the extractor $\mathcal {E}$ outputs content value $\mathcal {M}' \ne \mathcal {M}$ only with negligible probability.

The above says that the extractor $\mathcal {E}$ will be able to extract out the correct content value $\mathcal {M}' = \mathcal {M}$ if the malicious server $\widetilde{\mathcal {S}}$ can maintain a non-negligible probability of passing the Audit-protocol. This means the server must retain full knowledge of $\mathcal {M}$.

3.2 Security Definitions on Dynamic PoR

The security definitions for dynamic PoR systems are the same as those for static PoR systems, except that the oracles which the malicious server $\widetilde{\mathcal {S}}$ has access to are including Read, Write and Audit. Precisely, the security game for Authenticity is the same as the for static PoR schemes, except that the malicious server $\widetilde{\mathcal {S}}$ can get access to Read, Write and Audit oracles. This means that the specified operations $op_t$ by $\widetilde{\mathcal {S}}$ in the protocol sequence $P = (op_1, op_2, \cdots , op_{\mathrm {poly}(\lambda )})$ can be either Read, Write or Audit. Similarly, the security game for Retrievability is the same as that for static PoR systems, except that the malicious server $\widetilde{\mathcal {S}}$ can get access to Read, Write and Audit oracles. Note that the winning condition for both games remain unchanged.

4 Constructions

In this section we first give the construction of a static publicly verifiable PoR system. Then we discuss how to extend this static PoR scheme to support efficient dynamic updates.

Before presenting our proposed constructions, we analyze a trivial construction of a publicly verifiable PoR scheme using $i \mathcal {O}$. Let n be the number of file blocks, $\lambda _1$ be the size of a file block (here assume every file block is equally large), $\lambda _2$ be the size of a block tag $\sigma$ and I be the challenge index set requested by the verifier. Since $i \mathcal {O}$ can hide secret information, which is embedded into the obfuscated program, from the users, one might construct a scheme as: (1) set the tag for a file block $m_i$ as the output of a PRF $F(k, m_i)$ with secret key k; (2) embed key k into the verification program and obfuscate it; (3) this verification program simply checks the tags for the challenged file blocks to see if they are valid outputs of the PRF. Observe that this verification program takes as inputs a challenge index set, the challenged file blocks and the corresponding file tags. Therefore, the circuit for this verification program will be of size $O(poly(|I| \cdot \log n + |I| \cdot \lambda _1 + |I| \cdot \lambda _2))$, where |I| is the size of index set I and poly(x) is a polynomial in terms of x. Clearly, this method also costs much a lot of bandwidth due to the fact that it does not provide an aggregated proof.

While in our construction we modify the privately verifiable PoR scheme in [6]. For consistency with the above analysis, assume that file blocks are not further divided into sectors. Then the verification program takes as input a challenge index set I, an aggregation of the challenged file blocks $\mu$ and an aggregated $\sigma '$. Consequently the circuit for the verification program will have size $O(poly(|I| \cdot \log n + \lambda _1 + \lambda _2))$, which is much smaller than that in the trivial construction. Clearly, the trivial construction will lead to a significantly larger obfuscation of the verification program.

Similarly, we analyze the circuit’s size when a file block is further split into s sectors, as the scheme in [6] did. Let the size of a sector in a file block be $\lambda _3$. The circuit size in the trivial construction will remain unchanged, $O(poly(|I| \cdot \log n + |I| \cdot \lambda _1 + |I| \cdot \lambda _2))$. While the circuit in our construction will have size $O(poly(|I| \cdot \log n + s \cdot \lambda _3 + \lambda _3)) \approx O(poly(|I| \cdot \log n + \lambda _1 + \lambda _3))$, which is still much smaller than that in the trivial construction. As we can see, exploiting $i \mathcal {O}$ is not trivial although it is a powerful cryptographic primitive.

4.1 Static Publicly Verifiable PoR Scheme

We modify Shacham and Waters’ privately verifiable PoR scheme in [6] and combine it with $i \mathcal {O}$ to give a publicly verifiable PoR scheme. Recall that in the scheme in [6], a file F is processed using erasure code and then divided into n blocks. Also note that each block is split into s sectors. This allows for a tradeoff between storage overhead and communication overhead, as discussed in [6].

Before presenting the construction of the proposed static PoR scheme, we give a brief discussion on how we apply indistinguishability obfuscation to the PoR scheme in [6]. For doing that, we need to utilize a key technique introduced in [3], named punctured programs. At a very high-level, the idea of this technique is to modify a program (which is to be obfuscated) by surgically removing a key element of the program, without which the adversary cannot win the security game it must play, but in a way that does not change the functionality of the program. Note that, in Shacham and Waters’ PoR scheme, for each file block, $\sigma _i$ is set as $f_{prf}(i) + \sum ^s_{j=1} \alpha _j m_{ij}$, where the secret key $k_{prf}$ for PRF f is specific for one certain file M. That means for different files, it uses different PRF key $k_{prf}$’s. As to make it a punctured PRF that we want in the obfuscated program, we eliminate this binding between PRF key $k_{prf}$ and file M, and the same PRF key $k_{prf}$ will be used in storing many different files. Thus, the PRF key $k_{prf}$ will be randomly chosen in client KeyGen step, not in Store step. The security will be maintained after this modification, due to the fact that it still provides $\sigma _i$ with randomness without adversary getting the PRF key.

The second main change is related to the construction of a file tag t. Note that, in Shacham and Waters’ scheme, $t = n\Vert c \Vert \mathsf {MAC}_{k_{mac}}(n\Vert c)$, where $c = \mathsf {Enc}_{k_{enc}}(k_{prf}\Vert \alpha _1\Vert \cdots \Vert \alpha _s)$. In our proposed scheme, the randomly selected elements $\alpha _1, \cdots , \alpha _s$ will be removed. Instead, we use another PRF key $f_{prf'}$ to generate s pseudorandom numbers, which will reduce the communication cost by $(s \cdot \lceil \log p\rceil )$, where $\log p$ means each element $\alpha _i \in \mathbb {Z}_p$. As a consequence of these two changes, the symmetric key encryption component c is no longer needed and $\sigma _i$ will be made as $f_{prf}(i) + \sum ^s_{j=1} f_{prf'}(j) \cdot m_{ij}$.

Let $F_1(k_1, \cdot )$ be a puncturable PRF mapping $\lceil \mathrm {log}\ N \rceil$-bit inputs to $\lceil \mathrm {log}\ \mathbb {Z}_p \rceil$. Here N is a bound on the number of blocks in a file. Let $F_2(k_2, \cdot )$ be a puncturable PRF mapping $\lceil \mathrm {log}\ s \rceil$-bit inputs to $\lceil \mathrm {log}\ \mathbb {Z}_p \rceil$. Let $\mathsf {SSig}_{ssk}(x)$ be the algorithm generating a signature on x.

• KeyGen(). Randomly choose two PRF key $k_1 \in \mathcal {K}_1$, $k_2 \in \mathcal {K}_2$ and a random signing keypair $(svk, ssk) \mathop {\leftarrow }\limits ^{R} \mathsf {SK}_g$. Set the secret key $sk = (k_1, k_2, ssk)$. Let the public key be svk along with the verification key VK which is an indistinguishability obfuscation of the program Check defined as below.

• Store( sk ,  M ). Given file M and secret key $sk = (k_1, k_2, ssk)$, proceed as follows:

  • 1. apply the erasure code to M to obtain $M'$;

  • 2. split $M'$ into n blocks, and each block into s sectors to get $\{m_{ij}\}$ for $1 \le i \le n, 1 \le j \le s$;

  • 3. set the file tag $t = n\Vert \mathsf {SSig}_{ssk}(n)$

  • 4. for each i, $1 \le i \le n$, compute $\sigma _i = F_1(k_1, i) + \sum ^s_{j=1} F_2(k_2, j) \cdot m_{ij}$;

  • 5. set as the outputs the processed file $M' = \{m_{ij}\}$, $1 \le i \le n,1 \le j \le s$, the corresponding file tag t and $\{\sigma _i\},1 \le i \le n$.

• Verify( svk ,  VK ,  t ). Given the tag t, parse $t = n\Vert \mathsf {SSig}_{ssk}(n)$ and use svk to verify the signature on t; if the signature is invalid, reject and halt. Otherwise, pick a random l-element subset I from [1, n], and for each $i \in I$, pick a random element $v_i \in \mathbb {Z}_p$. Send set $Q=\{(i,v_i)\}$ to the prover. Parse the prover’s response to obtain $\mu _1,\cdots ,\mu _s, \sigma \in \mathbb {Z}^{s+1}_p$. If parsing fails, reject and halt. Otherwise, output VK$(Q = \{(i, v_i)\}_{i\in I}, \mu _1,\cdots ,\mu _s, \sigma )$.

  

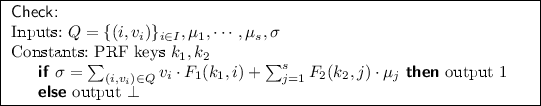
• Prove $(t,M')$. Given the processed file $M'$, $\{\sigma _i\},1\le i \le n$ and an l-element set Q sent by the verifier, parse $M' = \{m_{ij}\},1\le i\le n,1\le j\le s$ and $Q = \{(i, v_i)\}$. Then compute

  $$\begin{aligned} \mu _j = \sum _{(i,v_i) \in Q} v_i m_{ij}\ \mathrm {for}\ 1\le j\le s,\ \ \ \mathrm {and}\ \ \ \sigma =\sum _{(i,v_i)} v_i \sigma _i, \end{aligned}$$

  and send to the prove in response the values $\mu _1,\cdots ,\mu _s$ and $\sigma$.

4.2 PoR Scheme Supporting Efficient Dynamic Updates

A PoR scheme supporting dynamic updates means that it enables modification, deletion and insertion over the stored files. Note that, in the static PoR scheme, each $\sigma _i$ associated with ${m_{ij}}_{1\le j \le s}$ is also bound to a file block index i. If an update is executed in this static PoR scheme, it requires to change every $\sigma _i$ corresponding to the involved file blocks, and the cost could probably be expensive. Let’s say the client needs to insert a file block $F_i$ into position i. We can see that this insertion manipulation requires to update the indices in $\sigma _j$’s for all $i \le j \le n$. On average, a single insertion incurs updates on n/2 $\sigma _j$’s.

In order to offer efficient insertion, we need to disentangle $\sigma _i$ from index i. Concretely, $F_1(k_1, \cdot )$ should be erased in the computing of $\sigma _i$, which leads to a modified $\sigma '_i = \sum ^s_{j=1} F_2(k_2, j) \cdot m_{ij}$. However, this would make the scheme insecure, because a malicious server can always forge, e.g., $\sigma '_i/2 = \sum ^s_{j=1} F_2(k_2, j) \cdot (m_{ij}/2)$ for file block $\{m_{ij}/2\}_{1\le j \le s}$ with this $\sigma '_i$.

Instead, we build $\sigma _i$ as $F_1(k_1, r_i) + \sum ^s_{j=1} F_2(k_2, j) \cdot m_{ij}$, where $r_i$ is a random element from $\mathbb {Z}_p$. Clearly, we can’t maintain the order of the stored file blocks without associating $\sigma _i$ with index i. To provide the guarantee that every up-to-date file block is in the designated position, we use a modified B+ tree data structure with standard Merkle hash tree technique.

Observe that, unlike Shacham and Waters’ scheme where the file is split into n blocks after being erasure encoded, the construction here assumes that each file block is encoded ‘locally’. (Cash et al.’s work [17] also started with this point.) That is, instead of using an erasure code that takes the entire file as input, we use a code that works on small blocks. More precisely, the client divides the file M into n blocks, i.e., $M = (m_1, m_2, \cdots , m_n)$, and then encodes each file block $m_i$ individually into a corresponding codeword block $c_i = \mathsf {encode}(m_i)$. Next, the client performs the following PoR scheme to create $\sigma _i$ for each $c_i$. Auditing works as before: The verifier randomly selects l indices from [1, n] and l random values, and then challenges the server to respond with a proof that is computed with those l random values and corresponding codewords specified by the l indices. Note that, in this construction, each codeword $c_i$ will be further divided into s sectors, $(c_{i1}, c_{i2}, \cdots , c_{is})$ during the creation of $\sigma _i$. A more detailed discussion about this and analysis of how to better define block size can be found in the appendices in [6, 17].

Let $F_1(k_1, \cdot )$ be a puncturable PRF mapping $\lceil \mathrm {log}\ N \rceil$-bit inputs to $\lceil \mathrm {log}\ \mathbb {Z}_p \rceil$. Here N is a bound on the number of blocks in a file. Let $F_2(k_2, \cdot )$ be a puncturable PRF mapping $\lceil \mathrm {log}\ s \rceil$-bit inputs to $\lceil \mathrm {log}\ \mathbb {Z}_p \rceil$. Let $\mathsf {Enc}_k$/$\mathsf {Dec}_k$ be a symmetric key encryption/decryption algorithm, and $\mathsf {SSig}_{ssk}(x)$ be the algorithm generating a signature on x.

• KeyGen(). Randomly choose puncturable PRF keys $k_1 \in \mathcal {K}_1$ $k_2 \in \mathcal {K}_2$, a symmetric encryption key $k_{enc} \in \mathcal {K}_{enc}$ and a random signing keypair $(svk, ssk) \mathop {\leftarrow }\limits ^{R} \mathsf {SK}_g$. Set the secret key $sk = (k_1, k_2, k_{enc}, ssk)$. Let the public key be svk along with the verification key VK which is an indistinguishability obfuscation of the program CheckU defined as below.

• Store( sk ,  M ). Given file M and secret key $sk = (k_1, k_2, k_{enc}, ssk)$, proceed as follows:

  • 1. split $M'$ into n blocks and apply the erasure code to each block $m_i$ to obtain the codeword block $m'_i$, then divide each block $m'_i$ into s sectors to get $\{m'_{ij}\}$ for $1 \le i \le n, 1 \le j \le s$;

  • 2. for each i, $1 \le i \le n$, choose a random element $r_i \in \mathbb {Z}_p$ and compute $\sigma _i = F_1(k_1, r_i) + \sum ^s_{j=1} F_2(k_2, j) \cdot m'_{ij}$;

  • 3. set $c = \mathsf {Enc}_{k_{enc}}(r_1\Vert \cdots \Vert r_n)$ and the file tag $t = n\Vert c\Vert \mathsf {SSig}_{ssk}(n\Vert c)$;

  • 4. set as the outputs the processed file $M' = \{m'_{ij}\}$, $1 \le i \le n,1 \le j \le s$, the corresponding file tag t and $\{\sigma _i\},1 \le i \le n$.

• Verify( svk ,  VK ,  t ). Given the file tag t, parse $t = n\Vert c \Vert \mathsf {SSig}_{ssk}(n\Vert c)$ and use svk to verify the signature on t; if the signature is invalid, reject and halt. Otherwise, pick a random l-element subset I from [1, n], and for each $i \in I$, pick a random element $v_i \in \mathbb {Z}_p$. Sent set $Q = \{(i,v_i)\}$ to the prover. Parse the prover’s response to obtain $\mu _1,\cdots ,\mu _s, \sigma \in \mathbb {Z}^{s+1}_p$. If parsing fails, reject and halt. Otherwise, output VK$(Q = \{(i, v_i)\}_{i\in I}, \mu _1,\cdots ,\mu _s, \sigma , t)$.

  

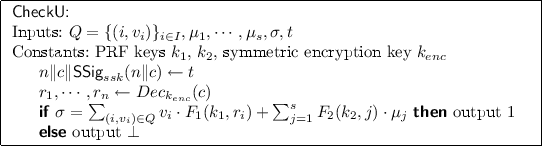
• Prove $(t,M')$. Given the processed file $M'$, $\{\sigma _i\},1\le i \le n$ and an l-element set Q sent by the verifier, parse $M' = \{m'_{ij}\},1\le i\le n,1\le j\le s$ and $Q = \{(i, v_i)\}$. Then compute

  $$\begin{aligned} \mu _j = \sum _{(i,v_i) \in Q} v_i m'_{ij}\ \mathrm {for}\ 1\le j\le s,\ \ \ \mathrm {and}\ \ \ \sigma =\sum _{(i,v_i)} v_i \sigma _i, \end{aligned}$$

  and send to the prove in response the values $\mu _1,\cdots ,\mu _s$ and $\sigma$.

Modified B+ Merkle tree. In our construction, we organize the data files using a modified B+ tree, and then apply a standard Merkle Hash tree to provides guarantees of freshness and authenticity. In this modified B+ tree, each node has at most three entries. Each entry in leaf node is data file’s $\sigma$ and is linked to its corresponding data file in the additional bottom level. The internal nodes will no longer have index information. Before presenting the tree’s construction, we first define some notations. We denote an entry’s corresponding computed $\sigma$ by $label(\cdot )$, the rank of an entry (i.e., the number of file blocks that can be reached from this entry) by $rank(\cdot )$, descendants of an entry by $child(\cdot )$, left/right sibling of an entry by $len(\cdot )/ren(\cdot )$.

• entry w in leaf node: $label(w)=\sigma$, len(w) (if w is the leftmost entry, $len(w) = 0$) and ren(w) ((if w is the rightmost entry, $ren(w) = 0$);

• entry v in internal node and root node: rank(v), child(v) len(v) and ren(v), where len(v) and ren(v) conform to the rules above.

Fig. 1.

An example of a modified B+ tree.

An example is illustrated in Fig. 1a. Following the definitions above, entry $v_1$ in root node R contains: (1) $rank(v_1)=3$, because $w_1, w_2$ and $w_3$ can be reached from $v_1$; (2) $child(v_1)=w_1\Vert w_2\Vert w_3$; (3) $len(v_1)=0$; (4) $ren(v_1)=v_2$. Entry $w_2$ in leaf node $W_1$ contains: (1) $label(w_2) = \sigma _2$; (2) $len(w_2) = w_1$; (3) $ren(w_2)=w_3$. Note that the arrows connecting the entries in leaf nodes with F’s means that each entry is associated with its corresponding file block. Precisely, e.g., entry $w_1$ is associated with the first data block $F_1$ and $label(w_1)=\sigma _1$.

To search for a $\sigma$ and its corresponding file block, we need two additional values of each entry, $low(\cdot )$ and $high(\cdot )$. $low(\cdot )$ gives the lowest-position data block that can be reached from an entry, and $high(\cdot )$ defines the highest-position data block that can be reached from an entry. Observe that these two values need not be stored for every entry in the tree. We can compute them on the fly using the ranks. For the current entry r, assume we know low(r) and high(r). Let $child(r) = v_1\Vert v_2\Vert v_3$. Then $low(v_i)$’s and $high(v_i)$’s can be computed with entry’s rank value in the following way: (1) $low(v_1) = low(r)$ and $high(v_1) = low(v_1) + rank(v_1) - 1$; (2) $low(v_2) = high(v_1) + 1$ and $high(v_2) = low(v_2) + rank(v_2) - 1$; (3) $low(v_3) = high(v_2) + 1$ and $high(v_3) = high(r)$.

Using the entries’ rank values, we can reach the i-th data block (i.e., i-th entry) in the leaf nodes. The search starts with entry $v_1$ in root node. Clearly, for the start entry of the tree, we have $low(v_1)=1$. On each entry v during the search, if $i \in [low(v),high(v)]$, we proceed the search along the pointer from v to its children; otherwise, check the next entry on v’s right side. We continue until we reach the i-th data block. For instance, say we want to read the 6-th data block in Fig. 1a. We start with entry $v_1$, and the search proceeds as follows:

• 1. compute $high(v_1) = low(v_1) + rank(v_1) - 1 = 3$;

• 2. $i = 6 \notin [low(v_1),high(v_1)]$, then check the next entry, $v_2$;

• 3. compute $low(v_2) = high(v_1) + 1 = 4, high(v_2) = low(v_2) + rank(v_2) - 1 = 6$;

• 4. $i \in [low(v_2),high(v_2)]$, then follow the pointer leading to $v_2$’s children;

• 5. get $child(v_2) = w_4\Vert w_5\Vert w_6$;

• 6. now in leaf node, check each entry from left to right, and find $w_6$ be the entry connecting to the wanted data block.

Now it is only left to define the Merkle hash tree on this modified B+ tree. Note that in our modified B+ tree, each node have at most 3 entries. Let upper case letter denote node and lower case one denote entry. For each entry, the hashing value is computed as follows:

• Case 0: w is an entry in a leaf node, compute $f(w) = h(label(w)) = h(\sigma )$,

• Case 1: v is an entry in an internal node and it’s descendent is node $V'$, compute $f(v) = h(rank(v)\Vert f(V'))$.

For each node (internal node or leaf node) consisting of entries $v_1, v_2, v_3$ from left to right, we define $f(V)=h(f(v_1)\Vert f(v_2)\Vert f(v_3))$. For instance, in Fig. 1.a, the hashing value for the root node is $f(R) = h(f(v_1)\Vert f(v_2)\Vert f(v_3))$, where $f(v_i) = h(rank(v_i)\Vert f(W_i))$ and $f(W_i) = h(f(w_{(i-1)*3 + 1})\Vert f(w_{(i-1)*3 + 2})\Vert f(w_{(i-1)*3 + 3}))$.

With this Merkle hash tree built over the modified B+ tree, the client keeps track of the root digest. Every time after fetching a data block, the client fetches its corresponding $\sigma$ as well. Also the client receives the hashing values associated with other entries in the same node along the path from root to the data block. Then the client can verify the authenticity and freshness with the Merkle tree. Say the client needs to verify the authenticity and freshness of block $F_3$ in Fig. 1a, where he/she possesses the root digest f(R). The path from root to $F_3$ will be $(R \rightarrow W_1)$. For verification, besides $\sigma _3$, the client also receives $f(w_1),f(w_2)$ in node $W_1$ and $f(v_2),f(v_3)$ in node R.

Update. The main manipulations are updating the data block and updating the Merkle tree. Note that the update affects only nodes along the path from a wanted data block to root on the Merkle tree. Therefore, the running time for updating the Merkle tree is O(log n). Also to update the Merkle tree, some hashing values along the path from a data block to root are needed from the server. Clearly, the size of those values will be O(log n). Update operations include Modification, Deletion and Insertion. The update operations over our modified B+ tree mostly conform to the procedures of standard B+ tree. A slight difference lies in the Insertion operation when splitting node, due to the fact that our modified B+ tree doesn’t have index information.

First, we discuss Modification and Deletion. To modify a data block, the client simply computes the data block’s new corresponding $\sigma$ and updates the Merkle tree with this $\sigma$ to obtain a new root digest. Then the client uploads the the new data block and the new $\sigma$. After receiving this new $\sigma$, the server just needs to update the Merkle tree along the path from the data block to root. To delete a data block, the server simply deletes the unwanted data block by the client and then updates the Merkle tree along the path from this data block to root.

Next, we give the details of Insertion. If the leaf node where the new data block will be inserted is not full, the procedure is the same as Modification. Otherwise, the leaf node needs to be split, and then the entry that leads to this leaf node will also be split into two entries, with one entry leading to each leaf node. Note that unlike operations on standard B+ tree, we don’t copy the index of the third entry (i.e., the index of the new generated node) to its parent’s node. Instead, we simply create a new entry with a pointer leading to the node and record the corresponding information as defined above. If the root node needs to be divided, the depth of this Merkle tree will increment by 1. An example of updating is shown as Fig. 1b and c. Say the client wants to insert a new file block $F_{10}$ in the 7-th position. First, it locates the position in the way mentioned above. Note that we can locate the 6-th position or the 7-th position. Here we choose to locate the 6-th position and insert a new entry $w_{10}$ behind $w_6$ in left node $W_2$ . (If choosing to locate the 7-th position, one should put the new entry before $w_7$.) Next, the information corresponding to this new file block $F_{10}$ will be written into entry $w_{10}$ with a pointer pointing from $w_{10}$ to $F_{10}$, as shown in Fig. 1b. Since it exceeds the maximum number of entries that a node can have, this leaf node $W_2$ needs to be split into two leaf nodes, $W'_2$ and $W_4$ with two non-empty entries in each node (this conforms to the rules of updating a B+ tree), as shown in Fig. 1c. At the same time, a new entry $v_4$ is created in the root node R with a pointer leading $v_4$ to leaf node $W_4$. Similarly, this root node R is split into two internal nodes, $V_1$ and $V_1$. Finally, a new root note $R'$ is built, which has two entries and two pointers leading to $V_1$ and $V_2$, respectively. Note that, now the root node has entries $r_1$ and $r_2$, where $r_1$ is the start entry of this tree, meaning $low(r_1) = 1$. We also have $rank(r_1) = rank(V_1) = rank(v_1) + rank(v_2) = 5$ and $rank(r_2) = 5$.

4.3 Security Proofs

Theorem 1

The proposed static PoR scheme satisfied Authenticity as specified in Sect. 3.1, assuming the existence of secure indistinguishability obfuscators, existentially unforgeable signature schemes and secure puncturable PRFs.

Theorem 2

The proposed static PoR scheme satisfies Retrievability as specified in Sect. 3.1.

The detailed proof for Theorem 1 is given in the full version of this paper [23]. The proof for Theorem 2 will be identical to that in [6], because in our scheme, a file is processed using erasure code before being divided into n blocks, the same as that in [6] where the proof was divided into two parts, Sects. 4.2 and 4.3.

5 Analysis and Comparisons

In this section, we give an analysis of our proposed scheme and then compare it with other two recently proposed schemes.

Our scheme requires the data owner to generate an obfuscated program during the preprocessing stage of the system. With the current obfuscator candidate, it indeed costs the data owner a somewhat large amount of overhead, but this is a one-time effort which can be amortized over plenty of operations in the future. Thus, we focus on the analysis on the computation and communication overheads incurred during writing and auditing operations rather than those in the preprocessing step. Like the private PoR system in [6] the data owner can efficiently store files on the cloud server, and it takes the cloud server less overhead during an auditing protocol than in a public-key-based scheme. The cost on the client device is mainly incurred by the operations over symmetric key primitives, which are known to be much faster than public key cryptographic primitives. The cost analysis on the server side is shown as Table 1.

Table 1. Comparison with existing dynamic PoRs.

In Table 1 showing a comparison with existing dynamic PoR schemes we let $\beta$ be the block size in number of bits, $\lambda$ be the security parameter and n be the number of blocks. We compare our scheme with the state-of-the-art scheme [18], since a comparison between Shi et al.’s scheme and Cash et al.’s scheme is given in [18]. Note that Shi et al.’s scheme needs amortized cost $O(\beta \log n)$ for writing on the server side, due to the fact that an erasure-coding needs to be done on the entire data file after $\varTheta (n)$ updates, while our scheme uses an erasure code that works on file blocks, instead of taking the entire file as inputs (more details and discussions can be found in Sect. 4). That means, in our system modifying a block does not require a change of the erasure codes of the entire file. Thus, the cost for writing is only proportional to the block size being written. On the other hand, during an auditing protocol, Shi et al.’s scheme incurs overhead $O(\beta \lambda \log n)$ on the server side, due to the features of the server-side storage layout. In their scheme, one single file will be stored as three parts, including raw data part R, erasure-coded copy of the entire file C and hierarchical log structure part H that stores the up-to-date file blocks in erasure-coded format. Thus, during one auditing operation, Shi et al.’s scheme needs to check $O(\lambda )$ random blocks from C and $O(\lambda )$ random blocks from each filled level in H. While, in our scheme, the server performs every writing over the wanted block directly, not storing the update block separately. Thus, our scheme only requires $O(\lambda )$ random blocks of one file to check authenticity during auditing. (Note that this $O(\lambda )$ usually would be $\Omega (\sqrt{n\beta })$ if no pseudorandom permutation over the locations of the file blocks is performed, because a small number proportional to $O(\lambda )$ might render the system insecure. Please refer to [17] for more details.) Note that it is most likely that the auditing protocol is executed between a well-equipped verification machine and the server, and the operations on server side only involve symmetric key primitives. Therefore, it will not have noticeable effects on the system’s overall performance.

Clearly, the improvement in our work mainly results from $i \mathcal {O}$’s power that secret keys can be embedded into the obfuscated verification program without secret keys being learnt by user. However, the current obfuscator candidate [2] provides a construction running in impractical, albeit polynomial, time. (Note that it is reasonable and useful that the obfuscated program is run on well-equipped machines.) Although $i \mathcal {O}$’s generation and evaluation is not fast now [30], studies on implementing practical obfuscation are developing fast [31]. It is plausible that obfuscations with practical performance will be achieved in the not too distant future. Note that the improvement on obfuscation will directly lead to an improvement on our schemes.

6 Conclusions

In this paper, we explore indistinguishability obfuscation to construct a publicly verifiable Proofs-of-Retrievability (PoR) scheme that is mainly built upon symmetric key cryptographic primitives. We also show how to modify the proposed scheme to support dynamic updates using a combination of a modified B+ tree and a standard Merkle hash tree. By analysis and comparisons with other existing schemes, we show that our scheme is efficient on the data owner side and the cloud server side. Although it consumes a somewhat large amount of overheads to generate an obfuscation, it is only a one-time effort during the preprocessing stage of the system. Therefore, this cost can be amortized over all of future operations. Also note that the improvement on obfuscation will directly lead to an improvement on our schemes.

A Discussions and Future Directions Towards \(i \mathcal {O}\)

As pointed out in [2], the current obfuscation constructions runs in impractical polynomial-time, and it is an important objective to improve the efficiency for $i \mathcal {O}$ usage in real life applications. Also Apon et al.’s showed the inefficiency in $i \mathcal {O}$’s generation and evaluation in [30]. In this section, we give discussions on three possible future directions in Obfuscation, in addition to those in [2].

1.1 A.1 Outsourced and Joint Generation of Indistinguishability Obfuscation

Image the scenario in our proposed publicly verifiable PoR system, where users store their data on the same cloud server using the same PoR scheme but with different secret keys. One naive approach with $i \mathcal {O}$ would be requiring each user to generate his/her own individual obfuscated program for public verification. This means that each user needs to afford the prohibitively expensive overhead for $i \mathcal {O}$’s generation on his/her own. Note that for the same PoR scheme, the verification procedures are the same but with different user’s secret key. Also note that each user “embeds” his/her own secret keys into the obfuscated verification in a way that anyone else can’t learn anything about the embedded secret values. Hence, we can have several users jointly and securely generate one obfuscated verification program, where each user uses his/her own secret key as part of the input to the generation. One promising way could be using Secure multiparty computation. Observe that this generated obfuscated program has almost the same computation as the one with only one user’s secret key embedded. The only differences between this jointly generated obfuscation and the individual-user-generated obfuscation are that (1) the jointly generated obfuscation is implanted with more than one user’s secret key; (2) the jointly generated obfuscation needs one more step to identify which user’s secret key it will use.

On the other hand, outsourced computing is useful in applications where relatively low-power devices need to compute expensive and time-consuming functions. Clearly, as for relatively low-power individual computers, the overhead caused by the current $i \mathcal {O}$ construction candidate is impractical. Thus, it would be promising to find a specific way to efficiently outsource $i \mathcal {O}$’s generation.

1.2 A.2 Reusability and Universality of Indistinguishability Obfuscation

Reusability is related to $i \mathcal {O}$’s joint generation to some extent. In the scenario considered above, the jointly generated obfuscated program is embedded with a group of users’ private key. This means that the same obfuscated program can be used by verifiers on behalf of different users in this group.

Universality is relevant to an obfuscated program’s functionalities. More Concretely, an universal $i \mathcal {O}$ is supposed to support multiple functionalities. A straightforward example would be the obfucation-based functional encryption scheme in [2]. Recall that in their construction, the secret key $sk_f$ for a function f is an obfuscated program. For this obfuscated program to become universal, $sk_f$ would need to be associated with more than one function. In this case, e.g., an universal obfuscated program $sk_f$ can be associated with a class of similar functions $f = (f_1, f_2, \cdots , f_k)$. This means that $sk_f$’s holder can obtain $f_1(m), f_2(m), \cdots , f_k(m)$ from an encryption of m.

Recently, Hohenberger et al. [32] has shown that $i \mathcal {O}$ can provide some other cryptographic primitives with universality. They employed $i \mathcal {O}$ to construct universal signature aggregators, which can aggregate across schemes in various algebraic settings (e.g., RSA, BLS). Prior to this universal signature aggregator, the aggregation of signatures can only be built if all the signers use the same signing algorithm and shared parameters. On the contrary, the universal signature aggregator enables the aggregation of the users’ signatures without requiring them to execute the same signing behavior, which indicates a compressed authentication overhead.

1.3 A.3 Obfuscation for Specific Functions

The current $i \mathcal {O}$ construction candidate provides a way for obfuscating general circuits and runs in impractical polynomial-time. Note that an obfuscation designed for some particular simple function with practical performance, such as computing two vectors’ inner product, can also be wanted. (like Wee’s work in STOC’05 [33]) This means that we want to obfuscate such simple functions in a practical way that might be specific for those functions. Note that, for example, a practical obfuscated program computing the inner product of two vectors, where one vector is an input to this program and the other one is embedded into the program without user learning its knowledge, could be useful in applications like computational biometrics. Also, it is really likely that such a practical obfuscation for a specified function can be used as a building block to construct an obfuscation supporting more complex functionalities by combining with other existing practical cryptographic primitives.