Enhancing the Efficiency of the Interval-Valued Fuzzy Rule-Based Classifier with Tuning and Rule Selection

Abstract

Interval-Valued fuzzy rule-based classifier with TUning and Rule Selection, IVTURS, is a state-of-the-art fuzzy classifier. One of the key point of this method is the usage of interval-valued restricted equivalence functions because their parametrization allows one to tune them to each problem, which leads to obtaining accurate results. However, they require the application of the exponentiation several times to obtain a result, which is a time demanding operation implying an extra charge to the computational burden of the method.

In this contribution, we propose to reduce the number of exponentiation operations executed by the system, so that the efficiency of the method is enhanced with no alteration of the obtained results. Moreover, the new approach also allows for a reduction on the search space of the evolutionary method carried out in IVTURS. Consequently, we also propose four different approaches to take advantage of this reduction on the search space to study if it can imply an enhancement of the accuracy of the classifier. The experimental results prove: 1) the enhancement of the efficiency of IVTURS and 2) the accuracy of IVTURS is competitive versus that of the approaches using the reduced search space.

1 Introduction

Classification problems [10], which consist of assigning objects into predefined groups or classes based on the observed variables related to the objects, have been widely studied in machine learning. To tackle them, a mapping function from the input to the output space, called classifier, needs to be induced applying a learning algorithm. That is, a classifier is a model encoding a set of criteria that allows a data instance to be assigned to a particular class depending on the value of certain variables.

Fuzzy Rule-Based Classification Systems (FRBCSs) [16] are applied to deal with classification problems, since they obtain accurate results while providing the user with a model composed of a set of rules formed of linguistic labels easily understood by humans. Interval-Valued FRBCSs (IVFRBCSs) [21], are an extension of FRBCSs where some (or all) linguistic labels are modelled by means of Interval-Valued Fuzzy Sets (IVFSs) [19].

IVTURS [22] is a state-of-the-art IVFRBCS built upon the basis of FARC-HD [1]. First, the two first steps of FARC-HD are applied to learn an initial fuzzy rule base, which is augmented with IVFSs to represent the inherent ignorance in the definition of the membership functions [20]. One of the key components of IVTURS is its Fuzzy Reasoning Method (FRM) [6], where all the steps consider intervals instead of numbers. When the matching degree between an example and the antecedent of a rule has to be computed, IVTURS makes usage of Interval-Valued Restricted Equivalence Functions (IV-REFs) [18]. These functions are introduced to measure the closeness between the interval membership degrees and the ideal ones, [1, 1]. Their interest resides in their parametric construction method, which allows them to be optimized for each specific problem. In fact, the last step of IVTURS applies an evolutionary algorithm to find the most appropriate values for the parameters used in their construction.

However, the accurate results obtained when using IV-REFs comes at the price of the computational cost. To use an IV-REF it is necessary to apply several exponentiation operations, which are very time demanding. Consequently, the aim of this contribution is to reduce the run-time of IVTURS by decreasing the number of exponentiation operations required to obtain the same results. To do so, we propose two modifications:

• A mathematical simplification of the construction method of IV-REFs, which allows one to reduce to half the number of exponentiation operations.

• Add a verification step to avoid making computations both with incompatible interval-valued fuzzy rules as well as with do not care labels.

Moreover, the mathematical simplification also offers the possibility of reducing the search space of the evolutionary process carried out in IVTURS. This reduction may imply a different behaviour of the classifier, which may derive to an enhancement of the results. In this contribution, we propose four different approaches to explore the reduced search space for the sake of studying whether they allow one to improve the system’s performance or not.

We use the same experimental framework that was used in the paper where IVTURS was defined [22], which consist of twenty seven datasets selected from the KEEL data-set repository [2]. We will test whether our two modifications reduce the run-time of IVTURS and the reduction rate achieved as well as the performance of the four different approaches considered to explore the reduced search space. To support our conclusions, we conduct an appropriate statistical study as suggested in the literature [7, 13].

The rest of the contribution is arranged as follows: in Sect. 2 we recall some preliminary concepts on IVFSs, IV-REFs and IVTURS. The proposals for speeding IVTURS up and those to explore the reduced search space are described in Sect. 3. Next, the experimental framework and the analysis of the results are presented in Sects. 4 and 5, respectively. Finally, the conclusions are drawn in Sect. 6.

2 Preliminaries

In this section, we review several preliminary concepts on IVFSs (Sect. 2.1), IV-REFs (Sect. 2.2) and IVFRBCSs (Sect. 2.3).

2.1 Interval-Valued Fuzzy Sets

This section is aimed at recalling the theoretical concepts related to IVFSs. We start showing the definition of IVFSs, whose history and relationship with other type of FSs as interval type-2 FSs can be found in [4].

Let L([0, 1]) be the set of all closed subintervals in [0, 1]:

$$\begin{array}{ll}&L([0,1])=\{\text{ x }=[\underline{x}, \overline{x}]|(\underline{x},\overline{x})\in [0,1]^2 \text{ and } \underline{x}\le \overline{x}\}.\end{array}$$

Definition 1

 [19] An interval-valued fuzzy set A on the universe $U\ne \emptyset$ is a mapping $A_{IV}:U\rightarrow L([0,1])$, so that

$$A_{IV}(u_i)=[\underline{A}(u_i),\overline{A}(u_i)]\in L([0,1]), \text{ for } \text{ all } u_i\in U.$$

It is immediate that $[\underline{A}(u_i),\overline{A}(u_i)]$ is the interval membership degree of the element $u_i$ to the IVFS A.

In order to model the conjunction among IVFSs we apply t-representable interval-valued t-norms [9] without zero divisors, that is, they verify that ${\text{ T }}(\text{ x },\text{ y })=0_L$ if and only if $\text{ x }=0_L$ or $\text{ y }=0_L$. We denote them $\mathbf{T} _{T_{a},T_{b}}$, since they are represented by $T_{a}$ and $T_{b}$, which are the t-norms applied over the lower and the upper bounds, respectively. That is, $\mathbf{T} _{T_{a},T_{b}}(\mathbf{x},\mathbf{y})=[T_a(\underline{x},\underline{y}), T_b(\overline{x},\overline{y}]$. Furthermore, we need to use interval arithmetical operations [8] to make some computations. Specifically, the interval arithmetic operations we need in the work are:

• Addition: $[\underline{x}, \overline{x}]+[\underline{y}, \overline{y}] = [\underline{x}+\underline{y}, \overline{x}+\overline{y}]$.

• Multiplication: $[\underline{x}, \overline{x}]*[\underline{y}, \overline{y}] = [\underline{x}*\underline{y}, \overline{x}*\overline{y}]$.

• Division: $\frac{[\underline{x}, \overline{x}]}{ [\underline{y}, \overline{y}]} = [\min (\min (\frac{\underline{x}}{\underline{y}},\frac{\overline{x}}{\overline{y}}),1), \min (\max (\frac{\underline{x}}{\underline{y}},\frac{\overline{x}}{\overline{y}}), 1)] \text{ with } {\underline{y}} \ne 0$.

where $[\underline{x}, \overline{x}]$, $[\underline{y}, \overline{y}]$ are two intervals in $\mathbb {R}^+$ so that x is larger than y.

Finally, when a comparison between interval membership degrees is necessary, we use the total order relationship for intervals defined by Xu and Yager [23] (see Eq. (1)), which is also an admissible order [5].

$$\begin{aligned}{}[\underline{x}, \overline{x}] \le [\underline{y}, \overline{y}] \text{ if } \text{ and } \text{ only } \text{ if } \underline{x} + \overline{x} < \underline{y} + \overline{y} \text{ or } \underline{x} + \overline{x} = \underline{y} + \overline{y} \text{ and } \overline{x} - \underline{x} \ge \overline{y} - \underline{y} \end{aligned}$$

(1)

Using Eq. (1) it is easy to observe that $0_L = [0, 0]$ and $1_L = [1, 1]$ are the smallest and largest elements in L([0, 1]), respectively.

2.2 Interval-Valued Restricted Equivalence Functions

In IVTURS [22], one of the key components are the IV-REFs [11, 18], whose aim is to quantify the equivalence degree between two intervals. They are the extension on IVFSs of REFs [3] and their definition is as follows:

Definition 2

 [11, 18] An Interval-Valued Restricted Equivalence Function (IV-REF) associated with a interval-valued negation N is a function

$$IV\text{- }REF: L([0,1])^{2} \rightarrow L([0,1])$$

so that:

• (IR1) $IV\text{- }REF(\mathbf{x} ,\mathbf{y} )=IV\text{- }REF(\mathbf{y} ,\mathbf{x} )$ for all $\mathbf{x} ,\mathbf{y} \in L([0,1])$;

• (IR2) $IV\text{- }REF(\mathbf{x} ,\mathbf{y} )=1_L$ if and only if $\mathbf{x} =\mathbf{y}$;

• (IR3) $IV\text{- }REF(\mathbf{x} ,\mathbf{y} )=0_L$ if and only if $\mathbf{x} =1_L$ and $\mathbf{y} =0_L$ or $\mathbf{x} =0_L$ and $\mathbf{y} =1_L$;

• (IR4) $IV\text{- }REF(\mathbf{x} ,\mathbf{y} )=IV\text{- }REF(N(\mathbf{x} ),N(\mathbf{y} ))$ with N an involutive interval-valued negation;

• (IR5) For all $\mathbf{x} ,\mathbf{y} ,\mathbf{z} \in L([0,1])$, if $\mathbf{x} \le _L \mathbf{y} \le _L \mathbf{z}$, then $IV\text{- }REF(\mathbf{x} ,\mathbf{y} ) \ge _L IV\text{- }REF(\mathbf{x} ,\mathbf{z} )$ and $IV\text{- }REF(\mathbf{y} ,\mathbf{z} ) \ge _L IV\text{- }REF(\mathbf{x} ,\mathbf{z} )$.

In this work we use the standard negation, that is, $N(x) = 1 - x$.

An interesting feature of IV-REFs is the possibility of parametrize them by means of automorphisms as follows.

Definition 3

An automorphism of the unit interval is any continuous and strictly increasing function $\phi :[0,1]\rightarrow [0,1]$ so that $\phi (0)=0$ and $\phi (1)=1$.

An easy way of constructing automorphisms is by means of a parameter $\lambda \in (0,\infty )$: $\varphi (x) = x^\lambda$, and hence, $\varphi ^{-1}(x) = x^{{1/\lambda }}$. Some automorphims constructed using different values of the parameter $\lambda$ are shown in Fig. 1.

Fig. 1.

Example of different automorphisms generated by different values of $\lambda$.

Then, the construction method of IV-REFs used in IVTURS can be seen in Eq. (2):

$$\begin{aligned} \begin{matrix} IV\text{- }REF(\mathbf{x} ,\mathbf{y} )= [T(\phi _{1}^{-1}(1 - |\phi _2(\underline{x}) - \phi _2(\underline{y})|), \phi _{1}^{-1}(1 - |\phi _2(\overline{x}) - \phi _2(\overline{y})|)), \\ S(\phi _{1}^{-1}(1 - |\phi _2(\underline{x}) - \phi _2(\underline{y})|), \phi _{1}^{-1}(1 - |\phi _2(\overline{x}) - \phi _2(\overline{y})|))] \end{matrix} \end{aligned}$$

(2)

where T is the minimum t-norm, S is the maximum t-conorm and $\varphi _1, \varphi _2$ are two automorphisms of the interval [0, 1] parametrized by $\lambda _1$ and $\lambda _2$, respectively. Therefore, the IV-REFs used in IVTURS are as follows:

$$\begin{aligned} \begin{matrix} IV\text{- }REF(\mathbf{x} ,\mathbf{y} )= [\min ((1 - |\underline{x}^{\lambda _2} - \underline{y}^{\lambda _2}|)^{1/\lambda _1}, (1 - |\overline{x}^{\lambda _2} - \overline{y}^{\lambda _2}|)^{1/\lambda _1}), \\ \max ((1 - |\underline{x}^{\lambda _2} - \underline{y}^{\lambda _2}|)^{1/\lambda _1}, (1 - |\overline{x}^{\lambda _2} - \overline{y}^{\lambda _2}|)^{1/\lambda _1})] \end{matrix} \end{aligned}$$

(3)

2.3 Interval-Valued Fuzzy Rule-Based Classification Systems

Solving a classification problem consists in learning a mapping function called classifier from a set of training examples, named training set, that allows new examples to be classified. The training set is composed of P examples, $x_p = (x_{p1}, \ldots , x_{pn}, y_p)$, where $x_{pi}$ is the value of the i-th attribute $(i=1,2,\ldots ,n)$ of the p-th training example. Each example belongs to a class $y_p \in \mathbb {C} = \{C_1,C_2,...,C_m\}$, where m is the number of classes of the problem.

IVFRBCSs are a technique to deal with classification problems [20], where each of the n attributes is described by a set of linguistic terms modeled by their corresponding IVFSs. Consequently, they provide an interpretable model as the antecedent part of the fuzzy rules is composed of a subset of these linguistic terms as shown in Eq. (4).

$$\begin{aligned} \text{ Rule } R_j: \text{ If } x_1 \text{ is } A_{j1} \text{ and } \ldots \text{ and } x_n \text{ is } A_{jn} \text{ then } \text{ Class } \text{= } C_j \text{ with } RW_j \end{aligned}$$

(4)

where $R_j$ is the label of the jth rule, $x = (x_1, \ldots ,x_n)$ is an n-dimensional pattern vector, $A_{ji}$ is an antecedent IVFS representing a linguistic term, $C_j$ is the class label, and $RW_j$ is the rule weight [17].

IVTURS [22] is an state-of-the-art IVFRBCSs, whose learning process is composed of two steps:

• 1. To build an IV-FRBCS. This step involves the following tasks:

  • The generation of an initial FRBCS by applying FARC-HD [1].

  • Modelling the linguistic labels of the learned FRBCS by means of IVFSs.

  • The generation of an initial IV-REF for each variable of the problem.

• 2. To apply an optimization approach with a double purpose:

  • To learn the best values of the IV-REFs’ parameters, that is, the values of the exponents of the automorphisms ($\lambda _1$ and $\lambda _2$).

  • To apply a rule selection process in order to decrease the system’s complexity.

In order to be able to classify new examples, $x_p = (x_{p1},\ldots ,x_{pn})$, IVTURS considers an Interval-Valued Fuzzy Reasoning Method [22] (IV-FRM), which uses the L interval-valued fuzzy rules composing the model as follows:

• 1. Interval matching degree: It quantifies the strength of activation of the if-part for all rules (L) in the system with the example $x_p$:

  $$\begin{aligned} \begin{array}{c} [\underline{{A_j}}(x_p),\overline{{A_j}}(x_p)] = \mathbf{T} _{T_{a},T_{b}}(IV\text{- }REF([\underline{A_{j1}}(x_{p1}),\overline{A_{j1}}(x_{p1})], [1, 1]),\ldots ,\\ IV\text{- }REF([\underline{A_{jn}}(x_{pn}),\overline{A_{jn}}(x_{pn})],[1, 1])), \qquad j = 1,\ldots , L. \end{array} \end{aligned}$$

  (5)

• 2. Interval association degree: for each rule, $R_j$, the interval matching degree is weighted by its rule weight $RW_j = [\underline{RW_j}, \overline{RW_j}]$::

  $$\begin{aligned} \text{[ }\underline{b_j}(x_p),\overline{b_j}(x_p)] = [\underline{\mu _{A_j}}(x_p), \overline{\mu _{A_j}}(x_p)] * [\underline{RW_{j}},\overline{RW_{j}}] \quad j = 1,\ldots , L. \end{aligned}$$

  (6)

• 3. Interval pattern classification soundness degree for all classes. The positive interval association degrees are aggregated by class applying an aggregation function f.

  $$\begin{aligned} \small [\underline{Y_k},\overline{Y_k}] = \displaystyle f_{R_j \in RB; \; C_j=k} ([\underline{b_j}(x_p),\overline{b_j}(x_p)] | [\underline{b_j}(x_p),\overline{b_j}(x_p)] > 0_L), \qquad k = 1, \ldots , m. \end{aligned}$$

  (7)

• 4. Classification. A decision function F is applied over the interval soundness degrees:

  $$\begin{aligned} F([\underline{Y_1},\overline{Y_1}], ..., [\underline{Y_m},\overline{Y_m}]) = \underset{k=1,\ldots ,m}{\text{ arg } \max ([\underline{Y_k},\overline{Y_k}])} \end{aligned}$$

  (8)

3 Enhancing the Efficiency of IVTURS

IVTURS provides accurate results when tackling classification problems. However, we are concerned about its computational burden as it may be an obstacle to use it in real-world problems. The most computationally expensive operation in IVTURS is the exponentiation operation required when computing the IV-REFs, which are constantly used in the IV-FRM (Eq. (5)). Though there are twelve exponentiation operations in Eq. (3), only four of them need to be computed because: 1) $\underline{y}=\overline{y}=1$, implying that the computation of $\underline{y}^{\lambda _2}$ and $\overline{y}^{\lambda _2}$ can be avoided as one raised to any number is one; 2) the lower and the upper bound of the resulting IV-REF are based on the minimum and maximum of the same operations, which reduces the number of operations to the half.

The aim of this contribution is to reduce the number of exponentiation operations needed to execute IVTURS, which will imply an enhancement of the system’s efficiency. To do so, we propose two modifications to the original IVTURS: 1) to apply a mathematical simplification of the IV-REFs that reduces to half the number of exponentiation operations (Sect. 3.1) and 2) to avoid applying IV-REFs with both do not care labels and incompatible interval-valued fuzzy rules (Sect. 3.2).

Furthermore, the mathematical simplification of IV-REFs, besides reducing the number of exponentiation operations while obtaining the same results, would also allow us to also reduce the search space of the evolutionary algorithm, possibly implying in a different behavior in the system. We will study whether this reduction of the search space could result in a better performance of the system by using four different approaches to explore it (Sect. 3.3).

3.1 IV-REFs Simplification

IV-REFs are used to measure the degree of closeness (equivalence) between two intervals. In IVTURS, they are used to compute the equivalence between the interval membership degrees and the ideal membership degree, that is, IV-REF$([\underline{x},\overline{x}],[1, 1])$. Precisely, because one of the input intervals is [1, 1], we can apply the following mathematical simplification.

$$\begin{aligned} IV-REF([\underline{x},\overline{x}],[1, 1]) = [(1 - |\underline{x}^{\lambda _2} - 1^{\lambda _2}|)^{{1}/{\lambda _1}}, (1 - |\overline{x}^{\lambda _2} - 1^{\lambda _2}|)^{{1}/{\lambda _1}}] = [\underline{x}^{{\lambda _2}/{\lambda _1}}, \overline{x}^{{\lambda _2}/{\lambda _1}}] \end{aligned}$$

(9)

Therefore, we can obtain the same result by just raising the value of the interval membership degree to the division of both exponents (${\lambda _2}/{\lambda _1}$), which imply reducing to half the number of operations.

3.2 Avoiding Incompatible Rules and Do Not Care Labels

When the inference process is applied to classify a new example, the interval matching degree has to be obtained for each rule of the system. The maximum number of antecedents of the interval-valued fuzzy rules used in IVTURS is limited to a certain hyper-parameter of the algorithm, $k_t$, whose default value is 3. This fact implies that in almost all the classification problems the usage of do not care labels is necessary, since the number of input attributes is greater than that of $k_t$. In order to program this feature of IVTURS, a do not care label is considered as an extra membership function that returns the neutral element for the t-representable interval-valued t-norm used ([1, 1] in this case as the product is applied). In this manner, when performing the conjunction of the antecedents the usage of do not care labels do not change the obtained result. However, this fact implies that when having a do not care label, it returns [1, 1] as interval membership degree and IV-REF ([1, 1], [1, 1]) needs to be computed ($[\underline{x},\overline{x}] = [1, 1]$). Consequently, a large number of exponentiation operations can be saved if we avoid computing IV-REF in this situations as the result is always [1, 1].

On the other hand, we also propose to avoid obtaining the interval matching degree and thus computing the associated IV-REFs when the example is not compatible with the antecedent of the interval-valued fuzzy rule. To do so, we need to perform an initial iteration where we check whether the example is compatible with the rule. Then, the interval matching degree is only computed when they are compatible. This may see to be an extra charge for the run-time but we take advantage of this first iteration to obtain the interval matching degrees, avoiding the do not care labels, and we send them to the function that computes the interval matching degree.

These two modifications could have a huge impact on the run-time of IVTURS because do not care labels are very common in the interval-valued fuzzy rules of the system and the proportion of compatible rules with an example is usually small.

3.3 Reducing the Search Space in the Evolutionary Process of IVTURS

In Sect. 3.1 we have presented a mathematical simplification of the IV-REFs that allows one to reduce the number of exponentiation operations obtaining exactly the same results than that obtained in the original formulation of IVTURS. However, according to Eq. (9) we can observe that both parameters of the simplified IV-REF ($\lambda _1,\lambda _2$) can be collapsed into a unique one ($\lambda$) as shown in Eq. (10).

$$\begin{aligned} IV-REF([\underline{x},\overline{x}],[1, 1]) = [\underline{x}^{{\lambda _2}/{\lambda _1}}, \overline{x}^{{\lambda _2}/{\lambda _1}}] = [ \underline{x}^\lambda , \overline{x}^\lambda ] \end{aligned}$$

(10)

In this manner, the search space of the evolutionary process carried out in IVTURS, where the values of $\lambda _1$ and $\lambda _2$ are tuned to each problem, can be also reduced to half because only the value of $\lambda$ needs to be tuned. Consequently, the behaviour of the algorithm can change and we aim at studying whether this reduction is beneficial or not. Specifically, the structure of the chromosome is: $C_i = (g_{\lambda _1},g_{\lambda _2},\ldots ,g_{\lambda _{n}})$, where $g_{\lambda _i}$, $i = 1,\ldots ,n$, are the genes representing the value of $\lambda _i$ and n is the number of input variables of the classification problem.

The parameter $\lambda$ can vary theoretically between zero and infinity. However, in IVTURS, $\lambda _1$ and $\lambda _2$ are limited to the interval [0.01, 100]. On the other hand, in the evolutionary process, those genes used to encode them are codified in [0.01, 1.99], $g_{\lambda _i}\in [0.01, 1.99]$, in such a way that the chances of learning values in [0.01, 1] and in (1, 100] are the same. Consequently, these genes have to be decoded so that they are in the range [0.01, 100] when used in the corresponding IV-REF. The decoding process is driven by the following equation:

$$\begin{aligned} g_{\lambda _i} = {\left\{ \begin{array}{ll} g_{\lambda _i}, &{} \text{ if } 0< g_{\lambda _i} \le 1 \\ \frac{1}{2-g_{\lambda _i}}, &{} \text{ if } 1< g_{\lambda _i} < 2 \\ \end{array}\right. } \end{aligned}$$

(11)

In [12], Galar et al. use REFs (the numerical counterpart of IV-REFs) to deal with the problem of difficult classes applying the OVO decomposition strategy. In this method, on the one hand, those genes used for representing the parameter $\lambda$ are coded in the range (0, 1). On the other hand, the decoding process of the genes is driven by Eq. 12.

$$\begin{aligned} \lambda _i = {\left\{ \begin{array}{ll} \displaystyle (2 \cdot g_{\lambda _i})^2&{} \text { if } g_{\lambda _i} \le 0.5 \\ \displaystyle \frac{1}{ (1 - 2 \cdot (g_{\lambda _i} - 0.5))^2}&{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(12)

There are two main differences between these two methods: 1) the decoded value by Eq. (11) is in the range [0.01, 100], whereas when using Eq. (12) the values are in $(0, \infty )$ and 2) the search space is explored in a different way as can be seen in the two first rows of Fig. 2, where the left and the right columns show how the final values when $\lambda _i \le 1.0$ and $\lambda _i > 1.0$ are obtained, respectively.

Looking at these two methods, we propose another two new ones:

• Linear exploration of the search space: we encode all the genes in the range [0.01, 1.99] and we decode them using a linear normalization in the ranges [0.0001, 1.0] and (1.0, 10000] for the genes in [0.01, 1.0] and (1.0, 1.99], respectively.

• Mixture of Eq. (11) and Eq. (12). Genes are encoded in (0, 1) and they are decoded using Eq. (11) for genes in (0, 0.5] (linear decoding: $2 \cdot g_{\lambda _i}$)and Eq. (12) for genes in (0.5, 1.0].

Fig. 2.

Effect of the decoding method of the parameter $g_{\lambda }$ on the way how the search space is explored.

4 Experimental Framework

We have considered the same datasets which were used in the paper where IVTURS was proposed. That is, we select twenty-seven real world data-sets from the KEEL data-set repository [2]. Table 1 summarizes their properties: number of examples (#Ex.), attributes (#Atts.) and classes (#Class.)¹. We apply a 5-fold cross-validation model using the standard accuracy rate to measure the performance of the classifiers.

Table 1. Description of the selected data-sets.

In this contribution we use the configuration of IVTURS that was used in the paper were it was defined:

• Fuzzy rule learning:

  • Minsup: 0.05.

  • Maxconf: 0.8.

  • $Depth_{max}$: 3.

  • $k_t$: 2.

• Evolutionary process

  • Population Size: 50 individuals.

  • Number of evaluations: 20,000.

  • Bits per gene for the Gray codification (for incest prevention): 30 bits.

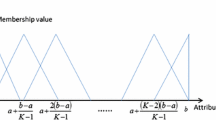
• IVFSs construction:

  • Number of linguistic labels per variable: 5 labels.

  • Shape: Triangular membership functions.

  • Upper bound: 50% greater than the lower bound ($W=0.25$).

• Configuration of the initial IV-REFs:

  • T-norm: minimum.

  • T-conorm: maximum.

  • First automorphism: $\phi _1(x)=x^1$ (a = 1).

  • Second automorphism: $\phi _2(x)=x^1$ (b = 1).

• Rule weight: fuzzy confidence (certainty factor) [17].

• Fuzzy reasoning method: additive combination [6].

• Conjunction operator: product interval-valued t-norm.

• Combination operator: product interval-valued t-norm.

5 Analysis of the Obtained Results

This section is aimed at showing the obtained results having a double aim:

• 1. To check whether the two modifications proposed for enhancing the run-time of IVTURS allow one to speed it up or not.

• 2. To study if the reduction of the search space made possible by the mathematical simplification of the IV-REFs allows one to improve the results of IVTURS.

In first place we show in Table 2 the run-time in seconds of the three versions of IVTURS², namely, the original IVTURS, IVTURS using the mathematical simplification of the IV-REFs ($IVTURS_{v1}$) and IVTURS avoiding the usage of incompatible interval-valued fuzzy rules and do not care labels ($IVTURS_{v2}$). For $IVTURS_{v1}$, the number in parentheses is the reduction rate achieved versus the original IVTURS, whereas in the case of $IVTURS_{v2}$ it is the reduction rate achieved with respect to $IVTURS_{v1}$.

Table 2. Run-time in seconds of IVTURS besides the two versions developed for speeding it up. The number in parentheses shows the reduction rate of the method in the column versus the method in its respective left column.

Looking at the obtained results we can conclude that the two versions allow IVTURS to be more efficient. In fact, $IVTURS_{v1}$ allows one to reduce to half the run-time of IVTURS as expected, since the number of exponentiation operations is also reduced to half. On the other hand, $IVTURS_{v2}$ exhibits a huge reduction on the run-time with respect to that of the original IVTURS as it is 7.839 times faster (1.95*4.02). These modifications allow IVTURS to be applied in a wider range of classification problems as its efficiency has been notably enhanced. The code of the IVTURS method using the two modification for speeding it up can be found at: https://github.com/JoseanSanz/IVTURS.

The second part of the study is to analyze whether the reduction of the search space enabled by the mathematical simplification if the IV-REFs allows one to improve the accuracy of the system or not. As we have explained in Sect. 3.3, we propose four approaches to codify and explore the reduced search space: 1) the same approach than that used in the original IVTURS but using the reduced search space (IVTURS$_{Red.}$); 2) the approach defined by Galar et al. [12] but extended on IVFSs (IVTURS$_{Galar}$); 3) the mixture of the two previous approaches (IVTURS$_{Mix.}$) and 4) the linear exploration of the search space (IVTURS$_{Linear}$).

In Table 3 we show the results obtained in testing by these four approach besides those obtained by the original IVTURS. We stress in bold-face the best result for each dataset. Furthermore, we also show the averaged performance in the 27 datasets (Mean).

Table 3. Testing results provided by IVTURS and the four approaches using the reduced search space.

According to the results shown in Table 3, we can observe that both methods using the approach defined by Galar et al. (IVTURS$_{Galar}$ and IVTURS$_{Mix.}$) allows one to improve the averaged accuracy of IVTURS. The reduction of the search space using the original approach defined in IVTURS, IVTURS$_{Red.}$, does not provide competitive results whereas the approach using a linear exploration of the search space also obtains worse results than those of the original IVTURS.

In order to give statistical support to our analysis we have carried out the Aligned Friedman’s ranks test [14] to compare these five methods, whose obtained p-value is 1.21E-4 that implies the existence of statistical differences among them. For this reason, we have applied the Holm’s post hoc test [15] to compare the control method (the one associated with the less rank) versus the remainder ones. In Table 4, we show both the ranks of the methods computed by the Aligned Friedman’s test as well as the Adjusted P-Value (APV) obtained when applying the Holm’s test.

Table 4. Results obtained by the Aligned Friedman’s rank test and the Holm’s test.

Looking at the results of the statistical study we can conclude that IVTURS, IVTURS$_{Mix.}$ and IVTURS$_{Galar.}$ are statistically similar. However, there are statistical differences with respect to IVTURS$_{Red.}$ and a trend in favour to the three former methods when compared versus IVTURS$_{Linear}$. All in all, we can conclude that the approach defined in the original IVTURS provides competitive results even when compared against methods whose search space is reduced to half.

6 Conclusion

In this contribution we have proposed two modifications over IVTURS aimed at enhancing its efficiency. On the one hand, we have used a mathematical simplification of the IV-REFs used in the inference process. On the other hand, we avoid making computations with both incompatible interval-valued fuzzy rules and do not care labels, since they do not affect the obtained results and they entail a charge to the computational burden of the method. Moreover, we have proposed a reduction of the search space of the evolutionary process carried out in IVTURS using four different approaches.

The experimental results have proven the improvement of the run-time of the method, since it is almost eight times faster that the original IVTURS when applying the two modifications. Regarding the reduction of the search space we have learned the following lessons: 1) the new methods based on the approach defined by Galar et al. allow one to improve the results without statistical differences versus IVTURS; 2) the simplification of the search space using the same setting defined in IVTURS does not provide competitive results, possibly due to the limited range where the genes are decoded when compared with respect the remainder approaches and 3) the linear exploration of the search space does not provide good results neither, which led us think that the most proper values are closer to one than to $\infty$.