New Methods for Comparing Interval-Valued Fuzzy Cardinal Numbers

Abstract

In this contribution the concept how to solve the problem of comparability in the interval-valued fuzzy setting and its application in medical diagnosis is presented. Especially, we consider comparability of interval-valued fuzzy sets cardinality, where order of its elements is most important. We propose an algorithm for comparing interval-valued fuzzy cardinal numbers (IVFCNs) and we evaluate it in a medical diagnosis decision support system.

This work was partially supported by the Centre for Innovation and Transfer of Natural Sciences and Engineering Knowledge of University of Rzeszów, Poland, the project RPPK.01.03.00-18-001/10.

1 Introduction

Many new methods and theories behaving imprecision and uncertainty have been proposed since fuzzy sets were introduced by Zadeh [26]. Extensions of classical fuzzy set theory, intuitionistic fuzzy sets [3] and interval-valued fuzzy sets [22, 25] are very useful in dealing with imprecision and uncertainty (cf. [5] for more details). In this setting, different proposals for comparability relations between interval-valued fuzzy sets have been proposed (e.g. [23, 30]). However, the motivation of the present paper is to propose a new methods to comparability between interval-valued fuzzy sets (and their special type which are interval-valued fuzzy cardinal numbers) taking into account the widths of the intervals. We assume that the precise membership degree of an element in a given set is a number included in the membership interval. For such interpretation, the width of the membership interval of an element reflects the lack of precise membership degree of that element. Hence, the fact that two elements have the same membership intervals does not necessarily mean that their corresponding membership values are the same. This is why we have taken into account the importance of the notion of width of intervals while proposing new algorithms.

Additionally, these developments are made according to the standard partial order between intervals, but also with respect to admissible orders [6], which are linear.

The paper is organized as follows. In Sect. 2 basic information on interval-valued setting are recalled. Especially, orders in interval setting and aggregation operators based on them are considered. Afterwards, in Sect. 3 we propose algorithm to compare interval values and finally in Sect. 4 we present mentioned methodology for comparing IVFCNs in the decision making used in the OvaExpert system (intelligent decision support system for the diagnosis of ovarian tumors) (see [12, 13, 29]).

2 Preliminaries

Firstly, we recall some facts from interval-valued fuzzy set theory.

2.1 Orders in the Interval-Valued Fuzzy Settings

Definition 1

(cf. [22, 25]). An interval-valued fuzzy set IVFS $\widetilde{A}$ in X is a mapping $\widetilde{A}: X \rightarrow L^I$ such that $\widetilde{A}(x) =[\underline{A}(x),\overline{A}(x)] \in L^I$ for $x \in X$, where

$$\widetilde{A}\cap \widetilde{B} = \big \{\langle x, \big [\min \{\underline{A}(x),\underline{B}(x)\}, \min \{\overline{A}(x),\overline{B}(x)\}\big ]\rangle :x\in X\big \}, $$

$$\widetilde{A}\cup \widetilde{B} = \big \{\langle x, \big [\max \{\underline{A}(x),\underline{B}(x)\}, \max \{\overline{A}(x),\overline{B}(x)\}\big ]\rangle :x\in X\big \}$$

and

$$L^I=\{[\underline{x},\overline{x}]:\;\underline{x},\overline{x}\in [0,1], \;\underline{x}\le \overline{x}\}.$$

The well-known classical monotonicity (partial order) for intervals is of the form

$$\begin{aligned}{}[\underline{x},\overline{x}]\le _{L^I} [\underline{y},\overline{y}] \Leftrightarrow \underline{x}\le \underline{y}, \; \overline{x}\le \overline{y}, \end{aligned}$$

where $[\underline{x},\overline{x}]<_{L^I} [\underline{y},\overline{y}]\Leftrightarrow$ $[\underline{x},\overline{x}] \le _{L^I} [\underline{y},\overline{y}] \;\;and\;\;(\underline{x}< \underline{y}\;\;or \;\;\overline{x} < \overline{y}).$

In $L^I$ the operations joint and meet are defined respectively

$$ [\underline{x},\overline{x}] \vee [\underline{y},\overline{y}] =[\max (\underline{x},\underline{y}),\max (\overline{x},\overline{y})], $$

$$ [\underline{x},\overline{x}] \wedge [\underline{y},\overline{y}] =[\min (\underline{x},\underline{y}),\min (\overline{x},\overline{y})]. $$

Note that the structure ($L^I, \vee , \wedge$) is a complete lattice, with the partial order $\le _{L^I}$, where

$$\mathbf 1 =[1,1]\;\; and \;\;\mathbf 0 = [0,0]$$

are the greatest and the smallest element of $(L^I, \le _{L^I})$, respectively.

We are interested in extending the partial order $\le _{L^I}$ to a linear order, solving the problem of existence of incomparable elements. We recall the notion of an admissible order, which was introduced in [6] and studied, for example, in [2] and [27]. The linearity of the order is needed in many applications of real problems, in order to be able to compare any two interval data [7].

Definition 2

(cf. [6]). An order $\le _{Adm}$ in $L^I$ is called admissible if it is linear and satisfies that for all $x,y \in L^I$, such that $x \le _{L^I} y$, then $x \le _{Adm} y$.

Proposition 1

(cf. [6]). Let $B_1,B_2 : [0,1]^2 \rightarrow [0, 1]$ be two continuous aggregation functions, such that, for all $x = [\underline{x}, \overline{x}], y = [\underline{y}, \overline{y}] \in L^I$, the equalities $B_1(\underline{x}, \overline{x}) = B_1(\underline{y}, \overline{y})$ and $B_2(\underline{x}, \overline{x}) = B_2(\underline{y}, \overline{y})$ hold if and only if $x = y$. If the order $\le _{B_{1,2}}$ on $L^I$ is defined by $x\le _{B_{1,2}}y$ if and only if

$$B_1(\underline{x}, \overline{x}) < B_1(\underline{y}, \overline{y}) \;\;\;{or} \;\;\; (B_1(\underline{x}, \overline{x}) = B_1(\underline{y}, \overline{y}) \ \;{and} \ B_2(\underline{x}, \overline{x}) \le B_2(\underline{y}, \overline{y})),$$

then $\le _{B_{1,2}}$ is an admissible order on $L^I$.

Example 1

(cf. [6]). The following are special cases of admissible linear orders on $L^I$:

• The Xu and Yager order:

  $$\begin{aligned}{}[\underline{x},\overline{x}] \le _{XY} [\underline{y}, \overline{y}]\Leftrightarrow&\underline{x}+\overline{x} < \underline{y} +\overline{y}\; or\; (\overline{x} + \underline{x} = \overline{y} + \underline{y}\;\; and \;\;\overline{x} - \underline{x} \le \overline{y} - \underline{y}). \end{aligned}$$

• The first lexicographical order (with respect to the first variable), $\le _{Lex1}$ defined as:

  $$[\underline{x},\overline{x}] \le _{Lex1} [\underline{y}, \overline{y}]\Leftrightarrow \underline{x} < \underline{y}\; or\; (\underline{x} = \underline{y}\;\; and \;\;\overline{x} \le \overline{y}).$$

• The second lexicographical order (with respect to the second variable), $\le _{Lex2}$ defined as:

  $$[\underline{x},\overline{x}] \le _{Lex2} [\underline{y}, \overline{y}]\Leftrightarrow \overline{x} < \overline{y} \;or\; (\overline{x} = \overline{y}\;\; and \;\;\underline{x} \le \underline{y}).$$

• The ${\alpha \beta }$ order, $\le _{\alpha \beta }$ defined as:

  $$\begin{aligned}{}[\underline{x},\overline{x}] \le _{\alpha \beta } [\underline{y},\overline{y}]\Leftrightarrow&K_{\alpha }(\underline{x},\overline{x}) < K_{\alpha }(\underline{y},\overline{y})\; or\; \\ {}&(K_{\alpha }(\underline{x},\overline{x}) = K_{\alpha }(\underline{y},\overline{y})\; and\; K_{\beta }(\underline{x},\overline{x}) \le K_{\beta }(\underline{y},\overline{y})) \end{aligned}$$

  for some ${\alpha \ne \beta } \in [0, 1]$ and $x, y \in L^I$, where $K_{\alpha }: [0, 1]^2 \rightarrow [0,1]$ is defined as $K_{\alpha }(x, y) = {\alpha }x + (1 -{\alpha })y$.

The orders $\le _{XY}$, $\le _{Lex1}$ and $\le _{Lex2}$ are special cases of the order $\le _{\alpha \beta }$ with $\le _{0.5\beta }$ (for $\beta > 0.5$), $\le _{1,0}$, $\le _{0,1}$, respectively. The orders $\le _{XY}$, $\le _{Lex1}$, $\le _{Lex2}$, and $\le _{\alpha \beta }$ are admissible linear orders $\le _{B_{1,2}}$ defined by pairs of aggregation functions, namely weighted means. In the case of the orders $\le _{Lex1}$ and $\le _{Lex2}$, the aggregations that are used are the projections $P_1$, $P_2$ and $P_2$, $P_1$, respectively.

Remark 1

In the later part we will use the notation $\le$ both for the partial or admissible linear order, with $\mathbf 0$ and $\mathbf 1$ as minimal and maximal element of $L^I$, respectively. Notation $\le _{L^I}$ will be used while the results for the admissible linear orders will be used with the notation $\le _{Adm}$.

2.2 Interval-Valued Aggregation Functions

Let us now recall the concept of an interval-valued aggregation function, or an aggregation function on $L^I$, which is an important notion for many applications. We consider interval-valued aggregation functions both with respect to $\le _{L^I}$ and $\le _{Adm}$. In many papers we may find the study of properties and possible applications of interval-valued operators/aggregation functions (e.g. [4, 5, 7, 14, 18, 20]).

Definition 3

(cf. [16, 27]). An operation $\mathcal {A}: (L^I)^n \rightarrow L^I$ is called an interval-valued aggregation function if it is increasing with respect to the order $\le$ (partial or total) and

$$\mathcal {A}(\underbrace{\mathbf{0 ,...,\mathbf 0 }}_{n \times })=\mathbf 0 ,\;\;\mathcal {A}(\underbrace{\mathbf{1 ,...,\mathbf 1 }}_{n \times })=\mathbf 1 . $$

A special class of interval-valued aggregation functions is the one formed by the so-called representable interval-valued aggregation functions.

Definition 4

(cf. [9, 11]). An interval-valued aggregation function $\mathcal {A}: (L^I)^n\rightarrow L^I$ is said to be representable if there exist aggregation functions $A_1,A_2: [0,1]^n\rightarrow [0,1]$ such that

$$\mathcal {A}(x_1,\ldots ,x_n)=[A_1(\underline{x}_1,\ldots \underline{x}_n),A_2(\overline{x}_1,\ldots ,\overline{x}_n)]$$

for all $x_1,\ldots ,x_n\in L^I$, provided that $A_1 \le A_2.$

Example 2

Lattice operations $\wedge$ and $\vee$ on $L^I$ are examples of representable aggregation functions on $L^I$ with respect to the partial order $\le _{L^I}$, with $A_1=A_2=\min$ in the first case and $A_1=A_2=\max$ in the second one. However, $\wedge$ and $\vee$ are not interval-valued aggregation functions with respect to $\le _{Lex1}$, $\le _{Lex2}$ or $\le _{XY}$.

The following are other examples of representable interval-valued aggregation functions with respect to $\le _{L^I}$.

• The representable arithmetic mean:

  $$\mathcal {A}_{mean}([\underline{x},\overline{x}],[\underline{y},\overline{y}])=[A_{mean}(\underline{x},\underline{y}),A_{mean}(\overline{x},\overline{y})]=[\frac{\underline{x}+\underline{y}}{2},\frac{\overline{x}+\overline{y}}{2}].$$

• The representable geometric mean:

  $$\mathcal {A}_{gmean}([\underline{x},\overline{x}],[\underline{y},\overline{y}])=[A_{gmean}(\underline{x},\underline{y}),A_{gmean}(\overline{x},\overline{y})]=[\sqrt{\underline{x}\underline{y}},\sqrt{\overline{x}\overline{y}}].$$

Representability is not the only possible way to build interval-valued aggregation functions with respect to $\le _{L^I}$. Moreover, we may built interval-valued aggregation functions with respect to the other orders, i.e. $\le _{Adm}$.

Let $A: [0,1]^2\rightarrow [0,1]$ be an aggregation function.

• The function $\mathcal {A}_1: (L^I)^2 \rightarrow L^I$, where

  $$\mathcal {A}_1(x,y)=\left\{ \begin{array}{ll} [1,1], &{} \;if\; (x,y)=([1,1],[1,1]), \\ {} [0,A(\underline{x},\overline{y})], &{} {otherwise} \end{array} \right. $$

  is a non-representable interval-valued aggregation function with respect to $\le _{L^I}$.

• The function $\mathcal {A}_2: (L^I)^2 \rightarrow L^I$ ([19]), where

  $$\mathcal {A}_2(x,y)=\left\{ \begin{array}{ll} [1,1], &{} \;if\; (x,y)=([1,1],[1,1]) \\ {} [0,A(\underline{x},\underline{y})], &{} {otherwise} \end{array} \right. $$

  is non-representable interval-valued aggregation functions with respect to $\le _{Lex1}$.

• $\mathcal {A}_{mean}$ is an aggregation function with respect to $\le _{\alpha \beta }$ (cf. [2]).

• The following function

  $$\mathcal {A}_{\alpha }(x,y)=[\alpha \underline{x}+(1-\alpha )\underline{y},\alpha \overline{x}+(1-\alpha )\overline{y}]$$

  is an interval-valued aggregation function on $L^I$ with respect to $\le _{Lex1}$, $\le _{Lex2}$ and $\le _{XY}$ for $x,y\in L^I$ and $\alpha \in [0,1]$ (cf. [27]).

3 Subsethood Measure

Subsethood, or inclusion, measures have been studied mainly from constructive and axiomatic approaches and have been introduced successfully into the theory of fuzzy sets and their extensions. Many researchers have tried to relax the rigidity of Zadeh’s definition of subsethood to get a soft approach which is more compatible with the spirit of fuzzy logic. For instance, Zhang and Leung (1996) defended that quantitative methods were the main approaches in uncertainty inference, a key problem in artificial intelligence, so they presented a generalized definition for subsethood measures, called including degrees.

3.1 Precedence Indicator

We use the notion of an interval subsethood measure for a pair of intervals with the partial and admissible orders and the width of intervals introduced and examined in [21].

Definition 5

A function $\mathrm {Prec}: (L^I)^2\rightarrow L^I$ is said to be a precedence indicator if it satisfies the following conditions for any $a,b,c\in L^I$

P1:

if $a=1_{L^I}$ and $b=0_{L^I}$, then $\mathrm {Prec}(a,b)=0_{L^I}$,

P2:

if $a< b$, then $\mathrm {Prec}(a,b)=1_{L^I}$ for any $a,b\in L^I$,

P3:

$\mathrm {Prec}(a,a)=[1-w(a),1]$ for any $a\in L^I$,

P4:

if $a\le b\le c$ and $w(a)=w(b)=w(c)$, then $\mathrm {Prec}(c,a)\le \mathrm {Prec}(b,a)$ and $\mathrm {Prec}(c,a)\le \mathrm {Prec}(c,b)$, for any $a,b,c\in L^I$, where

$$\begin{aligned} w(a)=\overline{a}-\underline{a}. \end{aligned}$$

(1)

The following construction method is based on the aggregation and negation functions which play important rule in many applications (e.g. [4, 9, 11, 14]) and is presented in the next theorem. Recall that an interval-valued fuzzy negation $N_{IV}$ is an antytonic operation that satisfies $N_{IV}({0}_{L^I})={1}_{L^I}$ and $N_{IV}({1}_{L^I})={0}_{L^I}$ ([1, 10]).

Proposition 2

([21]). For $a,b\in L^I$ the operation $\mathrm {Prec}_{\mathcal {A}}: (L^I)^2\rightarrow L^I$ is the precedence indicator

$$\mathrm {Prec}_{\mathcal {A}}(a,b)=\left\{ \begin{array}{ll} [1-w(a),1], &{} a=b,\\ {1}_{L^I}, &{} a<b,\\ \mathcal {A}(N_{IV}(a),b), &{} otherwise \end{array} \right. $$

for $a,b\in L^I$ and the interval-valued fuzzy negation $N_{IV}$, such that

$$N_{IV}(a)=[N(\overline{a}),N(\underline{a})]\le [1-\overline{a},1-\underline{a}],$$

where N is a fuzzy negation and $\mathcal {A}$ is a representable interval-valued aggregation such that $\mathcal {A}\le \vee$.

Using the construction methods from Proposition 2 we obtain the following examples.

Example 3

The following function is an interval subsethood measure with respect to $\le _{L^I}$:

$$\mathrm {Prec}_{\mathcal {A}_{meanL^I}}(x,y)=\left\{ \begin{array}{ll} [1-w(x),1], &{} x=y,\\ \mathbf {1}, &{} x<_{L^I}y,\\ {[\frac{1-\overline{x}+\underline{y}}{2},\frac{1-\underline{x}+\overline{y}}{2}]}, &{} otherwise, \end{array} \right. $$

where $N_{IV}(x)=[1-\overline{x},1-\underline{x}]$.

Moreover, the following function is a subsethood measure with respect to $\le _{Lex2}$:

$$\mathrm {Prec}_{\mathcal {A}_{meanLex2}}(x,y)=\left\{ \begin{array}{ll} [1-w(x),1], &{} x=y,\\ \mathbf {1}, &{} x<_{Lex2}y,\\ {[\frac{\underline{y}}{2},\frac{1-\overline{x}+\overline{y}}{2}]}, &{} otherwise. \end{array} \right. $$

Using the interval-valued aggregation function $\mathcal {A}_{\alpha }$ for $\alpha \in [0,1]$, we get the subsethood measure

$$\mathrm {Prec}_{\mathcal {A}_{\alpha }Lex2}(x,y)=$$

$$\left\{ \begin{array}{ll} [1-w(x),1], &{} x=y,\\ \mathbf {1}, &{} x<_{Lex2}y,\\ {[(1-\alpha )\underline{y},} &{} \\ \qquad {\alpha (1-\overline{x})+(1-\alpha )\overline{y}]}, &{} otherwise, \end{array} \right. $$

where

$$N_{IV}(x)=\left\{ \begin{array}{ll} \mathbf {1}, &{} x=\mathbf {0},\\ {[0,1-\overline{x}]}, &{} otherwise \end{array} \right. $$

is an interval-valued fuzzy negation with respect to $\le _{Lex2}$.

Remark 2

(cf. [27]). The aggregation $\mathcal {A}_{\alpha }$ preserves the width of the intervals of the same width.

Another construction method, which is inspired by the construction presented for generalization of the subsethood measure at paper [21], presents the following proposition.

Proposition 3

The operation

$$\mathrm {Prec}_{w}(a,b)= \left\{ \begin{array}{ll} 1_{L^I}, &{} a<b,\\ {[1-\max (w(a),r(a,b)),1-r(a,b)]}, &{} else \end{array} \right. $$

is the precedence indicator with respect to $\le$, where for $a,b\in L^I$

$r(a,b)=\max \{|\underline{a}-\underline{b}|,|\overline{a}-\overline{b}|\}$.

3.2 Interval-Valued Fuzzy Cardinal Numbers (IVFCNs)

In this section we briefly introduce main ideas about cardinalities of IVFSs. More details can be found in the monographs [12, 24]. Such numbers are of great importance in solving decision problems in which uncertainty occurs (see [8, 15, 28]). In further part we will use the following notations:

• For given fuzzy set A a symbol $[A]_{i}$ is defined as:

  $$\begin{aligned}{}[A]_{i}:=\bigvee \{t\in (0,1]:\;|A_{t}|\ge i\} \text{ for } i\in \mathbb {N}. \end{aligned}$$

• Function $f:[0,1]\rightarrow [0,1]$ is called cardinality pattern if it meets the following conditions:

  • 1. is nondecreasing i.e. $\forall _{a,b\in [0,1]} f(a)\le f(b)$ if $a\le b$,

  • 2. and meets limit conditions $f(0)=0$ i $f(1)=1$.

• Symbol $\cap _T$ means the triangular norm and N the fuzzy negation.

Generalized Fuzzy Cardinal Numbers

• 1. Generalized cardinal number FGCount is interpreted as a degree to which fuzzy set A has at least k elements

  $$FG_f(k):=f([A]_{1}) \cap _T f([A]_{2})\cap _T\ldots \cap _T f([A]_{k}) \; \text {for}\; k \in \mathbb {N}.$$

• 2. Generalized cardinal number FLCount is interpreter as a degree to which A includes at most k elements

  $$FL_f(k):=N(f([A]_{k+1}))\cap _T N(f([A]_{k+2}))\cap _T\cdot \cap _T \; N(f([A]_{n})) \; \text {for}\; k \in \mathbb {N}.$$

• 3. Generalized cardinal number FECount expresses the degree to which A has exactly k elements where

  $$FE_f (k):=f([A]_{1})\cap _T f([A]_{2})\cap _T\ldots \cap _T f([A]_{k})\cap _T$$
  $$N(f([A]_{k+1}))\cap _T N(f([A]_{k+2}))\cap _T\ldots \cap _T N(f([A]_{n})) \; \text {for}\; k \in \mathbb {N}.$$

$FE_f$ is the intersection of $FG_f$ and $FL_f$. It may be perceived as the ‘actual’ generalized cardinal number of a fuzzy set A.

Fuzzy Cardinality of IVFS. Cardinalities of interval-valued fuzzy sets are defined in a natural manner using cardinalities of fuzzy sets described in previous section.

For a finite interval-valued fuzzy set $\widetilde{A}=[\underline{A}, \overline{A}]$ fuzzy type cardinalities are defined as interval-valued fuzzy sets in $\mathbb {N}$ (see [24]).

Definition 6

(cf. [12, 24]).

• 1. f-FGCount of IVFS $\widetilde{A}$ for a given cardinality pattern f is defined as:

  $$\begin{aligned} \widetilde{FG}_f(\widetilde{A})=[FG_f(\underline{A}),FG_f(\overline{A})], \end{aligned}$$

  (2)

  i.e. for $k\in \mathbb {N}$:

  $$\begin{aligned} \begin{aligned} \widetilde{FG}_f(\widetilde{A})(k)=&[FG_f(\underline{A})(k),FG_f(\overline{A})(k)]= [f([\underline{A}]_k),f([\overline{A}]_k)], \end{aligned} \end{aligned}$$

  (3)

  where $FG_f(\underline{A})$ and $FG_f(\overline{A})$ are the fuzzy cardinalites defined in previous section.

• 2. f-FLCount of IVFS $\widetilde{A}$ for a given cardinality pattern f is defined as:

  $$\begin{aligned} \widetilde{FL}_f(\widetilde{A})=[FL_f(\overline{A}),FL_f(\underline{A})], \end{aligned}$$

  (4)

  i.e. for $k\in \mathbb {N}$:

  $$\begin{aligned} \begin{aligned} \widetilde{FL}_f(\widetilde{A})(k)=&[FL_f(\underline{A})(k),FL_f(\overline{A}(k)]=[1-f([\overline{A}]_{k+1}),1-f([\underline{A}]_k)], \end{aligned} \end{aligned}$$

  (5)

  where $FL_f(\underline{A})$ and $FL_f(\overline{A})$ are the fuzzy cardinalities defined in previous section.

• 3. f-FECount of IVFS $\widetilde{A}$ for a given cardinality pattern f is defined as:

  $$\begin{aligned} \widetilde{FE}_f(\widetilde{A})=\widetilde{FG}_f(\widetilde{A}) \cap \widetilde{FL}_f(\widetilde{A}), \end{aligned}$$

  (6)

  i.e. for $k\in \mathbb {N}$:

  $$\begin{aligned} \begin{aligned} \widetilde{FE}_f(\widetilde{A})(k)=[f([\underline{A}]_k) \wedge (1-f([\overline{A}]_{k+1})),f([\overline{A}]_k)\wedge (1-f([\underline{A}]_{k+1})]. \end{aligned} \end{aligned}$$

  (7)

To simplify the notations, f-FECount of an IVFS will be denoted by $\widetilde{\sigma }$ and we will call it Interval-Valued Fuzzy Cardinal Number (in short IVFCN).

Comparability Algorithm of IVFCNs. In many decision-making applications, an important problem to solve is comparing the cardinalities of IVFSs.

To define algorithm more formally, we need to introduce some basics notations.

Definition 7

Representative $Rep(x)\in \mathbb {R}$ of an interval $x\in L^I$ for $\alpha \in [0,1]$ is defined as:

$$\begin{aligned} Rep(x)=K_{\alpha }(x)=\underline{x}+\alpha *w(x), \end{aligned}$$

(8)

where w fulfills (1).

In a special case value of representative of an interval can lead to middle or bounds of interval:

• 1. if $a=0$ then $Rep(x)=\underline{x}$ - lower bound of the interval;

• 2. if $a=1$ then $Rep(x)=\overline{x}$ - upper bound of the interval;

• 3. if $a=0.5$ then $Rep(x)= (\underline{x}+\overline{x})/2$ - middle of the interval.

To order the IVFCNs we propose the following method inspired on [17] used in the next section for group decision making.

Algorithm for Ordering of IVFCNs

Step 1 (Inputs). Input data: interval-valued fuzzy cardinal numbers: $X_i \in IVFCNs$, $i=\{1,\ldots ,n\}$, $n\in \mathbb {N}$

$$X_i=\{[\underline{x}_k,\overline{x}_k],\;\; where \;\;k=\{1,\ldots ,m\}\;m\in \mathbb {N}\}.$$

Step 2 (Representatives). For input data with intervals data, we need the following process (representatives (see (8))):

$$Rep(x_k)=\underline{x}_k+\alpha *w(x_k),\;\; where\;\; \alpha \in [0,1]$$

and we obtain $\mathbf{x} _i=\{Rep(x_k)\}.$

Step 3 (Aggregations). For m elements support we construct aggregations matrix with difference aggregation functions Let $\mathbf{F}=(F_1,...F_m)$ be a sequence of m aggregation functions, $F_i:[0,1]^m\rightarrow [0,1]$, then we calculate

$$\begin{aligned} \begin{array}{l} F_1(\mathbf{x} _1),\ldots ,F_m(\mathbf{x} _1)\\ \ldots \\ F_1(\mathbf{x} _n),\ldots ,F_m(\mathbf{x} _n) \end{array} \end{aligned}$$

for $\mathbf{x} _1,...\mathbf{x} _n$ and we calculate for each $1\le i,j\le k$ the measure of connectivity for pairs of values $\mathbf{x} _i$ and $\mathbf{x} _j$, $i\ne j$,

$$CON(\mathbf{x} _i,\mathbf{x} _j)=\sum _{1\le l\le m}(F_l(\mathbf{x} _i(t))-F_l(\mathbf{x} _j(t))),\;\;\;1\le t\le n.$$

Step 4 (Selection). For each $1\le i,j\le n$ we find

$$\max _{1\le i,j\le n}CON(\mathbf{x} _i,\mathbf{x} _j)=CON(\mathbf{x} _z,\mathbf{x} _w), \;\;1\le z,w\le n;$$

The element $\mathbf{x} _{z}$ is chosen as most appropriate.

We repeat Step Selection by omitting the wining values $\mathbf{x} _{z}$ in the next iteration.

If $\max _{1\le i,j\le n}CON(\mathbf{x} _i,\mathbf{x} _j)=CON(\mathbf{x} _z,\mathbf{x} _w)=CON(\mathbf{x} _{z'},\mathbf{x} _{w'}), 1\le z,z',w,w'\le n,$ then we find

$$C_1:=\sum _{1\le w\le n}(\max (0,CON(\mathbf{x} _z,\mathbf{x} _w)))$$

and

$$C_2:=\sum _{1\le w'\le n}(\max ((0,CON(\mathbf{x} _{z'},\mathbf{x} _{w'}))).$$

If $C_1>C_2$ then the element $\mathbf{x} _{z}$ is chosen as the most appropriate otherwise the element $\mathbf{x} _{z'}$ is chosen as most appropriate. Otherwise if both $C_1$ and $C_2$ are equal than $\mathbf{x} _{z}= \mathbf{x} _{z'}$.

As a consequence we obtain the sequence: $\mathbf{x} _{z}\succeq \mathbf{x} _{z'}\succeq \ldots$ and thus $\mathbf{X} _{z}\succeq \mathbf{X} _{z'}\succeq \ldots$. In particular, if we compare only two IVFCNs, i.e two sequences of representatives $\mathbf{x} ,\mathbf{y}$, then $\mathbf{x} \succeq \mathbf{y}$ if $CON(\mathbf{x} ,\mathbf{y} )>CON(\mathbf{y} ,\mathbf{x} )$ else if $CON(\mathbf{x} ,\mathbf{y} )< CON(\mathbf{y} ,\mathbf{x} )$, then $\mathbf{x} \preceq \mathbf{y}$, otherwise they are equivalent.

4 Application in Decision Making

The presented methodology for comparing IVFCNs can be applied in the decision model used in the OvaExpert system. OvaExpert is an intelligent decision support system for the diagnosis of ovarian tumors. The system was developed as a result of joint research of two Polish research centers: the Division of Gynecologic Surgery of the Poznan University of Medical Sciences and the Department of Imprecise Information Processing Methods, Faculty of Mathematics. More detailed information about the system can be found in [12].

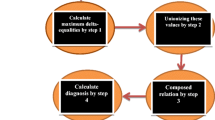
Figure 1 presents diagram showing OvaExpert counting approach for making decisions. This method of decision making utilised in the system is based on voting strategy with counting. On input system gets incomplete information about patient. In Step 1 many diagnostic models are computed and it results as IVFS of decisions. Then in Step 2 two IVFSNs are computed (which represents positive and negative diagnosis). And finally in Step 3 comparison of this two IVFSNs resulting decision. This step utilize methods presented earlier in this work.

Fig. 1.

OvaExpert counting approach for making medical decision

4.1 Decision Making Algorithm Based on Bipolar Voting Strategy

The idea behind decision algorithm is to use bipolar perspective on IVFS. Because such an IVFS contains information on uncertainty level, it carries both information supporting and rejecting the decision. This property of IVFS is used in decision algorithm. The basic idea behind this algorithm consists of a couple of steps:

• As an input we have two IVFS’s P and C (representing number of decision’s $D_{pro}$ and $D_{contra}$ supporting given decision):

  • $P=\sigma (D_{pro})$ - representing the number of decisions ‘for’;

  • $C=\sigma (D_{contra})$ - representing the number of decisions ‘against’;

• To make decisions, we must choose a set that is more numerous e.g. decide if (or vice versa):

  $$P<C.$$

For equivalency of P and C (see Algorithm. Ordering of IVFCNs) then we do not make decisions.

4.2 Results and Discussion

The presented algorithm have been tested on real medical data. These data described 388 cases of patients diagnosed and treated in the Division of Gynecological Surgery, Poznan University of Medical Sciences, between 2005 and 2015. Out of them 61% have been diagnosed as suffering from benign tumours and 39% as suffering from malign tumours. Moreover, 56% of patients had full diagnostic (no test required by diagnostic scales was missing), 40% had significant amounts of missing data varying from (0%, 50%], and for the remaining ones 50% of data was missing. Detailed description of data used for evaluation can be found in [12].

The goal of evaluation was to select a decision algorithm that would best classify malignity cases with the top possible decisiveness.

We tested the algorithm for the weighted average functions of $F_i$ in $\mathbf{F}$ (see Step 3 of Algorithm. Ordering of IVFCNs).

(Weighted Average). We will use the following case of aggregation functions, i.e. arithmetic weight mean ${AW}_{w}:([0,1])^m\rightarrow [0,1]$

$$\begin{aligned} {AW}_{w}(x_1,...,x_m)=\frac{\sum _{i=1}^m w_i{x}_i}{\sum _{i=1}^m w_i},\end{aligned}$$

(9)

where the adequate vectors $\mathbf{w}=(w_1,...w_m)$ we generate in the following way: In the first step divide a sum of supports of both IVFCNs $S=supp(P) \cup supp(C)$ into two equal parts $S_1$ and $S_2$. In the second step compare precedence indicators from both parts separately in the following way:

If $\mathrm {Prec}(P(x_i),C(x_i))\le \mathrm {Prec}(C(x_i),P(x_i)) \text{ on } S_1$

then we generate weights $w_i$ from [0.5, 1] otherwise from [0, 0.5];

If $\mathrm {Prec}(P(x_i),C(x_i))>\mathrm {Prec}(C(x_i),P(x_i)) \text{ on } S_2$

then we generate weights $w_i$ from [0.5, 1] otherwise from [0, 0.5], where:

$S_1=[min(S),{(max(S)-min(S)/2)}],\; S_2= [{(max(S)- min(S))/2},max(S)]$ and $\mathrm {Prec}\in \{\mathrm {Prec}_{\mathcal {A}},\mathrm {Prec}_w\}$ and $\le \in \{\le _{L^I},\le _{Adm}\}.$

Evaluation of the Algorithm. We use the following notations for evaluate the results of the classification: Accuracy  (acc), Sensitivity (sen), Specificity (spec) and Precision (prec) (cf. [12]).

Fig. 2.

Impact of $\alpha$ selection on decision quality

The Table 1 below presents analysis of different parameters of $\alpha$ (different methods to calculate representatives). We check values of $\alpha$ by different criteria, i.e., the best acc, sen, spec, prec, respectively. We present the best results obtained in series of tests for $\mathrm {Prec}_w$ and Xu and Yager linear order. We observe that we obtained comparable results to [12]. With comparison to OEA baseline model (which is current decision method in OvaExpert system) we see that new algorithm give the better results of specificity, but very similar values of other performance measures (like sensitivity and accurency). Figure 2 shows the impact of $\alpha$ selection on decision quality. So proposed algorithms are interesting from point of view possible applications and in other data also may be better methods to compare IV values.

Table 1. The best evaluation results for different $\alpha$

To obtain the best acc and sen values, the $\alpha$ values should be in the range of [0.15, 0.5], which indicates a strong relationship between these values and the designated representatives.

For spec and prec values, the initial range of [0, 0.45] is relatively neutral, only after exceeding the value of 0.45 for $\alpha$, the above variables have a decreasing trend. To obtain the best results for all parameters, the recommended alpha values should be in the range [0.15, 0.45].

5 Conclusions and Future Plans

In this presentation, we discuss possible algorithms for compare in interval-valued fuzzy setting, where these notions with widths of intervals involved. Moreover, new algorithms of comparing and ranking cardinalities of IVFS were applied in decision making algorithm. In future we will test presented algorithms for other types data. Moreover, we are currently working on several other types of ranking methods that uses aggregation functions.