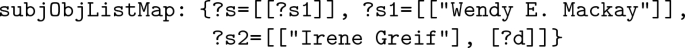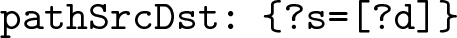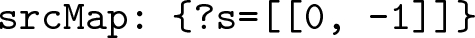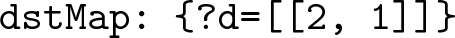Keywords

1 Introduction

Many applications have to find connections between entities in datasets. In graph theoretic terms, this amounts to querying for paths in graphs, between multiple sources and destinations. Often the sets of sources and destinations cannot be easily given explicitly but rather in terms of patterns to be matched in graphs. For example, to assess security risks for flights, security officials may want to know about relationships between p1 = passengers on any flights to a particular destination within a particular time window who purchased one-way tickets by cash, and p2 = countries on the CIA watchlist. Here p1 and p2 are patterns describing the set of sources and destinations of interest. Such inquiries also commonly occur when dealing with biological networks as well as in several non-traditional emerging applications e.g. networking. For the latter example, suppose there is a network composed of SDN ASs (Autonomous Systems), where an AS controller may want to compute a domain-level path from one node to another for an application where the query includes constraints related to business relationships with potential transit domains. Another feature of path queries as demonstrated by the networking example is that, there can be constraints on paths e.g. avoid domains of type T or constraints on path disjointedness (link- or node-disjoint for specific resilience level) or other structural constraints. Such constraints are more expressive than the property path queries which require a regular expression of the properties in path being searched for. In a sense, these queries are traditional path queries generalized to include graph patterns and path constraints. We refer to such queries as Generalized Path Queries - gpqs.

Property path expressions in SPARQL are also motivated by the need for graph traversal queries. However, they are fundamentally different from path queries in that the result of a property path expression is not paths but rather sets of endpoint nodes connected by paths that match the property path pattern. G-Core [15] presents a good discussion of different classes of graph queries. Existing graph-based query engines such as Neo4j [9], StarDog [13], Allegrogaph [14], AnzoGraph [6], Virtuoso [18] provide varying degrees of support for path querying. Some other platforms such as [19, 21,22,23,24, 30] have focused exclusively on the path querying.

A common thread across existing path querying evaluation strategies is that they are built on traditional graph algorithms. The challenge with graph theoretic interpretations of such queries is that the different constraints in gpqs may translate to different classes of graph problems, requiring different algorithms. For example, shortest path algorithms vs. subgraph isomorphism algorithms vs. subgraph homeomorphism, etc. From the point of view of query processing, this is a limited approach because of the limited opportunity for decomposition and reusability. On the other hand, adopting an algebraic perspective allows problems to be interpreted in a more generalized form. This also allows for more natural integration with algebraic graph pattern query engines. Considering such a strategy makes sense once one observes that gpqs are essentially comprised of four elements: graph pattern matching, joining/filtering of graph patterns, path computation, path filtering. Some existing platforms like [13] do partially interpret gpq-like queries algebraically. However, the absence of a complete algebraic query interpretation framework results on falling back on traditional graph algorithms in many situations.

In this paper, we propose an algebraic query evaluation technique for gpqs that delineates the four gpqs subquery elements and their mapping to algebraic query operations so that gpqs query planning translates to composition and ordering of query operations. More specifically, the paper presents.

  • a conceptual query evaluation model that integrates algebraic graph pattern matching with algebraic path problem solving.

  • an implementation model that perturbs the plan for graph pattern matching query generated by a SPARQL query compiler by splicing in algebraic path querying operators to produce a gpqs query plan. Another advantage of this strategy is that current SPARQL parsers and existing graph pattern matching compiler can be adopted without modification. An example implementation strategy using Apache Jena’s query compiler and Apache Tez’ DAG for physical execution is presented.

  • comparison of the performance and expressiveness of the integrated platform with a popular engine.

Section 2 presents the background on algebraic path problem solving and graph pattern matching. The relevant work, existing graph querying engines and their limitations are provided in Sect. 3. Section 4 discusses our approach both conceptually as well as the implementation model with evaluation presented in Sect. 5. Conclusion is in Sect. 6.

2 Background

2.1 Algebraic Path Problem Solving in Directed Graphs

We begin with a brief review of an efficient algebraic path problem solving approach due to [34]. An edge e in a directed labeled graph \(G = (V, E)\) is denoted as \(e=(v_1, v_2)\) with label \(\lambda (e)=l_e\), where \(v_1, v_2 \in V\) and \(e \in E\). A path p, in this graph \(G=(V,E)\), is defined as an alternating sequence of nodes and edge labels terminating in a node \(p=\{v_1, l_{e_1}, v_2, l_{e_2},..., v_n, l_{e_n}, v_{n+1}\}\), where \(v_1, v_2,...,v_n, v_{n+1} \in V\) and \(e_1, e_2,...,e_n \in E\). A path expression of type (s, d), PE(s, d) [34] is a 3-tuple \(\langle \)s, d, R\(\rangle \), where R is a regular expression over the set of edges defined using the standard operators union\((\cup )\), concatenation\((\bullet )\) and closure\((*)\) such that the language L(R) of R represents paths from s to d, where \(s,d \in V\). For example in Fig. 1(a) borrowed from [21], PE(2, 7) = \(\langle 2, 7, ((b \bullet c \bullet f)\cup (i \bullet f))\rangle \) is path expression of type (2,7) (for brevity, only edges are captured in the regular expression, no nodes). Path expressions may or may not be complete in terms of the subset of paths represented. For example, PE(2, 7) only represents two of the several paths between 2 and 7.

If a graph is ordered using any numbering scheme, path information can be represented using a particular ordering of path expressions called a Path-Sequence (PS) [21, 34]. Figure 1(b) shows the path-sequence that represents the example graph in Fig. 1(a). It can be observed that some path expressions are simple, e.g. representing only a single edge, while others are more complex. The formalization of a path sequence [34] defines what path expressions are in a path sequence. A particularly appealing property of a path-sequence is that many path problems can be solved using a simple propagation SOLVE algorithm [21, 34], that assembles path information as it scans the path-sequence from left to right. At every iteration of the SOLVE algorithm the following step is performed \(PE(s, w_i) \cup (PE(s,v_i) \bullet PE(v_i,w_i)) -> SA[w_i] \), where an existing path expression for \((s, w_i)\) is extended using concatenation of two subpath expressions and/or union of new path expression capturing additional paths for \((s, w_i)\). At the end of the scan and propagation phase, we are guaranteed completeness of the source node used to drive the propagation phase. The original single source SOLVE algorithm was generalized in [21] to multiple sources, with a particular emphasis on sharing computation across sources where subexpressions were common.

Fig. 1.
figure 1

Example explaining path-sequence and expression (a) Example graph (b) Path-sequence for the graph (c) Partial path expression for paths between nodes 2 to 7

Full size image

One of the main issues with graph computation is that every problem requires a different algorithm. A nice property of this algebraic framework as shown by [34] is that multiple path problems can be solved using the same algorithm by interpreting Union\((\cup )\) and concatenation\((\bullet )\) operators appropriately. For example, the shortest path problem has a very straightforward interpretation in terms of the Union\((\cup )\) operator, where rather than union multiple path expressions you ignore all but that with the least cost. Some problems can also be interpreted in terms of manipulation of the path expression produced by the unconstrained path problem. [17, 21, 23] all describe some examples. For problems in this category, a critical issue is that computationally efficient representations of path expressions are used rather than mere string representations. For example, there is a natural mapping from regular expressions to abstract syntax trees (AST) where the operators like union\((\cup )\) and concatenation\((\bullet )\) form the internal nodes while the edges form the leaves of the tree. Figure 1(c) shows the AST for the PE shown earlier. In this context, path filter operators can then be defined in terms of manipulation of path expression representations.

2.2 Algebraic Query Evaluation of Graph Pattern Matching

It is well known that RDF admits a directed graph model. SPARQL [29] is the standard RDF query language with its main query primitive being a graph pattern. Evaluation of graph pattern matching query is usually performed using operators with an algebraic query plan where we typically use relational-like query operators. The graph patterns are compiled into an algebraic logical plan representation, which is generally a sequence of query operators with an implied execution ordering. For example, Jena ARQ [4, 28] is a popular query engine that supports SPARQL queries and it creates a SPARQL Syntax-Expression(SSE) as an algebraic logical query plan. The last step in query evaluation is transforming the logical plan to a physical plan which depends on the physical execution environment.

3 Related Work

[16, 35] provides a good survey of graph query languages. For running queries that have both graph pattern matching and path computation components, in most cases, users have to use two different platforms. Those platforms that do allow both components mostly focus on finding shortest paths and not necessarily all paths. Platforms like Virtuoso [18], RDFPath [30], Blazegraph [5] use property paths [12] supported by SPARQL 1.1 [25]. However, using property paths, it is only possible to know the specific sources and destination, but not the exact paths. Also, the users would need to write a regular expression of the properties in the paths they are looking for, requiring the user to know the exact properties in the path as well as have some idea of the sequence of these properties. Gremlin [32], the query language for JanusGraph [8] and Neptune [2] also requires the predicates of the path to be specified in the query. Oracle’s PGQL [10, 11, 31, 33] finds paths using general expressions over vertices and edges of the graph. The user needs to have knowledge of the sequence of edges in the paths being searched for in this case as well.

Neo4j [9], AgensGraph [1] use Cypher [7, 20] as their query language. Cypher uses a fast bidirectional breadth-first search algorithm for optimizing path queries. However, this fast algorithm is used only in certain scenarios like finding shortest path. When finding all paths, Cypher uses a much slower exhaustive depth-first search algorithm. Even for shortest path queries, the fast algorithm is used only if the predicates in the path query can be evaluated on the fly. For path queries, with predicates for which they need to examine the whole path before making a decision on filtering, Cypher’s query evaluation falls back to exhaustive search. Cypher has another drawback, where its shortest path algorithm produces incomplete results when the start and end nodes are the same. Such a scenario might occur when performing a shortestPath search where the sources and destinations are overlapping sets of nodes.

Stardog [13] uses more traditional SPARQL operators for query evaluation. For any path query with start and end variable patterns Stardog first finds all possible paths that match PQ which is a regular expression similar to that used by property paths. The resulting set of paths is then joined with the end graph pattern, followed by the start graph pattern. This approach of applying filter first and then joining with source and destination patterns might be useful when the filter is highly restrictive. However, if the path query filter is not restrictive it will produce a large resultset resulting in poor performance when joining with the start and end patterns.

4 Approach

Introducing a new query class would typically require the extension of query language and processing framework. However, we adopted an approach of introducing a syntactic sugar that avoided the need for changing SPARQL’s query syntax. A second simplifying but reasonable strategy is the use of a fixed order between the graph pattern matching phase and the path computation phase. The rationale here is that in gpqs, pattern matching serves to compute the set of sources, destinations and/or intermediate nodes in constraints. In other words, the output of graph pattern matching can be seen as input to the path problem phase. Interpreting this in terms of query plans implies that the path computation and path filter operators will always be at the root of the tree for any gpqs query plans. In the sequel, we elaborate our realization of the above implied strategy.

Fig. 2.
figure 2

(a) An example path query in our implementation of the integrated platform. (b) The SSE produced by Jena’s parser and compiler

Full size image

4.1 Identifying GPQ Sub-Query Components in SPARQL* Queries

Our syntactic sugar is based on adopting a pre-defined variable name ?pathVar as the path operator. We acknowledge the risk of other users using this variable in their queries, but assume this risk to be small. Since this a legal variable that is recognized by the graph pattern matching platform’s parser, the unaltered parser can parse and compile path queries without failing due to syntax issues. Here, we refer to SPARQL with our pre-defined variable ?pathVar as SPARQL*.

Implementation Strategy: In this section, we describe the approach followed to identify the source and destination variables using the pre-defined path variable ?pathVar and then project them out from the graph patterns. The last triple pattern in example query in Fig. 2(a), \(\langle \)?s ?pathVar ?d\(\rangle \) denotes the path computation between all bindings to the variable ?s and the variable ?d. Presence of the ?pathVar variable in the predicate position implies that it is a path query. Now, we must keep track of the position of the source and destination variables in the graph patterns and finally, after all the joins have taken place we must project out only the bindings of the source and destination variables. These bindings would then go into the path operator. To do this, we create the required datastructures to hold the position information of the source and destination variables in the query. This information will be later required when we create the final physical plan of the query.

For our proof-of-concept prototype, we implemented by integrating Semstorm [27] as the graph pattern matching platform and Serpent [21, 23] as the path query computation platform. Semstorm uses the below two main datastructures as query plan representation to hold the position information of the different triple patterns in the submitted query.

  • subjObjListMap holds the mapping between the subjects and the corresponding objects in the query. The subjObjListMap for the query in Fig. 2(a) would be

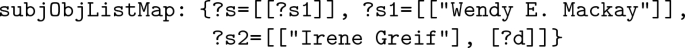
    figure a

  • subjPropListMap holds the mapping between the subjects and the properties or predicates in the triple patterns in the query. The subjPropListMap of the query in Fig. 2(a) would be

    figure b

In addition to these, the following datastructures have been added to facilitate path computation and provide required location information to the path operator.

  • pathSrcDst is a map that shows the mapping between the source variable and its corresponding destination variable. For the query in Fig. 2(a), the pathSrcDst would be

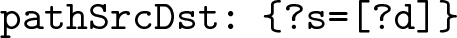
    figure c

  • srcMap contains the source variable in the key position and a list of integers in the value position. The list of integers denote the exact position of the source variable in the subjObjListMap datastructure. The srcMap of the query in Fig. 2(a) would be

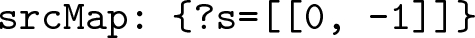
    figure d

  • dstMap is similar to the srcMap, except that its key contains the destination variable and the list of integers in its value position denote the position of the destination variable. The dstMap of the query in Fig. 2(a) would be

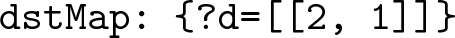
    figure e

  • cndMap is also same as the srcMap and dstMap except that it hold the constraints information. For example, some query might want to restrict paths to the ones which contain at least one akt:has-affiliation property or predicate. Then, this triple will be a part of the constraints and the position of this triple would be captured in the cndMap. The query in Fig. 2(a) is not a constrained query and hence, its cndMap would be empty.

The list of integers in the value position of the srcMap, dstMap and cndMap all denote the position of the respective variables in subjObjListMap. For example, {?s = [[0, \(\,-\,\)1]]} means the variable ?s is in the first BGP of subjObjListMap (indexing starts at 0) and −1 denotes that it is the subject of the BGP. {?d = [[2, 1]]} means that the variable ?d is in the third BGP and it is the second object of that BGP. Sometimes these variables might also be the join variable between two graph patterns and so, they can exist in multiple BGPs and the value of the respective maps will have a list of integer pairs, identifying the position of the variable in subjObjListMap.

Fig. 3.
figure 3

Query plan transformation from graph pattern matching query to ggpq

Full size image

4.2 Logical Query Plan Transformation

Our query planning approach is based on transforming the query plan produced by graph pattern matching engine. The intuition is that the subqueries which are the graph patterns defining the sets of sources, destinations, etc for path computation can be translated to query plans in the usual manner. However, the semantics of such queries will usually imply a cross-product of intermediate results (since the subgraph patterns will be disconnected). We illustrate this idea with the example query in Fig. 2(a) (but ignoring the last triple pattern \(\langle \)?s ?pathVar ?d\(\rangle \) which is our syntactic sugar for the path variable triple pattern). Figure 2(b) shows the SSE created by Jena’s parser and compiler and Fig. 3(a) shows the SSE as a tree. To achieve the correct query semantics, the cross-product and projection operators have to be removed and query operators associated with path computation introduced. The final operator in the plan is a path filter operator (if path filtering constraints are specified - absent in example). The newly introduced components of the query plan are enclosed in a dotted box in Fig. 3(b).

Implementation Strategy: Our graph pattern matching platform, Semstorm [27] is an RDF processing platform that is targeted for Cloud-processing and uses Apache Hadoop/Tez execution environment. Semstorm’s compiler builds on Jena’s parser, using Jena’s SSE to create a Tez [3] DAG as the physical query plan based on Semstorm’s query algebra. To achieve an equivalent physical query plan transformation, similar to the logical plan transformation in Fig. 3, new physical query operators have to be introduced. Since our physical execution environment is Tez, the new physical operators are nothing but new Tez Vertices. The following new Tez vertex types were added that act as the physical query operators.

Fig. 4.
figure 4

The Tez DAG representating the physical plan for the query shown in Fig. 2

Full size image

  • Annotator Vertex for Source, Destination and Constraint Variables. Semstorm is meant to run SELECT * WHERE queries and so, it propagates the data for all of the variables in the query. However, the path computation platform Serpent expects three lists of nodes that denote sources, destinations and constraints respectively. Hence, annotators were required to identify the source, destination or constraint variables and then, allow only the bindings for that variable to pass through, discarding the rest of the bindings. While this might seem to be a less optimized method, it must be noted that bindings to other variables cannot be discarded before all joins have completed since the source, destination or constraint variable may not always be the join variable.

  • PathComputer Vertex. This is the path operator which performs the path computation. It takes the sources, destinations and constraints as input, converts these into three String arrays as is required by Serpent and then calls the appropriate method in the Serpent platform. For every path query DAG this vertex will always be at the root.

Figure 4 shows the final Tez DAG that needs to be generated for the example query in Fig. 2(a). The TypeScanner::?s vertex in the DAG identifies and reads all triples that match the pattern {?s akt:has-author ?s1} from the data file. Similarly, the other TypeScanner vertices read the respective matching triples. The output of the TypeScanner::?s and TypeScanner::?s1 vertices go to Annotator(?s1):0 and Annotator(?s1):1 vertices respectively. These annotator vertices identify the join variable and its position in the graph pattern. The Packager::?s,?s1 vertex performs the actual join operation between the two graph patterns and provides the joined output of the two input graph patterns.

If a simple pattern matching query is submitted to Semstorm, it would add a Producter vertex that would take inputs from the Packager::?s,?s1 and TypeScanner::?s2 vertices and the output of the Producter vertex would go into a Flattener vertex which would write out the final query output to an output file on disk. In our integrated version, we created a fork at this point, where for a path query, we do not add the Producter and Flattener vertices. After joins, we add the Annotator- Source:[[0,−1]] and Annotator-Destination:[[2,1]] to annotate the source and destination respectively. We also add the value from the srcMap and dstMap to the respective vertex name. Since the destination vertex in our example is not involved in any joins the destination annotator vertex gets its input directly from the typeScanner vertex that has the destination variable. The PathComputer::Src:?s, Dst:?d vertex comes at the root of the DAG since this will be executed last. While creating this vertex, information about the source variable ?s and destination variable ?d are added to it using the configuration payload. This DAG is submitted to the query execution framework of Semstorm, which executes the DAG and produces the final path output.

Fig. 5.
figure 5

Size of source and destination sets for each query

Full size image

4.3 Path Constraints

Some path constraints can be evaluated by reinterpreting the union and concatenation operations during the propagation algorithm (SOLVE) e.g. for shortest paths. Others will be defined as manipulations over the path expression produced by unconstrained version of the problem e.g. finding paths that contain a given set of nodes (no order specified). Those manipulations will be encapsulated in operators that are parent nodes of the pathComputer node in operator plan tree. The efficiency of the such operations will depend on the nature of path expression representation e.g. a binary encoded representation. However, a detailed discussion path constraints is outside scope of this paper.

5 Evaluation

5.1 Test Setup

The primary goal of our evaluation was to compare our integrated system with an existing platform on the following parameters.

  1. 1.

    Query compilation time comparison for our platform with and without path operator.

  2. 2.

    Performance, i.e., time taken to run the same queries.

  3. 3.

    Completeness of results, i.e., whether the platform returns all paths expected.

  4. 4.

    Expressiveness, i.e., what level of queries can be expressed in each platform.

Dataset and Queries: Our queries were ran on the BTC500M dataset [26] (size 0.5 GB, 2.5 million triples). While formulating queries, we focused on finding paths that are at least three hops long. The queries we ran varies from small set of sources and destinations to very large set of sources and destinations. We ran five small queries and five large queries where small and large indicate the size of the set of sources and destinations shown in Fig. 5. In the charts Small Queries and Large Queries have been abbreviated to SQ and LQ respectively. The same queries were modified to add constraints to run constrained query experiments.

All the comparisons have been done with Stardog. We also considered Neo4j, but while trying to run queries using Cypher we found that all-paths queries on this dataset were running indefinitely and causing the Neo4j server to crash. We were able to run shortest path queries on Neo4j but that result is not included in this paper as finding shortest path was not an evaluation goal for this paper.

Hardware Configuration: Evaluation was conducted on single node server running HDFS in a privately owned RedHat Enterprise Server server, housed in the University’s server lab. The server is equipped with Xeon octa core x86_64 CPU (2.33 GHz), 40 GB RAM, and two HDDs (3.6 TB and 445 GB). All results have been averaged over five trials. In all the charts our platform has been labelled as “Sem-Ser”.

5.2 Evaluation Results

Query Compilation Time Comparison: Figure 6 shows the time taken for query compilation on our platform for queries which have the path operator compared with the same queries without the path operator. The path operator does not have much effect on the query compilation time and in most cases the compilation time increased by less than one second.

Fig. 6.
figure 6

Chart showing compilation time comparison

Full size image

Performance Evaluation: When comparing absolute time taken by our platform with that of Stardog, we found that Stardog performed better in all queries except for \(SQ_1\), \(LQ_1\) and \(LQ_2\). \(LQ_2\) timed out and produced only partial results on Stardog and took the longest time (5.5 min) and produced the largest number of paths (0.8 million paths) on our platform. This is mainly because the graph patterns provided for the source and destination nodes was quite general, thus, leading to large number of matching sources and destinations. Consequently, there were a large number of paths connecting these nodes.

Fig. 7.
figure 7

Chart showing comparison of number of paths identified

Full size image
Fig. 8.
figure 8

Chart showing the comparison of time taken per path identified

Full size image

Completeness of Results: Figure 7(a) and (b) show the number of paths identified by small and large queries respectively. \(LQ_2\) has been marked with an asterix since it did not finish in Stardog and hence, all the charts have only one value for this query. For all the queries, Stardog produced incomplete results and also duplicate paths. This dataset has a lot of triples such as \(\langle \)acm:58567 akt:has-publication-reference acm:58567\(\rangle \). In this triple the subject and the object is the same uri acm:58567 and hence, this is called a loop or self-loop. The BTC dataset has a lot of such triples and Stardog does not consider the self loops in the paths it identifies. For example, suppose we have an RDF graph consisting of the triples \(\langle \)A p1 A\(\rangle \) \(\langle \)A p2 B\(\rangle \) \(\langle \)B p3 B\(\rangle \) and a path query with A as source node and B as destination node. On execution of the path query Stardog will ignore the self-loops \(\langle \)A p1 A\(\rangle \) and \(\langle \)B p3 B\(\rangle \) and will output only one path (A p2 B). However, our platform will find four paths (A p2 B), (A p1 A p2 B), (A p2 B p3 B) and (A p1 A p2 B p3 B). This is the reason behind Stardog mostly finding less paths as compared to our platform.

In some queries (\(SQ_1\), \(LQ_1\)), Stardog does find more number of paths. However, these results contain duplicate paths. For example, although Stardog produces 40 paths for \(SQ_1\) the number of unique paths is 6. Since there was a huge mismatch between the number of paths found by our platform and Stardog we compared the time taken per path identified rather than the absolute time taken for executing each query. Figure 8(a) and (b) shows the time per path comparison for the small and large queries respectively.

Expressiveness: All types of graph patterns can be expressed in Neo4j, Stardog as well as our platform. However, Stardog does not support constraints such as ALL, ANY, NONE. Figure 9 shows the comparison of the expressiveness of our platform with that of Stardog and Neo4j. Neo4j has predicate functions (all, any, exists, none, single) which can be used for the same purpose of filtering. However, since we were not able to run all paths queries on Neo4j it was not possible to compare constrained queries on our platform with that on Neo4j.

Fig. 9.
figure 9

Table showing comparison of the level of expressiveness of our platform with Neo4j and Stardog

Full size image
Fig. 10.
figure 10

Execution Time of constrained queries vs unconstrained queries

Full size image

Figure 10 shows the time taken for constrained queries as compared to unconstrained queries on our platform. All of the constrained queries understandably taken longer time to complete query execution, since these queries include an extra filtering step. For all of the small queries, the increase in execution time is minimal mainly because the size of the resulting set of paths before filtering is also small. For the large queries, the increase in execution time is more noticeable due to the larger size of the resultset prior to filtering.

6 Conclusion

This paper presents an algebraic query evaluation strategy to evaluate generalized path queries with declaratively defined source and destination nodes. This paper also presents a general framework and steps to integrate any existing graph pattern matching platform with a path computation platform. Lastly, this paper describes an implementation of such an integrated platform and shows performance comparison with this integrated platform with that of popular platforms that can handle such generalized path queries.