Implementing YewPar: A Framework for Parallel Tree Search

Abstract

Combinatorial search is central to many applications yet hard to parallelise. We argue for improving the reuse of parallel searches, and present the design and implementation of a new parallel search framework. YewPar generalises search by abstracting search tree generation, and by providing algorithmic skeletons that support three search types, together with a set of search coordination strategies. The evaluation shows that the cost of YewPar generality is low (6.1%); global knowledge is inexpensively shared between workers; irregular tasks are effectively distributed; and YewPar delivers good runtimes, speedups and efficiency with up to 255 workers on 17 localities.

1 Introduction

Exact combinatorial search is essential to a wide range of applications including constraint programming, graph matching, and computer algebra. Combinatorial problems are solved by systematically exploring a search space, and doing so is computationally hard both in theory and in practice, encouraging the use of approximate algorithms.

Alternatively, exact search can be parallelised to reduce execution time. Parallel search is, however, extremely challenging due to huge and highly irregular search trees, and the need to preserve search heuristics. The state of the art is parallel searches that (1) are single purpose, i.e. for a specific search application, e.g. Embarrassingly Parallel Search [12] supports constraint programming only; and (2) use hand crafted parallelism, e.g parallel MaxClique [13], with almost no reuse of parallelism between search applications. Hence typically an application is parallelised just once in an heroic effort.

We provide a high-level approach to parallel search that allows non-expert users to benefit from increasing CPU core counts. Specifically YewPar supports algorithmic skeletons that provide reusable implementations of common parallel search patterns.

Contributions. We present for the first time the design (Sect. 3) and implementation (Sect. 4) of YewPar, a new C++ parallel search framework. YewPar provides both high-level skeletons and low-level search specific schedulers and utilities to deal with the irregularity of search and knowledge exchange between workers. YewPar uses the HPX library for distributed task-parallelism [11], allowing search on multi-cores, clusters, HPC etc.

A novel element of YewPar is the depth-pool, a search-specific distributed workpool that aims to preserve search heuristics. We describe the depth-pool and show average runtime performance very similar to the widely-used deque, yet dramatically reduced variance for some searches (Sect. 5).

We evaluate YewPar using around 15 instances of two search applications covering two search types. The applications are evaluated on standard challenge instances, e.g. the DIMACS benchmark suite [10]. We investigate how YewPar shares knowledge between search threads (workers), and how effectively it scales from 15 to 255 workers, on a Beowulf cluster. The sequential YewPar overheads are low, with a mean 6.1% slowdown compared to a hand-coded sequential implementation.

2 Existing Search Approaches

Fig. 1.

MaxClique: graph with maximum clique $\{a,d,f,g\}$ and search tree

Conceptually exact combinatorial search proceeds by generating and traversing a tree representing alternative options. In practice the trees are huge and grow exponentially, e.g. $378\times {}10^{12}$ nodes at depth 67 with a growth rate of 1.62 in [9], and as such are not materialised fully during search.

There are three main search types: enumeration, which searches for all solutions matching some property, e.g. all maximal cliques in a graph; decision, which looks for a specific solution, e.g. a clique of size $k$; or optimisation, which finds a solution that minimises/maximises an objective function, e.g. finding a maximum clique. To illustrate, Fig. 1 shows a small graph, and a fragment of the search tree generated during a maximum clique search. The search proceeds depth-first, repeatedly adding nodes to extend the current clique. After exploring the subtree rooted at c it backtracks to explore the subtree rooted at f, which comes heuristically after c.

Although decades of algorithmic research have developed search heuristics that minimise search time, the scale of the search trees mean that many can take days to solve [9]. Alongside algorithmic improvements, parallel search is often used to increase the range of problems that can be practically solved.

Parallel search comes in three main variants: parallel node processing, where children of a node are generated in parallel; portfolio methods, where multiple sequential searches (with differing strategies) race to find an optimal solution; and space-splitting, where distinct areas of the search tree are searched in parallel. Space-splitting search follows a task parallel approach, where a task searches a given subtree. We focus on space-splitting techniques as they are application independent and scalable, making them ideal for general purpose frameworks such as YewPar.

There are three main work generation approaches for tree search:

• (1) Static work generation, as in embarrassingly parallel search [12], creates all tasks at startup and stores them in a (global) workpool, where they are picked up by idle workers. To balance load these approaches need to generate vastly more tasks than the number of workers, which increases startup cost.

• (2) Periodic work generation intersperses search with work generation. In mts [4], for example, workers that do not complete a task within a given budget (e.g. time, or number of nodes traversed) stop and store their unexplored subtrees in a workpool, where idle workers will pick them up.

• (3) On-demand work generation bypasses workpools; instead idle workers steal unexplored subtrees directly from other workers. Abu-khzam et al. [1] show such techniques to be highly scalable e.g. up to 131,072 workers.

The Need for a New Search Framework. Many existing parallel search approaches were designed for a single application, with search code intertwined with parallelism code, limiting reuse. Frameworks that support multiple search applications often only support a single work generation approach, yet no approach works best for all applications, making it difficult to choose an appropriate framework [2].

YewPar solves this by providing a more general, i.e. more reusable approach for parallel search, supporting all of the above work generation approaches, i.e. static, periodic and on-demand. A user writes their application once and has access to a library of parallel skeletons that realise common parallel search patterns. Importantly, the user never writes code for parallelisation, making it easy to port existing sequential search applications and experiment with the different parallelism configurations that YewPar provides.

While existing task-parallel frameworks such as Cilk [8] appear to provide suitable parallelism, key aspects of their implementations are entirely inappropriate for search. For example, deque-based work-stealing can break heuristic search orderings [13], and the common assumption that the number of tasks in a workpool is a good measure of load is invalid when learned knowledge during search is globally distributed, pruning search tasks. YewPar instead provides parallel coordinations and a workpool that are all specialised for search.

Fig. 2.

Creating search skeletons and applications

3 YewPar Design

YewPar parallelises tree search using distributed task parallelism that adapts to the dynamic and irregular nature of search, and enables scaling on common distributed-memory platforms.

Users construct search applications by combining a YewPar search skeleton with a lazy node generator that they implement to characterise their search problem, as shown in Fig. 2. The lazy node generator specifies how to generate the search tree on demand and in which order to traverse the tree. Each skeleton comprises a search coordination, e.g. Depth-Bounded (Sect. 3.1), and a search type, e.g Decision. For example, YewPar’s DepthBoundedEnumeration skeleton statically generates work and enumerates the search space. The skeleton library is extensible, allowing new search coordination methods to be added.

3.1 Search Coordination Methods

During a search potentially any node in the search tree may be converted to a task, but to minimise search time it is critical to choose heuristically a good node. We follow existing work e.g. [14], using search heuristics, as encoded in the lazy node generator, and select subtrees close to the root as we expect these to be large; minimising scheduling overheads.

YewPar provides a range of standard search coordinations. A novel parallel operational semantics for each coordination is provided in Chapter 4 of [2]. Sequential coordination is provided for reference and simply searches the tree without generating any tasks.

Depth-Bounded coordination implements semi-static work generation by converting all nodes below a user-defined cut-off depth ($d_{ cutoff }$) into tasks and placing them in a workpool. New tasks are generated throughout the computation as subtrees with nodes below $d_{ cutoff }$ are stolen rather than being generated upfront.

Budget coordination uses periodic work generation. On stealing a new task, a worker is given a user-defined backtrack budget. If the worker reaches the backtracking limit before completing the task, it offloads all unexplored subtrees at the lowest depth, i.e. closest to the root, into a workpool, before resetting the budget and continuing to search the remaining subtrees.

Stack-Stealing coordination provides on-demand work generation, triggered by work-stealing, similar to [1]. On receiving a steal request, the victim ships the lowest unexplored subtree from its own stack to the thief. Victim selection is random but biased to favour local over remote steals in order to minimise steal latency. YewPar combines work-stealing with work-pushing on startup in order to distribute tasks quickly.

Fig. 3.

YewPar system stack

4 YewPar Implementation

YewPar¹ is C++ parallel search framework. It supports the parallel algorithmic skeletons of Sect. 3 and provides low-level components such as schedulers, workpools, and global knowledge management so that new skeletons can be created. For efficiency and type safety, YewPar uses C++ templates to compile search applications. This specialises code to the specific application types, e.g. the node type, and enables type directed optimisations.

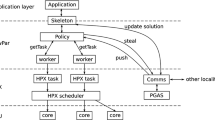
For distributed-memory parallelism YewPar uses HPX [11], a library designed for Exascale computing ($10^{18}$ FLOPS). Figure 3 shows the YewPar system stack. The implementation achieves scalability using asynchronous task-parallelism and lightweight, user-space threads (HPX-threads). Distributed load management has been implemented directly in YewPar as HPX does not provide it. Crucially the load management aims to maintain search order heuristics (Sect. 5).

HPX is selected as the distributed task library as it does not require a bespoke compiler and provides APIs for user-level access to tasks, futures, schedulers etc. Alternatively, parallel languages with distributed tasks could also be used, such as Chapel [6] or X10 [7].

Application-Level Scheduling: YewPar divides operating system threads, one per physical core, into two types: (1) worker threads that run the scheduling loop until they are terminated, and (2) HPX manager threads. YewPar has one HPX manager thread per locality for processing of active messages, synchronisation, and PGAS updates. In order to minimise latency, YewPar also reserves one CPU core for this manager thread.

Distributed Scheduling Policies. Conceptually, idle workers request new tasks from a scheduling policy, that is determined by the coordination method, for example Depth-Bounded relies on a workpool whereas Stack-Stealing does not. Policies communicate directly with HPX to either push work to remote localities, or receive stolen tasks from other localities. Two scheduling policies are currently available, more could be added.

• 1. The distributed workpool policy, used by Depth-Bounded and Budget, features one workpool per locality that stores all locally generated tasks. Steals, both local and remote, are directed to the workpool, which aims to serve thiefs tasks in heuristic order (Sect. 5).

• 2. The pickpocket policy, used by Stack-Stealing, has no workpools as Stack-Stealing generates tasks only on demand. Instead, there is a special component per locality, the pickpocket. Steals, both local and remote, are directed to the pickpocket, which requests an unexplored subtree from a busy local worker and serves it to the thief. Like the workpool, the pickpocket aims to pick unexplored subtrees in heuristic order.

Both policies follow the same victim selection strategy when stealing. Victims are chosen at random, with two provisos: (1) Local steals take priority; remote steals are attempted only if there is no work locally. (2) Remote steals are biased towards the victim of the most recent successful steal, in the hope that it still has more work.

Global Knowledge Management. Current search results are shared between workers. YewPar provides each locality with a registry that shares search specific variables – for example current bounds and skeleton parameters – between all workers of a locality. Although primary access to this state is local, it supports global updates via active messages, e.g. when receiving improved bounds.

The global incumbent object, e.g. the current solution for a decision/optimisation problem, is stored in HPX’s Partitioned Global Address Space (PGAS) making it accessible to any worker. On receiving an update message the incumbent checks that no better solution has been found and, if so, updates the stored solution and broadcasts the new bound to all localities. Section 6.2 shows that one global object suffices due to the infrequent and irregular access patterns.

5 Depth-Pool: A Workpool that Respects Search Heuristics

The performance of many tree searches depends heavily on a search heuristic that prescribes the order the search tree is traversed, aiming to find good solution(s) quickly and to minimise the search space through pruning. Failure to follow a good heuristic can cause detrimental search anomalies where large parts of the search tree are traversed that could have been pruned [5].

Workpool choice is key to ensuring search heuristics are maintained. Most work-stealing workpools use deques, where local steals pick the youngest tasks from one end, and remote steals pick the oldest tasks from the other. This works well for divide-and-conquer workloads, as Cilk [8] has shown, but not for tree searches that depend on heuristics [13]. The reason is that deque-based workpools do not maintain heuristic orderings; worse still the steal policy selects tasks that are heuristically unfavourable.

Fully respecting heuristic orderings entirely eliminates search anomalies but centralises task selection, severely limiting scalability [3]. At larger scale, a distributed workpool is needed that (1) preserves heuristic ordering as far as possible, (2) biases remote steals towards big tasks (i.e. subtrees close to the root), and (3) has low steal latency. Low steal latency is crucial since standard latency hiding techniques such as task pre-fetching disrupt the heuristic ordering. To this end, we propose a new workpool, the depth-pool, illustrated in Fig. 4.

Fig. 4.

Depth-pool structure. $T^{1}_{0}$ is a task with id 1 and heuristic position 0. Lower implies better heuristic position.

The central data structure is an array of first-in-first-out (FIFO) queues. The array is indexed by the depth in the search tree, i.e. the i-th queue holds tasks spawned at depth i. The depth-pool biases remote steals towards the root of the tree, where tasks are likely bigger, while biasing local steals to the deepest depth, thereby improving locality. By using FIFO queues the heuristic ordering is maintained at each depth, which avoids the heuristically poor choices made by deque-based scheduling. Steal latency is low as a HPX manager thread is available to handle steals.

As the depth-pool is more complex than a deque, one might expect higher overheads, but maintaining the search heuristics should reduce runtime variance. All of the results in the following section use the depthpool, and show good performance. Moreover, a direct comparison of depth-pools and deques for 7 instances of two search applications shows very similar performance, with depth-pool delivering dramatically lower variance in at least one instance (Figure 6.6 of [2]).

6 Evaluation

We evaluate YewPar performance on a cluster of 17 localities each with dual 8-core Intel Xeon E5-2640v2 CPUs (2 Ghz; no hyper-threading), 64 GB of RAM and running Ubuntu 14.04.3 LTS. Datasets underpinning the experiments are available online².

Input datasets, e.g. particular graphs, to search applications are known as instances. YewPar is evaluated in [2] with 25 instances across seven search applications that cover all three search types. Here we report results for a selection of instances of the following two state-of-the-art search applications covering two search types.

MaxClique searches a graph for the largest set of vertices (optimisation search) where each vertex is adjacent to all other vertices in the set. We implement Prosser’s MCSa1 algorithm [15], as sketched in Fig. 1. The instances are drawn from the DIMACS benchmark suite [10].

Numerical Semigroups (NS) enumerates the numerical semigroups with a genus $\le g$. A numerical semigroup is defined over the set of natural numbers with a set of numbers removed (holes) such that the remaining set still forms a semi-group under addition. The genus of a numerical semigroup is the number of holes. The implementation is closely based on, and uses the efficient bit representation for semigroups, of  [9]. Each step in the search removes a number from the group generator and adds additional elements to maintain the group property.

Section 6.1 compares YewPar sequential performance with a state-of-the-art MaxClique solver. However parallel performance comparisons are made only with other YewPar implementations as no other parallel comparator is available. That is, there is no other system that allows both MaxClique and Numerical Semigroups to be implemented, nor is there another distributed-memory parallel version of the MCSa1 algorithm [3].

6.1 Skeleton Overheads

The generality of the YewPar skeletons incurs performance overheads compared with search specific implementations. For example lazy node generation requires that nodes are duplicated rather than updated in place. Compared with hand written sequential clique search, YewPar shows low overheads with a geometric mean overhead of only 6.1% across 21 DIMACS MaxClique instances (Table 6.1 of [2]).

6.2 Global Knowledge Exchange

Searches share global knowledge, e.g. the current incumbent in an optimisation search, and YewPar uses HPX’s broadcasts and PGAS to do so. We evaluate the performance implications using MaxClique instances on 255 workers (17 localities) with Depth-Bounded coordination and $d_{ cutoff } = 2$.

Figure 5a shows the mean number of attempted incumbent updates (to the nearest integer) for each instance. Failure to update occurs when a better solution was found before the update message arrived. For most instances, regardless of their runtime, the total number of updates is small: often less than 50. In instances with more updates, a greater proportion are unsuccessful. Moreover Fig. 5b shows how most updates occur early in the search.

While the number of successful updates is bounded by the size of the maximum clique, the variation in the number of successful and unsuccessful steals is instance specific and depends, for example, on how many branches near the start of the search report similar incumbent values (before bound propagation occurs). This non-predictability is a key challenge in parallel search.

Fig. 5.

Incumbent updates.

Given the small amount of global knowledge exchanged, YewPar’s approach combining PGAS and broadcast is appropriate and likely scales beyond the current architecture. Crucially, although message delays may reduce performance, they do not affect the correctness of the search.

6.3 Work-Stealing Performance

Effective work-stealing is crucial to obtaining good performance in task parallel search. We investigate this using three representative MaxClique instances, brock400_1, brock800_4 and brock400_3, to show that performance portability is achievable. We report results from a single execution on 8 localities with Depth-bounded, Stack-Stealing, and Budget search coordinations.

Fig. 6.

Sample per-locality work generation and stealing statistics.

Figure 6a shows the number of spawns, and local/distributed steals per locality for brock400_1 with Depth-Bounded coordination. A uniform distribution of tasks across localities is unlikely given the huge variance in task runtime. Rather, YewPar effectively ensures that all localities have work, i.e. almost all localities have 2000+ tasks.

Tasks are well distributed across the localities as they are spawned during the search rather than upfront. A large proportion of the steals occur locally as there are many localities with < 500 distributed steals. YewPar handles the large numbers of tasks efficiently, scheduling and running 26924 tasks in 3.5s (7692 tasks per second).

Figure 6b summarises the work-stealing statistics for brock800_4 with Stack-Stealing coordination. As work is generated on demand, there is no spawn count. As steals can occur at any depth in the search tree many local steals are successful. Locality 0 steals little, probably because it holds the largest tasks.

Figure 6c summarises work-stealing statistics for brock800_4 with Budget coordination. Like Depth-Bounded the work is well spread across the localities, with almost all having 2000+ tasks. Locality 4 has relatively few tasks despite stealing successfully, and we infer that most of the tasks stolen are small.

In summary, YewPar efficiently handles searches with thousands of tasks spread over 120 workers. All search coordinations work well with MaxClique ensuring a sufficient number of tasks per locality despite the high degree of irregularity common in search applications.

6.4 Scalability of YewPar

To investigate scalability we evaluate the runtimes and relative speedups of large instances of both MaxClique instances and Numerical Semigroups on 255 workers across 17 localities. Speedup is relative to a single locality with 15 workers as one worker runs take a significant time, i.e. around 2–3 hours per instance.

Fig. 7.

Scaling performance of MaxClique. Error bars show min/max runtimes.

Figure 7 shows the runtime and relative speedup for the three search coordinations on two MaxClique instances. Depth-Bounded is best with a super-linear speedup, caused by subtree pruning, of 31.0 on 16 localities. We deduce that tasks searching subtrees at $d_{ cutoff }$ are generally long running. In comparison, Stack-Stealing and Budget are slower as they interrupt search more frequently.

Parameter values like $d_{ cutoff }$ and budget can have a large impact of parallel performance (see 6.5 and 6.7 of [2]). Techniques that guide users to chose good, or low-risk, values remains an open problem.

Fig. 8.

Scaling performance of Numerical Semigroups. Error bars show min/max runtimes.

Figure 8 shows the runtime and relative speedups of Numerical Semigroups. Budget is best with a maximum speedup of 15.4 on 17 localities. Depth-Bounded performs worst, timing out after 30 min regardless of the number of workers. This illustrates the need for a search framework like YewPar to provide multiple search coordinations that are suitable for different search applications; allowing it to often achieve an average efficiency of >50% even for these highly irregular computations.

7 Conclusion

Parallel combinatorial search is challenging and we argue for improving the reuse of parallel searches. For this purpose we present the design and implementation a new parallel search framework. YewPar generalises search by abstracting the search tree generation, and by providing algorithmic skeletons that support three search types, and a set of standard search coordination strategies. A novel feature is the depth-pool, a new distributed workpool that preserves search heuristics to minimise runtime variance.

Evaluating YewPar on around 15 instances of two search applications (MaxClique and Numerical Semigroups) demonstrates its generality and effectiveness. The cost of YewPar generality is low: averaging 6.1% compared with a specific implementation. Moreover global knowledge is inexpensively shared between search tasks; the irregular tasks are effectively distributed; and YewPar delivers good runtimes, speedups and efficiency with up to 255 workers on 17 locations.