Abstract
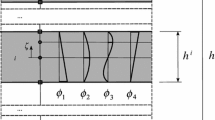
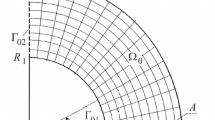
On the basis of a simplified rigid model of a layered elastic body, an engineering technique for determining the parameters of a contact is proposed for the indentation of a spherical indenter into it. The model is based on the dependence of the displacement of the points of the half-space along the axis of symmetry on the magnitude of the applied distributed load. The reduced elasticity modulus and the Poisson’s ratio are determined depending on the elastic properties of the base and coating materials, the thickness of the coating, and the radius of the contact area. Equations are given for determining the parameters of a contact when a spherical indenter is indented into a layered body. The obtained results are compared with the exact solution of the spatial axisymmetric problem for describing the stress-strain state in an elastic layer when a spherical indenter is indented into it, obtained by A. P. Makushkin using the Fourier–Bessel integral transformation method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Kovalev EP, Ignat’ev MB, Semenov AP et al (2004) J Friction Wear 25:316–336
Makushkin AP (1993) Polymers in friction and seal assemblies at low temperatures. Mechanical Engineering, Moscow
Torskaya EV (2014) Modeling of frictional interaction of bodies with coverings. Dissertation, Moscow
Aleksandrov VM, Mkhitaryan SM (1983) Contact problems for bodies with elastic coatings and interlayers. Nauka, Moscow
Giannakopoulos AT, Suresh T (1997) Indentation of solids with gradients in elastic properties. J Solids Struct 34:2357–2392
Aizikovich SM, Aleksandrov VM, Vasiliev AS, Krenev LI, Trubchik IS (2011) Analytic solutions of mixed axisymmetric problems for functional gradient media. Fizmatlit, Moscow
Potelezhko VP (2006) The Bousinescu problem for a two-layer half-space. Mech Phy Process Surf Contact of Solid Bodies Mach Parts 2:27–32
Argatov II (2004) Approximate solution of an axisymmetric contact problem for an elastic layer of finite thickness. Probl Mech Eng Reliab Mach 6:35–40
Voronin NA (1993) Application of the theory of the elastic Hertz contact to the calculation of the stress-strain state of a layered elastic body. Friction and Wear 14:250–258
Voronin NA (2002) Calculation of elastic contact parameters and effective characteristics of the topocomposite for the case of interaction of the latter with a spherical indenter. Friction Wear 23:583–596
Ogar PM, Tarasov VA, Fedorov IB (2013) Control of stiffness of contact systems of sealing joints modern technologies. Syst Anal Model 1:2–27
Ogar PM, Tarasov VA (2013) Determination of the elastic characteristics of bodies with thin coatings. Adv Mater Res 677:267–272
Ogar PM, Gorokhov DB, Kozhevnikov AS (2016) Effective modulus of elasticity of a layered body. Modern technologies. Syst Anal Model 4(52):37–42
Kozhevnikov AS (2017) Simplified model of a layered body. Mech XXI Century 16:211–217
Ogar P, Kozhevnikov A, Fedorov V (2018) The reduced modulus of elasticity of a layered half-space. MATEC Web Conf 224:02051
Johnson K (1989) Contact mechanics. Mir, Moscow
Argatov II, Dmitriev NN (2003) Fundamentals of the theory of elastic discrete contact. Politechnica, St.-Peterburg
O’Sullivan TC, King RB (1988) Sliding contact stress field due to a spherical indenter on a layered elastic half-space, ASME. J Tribol 110:235–240
Peng W, Bhushan B (2001) Three-dimensional contact analysis of layered elastic/plastic solids with rough surfaces. Wear 249:741–760
Peng W (2001) Contact mechanics of multilayered rough surfaces in tribology. Dissertation, The Ohio State University
Ogar P, Alpatov Yu, Gorokhov D (2018) Relative contact area in metal-polymer joints. MATEC Web Conf 224:02051
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Ogar, P., Kozhevnikov, A., Kushnarev, V. (2020). Modeling Introduction of Rigid Sphere into Layered Elastic Body. In: Radionov, A., Kravchenko, O., Guzeev, V., Rozhdestvenskiy, Y. (eds) Proceedings of the 5th International Conference on Industrial Engineering (ICIE 2019). ICIE 2019. Lecture Notes in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-030-22041-9_125
Download citation
DOI: https://doi.org/10.1007/978-3-030-22041-9_125
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22040-2
Online ISBN: 978-3-030-22041-9
eBook Packages: EngineeringEngineering (R0)