Abstract
We present an extensive collection of quantitative models to facilitate the development, comparison, and benchmarking of new verification algorithms and tools. All models have a formal semantics in terms of extensions of Markov chains, are provided in the Jani format, and are documented by a comprehensive set of metadata. The collection is highly diverse: it includes established probabilistic verification and planning benchmarks, industrial case studies, models of biological systems, dynamic fault trees, and Petri net examples, all originally specified in a variety of modelling languages. It archives detailed tool performance data for each model, enabling immediate comparisons between tools and among tool versions over time. The collection is easy to access via a client-side web application at qcomp.org with powerful search and visualisation features. It can be extended via a Git-based submission process, and is openly accessible according to the terms of the CC-BY license.
Authors are listed alphabetically. This work was supported by DFG grant 389792660 (part of CRC 248), ERC Advanced Grants 695614 (POWVER) and 781914 (FRAPPANT), NWO and BetterBe grant 628.010.006, and NWO VENI grant 639.021.754.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Quantitative verification is the analysis of formal models and requirements that capture probabilistic behaviour, hard and soft real-time aspects, or complex continuous dynamics. Its applications include probabilistic programs, safety-critical and fault-tolerant systems, biological processes, queueing systems, and planning in uncertain environments. Quantitative verification tools can, for example, compute the worst-case probability of failure within a time bound, the minimal expected cost to achieve a goal, or a Pareto-optimal control strategy balancing energy consumption versus the probability of unsafe behaviour. Two prominent such tools are Prism [15] for probabilistic and Uppaal [17] for real-time systems.
Over the past decade, various improvements and extensions have been made to quantitative model checking algorithms, with different approaches implemented in an increasing number of tools, e.g. [7, 8, 11, 13, 18]. Researchers, tool developers, non-academic users, and reviewers can all greatly benefit from a common set of realistic and challenging examples that new algorithms and tools are consistently benchmarked and compared on and that may indicate the practicality of a new method or tool. Such sets, and the associated push to standardised semantics, formats, and interfaces, have proven their usefulness in other areas such as software verification [4] and SMT solving [3].
In quantitative verification, the Prism Benchmark Suite (PBS) [16] has served this role for the past seven years. It provides 24 distinct examples in the Prism language covering discrete- and continuous time Markov chains (DTMC and CTMC), discrete-time Markov decision processes (MDP), and probabilistic timed automata (PTA). To date, it has been used in over 60 scientific papers. Yet several developments over the past seven years are not adequately reflected or supported by the PBS. New tools (1) support other modelling languages and semantics (in particular, several tools have converged on the Jani model exchange format [6]), and (2) exploit higher-level formalisms like Petri nets or fault trees. In addition, (3) today’s quantitative verification tools employ a wide range of techniques, whereas the majority of models in the PBS work best with Prism’s original BDD-based approach. Furthermore, (4) probabilistic verification and planning have been connected (e.g. [14]), and (5) MDP have gained in prominence through recent breakthroughs in AI and learning.
We present the Quantitative Verification Benchmark Set (QVBS): a new and growing collection of currently 72 models (Sect. 2) in the Jani format, documented by comprehensive metadata. It includes all models from the PBS plus a variety of new examples originally specified in significantly different modelling languages. It also covers decision processes in continuous stochastic time via Markov automata (MA [9]). The QVBS aggregates performance results obtained by different tools on its models (Sect. 3). All data is accessible via a client-side web application with powerful search and visualisation capabilities (Sect. 4).
2 A Collection of Quantitative Models
The Quantitative Verification Benchmark Set is characterised by commonality and diversity. All models are available in the Jani model exchange format [6], and they all have a well-defined formal semantics in terms of five related automata-based probabilistic models based on Markov chains. At the same time, the models of the QVBS originate from a number of different application domains, were specified in six modelling languages (with the original models plus information on the Jani conversion process being preserved in the QVBS), and pose different challenges including state space explosion, numeric difficulties, and rare events.
Syntax and semantics. The QVBS accepts any interesting model with a Jani translation to the DTMC, CTMC, MDP, MA, and PTA model types. Its current models were originally specified in Galileo for fault trees [20], GreatSPN [2] for Petri nets, the Modest language [5], PGCL for probabilistic programs [10], PPDDL for planning domains [21], and the Prism language [15]. By also storing the original model, structural information (such as in Petri nets or fault trees) that is lost by a conversion to an automata-based model is preserved for tools that can exploit it. We plan to broaden the scope to e.g. stochastic timed automata [5] or stochastic hybrid systems [1] in coordination with interested tool authors.
Sources and application domains. 41 of the QVBS’s current 72 models stem from existing smaller and more specialised collections: 24 from the PRISM Benchmark Suite (PBS) [16], 10 from the probabilistic/uncertainty tracks of the 2006 and 2008 International Planning Competitions (IPPC) [21], and 7 repairable dynamic fault trees from the Twente Arberretum (TA) [19]. 65 of the models can be categorised as representing systems from six broad application domains: models of communication protocols (com), of more abstract randomised and distributed algorithms (rda), for dependability and performance evaluation (dpe), of planning, scheduling and operations management scenarios (pso), of biological processes (bio), and of mechanisms for security and privacy (sec). We summarise the sources and application domains of the QVBS models in Table 1.
Metadata. Alongside each model, in original and Jani format, we store a comprehensive set of structured Json metadata to facilitate browsing and data mining the benchmark set. This includes basic information such as a description of the model, its version history, and references to the original source and relevant literature. Almost all models are parameterised such that the difficulty of analysing the model can be varied: some parameters influence the size of the state spaces, others may be time bounds used in properties, etc. The metadata documents all parameters and the ranges of admissible values. It includes sets of “proposed” parameter valuations with corresponding state space sizes and reference results. Each model contains a set of properties to be analysed; they are categorised into probabilistic unbounded and bounded reachability (P and Pb), unbounded and bounded expected rewards (E and Eb), and steady-state queries (S). Table 2 summarises the number of properties of each type (left), and the number of suggested parameter valuations (right) per resulting state space size (if available), where e.g. column “\(10^6\)” lists the numbers of valuations yielding \(10^4\) to \(10^6\) states.
3 An Archive of Results
The Quantitative Verification Benchmark Set collects not only models, but also results: the values of the properties that have been checked and performance data on runtime and memory usage. For every model, we archive results obtained with different tools/tool versions and settings on different hardware in a structured Json format. The aim is to collect a “big dataset” of performance information that can be mined for patterns over tools, models, and time. It also gives developers of new tools and algorithms a quick indication of the relative performance of their implementation, saving the often cumbersome process of installing and running many third-party tools locally. Developers of existing tools may profit from an archive of the performance of their own tool, helping to highlight performance improvements—or pinpoint regressions—over time. The QVBS includes a graphical interface to aggregate and visualise this data (see Sect. 4 below).
4 Accessing the Benchmark Set
The models and results data of the Quantitative Verification Benchmark Set are managed in a Git repository at github.com/ahartmanns/qcomp. A user-friendly interface is provided at qcomp.org/benchmarks via a web application that dynamically loads the Json data and presents it in two views:
The model browser presents a list of all models with key metadata. The list can be refined by a full-text search over the models’ names, descriptions and notes, and by filters for model type, original modelling language, property types, and state space size. For example, a user could request the list of all Modest MDP models with an expected-reward property and at least ten million states. Every model can be opened in a detail view that links to the Jani and original files, shows all metadata including parameters, proposed valuations, and properties with reference results, and provides access to all archived results. Figure 1 shows the model browser filtered to GreatSPN models that include a bounded probabilistic reachability property. The flexible-manufacturing model is open in detail view.
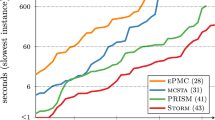
The results browser is accessed by selecting one or more models in the model browser and opening the “compare results” link. It provides a flexible, summarising view of the performance data collected from all archived results for the selected models. The data can be filtered to include select properties or parameter valuations only. It is visualised as a table or different types of charts, including bar charts and scatter plots. Figure 2 shows the result browser for the beb and breakdown-queues models, comparing the performance of mcsta [13] with default settings to Storm [8] in its slower “exact” mode. The performance data can optionally be normalised by the benchmark scores of the CPU used to somewhat improve comparability, although this still disregards many other important factors (like memory bandwidth and storage latency), of course.
The web application is entirely client-side: all data is loaded into the user’s browser as needed. All aggregation, filtering, and visualisation is implemented in Javascript. The application thus has no requirements on the server side. It is part of the Git repository and can be downloaded and opened offline by anyone.
5 Conclusion
Building upon the successful foundation of the Prism Benchmark Suite, the new Quantitative Verification Benchmark Set not only expands the number and diversity of easily accessible benchmarks, but also professionalises the collection and provision of benchmark data through its Json-based formats for metadata and results. We expect its associated web application to become a valuable tool for researchers, tool authors, and users alike. The QVBS is also an open dataset: all content is available under the CC-BY license, and new content—new models, updates, and results—can be contributed via a well-defined Git-based process. The Quantitative Verification Benchmark Set is the sole source of models for QComp 2019 [12], the first friendly competition of quantitative verification tools.
References
Abate, A., Blom, H., Cauchi, N., Haesaert, S., Hartmanns, A., Lesser, K., Oishi, M., Sivaramakrishnan, V., Soudjani, S., Vasile, C.I., Vinod, A.P.: ARCH-COMP18 category report: stochastic modelling. In: ARCH Workshop at ADHS. EPiC Series in Computing, vol. 54, pp. 71–103. EasyChair (2018)
Amparore, E.G., Balbo, G., Beccuti, M., Donatelli, S., Franceschinis, G.: 30 years of GreatSPN. In: Fiondella, L., Puliafito, A. (eds.) Principles of Performance and Reliability Modeling and Evaluation. SSRE, pp. 227–254. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-30599-8_9
Barrett, C., Fontaine, P., Tinelli, C.: SMT-LIB benchmarks. http://smtlib.cs.uiowa.edu/benchmarks.shtml
Beyer, D.: Software verification with validation of results. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10206, pp. 331–349. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54580-5_20
Bohnenkamp, H.C., D’Argenio, P.R., Hermanns, H., Katoen, J.P.: MoDeST: a compositional modeling formalism for hard and softly timed systems. IEEE Trans. Software Eng. 32(10), 812–830 (2006)
Budde, C.E., Dehnert, C., Hahn, E.M., Hartmanns, A., Junges, S., Turrini, A.: JANI: quantitative model and tool interaction. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10206, pp. 151–168. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54580-5_9
David, A., Jensen, P.G., Larsen, K.G., Mikučionis, M., Taankvist, J.H.: Uppaal Stratego. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 206–211. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_16
Dehnert, C., Junges, S., Katoen, J.-P., Volk, M.: A Storm is coming: a modern probabilistic model checker. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 592–600. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_31
Eisentraut, C., Hermanns, H., Zhang, L.: On probabilistic automata in continuous time. In: LICS, pp. 342–351. IEEE Computer Society (2010)
Gordon, A.D., Henzinger, T.A., Nori, A.V., Rajamani, S.K.: Probabilistic programming. In: FOSE, pp. 167–181. ACM (2014)
Hahn, E.M., Li, Y., Schewe, S., Turrini, A., Zhang, L.: iscasMc: a web-based probabilistic model checker. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 312–317. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06410-9_22
Hartmanns, A., Hensel, C., Klauck, M., Klein, J., Kretínský, J., Parker, D., Quatmann, T., Ruijters, E., Steinmetz, M.: The 2019 comparison of tools for the analysis of quantitative formal models. In: Beyer, D., Huisman, M., Kordon, F., Steffen, B. (eds.) TACAS 2019. LNCS, vol. 11429, pp. 69–92. Springer, Cham (2019)
Hartmanns, A., Hermanns, H.: The Modest Toolset: an integrated environment for quantitative modelling and verification. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 593–598. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_51
Klauck, M., Steinmetz, M., Hoffmann, J., Hermanns, H.: Compiling probabilistic model checking into probabilistic planning. In: ICAPS. AAAI Press (2018)
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Kwiatkowska, M.Z., Norman, G., Parker, D.: The PRISM benchmark suite. In: QEST, pp. 203–204. IEEE Computer Society (2012)
Larsen, K.G., Lorber, F., Nielsen, B.: 20 years of UPPAAL enabled industrial model-based validation and beyond. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11247, pp. 212–229. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03427-6_18
Legay, A., Sedwards, S., Traonouez, L.-M.: Plasma Lab: a modular statistical model checking platform. In: Margaria, T., Steffen, B. (eds.) ISoLA 2016. LNCS, vol. 9952, pp. 77–93. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-47166-2_6
Ruijters, E., et al.: The Twente Arberretum. https://dftbenchmarks.utwente.nl/
Sullivan, K.J., Dugan, J.B., Coppit, D.: The Galileo fault tree analysis tool. In: FTCS-29, pp. 232–235. IEEE Computer Society (1999)
Younes, H.L.S., Littman, M.L., Weissman, D., Asmuth, J.: The first probabilistic track of the International Planning Competition. J. Artif. Intell. Res. 24, 851–887 (2005)
Acknowledgments
The authors thank Paul Gainer (University of Liverpool), Sebastian Junges (RWTH Aachen), Joachim Klein (Technische Universität Dresden), Matthias Volk (RWTH Aachen), and Zhen Zhang (Utah State University) for submitting models to the QVBS, Gethin Norman (University of Glasgow) for his contributions to the Prism Benchmark Suite, and Marcel Steinmetz (Saarland University) for translating the IPPC benchmarks.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Hartmanns, A., Klauck, M., Parker, D., Quatmann, T., Ruijters, E. (2019). The Quantitative Verification Benchmark Set. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11427. Springer, Cham. https://doi.org/10.1007/978-3-030-17462-0_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-17462-0_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17461-3
Online ISBN: 978-3-030-17462-0
eBook Packages: Computer ScienceComputer Science (R0)