Abstract
We present a behavioural typing system for a higher-order timed calculus using session types to model timed protocols. Behavioural typing ensures that processes in the calculus perform actions in the time-windows prescribed by their protocols. We introduce duality and subtyping for timed asynchronous session types. Our notion of duality allows typing a larger class of processes with respect to previous proposals. Subtyping is critical for the precision of our typing system, especially in the presence of session delegation. The composition of dual (timed asynchronous) types enjoys progress when using an urgent receive semantics, in which receive actions are executed as soon as the expected message is available. Our calculus increases the modelling power of extant calculi on timed sessions, adding a blocking receive primitive with timeout and a primitive that consumes an arbitrary amount of time in a given range.
This work has been partially supported by EPSRC EP/N035372/1, EP/K011715/1, EP/N027833/1, EP/K034413/1, EP/L00058X/1, EP/N028201/1, Aut. Reg. of Sardinia projects Sardcoin and Smart collaborative engineering, FCT through project Confident PTDC/EEI-CTP/4503/2014 and the LASIGE Research Unit UID/CEC/00408/2019. We thank Julien Lange for his advise and comments.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Time is at the basis of many real-life protocols. These include common client-server interactions as for example, “An SMTP server SHOULD have a timeout of at least 5 minutes while it is awaiting the next command from the sender” [22]. By protocol, we intend application-level specifications of interaction patterns (via message passing) among distributed applications. An extensive literature offers theories and tools for formal analysis of timed protocols, modelled for instance as timed automata [3, 26, 34] or Message Sequence Charts [2]. These works allow to reason on the properties of protocols, defined as formal models. Recent work, based on session types, focus on the relationship between time-sensitive protocols, modelled as timed extensions of session types, and their implementations abstracted as processes in some timed calculus. The relationship between protocols and processes is given in terms of static behavioural typing [12, 15] or run-time monitoring [6, 7, 30] of processes against types. Existing work on timed session types [7, 12, 15, 30] is based on simple abstractions for processes which do not capture time sensitive primitives such as blocking (as well as non-blocking) receive primitives with timeout and time consuming actions with variable, yet bound, duration. This paper provides a theory of asynchronous timed session types for a calculus that features these two primitives. We focus on the asynchronous scenario, as modern distributed systems (e.g., web) are often based on asynchronous communications via FIFO channels [4, 33]. The link between protocols and processes is given in terms of static behavioural typing, checking for punctuality of interactions with respect to protocols prescriptions. Unlike previous work on asynchronous timed session types [12], our type system can check processes against protocols that are not wait-free. In wait-free protocols, the time-windows for corresponding send and receive actions have an empty intersection. We illustrate wait-freedom using a protocol modelled as two timed session types, each owning a set of clocks (with no shared clocks between types).

The protocol in (1) involves a client \(S_{\mathtt {C}}\) with a clock x, and a server \(S_{\mathtt {S}}\) with a clock y (with both x and y initially set to 0). Following the protocol, the client must send a message of type \(\mathtt {Command}\) within 5 min, reset x, and continue as \(S_\mathtt {C}'\). Dually, the server must be ready to receive a command with a timeout of 5 min, reset y, and continue as \( S_{\mathtt {S}}'\). The model in (1) is not wait-free: the intersection of the time-windows for the send and receive actions is non-empty (the time-windows actually coincide). The protocol in (2), where the server must wait until after the client’s deadline to read the message, is wait-free.

Patterns like the one in (1) are common (e.g., the SMPT fragment mentioned at the beginning of this introduction) but, unfortunately, they are not wait-free, hence ruled out in previous work [12]. Arguably, (2) is an unpractical wait-free variant of (1): the client must always wait for at least 5 min to have the message read, no matter how early this message was sent. The definition of protocols for our typing system (which allows for not wait-free protocols) is based on a notion of asynchronous timed duality, and on a subtyping relation that provides accuracy of typing, especially in the case of channel passing.
Asynchronous timed duality. In the untimed scenario, each session type has one unique dual that is obtained by changing the polarities of the actions (send vs. receive, and selection vs. branching). For example, the dual of a session type \(S\) that sends an integer and then receives a string is a session type \(\overline{S}\) that receives an integer and then sends a string.

Duality characterises well-behaved systems: the behaviour described by the composition of dual types has no communication mismatches (e.g., unexpected messages, or messages with values of unexpected types) nor deadlocks. In the timed scenario, this is no longer true. Consider a timed extension of session types (using the model of time in timed automata [3]), and of (untimed) duality so that dual send/receive actions have equivalent time constraints and resets. The example below shows a timed type S with its dual \(\overline{S}\), where S owns clock x, and \(\overline{S}\) owns clock y (with x and y initially set to 0):

Here \(S\) sends an integer at any time satisfying \(x\leqslant 1\), and then resets x. After that, \(S\) receives a string at any time satisfying \(x\leqslant 2\). The timed dual of \(S\) is obtained by keeping the same time constraints (and renaming the clock—to make it clear that clocks are not shared). To illustrate our point, we use the semantics from timed session types [12], borrowed from Communicating Timed automata [23]. This semantics is separated, in the sense that only time actions may ‘take time’, while all other actions (e.g., communications) are instantaneous.Footnote 1 The aforementioned semantics allows for the following execution of \(S\mid \overline{S}\):

where: (i) the system makes a time step of 0.4, then S sends the integer and resets x, yielding a state where \(x=0\) and \(y=0.4\); (ii) the system makes a time step of 0.6, then \(\overline{S}\) receives the integer and resets y, yielding a state where \(x=0.6\) and \(y=0\); (iii) the system makes a time step of 2, then the continuation of \(\overline{S}\) sends the string, when \(y=2\) and \(x=2.6\). In (iii), the string was sent too late: constraint \(x\leqslant 2\) of the receiving endpoint is now unsatisfiable. The system cannot do any further legal step, and is stuck.
Urgent receive semantics. The example above shows that, in the timed asynchronous scenario, the straightforward extension of duality to the timed scenario does not necessarily characterise well-behaved communications. We argue, however, that the execution of \(S\mid \overline{S}\), in particular the time reduction with label 0.6, does not reflect the semantics of most common receive primitives. In fact, most mainstream programming languages implement urgent receive semantics for receive actions. We call a semantics urgent receive when receive actions are executed as soon as the expected message is available, given that the guard of that action is satisfied. Conversely, non-urgent receive semantics allows receive actions to fire at any time satisfying the time constraint, as long as the message is in the queue. The aforementioned reduction with label 0.6 is permitted by non-urgent receive semantics such as the one in [23], since it defers the reception of the integer despite the integer being ready for reception and the guard (\(y\leqslant 2\)) being satisfied, but not by urgent receive semantics. Urgent receive semantics allows, instead, the following execution for \(S\mid \overline{S}\):

If S sends the integer when \(x=0.4\), then \(\overline{S}\) must receive the integer immediately, when \(y=0.4\). At this point, both endpoints reset their respective clocks, and the communication will continue in sync. Urgent receive primitives are common; some examples are the non-blocking \(\mathtt {WaitFreeReadQueue.read()}\) and blocking \(\mathtt {WaitFreeReadQueue.waitForData()}\) of Real-Time Java [13], and the receive primitives in Erlang and Golang. Urgent receive semantics make interactions “more synchronous” but still as asynchronous as real-life programs.
A calculus for timed asynchronous processes. Our calculus features two time-sensitive primitives. The first is a parametric receive operation \(a^{n}(b).\, P\) on a channel a, with a timeout n that can be \(\infty \) or any number in \(\mathbf {R}_{\geqslant 0}\). The parametric receive captures a range of receive primitives: non-blocking (\(n=0\)), blocking without timeout (\(n=\infty \)), or blocking with timeout (\(n\in \mathbf {R}_{> 0}\)). The second primitive is a time-consuming action, \(\mathtt {delay}(\delta ).\, P\), where \(\delta \) is a constraint expressing the time-window for the time consumed by that action. Delay processes model primitives like \(\mathtt {Thread.sleep}(n)\) in real-time Java [13] or, more generally, any time-consuming action, with \(\delta \) being an estimation of the delay of computation.
Processes in our calculus abstract implementations of protocols given as pairs of dual types. Consider the processes below.

Processes abiding the protocols in (2) could be as follows: \(P_C\) for the client \(S_C\), and \(P_S\) for the server \(S_S\). The client process \(P_C\) performs a time consuming action for up to 3 min, then sends command \(\mathtt {HELO}\) to the server, and continues as \(P_C'\). The server process \(P_S\) sleeps for exactly 5 min, receives the message immediately (without blocking), and continues as \(P_S'\). A process for the protocol in (1) could, instead be the parallel composition of \(P_C\), again for the client, and \(Q_S\) for the server. Process \(Q_S\) uses a blocking primitive with timeout; the server now blocks on the receive action with a timeout of 5 min, and continues as \(Q_S'\) as soon as a message is received. The blocking receive primitive with timeout is crucial to model processes typed against protocols one can express with asynchronous timed duality, in particular those that are not wait-free.
A type system for timed asynchronous processes. The relationship between types and processes in our calculus is given as a typing system. Well-typed processes are ensured to communicate at the times prescribed by their types. This result is given via Subject Reduction (Theorem 4), establishing that well-typedness is preserved by reduction. In our timed scenario, Subject Reduction holds under receive liveness, an assumption on the interaction structure of processes. This assumption is orthogonal to time. To characterise the interaction structures of a timed process we erase timing information from that processes (time erasure). Receive liveness requires that, whenever a time-erased processes is waiting for a message, the corresponding message is eventually provided by the rest of the system. While receive liveness is not needed for Subject Reduction in untimed systems [21], it is required for timed processes. This reflects the natural intuition that if an untimed-process violates progress, then its timed counterpart may miss deadlines. Notably, we can rely on existing behavioural checking techniques from the untimed setting to ensure receive liveness [17].
Receive liveness is not required for Subject Reduction in a related work on asynchronous timed session types [12]. The dissimilarity in the assumptions is only apparent; it derives from differences in the two semantics for processes. When our processes cannot proceed correctly (e.g., in case of missed deadlines) they reduce to a failed state, whereas the processes in [12] become stuck (indicating violation of progress).
Synopsis. In Sect. 2 we introduce the syntax and the formation rules for asynchronous timed session types. In Sect. 3, we give a modular Labelled Transition System (LTS) for types in isolation (Sect. 3.1) and for compositions of types (Sect. 3.3). The subtyping relation is given in Sect. 3.2 and motivated in Example 8, after introducing the typing rules. We introduce timed asynchronous duality and its properties in Sect. 4. Remarkably, the composition of dual timed asynchronous types enjoys progress when using an urgent receive semantics (Theorem 1). Section 5 presents a calculus for timed processes and Sect. 6 introduces its typing system. The properties of our typing system—Subject Reduction (Theorem 4) and Time Safety (Theorem 5)—are introduced in Sect. 7. Conclusions and related works are in Sect. 8. Proofs and additional material can be found in the online report [11].
2 Asynchronous Timed Session Types
Clocks and predicates. We use the model of time from timed automata [3]. Let \(\mathbb {X}\) be a finite set of clocks, let \(x_1, \ldots , x_n\) range over clocks, and let each clock take values in \(\mathbf {R}_{\geqslant 0}\). Let \(t_1, \ldots , t_n\) range over non-negative real numbers and \(n_1, \ldots , n_n\) range over non-negative rationals. The set \(\mathcal {G}(\mathbb {X})\) of predicates over \(\mathbb {X}\) is defined by the following grammar.

We derive \(\mathtt {false}\), <, \(\geqslant \), \(\leqslant \) in the standard way. Predicates in the form \(x- y> n\) and \(x- y= n\) are called diagonal predicates; in these cases we assume \(x\ne y\). Notation \( cn (\delta )\) stands for the set of clocks in \(\delta \).
Clock valuation and resets. A clock valuation \(\nu : \mathbb {X}\mapsto \mathbf {R}_{\geqslant 0}\) returns the time of the clocks in \(\mathbb {X}\). We write \(\nu +t\) for the valuation mapping all \(x\in \mathbb {X}\) to \(\nu (x)+t\), \(\nu _0\) for the initial valuation (mapping all clocks to 0), and, more generally, \(\nu _t\) for the valuation mapping all clocks to t. Let \(\nu \models \delta \) denote that \(\delta \) is satisfied by \(\nu \). A reset predicate \(\lambda \) over \(\mathbb {X}\) is a subset of \(\mathbb {X}\). When \(\lambda \) is  then no reset occurs, otherwise the assignment for each \(x\in \lambda \) is set to 0. We write \(\nu \, [\lambda \mapsto 0]\) for the clock assignment that is like \(\nu \) everywhere except that its assigns 0 to all clocks in \(\lambda \).
then no reset occurs, otherwise the assignment for each \(x\in \lambda \) is set to 0. We write \(\nu \, [\lambda \mapsto 0]\) for the clock assignment that is like \(\nu \) everywhere except that its assigns 0 to all clocks in \(\lambda \).
Types. Timed session types, hereafter just types, have the following syntax:

Sorts \(T\) include base types ( ,
,  , etc.), and sessions \((\delta , S)\). Messages of type \((\delta , S)\) allow a participant involved in a session to delegate the remaining behaviour \(S\); upon delegation the sender will no longer participate in the delegated session and receiver will execute the protocol described by \(S\) under any clock assignment satisfying \(\delta \). We denote the set of types with \(\mathbb {T}\).
, etc.), and sessions \((\delta , S)\). Messages of type \((\delta , S)\) allow a participant involved in a session to delegate the remaining behaviour \(S\); upon delegation the sender will no longer participate in the delegated session and receiver will execute the protocol described by \(S\) under any clock assignment satisfying \(\delta \). We denote the set of types with \(\mathbb {T}\).
Type  models a send action of a payload with sort \(T\). The sending action is allowed at any time that satisfies the guard \(\delta \). The clocks in \(\lambda \) are reset upon sending. Type
models a send action of a payload with sort \(T\). The sending action is allowed at any time that satisfies the guard \(\delta \). The clocks in \(\lambda \) are reset upon sending. Type  models the dual receive action of a payload with sort \(T\). The receiving types require the endpoint to be ready to receive the message in the precise time window specified by the guard.
models the dual receive action of a payload with sort \(T\). The receiving types require the endpoint to be ready to receive the message in the precise time window specified by the guard.
Type  is a select action: the party chooses a branch \(i\in I\), where I is a finite set of indices, selects the label \(l_i\), and continues as prescribed by \(S_i\). Each branch is annotated with a guard \(\delta \) and reset \(\lambda \). A branch j can be selected at any time allowed by \(\delta _j\). The dual type is
is a select action: the party chooses a branch \(i\in I\), where I is a finite set of indices, selects the label \(l_i\), and continues as prescribed by \(S_i\). Each branch is annotated with a guard \(\delta \) and reset \(\lambda \). A branch j can be selected at any time allowed by \(\delta _j\). The dual type is  for branching actions. Each branch is annotated with a guard and a reset. The endpoint must be ready to receive the label for j at any time allowed by \(\delta _j\) (or until another branch is selected).
for branching actions. Each branch is annotated with a guard and a reset. The endpoint must be ready to receive the label for j at any time allowed by \(\delta _j\) (or until another branch is selected).
Recursive type \(\mu \alpha . S\) associates a type variable \(\alpha \) to a recursion body \(S\). We assume that type variables are guarded in the standard way (i.e., they only occur under actions or branches). We let \(\mathcal {A}\) denote the set of type variables.
Type \(\mathtt {end}\) models successful termination.
2.1 Type Formation
The grammar for types allow to generate types that are not implementable in practice, as the one shown in Example 1.
Example 1 (Junk-types)
Consider \(S\) in (3) under initial clock valuation \(\nu _0\).

The specified endpoint must be ready to receive a message in the time-window between 0 and 5 time units, as we evaluate \(x<5\) in \(\nu _0\). Assume that this receive action happens when \(x=3\), yielding a new state in which: (i) the clock valuation maps x to 3, and (ii) the endpoint must perform a send action while \(x<2\). Evidently, (ii) is no longer possible in the new clock valuation, as the \(x<2\) is now unsatisfiable. We could amend (3) in several ways: (a) by resetting x after the receive action; (b) by restricting the guard of the receive action (e.g., \(x<2\) instead of \(x<5\)); or (c) by relaxing the guard of the send action. All these amendments would, however, yield a different type.
In the remainder of this section we introduce formation rules to rule out junk types as the one in Example 1 and characterise types that are well-formed. Intuitively, well-formed types allow, at any point, to perform some action in the present time or at some point in the future, unless the type is \(\mathtt {end}\).
Judgments. The formation rules for types are defined on judgments of the form
where A is an environment assigning type variables to guards, and \(\delta \) is a guard in \(\mathcal {G}(\mathbb {X})\). A is used as an invariant to form recursive types. Guard \(\delta \) collects the possible ‘pasts’ from which the next action in \(S\) could be executed (unless \(S\) is \(\mathtt {end}\)). We use notation \(\mathbin {\downarrow {\delta }}\) (the past of \(\delta \)) for a guard \(\delta '\) such that \(\nu \models \delta '\) if and only if \(\exists t: \nu + t\models \delta \). For example, \(\mathbin {\downarrow {(1\leqslant x\leqslant 2)}} = x\leqslant 2\) and \(\mathbin {\downarrow {(x \geqslant 3)}} = \mathtt {true}\). Similarly, we use the notation \(\delta [\lambda \mapsto 0]\) to denote a guard in which all clocks in \(\lambda \) are reset. For example, \((x\leqslant 3\wedge y \leqslant 2)[{x}\mapsto 0] = (x=0 \wedge y\leqslant 2)\). We use the notation \(\delta _1 \subseteq \delta _2\) whenever, for all \(\nu \), \(\nu \models \delta _1 \implies \nu \models \delta _2\). The past and reset of a guard can be inferred algorithmically, and \(\subseteq \) is decidable [8].

Rule \({~[\mathtt {end}]~}\) states that the terminated type is well-formed against any A. The guard of the judgement is \(\mathtt {true}\) since \(\mathtt {end}\) is a final state (as \(\mathtt {end}\) has no continuation, morally, the constraint of its continuation is always satisfiable). Rule \({~[\mathtt {interact}]~}\) ensures that the past of the current action \(\delta \) entails the past of the subsequent action \(\gamma \) (considering resets if necessary): this rules out types in which the subsequent action can only be performed in the past. Rules \({~[\mathtt {end}]~}\) and \({~[\mathtt {interact}]~}\) are illustrated by the three examples below.
Example 2
The judgment below shows a type being discarded after an application of rule \({~[\mathtt {interact}]~}\):

The premise of \({~[\mathtt {interact}]~}\) would be  , which does not hold for \(\delta = 1 \leqslant x \leqslant 3\) and \(\mathbin {\downarrow {\gamma }}= x\leqslant 2\). This means that guard
, which does not hold for \(\delta = 1 \leqslant x \leqslant 3\) and \(\mathbin {\downarrow {\gamma }}= x\leqslant 2\). This means that guard  of the first action may lead to a state in which guard \(1 \leqslant x \leqslant 2\) for the subsequent action is unsatisfiable. If we amend the type in (4) by adding a reset in the first action, we obtain a well-formed type. We show its formation below, where for simplicity we omit obvious preconditions like
of the first action may lead to a state in which guard \(1 \leqslant x \leqslant 2\) for the subsequent action is unsatisfiable. If we amend the type in (4) by adding a reset in the first action, we obtain a well-formed type. We show its formation below, where for simplicity we omit obvious preconditions like  base type, etc.
base type, etc.

Rule \({~[\mathtt {delegate}]~}\) behaves as \({~[\mathtt {interact}]~}\), with two additional premises on the delegated session: (1) \(S'\) needs to be well-formed, and (2) the guard of the next action in \(S'\) needs to be satisfiable with respect to \(\delta '\). Guard \(\delta '\) is used to ensure a correspondence between the state of the delegating endpoint and that of the receiving endpoint. Rule \({~[\mathtt {choice}]~}\) is similar to \({~[\mathtt {interact}]~}\) but requires that there is at least one viable branch (this is accomplished by considering the weaker past \(\mathbin {\downarrow {\bigvee }}_{i\in I}\delta _i\)) and checking each branch for formation. Rules \({~[\mathtt {rec}]~}\) and \({~[\mathtt {var}]~}\) are for recursive types and variables, respectively. In \( {~[\mathtt {rec}]~}\) the guard \(\delta \) can be easily computed by taking the past of the next action of the in \(S\) (or the disjunction if \(S\) is a branching or selection). An algorithm for deciding type formation can be found in [11].
Definition 1 (Well-formed types)
We say that \(S\) is well-formed against clock valuation \(\nu \) if  and \(\nu \models \delta \), for some guard \(\delta \). We say that \(S\) is well-formed if it is well formed against \(\nu _0\).
and \(\nu \models \delta \), for some guard \(\delta \). We say that \(S\) is well-formed if it is well formed against \(\nu _0\).
We will tacitly assume types are well-formed, unless otherwise specified. The intuition of well-formedness is that if \(A ; \ \delta \, \vdash \,S\) then \(S\) can be run (using the types semantics given in Sect. 3) under any clock valuation \(\nu \) such that \(\nu \models \delta \). In the sequel, we take (well-formed) types equi-recursively [31].
3 Asynchronous Session Types Semantics and Subtyping
We give a compositional semantics of types. First, we focus on types in isolation from their environment and from their queues, which we call simple type configurations. Next we define subtyping for simple type configurations. Finally, we consider systems (i.e., composition of types communicating via queues).
3.1 Types in Isolation
The behaviour of simple type configurations is described by the Labelled Transition System (LTS) on pairs \((\nu ,S)\) over \((\mathbb {V} \times \mathcal {S})\), where clock valuation \(\nu \) gives the values of clocks in a specific state. The LTS is defined over the following labels

Label !m denotes an output action of message m and ?m an input action of m. A message m can be a sort \(T\) (that can be either a higher order message \((\delta , S)\) or base type), or a branching label  . The LTS for single types is defined as the least relation satisfying the rules in Fig. 1. Rules [snd], [rcv], [sel], and [bra] can only happen if the constraint of the next action is satisfied in the current clock valuation. Rule [rec] unfolds recursive types, and [time] always lets time elapse.
. The LTS for single types is defined as the least relation satisfying the rules in Fig. 1. Rules [snd], [rcv], [sel], and [bra] can only happen if the constraint of the next action is satisfied in the current clock valuation. Rule [rec] unfolds recursive types, and [time] always lets time elapse.
Let \(\mathbf {s}\), \(\mathbf {s}'\), \(\mathbf {s}_i\) (\(i\in \mathbb {N}\)) range over simple type configurations \((\nu , S)\). We write \(\mathbf {s}{\mathop {\longrightarrow }\limits ^{\ell }}\) when there exists \(\mathbf {s}'\) such that \(\mathbf {s}{\mathop {\longrightarrow }\limits ^{\ell }}\mathbf {s}'\), and write \(\mathbf {s}{\mathop {\longrightarrow }\limits ^{t \, \ell }}\) for \(\mathbf {s}{\mathop {\longrightarrow }\limits ^{t}} {\mathop {\longrightarrow }\limits ^{\ell }}\).
3.2 Asynchronous Timed Subtyping
We define subtyping as a partial relation on simple type configurations. As in other subtyping relations for session types we consider send and receive actions dually [14, 16, 19]. Our subtyping relation is covariant on output actions and contra-variant on input actions, similarly to that of [14]. In this way, our subtyping \(S <\,:S'\) captures the intuition that a process well-typed against S can be safely substituted with a process well-typed against \(S'\). Definition 2, introduces a notation that is useful in the rest of this section.
Definition 2 (Future enabled send/receive)
Action \(\ell \) is future enabled in \(\mathbf {s}\) if \(\exists t: \mathbf {s}{\mathop {\longrightarrow }\limits ^{t \, \ell }}\). We write \(\mathbf {s} {\mathop {\Rightarrow }\limits ^{!}}\) (resp. \(\mathbf {s} {\mathop {\Rightarrow }\limits ^{?}}\)) if there exists a sending action !m (resp. a receiving action ?m) that is future enabled in \(\mathbf {s}\).
As common in session types, the communication structure does not allow for mixed choices: the grammar of types enforces choices to be either all input (branching actions), or output (selection actions). From this fact it follows that, given \(\mathbf {s}\), reductions \(\mathbf {s} {\mathop {\Rightarrow }\limits ^{!}}\) and \(\mathbf {s} {\mathop {\Rightarrow }\limits ^{?}}\) cannot hold simultaneously.
Definition 3 (Timed Type Simulation)
Fix \(\mathbf {s}_1 = (\nu _1,S_1)\) and \(\mathbf {s}_2=(\nu _2,S_2)\). A relation \(\mathcal {R}\in (\mathbb {V} \times \mathcal {S})^2\) is a timed type simulation if \((\mathbf {s}_1,\mathbf {s}_2)\in \mathcal {R}\) implies the following conditions:
-
1.
\(S_1 = \mathtt {end}\) implies \(S_2 = \mathtt {end}\)
-
2.
\(\mathbf {s}_1 {\mathop {\longrightarrow }\limits ^{t \, !m_1}}\mathbf {s}_1'\) implies \(\exists \mathbf {s}_2',m_2:\mathbf {s}_2{\mathop {\longrightarrow }\limits ^{t \, !m_2}}\mathbf {s}_2'\), \((m_2,m_1) \in \mathcal {S}, (\mathbf {s}_1',\mathbf {s}_2')\in \mathcal {R}\)
-
3.
\(\mathbf {s}_2{\mathop {\longrightarrow }\limits ^{t \, ?m_2}}\mathbf {s}_2'\) implies \(\exists \mathbf {s}_1',m_1: \mathbf {s}_1{\mathop {\longrightarrow }\limits ^{t \, ?m_1}}\mathbf {s}_1'\), \((m_1,m_2) \in \mathcal {S}\), \((\mathbf {s}_1',\mathbf {s}_2')\in \mathcal {R}\)
-
4.
\(\mathbf {s}_1 {\mathop {\Rightarrow }\limits ^{?}}\) implies \(\mathbf {s}_2 {\mathop {\Rightarrow }\limits ^{?}}\) and \(\mathbf {s}_2 {\mathop {\Rightarrow }\limits ^{!}}\) implies \(\mathbf {s}_1 {\mathop {\Rightarrow }\limits ^{!}}\)
where \(\mathcal {S}\) is the following extension of \(\mathcal {R}\) to messages: (1) \((T,T') \in \mathcal {S}\) if T and \(T'\) are base types, and \(T'\) is a subtype of T by sorts subtyping, e.g., \((\mathtt {int},\mathtt {nat}) \in \mathcal {S}\); (2)  ; (3) \(((\delta _1, S_1),(\delta _2, S_2)) \in \mathcal {S}\), if \(\forall \nu _1\models \delta _1 \, \exists \nu _2\models \delta _2 : ((\nu _1, S_1),(\nu _2, S_2)) \in \mathcal {R}\) and \(\forall \nu _2\models \delta _2 \, \exists \nu _1\models \delta _1 : ((\nu _1, S_1),(\nu _2, S_2)) \in \mathcal {R}\).
; (3) \(((\delta _1, S_1),(\delta _2, S_2)) \in \mathcal {S}\), if \(\forall \nu _1\models \delta _1 \, \exists \nu _2\models \delta _2 : ((\nu _1, S_1),(\nu _2, S_2)) \in \mathcal {R}\) and \(\forall \nu _2\models \delta _2 \, \exists \nu _1\models \delta _1 : ((\nu _1, S_1),(\nu _2, S_2)) \in \mathcal {R}\).
Intuitively, if \((\mathbf {s}_1,\mathbf {s}_2)\in \mathcal {R}\) then any environment that can safely interact with \(\mathbf {s}_2\), can do so with \(\mathbf {s}_1\). We write that \(\mathbf {s}_2\) simulates \(\mathbf {s}_1\) whenever \(\mathbf {s}_1\) and \(\mathbf {s}_2\) are in a timed type simulation. Below, \(\mathbf {s}_2\) simulates \(\mathbf {s}_1\):

Conversely, \(\mathbf {s}_1\) does not simulate \(\mathbf {s}_2\) because of condition (2). Precisely, \(\mathbf {s}_2\) can make a transition \(\mathbf {s}_2 {\mathop {\longrightarrow }\limits ^{10 \, !\mathtt {int}}}\) that cannot be matched by \(\mathbf {s}_1\) for two reasons: guard \(x<5\) is no longer satisfiable when \(x=10\), and \((\mathtt {nat},\mathtt {int})\not \in \mathcal {S}\) since \(\mathtt {int}\) is not a subtype of \(\mathtt {nat}\). For receive actions, instead, we could substitute \(\mathbf {s}\) with \(\mathbf {s}'\) if \(\mathbf {s}'\) had at least the receiving capabilities of \(\mathbf {s}\). Condition (4) in Definition 3 rules out relations that include, e.g.,  .
.
Live simple type configurations. In our subtyping definition we are interested in simple type configurations that are not stuck. Consider the example below:

The simple type configuration in (5) would not be stuck if \(\nu = \nu _0\), but would be stuck for any \(\nu =\nu '[x\mapsto 10]\). Definition 4 gives a formal definition of simple type configurations that are not stuck, i.e., that are live.
Definition 4 (Live simple type configuration)
A simple configuration \((\nu ,S)\) is said live if:

Observe that for all well-formed \(S\), \((\nu _0, S)\) is live.
Subtyping for simple type configurations. We can now define subtyping for simple type configurations and state its decidability.
Definition 5 (Subtyping)
\(\mathbf {s}_1\) is a subtype of \(\mathbf {s}_2\), written \(\mathbf {s}_1 <\,:\mathbf {s}_2\), if there exists a timed type simulation \(\mathcal {R}\) on live simple type configurations such that \((\mathbf {s}_1,\mathbf {s}_2)\in \mathcal {R}\). We write \(S_1<\,:S_2\) when \((\nu _0, S_1) <\,:(\nu _0,S_2)\). Abusing the notation, we write \( m <\,:m'\) iff there exists \(\mathcal {S}\) such that \((m,m')\in \mathcal {S}\).
Subtyping has been shown to be decidable in the untimed setting [19] and in the timed first order setting [6]. In [6], decidability is shown through a reduction to model checking of timed automata networks. The result in [6] can be extended to higher-order messages using the techniques in [3], based on finite representations (called regions) of possibly infinite sets of clock valuations.
Proposition 1 (Decidability of subtyping)
Checking if \((\delta _1, S_1) <\,:(\delta _2, S_2)\) is decidable.
3.3 Types with Queues, and Their Composition
As interactions are asynchronous, the behaviour of types must capture the states in which messages are in transit. To do this, we extend simple type configurations with queues. A configuration \(\mathbf {S}\) is a triple \((\nu ,S, \mathtt {M})\) where \(\nu \) is clock valuation, \(S\) is a type and \(\mathtt {M}\) a FIFO unbounded queue of the following form:

\(\mathtt {M}\) contains the messages sent by the co-party of \(S\) and not yet received by \(S\). We write \(\mathtt {M}\) for  , and call \((\nu ,S, \mathtt {M})\) initial if \(\nu =\nu _0\) and
, and call \((\nu ,S, \mathtt {M})\) initial if \(\nu =\nu _0\) and  .
.
Composing types. Configurations are composed into systems. We denote \(\mathbf {S}\mid \mathbf {S}'\) as the parallel composition of the two configurations \(\mathbf {S}\) and \(\mathbf {S}'\).
The labelled transition rules for systems are given in Fig. 2. Rule (snd) is for send actions. A send action can occur only if the time constraint of \(S\) is satisfied (by the premise, which uses either rule [snd] or [sel] in Fig. 1). Rule (que) models actions on queues. A queue is always ready to receive any message m. Rule (rcv) is for receive actions, where a message is read from the queue. A receiving action can only occur if the time constraint of \(S\) is satisfied (by the premise, which uses either rule [rcv] or [bra] in Fig. 1). The message is removed from the head of the queue of the receiving configuration. The third clause in the premise uses the notion of subtyping (Definition 3) for basic sorts, labels, and higher order messages. Rule (crcv) is the action of a configuration pulling a message of its queue. Rule (com) is for communication between a sending configuration and a buffer. Rule (ctime) lets time elapse in the same way for all configurations in a system. Rule (time) models time passing for single configurations. Time passing is subject to two constrains, expressed by the second and third conditions in the premise. Condition \((\nu ,S) {\mathop {\Rightarrow }\limits ^{!}}\) requires the time action \(t\) to preserve the satisfiability of some send action. For example, in configuration  , a transition with label 2 would not preserve any send action (hence would not be allowed), while a transition with label 1.8 would be allowed by condition \((\nu ,S) {\mathop {\Rightarrow }\limits ^{!}}\). Condition \(\forall t' < t: (\nu + t',S,\mathtt {M}) {{\mathop {\nrightarrow }\limits ^{\tau }}}\) in the premise of rule (time) checks that there is no ready message to be received in the queue. This is to model urgency: when a configuration is in a receiving state and a message is in the queue then the receiving action must happen without delay. For example,
, a transition with label 2 would not preserve any send action (hence would not be allowed), while a transition with label 1.8 would be allowed by condition \((\nu ,S) {\mathop {\Rightarrow }\limits ^{!}}\). Condition \(\forall t' < t: (\nu + t',S,\mathtt {M}) {{\mathop {\nrightarrow }\limits ^{\tau }}}\) in the premise of rule (time) checks that there is no ready message to be received in the queue. This is to model urgency: when a configuration is in a receiving state and a message is in the queue then the receiving action must happen without delay. For example,  can make a transition with label 1, but
can make a transition with label 1, but  cannot make any time transition. Below we show two examples of system executions. Example 3 illustrates a good communication, thanks to urgency. We also illustrate in Example 4 that without an urgent semantics the system in Example 3 gets stuck.
cannot make any time transition. Below we show two examples of system executions. Example 3 illustrates a good communication, thanks to urgency. We also illustrate in Example 4 that without an urgent semantics the system in Example 3 gets stuck.
Example 3 (A good communication)
Consider the following types:

System  can make a time step with label 0.5 by \(\text {(ctime)}\), yielding the system in (6)
can make a time step with label 0.5 by \(\text {(ctime)}\), yielding the system in (6)

The system in (6) can move by a \(\tau \) step thanks to \({\text {(com)}}\): the left-hand side configuration makes a step with label !T by \({\text {(snd)}}\) while the right-hand side configuration makes a step ?T by \({\text {(que)}}\), yielding system (7) below.

The right-hand side configuration in the system in (7) must urgently receive message T due to the third clause in the premise of rule \(\text {(time)}\). Hence, the only possible step forward for (7) is by \(\text {(crcv)}\) yielding the system in (8).

Example 4 (In absence of urgency)
Without urgency, the system in (7) from Example 3 may get stuck. Assume the third clause of rule \(\text {(time)}\) was removed: this would allow (7) to make a time step with label 0.5, followed by a step by \(\text {(rcv)}\) yielding the system in (9), where clock y is reset after the receive action.

followed by a \(\tau \) step by \(\text {(com)}\) reaching the following state:

The message in the queue in (10) will never be received as the guard \(x\leqslant 2\) is not satisfiable now or at any point in the future. This system is stuck. Instead, thanks to urgency, the clocks of the configurations of system (8) have been ‘synchronised’ after the receive action, preventing the system from getting stuck.
4 Timed Asynchronous Duality
We introduce a timed extension of duality. As in untimed duality, we let each send/select action be complemented by a corresponding receive/branching action. Moreover, we require time constraints and resets to match.
Definition 6 (Timed duality)
The dual type \(\overline{S}\) of \(S\) is defined as follows:

Duality with urgent receive semantics enjoys the following properties: systems with dual types fulfil progress (Theorem 1); behaviour (resp. progress) of a system is preserved by the substitution of a type with a subtype (Theorem 2) (resp. Theorem 3). A system enjoys progress if it reaches states that are either final or that allow further communications, possibly after a delay. Recall that we assume types to be well-formed (cf. Definition 1): Theorems 1, 2, and 3 rely on this assumption.
Definition 7 (Type progress)
We say that a system \((\nu , {S}, \mathtt {M}) \) is a success if \(S= \mathtt {end}\) and  . We say that \(\mathbf {S}_1 \mid \mathbf {S}_2\) satisfies progress if:
. We say that \(\mathbf {S}_1 \mid \mathbf {S}_2\) satisfies progress if:

Theorem 1 (Duality progress)
System  enjoys progress.
enjoys progress.
We show that subtyping does not introduce new behaviour, via the usual notion of timed simulation [1]. Let \(\mathbf {c}, \mathbf {c}_1, \mathbf {c}_2\) range over systems. Fix \(\mathbf {c}_1= (\nu _1^1, S_1^1, \mathtt {M}_1^1)\mid (\nu _2^1, S_2^1, \mathtt {M}_2^1)\), and \(\mathbf {c}_2 = (\nu _1^2, S_1^2, \mathtt {M}_1^2)\mid (\nu _2^2, S_2^2, \mathtt {M}_2^2)\). We say that a binary relation over systems preserves \(\mathtt {end}\) if:  iff
iff  for all \(i\in \{1,2\}\). Write \(\mathbf {c}_1 \lesssim \mathbf {c}_2\) if \((\mathbf {c}_1, \mathbf {c}_2)\) are in a timed simulation that preserves \(\mathtt {end}\).
for all \(i\in \{1,2\}\). Write \(\mathbf {c}_1 \lesssim \mathbf {c}_2\) if \((\mathbf {c}_1, \mathbf {c}_2)\) are in a timed simulation that preserves \(\mathtt {end}\).
Theorem 2 (Safe substitution)
If \(S' <\,:\overline{S}\), then  .
.
Theorem 3 (Progressing substitution)
If \(S' <\,:\overline{S}\), then  satisfies progress.
satisfies progress.
5 A Calculus for Asynchronous Timed Processes
We introduce our asynchronous calculus for timed processes. The calculus abstracts implementations that execute one or more sessions. We let \(P, P', Q, \ldots \) range over processes, \(X\) range over process variables, and define \(n\in \mathbb {R}_{\geqslant 0} \cup \{\infty \}\). We use the notation \(\mathbf {a}\) for ordered sequences of channels or variables.

 sends a value v on channel \(a\) and continues as P. Similarly,
sends a value v on channel \(a\) and continues as P. Similarly,  sends a label
sends a label  on channel \(a\) and continue as P. Process
on channel \(a\) and continue as P. Process  behaves as either P or Q depending on the boolean value v. Process \(P\mid Q\) is for parallel composition of P and Q, and \(0\) is the idle process. \(\mathtt {def}\;D\;\mathtt {in}\;P\) is the standard recursive process: D is a declaration, and P is a process that may contain recursive calls. In recursive calls
behaves as either P or Q depending on the boolean value v. Process \(P\mid Q\) is for parallel composition of P and Q, and \(0\) is the idle process. \(\mathtt {def}\;D\;\mathtt {in}\;P\) is the standard recursive process: D is a declaration, and P is a process that may contain recursive calls. In recursive calls  the first list of parameters has to be instantiated with values of ground types, while the second with channels. Recursive calls are instantiated with equations
the first list of parameters has to be instantiated with values of ground types, while the second with channels. Recursive calls are instantiated with equations  in D. Process \((\nu ab) P\) is for scope restriction of endpoints \(a\) and \(b\). Process \(ab: h\) is a queue with name \( ab\) (colloquially used to indicate that it contains messages in transit from \(a\) to \(b\)) and content \(h\). \((\nu ab)\) binds endpoints \( a\) and \(b\), and queues \( ab\) and \( ba\) in P.
in D. Process \((\nu ab) P\) is for scope restriction of endpoints \(a\) and \(b\). Process \(ab: h\) is a queue with name \( ab\) (colloquially used to indicate that it contains messages in transit from \(a\) to \(b\)) and content \(h\). \((\nu ab)\) binds endpoints \( a\) and \(b\), and queues \( ab\) and \( ba\) in P.
There are two kind of time-consuming processes: those performing a time-consuming action (e.g., method invocation, sleep), and those waiting to receive a message. We model the first kind of processes with \(\mathtt {delay}(\delta ).\, P\), and the second kind of processes with  (receive) and
(receive) and  (branching). In \(\mathtt {delay}(\delta ).\, P\), \(\delta \) is a constraints as those defined for types, but on one single clock \(x\). The name of the clock here is immaterial: clock \(x\) is used as a syntactic tool to define intervals for the time-consuming (delay) action. In this sense, assume x is bound in \(\mathtt {delay}(\delta ).\, P\). Process \(\mathtt {delay}(\delta ).\, P\) consumes any amount of time t such that t is a solution of \(\delta \). For example \(\mathtt {delay}(x\leqslant 3).\, P\) consumes any value between 0 to 3 time units, then behaves as P. Process \(a^{n}(b).\, P\) receive a message on channel \(a\), instantiates \(b\) and continue as P. Parameter \(n\) models different receive primitives: non-blocking (\(n=0\)), blocking (\(n=\infty \)), and blocking with timeout (\(n\in \mathbb {R}^{\geqslant 0}\)). If \(n\in \mathbb {R}^{\geqslant 0}\) and no message is in the queue, the process waits \(n\) time units before moving into a failed state. If \(n\) is set to \(\infty \) the process models a blocking primitive without timeout. Branching process
(branching). In \(\mathtt {delay}(\delta ).\, P\), \(\delta \) is a constraints as those defined for types, but on one single clock \(x\). The name of the clock here is immaterial: clock \(x\) is used as a syntactic tool to define intervals for the time-consuming (delay) action. In this sense, assume x is bound in \(\mathtt {delay}(\delta ).\, P\). Process \(\mathtt {delay}(\delta ).\, P\) consumes any amount of time t such that t is a solution of \(\delta \). For example \(\mathtt {delay}(x\leqslant 3).\, P\) consumes any value between 0 to 3 time units, then behaves as P. Process \(a^{n}(b).\, P\) receive a message on channel \(a\), instantiates \(b\) and continue as P. Parameter \(n\) models different receive primitives: non-blocking (\(n=0\)), blocking (\(n=\infty \)), and blocking with timeout (\(n\in \mathbb {R}^{\geqslant 0}\)). If \(n\in \mathbb {R}^{\geqslant 0}\) and no message is in the queue, the process waits \(n\) time units before moving into a failed state. If \(n\) is set to \(\infty \) the process models a blocking primitive without timeout. Branching process  is similar, but receives a label
is similar, but receives a label  and continues as \(P_i\).
and continues as \(P_i\).
Run-time processes are not written by programmers and only appear upon execution. Process \(\mathtt {failed}\) is the process that has violated a time constraint. We say that P is a failed state if it has \(\mathtt {failed}\) as a syntactic sub-term. Process \(\mathtt {delay}(t).\, P \) delays for exactly \(t\) time units.
Well-formed processes. Sessions are modelled as processes of the following form
where P is the process for endpoints \(a\) and \(b\), \(ab\) is the queue for messages from \(a\) to \(b\), and \(ba\) is the queues for messages from \(b\) to \(a\). A process can have more than one ongoing session. For each, we expect that all necessary queues are present and well-placed. We ensure that queues are well-placed via a well-formedness property for processes (see [11] for an inductive definition). Well-formedness rules out processes of the following form:

The process in (11) in not well-formed since queue \(ba\) for communications to endpoint \(a\) is not usable as it is in the continuation of the receive action. Well-formedness of processes is necessary to our safety results. We check well-formedness orthogonally to the typing system for the sake of simpler typing rules. While well-formedness ensures the absence of misplaced queues, the presence of an appropriate pair of queues for every session is ensured by the typing rules.
Session creation. Usually well-formedness is ensured by construction, as sessions are created by a specific (synchronous) reduction rule [10, 21]. This kind of session creation is cumbersome in the timed setting as it allows delays that are not captured by protocols, hence well-typed processes may miss deadlines. Other work on timed session types [12] avoids this problem by requiring that all session creations occur before any delay action. Our calculus allows session to be created at any point, even after delays. In (12) a session with endpoints c and d is created after a send action (assume P includes the queues for this new session).

A process like the one in (12) may be thought as a dynamic session creation that happens synchronously (as in [10, 21]), but assuming that all participants are ready to engage without delays. Our approach yields a simplification to the calculus (syntax and reduction rules) and, yet, a more general treatment of session initiation than the work in [12].
Reduction for processes. Processes are considered modulo structural equivalence, denoted by \(\equiv \), and defined by adding the following rule for delays to the standard ones [28]: \(\mathtt {delay}(0).\, P\equiv P\). Reduction rules for processes are given in Fig. 3. A reduction step \(\longrightarrow \) can happen because of either an instantaneous step \(\rightharpoonup \) by \([\mathtt {Red1}]\) or time-consuming step \(\rightsquigarrow \) by \([\mathtt {Red2}]\). Rules \([\mathtt {Send}]\), \([\mathtt {Rcv}]\), \([\mathtt {Sel}]\), and \([\mathtt {Bra}]\) are the usual asynchronous communication rules. Rule \([\mathtt {Det}]\) models the random occurrence of a precise delay t, with t being a solution of \(\delta \). The other untimed rules, \([\mathtt {IfT}]\), \([\mathtt {Par}]\), \([\mathtt {Def}]\), \([\mathtt {Rec}]\), \([\mathtt {AStr}]\), and \([\mathtt {AScope}]\) are standard. Note that rule \([\mathtt {Par}]\) does not allow time passing, which is handled by rule \([\mathtt {Delay}]\). Rule \([\mathtt {TStr}]\) is the timed version of \([\mathtt {AStr}]\). Rule \([\mathtt {Delay}]\) applies a time-passing function \(\varPhi _{t}\) (defined in Fig. 4) which distributes the delay t across all the parts of a process. \(\varPhi _{t}(P)\) is a partial function: it is undefined if P can immediately make an urgent action, such as evaluation of expressions or output actions. If \(\varPhi _{t}(P)\) is defined, it returns the process resulting from letting \(t\) time units elapse in P. \(\varPhi _t(P)\) may return a failed state, if delay t makes a deadline in P expire. The definition of \(\varPhi _t(P_1 \mid P_2)\) relies on two auxiliary functions: \(\mathtt {Wait}(P)\) and \(\mathtt {NEQueue}(P)\) (see [11] for the full definition). \(\mathtt {Wait}(P)\) returns the set of channels on which P (or some syntactic sub-term of P) is waiting to receive a message/label. \(\mathtt {NEQueue}(P)\) returns the set of endpoints with a non-empty inbound queue. For example,  and \(\mathtt {NEQueue}(ba: h)=\{a\}\) given that
and \(\mathtt {NEQueue}(ba: h)=\{a\}\) given that  . \(\varPhi _t(P_1 \mid P_2)\) is defined only if no urgent action could immediately happen in \(P_1\mid P_2\). For example, \(\varPhi _t(P_1 \mid P_2)\) is undefined for \(P_1= a^{t}(b).\, Q\) and \(P_2=ba:v\).
. \(\varPhi _t(P_1 \mid P_2)\) is defined only if no urgent action could immediately happen in \(P_1\mid P_2\). For example, \(\varPhi _t(P_1 \mid P_2)\) is undefined for \(P_1= a^{t}(b).\, Q\) and \(P_2=ba:v\).
In the rest of this section we show the reductions of two processes: one with urgent actions (Example 5), and one to a failed state (Example 6). We omit processes that are immaterial for the illustration (e.g., unused queues).
Example 5
(Urgency and undefined \(\varPhi _t\)). We show the reduction of process  that has an urgent action. Process P can make the following reduction by \([\mathtt {Send}]\):
that has an urgent action. Process P can make the following reduction by \([\mathtt {Send}]\):

At this point, to apply rule \([\mathtt {Delay}]\), say with \(t = 5\), we need to apply the time-passing function as shown below:

which is undefined.  is undefined because
is undefined because  . Since \(\varPhi _5(P')\) is undefined. Instead, the message in queue \(ab\) can be received by rule \([\mathtt {Rcv}]\):
. Since \(\varPhi _5(P')\) is undefined. Instead, the message in queue \(ab\) can be received by rule \([\mathtt {Rcv}]\):

Example 6
(An execution with failure). We show a reduction to a failing state of a process with a non-blocking receive action (expecting a message immediately) composed with another process that sends a message after a delay.

The application of the time-passing function to \(P'\) yields a failing state (a message is not received in time) as shown below, where the second equality holds since  :
:

6 Typing for Asynchronous Timed Processes
We validate programs against specifications using judgements of the form  . Environments are defined as follows:
. Environments are defined as follows:

Environment \(\varDelta \) is a session environment, used to keep track of the ongoing sessions. When \(\varDelta (a)=(\nu , S)\) it means that the process being validated is acting as a role in session \(a\) specified by \(S\), and \(\nu \) is the clock valuation describing a (virtual) time in which the next action in \(S\) may be executed. We write \(\mathrm {dom}(\varDelta )\) for the set of variables and channels in \(\varDelta \). Environment \(\varGamma \) maps variables \(a\) to sorts \(T\) and process variables \(X\) to pairs \((\mathbf {T};\varTheta )\), where \(\mathbf {T}\) is a vector of sorts and \(\varTheta \) is a set of session environments. The mapping of process variable is used to type recursive processes: \(\mathbf {T}\) is used to ensure well-typed instantiation of the recursion parameters, and \(\varTheta \) is used to model the set of possible scenarios when a new iteration begins.
Notation, assumptions, and auxiliary definitions. We write \(\varDelta + t\) for the session environment obtained by incrementing all clock valuations in the codomain of \(\varDelta \) by t.
Definition 8
We define the disjoint union \(A \uplus B\) of sets of clocks A and B as:

where \(in_l\) and \(in_r\) are one to one endofunctions on clocks and, for all \(x\in A\) and \(y\in B\), \(in_l(x) \ne in_r(y)\). With an abuse of notation, we define the disjoint union of clock valuations \(\nu _1,\nu _2\), in symbols \(\nu _1 \uplus \nu _2\), as a clock valuation satisfying:

We use the symbol \(\biguplus \) for the iterate disjoint union.
For a configuration \((\nu ,S)\) we define \(\mathtt {val((\nu ,S))} = \nu \), and \(\mathtt {type((\nu ,S))} = S\). We overload function \(\mathtt {val}\) to session environments \(\varDelta \) as follows:
We require \(\varTheta \) to satisfy the following three conditions:
-
1.
If \(\varDelta \in \varTheta \) and \(\varDelta (a)=(\nu , S)\), then \(S\) is well-formed (Definition 1) against \(\nu \);
-
2.
For all \(\varDelta _1 \in \varTheta \), \(\varDelta _2 \in \varTheta \): \(\mathtt {type}(\varDelta _1(a)) = S\) iff \(\mathtt {type}(\varDelta _2(a)) = S\);
-
3.
There is guard \(\delta \) such that:
$$ \{\nu \mid \nu \models \delta \} = \bigcup _{\varDelta \in \varTheta } \mathtt {val}(\varDelta ). $$
The last condition ensures that \(\varTheta \) is finitely representable, and is key for decidability of type checking.
Example 7
We show some examples of \(\varTheta \) that do or do not satisfy the last requirement above. Let  and
and  , and let:
, and let:

We have that \(\varTheta _1\) satisfies condition (3): let \(\delta _1 = x\leqslant 2 \wedge y- x= 0\). It is easy to see that \(\{\nu \mid \nu \models \delta _1\} = \bigcup _{\varDelta \in \varTheta } \mathtt {val}(\varDelta )\). For \(\varTheta _2\), a candidate proposition would be \(\delta _2 = x\leqslant \sqrt{2} \wedge y- x= 0\). However, \(\delta _2\) can not be derived with the syntax of propositions, as \(\sqrt{2}\) is irrational. Indeed, \(\varTheta _2\) does not satisfy the condition. For \(\varTheta _3\), let \(\delta _3 = x+ y= 2\). Again, \(\delta _3\) is not a guard, as additive constraints in the form \(x+ y= n\) are not allowed. Indeed, also \(\varTheta _3\) does not satisfy the condition.
In the following, we write \(\mathbf {a}:\mathbf {T}\) for \(a_1 : T_1, \ldots , a_n : T_n\) when \(\mathbf {a}= a_1 , \ldots , a_n \) and \(\mathbf {T}= T_1, \ldots , T_n\) (assuming \(\mathbf {a}\) and \(\mathbf {T}\) have the same number of elements). Similarly for \(\mathbf {b}:\mathbf {(\nu ,S)}\). In the typing rules, we use a few auxiliary definitions: Definition 9 (\(t\)-reading \(\varDelta \)) checks if any ongoing sessions in a \(\varDelta \) can perform an input action within a given timespan, and Definition 10 (Compatibility of configurations) extends the notion of duality to systems that are not in an initial state.
Definition 9
(\(t\)-reading \(\varDelta \)). Session environment \(\varDelta \) is \(t\)-reading if there exist some \(a\in \mathrm {dom}(\varDelta )\), \(t' < t\) and m such that: \(\varDelta (a) = (\nu ,S) \wedge (\nu + t',S) {\mathop {\longrightarrow }\limits ^{?m}}\).
Namely, \(\varDelta \) is \(t\)-reading if any of the open sessions in the mapping prescribe a read action within the time-frame between \(\nu \) and \(\nu +t\). Definition 9 is used in the typing rules for time-consuming processes – \([\mathtt {Vrcv}]\), \([\mathtt {Drcv}]\), and \([\mathtt {Del\textit{t}}]\) – to ‘disallow’ derivations when a (urgent) receive may happen.
Definition 10
(Compatibility of configurations). Configuration \((\nu _1,\) \(S_1, \mathtt {M}_1)\) is compatible with \((\nu _2,S_2, \mathtt {M}_2)\), written \((\nu _1,S_1, \mathtt {M}_1) \bot (\nu _2,S_2, \mathtt {M}_2)\), if:
-
1.
 ,
, -
2.
 ,
, -
3.
 .
.
By condition (3) initial configurations are compatible when they include dual types, i.e.,  . By condition (2) two configurations may temporarily misalign as execution proceeds: one may have read a message from its queue, while the other has not, as long as the former is ready to receive it immediately. Thanks to the particular shape of type’s interactions, initial configurations – of the form
. By condition (2) two configurations may temporarily misalign as execution proceeds: one may have read a message from its queue, while the other has not, as long as the former is ready to receive it immediately. Thanks to the particular shape of type’s interactions, initial configurations – of the form  – will only reach systems, say \((\nu _1,S_1, \mathtt {M}_1) \bot (\nu _2,{S_2}, \mathtt {M}_2)\), in which at least one between \(\mathtt {M}_1\) and \(\mathtt {M}_2\) is empty. Condition (1) requires compatible configurations to satisfy this basic property.
– will only reach systems, say \((\nu _1,S_1, \mathtt {M}_1) \bot (\nu _2,{S_2}, \mathtt {M}_2)\), in which at least one between \(\mathtt {M}_1\) and \(\mathtt {M}_2\) is empty. Condition (1) requires compatible configurations to satisfy this basic property.
Typing rules. The typing rules are given in Fig. 5. Rule \([\mathtt {Vrcv}]\) is for input processes. The first premise consists of two conditions requiring the time-span \([\nu ,\nu + n]\) in which the process can receive the message to coincide with \(\delta \):
-
\(\nu + t\models \delta \Rightarrow t\leqslant n\) rules out processes that are not ready to receive a message when prescribed by the type.
-
\(t\leqslant n\Rightarrow \nu + t\models \delta \) requires that \(a^{n}(b).\, P\) can read only at times that satisfy the type prescription \(\delta \).Footnote 2
The second premise of \([\mathtt {Vrcv}]\) requires the continuation P to be well-typed against the continuation of the type, for all possible session environments where the virtual time is somewhere between \([\nu ,\nu +n]\), where the virtual valuation \(\nu \) in the mapping of session \(a\) is reset according to \(\lambda \). Rule \([\mathtt {Drcv}]\), for processes receiving delegated sessions, is like \([\mathtt {Vrcv}]\) except: (a) the continuation P is typed against a session environment extended with the received session \(S'\), and (b) the clock valuation \(\nu '\) of the receiving session must satisfy \(\delta '\). Recall that by formation rules (Sect. 2.1) \(S'\) is well-formed against all \(\nu '\) that satisfy \(\delta '\).
Rule \([\mathtt {Vsend}]\) is for output processes. Send actions are instantaneous, hence the type current \(\nu \) needs to satisfy \(\delta \). As customary, the continuation of the process needs to be well-typed against the continuation of the type (with \(\nu \) being reset according to \(\lambda \), and \(\varGamma \) extended with information on the sort of b). \([\mathtt {Dsend}]\) for delegation is similar but: (a) the delegated session is removed from the session environment (the process can no longer engage in the delegated session), and (b) valuation \(\nu '\) of the delegated session must satisfy guard \(\delta '\).
Rule \([\mathtt {Del\delta }]\) checks that P is well-typed against all possible solutions of \(\delta \). Rule \([\mathtt {Del\textit{t}}]\) shifts the virtual valuations in the session environment of \(t\). This is as the corresponding rule in [12] but with the addition of the check that \(\varDelta \) is not \(t\)-reading, needed because of urgent semantics.
Rule \([\mathtt {Res}]\) is for processes with scopes.
Rule \([\mathtt {Rec}]\) is for recursive processes. The rule is as usual [21] except that we use a set of session environments \(\varTheta \) (instead of a single \(\varDelta \)) to capture a set of possible scenarios in which a recursion instance may start, which may have different clock valuations. Rule \([\mathtt {Var}]\) is also as expected except for the use of \(\varTheta \).
Rules \([\mathtt {Par}]\) and \([\mathtt {Subt}]\) straightforward.
Example 8 (Typing with subtyping)
Subtyping substantially increases the power of our type system, in particular in the presence of channel passing. Intuitively, without subtyping, the type of any higher-order send action should be an equality constraint (e.g., \(x = 1\)) rather than more general timeout (e.g., \(x<1\)). We illustrate our point using P defined below:

where Q contains empty queues of the involved endpoints. Intuitively, P proceeds as follows: (1) \(P_1\) sends channel \(a_2\) to \(P_2\) within one time unit, and terminates; (2) \(P_2\) reads the message as soon as it arrives, and listens for a message across the received channel (\(a_2\)) for two time units; (3) \(P_3\) sends value \(\mathtt {true}\) through channel \(b_2\) at a time in between 1 and 2, unaware that now she is communicating with \(P_2\), and then terminates; (4) \(P_2\) reads the message immediately and terminates. See below for one possible reduction:

Although P executes correctly, the involved processes are well-typed against types that are not dual:

for  ,
,  ,
,  . In order to type-check P, we need to apply rule \([\mathtt {Res}]\), requiring endpoints of the same session to have dual types. But clearly:
. In order to type-check P, we need to apply rule \([\mathtt {Res}]\), requiring endpoints of the same session to have dual types. But clearly:  . Without subtyping, P would not be well-typed. By subtyping, however, \((y \leqslant 1,S_2) <\,:(y = 0,S_2')\) with
. Without subtyping, P would not be well-typed. By subtyping, however, \((y \leqslant 1,S_2) <\,:(y = 0,S_2')\) with  , and then \(S_1' <\,:\overline{S_1'}\). Thanks to the subtyping rule [subt] we can derive
, and then \(S_1' <\,:\overline{S_1'}\). Thanks to the subtyping rule [subt] we can derive  and, in turn,
and, in turn,  .
.
7 Subject Reduction and Time Safety
The main properties of our typing system are Subject Reduction and Time Safety. Time Safety ensures that the execution of well-typed processes will only reach fail-free states. Recall, P is fail-free when none of its sub-terms is the process \(\mathtt {failed}\). Time Safety builds on a condition that is not related with time, but with the structure of the process interactions. If an untimed process gets stuck due to mismatches in its communication structure, a timed process with the same communication structure may move to a failed state. Consider P below:

P is well-typed:  with
with  . However, P can only make time steps, and when, overall, more than 5 time units elapse (e.g., 6 in the reduction below) P reaches a failed state due to a circular dependency between actions of sessions \((\nu a b)\) and \((\nu c d)\):
. However, P can only make time steps, and when, overall, more than 5 time units elapse (e.g., 6 in the reduction below) P reaches a failed state due to a circular dependency between actions of sessions \((\nu a b)\) and \((\nu c d)\):
Our typing system does not check against such circularities across different interleaved sessions. This is common in work on untimed [21] and timed [12] session types. However, in the untimed scenario, progress for interleaved sessions can be guaranteed by means of additional checks on processes [17]. Time Safety builds on the results in [17] by using an assumption (receive liveness) on the underneath structure of the timed processes. This assumptions is formally captured in Definition 11, which is based on an untimed variant of our calculus.
The untimed calculus. We define untimed processes, denoted by \(\hat{P}\), as processes obtained from the grammar given for timed processes (Sect. 5) without delays and failed processes. In untimed processes, time annotations of branching/receive processes are immaterial, hence omitted in the rest of the paper.
Given a (timed) process P, one can obtain its untimed counter-part by erasing delays and failed processes; we denoted the result of such erasure on P by \(\mathtt {erase}(P)\). The semantics of untimed processes is defined as the one for timed processes (Sect. 5) except that reduction rules \([\mathtt {Delay}]\), \([\mathtt {TStr}]\), and \([\mathtt {Red2}]\), are removed. Abusing the notation, we write \(\hat{P}{\mathop {\longrightarrow }\limits ^{}} \hat{P'}\) when an untimed process \(\hat{P}\) moves to a state \(\hat{P'}\) using the semantics for untimed processes. The definitions of \(\mathtt {Wait}(\hat{P})\) and \(\mathtt {NEQueue}(\hat{P})\) can be derived from the definitions for timed processes in the straightforward way.
Definition 11 (receive liveness) formalises our assumption on the interaction structures of a process.
Definition 11 (Receive liveness)
\(\hat{P}\) is said to satisfy receive liveness (or is live, for short) if, for all \(\hat{P'}\) such that \(\hat{P}~~\longrightarrow ^*~~\hat{P'}\):

In any reachable state \(\hat{P}'\) of a live untimed process \(\hat{P}\), if any endpoint a in \(\hat{P}'\) is waiting to receive a message (\(a\in \mathtt {Wait}(\hat{Q})\)), then the overall process is able to reach a state \(\hat{Q}'\) where a can perform the receive action (\(a\in \mathtt {NEQueue}(\hat{Q}')\)).
Consider process P in (13). The untimed process \(\mathtt {erase}(P)\) is not live because \(\mathtt {Wait}(\mathtt {erase}(P)) = \{a,c\}\) and \(a,c\not \in \mathtt {NEQueue}(\mathtt {erase}(P))\), since \(\mathtt {NEQueue}(\mathtt {erase}(P))\) is the empty set. Syntactically, \(\mathtt {erase}(P)\) is as P, but it does not have the same behaviour. P can only make time steps, reaching a failed process, while \(\mathtt {erase}(P)\) is stuck, as untimed processes only make communication steps.
Properties. Time safety relies on Subject Reduction Theorem 4, which establishes a relation (preserved by reduction) of well-typed processes and their types.
Theorem 4 (Subject reduction for closed systems)
Let \(\mathtt {erase}(P)\) be live. If  and \(P ~~\longrightarrow ~~P'\) then
and \(P ~~\longrightarrow ~~P'\) then  .
.
Note that Subject Reduction assumes \(\mathtt {erase}(P)\) to be live. For instance, the example of P in (13) is well-typed, but \(\mathtt {erase}(P)\) is not live. The process can reduce to a failed state (as illustrated earlier in this section) that cannot be typed (failed processes are not well-typed). Time Safety establishes that well-typed processes only reduce to fail-free states.
Theorem 5 (Time safety)
If \(\mathtt {erase}(P)\) is live,  and \(P ~~\longrightarrow ^*~~P'\), then \(P'\) is fail-free.
and \(P ~~\longrightarrow ^*~~P'\), then \(P'\) is fail-free.
Typing is decidable if one uses processes annotated with the following information: (1) scope restrictions \((\nu ab:S) P\) are annotated with the type \(S\) of the session for endpoint \(a\) (the type of \(b\) is implicitly assumed to be \(\overline{S}\) and both endpoints are type checked in the initial clock valuation \(\nu _0\)); (2) receive actions \(a^{n}(b:T).\, P\) are annotated with the type \(T\) of the received message; (3) recursion \(X(\mathbf {a:T} \; ; \, \mathbf {a:S},\delta )=P\) are annotated with types for each parameter, and a guard modelling the state of the clocks. We call annotated programs those annotated processes derived without using productions marked as run-time (i.e., \(\mathtt {failed}\) and \(\mathtt {delay}(t).\, P\)), and where \(n\) in \(a^{n}(b:T).\, P\) ranges over \(\mathbb {Q}_{\geqslant 0} \cup \{\infty \}\).
Proposition 2
Type checking for annotated programs is decidable.
8 Conclusion and Related Work
We introduced duality and subtyping relations for asynchronous timed session types. Unlike for untimed and timed synchronous [6] dualities, the composition of dual types does not enjoy progress in general. Compositions of asynchronous timed dual types enjoy progress when using an urgent receive semantics. We propose a behavioural typing system for a timed calculus that features non-blocking and blocking receive primitives (with and without timeout), and time consuming primitives of arbitrary but constrained delays. The main properties of the typing system are Subject Reduction and Time Safety; both results rely on an assumption (receive liveness) of the underneath interaction structure of processes. In related work on timed session types [12], receive liveness is not required for Subject Reduction; this is because the processes in [12] block (rather than reaching a failed state) whenever they cannot progress correctly, hence e.g., missed deadline are regarded as progress violations. By explicitly capturing failures, our calculus paves the way for future work on combining static checking with run-time instrumentation to prevent or handle failures.
Asynchronous timed session types have been introduced in [12], in a multiparty setting, together with a timed \(\pi \)-calculus, and a type system. The direct extension of session types with time introduces unfeasible executions (i.e., types may get stuck), as we have shown in Example 1. [12] features a notion of feasibility for choreographies, which ensures that types enjoy progress. We ensure progress of types by formation and duality. The semantics of types in [12] is different from ours in that receive actions are not urgent. The work in [12] gives one extra condition on types (wait-freedom), because feasible types may still yield undesirable executions in well-typed processes. Thanks to our duality, subtyping, and calculus (in particular the blocking receive primitive with timeout) this condition is unnecessary in this work. As a result, our typing system allows for types that are not wait-free. By dropping wait-freedom, we can type a class of common real-world protocols in which processes may be ready to receive messages even before the final deadline of the corresponding senders. Remarkably, SMTP mentioned in the introduction is not wait-free. For some other aspects, our work is less general than the one in [12], as we consider binary sessions rather than multiparty sessions. A theory of timed multiparty asynchronous protocols that encompasses the protocols in [12] and those considered here is an interesting future direction. The work in [6] introduces a theory of synchronous timed session types, based on a decidable notion of compatibility, called compliance, that ensures progress of types, and is equivalent to synchronous timed duality and subtyping in a precise sense [6]. Our duality and subtyping are similar to those in [6], but apply to the asynchronous scenario. The work in [15] introduces a typed calculus based on temporal session types. The temporal modalities in [15] can be used as a discrete model of time. Timed session types, thanks to clocks and resets, are able to model complex timed dependencies that temporal session types do not seem able to capture. Other work studies models for asynchronous timed interactions, e.g., Communicating Timed Automata [23] (CTA), timed Message Sequence Charts [2], but not their relationships with processes. The work in [5] introduces a refinement for CTA, and presents a notion of urgency similar to the one used in this paper, preliminary studied also in [29].
Several timed calculi have been introduced outside the context of behavioural types. The work in [32] extends the \(\pi \)- calculus with time primitives inspired in CTA and is closer, in principle, to our types than our processes. Another timed extension of the \(\pi \)-calculus with time-consuming actions has been applied to the analysis the active times of processes [18]. Some works focus on specific aspects of timed behaviour, such as timeouts [9], transactions [24, 27], and services [25]. Our calculus does not feature exception handlers, nor timed transactions. Our focus in on detecting time violations via static typing, so that a process only moves to fail-free states.
The calculi in [7, 12, 15] have been used in combination with session types. The calculus in [12] features a non-blocking receive primitive similar to our \(a^{0}(b).\, P\), but that never fails (i.e., time is not allowed to flow if a process tries to read from an empty buffer—possibly leading to a stuck process rather than a failed state). The calculus in [7] features a blocking receive primitive without timeout, equivalent to our \(a^{\infty }(b).\, P\). The calculus in [15], seems able to encode a non-blocking receive primitive like the one of [12] and a blocking receive primitive without timeout like our \(a^{\infty }(b).\, P\). None of these works features blocking receive primitives with timeouts. Furthermore, existing works feature [7, 12] or can encode [15] only precise delays, equivalent to \(\mathtt {delay}(x=n).\, P\). Such punctual predictions are often difficult to achieve. Arbitrary but constrained delays are closer abstractions of time-consuming programming primitives (and possibly, of predictions one can derive by cost analysis, e.g., [20]).
As to applications, timed session types have been used for run-time monitoring [7, 30] and static checking [12]. A promising future direction is that of integrating static typing with run-time verification and enforcement, towards a theory of hybrid timed session types. In this context, extending our calculus with exception handlers [9, 24, 27] could allow an extension of the typing system, that introduces run-time instrumentation to handle unexpected time failures.
Notes
- 1.
Separated semantics can describe situations where actions have an associated duration.
- 2.
While not necessary for our safety results, this constraint simplifies our theory. Timing variations between types and programs are all handled in one place: rule \([\mathtt {Subt}]\).
References
Aceto, L., Ingólfsdóttir, A., Larsen, K.G., Srba, J.: Reactive Systems: Modelling, Specification and Verification. Cambridge University Press, Cambridge (2007). https://doi.org/10.1017/CBO9780511814105
Akshay, S., Gastin, P., Mukund, M., Kumar, K.N.: Model checking time-constrained scenario-based specifications. In: FSTTCS. LIPIcs, vol. 8, pp. 204–215. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2010). https://doi.org/10.4230/LIPIcs.FSTTCS.2010.204
Alur, R., Dill, D.L.: A theory of timed automata. TCS 126, 183–235 (1994)
Advanced Message Queuing Protocols (AMQP). https://www.amqp.org/
Bartoletti, M., Bocchi, L., Murgia, M.: Progress-preserving refinements of CTA. In: CONCUR. LIPIcs, vol. 118, pp. 40:1–40:19. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018). https://doi.org/10.4230/LIPIcs.CONCUR.2018.40
Bartoletti, M., Cimoli, T., Murgia, M.: Timed session types. Log. Methods Comput. Sci. 13(4) (2017). https://doi.org/10.23638/LMCS-13(4:25)2017
Bartoletti, M., Cimoli, T., Murgia, M., Podda, A.S., Pompianu, L.: A contract-oriented middleware. In: Braga, C., Ölveczky, P.C. (eds.) FACS 2015. LNCS, vol. 9539, pp. 86–104. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-28934-2_5
Bengtsson, J., Yi, W.: Timed automata: semantics, algorithms and tools. In: Desel, J., Reisig, W., Rozenberg, G. (eds.) ACPN 2003. LNCS, vol. 3098, pp. 87–124. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27755-2_3
Berger, M., Yoshida, N.: Timed, distributed, probabilistic, typed processes. In: Shao, Z. (ed.) APLAS 2007. LNCS, vol. 4807, pp. 158–174. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76637-7_11
Bettini, L., Coppo, M., D’Antoni, L., De Luca, M., Dezani-Ciancaglini, M., Yoshida, N.: Global progress in dynamically interleaved multiparty sessions. In: van Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 418–433. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85361-9_33
Bocchi, L., Murgia, M., Vasconcelos, V., Yoshida, N.: Asynchronous timed session types: from duality to time-sensitive processes (2018). https://www.cs.kent.ac.uk/people/staff/lb514/tstp.html
Bocchi, L., Yang, W., Yoshida, N.: Timed multiparty session types. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 419–434. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44584-6_29
Bruno, E.J., Bollella, G.: Real-Time Java Programming: With Java RTS, 1st edn. Prentice Hall PTR, Upper Saddle River (2009)
Chen, T.C., Dezani-Ciancaglini, M., Yoshida, N.: On the preciseness of subtyping in session types. In: PPDP, pp. 135–146. ACM (2014). https://doi.org/10.1145/2643135.2643138
Das, A., Hoffmann, J., Pfenning, F.: Parallel complexity analysis with temporal session types. Proc. ACM Program. Lang. 2(ICFP), 91:1–91:30 (2018). https://doi.org/10.1145/3236786
Demangeon, R., Honda, K.: Full abstraction in a subtyped pi-calculus with linear types. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 280–296. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23217-6_19
Dezani-Ciancaglini, M., de’Liguoro, U., Yoshida, N.: On progress for structured communications. In: Barthe, G., Fournet, C. (eds.) TGC 2007. LNCS, vol. 4912, pp. 257–275. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78663-4_18
Fischer, M., Förster, S., Windisch, A., Monjau, D., Balser, B.: A new time extension to \(\pi \)-calculus based on time consuming transition semanticss. In: Grimm, C. (ed.) Languages for System Specification, pp. 271–283. Springer, Boston (2004). https://doi.org/10.1007/1-4020-7991-5_17
Gay, S.J., Hole, M.: Subtyping for session types in the pi calculus. Acta Inf. 42(2–3), 191–225 (2005). https://doi.org/10.1007/s00236-005-0177-z
Hoffmann, J., Shao, Z.: Automatic static cost analysis for parallel programs. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 132–157. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_6
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL, pp. 273–284. ACM (2008)
Klensin, J.: Simple mail transfer protocol. RFC 5321, October 2008. https://tools.ietf.org/html/rfc5321
Krcal, P., Yi, W.: Communicating timed automata: the more synchronous, the more difficult to verify. In: Ball, T., Jones, R.B. (eds.) CAV 2006. LNCS, vol. 4144, pp. 249–262. Springer, Heidelberg (2006). https://doi.org/10.1007/11817963_24
Laneve, C., Zavattaro, G.: Foundations of web transactions. In: Sassone, V. (ed.) FoSSaCS 2005. LNCS, vol. 3441, pp. 282–298. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31982-5_18
Lapadula, A., Pugliese, R., Tiezzi, F.: CWS: a timed service-oriented calculus. In: Jones, C.B., Liu, Z., Woodcock, J. (eds.) ICTAC 2007. LNCS, vol. 4711, pp. 275–290. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75292-9_19
Larsen, K.G., Pettersson, P., Yi, W.: Uppaal in a nutshell. Int. J. Softw. Tools Technolo. Transf. 1, 134–152 (1997)
López, H.A., Pérez, J.A.: Time and exceptional behavior in multiparty structured interactions. In: Carbone, M., Petit, J.-M. (eds.) WS-FM 2011. LNCS, vol. 7176, pp. 48–63. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29834-9_5
Milner, R.: Communicating and Mobile Systems: The \(\pi \)-calculus. Cambridge University Press, New York (1999)
Murgia, M.: On urgency in asynchronous timed session types. In: ICE. EPTCS, vol. 279, pp. 85–94 (2018). https://doi.org/10.4204/EPTCS.279.9
Neykova, R., Bocchi, L., Yoshida, N.: Timed runtime monitoring for multiparty conversations. Formal Asp. Comput. 29(5), 877–910 (2017). https://doi.org/10.1007/s00165-017-0420-8
Pierce, B.C.: Types and Programming Languages. MIT Press, Cambridge (2002)
Saeedloei, N., Gupta, G.: Timed \(\pi \)-calculus. In: Abadi, M., Lluch Lafuente, A. (eds.) TGC 2013. LNCS, vol. 8358, pp. 119–135. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-05119-2_8
Vinoski, S.: Advanced message queuing protocol. IEEE Internet Comput. 10(6), 87–89 (2006). https://doi.org/10.1109/MIC.2006.116
Yovine, S.: Kronos: a verification tool for real-time systems. (Kronos user’s manual release 2.2). Int. J. Softw. Tools Technol. Transf. 1, 123–133 (1997)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Bocchi, L., Murgia, M., Vasconcelos, V.T., Yoshida, N. (2019). Asynchronous Timed Session Types. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)






 is omitted for brevity.
is omitted for brevity.  ,
, ,
,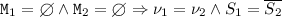 .
.
