Orthogonal and Smooth Orthogonal Layouts of 1-Planar Graphs with Low Edge Complexity

Abstract

While orthogonal drawings have a long history, smooth orthogonal drawings have been introduced only recently. So far, only planar drawings or drawings with an arbitrary number of crossings per edge have been studied. Recently, a lot of research effort in graph drawing has been directed towards the study of beyond-planar graphs such as 1-planar graphs, which admit a drawing where each edge is crossed at most once. In this paper, we consider graphs with a fixed embedding. For 1-planar graphs, we present algorithms that yield orthogonal drawings with optimal curve complexity and smooth orthogonal drawings with small curve complexity. For the subclass of outer-1-planar graphs, which can be drawn such that all vertices lie on the outer face, we achieve optimal curve complexity for both, orthogonal and smooth orthogonal drawings.

This work started at Dagstuhl seminar 16452 “Beyond-Planar Graphs: Algorithmics and Combinatorics”. We thank the organizers and the other participants. The full version of this article is available at arxiv.org/abs/1808.10536.

1 Introduction

Orthogonal drawings date back to the 1980’s, with Valiant’s [24], Leiserson’s [17] and Leighton’s [16] work on VLSI layouts and floor-planning applications and have been extensively studied over the years. The quality of an orthogonal drawing can be judged based on several aesthetic criteria such as the required area, the total edge length, the total number of bends, or the maximum number of bends per edge. While schematic drawings such as orthogonal layouts are very popular for technical applications (such as UML diagrams) still to date, from a cognitive point of view, schematic drawings in other applications like subway maps seem to have disadvantages over subway maps drawn with smooth Bézier curves, for example, in the context of path finding [19]. In order to “smoothen” orthogonal drawings and to improve their readability, Bekos et al. [6] introduced smooth orthogonal drawings that combine the clarity of orthogonal layouts with the artistic style of Lombardi drawings [11] by replacing sequences of “hard” bends in the orthogonal drawing of the edges by (potentially shorter) sequences of “smooth” inflection points connecting circular arcs. Formally, our drawings map vertices to points in $\mathbb R^2$ and edges to curves of one of the following two types.

• Orthogonal Layout: Each edge is drawn as a sequence of vertical and horizontal line segments. Two consecutive segments of an edge meet in a bend.

• Smooth Orthogonal Layout [6]: Each edge is drawn as a sequence of vertical and horizontal line segments as well as circular arcs: quarter arcs, semicircles, and three-quarter arcs. Consecutive segments must have a common tangent.

The maximum vertex degree is usually restricted to four since every vertex has four available ports (North, South, East, West), where the edges enter and leave a vertex with horizontal or vertical tangents. In addition, the usual model insists that no two edges incident to the same vertex can use the same port. Throughout this paper, we restrict ourselves to graphs of maximum degree four.

The curve complexity of a drawing is the maximum number of segments used for an edge. An OC$_{k}$-layout is an orthogonal layout with curve complexity k, that is, an orthogonal layout with at most $k-1$ bends per edge. An SC$_{k}$-layout is a smooth orthogonal layout with curve complexity k. For results, see Table 1.

Fig. 1.

Two 2-planar drawings of $K_5$.

The well-known algorithm of Biedl and Kant [7] draws any connected graph of maximum degree 4 orthogonally on a grid of size $n \times n$ with at most $2n + 2$ bends, bending each edge at most twice (and, hence, yielding OC$_{3}$-layouts). For the output of their algorithm applied to $K_5$, see Fig. 1a. Note that their approach introduces crossings to the produced drawing. For planar graphs, they describe how to obtain planar orthogonal drawings with at most two bends per edge, except possibly for one edge on the outer face.

So far, smooth orthogonal drawings have been studied nearly exclusively for planar graphs. Bekos et al. [5] showed how to compute an SC$_{1}$-layout for any maximum degree 4 graph, but their algorithm does not consider the embedding of the given graph. For a drawing of $K_5$ computed by their algorithm, see Fig. 1b. Also, in the produced drawings, the number of crossings that an edge may have is not bounded. Bekos et al. also showed that, if one does not restrict vertex degrees, many planar graphs do not admit (planar) SC$_{1}$-layouts under the Kandinsky model, where the number of edges using the same port is unbounded. They proved, however, that all planar graphs of maximum degree 3 admit an SC$_{1}$-layout (under the usual port constraint). For the same class of graphs, Alam et al. [1] showed how to get a polynomial drawing area ($O(n^2) \times O(n)$) when increasing the curve complexity to SC$_{2}$. Further, they showed that every planar graph of maximum degree 4 admits an SC$_{2}$-layout, but not every such graph admits an SC$_{1}$-layout where the vertices lie on a polynomial-sized grid. They also proved that every biconnected outerplane graph of maximum degree 4 admits an SC$_{1}$-layout (respecting the given embedding).

In this paper, we study orthogonal and smooth orthogonal layouts of non-planar graphs, in particular, 1-planar graphs. Recall that k-planar graphs are those graphs that admit a drawing in the plane where each edge has at most k crossings. Our goal is to extend the well-established aesthetic criterion ‘curve complexity’ of (smooth) orthogonal drawings from planar to 1-planar graphs.

1-planar graphs, introduced by Ringel [18], probably form the most-studied class of the beyond-planar graphs, which extend the notion of planarity. There are recent surveys on both 1-planar graphs [15] and beyond-planar graphs [10]. Mostly, straight-line drawings have been studied for 1-planar graphs. While every planar graph has a planar straight-line drawing (due to Fáry’s theorem), this is not true for 1-planar graphs [12, 23]. For the 3-connected case, the statement holds except for at most one edge on the outer face [2]. Given a drawing of a 1-planar graph, one can decide in linear time whether it can be “straightened” [14].

An important subclass of 1-planar graphs are outer-1-planar graphs. These are the graphs that have a 1-planar drawing where every vertex lies on the outer (unbounded) face. They are planar graphs, can be recognized in linear time [4, 13], and can be drawn with straight-line edges and right-angle crossings [9].

We are specifically interested in 1-plane and outer-1-plane graphs, which are 1-planar and outer-1-planar graphs together with an embedding. Such an embedding determines the order of the edges around each vertex, but also which edges cross and in which order. By the layout of a 1-plane graph we mean that the layout respects the given embedding, without stating this again. In contrast, the layout of a 1-planar graph can have any 1-planar embedding.

Our Contribution. Previous results and our contribution on (smooth) orthogonal layouts are listed in Table 1. We present new layout algorithms for 1-planar graphs in the orthogonal model (Sect. 3) and in the smooth orthogonal model (Sect. 4), achieving low curve complexity and preserving 1-planarity. We study 1-plane graphs as well as the special case of outer-1-plane graphs, where all vertices lie on the outer face. We conclude with some open problems; see Sect. 5.

In particular, we show that all 1-plane graphs admit OC$_{4}$-layouts (Theorem 2) and SC$_{3}$-layouts (Theorem 5). We also prove that all biconnected outer-1-plane graphs admit OC$_{3}$-layouts (Theorem 4) and SC$_{2}$-layouts (Theorem 7). Three out of these four results are worst-case optimal: There exist biconnected 1-plane graphs that do not admit an OC$_{3}$-layout (Theorem 1) and biconnected outer-1-plane graphs that do not admit OC$_{2}$-layouts (Theorem 3) and SC$_{1}$-layouts (Theorem 6).

Table 1. Comparison of our results to previous work. The model K(andinsky)-SC$_{1}$ does not restrict the number of edges per port to one. ($^\star$) except for the octahedron (OC$_{4}$). “Super-poly” means that the drawings are not known to be of polynomial size.

2 1-Planar Bar Visibility Representation

As an intermediate step towards orthogonal drawings, we introduce 1-planar bar visibility representations: Each vertex is represented as a horizontal segment – called bar – and each edge is represented as either a vertical segment or a polyline composed of a vertical segment and a horizontal segment between the bars of its adjacent vertices. Edges must not intersect other bars. If an edge has a horizontal segment, we call it red. The horizontal segment of a red edge must be on top of its vertical segment and crosses exactly one vertical segment of another edge – which is called blue. The vertical segment of a red edge must not be crossed; see Fig. 2. We consider every edge as a pair of two half-edges, one for each of its two endpoints. Red edges are split at their bend – the construction bend, such that each half-edge consists of either a vertical or a horizontal segment. Observe that horizontal half-edges are always red. We show that every 1-planar graph has a 1-planar bar visibility representation, following the approach of Brandenburg [8]:

For a 1-planar embedding, we define a kite to be a $K_4$ induced by the end vertices of two crossing edges with the property that each of the four triangles induced by the crossing point and one end vertex of each of the two crossing edges is a face. A crossing is caged if its end vertices induce a kite. Let now G be a 1-planar graph. As a preprocessing step, G is augmented to a not necessarily simple graph $G'$, with the property that any crossing is caged and no planar edge can be added to $G'$ without creating a new crossing or a double edge [2].

After the preprocessing step, all crossing edges are removed and a bar visibility representation for the produced plane graph $G_p$ is computed [20, 22]. To this end an st-ordering of a biconnected supergraph of $G_p$ is computed, i.e., an ordering $s=v_0$, $v_1$, $\ldots$, $v_{n-2}$, $v_{n-1}=t$ of the vertices such that each vertex except s and t is adjacent to both, a vertex with a greater and a lower index. The st-number is the index of a vertex. The y-coordinate of each bar is chosen to be the st-number of the respective vertex.

Faces of size four that correspond to the kites of G have three possible configurations: left/right wing or diamond configuration. Figure 2 shows the configurations and how to insert the crossing edges in order to obtain a 1-planar bar visibility representation of $G'$. Removing the caging edges results in a 1-planar bar visibility representation of G.

Fig. 2.

Different configurations for kites in a 1-planar bar visibility representation (Color figure online).

An edge is a left, right, top or bottom edge for a bar if it is attached to the respective side of that bar. Note that only red edges of G can be left or right edges for exactly one of their endpoints (and top edge for their other endpoint). If a bar has no bottom (top) edges, it is a bottom (top) bar, respectively. Otherwise it is a middle bar. For a bottom (top) bar, consider the x-coordinates of the touching points of its edges. We define its leftmost and rightmost edge to be the edge with the smallest and largest x-coordinate, respectively. If such a bar has a left or right edge then, by the previous definition, this is its leftmost or rightmost edge, respectively. Note that by the construction of the bar visibility representation, each bar has at most one left and at most one right red edge.

3 Orthogonal 1-Planar Drawings

In this section, we examine orthogonal 1-planar drawings. In particular, we give a counterexample showing that not every biconnected 1-plane graph of maximum degree 4 admits an OC$_{3}$-layout. On the other hand, we prove that every 1-plane graph of maximum degree 4 admits an OC$_{4}$-layout that preserves the given embedding. For biconnected outer-1-plane graphs we achieve optimal curve complexity 3.

3.1 Orthogonal Drawings for General 1-Planar Graphs

Theorem 1

Not every biconnected 1-plane graph of maximum degree 4 admits an OC$_{3}$-layout. Moreover, there is a family of graphs requiring a linear number of edges of complexity at least 4 in any OC$_{4}$-layout respecting the embedding.

Proof

Consider the 1-planar embedding of a $K_5$ as shown in Fig. 3a. The outer face is a triangle T and all vertices have their free ports in the interior of T. Hence, T has at least 7 bends, and at least one edge of T has at least 3 bends.

For another example refer to Fig. 3b, where vertices a, b, and c create a triangle with the same properties. We use t copies of the graph of Fig. 3b in a column and glue them together by connecting the top and bottom gray vertices of consecutive copies with an edge, as well as the topmost vertex of the topmost copy and the bottommost vertex of the bottommost copy. The graph has $n=9t$ vertices and at least t edges of complexity at least 4.    $\square$

Fig. 3.

Biconnected 1-plane graphs without OC$_{3}$-layout

In order to achieve an OC$_{4}$-layout for 1-plane graphs, we will use a general property of orthogonal drawings of planar graphs: Consider two consecutive bends on an edge e with an incident face f. We say that the pair of bends forms a U-shape if they are both convex or both concave in f and an S-shape, otherwise. It follows from the flow model of Tamassia [21] that if a planar graph has an orthogonal drawing with an S-shape then it also has an orthogonal drawing with the identical sequence of bends on all edges except for the two bends of the S-shape that are removed. Thus, by planarization, any pair of S-shape bends can be removed as long as the two bends are not separated by crossings.

Theorem 2

Every n-vertex 1-plane graph of maximum degree 4 admits an OC$_{4}$-layout on a grid of size $O(n) \times O(n)$.

Proof

Let G be a 1-planar graph of maximum degree 4 and consider a 1-planar bar visibility representation of G. If G is not connected, we draw each connected component separately, therefore we assume that G is connected.

Each vertex is placed on its bar. Figures 4 and 5 indicate how to route the adjacent half-edges. Recall that the S-shape bend pairs can be eliminated. Thus, a horizontal half-edge gets at most one extra bend and a vertical half-edge gets at most two extra bends; see Fig. 5. We call a half-edge extreme if it was horizontal and got one bend or vertical and got two bends that create a U-shape.

Fig. 4.

Replacing a middle bar with a vertex in the presence of (a)–(c) zero, (d)–(e) one, and (f) two horizontal half-edges

Fig. 5.

Replacing a bottom bar of degree 4 with a vertex.

It suffices to show that the edges can be routed such that no edge is composed of two extreme half-edges. Even for red edges where we have the construction bend, we either get one extra bend from the horizontal (extreme) half-edge or two extra bends from the vertical (extreme) half-edge. Observe that an edge is extreme if and only if it is the rightmost or leftmost edge of a bottom or top bar, respectively, and it is attached to the bottom or top of the vertex, respectively. For each bottom or top bar we have the free choice to set either its rightmost or leftmost half-edge to become extreme. Consider the following bipartite graph H. The vertices of H are the top and bottom bars, as well as their leftmost and rightmost edges. A bar-vertex and an edge-vertex are adjacent in H if and only if the bar and the edge are incident. Observe that each bar-vertex has degree two and each edge-vertex has degree at most two, thus H is a union of disjoint paths and cycles and there is a matching of H in which each bar-vertex is matched. This matching defines the extreme half-edges. It assigns exactly one half-edge to every bottom or top-bar and matches at most one half-edge of each edge.    $\square$

3.2 Orthogonal Drawings of Outer-1-Plane Graphs

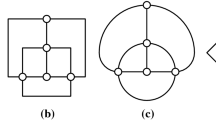
Since outer-1-planar graphs are planar graphs [4], a planar orthogonal layout could be computed with curve complexity at most three. For example, in Fig. 6a we can see an outer-1-plane graph with a planar embedding in Fig. 6b. Arguing similarly as we did for the proof of Theorem 1 it follows that there will be at least two bends on an edge of the outer face. In this particular case, Fig. 6c shows an outer-1-planar drawing of the same graph with at most two bends per edge. In the following we compute 1-planar orthogonal layouts for biconnected outer-1-planar graphs with optimal curve complexity three that also preserve the initial outer-1-planar embedding.

Fig. 6.

An outer-1-plane graph.

Theorem 3

Not every biconnected outer-1-plane graph of maximum degree 4 admits an OC$_{2}$-layout.

Fig. 7.

Constructing a biconnected outer-1-plane graph that does not admit an OC$_{2}$-layout with the same embedding.

Proof

$K_4$ is a biconnected outer-1-plane graph. Actually, it has a unique OC$_{2}$-layout as shown in Fig. 7a. When connecting two copies of $K_4$ by two intersecting edges as in Fig. 7b, it is not possible to draw the resulting graph such that the connector edges intersect and have curve complexity two.    $\square$

Theorem 4

Every biconnected outer-1-plane graph of maximum degree 4 admits an OC$_{3}$-layout in an $O(n) \times O(n)$ grid, where n is the number of vertices.

Proof

(sketch). Let G be an outer-1-planar graph of maximum degree 4. Observe that all crossings can be caged without changing the embedding: A maximal outer-1-planar graph always admits a straight-line outer-1-planar drawing in which all faces are convex [9, 12]. We would directly obtain the required curve complexity if there were no top or bottom bars of degree 4. Instead, our proof is based on a 1-planar bar visibility representation of G produced by a specific st-ordering. Let s and t be two vertices on the outer face. Define $S_l$ and $S_r$ to be the sequences of vertices on the left path and on the right path from s to t along the outer face of G, respectively. We choose $s,S_l,S_r,t$ as our st-ordering. Observe that this is also an st-ordering of the caged and planarized graph $G_p$.

We process middle bars as in the algorithm of Theorem 2. For the top and bottom bars of degree 4 we choose differently which half-edge will be attached to the north or south port, respectively. Let v be a vertex such that b(v) is a top or bottom bar of degree 4. Let $e_l=(v,v_l)$ and $e_r=(v,v_r)$ be its leftmost and rightmost edge, respectively. Assume that $v \in S_l \cup \{s\}$ and b(v) is a bottom bar. If $v_l\in S_l$, we choose edge $e_l$ to be attached to the south port of v, otherwise we choose edge $e_r$. If b(v) is a top bar of degree 4 we choose its leftmost edge $e_l$ to be attached to the north port of v. Symmetrically, if $v\in S_r \cup \{t\}$ and b(v) is a top bar, we choose $e_r$ for the north port of v if $v_r\in S_r$, otherwise we choose $e_l$. If b(v) is a bottom bar we choose its rightmost edge $e_r$ for the south port of v.

The above choice has the following property (see the full version [3] for a detailed proof): Any edge with three or four bends contains two consecutive bends that create an S-shape. The two bends are always connected with a vertical segment. If this is an uncrossed edge of G, the S-shape can be eliminated. For crossing edges, we prove that only one edge per crossing may have more than two bends. If the vertical segment connecting the two bends of the S-shape is crossed, we apply the flow technique of Tamassia [21] around the crossing point and reduce the number of bends (for details see the full version [3]).    $\square$

4 Smooth Orthogonal 1-Planar Drawings

In this section we examine smooth orthogonal 1-planar drawings. In particular, we show that every 1-plane graph of maximum degree 4 admits an SC$_{3}$-layout that preserves the given embedding. For biconnected outer-1-plane graphs, we achieve SC$_{2}$, which is optimal for this graph class.

Fig. 8.

Smoothing process of U-shapes created by top (bottom) bars.

4.1 Smooth Orthogonal Drawings for General 1-Planar Graphs

Theorem 5

Every 1-plane graph of maximum degree 4 admits an SC$_{3}$-layout in $O(n) \times O(n^2)$ area.

Proof

We compute an SC$_{3}$-layout based on an OC$_{4}$-layout computed by the algorithm of Theorem 2. Observe that in the OC$_{4}$-layouts calculated by our approach, the area bounded U-shaped half-edges created at top and bottom bars is vertex-free (see gray area in Fig. 8a), and, each vertex is located on a separate level. We replace one bend of each U-shaped half-edge by a dummy vertex; see Fig. 8a. By doing so, we split each U-shaped half-edge into a vertical edge and an L-shaped half-edge. In the following, we treat the L-shaped half-edge as if the bend was on an L-shaped half-edge incident to the dummy vertex. We process $V=\{v_1,v_2,\ldots ,v_n\}$ in the ascending vertical order of vertices (including dummy vertices). For $v_i$, let $\varDelta ^\uparrow _i$ be the largest horizontal distance between $v_i$ and any bend on incident L-shaped half-edges leading to neighbors with larger index. Let $\varDelta ^\downarrow _i$ be the corresponding value for bends at incident L-shaped half-edges and construction bends of red edges incident to edges leading to neighbors with smaller index. We increase the y-coordinate of all $v_j$ with $j \ge i$ by $\varDelta ^\downarrow _i$ units and then the y-coordinate of all $v_k$ with $k > i$ by $\varDelta ^\uparrow _i$ units. Bends on L-shaped half-edges and construction bends of red edges leading to neighbors with smaller index will be moved together with the corresponding vertex. Note that the region enclosed by U-shapes created at top and bottom bars remains empty; see Fig. 8b. After the stretching, we remove the additional dummy vertices.

Each U-shaped half-edge will be replaced by a semi-circle which fits into the corresponding stretched empty region. We place the semi-circle directly incident to the endpoint which created the U-shape; see Fig. 8c. Then we replace each intersected S-shaped half-edge formed by a construction bend of a red edge by two consecutive quarter arcs incident to the top endpoint of the edge. Recall that if a red edge has an S-shape from its top vertex, it has no bend from its bottom vertex. Further we replace each remaining bend by a quarter arc starting at the corresponding endpoint. Arcs at the two endpoints will be connected by a vertical segment. The correctness follows from the fact that the regions stretched to make space for drawing arcs were empty in the initial drawing.

The area of the resulting drawing is $O(n) \times O(n^2)$ as the input drawing had $O(n)\times O(n)$ area and for every vertex the stretching operation increases the height by at most the length of the longest horizontal segment (i.e. O(n)).    $\square$

4.2 Smooth Orthogonal Drawings for Outer-1-Plane Graphs

We focus on smooth layouts of outer-1-plane graphs. We demonstrate that curve complexity one is not always possible, but curve complexity two can be achieved for biconnected outer-1-plane graphs. We start with the following observation. The complete graph on four vertices with free ports towards its outer face has a unique SC$_{1}$-layout, shown in Fig. 9a. Removing one edge and restricting all ports towards its outer face, there exist two SC$_{1}$-layouts, see Figs. 9b and c.

Fig. 9.

(a) SC$_{1}$-layouts for $K_4$ and (b)–(c) for $K_4-e$ with restricted ports. (d) A biconnected outer-1-plane graph that does not have an SC$_{1}$-layout. (e)-(g) SC$_{1}$-layouts of a subgraph of (d).

Theorem 6

Not every biconnected outer-1-plane graph of maximum degree 4 has an SC$_{1}$-layout.

Proof

Take the graph in Fig. 9d. It has two subgraphs isomorphic to $K_4-e$ (with restricted ports) that share a vertex. Combining two drawings for both copies gives rise to the three drawings in Figs. 9e–g in which the edge between the two highlighted vertices cannot be added with curve complexity one.    $\square$

To achieve SC$_{2}$-layouts for biconnected outer-1-plane graphs (see Fig. 11 for an example), we modify the algorithm of Alam et al. [1] for outerplane graphs; see the full version [3] for details.

Theorem 7

Every biconnected outer-1-plane graph of maximum degree 4 has an SC$_{2}$-layout. The drawing area may be super-polynomial.

Proof

(sketch). The algorithm of Alam et al. [1] processes the faces of the graph along the weak-dual, i.e., the dual graph omitting the outer face and rooted at some inner face. For the next face, one of its edges (the reference edge) is already drawn and imposes the drawing of the face. Figures 10a–f show the different cases.

We define an auxiliary graph $G'$: Let G be a biconnected outer-1-plane graph, and let $G_\mathrm {p}$ be the planarized graph of G, where crossing points are replaced with dummy vertices. Three types of dummy vertices exist in $G_\mathrm {p}$: dummy-cuts (cut vertices), in-dummies (only incident to inner faces), and out-dummies. $G'$ contains all in-dummy and out-dummy vertices of $G_\mathrm {p}$, while dummy-cuts are replaced by a caging cycle. The face inside a caging cycle is called a cut-face. All other faces are called normal. Faces are processed along a traversal of the weak dual of $G'$. As $G'$ may not be outerplanar, its weak dual does not have to be acyclic. It contains cycles of length four around in-dummies (see Fig. 10m). The auxiliary graph $G'$ also contains virtual edges that are red. These are edges added for caging dummy-cuts and edges added to complete the process of faces around an in-dummy. Figures 10g–j show how to process normal faces not appearing in Alam et al. [1]. When processing a cut-face, we draw the crossing edges instead of the caging cycles; see Figs. 10k–l for two out of ten cases. Finally, in order to draw the fourth face around an in-dummy, we ensure that the edge-segments incident to the dummy vertex have the same length; see Fig. 10n for an example.

   $\square$

Fig. 10.

Constructing an SC$_{2}$-drawing of biconnected outer 1-planar graphs (Color figure online).

Fig. 11.

SC$_{2}$-layout of an outer-1-plane graph produced by our algorithm, which is based on the algorithm of Alam et al. [1]. The largest 3/4-arc is only partially drawn.

5 A List of Open Problems

• Can we improve our curve complexity bounds if we restrict ourselves to more strongly connected classes of graphs (of maximum degree 4)?

• Candidate subclasses of outer-1-plane graphs for SC$_{1}$-layouts are for example outer-IC-plane graphs where crossings are independent. A possible variant would be to allow degenerate layouts where pairs of edges can touch but not cross.

• Is there a 1-plane graph that does not admit an SC$_{2}$-layout?

• Do biconnected outer-1-plane graphs admit an SC$_{2}$-layout with polynomial drawing area?

• Do similar results also hold for 2-planar graphs and more generally beyond-planar graphs?