Drawing Subcubic 1-Planar Graphs with Few Bends, Few Slopes, and Large Angles

Abstract

We show that the 1-planar slope number of 3-connected cubic 1-planar graphs is at most 4 when edges are drawn as polygonal curves with at most 1 bend each. This bound is obtained by drawings whose vertex and crossing resolution is at least $\pi /4$. On the other hand, if the embedding is fixed, then there is a 3-connected cubic 1-planar graph that needs 3 slopes when drawn with at most 1 bend per edge. We also show that 2 slopes always suffice for 1-planar drawings of subcubic 1-planar graphs with at most 2 bends per edge. This bound is obtained with vertex resolution $\pi /2$ and the drawing is RAC (crossing resolution $\pi /2$). Finally, we prove lower bounds for the slope number of straight-line 1-planar drawings in terms of number of vertices and maximum degree.

1 Introduction

A graph is 1-planar if it can be drawn in the plane such that each edge is crossed at most once. The notion of 1-planarity naturally extends planarity and received considerable attention since its first introduction by Ringel in 1965 [33], as witnessed by recent surveys [14, 27]. Despite the efforts made in the study of 1-planar graphs, only few results are known concerning their geometric representations (see, e.g., [1, 4, 7, 11]). In this paper, we study the existence of 1-planar drawings that simultaneously satisfy the following properties: edges are polylines using few bends and few distinct slopes for their segments, edge crossings occur at large angles, and pairs of edges incident to the same vertex form large angles. For example, Fig. 1d shows a 1-bend drawing of a 1-planar graph (i.e., a drawing in which each edge is a polyline with at most one bend) using 4 distinct slopes, such that edge crossings form angles at least $\pi /4$, and the angles formed by edges incident to the same vertex are at least $\pi /4$. In what follows, we briefly recall known results concerning the problems of computing polyline drawings with few bends and few slopes or with few bends and large angles.

Related Work. The k-bend (planar) slope number of a (planar) graph G with maximum vertex degree $\varDelta$ is the minimum number of distinct edge slopes needed to compute a (planar) drawing of G such that each edge is a polyline with at most k bends. When $k=0$, this parameter is simply known as the (planar) slope number of G. Clearly, if G has maximum vertex degree $\varDelta$, at least $\lceil \varDelta /2 \rceil$ slopes are needed for any k. While there exist non-planar graphs with $\varDelta \ge 5$ whose slope number is unbounded with respect to $\varDelta$ [3, 32], Keszegh et al. [24] proved that the planar slope number is bounded by $2^{O(\varDelta )}$. Several authors improved this bound for subfamilies of planar graphs (see, e.g., [21, 26, 28]).

Concerning k-bend drawings, Angelini et al. [2] proved that the 1-bend planar slope number is at most $\varDelta -1$, while Keszegh et al. [24] proved that the 2-bend planar slope number is $\lceil \varDelta /2 \rceil$ (which is tight). Special attention has been paid in the literature to the slope number of (sub)cubic graphs, i.e., graphs having vertex degree (at most) 3. Mukkamala and Pálvölgyi showed that the four slopes $\{0, \frac{\pi }{4}, \frac{\pi }{2}, \frac{3\pi }{4}\}$ suffice for every cubic graph [31]. For planar graphs, Kant and independently Dujmović et al. proved that cubic 3-connected planar graphs have planar slope number 3 disregarding the slopes of three edges on the outer face [15, 22], while Di Giacomo et al. [13] proved that the planar slope number of subcubic planar graphs is 4. We also remark that the slope number problem is related to orthogonal drawings, which are planar and with slopes $\{0, \frac{\pi }{2}\}$ [16], and with octilinear drawings, which are planar and with slopes $\{0, \frac{\pi }{4}, \frac{\pi }{2}, \frac{3\pi }{4}\}$ [5]. All planar graphs with $\varDelta \le 4$ (except the octahedron) admit 2-bend orthogonal drawings [6, 29], and planar graphs admit octilinear drawings without bends if $\varDelta \le 3$ [13, 22], with 1 bend if $\varDelta \le 5$ [5], and with 2 bends if $\varDelta \le 8$ [24].

Of particular interest for us is the k-bend 1-planar slope number of 1-planar graphs, i.e., the minimum number of distinct edge slopes needed to compute a 1-planar drawing of a 1-planar graph such that each edge is a polyline with at most $k \ge 0$ bends. Di Giacomo et al. [12] proved an $O(\varDelta )$ upper bound for the 1-planar slope number ($k=0$) of outer 1-planar graphs, i.e., graphs that can be drawn 1-planar with all vertices on the external boundary.

Finally, the vertex resolution and the crossing resolution of a drawing are defined as the minimum angle between two consecutive segments incident to the same vertex or crossing, respectively (see, e.g., [17, 20, 30]). A drawing is RAC (right-angle crossing) if its crossing resolution is $\pi /2$. Eades and Liotta proved that 1-planar graphs may not have straight-line RAC drawings [18], while Chaplick et al. [8] and Bekos et al. [4] proved that every 1-planar graph has a 1-bend RAC drawing that preserves the embedding.

Our Contribution. We prove upper and lower bounds on the k-bend 1-planar slope number of 1-planar graphs, when $k \in \{0,1,2\}$. Our results are based on techniques that lead to drawings with large vertex and crossing resolution.

In Sect. 3, we prove that every 3-connected cubic 1-planar graph admits a 1-bend 1-planar drawing that uses at most 4 distinct slopes and has both vertex and crossing resolution $\pi /4$. In Sect. 4, we show that every subcubic 1-planar graph admits a 2-bend 1-planar drawing that uses at most 2 distinct slopes and has both vertex and crossing resolution $\pi /2$. These bounds on the number of slopes and on the vertex/crossing resolution are clearly worst-case optimal. In Sect. 5.1, we give a 3-connected cubic 1-plane graph for which any embedding-preserving 1-bend drawing uses at least 3 distinct slopes. The lower bound holds even if we are allowed to change the outer face. In Sect. 5.2, we present 2-connected subcubic 1-plane graphs with n vertices such that any embedding-preserving straight-line drawing uses $\varOmega (n)$ distinct slopes, and 3-connected 1-plane graphs with maximum degree $\varDelta \ge 3$ such that any embedding-preserving straight-line drawing uses at least $9(\varDelta -1)$ distinct slopes, which implies that at least 18 slopes are needed if $\varDelta =3$.

Preliminaries can be found in Sect. 2, while open problems are in Sect. 6.

2 Preliminaries

We only consider simple graphs with neither self-loops nor multiple edges. A drawing $\varGamma$ of a graph G maps each vertex of G to a point of the plane and each edge to a simple open Jordan curve between its endpoints. We always refer to simple drawings where two edges can share at most one point, which is either a common endpoint or a proper intersection. A drawing divides the plane into topologically connected regions, called faces; the infinite region is called the outer face. For a planar (i.e., crossing-free) drawing, the boundary of a face consists of vertices and edges, while for a non-planar drawing the boundary of a face may also contain crossings and parts of edges. An embedding of a graph G is an equivalence class of drawings of G that define the same set of faces and the same outer face. A (1-)plane graph is a graph with a fixed (1-)planar embedding. Given a 1-plane graph G, the planarization $G^*$ of G is the plane graph obtained by replacing each crossing of G with a dummy vertex. To avoid confusion, the vertices of $G^*$ that are not dummy are called real. Moreover, we call fragments the edges of $G^*$ that are incident to a dummy vertex. The next lemma will be used in the following and can be of independent interest, as it extends a similar result by Fabrici and Madaras [19]. The proof is given in the full version [25].

Lemma 1

Let $G=(V,E)$ be a 1-plane graph and let $G^*$ be its planarization. We can re-embed G such that each edge is still crossed at most once and (i) no cutvertex of $G^*$ is a dummy vertex, and (ii) if G is 3-connected, then $G^*$ is 3-connected.

A drawing $\varGamma$ is straight-line if all its edges are mapped to segments, or it is k-bend if each edge is mapped to a chain of segments with at most $k>0$ bends. The slope of an edge segment of $\varGamma$ is the slope of the line containing this segment. For convenience, we measure the slopes by their angle with respect to the x-axis. Let $\mathcal S=\{\alpha _1,\dots ,\alpha _t\}$ be a set of t distinct slopes. The slope number of a k-bend drawing $\varGamma$ is the number of distinct slopes used for the edge segments of $\varGamma$. An edge segment of $\varGamma$ uses the north (N) port (south (S) port) of a vertex v if it has slope $\pi /2$ and v is its bottommost (topmost) endpoint. We can define analogously the west (W) and east (E) ports with respect to the slope 0, the north-west (NW) and south-east (SE) ports with respect to slope $3\pi /4$, and the south-west (SW) and north-east (NE) ports with respect to slope $\pi /4$. Any such port is free for v if there is no edge that attaches to v by using it.

We will use a decomposition technique called canonical ordering [23]. Let $G=(V,E)$ be a 3-connected plane graph. Let $\delta = \{\mathcal {V}_1,\dots ,\mathcal {V}_K\}$ be an ordered partition of V, that is, $\mathcal {V}_1 \cup \dots \cup \mathcal {V}_K = V$ and $\mathcal {V}_i \cap \mathcal {V}_j = \emptyset$ for $i \ne j$. Let $G_i$ be the subgraph of G induced by $\mathcal {V}_1 \cup \dots \cup \mathcal {V}_i$ and denote by $C_i$ the outer face of $G_i$. The partition $\delta$ is a canonical ordering of G if: (i) $\mathcal {V}_1=\{v_1,v_2\}$, where $v_1$ and $v_2$ lie on the outer face of G and $(v_1,v_2) \in E$. (ii) $\mathcal {V}_K = \{v_n\}$, where $v_n$ lies on the outer face of G, $(v_1,v_n) \in E$. (iii) Each $C_i$ ($i > 1$) is a cycle containing $(v_1,v_2)$. (iv) Each $G_i$ is 2-connected and internally 3-connected, that is, removing any two interior vertices of $G_i$ does not disconnect it. (v) For each $i \in \{2, \dots , K-1\}$, one of the following conditions holds: (a) $\mathcal {V}_i$ is a singleton $v^i$ that lies on $C_i$ and has at least one neighbor in $G \setminus G_i$; (b) $\mathcal {V}_i$ is a chain $\{v^i_1,\dots , v^i_l\}$, both $v^i_1$ and $v^i_l$ have exactly one neighbor each in $C_{i-1}$, and $v^i_2, \ldots , v^i_{l-1}$ have no neighbor in $C_{i-1}$. Since G is 3-connected, each $v^i_j$ has at least one neighbor in $G \setminus G_i$.

Let v be a vertex in $\mathcal {V}_i$, then its neighbors in $G_{i-1}$ (if $G_{i-1}$ exists) are called the predecessors of v, while its neighbors in $G\setminus G_{i}$ (if $G_{i+1}$ exists) are called the successors of v. In particular, every singleton has at least two predecessors and at least one successor, while every vertex in a chain has either zero or one predecessor and at least one successor. Kant [23] proved that a canonical ordering of G always exists and can be computed in O(n) time; the technique in [23] is such that one can arbitrarily choose two adjacent vertices u and w on the outer face so that $u=v_1$ and $w=v_2$ in the computed canonical ordering.

An n-vertex planar st-graph $G=(V,E)$ is a plane acyclic directed graph with a single source s and a single sink t, both on the outer face [10]. An st-ordering of G is a numbering $\sigma : V \rightarrow \{1,2,\dots ,n\}$ such that for each edge $(u,v) \in E$, it holds $\sigma (u) < \sigma (v)$ (thus $\sigma (s)=1$ and $\sigma (t)=n$). For an st-graph, an st-ordering can be computed in O(n) time (see, e.g., [9]) and every biconnected undirected graph can be oriented to become a planar st-graph (also in linear time).

3 1-Bend Drawings of 3-Connected Cubic 1-Planar Graphs

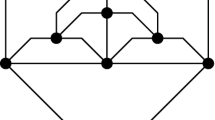
Let G be a 3-connected 1-plane cubic graph, and let $G^*$ be its planarization. We can assume that $G^*$ is 3-connected (else we can re-embed G by Lemma 1). We choose as outer face of G a face containing an edge $(v_1,v_2)$ whose vertices are both real (see Fig. 1a). Such a face exists: If G has n vertices, then $G^*$ has fewer than 3n / 4 dummy vertices because G is subcubic. Hence we find a face in $G^*$ with more real than dummy vertices and hence with two consecutive real vertices. Let $\delta = \{\mathcal {V}_1,\dots ,\mathcal {V}_K\}$ be a canonical ordering of $G^*$, let $G_i$ be the graph obtained by adding the first i sets of $\delta$ and let $C_i$ be the outer face of $G_i$.

Note that a real vertex v of $G_i$ can have at most one successor w in some set $\mathcal {V}_j$ with $j>i$. We call w an L-successor (resp., R-successor) of v if v is the leftmost (resp., rightmost) neighbor of $\mathcal {V}_j$ on $C_{i}$. Similarly, a dummy vertex x of $G_i$ can have at most two successors in some sets $\mathcal {V}_j$ and $\mathcal {V}_l$ with $l \ge j > i$. In both cases, a vertex v of $G_i$ having a successor in some set $\mathcal {V}_j$ with $j>i$ is called attachable. We call v L-attachable (resp., R-attachable) if v is attachable and has no L-successor (resp., R-successor) in $G_i$. We will draw an upward edge at u with slope $\pi /4$ (resp., $3\pi /4$) only if it is L-attachable (resp., R-attachable).

Fig. 1.

(a) A 3-connected 1-plane cubic graph G; (b) a canonical ordering $\delta$ of the planarization $G^*$ of G—the real (dummy) vertices are black points (white squares); (c) the edges crossed by the dashed line are a uv-cut of $G_5$ with respect to (u, w)—the two components have a yellow and a blue background, respectively; (d) a 1-bend 1-planar drawing with 4 slopes of G (Color figure online)

Let u and v be two vertices of $C_i$, for $i>1$. Denote by $P_i(u,v)$ the path of $C_i$ having u and v as endpoints and that does not contain $(v_1,v_2)$. Vertices u and v are consecutive if they are both attachable and if $P_i(u,v)$ does not contain any other attachable vertex. Given two consecutive vertices u and v of $C_i$ and an edge e of $C_i$, a uv-cut of $G_i$ with respect to e is a set of edges of $G_i$ that contains both e and $(v_1,v_2)$ and whose removal disconnects $G_i$ into two components, one containing u and one containing v (see Fig. 1c). We say that u and v are L-consecutive (resp., R-consecutive) if they are consecutive, u lies to the left (resp., right) of v on $C_i$, and u is L-attachable (resp., R-attachable).

We construct an embedding-preserving drawing $\varGamma _i$ of $G_i$, for $i=2,\dots ,K$, by adding one by one the sets of $\delta$. A drawing $\varGamma _i$ of $G_i$ is valid, if:

P1 :

It uses only slopes in the set $\{0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4}\}$;

P2 :

It is a 1-bend drawing such that the union of any two edge fragments that correspond to the same edge in G is drawn with (at most) one bend in total.

A valid drawing $\varGamma _K$ of $G_K$ will coincide with the desired drawing of G, after replacing dummy vertices with crossing points.

Construction of $\varGamma _2$. We begin by showing how to draw $G_2$. We distinguish two cases, based on whether $\mathcal {V}_2$ is a singleton or a chain, as illustrated in Fig. 2.

Construction of $\varGamma _i$, for $2< i < K$. We now show how to compute a valid drawing of $G_i$, for $i=3,\dots ,K-1$, by incrementally adding the sets of $\delta$.

We aim at constructing a valid drawing $\varGamma _i$ that is also stretchable, i.e., that satisfies the following two more properties; see Fig. 3. These two properties will be useful to prove Lemma 2, which defines a standard way of stretching a drawing by lengthening horizontal segments.

Fig. 2.

Construction of $\varGamma _2$: (a) $\mathcal {V}_2$ is a real singleton; (b) $\mathcal {V}_2$ is a dummy singleton; (c) $\mathcal {V}_2$ is a chain.

Fig. 3.

$\varGamma _i$ is stretchable.

P3 :

The edge $(v_1,v_2)$ is drawn with two segments $s_1$ and $s_2$ that meet at a point p. Segment $s_1$ uses the SE port of $v_1$ and $s_2$ uses the SW port of $v_2$. Also, p is the lowest point of $\varGamma _i$, and no other point of $\varGamma _i$ is contained by the two lines that contain $s_1$ and $s_2$.

P4 :

For every pair of consecutive vertices u and v of $C_i$ with u left of v on $C_i$, it holds that (a) If u is L-attachable (resp., v is R-attachable), then the path $P_i(u,v)$ is such that for each vertical segment s on this path there is a horizontal segment in the subpath before s if s is traversed upwards when going from u to v (resp., from v to u); (b) if both u and v are real, then $P_i(u,v)$ contains at least one horizontal segment; and (c) for every edge e of $P_i(u,v)$ such that e contains a horizontal segment, there exists a uv-cut of $G_i$ with respect to e whose edges all contain a horizontal segment in $\varGamma _i$ except for $(v_1,v_2)$, and such that there exists a y-monotone curve that passes through all and only such horizontal segments and $(v_1,v_2)$.

Lemma 2

Suppose that $\varGamma _i$ is valid and stretchable, and let u and v be two consecutive vertices of $C_i$. If u is L-attachable (resp., v is R-attachable), then it is possible to modify $\varGamma _i$ such that any half-line with slope $\pi /4$ (resp., $3\pi /4$) that originates at u (resp., at v) and that intersects the outer face of $\varGamma _i$ does not intersect any edge segment with slope $\pi /2$ of $P_i(u,v)$. Also, the modified drawing is still valid and stretchable.

Proof Sketch

Crossings between such half-lines and vertical segments of $P_i(u,v)$ can be solved by finding suitable uv-cuts and moving everything on the right/left side of the cut to the right/left. The full proof is given in the full version [25].    $\square$

Let P be a set of ports of a vertex v; the symmetric set of ports $P'$ of v is the set of ports obtained by mirroring P at a vertical line through v. We say that $\varGamma _i$ is attachable if the following two properties also apply.

P5 :

At any attachable real vertex v of $\varGamma _i$, its N, NW, and NE ports are free.

P6 :

Let v be an attachable dummy vertex of $\varGamma _i$. If v has two successors, there are four possible cases for its two used ports, illustrated with two solid edges in Fig. 4a–d. If v has only one successor not in $\varGamma _i$, there are eight possible cases for its three used ports, illustrated with two solid edges plus one dashed or one dotted edge in Fig. 4a–e.

Fig. 4.

Illustration for P6. If v has two successors not in $\varGamma _i$, then the edges connecting v to its two neighbors in $\varGamma _i$ are solid. If v has one successor in $\varGamma _i$, then the edge between v and this successor is dashed or dotted.

Observe that $\varGamma _2$, besides being valid, is also stretchable and attachable by construction (see also Fig. 2). Assume that $G_{i-1}$ admits a valid, stretchable, and attachable drawing $\varGamma _{i-1}$, for some $2 \le i < K-1$; we show how to add the next set $\mathcal {V}_i$ of $\delta$ so to obtain a drawing $\varGamma _i$ of $G_i$ that is valid, stretchable and attachable. We distinguish between the following cases.

Case 1. $\mathcal {V}_i$ is a singleton, i.e., $\mathcal {V}_i=\{v^i\}$. Note that if $v^i$ is real, it has two neighbors on $C_{i-1}$, while if it is dummy, it can have either two or three neighbors on $C_{i-1}$. Let $u_l$ and $u_r$ be the first and the last neighbor of $v^i$, respectively, when walking along $C_{i-1}$ in clockwise direction from $v_1$. We will call $u_l$ (resp., $u_r$) the leftmost predecessor (resp., rightmost predecessor) of $v^i$.

Case 1.1. Vertex $v^i$ is real. Then, $u_l$ and $u_r$ are its only two neighbors in $C_{i-1}$. Each of $u_l$ and $u_r$ can be real or dummy. If $u_l$ (resp., $u_r$) is real, we draw $(u_l,v^i)$ (resp., $(u_r,v^i)$) with a single segment using the NE port of $u_l$ and the SW port of $v^i$ (resp., the NW port of $u_r$ and the SE port of $v^i$). If $u_l$ is dummy and has two successors not in $\varGamma _{i-1}$, we distinguish between the cases of Fig. 4 as shown in Fig. 5. The symmetric configuration of C3 is only used for connecting to $u_r$.

Fig. 5.

A real singleton when $u_l$ is dummy with two successors not in $\varGamma _{i-1}$

If $u_l$ is dummy and has one successor not in $\varGamma _{i-1}$, we distinguish between the various cases of Fig. 4 as indicated in Fig. 6. Observe that C1 requires a local reassignment of one port of $u_l$. The edge $(u_r,v^i)$ is drawn by following a similar case analysis. Vertex $v^i$ is then placed at the intersection of the lines passing through the assigned ports, which always intersect by construction. In particular, the S port is only used when $u_l$ has one successor, but the same situation cannot occur when drawing $(u_r,v^i)$. Otherwise, there is a path of $C_{i-1}$ from $u_l$ via its successor x on $C_{i-1}$ to $u_r$ via its successor y on $C_{i-1}$. Note that $x=y$ is possible but $x\ne u_r$. Since the first edge on this path goes from a predecessor to a successor and the last edge goes from a successor to a predecessor, there has to be a vertex z without a successor on the path; but then $u_l$ and $u_r$ are not consecutive. To avoid crossings between $\varGamma _{i-1}$ and the new edges $(u_l,v^i)$ and $(u_r,v^i)$, we apply Lemma 2 to suitably stretch the drawing. In particular, possible crossings can occur only with vertical edge segments of $P_{i-1}(u_l,u_r)$, because when walking along $P_{i-1}(u_l,u_r)$ from $u_l$ to $u_r$ we only encounter a (possibly empty) set of segments with slopes in the range $\{3\pi /4,\pi /2,0\}$, followed by a (possibly empty) set of segments with slopes in the range $\{\pi /2,\pi /4,0\}$.

Fig. 6.

Some cases for the addition of a real singleton when $u_l$ is dummy with one successor not in $\varGamma _{i-1}$

Fig. 7.

Illustration for the addition of a dummy singleton

Case 1.2. Vertex $v^i$ is dummy. By 1-planarity, the two or three neighbors of $v^i$ on $C_{i-1}$ are all real. If $v^i$ has two neighbors, we draw $(u_l,v^i)$ and $(u_r,v^i)$ as shown in Fig. 7a, while if $v^i$ has three neighbors, we draw $(u_l,v^i)$ and $(u_r,v^i)$ as shown in Fig. 7b. Analogous to the previous case, vertex $v^i$ is placed at the intersection of the lines passing through the assigned ports, which always intersect by construction, and avoiding crossings between $\varGamma _{i-1}$ and the new edges $(u_l,v^i)$ and $(u_r,v^i)$ by applying Lemma 2. In particular, if $v^i$ has three neighbors on $C_{i-1}$, say $u_l$, w, and $u_r$, by P4 there is a horizontal segment between $u_l$ and w, as well as between w and $u_r$. Thus, Lemma 2 can be applied not only to resolve crossings, but also to find a suitable point where the two lines with slopes $\pi /4$ and $3\pi /4$ meet along the line with slope $\pi /2$ that passes through w.

Case 2. $\mathcal {V}_i$ is a chain, i.e., $\mathcal {V}_i=\{v^i_1,v^i_2,\dots ,v^i_l\}$. We find a point as if we had to place a vertex v whose leftmost predecessor is the leftmost predecessor of $v^i_1$ and whose rightmost predecessor is the rightmost predecessor of $v^i_l$. We then draw the chain slightly below this point by using the same technique used to draw $\mathcal {V}_2$. Again, Lemma 2 can be applied to resolve possible crossings.

We formally prove the correctness of our algorithm in the full version [25].

Lemma 3

Drawing $\varGamma _{K-1}$ is valid, stretchable, and attachable.

Fig. 8.

Illustration for the addition of $\mathcal {V}_k$

Construction of $\varGamma _K$. We now show how to add $\mathcal {V}_K=\{v_n\}$ to $\varGamma _{K-1}$ so as to obtain a valid drawing of $G_K$, and hence the desired drawing of G after replacing dummy vertices with crossing points. Recall that $(v_1,v_n)$ is an edge of G by the definition of canonical ordering. We distinguish whether $v_n$ is real or dummy; the two cases are shown in Fig. 8. Note that if $v_n$ is dummy, its four neighbors are all real and hence their N, NW, and NE ports are free by P5. If $v_n$ is real, it has three neighbors in $\varGamma _{K-1}$, $v_1$ is real by construction, and the S port can be used to attach with a dummy vertex. Finally, since $\varGamma _{K-1}$ is attachable, we can use Lemma 2 to avoid crossings and to find a suitable point to place $v_n$. A complete drawing is shown in Fig. 1d.

The theorem follows immediately by the choice of the slopes.

Theorem 1

Every 3-connected cubic 1-planar graph admits a 1-bend 1-planar drawing with at most 4 distinct slopes and angular and crossing resolution $\pi /4$.

4 2-Bend Drawings

Liu et al. [29] presented an algorithm to compute orthogonal drawings for planar graphs of maximum degree 4 with at most 2 bends per edge (except the octahedron, which requires 3 bends on one edge). We make use of their algorithm for biconnected graphs. The algorithm chooses two vertices s and t and computes an st-ordering of the input graph. Let $V=\{v_1,\ldots ,v_n\}$ with $\sigma (v_i)=i$, $1\le i\le n$. Liu et al. now compute an embedding of G such that $v_2$ lies on the outer face if $\deg (s)=4$ and $v_{n-1}$ lies on the outer face if $\deg (t)=4$; such an embedding exists for every graph with maximum degree 4 except the octahedron.

The edges around each vertex $v_i,1\le i\le n$, are assigned to the four ports as follows. If $v_i$ has only one outgoing edge, it uses the N port; if $v_i$ has two outgoing edges, they use the N and E port; if $v_i$ has three outgoing edges, they use the N, E, and W port; and if $v_i$ has four outgoing edges, they use all four ports. Symmetrically, the incoming edges of $v_i$ use the S, W, E, and N port, in this order. The edge (s, t) (if it exists) is assigned to the W port of both s and t. If $\deg (s)=4$, the edge $(s,v_2)$ is assigned to the S port of s (otherwise the port remains free); if $\deg (t)=4$, the edge $(t,v_{n-1})$ is assigned to the N port of t (otherwise the port remains free). Note that every vertex except s and t has at least one incoming and one outgoing edge; hence, the given embedding of the graph provides a unique assignment of edges to ports. Finally, they place the vertices bottom-up as prescribed by the st-ordering. The way an edge is drawn is determined completely by the port assignment, as depicted in Fig. 9.

Let $G=(V,E)$ be a subcubic 1-plane graph. We first re-embed G according to Lemma 1. Let $G^*$ be the planarization of G after the re-embedding. Then, all cutvertices of $G^*$ are real vertices, and since they have maximum degree 3, there is always a bridge connecting two 2-connected components. Let $G_1,\ldots ,G_k$ be the 2-connected components of G, and let $G_i^*$ be the planarization of $G_i,1\le i\le k$. We define the bridge decomposition tree $\mathcal {T}$ of G as the graph having a node for each component $G_i$ of G, and an edge $(G_i,G_j)$, for every pair $G_i, G_j$ connected by a bridge in G. We root $\mathcal {T}$ in $G_1$. For each component $G_i,2\le i\le k$, let $u_i$ be the vertex of $G_i$ connected to the parent of $G_i$ in $\mathcal T$ by a bridge and let $u_1$ be an arbitrary vertex of $G_1$. We will create a drawing $\varGamma _i$ for each component $G_i$ with at most 2 slopes and 2 bends such that $u_i$ lies on the outer face.

To this end, we first create a drawing $\varGamma _i^*$ of $G_i^*$ with the algorithm of Liu et al. [29] and then modify the drawing. Throughout the modifications, we will make sure that the following invariants hold for the drawing $\varGamma _i^*$.

• (I1) $\varGamma _i^*$ is a planar orthogonal drawing of $G_i^*$ and edges are drawn as in Fig. 9;

• (I2) $u_i$ lies on the outer face of $\varGamma _i^*$ and its N port is free;

• (I3) every edge is y-monotone from its source to its target;

• (I4) every edge with 2 bends is a C-shape, there are no edges with more bends;

• (I5) if a C-shape ends in a dummy vertex, it uses only E ports; and

• (I6) if a C-shape starts in a dummy vertex, it uses only W ports.

Fig. 9.

The shapes to draw edges

Lemma 4

Every $G_i^*$ admits a drawing $\varGamma _i^*$ that satisfies invariants (I1)–(I6).

Proof Sketch

We choose $t=u_i$ and some real vertex s and use the algorithm by Liu et al. to draw $G_i$. Since s and t are real, there are no U-shapes. Since no real vertex can have an outgoing edge at its W port or incoming edge at its E port, the invariants follow. The full proof is given in the full version [25].    $\square$

We now iteratively remove the C-shapes from the drawing while maintaining the invariants. We make use of a technique similar to the stretching in Sect. 3. We lay an orthogonal y-monotone curve S through our drawing that intersects no vertices. Then we stretch the drawing by moving S and all features that lie right of S to the right, and stretching all points on S to horizontal segments. After this stretch, in the area between the old and the new position of S, there are only horizontal segments of edges that are intersected by S. The same operation can be defined symmetrically for an x-monotone curve that is moved upwards.

Lemma 5

Every $G_i$ admits an orthogonal 2-bend drawing such that $u_i$ lies on the outer face and its N port is free.

Proof Sketch

We start with a drawing $\varGamma _i^*$ of $G_i^*$ that satisfies invariants (I1)–(I6), which exists by Lemma 4. By (I2), $u_i$ lies on the outer face and its N port is free. If no dummy vertex in $\varGamma _i^*$ is incident to a C-shape, by (I4) all edges incident to dummy vertices are drawn with at most 1 bend, so the resulting drawing $\varGamma _i$ of $G_i$ is an orthogonal 2-bend drawing. Otherwise, there is a C-shape between a real vertex u and a dummy vertex v. We show how to eliminate this C-shape without introducing new ones while maintaining all invariants.

We prove the case that (u, v) is directed from u to v, so by (I5) it uses only E ports; the other case is symmetric. We do a case analysis based on which ports at u are free. We show one case here and the rest in the full version [25].

Case 1. The N port at u is free; see Fig. 10. Create a curve S as follows: Start at some point p slightly to the top left of u and extend it downward to infinity. Extend it from p to the right until it passes the vertical segment of (u, v) and extend it upwards to infinity. Place the curve close enough to u and (u, v) such that no vertex or bend point lies between S and the edges of u that lie right next to it. Then, stretch the drawing by moving S to the right such that u is placed below the top-right bend point of (u, v). Since S intersected a vertical segment of (u, v), this changes the edge to be drawn with 4 bends. However, now the region between u and the second bend point of (u, v) is empty and the N port of u is free, so we can make an L-shape out of (u, v) that uses the N port at u. This does not change the drawing style of any edge other than (u, v), so all the invariants are maintained and the number of C-shapes is reduced by one.    $\square$

Fig. 10.

Proof of Lemma 5, Case 1

Finally, we combine the drawings $\varGamma _i$ to a drawing $\varGamma$ of G. Recall that every cutvertex is real and two biconnected components are connected by a bridge. Let $G_j$ be a child of $G_i$ in the bridge decomposition tree. We have drawn $G_j$ with $u_j$ on the outer face and a free N port. Let $v_i$ be the neighbor of $u_j$ in $G_i$. We choose one of its free ports, rotate and scale $\varGamma _j$ such that it fits into the face of that port, and connect $u_j$ and $v_i$ with a vertical or horizontal segment. Doing this for every biconnected component gives an orthogonal 2-bend drawing of G.

Theorem 2

Every subcubic 1-plane graph admits a 2-bend 1-planar drawing with at most 2 distinct slopes and both angular and crossing resolution $\pi /2$.

5 Lower Bounds for 1-Plane Graphs

5.1 1-Bend Drawings of Subcubic Graphs

Theorem 3

There exists a subcubic 3-connected 1-plane graph such that any embedding-preserving 1-bend drawing uses at least 3 distinct slopes. The lower bound holds even if we are allowed to change the outer face.

Proof

Let G be the $K_4$ with a planar embedding. The outer face is a 3-cycle, which has to be drawn as a polygon $\varPi$ with at least four (nonreflex) corners. Since we allow only one bend per edge, one of the corners of $\varPi$ has to be a vertex of G. The vertex in the interior has to connect to this corner, however, all of its free ports lie on the outside. Thus, no drawing of G is possible.    $\square$

5.2 Straight-Line Drawings

The full proofs for this section are given in the full version [25].

Theorem 4

There exist 2-regular 2-connected 1-plane graphs with n vertices such that any embedding-preserving straight-line drawing uses $\varOmega (n)$ distinct slopes.

Fig. 11.

The constructions for the results of Sect. 5

Proof Sketch

Let $G_k$ be the graph given by the cycle $a_1\ldots ,a_{k+1},b_{k+1},\ldots ,b_1,a_1$ and the embedding shown in Fig. 11a. Walking along the path $a_1,\ldots ,a_{k+1}$, we find that the slope has to increase at every step.    $\square$

Lemma 6

There exist 3-regular 3-connected 1-plane graphs such that any embedding-preserving straight-line drawing uses at least 18 distinct slopes.

Proof Sketch

Consider the graph depicted in Fig. 11b. We find that the slopes of the edges $(a_i,b_i),(a_i,c_i),(c_i,d_i),(c_i,e_i),(e_i,d_i),(e_i,a_{i+1})$ have to be increasing in this order for every $i=1,2,3$.    $\square$

Theorem 5

There exist 3-connected 1-plane graphs such that any embedding-preserving straight-line drawing uses at least $9(\varDelta -1)$ distinct slopes.

Proof Sketch

Consider the graph depicted in Fig. 11c. The degree of $a_i$, $c_i$, and $e_i$ is $\varDelta$. We repeat the proof of Lemma 6, but observe that the slopes of the $9(\varDelta -3)$ added edges lie between the slopes of $(a_i,b_i),(a_i,c_i),(c_i,e_i)$, and $(e_i,a_{i+1})$.    $\square$

6 Open Problems

The research in this paper gives rise to interesting questions, among them: (1) Is it possible to extend Theorem 1 to all subcubic 1-planar graphs? (2) Can we drop the embedding-preserving condition from Theorem 3? (3) Is the 1-planar slope number of 1-planar graphs bounded by a function of the maximum degree?