Abstract
Ring signatures, as introduced by Rivest, Shamir, and Tauman (Asiacrypt ’01), allow to generate a signature for a message on behalf of an ad-hoc set of parties. To sign a message, only the public keys must be known and these can be generated independently. It is furthermore not possible to identify the actual signer based on the signature. Ring signatures have recently gained attention due to their applicability in the construction of practical anonymous cryptocurrencies, where they are used to secure transactions while hiding the identity of the actual spender. To be applicable in that setting, ring signatures must allow to determine when a party signed multiple transactions, which is done using a property called linkability.
This work presents a linkable ring signature scheme constructed from a lattice-based collision-resistant hash function. We follow the idea of existing schemes which are secure based on the hardness of the discrete logarithm problem, but adapt and optimize ours to the lattice setting. In comparison to other designs for (lattice-based) linkable ring signatures, our approach avoids the standard solution for achieving linkability, which involves proofs about correct evaluation of a pseudorandom function using heavy zero-knowledge machinery.
C. Baum—Supported by the BIU Center for Research in Applied Cryptography and Cyber Security in conjunction with the Israel National Cyber Bureau in the Prime Minister’s Office.
S. Oechsner—This work has been supported by the European Research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme under grant agreement No. 669255 (MPCPRO). Part of work done while visiting NTT Secure Platform Laboratories.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Digital signatures are one of the most important concepts in the area of cryptography. They permit a party to generate a key pair (SK, PK), give PK to the public and add certain information \(\varOmega \) - called the signature - to a message m. \(\varOmega \) is derived using the private (or signing) key SK and later allows a verifier, equipped with the public verification key PK, to attest that the signer indeed generated \(\varOmega \) for this specific message m. Verification is done in a way such that only a party who possesses certain secret information that only the signer has, namely the secret signing key SK, can generate a valid signature for PK.
Ring signatures, which were first suggested by Rivest, Shamir, and Tauman [40], relax the condition of having exactly one pair (SK, PK) for signing and verification to a certain extent. They allow a party among a set of N participants to sign a message on behalf of all of them. Here it is crucial that the verifier cannot identify the party that signed the message, while nobody outside of the N participants should be able to sign a message as if he was a participant himself. In comparison to group signatures, the set of parties does not need to be known ahead of time, but only when the signature is generated. Therefore, no key-generation algorithm which generates correlated randomness for all N parties needs to be involved and the rings can be set up ad-hocFootnote 1.
For such a ring signature, each signer could issue an arbitrary number of signatures. Fujisaki and Suzuki introduced the notion of traceable ring signatures [17], where the signer signs a message with respect to a list of ring members and a public issue such as an election. There is a public procedure to determine whether two signatures come from one signer, i.e., the signer is linked if a signer signs the same message with respect to the same list of ring member and same issue twice [16]. A related idea is so-called linkable ring signatures, in which case the true signer will be linked when he signs two messages (different or identical) with respect to the same ring. In a more restricted version of linkable ring signatures, one-time linkable ring signatures, a signer is linked as soon as he reveals two signatures. This property has proven to be vital in the construction of cryptocurrencies, such as to prevent double spending attacks and to preserve the anonymity of a spender since the address or the respective secret key in the design of the anonymous cryptocurrency is supposed to be one-time [37].
1.1 Related Work
Lattice-Based Signature Schemes. The line of work on lattice-based signature schemes was, to the best of our knowledge, initiated by Goldreich et al. [19], while the first practical construction was based on NTRU [22]. A scheme that fits into this line of work is the provably secure construction due to Gentry et al., also called hash-and-sign [18]. This approach, where the signing key is a secret trapdoor which is used to sample a short lattice vector, was further developed in [9, 15]. A different direction, called Fiat Shamir with Aborts, was first explored by Lyubashevsky [28, 29]. Very efficient signature schemes such as Tesla [21] and Dilithium [14] have been designed within this framework.
(Linkable) Ring Signature Schemes. There exists a wealth of literature on ring signature and linkable ring signature schemes such as [6, 16, 17, 27, 40] and we only list some of the relevant works here. However, the above mentioned signature schemes have a signature size that is linearly dependent on the number of users N in the ring. The Groth-Kohlweiss framework [20] is based on homomorphic commitments and provides a ring signature scheme with a logarithmic signature size. Franklin and Zhang [16] propose a general framework for linkable ring signatures. They extend the “PRF made public” paradigm by Bellare and Goldwasser [5] in order to provide linkability by combining a PRF evaluation of the secret key with a NIZK proof of correct evaluation. The smallest ring signatures to date have constant signature size and are based on accumulators. The construction by Dodis et al. [13] uses accumulators based on the strong RSA assumption, while Nguyen’s [36] relies on pairing-based cryptography. There exists also a linkable version of [13] by Tsang and Wei [42] that retains the constant-sized signatures. There exist candidates for post-quantum ring signature schemes such as hash-based [12, 23] or multi-variate-quadratic-equation based constructions [35]. Neither of them provide linkability in their current form, but they can potentially be extended to do so.
Lattice-Based Ring Signature Schemes. Lattice-based ring signatures were first introduced explicitly through the work of Brakerski and Tauman-Kalai [10] who proposed a general framework for ring signatures in the standard model and showed how to instantiate it based on the SIS assumption. The resulting signatures have size O(mN) for message length m and ring size N. Subsequently, Wang and Sun [43] proposed two ring signatures schemes from the SIS assumption in the random oracle and standard model, respectively, both of linear signature size. The first ring signature scheme based on the LWE assumption was proposed by Melchor et al. [33] and is an extension of [28] to the ring signature setting. Like the previous schemes, it yields signatures of linear size. Recently, Libert et al. [25] proposed the first lattice-based ring signature scheme with only logarithmic signature size using a Merkle-tree based construction.
Concurrent Work. In concurrent work, Torres et al. [41] present a construction that is very similar to ours. When comparing the actual parameters of both, we have a larger size of the public keys, but compare favorably in the signature size.
1.2 Our Contribution
We present a lattice-based linkable ring signature scheme based on the Module-SIS and Module-LWE problem. Our scheme has a signature size which is linear in N. It is therefore asymptotically less efficient than e.g. [12, 23, 25]. However, we show that in terms of signature size our construction outperforms or performs as good as [12, 25] for comparable security levels for ring sizes \(N\lessapprox 128\) and beats [23] for rings of small size. A comparison can be found in Table 1 below.
The authors of [12] present two different, highly optimized constructions of ring signatures in their work. We mention numbers for both to allow for fair comparison (outperforming one of the two for \(N=128\)). We want to stress that using known techniques [14] and by choosing parameters more aggressively it is possible to reduce the public key and signature size in our setting further, but such optimizations are beyond the scope of this work. Furthermore, [12, 23, 25] are not linkable in their current form, so one can expect a further increase in their proof size to compute a linkability tag. Though our work only outperforms [23] for small (\(N \le 20\)) ring sizes, this is exactly the range that cryptocurrencies need: the recommended ring size of the most popular cryptocurrency using linkable ring signatures, Monero, at the time of writing was \(N=5\). As mentioned before, using [14], would make it possible to reduce the ring signature size further to also outperform [23] for \(N\lessapprox 64\).
1.3 Technical Overview
As mentioned before, the standard approach for transforming a ring signature scheme into a linkable ring signature scheme, following Franklin and Zhang [16], is to add a PRF evaluation of the signer’s secret key to the signature, as well as a zero-knowledge proof of correct evaluation of the PRF under one of the secret keys corresponding to the public keys. This generic approach applies to any ring signature scheme and was explored for lattice-based PRFs in [25, 26, 44]. However, such proofs come with quite a substantial overhead. Our construction instead follows the approach of Liu et al. [27] that avoids this technique. The main observation is that the signer in their scheme has two “public” keys: One that is published before signature generation as part of the ring of signers, and the other one that is appended to each signature. Hence, another“public key” under different public parameters that corresponds to the signer’s secret signing key can be used as linkability tag. Since both kinds of public keys share the same algebraic structure, the two “public keys” of the signer, i.e. the actual public key and the linkability tag, can be tied together without appending another non-interactive zero-knowledge proof to the signature.
Since our construction will be based on the (Module-)SIS and (Module-)LWE problem, the public keys of the parties are of the form \(PK = \varvec{A}\varvec{r}\) for secret key \(\varvec{r}\) and public matrix \(\varvec{A}\). Linkability will be ensured by providing linkability tags \(I = \varvec{B}\varvec{r}\) for another public matrix \(\varvec{B}\). Interestingly, the reason why our construction achieves only one-time linkability is inherent in this approach: any evaluation \(\varvec{B} \varvec{r}\) leaks information about \(\varvec{r}\). If a fresh matrix \(\varvec{B}\) is generated for each ring, then a malicious party can receive more leakage on \(\varvec{r}\) than intended and hence may be able to recover the signer’s secret key.
In order to obtain more efficient lattice-based (linkable) ring signatures, it may be tempting to try to instantiate current sublinear-size ring signatures in the lattice setting. Note, however, that this is far from trivial, as these solutions are specifically tailored to a certain assumption like Dodis et al.’s accumulator-based ring signatures [13], or suffer from the well-known problem that hard lattice assumptions do not provide enough algebraic structure to support existing sublinear approaches based on homomorphic operations like that of Groth and Kohlweiss [20].
Paper Organization
In Sect. 2 we will introduce some definitions and lemmas concerning lattice-based constructions which we will need throughout this work. Moreover, we will give definitions for linkable ring signatures (following previous work). Section 3 contains the construction and security statements. The main parts of the proofs are deferred to Appendix A, whereas we discuss the practicality of our scheme in Sect. 4. In this Section, we also provide a sample parameter set for our construction together with estimates for the size of signatures.
2 Preliminaries
We will use [N] as shorthand for the set \(\{1, \dots , N\}\). Let R be the cyclotomic ring  , where \(\nu =2^p\) and \(p \in \mathbb {N}^+\). Let q be an odd prime and define
, where \(\nu =2^p\) and \(p \in \mathbb {N}^+\). Let q be an odd prime and define  . Here \(\mathbb {Z}_q\) denotes the integers modulo q, which will be represented as elements from the interval \(\left[ - {\frac{{q - 1}}{2}}, {\frac{{q - 1}}{2}} \right] \). For \(f=\sum _i f_i X^i \in R\), the norms of f are defined as
. Here \(\mathbb {Z}_q\) denotes the integers modulo q, which will be represented as elements from the interval \(\left[ - {\frac{{q - 1}}{2}}, {\frac{{q - 1}}{2}} \right] \). For \(f=\sum _i f_i X^i \in R\), the norms of f are defined as
If \(f \in R_q\), then we will represent each coset from \(\mathbb {Z}_q\) with its unique representative from the aforementioned interval and consider the norm of the obtained \(\mathbb {Z}\)-vector. Let \(S_{\beta }\) denote the set of elements \(x \in R\) with \(l_\infty \)-norm at most \(\beta \). Let \(\mathbf {0}_v\in \mathbb {Z}^{v \times v}\) and \(\mathbf {I}_v \in \mathbb {Z}^{v \times v}\) denote the zero and identity matrix over \(\mathbb {Z}\).
Remark 1
We use the following standard relations among different l-norms of a vector in R as defined above:
-
1.
If \(f, g \in R\) such that \(\left\| f\right\| _\infty \le \beta \), \(\left\| g\right\| _1 \le \gamma \), then \(\left\| fg\right\| _\infty \le \beta \gamma \).
-
2.
If \(f \in R\), \(\varvec{g} \in R^v\) satisfy that \(\left\| f\right\| _2 \le \beta \), \(\left\| \varvec{g}\right\| _\infty \le \gamma \), then \(\left\| f\varvec{g}\right\| _2 \le \sqrt{v}\nu \beta \gamma \).
We require a subset D of \(R_q\) which consists of short invertible elements such that the difference of any two distinct elements from this set is also invertible. It was shown in [32] that as long as q is a prime that satisfies \(q=17\mod 32\) and \(q>2^{20}\), then the set \(D=\left\{ {d \in {R_q}|{{\left\| d \right\| }_\infty } \le 1,{{\left\| d \right\| }_1} \le \kappa } \right\} \) satisfies this requirement. We use \(\bar{D}\) to denote the set of values \(D+D\) excluding 0.
2.1 Normal Distribution and Rejection Sampling
The continuous normal distribution over \(\mathbb {R}^\nu \) centered at \(\varvec{u}\in \mathbb {R}^\nu \) with standard deviation \(\sigma \) has probability density function
The discrete normal distribution over \(R^v\) centered at \(\varvec{u}\in R^v\) with standard deviation \(\sigma \) is given by the distribution function (for all \(\varvec{x} \in R^{v}\))
where we omit the subscript \(\varvec{u}\) when it is zero. We use the following standard tail-bound due to Banaszczyk:
Lemma 1
Let \(\mathcal {N}_{\varvec{u},\sigma }\) be defined as above. Then
For our ring signature scheme, we use rejection sampling to hide the secret signing key. The basic idea of rejection sampling is to abort the protocol with a certain probability such that the distribution of the response is independent of the secret input. We adopt the rejection sampling lemma from [29]:
Lemma 2
Let V be a subset of \(R^v\) in such that all elements have \({\left\| \cdot \right\| _2}\)-norms less than T, \(\sigma \in \mathbb {R}\) such that \(\sigma =\omega (T \sqrt{\log (v\nu )})\), and \(h: V \rightarrow \mathbb {R}\) be a probability distribution. Then there exists an \(M=O(1)\) such that the output distribution of the following two algorithms \(\mathcal {A}\), \(\mathcal {S}\) is within statistical distance \(2^{-\omega (\log (v\nu ))}/M\):
-
\(\mathcal {A}\) :
-
1.
\(\varvec{u} \leftarrow h\)
-
2.
\(\varvec{z} \leftarrow \mathcal {N}^v_{\varvec{u},\sigma }\)
-
3.
output \(\left( {\varvec{u},\varvec{z}} \right) \) with probability \(\min \left( {\frac{1}{M} {\frac{{{\mathcal{N}^v_\sigma }\left( \varvec{z} \right) }}{{{\mathcal{N}_{\varvec{u},\sigma }^v}\left( { \varvec{z}} \right) }}} ,1} \right) \)
-
1.
-
\(\mathcal {S}\) :
-
1.
\(\varvec{u} \leftarrow h\)
-
2.
\(\varvec{z} \leftarrow \mathcal {N}^v_{\sigma }\)
-
3.
output \(\left( {\varvec{u},\varvec{z}} \right) \) with probability 1/M
-
1.
Moreover, the probability that \(\mathcal {A}\) outputs a value is at least \(\frac{1-2^{-\omega (\log (v\nu ))}}{M}\).
In [29], the author remarks that if \(\sigma = \alpha T, \alpha >0\) and \(M=\exp \left( 12/\alpha +1/(2\alpha ^2)\right) \) then the output of both algorithms will be within statistical distance \(2^{-100}/M\) and \(\mathcal {A}\) will output a value with probability at least \(\dfrac{1-2^{-100}}{M}\). As an example, assume that we want the signing algorithm to succeed in each iteration with probability 1/3, i.e. we want to set \(M=3\). Then following the reasoning in [29], we can set \(\sigma =11\cdot T \). This means that the output of the signing algorithm is indistinguishable from the simulator except with probability \({\approx }\,\,2^{-98}\), which we deem sufficient for our application.
2.2 Module-SIS and Module-LWE
The security of our linkable ring signature scheme will be based on the hardness of two problems, Module-SIS and Module-LWE [24]. These problems are variants of the well-known SIS [1] and LWE [39] problems, but over modules that are defined over polynomial rings. This is a generalized version of the Ring-SIS and Ring-LWE problems [30, 31, 38]. Using Module-lattice assumptions comes with two advantages: (i) while they are a generalization of ideal-lattice assumptions, they still retain some structure which is necessary to construct a large space of short, invertible elements which is necessary for our construction; and (ii) there is evidence that module lattices of larger rank are less prone to certain attacks than ideal-lattices [3, 8].
The homogeneous Module-SIS problem consists of finding a vector \(\varvec{r}\) of small norm such that \(\varvec{A}\varvec{r}=0\) for a given, structured matrix \(\varvec{A}\).
Definition 1
\((\textsc {MSIS}_{h, v, t}).\) Given \(\varvec{A} \leftarrow R_q^{h \times v}\), find \(\varvec{r} \in R^v\) such that
\(\varvec{A} \varvec{r} = 0\) and \(0 < {\left\| \varvec{r} \right\| _2} \le t\).
Our scheme also uses the Decisional Module-LWE problem. In \(\textsc {D}\hbox {-}\textsc {MLWE}\), the problem consists of distinguishing noisy linear equations from random.
Definition 2
\((\textsc {D}\hbox {-}\textsc {MLWE}_{h, v, \beta }).\) Let \(\varvec{A} \leftarrow R_q^{h \times v}\). Then distinguish the distributions
where \(\varvec{r} \leftarrow S^v_\beta \) and \(\varvec{u} \leftarrow R_q^h\).
Here, we use a special instance of the Module-LWE problem where the secret has the same distribution as the noiseFootnote 2.
If two samples (with different matrices, but same secret vector \(\varvec{r}\)) are issued by the challenger, then this can still be related to a \(\textsc {D}\hbox {-}\textsc {MLWE}\) instance but with different parameters, as the following proposition shows.
Proposition 1
Let \(\varvec{A}, \varvec{B} \leftarrow R_q^{h\times v}\), \(\varvec{r} \leftarrow S_\beta ^v\) and \(\varvec{c}, \varvec{d} \leftarrow R_q^h\). Then
given the \(\textsc {D}\hbox {-}\textsc {MLWE}_{2h, v, \beta }\)-problem is hard.
Proof
Consider the matrices \(\varvec{E} = \left[ {\begin{array}{*{20}{c}} \varvec{A}\\ \varvec{B} \end{array}} \right] \), and \(\varvec{E}\varvec{r}=\left[ {\begin{array}{*{20}{c}} \varvec{A}\varvec{r}\\ \varvec{B}\varvec{r} \end{array}} \right] \). Then distinguishing the above distributions is equivalent to distinguishing
This is the definition of the \(\textsc {D}\hbox {-}\textsc {MLWE}_{2h, v, \beta }\) problem. \(\square \)
Our construction will moreover rely on a third problem, namely the Search Module-LWE problem. It can be seen as an inhomogeneous \(\textsc {MSIS}\) instance where the target is known to have a short preimage under \(\varvec{A}\).
Definition 3
\((\textsc {S}\hbox {-}\textsc {MLWE}_{h, v, \beta }).\) Sample a uniformly random \(\varvec{r}\leftarrow S_\beta ^v\). Given \(\left( \varvec{A} \leftarrow R_q^{h \times v}\!\!,\right. \left. \varvec{s}=\varvec{A}\varvec{r} \right) \) find \(\varvec{r}' \in R^v\) such that \(\varvec{A} \varvec{r}' = \varvec{s}\) and \(0 < {\left\| \varvec{r}' \right\| _\infty } \le \beta \).
Fixing \(h,v,\beta \) of an \(\textsc {S}\hbox {-}\textsc {MLWE}\)-instance, it is easy to see that any algorithm \(\mathcal {A}\) that solves \(\textsc {S}\hbox {-}\textsc {MLWE}\)-instances can also solve \(\textsc {D}\hbox {-}\textsc {MLWE}\)-instances with the same parameters in comparable time and with similar probability. For the converse direction, Langlois and Stehlé [24] showed that, for certain parameter sets, \(\textsc {S}\hbox {-}\textsc {MLWE}\) can be reduced to \(\textsc {D}\hbox {-}\textsc {MLWE}\).
2.3 Linkable Ring Signatures
The formal syntax and security model of linkable ring signatures, sometimes also called linkable spontaneous anonymous group signatures, can be found in [17, 27]. Definitions of linkable ring signatures with adaptation to the cryptocurrency scenario can be found in [37]. Our definitions are in the spirit of [17, 20, 27].
Definition 4
(Linkable Ring Signature). A linkable ring signature scheme consists of five algorithms:
-
\(\mathbf {Setup}(1^\lambda )\): Generates and outputs public parameters PP available to all users.
-
\(\mathbf {KGen}(PP)\): Generates a public key PK and a private signing key SK.
-
\(\mathbf {Sign}_{PP, SK_\ell }(m, L)\): Outputs a signature \(\varOmega \) on the message \(m \in \{0, 1\}^\star \) with respect to the ring \(L=(PK_1, \dots , PK_N)\). Here, (\(PK_\ell , SK_\ell \)) is a valid key pair output by \(\mathbf {KGen} (PP)\), and \(PK_\ell \in L\).
-
\(\mathbf {Vfy}(m, L, \varOmega )\): Verifies a purported ring signature \(\varOmega \) on a message m with respect to the ring of public keys L. It outputs a bit \(b\in \{0,1\}\).
-
\(\mathbf {Link}(m_1, m_2,\varOmega _1,\varOmega _2)\)Footnote 3: Takes as inputs two messages \(m_1, m_2\) as well as two signatures \(\varOmega _1\) and \(\varOmega _2\) and outputs \(b\in \{0,1\}\).
The above algorithms form a linkable ring signature scheme if the following three definitions of correctness, signer anonymity, linkability and exculpability are fulfilled.
Definition 5
(Correctness). Let \(N\ge 1\). Then \(\forall t\in [N],~\forall \{i_1,\ldots , i_t\} \subset [N], k\in \{i_1,\ldots , i_t\} \) and \(\forall m\in \{0,1\}^*\) it holds that
Signer anonymity captures the intuition that if the targeted signer is not corrupted, then the probability that the adversary can identify him as the true signer among all uncorrupted parties is negligible.
Definition 6
(Signer Anonymity). Let \(L=(PK_1,\dots ,PK_N)\) be a list of public keys and \(D_t\) be any set of \(0\le t<N\) signing keys such that \(\forall SK_i \in D_t ~ \exists PK_i \in L: ~ (PK_i, SK_i) \text { is generated by }{} \mathbf {KGen} \). A ring signature scheme is signer anonymous if for any PPT algorithm \(\mathcal {E}\), on inputs of any message m, sets \(L,D_t\) as defined above and any valid signature \(\varOmega \) on L and m generated using \(SK_\ell \not \in D_t\), then
Let \(PP\leftarrow \mathbf {Setup}(1^\lambda )\). For the following two definitions we assume the existence of two oracles \(\mathcal {O}_K, \mathcal {O}_S\):
-
Key generation oracle \(\mathcal {O}_K\): On input of a bit b generate a random keypair (PK, SK) \(\leftarrow \mathbf {KGen}(PP)\). If \(b=0\) then output PK, otherwise (PK, SK).
-
Signing oracle \(\mathcal {O}_S\): On input (L, m, i) where \(L=(PK_1,\dots ,PK_N)\) are public keys generated by \(\mathcal {O}_K\), \(i\in [N]\) and \(\mathcal {O}_K\) did not output \(SK_i\) and \(m\in \{0,1\}^*\), return \(\varOmega \leftarrow \mathbf {Sign}_{PP,SK_i}(m,L)\). If a key in L was not queried before, then output \(\bot \).
The idea behind the Linkability definition is as follows: if the same signer generates two signatures, then the algorithm \(\mathbf {Link}\) will identify this with overwhelming probability. It is important that this not only holds against honest use of the algorithm \(\mathbf {Sign}\), but arbitrary adversaries.
Definition 7
(Linkability). Let \(\mathcal {A}\) be a PPT algorithm with oracle access to \(\mathcal {O}_K, \mathcal {O}_S\). \(\mathcal {A}\) is given \(1^\lambda \) and PP as input and outputs a list \(L\subseteq \overline{L}\) (where \(\overline{L}\) is the set of all keys queried from \(\mathcal {O}_K\)) of length N together with \(N+1\) values \(\{(m_i, \varOmega _i)\}_{i \in [N+1]}\). Then the scheme is linkable if, for every such \(\mathcal {A}\),
The above only talks about the setting of generating signatures without being traceable. Equally important is the setting where signatures are signed by two different parties, where we require that their tags must be distinct. This then, of course, in particular includes the case of the \(\mathbf {Sign}\) algorithm. This property is important in the setting of cryptocurrencies where one might otherwise be able to issue fake transactions on behalf of another party.
Definition 8
(Exculpability). Let \(\mathcal {A}\) be a PPT algorithm with oracle access to \(\mathcal {O}_K, \mathcal {O}_S\). \(\mathcal {A}\) is given \(1^\lambda \) and PP as input and outputs a list \(L\subseteq \overline{L}\) (where \(\overline{L}\) is the set of all keys queried from \(\mathcal {O}_K\)) of length N together with two pairs \((m_1, \varOmega _1), (m_2,\varOmega _2)\) with \(\mathbf {Vfy} (m_1,L,\varOmega _1)=\mathbf {Vfy} (m_2, L,\varOmega _2)=1\), not both queried to \(\mathcal {O}_S\). Let \(M\subset L\) be set of \(PK_i\) for which \(\mathcal {A}\) did not obtain \(SK_i\) from \(\mathcal {O}_K\). Then
Remark 2
In our scheme, we do not give a definition and proof for existential unforgeability. As was observed in [17] the above definitions imply this property, as any algorithm breaking existential unforgeability can be used in a black-box setting to break exculpability (see [17, Theorem 2.6]).
3 Constructing Linkable Ring Signatures
In this section, we will describe our linkable ring signature scheme and prove its security. Our proposed scheme can be considered as an adaption of the linkable ring signature scheme proposed in [27] to the lattice setting. However, while most linkable signature schemes such as the one proposed in [16] require the use of a pseudorandom function to achieve linkability, our scheme demonstrates that the linkability for one-time ring signature schemes can be obtained without using a pseudorandom function to generate the tag.
If a scheme is not one-time, then this PRF is evaluated on the secret (or public) key of the signing party and a description of the actual ring L. In our case, it is not necessary to include the ring L into the tag computation (as the scheme is one-time) and we attach a tag derived from the secret key only. Concretely, each party will have a private key \(\varvec{r}_i\) together with a public key \(PK_i = \varvec{A} \varvec{r}_i\), where \(\varvec{A}\) is a random length-compressing matrix and \(\varvec{r}_i\) is a vector of small norm. Thus, \(PK_i\) is an evaluation of the public collision-resistant hash function \(f_{\varvec{A}}(\cdot ): \varvec{x} \mapsto \varvec{A} \varvec{x}\) on the private input \(\varvec{r}_i\).
During the signing process, the signer will generate two rings of signatures (similar to [27, 40] but twice): the first is a ring consisting of signatures for all the N public keys and generated using \(f_{\varvec{A}}\) whereas the second ring uses a different CRHF \(f_{\varvec{B}}\). This function \(f_{\varvec{B}}(\cdot ): \varvec{x} \mapsto \varvec{B} \varvec{x}\) uses a different public matrix \(\varvec{B}\) having the same dimensions as \(\varvec{A}\). The crucial point to interleave these rings is that they are built simultaneously, using the same challenges and blinding value in each step. For this to be verifiable, the signer must now include his \(I_i\) in the signature, which serves the same purpose as the public key \(PK_i\) in the first ring. We will show that the signer is bound to use his own value \(I_i\) if he wants to generate a valid signature and will therefore produce a collision if a second signature is revealed.
Let \(H: \{0,1\}^* \rightarrow D\) be a cryptographic hash function where D is the challenge space defined in Sect. 2. The algorithms of our scheme are defined as follows:
-
\(\mathbf {Setup}(1^\lambda )\): Sample two random matrices \(\varvec{A}, \varvec{B} \leftarrow R_q^{h \times v}\) and set \(PP=(\varvec{A}, \varvec{B})\).
-
\(\mathbf {KGen}(PP)\): Sample \(\varvec{r} \leftarrow S_{\beta }^v\) and then generate the public key \(PK = \varvec{A}\varvec{r}\) as well as the signing key \(SK = \varvec{r}\).
-
\(\mathbf {Sign}_{PP, SK_\ell }(m, L)\):
-
1.
Compute the tag \(I_\ell = \varvec{B} \varvec{r}_\ell \).
-
2.
Sample \(\varvec{u} \leftarrow \mathcal {N}_{\sigma }^{v}\) and set \(d_{\ell +1}\leftarrow H(L, I_\ell , m, \varvec{A} \varvec{u}, \varvec{B} \varvec{u})\).
-
3.
For each \(i=\ell +1, \dots , N, 1, \dots , \ell -1\):
-
(a)
Sample \(\varvec{r}_{z, i} \leftarrow {\mathcal {N}_{\sigma }^{v}}\).
-
(b)
Set \({t_{i,1}} = \varvec{A} \varvec{r}_{z,i} - {d_i} P{K_{i}}\) and \({t_{i,2}} = \varvec{B}\varvec{r}_{z,i} - {d_i}{I_\ell }\) as well as \(d_{(i\mod N)+1} \leftarrow H(L, I_\ell , m, t_{i,1}, t_{i,2})\).
-
(a)
-
4.
Compute \({\varvec{r}_{z,\ell }} ={\varvec{u} } + {d_{\ell }}{\varvec{r}_\ell }\).
-
5.
Abort with probability \(1 - \min \left( {1,\frac{{\mathcal{N}_\sigma ^v\left( {{\varvec{r}_{z,\ell }}} \right) }}{{M\cdot \mathcal{N}_{{d_\ell }{{\varvec{r}}_\ell },\sigma }^v\left( {{\varvec{r}_{z,\ell }}} \right) }}} \right) \), otherwise output the signature \(\varOmega =\left( {{d_1}, \left( \varvec{r}_{z,i}\right) _{i \in [N]},{I_\ell }} \right) \).
-
1.
-
\(\mathbf {Vfy}(m, L, \varOmega )\):
-
1.
For \(i \in [ N]\), check whether \(\left\| { {{{\varvec{r}}_{z,i}}} }\right\| _2 \le 2\sigma \sqrt{\nu v}\), else output 0.
-
2.
For \(i \in [N]\), compute \({t'_{i,1}} = \varvec{A} \varvec{r}_{z,i} - {d_i}P{K_{i}}\), \({t'_{i,2}} = \varvec{B} \varvec{r}_{z,i} - {d_i}{I_\ell }\) as well as
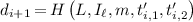 .
. -
3.
If
 then output 1, else output 0.
then output 1, else output 0.
-
1.
-
\(\mathbf {Link}(\varOmega _1, \varOmega _2)\): Given
$$\varOmega _1=\left( {{d_1^{(1)}},\left( \varvec{r}_{z,i}^{(1)}\right) _{i \in [N]},{I^{(1)}_\ell }} \right) \text { and } \varOmega _2=\left( {{d_1^{(2)}},\left( \varvec{r}_{z,i}^{(2)}\right) _{i \in [N]},{I^{(2)}_\ell }} \right) , $$return 1 if \(I^{(1)}_\ell =I^{(2)}_\ell \) and 0 otherwise.
Correctness can easily be verified using Lemmas 1 and 2.
3.1 Security
We now give the security statements of our construction. Due to length constraints, the proofs for these can be found in Appendix A.
Theorem 1
(Signer Anonymity). The proposed ring signature scheme provides signer anonymity in the (programmable) random oracle model assuming hardness of the \(\textsc {D}\hbox {-}\textsc {MLWE}_{2h,v,\beta }\)-problem.
Theorem 2
(Linkability). Assume that there exists an algorithm \(\mathcal {A}\) that breaks linkability with probability \(\epsilon \), in time at most s, with at most \(q_H\) queries to \(\mathcal {O}_K\) and \(q_S\) queries to \(\mathcal {O}_S\). Then there exists an algorithm \(\mathcal {M}\) that breaks a \(\textsc {MSIS}_{h,v,t}\)-instance with probability \(\left( \epsilon - \frac{1}{|\overline{D}|-q_H-Nq_S}\right) ^2 /\left( (N^2+N) q_H\right) ^2\) in time \(O(N^2\cdot q_H\cdot s)\) where \(t=4\sigma \sqrt{v \cdot \nu } + 2\cdot \kappa \cdot v \cdot \nu ^{1.5}\cdot \beta \).
Theorem 3
(Exculpability). Assume that there exists an algorithm \(\mathcal {A}\) that breaks exculpability with probability \(\epsilon \), in time at most s, with at most \(q_H\) queries to \(\mathcal {O}_K\) and \(q_S\) queries to \(\mathcal {O}_S\). Then there exists an algorithm \(\mathcal {M}\) that either breaks an \(\textsc {S}\hbox {-}\textsc {MLWE}_{2h,v,\beta }\) instance or an \(\textsc {MSIS}_{h,v,t}\)-instance with probability
in time \(O(N\cdot q_H\cdot s)\) where \(t=4\sigma \sqrt{v \cdot \nu } + 2\cdot \kappa \cdot v \cdot \nu ^{1.5}\cdot \beta \).
4 Discussion
We now discuss questions surrounding the practicality of our scheme and hint at future research directions.
Practical Considerations. The runtime of \(\mathbf {Vfy}\) is essentially the N-fold runtime of the verification of a regular lattice-based signature scheme. For signing, the computation and sampling of \(I_\ell ,\varvec{u}\) as well as \(\varvec{r}_{r,j}, \varvec{A} \varvec{r}_{z,j},\varvec{B} \varvec{r}_{z,j}\) for \(j\ne \ell \) can be done offline. The size of the total signature is approximately the size of N individual lattice-based signatures, as can be seen in Table 2.
As the basis of our construction, we chose a simple signature scheme without optimizations. Following the outline of our algorithms, one can instantiate it with e.g. [14] and then use their key-compression technique: this optimization is important when it comes to signature size.
Parameter Selection. In our construction, the \(\textsc {D}\hbox {-}\textsc {MLWE}\)-instance from Theorem 1 and the \(\textsc {S}\hbox {-}\textsc {MLWE}\)-instance in Theorem 3 have the same dimensions and bounds. Moreover, it was already mentioned in Sect. 2.2 that any algorithm which solves the \(\textsc {S}\hbox {-}\textsc {MLWE}\) problem in time h with success probability \(\epsilon \) can be turned into a distinguisher for \(\textsc {D}\hbox {-}\textsc {MLWE}\) for the same dimension with essentially the same runtime and success probability. It thus suffices in the parameter selection to look at the \(\textsc {D}\hbox {-}\textsc {MLWE}\)-instance only.
Unfortunately, it seems like the security reduction cannot be used for the choice of parameters, as it is inherently non-tight: from the proofs in Sect. 3, we see that the reductions have a huge loss in terms of success probability (both due to the use of the Forking Lemma and because the runtime is proportional to the number of queries of \(\mathcal {A}\) to H). If one attempts to obtain a good success probability of the reduction, the estimated runtime gets rather large. We leave a proof with a tighter reduction that can be used to instantiate our construction as an open problem.
Instead, we chose the parameters of our scheme such that the \(\textsc {MSIS},\textsc {D}\hbox {-}\textsc {MLWE}\)-problems are hard given that the reduction succeeds (see Table 2). As baseline, we assume hardness of at least 128 bits using all currently known lattice reduction attacks. This is reflected by requiring that lattice reduction will have to achieve a Root Hermite factor of less than 1.003 to break our scheme. For the given parameters, the security relies only on Module-SIS/LWE with \(h=1\) i.e. Ring-SIS/LWE, but increasing \(h,v,\kappa \) and thus decreasing \(\nu \) would allow to base the hardness on Module-SIS/LWE with a larger rank with only a minor increase in the size of the signature.
To choose actual parameters, we use the LWE simulator with sparse secrets from [2, 4] for \(\textsc {D}\hbox {-}\textsc {MLWE}\). Moreover, we use [34] to assess the hardness of our obtained SIS instanceFootnote 4. The size estimates in Table 2 are in Kilobytes/Megabytes (as in related work), we bound the size of each coefficient of \(\varvec{r}_{z,i}\) assuming it is within a \(6\sigma \)-interval.
Post-Quantum Security. It is widely believed that hardness assumptions used in our scheme may offer security in a post-quantum era. On the other hand, it is unlikely that our security proofs carry over to the Quantum Random Oracle Model (QROM, see e.g. [7]): we use adaptive programming of the RO H in Theorem 1, and adaptive rewinding in Theorems 2 and 3. Both of these proof techniques are somewhat inherent to the construction.
We note that other candidate constructions in the QROM such as [11, 14] also use a form of RO programming (even though not adaptively). Moreover, though it seems unlikely that the Forking Lemma can be proven in the QROM, there exist no attacks on protocols using these proof techniques which stem from this use of the RO, to the best of our knowledge.
Notes
- 1.
We relax this a bit and assume that there exists a CRS which is known to all parties and which allows them to derive their respective key pairs (SK, PK).
- 2.
This equivalent formulation is possible in our setting, as only one LWE sample will be issued per secret. The definition might seem unusual at first, as one regularly defines the LWE distribution as \(\varvec{A}\varvec{s}_1+\varvec{s}_2\). We can use the following transformation, which is well-known: note that the given equation is equivalent to writing \(\varvec{A}\varvec{s}_1+\varvec{I}_h\varvec{s}_2\) instead. By aligning this into a single matrix product of \(\varvec{A}'\) with \((\varvec{s}_1|\varvec{s}_2)\) and multiplying the resulting challenge with a uniformly random \(r\in R_q\), we obtain Definition 2.
- 3.
- 4.
While there might be newer methods to assess the hardness of SIS more precisely, [34] suffices for an estimation of parameters. Moreover, it turned out that using different methods yields hardness estimates (in terms of the Root Hermite factor) that are very close to [34]. Our parameter choices were considered secure at the time of writing, but the reader should refer to the full version of this work for updated parameters.
- 5.
These indirect queries are not important when we discuss a signature that does not correspond to any public key.
- 6.
We will describe the explicit construction of \(\mathcal R\) in the full version of this work, but it follows a standard approach using a version of the Forking Lemma.
- 7.
The anonymity simulation does only provide computational indistinguishability as it uses Proposition 1. Here the correctly generated \(I_j\) is known and the simulation is statistically indistinguishable, not just computationally.
References
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: STOC, pp. 99–108 (1996)
Albrecht, M.R., et al.: Estimate all the LWE, NTRU schemes! (2018). https://eprint.iacr.org/2018/331
Albrecht, M.R., Deo, A.: Large modulus ring-LWE \(\ge \) module-LWE. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 267–296. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_10
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9(3), 169–203 (2015)
Bellare, M., Goldwasser, S.: New paradigms for digital signatures and message authentication based on non-interactive zero knowledge proofs. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 194–211. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_19
Bender, A., Katz, J., Morselli, R.: Ring signatures: stronger definitions, and constructions without random oracles. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 60–79. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_4
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Bos, J., et al.: CRYSTALS - kyber: a CCA-secure module-lattice-based KEM (2017). https://eprint.iacr.org/2017/634
Boyen, X.: Lattice mixing and vanishing trapdoors: a framework for fully secure short signatures and more. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 499–517. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_29
Brakerski, Z., Kalai, Y.T.: A framework for efficient signatures, ring signatures and identity based encryption in the standard model (2010). http://eprint.iacr.org/2010/086
del Pino, R., Lyubashevsky, V., Neven, G., Seiler, G.: Practical quantum-safe voting from lattices. In: CCS 2017 (2017)
Derler, D., Ramacher, S., Slamanig, D.: Post-quantum zero-knowledge proofs for accumulators with applications to ring signatures from symmetric-key primitives. In: Lange, T., Steinwandt, R. (eds.) PQCrypto 2018. LNCS, vol. 10786, pp. 419–440. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-79063-3_20
Dodis, Y., Kiayias, A., Nicolosi, A., Shoup, V.: Anonymous identification in Ad Hoc groups. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 609–626. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_36
Ducas, L., Lepoint, T., Lyubashevsky, V., Schwabe, P., Seiler, G., Stehle, D.: Crystals - dilithium: Digital signatures from module lattices (2017). http://eprint.iacr.org/2017/633
Ducas, L., Micciancio, D.: Improved short lattice signatures in the standard model. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 335–352. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_19
Franklin, M., Zhang, H.: A framework for unique ring signatures (2012). http://eprint.iacr.org/2012/577
Fujisaki, E., Suzuki, K.: Traceable ring signature. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 181–200. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_13
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC, pp. 197–206. ACM (2008)
Goldreich, O., Goldwasser, S., Halevi, S.: Public-key cryptosystems from lattice reduction problems. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 112–131. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052231
Groth, J., Kohlweiss, M.: One-out-of-many proofs: or how to leak a secret and spend a coin. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 253–280. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_9
Güneysu, T., Lyubashevsky, V., Pöppelmann, T.: Practical lattice-based cryptography: a signature scheme for embedded systems. In: Prouff, E., Schaumont, P. (eds.) CHES 2012. LNCS, vol. 7428, pp. 530–547. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33027-8_31
Hoffstein, J., Pipher, J., Silverman, J.H.: NSS: an NTRU lattice-based signature scheme. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 211–228. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_14
Katz, J., Kolesnikov, V., Wang, X.: Improved non-interactive zero knowledge with applications to post-quantum signatures (2018). https://eprint.iacr.org/2018/475
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 75(3), 565–599 (2015)
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based accumulators: logarithmic-size ring signatures and group signatures without trapdoors. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 1–31. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_1
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based PRFs and applications to e-cash. ASIACRYPT 2017 (2017). http://eprint.iacr.org/2017/856
Liu, J.K., Wei, V.K., Wong, D.S.: Linkable and anonymous signature for ad hoc groups. In: ACISP 2004. LNCS, vol. 3108, pp. 325–335. Citeseer (2004)
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Lyubashevsky, V., Micciancio, D.: Generalized compact Knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Lyubashevsky, V., Seiler, G.: Partially splitting rings for faster lattice-based zero-knowledge proofs. In: EUROCRYPT 2018 (2018). https://eprint.iacr.org/2017/523
Aguilar Melchor, C., Bettaieb, S., Boyen, X., Fousse, L., Gaborit, P.: Adapting Lyubashevsky’s signature schemes to the ring signature setting. In: Youssef, A., Nitaj, A., Hassanien, A.E. (eds.) AFRICACRYPT 2013. LNCS, vol. 7918, pp. 1–25. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38553-7_1
Micciancio, D., Regev, O.: Lattice-based cryptography. In: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds.) Post-Quantum Cryptography, pp. 147–191. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-540-88702-7_5
Mohamed, M.S.E., Petzoldt, A.: RingRainbow – an efficient multivariate ring signature scheme. In: Joye, M., Nitaj, A. (eds.) AFRICACRYPT 2017. LNCS, vol. 10239, pp. 3–20. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57339-7_1
Nguyen, L.: Accumulators from bilinear pairings and applications. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 275–292. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_19
Noether, S., Mackenzie, A.: Ring confidential transactions. Ledger 1, 1–18 (2016)
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_8
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC, pp. 84–93 (2005)
Rivest, R.L., Shamir, A., Tauman, Y.: How to leak a secret. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_32
Torres, W.A., et al.: Post-quantum one-time linkable ring signature and application to ring confidential transactions in blockchain (lattice RingCT v1.0) (2018). https://eprint.iacr.org/2018/379
Tsang, P.P., Wei, V.K.: Short linkable ring signatures for e-voting, e-cash and attestation. In: Deng, R.H., Bao, F., Pang, H.H., Zhou, J. (eds.) ISPEC 2005. LNCS, vol. 3439, pp. 48–60. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31979-5_5
Wang, J., Sun, B.: Ring signature schemes from lattice basis delegation. In: Qing, S., Susilo, W., Wang, G., Liu, D. (eds.) ICICS 2011. LNCS, vol. 7043, pp. 15–28. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25243-3_2
Yang, R., Au, M.H., Lai, J., Xu, Q., Yu, Z.: Lattice-based techniques for accountable anonymity: composition of abstract Stern’s protocols and weak PRF with efficient protocols from LWR. Cryptology ePrint Archive, Report 2017/781 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proof of Security
A Proof of Security
1.1 A.1 Simulation
The simulation strategy follows a similar pattern as in [27, 40]. In an honestly generated ring signature (where the secret key \(SK_{\ell }\) is known) the \(\mathbf {Sign}\) algorithm simulates \(N-1\) individual signatures consecutively for all public keys but the one to which its secret key \(SK_{\ell }\) belongs. For this last public key, it uses the challenge \(d_\ell \) that is obtained for the last signature to close the ring using the secret key \(SK_\ell \). A simulator has no secret key and will instead generate all N individual signatures consecutively this way. To close the ring, it needs to reprogram the random oracle H on the last query to exactly yield the challenge \(d_1\) that is necessary to make all tests in \(\mathbf {Vfy}\) go through. Even though this reprogramming takes place, the challenge \(d_1\) that the RO returns will be fixed in the simulation ahead of time but be chosen uniformly at random. This means that the reprogramming is not detectable. Furthermore, Lemma 2 ensures that the simulation of the ring is indistinguishable.
Concerning the simulation and consistency of the second ring which involves I we note that here I is not obtained from the same secret input \(\varvec{r}\) that is used to derive PK from \(\varvec{A}\) since the simulator does not know SK. Instead, it will choose this value I uniformly at random from the appropriate set. An adversary cannot distinguish between I and the correctly generated counterpart due to Proposition 1.
In fact, the D-MLWE\({_{2h,v,\beta }}\) assumption of Proposition 1 attests to the indistinguishability of a pair of quadruples: \(\left( \varvec{A}, \varvec{B}, \varvec{A} \cdot \varvec{r}, \varvec{B} \cdot \varvec{r}\right) \sim \left( \varvec{A}, \varvec{B}, u, v\right) \), where u, v are random. One can further reduce the indistinguishability of another pair of quadruples: \(\left( \varvec{A}, \varvec{B}, u, v\right) \sim \left( \varvec{A}, \varvec{B}, \varvec{A} \cdot \varvec{r}, v\right) \) to D-MLWE\({_{h,v,\beta }}\) problem, the hardness of which can be deduced from that of D-MLWE\({_{2h,v,\beta }}\). Based on hybrid argument, the indistinguishability of the following two quadruples \(\left( \varvec{A}, \varvec{B}, \varvec{A} \cdot \varvec{r}, v\right) \sim \left( \varvec{A}, \varvec{B}, \varvec{A} \cdot \varvec{r}, \varvec{B} \cdot \varvec{r}\right) \) is reduced to the D-MLWE\({_{2h,v,\beta }}\) assumption.
1.2 A.2 Linkability
Assume that a PPT algorithm \(\mathcal {A}\) is run with some certain input and that it generates an output as in the linkability definition. \(\mathcal {A}\) makes queries to both the random oracle H and to the two oracles \(\mathcal {O}_K,\mathcal {O}_S\) in order to generate these signatures. We construct an algorithm \(\mathcal {R}\) which will run \(\mathcal {A}\) with multiple inputs and will attempt to rewind it on one of these inputs with different outputs from the random oracle. During a run, \(\mathcal {A}\) will be allowed to make \(q_H\) queries to the random oracle directly, but also \(\mathcal {O}_S\) indirectlyFootnote 5 makes \(N\cdot q_S\) queries to H to generate all the queried signatures. \(\mathcal R\) will simulate \(H,\mathcal {O}_S,\mathcal {O}_K\) honestly and will rewind \(\mathcal A\) with the goal of finding two signatures \(\varOmega , \hat{\varOmega }\) that for some index \(\pi \in [N]\) used in signature verification have the same RO query \((L,I,m, t_\pi ,t_\pi ')\), but differing \(d, \hat{d}, \varvec{r}, \hat{\varvec{r}}\) which go into generating this query for each individual signature. Furthermore, we require that the used I has a public key \(PK_\pi \) that was not generated by the simulated oracleFootnote 6. In the full version, we show how to construct such \(\mathcal R\) that succeeds with probability \(\left( \epsilon - \frac{1}{|\overline{D}|-q_H-Nq_S}\right) ^2 /\left( (N^2+N) q_H\right) ^2\) in time \(O(N^2\cdot q_H\cdot s)\).
Using this algorithm \(\mathcal R\), we construct another PPT TM \(\mathcal M\). This algorithm will obtain a MSIS-challenge \(\varvec{A}\), use it as the matrix that generates public keys and uses \(\mathcal R\) to compute the aforementioned signatures. We obtain \(d, \hat{d}, \varvec{r}, \hat{\varvec{r}},\pi \) such that \( (d-\hat{d})PK_{\pi } = \varvec{A} (\varvec{r}- \hat{\varvec{r}})\) and \((d-\hat{d})I = \varvec{B} (\varvec{r}- \hat{\varvec{r}})\).
\(PK_\pi \) was generated honestly by \(\mathcal {O}_K\) and we have \(\varvec{r}_\pi \) such that \(PK_\pi = A\varvec{r}_\pi \). Rewrite the above as \(\varvec{A} (d-\hat{d}) \varvec{r}_\pi = \varvec{A} (\varvec{r}- \hat{\varvec{r}})\). Assume that \((d-\hat{d}) \varvec{r}_\pi = (\varvec{r}- \hat{\varvec{r}}) \) then by the invertibility of \((d-\hat{d})\) it holds that \( I_\pi = \varvec{B} \varvec{r}_\pi = \varvec{B} \left( (\varvec{r}- \hat{\varvec{r}})\cdot (d-\hat{d})^{-1} \right) = I\) which contradicts the assumption that I is different from all honestly generated tags. Hence \((d-\hat{d}) \varvec{r}_\pi \ne (\hat{\varvec{r}}-\varvec{r}) \) and thus \(\varvec{s} = (d-\hat{d}) \varvec{r}_\pi - (\hat{\varvec{r}}-\varvec{r}) \ne 0\), while \( 0 = \varvec{A} \varvec{s} \) which yields a solution \(\varvec{s}\) to the \(\textsc {MSIS}\)-instance as in Definition 1.
1.3 A.3 Exculpability
The algorithm \(\mathcal {M}\) which we will construct in the course of this proof will either use the matrix \(\varvec{A}\) in \(\mathbf {Setup}\) to implant an \(\textsc {MSIS}\)-challenge or alternatively choose \(\varvec{A},\varvec{B} \) from an \(\textsc {S}\hbox {-}\textsc {MLWE}\) instance. Whereas in the former case the proof works as above, in the latter one we use a randomly chosen public key and its corresponding tag to embed an \(\textsc {S}\hbox {-}\textsc {MLWE}\) challenge. This then means that we cannot correctly simulate the \(\mathcal {O}_S\)-oracle as we would need the secret key for it - which is the secret we want to extract! Instead, the proof uses a version of the simulator from signer anonymity.
With respect to the \(\mathbf {Link}\) algorithm from our construction, the definition translates into the requirement that the tags \(I^{(1)},I^{(2)}\) from \(\varOmega _1,\varOmega _2\) are equal. Moreover, each \(I^{(i)}\) must be identical to an honestly generated identification tag for one of the public keys in L, and \(\mathcal {A}\) did not obtain both signatures from \(\mathcal {O}_S\) and does not possess the secret key for this public key. Let \(I=I^{(1)}=I^{(2)}\). The algorithm \(\mathcal {M}\) will first fairly flip a bit \(b\leftarrow \mathcal {B}_{1/2}\). Then it does the following, based on the value of b:
-
\(b=0\): \(\mathcal {M}\) will take a \(\textsc {S}\hbox {-}\textsc {MLWE}\) instance \((\varvec{D}, \varvec{t})\) where \(\varvec{D} = \begin{pmatrix} \varvec{A} \\ \varvec{B} \end{pmatrix} \in R_q^{2h \times v}\) and \(\varvec{t} = \begin{pmatrix} \varvec{t}_0 \\ \varvec{t}_1 \end{pmatrix} \in R_q^{2h}\) such that \(\varvec{A}, \varvec{B} \in R_q^{h\times v}\) and \(\varvec{t}_0\), \(\varvec{t}_1 \in R_q^{h}\). Assign \(PP=(\varvec{A}, \varvec{B})\) and choose an index \(k\in [N]\). For \(j\in [N]\) set
$$ (PK_j,SK_j) = {\left\{ \begin{array}{ll} (\varvec{A} \varvec{r}_j, (\varvec{r}_j, \varvec{B} \varvec{r}_j)) &{} \text { if } k\ne j \text { and for } \varvec{r}_j\leftarrow S_\beta ^v \\ (\varvec{t}_0, (\bot , \varvec{t}_1)) &{} \text { if } k = j \end{array}\right. } $$We then set the counter \(j=1\). Whenever \(\mathcal {A}\) requests a public key from \(\mathcal {O}_K\), then output \(PK_j\) and increase j by 1. If \(j=k\) and \(\mathcal {A}\) requests the secret key then abort. Whenever \(\mathcal {O}_S\) is queried, then sign the signature for the queried key s correctly if \(s\ne k\), otherwise use the back-patching simulator from the Signer Anonymity proofFootnote 7, but with \(I_j=\varvec{t}_1\).
-
\(b=1\): \(\mathcal {M}\) will take a \(\textsc {MSIS}\) instance \(\varvec{A} \in R_q^{h \times v}\) as input, sample \(\varvec{B} \leftarrow R_q^{h \times v}\) uniformly at random and set \(PP=(\varvec{A}, \varvec{B})\). It will additionally choose \(k\in [N]\) uniformly at random. \(\mathcal {O}_K\) will generate all keys honestly, but abort if \(\mathcal {A}\) queries \(SK_k\). \(\mathcal {O}_S\) will run \(\mathbf {Sign}\) honestly.
Assume that \(\mathcal {A}\) does not query for \(SK_k\), then the output of \(\mathcal {A}\) will be independent of the choice of b due to Theorem 1. If \(b=0\) then \(\mathcal {A}\) will be stopped if \(SK_k\) is queried, but observe that this abort probability is the same in case \(b=1\) as the key \(PK_k\) is perfectly indistinguishable from honestly generated public key \(PK_j\). Moreover, the abort probability in the presence of \(\mathcal {O}_S\) is identical due to the construction of the oracle, so the probability that \(\mathcal {A}\) outputs something is independent of b. This output probability is \(\epsilon '=\epsilon \cdot (N-1)/N\) by the random choice of k.
In the next step, \(\mathcal {M}\) now runs \(\mathcal {A}\) using the algorithm \(\mathcal {R}'\) (similar to \(\mathcal R\) from the previous proof it implements a Forking Lemma-type algorithm) which succeeds with probability \(\left( \epsilon - \frac{1}{|\overline{D}|-q_H-Nq_S}\right) ^2 /\left( (N^2+N)(q_H+N\cdot q_S)\right) ^2\) in time \(O(N\cdot q_H\cdot s)\) to obtain signatures that have identical inputs to the random oracle. From \(\mathcal R'\) obtain values \(d, \hat{d}, \varvec{r}, \hat{\varvec{r}},\pi \) such that \( (d-\hat{d})\varvec{A}\varvec{r}_\pi = (d-\hat{d})PK_\pi = \varvec{A}(\varvec{r}-\hat{\varvec{r}}) \) and \((d-\hat{d})I = \varvec{B}(\varvec{r}-\hat{\varvec{r}})\) where \(\varvec{r}_\pi \) is the secret key belonging to \(PK_\pi \). We might either have that \((d-\hat{d})\varvec{r}_\pi = \varvec{r}-\hat{\varvec{r}}\) or that inequality holds. Now if the values are not equal, then we can use the same argument as in linkability to extract a \(\textsc {MSIS}\) solution (this covers the case when \(b=1\)). But in case of equality the approach does not work - unless we are in the setting where the algorithm \(\mathcal {M}\) chose \(b=0\). Now we know that equality holds and \(\varvec{r}_\pi \) is known to exist as \(PK_\pi \) is a \(\textsc {S}\hbox {-}\textsc {MLWE}\) challenge, which we can therefore extract.
More formally, if \(b=0\) and \(k=\pi \) then \(\mathcal {M}\) will output \(\varvec{r}_\pi = (\varvec{r}-\hat{\varvec{r}})\cdot (d-\hat{d})^{-1}\) as \(d-\hat{d}\in D'\). If \(b=1\) then it will instead output \((d-\hat{d})\varvec{r}_\pi + \hat{\varvec{r}}-\varvec{r}\). We now calculate the probability that the algorithm \(\mathcal {M}\) will output a correct answer to either of the two challenges. Therefore, denote with \(\mathsf {X}_{=}\) the event that \((d-\hat{d})\varvec{r}_\pi = \varvec{r}-\hat{\varvec{r}} \), and with \(\mathsf {X}_{\ne }\) the opposite event. Let \(\mathsf {M}\) denote the event that \(\mathcal {M}\) outputs something. As our goal is to lower-bound the probability that the output of \(\mathcal {M}\) is correct, we need to determine
If \(b=0\), then by the choice of k, the probability that \(\pi =k\) is at least 1/|L| and therefore \(\Pr \left[ \mathsf {M} | \mathsf {X}_{=},b=0 \right] \ge 1/N\). Using Bayes’ Theorem, we obtain that
where we use in the last step that the occurrence of \(\mathsf {X}_{=}\) is independent of b.
In case of \(b=1\) we always give output, so we have that \(\Pr \left[ \mathsf {M} | \mathsf {X}_{\ne }, b=1 \right] =1\). Using the same reasoning as above, we obtain that \(\Pr \left[ \mathsf {X}_{\ne },b=1 | \mathsf {M} \right] \ge 1/2 \cdot \Pr \left[ \mathsf {X}_{\ne } \right] \) which yields an overall bound of \( \Pr \left[ \mathcal {M}\text { gives correct output}\right] \ge 1/2N \).
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Baum, C., Lin, H., Oechsner, S. (2018). Towards Practical Lattice-Based One-Time Linkable Ring Signatures. In: Naccache, D., et al. Information and Communications Security. ICICS 2018. Lecture Notes in Computer Science(), vol 11149. Springer, Cham. https://doi.org/10.1007/978-3-030-01950-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-01950-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-01949-5
Online ISBN: 978-3-030-01950-1
eBook Packages: Computer ScienceComputer Science (R0)





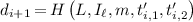 .
. then output 1, else output 0.
then output 1, else output 0.