Some Technical Aspects of Factorization Algebras on Manifolds

Abstract

We describe the basic ideas of factorization algebras on manifolds and topological chiral homology, with emphasis on their gluing properties.

Appendix

A Factorization Algebra on an Orbifold

• 1 Let $\mathscr {A}$ be as in Sect. 3. Then Theorem 25 implies that the contravariant functor $M\mapsto \mathrm {Alg}^\mathrm {loc}_M(\mathscr {A})$ on the category $\mathrm {Man}^{}$ of manifolds and open embeddings, extends uniquely to a sheaf on the category (enriched in groupoids) of orbifolds and local diffeomorphisms (or “étale” maps) between them. Indeed the ($\infty , 1$)- (or 2-) categories of sheaves (of e.g., ($\infty , 1$)-categories) on these categories are equivalent.

  For an orbifold X, it would perhaps make sense to refer to the value associated to X by this extended sheaf, as the ($\infty , 1$)-category “of locally constant factorization algebras on X”. This defines a notion of locally constant factorization algebra on X.

  The purpose of this appendix is to give a concrete description of this notion of locally constant factorization algebra on an orbifold, which also leads to a very simple description of the functoriality of the ($\infty , 1$)-category of locally constant factorization algebras with respect to local diffeomorphisms.

• 2 Let us denote by $\mathrm {Orb}$, the category enriched in groupoids of orbifolds with local diffeomorphisms as morphisms. We denote by $\bar{\mathrm {Man}}\phantom {{\mathrm {Man}}}^{}$, the category of manifolds with local diffeomorphisms as morphisms. We have a non-full and full inclusions

  

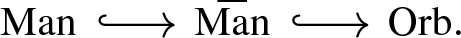
  (As any other category, we treat all these categories as ($\infty , 1$)-categories.)

  Let X be an orbifold. Then by ${{\,\mathrm{LocDiff}\,}}(X)$, we mean $\mathrm {Man}^{}_{/X}$. The coCartesian symmetric monoidal structure on $\bar{\mathrm {Man}}\phantom {{\mathrm {Man}}}^{}_{/X}$ (i.e., the symmetric monoidal structure given by the finite coproduct operations) restricts to a symmetric monoidal structure on ${{\,\mathrm{LocDiff}\,}}(X)$.

  Given an object $(M,f)\in {{\,\mathrm{LocDiff}\,}}(X)$, where M is a manifold, and $f:M\rightarrow X$ is a local diffeomorphism, we obtain an induced symmetric monoidal functor $f_!:\mathrm {Open}(M)\rightarrow {{\,\mathrm{LocDiff}\,}}(X)$. Thus, we obtain from a symmetric monoidal functor $A:{{\,\mathrm{LocDiff}\,}}{X}\rightarrow \mathscr {A}$, a prefactorization algebra $f^*A:=A\circ f_!$ on M.

  One sees from the definitions, that a locally constant factorization algebra on X is equivalent as a datum to a symmetric monoidal functor ${{\,\mathrm{LocDiff}\,}}(X)\rightarrow \mathscr {A}$ for which $f^*A$ is a locally constant factorization algebra on M for every object (M, f) of ${{\,\mathrm{LocDiff}\,}}(X)$. Equivalently, A should be locally constant in disks over X (i.e., on $\bar{\mathrm {Disk}}\phantom {{\mathrm {Disk}}}(X)$ defined below), and such that the canonical map $A(M,f)\leftarrow {{\,\mathrm{colim}\,}}_{\mathrm {Disj}(M)}f^*A$ is an equivalence for every (M, f).

• 3 We can also express a locally constant factorization algebra on X as a locally constant algebra over suitable disks over X.

  Let $\bar{\mathrm {Disk}}\phantom {{\mathrm {Disk}}}(X)$ denote the full submulticategory of (the underlying multicategory of) ${{\,\mathrm{LocDiff}\,}}(X)$, where the object $(U,i)\in {{\,\mathrm{LocDiff}\,}}(X)$ for a manifold U and a local diffeomorphism $i:U\rightarrow X$, belongs to $\bar{\mathrm {Disk}}\phantom {{\mathrm {Disk}}}(X)$ if there exists a diffeomorphism of U with a finite dimensional Euclidean space.

  Now, given a general object (M, f) of ${{\,\mathrm{LocDiff}\,}}(X)$, locally constant factorization algebras on M were equivalent to locally constant $\mathrm {Disk}(M)$-algebras, but the functor $f_!$ identifies multimaps in $\mathrm {Disk}(M)$ with multimaps in $\bar{\mathrm {Disk}}\phantom {{\mathrm {Disk}}}(X)$. It follows that a locally constant factorization on X is equivalent as a datum to a locally constant algebra on $\bar{\mathrm {Disk}}\phantom {{\mathrm {Disk}}}(X)$.

• 4 Let $f:X\rightarrow Y$ be local diffeomorphism of orbifolds. For a locally constant factorization algebra A on Y, we obtain a simple description of the pull-back $f^*A$ of A by f. Indeed, we obtain the induced symmetric monoidal functor $f_!:{{\,\mathrm{LocDiff}\,}}(X)\rightarrow {{\,\mathrm{LocDiff}\,}}(Y)$, and, it follows from the above description of locally constant factorization algebras on orbifolds, that there is a natural equivalence

  $$\begin{aligned} f^*A=A\circ f_! \end{aligned}$$

  (46)

  of symmetric monoidal functors on ${{\,\mathrm{LocDiff}\,}}(X)$.

Proposition 47

Let $p:U\rightarrow X$ be a surjective local diffeomorphism of orbifolds. Then a symmetric monoidal functor $A:{{\,\mathrm{LocDiff}\,}}(X)\rightarrow \mathscr {A}$ is a locally constant factorization algebra on X if and only if $A\circ p_!:{{\,\mathrm{LocDiff}\,}}(U)\rightarrow \mathscr {A}$ is a locally constant factorization algebra on U.

Proof

The necessity is clear from the equivalence (46).

For the converse, assume that $A\circ p_!$ is a locally constant factorization algebra on U. Then, for a manifold M and a local diffeomorphism $f:M\rightarrow X$, we need to prove that the prefactorization algebra $f^*A$ on M is a locally constant factorization algebra.

The assumption implies that $U_M:=U\times _XM$ is a manifold, and the projection $p_M:U_M\rightarrow M$ is a surjective local diffeomorphism. Therefore, it suffices by Theorem 25, to prove for every $V\in \mathrm {Open}(U_M)\times _{{{\,\mathrm{LocDiff}\,}}(M)}\mathrm {Open}(M)$, that $(f^*A)\mathclose {|}_{V}$ is a locally constant factorization algebra on V.

However, the composite $\mathrm {Open}(V)\hookrightarrow \mathrm {Open}(M)\xrightarrow {f_!}{{\,\mathrm{LocDiff}\,}}(X)$ is isomorphic to the composite

where $g:V\rightarrow U$ denotes the inclusion $V\hookrightarrow U_M$ followed by the projection $U_M\rightarrow U$, which is a local diffeomorphism.