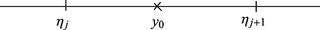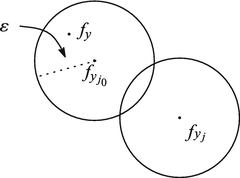Skip to main content
SpringerLink
Log in
Book cover

Fourier Analysis of Economic Phenomena pp 245–278Cite as

Almost Periodic Functions and Weakly Stationary Stochastic Processes

  • Chapter
  • First Online:

  • 707 Accesses

Part of the book series: Monographs in Mathematical Economics ((MOME,volume 2))

Abstract

It is a basic idea for the classical theory of Fourier series to express periodic functions as compositions of harmonic waves. This idea can be successfully extended to nonperiodic functions by means of Fourier transforms. However, we will be confronted with a lot of obstacles when we consider \(\mathfrak {L}^p\)-function spaces in the case p > 2.

This is a preview of subscription content, log in via an institution.

Chapter
USD   29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD   109.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD   139.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Notes

  1. 1.

    I am much indebted to Dunford and Schwartz [7] pp. 281–285, Katznelson [8] pp. 191–200, Kawata [9] II, pp. 96–103, 149–152, [10], [11] pp. 78–86, Loomis [12], Rudin [16, 17] for the contents of this chapter. The classical works cited above are Bohr [4, 5], von Neumann [19], Bochner [2] and Bochner and von Neumann [3].

  2. 2.

    In fact, we note that f(0) = 2 and f(x) ≠ 2 if x ≠ 0. If f(x) = 2, we must have \(\cos x=\cos \pi x=1\). It follows that both \(x=2k\pi \; (k\in \mathbb {Z})\) and \(\pi x=2k\pi \; (k\in \mathbb {Z})\) would have to hold good at the same time. However, it is impossible.

  3. 3.

    For any ε > 0, there exists some δ > 0 such that

    $$\displaystyle \begin{aligned} |f(u)-f(v)|<\frac{\varepsilon}{2} \quad \text{if}\quad |u-v|<\delta. \end{aligned} $$

    We make a decomposition \(\eta _j(1 \leqq j \leqq J)\) of [0, Λ] so that distances of any two adjacent points are less than δ. y 0 ∈ [0, Λ] is contained in a small interval [η j, η j+1]. Hence

    $$\displaystyle \begin{aligned} |f(x-y_0)-f(x-\eta_j)|&<\frac{\varepsilon}{2}. \\ (\text{Note that}\; |(x-y_0)-(x-\eta_j)|&=|y_0-\eta_j|<\delta. ) \end{aligned} $$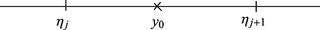

    This holds good for any \(x \in \mathbb {R}\), and so (9.5) follows.

  4. 4.
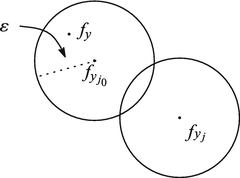
  5. 5.

    This delicate result is called Steinhaus’ theorem. See Dudley [6] p. 80 and Stromberg [18] pp. 297–298.

  6. 6.

    \(\bar {\mathrm {co}}A\) is the closed convex hull of a set A. coA is the convex hull of A.

  7. 7.

    Select some c n ∈{c 1, c 2, ⋯, c N} such that \(\|(b_1,b_2,\cdots ,b_J)-c_n\|{ }_1<\varepsilon J^{-1}\|f\|{ }_\infty ^{-1}\) and express this c n as

    $$\displaystyle \begin{aligned} c_n=(c_{n,1}, c_{n,2}, \cdots ,c_{n,J})=(b_1^{\prime},b_2^{\prime},\cdots,b_J^{\prime}). \end{aligned}$$

    Then the following evaluation follows.

    $$\displaystyle \begin{aligned} \bigg\|\sum_jb_jf_{y_j}(x)-\sum_jc_{n,j}f_{y_j}(x)\bigg\|{}_\infty \leqq \bigg\|\sum_j(b_j-c_{n,j})f_{y_j}(x)\bigg\|{}_\infty =\bigg\|\sum_j(b_j-b_j^{\prime})f_{y_j}(x)\bigg\|{}_\infty <\varepsilon . \end{aligned}$$
  8. 8.

    cf. Appendix C, p. 397.

  9. 9.

    In fact, we have

    $$\displaystyle \begin{aligned} \widehat{f_y}(\varphi)&=f_y(\hat{\varphi}) =\frac{1}{\sqrt{2\pi}}\int \int \varphi(\xi)e^{-i\xi x}d\xi f(x-y)dx \\ &=\frac{1}{\sqrt{2\pi}}\int \int \varphi(\xi)e^{-i\xi(y+z)}d\xi f(z)dz \\ &=f(\widehat{\varphi\cdot e^{-i\xi y}})=\hat{f}(\varphi\cdot e^{-i\xi y}) = e^{-i\xi y}\hat{f}(\varphi) \end{aligned} $$

    for any \(\varphi \in \mathfrak {S}\) by the definition of the Fourier transform of distributions. Hence \(\widehat {f}_y=e^{-i\xi y}\hat {f}\). In the course of computations, f(⋅) and f y(⋅) are tempered distributions defined by the functions f and f y. cf. Appendix C, Sect. C.3, p. 389.

  10. 10.

    We shall give a brief proof. Since g ∈ W(f), there exists a sequence {g n} of functions of the form

    $$\displaystyle \begin{aligned} \sum a_k f_{x_k},\; x_k\in\mathbb{R},\; \sum |a_k|\leqq 1 \end{aligned}$$

    such that ∥g n − g∥∞→ 0 (as n →∞), by Remark 9.1, 1∘. Hence it is easy to see that the sequence of tempered distributions defined by g n’s simply converges to the tempered distribution defined by g. Consequently, \(\hat {g_n}\) also simply converges to \(\hat {g}\) in \(\mathfrak {S}'\) (cf. 2∘ on p. 86). If the support of a function \(\varphi \in \mathfrak {S}\) is contained outside \(\mathrm {supp}\hat {f}\), \(\hat {g}_n(\varphi )=0\) since \(\mathrm {supp}\hat {f}_{x_k}=\mathrm {supp}\hat {f}\). Therefore \(\displaystyle \hat {g}(\varphi )=\lim _{n\rightarrow \infty }\hat {g_n}(\varphi )=0\). We conclude \(\mathrm {supp}\hat {g}\subset \mathrm {supp}\hat {f}\).

  11. 11.

    The Fourier transform of e iξx can be evaluated as in Example 4.9 on p. 85. For any \({\varphi \in \mathfrak {S}}\), we have

    $$\displaystyle \begin{aligned}\widehat{e^{i\xi x}}(\varphi)=\int_{-\infty}^\infty e^{i\xi x}\hat{\varphi}(x)dx =\sqrt{2\pi}\varphi(\xi).\end{aligned}$$

    Hence

    $$\displaystyle \begin{aligned} \widehat{e^{i\xi x}}=\sqrt{2\pi}\delta_\xi \end{aligned}$$

    is derived.

  12. 12.

    Since \(F\in \mathfrak {L}^1\), the mapping \(y\mapsto \tau _y F\;(\mathbb {R}\rightarrow \mathfrak {L}^1)\) is uniformly continuous by Theorem 5.1 (p. 1). It is, of course, continuous at y = 0. Hence there exists some θ > 0, for each ε > 0, such that ∥τ y F − F∥1 < ε provided that |y| < θ. Combining this result and 1∘, we obtain 2∘.

  13. 13.

    Obviously (9.26) holds good if we use f instead of h.

  14. 14.

    It can be verified by

    $$\displaystyle \begin{aligned} \eta F(\eta x)\ast c=\int_{\mathbb{R}}\eta F(\eta(x-y))cdy =c\int_{\mathbb{R}}\eta F(\eta&(x-y))dy=c\int_{\mathbb{R}}F(u)du=c \\ &(\text{changing variables: } \eta(x-y)=u ). \end{aligned} $$
  15. 15.

    By definition of W(f), we have 0 ∈ σ(f).

  16. 16.

    Katznelson [8] 2nd edn., pp. 159–160. There is a difference in the explanation of this result between the second edition and the third one. The latter seems to contain a slip.

  17. 17.

    \(\hat {f}\) is the Fourier transform of f in the sense of distribution.

  18. 18.

    \(\hat {f}\) is the Fourier transform of the tempered distribution defined by f.

  19. 19.

    See Chap. 5, Sect. 5.4. \(\displaystyle K(x)=\frac {1}{2\pi }\bigg (\sin \frac {x}{2} \bigg /\frac {x}{2}\bigg )^2\).

  20. 20.

    \(\hat {f}\), \(\hat {g}_\eta \) are the Fourier transforms of distributions.

  21. 21.

    We use such a notation because we wish to interpret the Fourier transform of f as something like a measure and its value at ξ as the mass at ξ.

  22. 22.

    In the case n = 1, \(P(x)=e^{i\xi _1 x}\) works. Next assume that there exist λ 1, λ 2, ⋯, λ q which satisfy (a) and (b) for ξ 1, ξ 2, ⋯, ξ n−1. Consider ξ 1, ξ 2, ⋯, ξ n. We may assume that

    $$\displaystyle \begin{aligned} \xi_n\notin \sum_{h=1}^q\lambda_h\mathbb{Z} \end{aligned}$$

    for any λ 1, λ 2, ⋯, λ q which satisfy (a) and (b). (Otherwise ξ n is also expressible in the form (b) by using λ 1, λ 2, ⋯λ q.) Define λ by

    $$\displaystyle \begin{aligned} \lambda=\xi_n-\sum_{h=1}^q\lambda_hz_h \quad \text{for}\quad z_h \in \mathbb{Z}.\end{aligned}$$

    Assume that

    $$\displaystyle \begin{aligned} \sum_{h=1}^q\theta_h\lambda_h+\theta\lambda=0,\quad \theta_h,\theta\in \mathbb{Q}. \end{aligned}$$

    If θ = 0, then θ h = 0 (h = 1, 2, ⋯, q) by (a). Hence we may concentrate at the case θ ≠ 0. Since

    $$\displaystyle \begin{aligned} \sum_{h=1}^q\theta_h\lambda_h+\theta\lambda=\sum_{h=1}^q\theta_h\lambda_h +\theta\bigg(\xi_n-\sum_{h=1}^q\lambda_hz_h\bigg)=\sum_{h=1}^q(\theta_h-\theta z_h)\lambda_h+\theta\xi_n=0, \end{aligned}$$

    it is obvious that

    $$\displaystyle \begin{aligned} \xi_n=-\sum_{h=1}^q\frac{\theta_h-\theta z_h}{\theta}\lambda_h. \end{aligned}$$

    Expressing \(\theta _h/\theta =v_h/u_h \; (u_h, v_h\in \mathbb {Z},\, h=1,2,\cdots ,q)\), we denote by u ∗ the least common multiple of u h’s. If we write \(\theta _h/\theta =v_h^*/u^*\), we obtain

    $$\displaystyle \begin{aligned} \xi_n=-\sum_{h=1}^q\bigg(\frac{v_h^*}{u^*}-z_h\bigg)\lambda_h=-\sum_{h=1}^q(v_h^*-u^*z_h)\frac{\lambda_h}{u^*}. \end{aligned}$$

    Furthermore, if we write \(\lambda _h^*=\lambda _h/u^*\;(h=1,2,\cdots, q)\), ξ j’s can be reexpressed as

    $$\displaystyle \begin{aligned} \xi_j&=\sum_{h=1}^qu^*A_{j,h}\lambda_h^*,\; j=1,2,\cdots,n-1, \\ \xi_n&=-\sum_{h=1}^q(v_h^*-u^*z_h)\lambda_h^*. \end{aligned} $$

    Thus \(\lambda _1^*,\lambda _2^*,\cdots ,\lambda _q^*\) satisfy (a) and (b) for ξ 1, ξ 2, ⋯, ξ n−1 and also

    $$\displaystyle \begin{aligned} \xi_n\in \sum_{h=1}^q\lambda_h^*\mathbb{Z}. \end{aligned}$$

    This contradicts our assumption. Hence θ must be zero.

  23. 23.

    The proof of (i)⇔(ii) is due to Kawata [11] pp. 80–82.

  24. 24.

    A function of the form

    $$\displaystyle \begin{aligned}f(x)=\sum_{j=1}^na_je^{-i\xi_j u}\quad (\xi_j\in \mathbb{R}) \end{aligned}$$

    is called a trigonometric polynomial. Any trigonometric polynomial is almost periodic.

  25. 25.

    This observation is based upon Maruyama [15].

References

  1. Billingsley, P.: Convergence of Probability Measures. Wiley, New York (1968)

    MATH  Google Scholar 

  2. Bochner, S.: Beiträge zur Theorie der fastperiodischen Funktionen, I, II. Math. Ann. 96, 119–147, 383–409 (1927)

    Google Scholar 

  3. Bochner, S., von Neumann, J.: Almost periodic functions in a group, II. Trans. Amer. Math. Soc. 37, 21–50 (1935)

    MathSciNet  MATH  Google Scholar 

  4. Bohr, H.: Zur Theorie der fastperiodischen Funktionen. I–III. Acta Math. 45, 29–127 (1925); 46, 101–214 (1925); 47, 237–281 (1926)

    Google Scholar 

  5. Bohr, H.: Fastperiodische Funktionen. Springer, Berlin (1932)

    Book  Google Scholar 

  6. Dudley, R.M.: Real Analysis and Probability. Wadsworth and Brooks, Pacific Grove (1988)

    Google Scholar 

  7. Dunford, N., Schwartz, J.T.: Linear Operators, Part 1, Interscience, New York (1958)

    Google Scholar 

  8. Katznelson, Y.: An Introduction to Harmonic Analysis, 3rd edn. Cambridge University Press, Cambridge (2004)

    Google Scholar 

  9. Kawata, T.: Ohyo Sugaku Gairon (Elements of Applied Mathematics). I, II. Iwanami Shoten, Tokyo (1950, 1952) (Originally published in Japanese)

    Google Scholar 

  10. Kawata, T.: On the Fourier series of a stationary stochastic process, I, II. Z. Wahrsch. Verw. Gebiete, 6, 224–245 (1966); 13, 25–38 (1969)

    Google Scholar 

  11. Kawata, T.: Teijo Kakuritsu Katei (Stationary Stochastic Processes). Kyoritsu Shuppan, Tokyo (1985) (Originally published in Japanese)

    Google Scholar 

  12. Loomis, L.: The spectral characterization of a class of almost periodic functions. Ann. Math. 72, 362–368 (1960)

    Article  MathSciNet  Google Scholar 

  13. Malliavin, P.: Integration and Probability. Springer, New York (1995)

    Book  Google Scholar 

  14. Maruyama, T.: Sekibun to Kansu-kaiseki (Integration and Functional Analysis). Springer, Tokyo (2006) (Originally published in Japanese)

    Google Scholar 

  15. Maruyama, T.: Fourier analysis of periodic weakly stationary processes. A note on Slutsky’s observation. Adv. Math. Econ. 20, 151–180 (2016)

    Article  Google Scholar 

  16. Rudin, W.: Weak almost periodic functions and Fourier–Stieltjes transforms. Duke Math. J. 26, 215–220 (1959)

    Article  MathSciNet  Google Scholar 

  17. Rudin, W.: Fourier Analysis on Groups. Interscience, New York (1962)

    Google Scholar 

  18. Stromberg, K.R.: An Introduction to Classical Real Analysis. American Mathematical Society, Providence (1981)

    Google Scholar 

  19. von Neumann, J.: Almost periodic functions in a group, I. Trans. Amer. Math. Soc. 36, 445–492 (1934)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Professor Emeritus, Keio University, Tokyo, Japan

    Toru Maruyama

Authors
  1. Toru Maruyama
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer Nature Singapore Pte Ltd.

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Maruyama, T. (2018). Almost Periodic Functions and Weakly Stationary Stochastic Processes. In: Fourier Analysis of Economic Phenomena. Monographs in Mathematical Economics, vol 2. Springer, Singapore. https://doi.org/10.1007/978-981-13-2730-8_9

Download citation

Publish with us

Policies and ethics

Search

Navigation