Systematisch vorgehen

Kapitelvorwort

Viele mathematische Probleme erscheinen auf den ersten Blick sehr komplex und oft unlösbar zu sein. Eine wichtige Hilfe ist es dann, wenn man die Lösungsschritte sorgfältig plant, strukturiert durchführt und anschließend den Lösungsweg, selbst wenn er nicht zum Erfolg geführt hat, reflektiert.

In diesem Kapitel machen Sie sich solche Vorgehensweisen an Beispielen bewusst und verbessern so Ihre eigene Arbeitsweise.

Achtung  Systematisch vorgehen zu können, gehört zu den allgemeinen mathematischen Kompetenzen. In einigen Beispielen und Übungsaufgaben dieses Kapitels werden auch Rechentechniken und Lösungsverfahren verwendet, die in den späteren Kapiteln eingehend behandelt werden. Bitte folgen Sie in solchen Fällen den Verweisen im Text.

Appendices

Aufgaben

2.1

Faktorisieren Sie die Terme so weit wie möglich. ($\rightarrow$ Abschn. 9.5)

• a) $2x^{3}+2x^{2}-8x-8$

• b) $0{,}1x^{4}-0{,}4x^{2}+0{,}4$

• c) $3x^{6}-4x^{5}-3x^{4}+4x^{3}$

2.2

Geben Sie eine innere Funktion $g$ und eine äußere Funktion $h$ an, sodass die Funktion $f$ als Verkettung von $h$ nach $g$, also durch $f(x)=h(g(x))$ dargestellt werden kann. ($\rightarrow$ Abschn. 12.4)

• a) $f(x)=e^{-0{,}5x^{2}}$

• b) $f(x)=\frac{1}{1+e^{-0{,}5x}}$

• c) $f(x)=\ln\left(x^{2}+1\right)$

2.3

Beschreiben Sie das Verhalten der Werte folgender Funktionen für $x\to\infty$ und für $x\to-\infty$. ($\rightarrow$ Abschn. 13.2)

• a) $f(x)=x-1+e^{-x}$

• b) $f(x)=\frac{1}{2}\left(e^{x}+e^{-x}\right)$

2.4

Erklären Sie an einer Skizze die Formel für das Volumen eines Kegelstumpfes:

$$\begin{aligned}\displaystyle V=\frac{\pi\cdot h}{3}\cdot\frac{R^{3}-r^{3}}{R-r}\end{aligned}$$

Dabei sind $R$ der Radius der Grundfläche, $r$ der Radius der Deckfläche und $h$ die Höhe des Kegelstumpfes.

2.5

Skizzieren Sie die Graphen der durch die folgenden Funktionsterme abschnittsweise definierten Funktionen:

$$\begin{aligned}\displaystyle f(x)&\displaystyle=\left\{\begin{array}[]{ccl}x^{2}-4&\textnormal{f{\"u}r}&x\in[-2;2]\\ 5&\textnormal{sonst}\end{array}\right.\\ \displaystyle g(x)&\displaystyle=\left\{\begin{array}[]{ccl}x+4&\textnormal{f{\"u}r}&x\leq 0\\ 8-x&\textnormal{f{\"u}r}&0<x<4\\ (x-2)^{2}&\textnormal{f{\"u}r}&x\geq 4\end{array}\right.\\ \displaystyle h(x)&\displaystyle=x-k;\quad x\in[k;k+1{[},\leavevmode\nobreak\ k\in\mathbb{Z}\end{aligned}$$

2.6

Untersuchen Sie die Anzahl der Lösungen folgender Gleichungen in Abhängigkeit von $m$.

• a) $(x+2)(x^{2}-m^{2})=0$

• b) $x(x-1)(x-m)=0$

• c) $mx^{2}+x+m=0$

2.7

Geben Sie die Fallunterscheidungen an, die zum Lösen der folgenden Ungleichungen notwendig sind.

• a) $|2x-1|<x+1$

• b) $|3-x|\leq 5-|x|$

• c) $\displaystyle\frac{2}{3x+1}<5$

• d) $\displaystyle\frac{1}{x-1}> \frac{3}{2x}+1$

2.8

Gegeben ist eine integrierbare Funktion, die im Intervall $[a;b]$ eine Nullstelle hat, in der sich ihr Vorzeichen ändert.

Vergleichen Sie die Werte der beiden Ausdrücke $\int_{a}^{b}|f(x)|\,dx$ und $\left|\int_{a}^{b}f(x)\,dx\right|$. ($\rightarrow$ Abschn. 14.6)

2.9

Toni löst eine Gleichung:

$$\begin{aligned}\displaystyle\boxed{\begin{array}[]{l@{\quad}r@{\;}c@{\;}l@{\qquad}l}\quad&x+4\;&=\;&2x+3\hfil\qquad&|\leavevmode\nobreak\ {}-5\\ \Leftrightarrow\hfil\quad&x-1\;&=\;&2x-2\hfil\qquad&\\ \Leftrightarrow\hfil\quad&x-1\;&=\;&2(x-1)\hfil\qquad&|\leavevmode\nobreak\ {}:(x-1)\\ \Leftrightarrow\hfil\quad&1\;&=\;&2\hfil\qquad&\\ \quad&\multicolumn{3}{c}{\textnormal{Keine L{\"o}sung}}\;&\;\\ \quad\end{array}}\end{aligned}$$

Wo liegt der Fehler?

2.10

• a) Die Funktion $x\mapsto e^{x}$ hat an der Stelle $\ln(2)\approx 0{,}693\,147\,2$ den Wert $2$. Auf wie viele Stellen kann man $\ln(2)$ runden, wenn der Funktionswert an der Näherungsstelle um höchstens $0{,}5\,\%$ von $2$ abweichen soll?

• b) Schätzen Sie, ohne ein elektronisches Hilfsmittel zu verwenden, wie groß die relative Abweichung des berechneten Volumens eines Würfels mit der Kantenlänge $\sqrt{3}\,\textnormal{m}$ vom exakten Volumen ist, wenn man für $\sqrt{3}\approx 1{,}732$ den Näherungswert $1{,}7$ verwendet.

Lösungen zu den Aufgaben

2.1

• a) $2x^{3}+2x^{2}-8x-8=2(x+1)(x+2)(x-2)$

• b) $0{,}1x^{4}-0{,}4x^{2}+0{,}4=0{,}1\left(x-\sqrt{2}\right)^{2}\left(x+\sqrt{2}\right)^{2}$

• c) $3x^{6}-4x^{5}-3x^{4}+4x^{3}=x^{3}(x-1)(x+1)(3x-4)$

2.2

• a) $f(x)=h(g(x))$ mit $g(x)=-0{,}5x^{2}$ und $h(z)=e^{z}$

• b) $f(x)=h(g(x))$ mit $g(x)=1+e^{-0{,}5x}$ und $h(z)=\frac{1}{z}$ oder $g(x)=e^{-0{,}5x}$ und $h(z)=\frac{1}{1+z}$

• c) $f(x)=h(g(x))$ mit $g(x)=x^{2}+1$ und $h(z)=\ln(z)$

2.3

• a) $f(x)\to\infty$ für $x\to\infty$ und für $x\to-\infty$

• b) $f(x)\to\infty$ für $x\to\infty$ und für $x\to-\infty$

2.4

Volumen des Gesamtkegels: $V_{g}=\frac{\pi}{3}R^{2}(h+h_{o})$

Volumen des abgeschnittenen Kegels: $V_{o}=\frac{\pi}{3}r^{2}h_{o}$

$$\begin{aligned}\displaystyle\frac{h_{o}}{h+h_{o}}=\frac{r}{R}\quad\Leftrightarrow\quad h_{0}=\frac{r}{R-r}h\textnormal{ und }h+h_{0}=\frac{R}{R-r}h\end{aligned}$$

Volumen des Kegelstumpfes:

$$\begin{aligned}\displaystyle V=V_{g}-V_{o}=\frac{\pi\cdot h}{3}\cdot\frac{R^{3}-r^{3}}{R-r}\end{aligned}$$

2.5

• a)

  

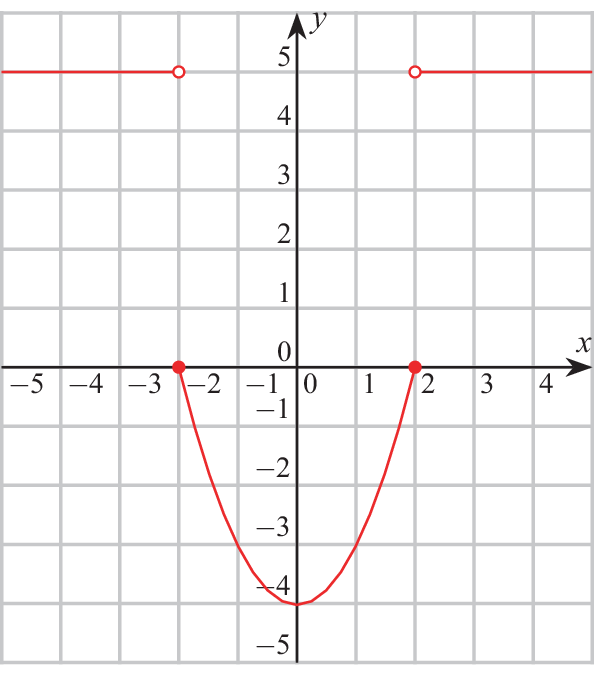
• b)

  

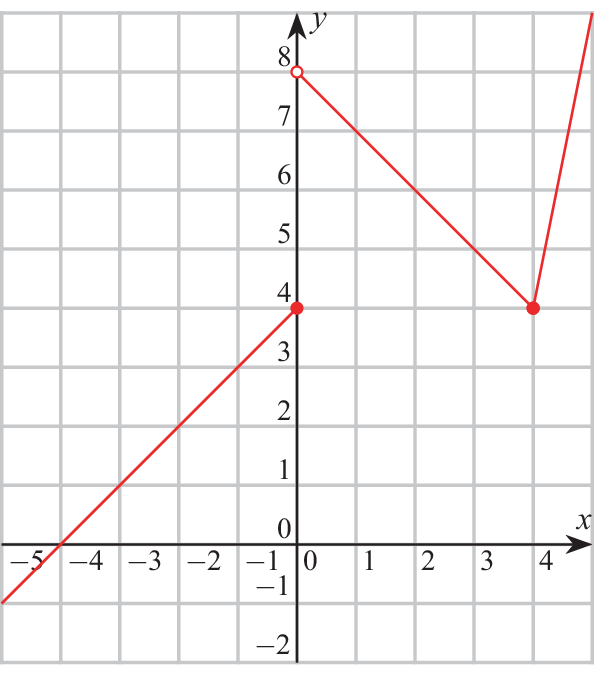
• c)

  

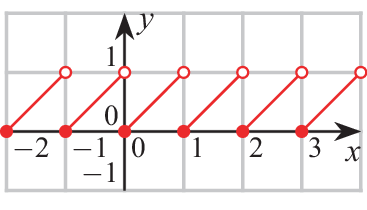
2.6

• a) Jeder Klammerterm kann den Wert null haben, also hat die Gleichung

  • drei Lösungen für $m\in\mathbb{R}\backslash\{0;2;-2\}$

  • genau zwei Lösungen für $m\in\{0;2;-2\}$.

• b) Wie bei a):

  • drei Lösungen für $m\in\mathbb{R}\backslash\{0;1\}$

  • genau zwei Lösungen für $m\in\{0;1\}$.

• c)

  • genau eine Lösung für $m\in\left\{0;-\frac{1}{2};\frac{1}{2}\right\}$

  • keine Lösung für $m\in\mathbb{R}\backslash\left[-\frac{1}{2};\frac{1}{2}\right]$

  • zwei Lösungen für $m\in\left]{-\frac{1}{2}};\frac{1}{2}\right[\backslash\{0\}$.

2.7

• a) 1. Fall: $x\geq 0{,}5$

  2. Fall: $x<0{,}5$

• b) 1. Fall: $0\leq x\leq 3$

  2. Fall: $x> 3$

  3. Fall: $x<0$

• c) 1. Fall: $x> -\frac{1}{3}$

  2. Fall: $x<-\frac{1}{3}$

• d) Multiplikation mit $x(x-1)$

  1. Fall: $x\in{]}0;1{[}$

  2. Fall: $x\in\mathbb{R}\backslash[0;1]$

2.8

Links ist ein möglicher Graph von $f$, rechts der Graph von $|f|$.

Es gilt $\int_{a}^{b}\left|f(x)\right|\,dx\geq\left|\int_{a}^{b}f(x)\,dx\right|\geq 0$.

2.9

Bei der Division durch $(x-1)$ muss man ausschließen, dass $x=1$ ist. 1 ist eine Lösung der Gleichung.

2.10

• a) Die relative Abweichung ist

  $$\begin{aligned}\displaystyle D=\left|\frac{2-e^{c}}{2}\right|.\end{aligned}$$

  Für $c=0{,}69$ ist $D\approx 0{,}003$, also kleiner also $0{,}5\,\%$.

• b) Die relative Abweichung ist

  $$\begin{aligned}\displaystyle D=\frac{\sqrt{3}^{3}-1{,}7^{3}}{\sqrt{3}^{3}}=1-\left(\frac{1{,}7}{\sqrt{3}}\right)^{3}.\end{aligned}$$

  Mit $1{,}73<\sqrt{3}<1{,}74$ erhält man

  $$\begin{aligned}\displaystyle 1-\left(\frac{1{,}7}{1{,}73}\right)^{3}<D<1-\left(\frac{1{,}7}{1{,}74}\right)^{3},\end{aligned}$$

  also

  $$\begin{aligned}\displaystyle 0{,}051<D<0{,}067.\end{aligned}$$

  Die relative Abweichung liegt zwischen $5{,}1$ und $6{,}7\,\%$.

Ausführliche Lösungen zu den Aufgaben finden Sie im Online-Material.

tiny.cc/to5l1y