Abstract
Traditional approaches to Quantitative Information Flow (QIF) represent the adversary’s prior knowledge of possible secret values as a single probability distribution. This representation may miss important structure. For instance, representing prior knowledge about passwords of a system’s users in this way overlooks the fact that many users generate passwords using some strategy. Knowledge of such strategies can help the adversary in guessing a secret, so ignoring them may underestimate the secret’s vulnerability. In this paper we explicitly model strategies as distributions on secrets, and generalize the representation of the adversary’s prior knowledge from a distribution on secrets to an environment, which is a distribution on strategies (and, thus, a distribution on distributions on secrets, called a hyper-distribution). By applying information-theoretic techniques to environments we derive several meaningful generalizations of the traditional approach to QIF. In particular, we disentangle the vulnerability of a secret from the vulnerability of the strategies that generate secrets, and thereby distinguish security by aggregation—which relies on the uncertainty over strategies—from security by strategy—which relies on the intrinsic uncertainty within a strategy. We also demonstrate that, in a precise way, no further generalization of prior knowledge (e.g., by using distributions of even higher order) is needed to soundly quantify the vulnerability of the secret.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Two core principles within the field of quantitative information flow (QIF) are: (i) a secret is considered “vulnerable” to the extent the adversary’s prior knowledge about secret values has low entropy; and (ii) the leakage of information in a system is a measure of how much the observable behavior of the system, while processing a secret value, degrades that entropy. These principles have been used to create ever more sophisticated QIF frameworks to model systems and reason about leakage. (See, for example, [1,2,3,4,5,6,7,8,9,10,11,12,13].)
Traditional approaches to QIF represent the adversary’s prior knowledge as a probability distribution on secret values. This representation is adequate when secrets are generated according to a single, possibly randomized, procedure that is known to the adversary (e.g., when a cryptographic key is randomly generated according to a known algorithm). However, in some important situations secrets are generated according to a more complex structure. In these cases, representing the prior as a distribution loses important, security-relevant information.
Consider the example of passwords. If an adversary gains access to a large collection of passwords (without the associated user identities), his prior knowledge can be modeled as the probability distribution over passwords corresponding to the relative frequency of passwords in the collection. It would be wrong to believe, however, that passwords are generated by a function exactly described by this distribution. This representation of prior knowledge aggregates a population of users into a single expected probabilistic behavior, whereas in fact it is more likely that individual users generate passwords according to some (not completely random) strategy. Some user born in 1983, for instance, may have a strategy of generally picking passwords containing the substring “1983”. If an adversary knows this, he can guess relevant passwords more quickly. In addition, on a system that mandates password changes, he may have an advantage when guessing that a changed password by the same user contains “1983” as a substring. In short, if the adversary learns something about the secret-generating strategy, he may obtain additional information about the secret itself.
Generally speaking, knowledge of strategies can be useful when multiple secrets are produced by a same source. For example, the same user might use a similar strategy to generate passwords on different web sites. If we consider locations as secret, then changes in location are surely correlated, e.g., based on time of day. Learning someone’s strategy for moving in a city may increase the chances of guessing this person’s location at a future point in time. Perhaps surprisingly, an evolving secret subject to repeated observations, in some cases, can be learned faster if it is changed (and observed) more often [14]. The reason is that the strategy by which the secret changes is revealed faster if more samples from the strategy are visible to an adversary; and if the strategy has little randomness in it, the adversary has an increased accuracy in determining past, current, and even future secret values.
This paper develops the idea that when secrets are generated according to a plurality of strategies, as in the above examples, it is advisable to represent the adversary’s prior as a hyper-distribution of secrets, i.e., a distribution of distributions. To show this, we first define a system model that explicitly considers strategies for generating secrets. We formalize a strategy as a probability distribution from which secrets can be sampled. We assume there is a probability distribution on strategies themselves, which we call an environment, representing how likely it is that each strategy will be used for generating the secret. Returning to the password example, each user would have his own probability distribution for generating secrets (i.e., his own strategy), and the environment would consist in a probability distribution over these strategies, representing the chance of each user being the one logging into the system.
In this model, representing the adversary’s prior as a distribution on secrets would reflect the expected behavior of all possible strategies in the environment. By quantifying the prior vulnerability as a function of this single distribution, traditional approaches would miss relevant information, underestimating the vulnerability of the secret for adversaries able to learn the strategy being used. By modeling the prior as a hyper-distribution, and applying information-theoretic reasoning on it, we can do better, generalizing the traditional approach to QIF. More specifically, we make the following contributions.
-
We generalize the traditional measure of prior adversarial vulnerability to environmental vulnerability, which takes into account that the adversary can learn the strategy for generating secrets (Sect. 3).
-
We define a measure of strategy vulnerability, which quantifies how certain an adversary is about the secret-generating strategy itself. We demonstrate that the traditional measure of prior vulnerability on secrets neatly decomposes into environmental and strategy vulnerability. Using this decomposition, we are able to disentangle two types of security usually conflated in the traditional approach to QIF: security by strategy, which arises from the intrinsic randomness of secret-generating strategies, and security by aggregation, which arises from the adversary’s inability to identify particular strategies in the secret-generation process (Sect. 4).
-
We define models of knowledge for adversaries who can only partially identify strategies, and we provide measures of the vulnerability of the secret and of the strategies themselves for this type of adversary (Sect. 5).
-
We demonstrate that the modeling of the adversary’s prior knowledge as a hyper-distribution on secrets is sufficiently precise: more complicated models (e.g., distributions on distributions on distributions on secrets, and such “higher order distributions”) add no expressive power (Sect. 6).
-
Our work lays a foundation for reasoning about real-world scenarios. In this paper we develop an example based on a real password dataset (Sect. 7).
The next section introduces some preliminary concepts while Sects. 3, 4, 5, 6 and 7 present our main results. Finally, Sect. 8 discusses related work, and Sect. 9 concludes. Full proofs appear in the corresponding technical report [15].
2 Preliminaries
We briefly review standard concepts and notation from quantitative information flow (QIF). Notably we define notions of “secret”, an adversary’s “prior knowledge” about the secret (or simply, “prior”), and an “information measure” to gauge that knowledge. We also define “channels”, probabilistic mappings from a set of secrets to another set, which have the effect of updating the adversary’s uncertainty about the secret from a prior probability distribution to a distribution on distributions on secrets, called a “hyper-distribution”.
Secrets and vulnerability. A secret is some piece of sensitive information we want to protect, such as a user’s password, social security number or current location. An adversary usually only has partial information about the value of a secret, referred to as “the prior.” Traditionally, the prior is represented as a probability distribution; our aim in this paper is to show that an alternative representation can be more useful. We denote by \(\mathcal {X}\) the set of possible secrets and by \(\mathbb {D}{\mathcal {X}}\) the set of probability distributions over \(\mathcal {X}\). We typically use \(\pi \) to denote a probability distribution, and \(\left\lceil \pi \right\rceil \) for its support (the set of values with non-zero probability).
An information measure is a function \(\mathbb {V}_{X}{:}\mathbb {D}{\mathcal {X}}{\rightarrow }\mathbb {R}\) mapping distributions on secrets to real numbers. An information measure can gauge vulnerability—the higher the value, the less secure the secret is—or uncertainty/entropy—the higher the value, the more secure the secret is. There are several definitions of information measures in the literature, varying according to the operational interpretation of the measure. Popular instances include Bayes vulnerability [8] and Bayes risk [16], Shannon entropy [17], and guessing entropy [18]. The g-vulnerability framework [19] was recently introduced to express information measures having richer operational interpretations; we discuss it further below.
Hypers and channels. A hyper-distribution [20] (or hyper for short) is a distribution on distributions. As we will see in the next section, we propose that the prior can be profitably represented as a hyper. A hyper on the set \(\mathcal {X}\) is of type \(\mathbb {D}^{2}{\mathcal {X}}\), which stands for \(\mathbb {D}(\mathbb {D}{\mathcal {X}})\), a distribution on distributions on \(\mathcal {X}\). The elements of \(\mathbb {D}{\mathcal {X}}\) are called the inner-distributions (or inners) of the hyper. The distribution the hyper has on inners is called the outer-distribution (or outer). We usually use \(\mathsf {H}\) to denote a hyper, \(\left\lceil \mathsf {H} \right\rceil \) for its support (the set of inners with non-zero probability), and \([\pi ]\) to denote the point-hyper assigning probability 1 to the inner \(\pi \).
An (information theoretic) channel is a triple \((\mathcal {X},\mathcal {Y},C)\), where \(\mathcal {X},\mathcal {Y}\) are finite sets of input values and output values, resp., and C is a \(|\mathcal {X}|\) \(\times \) \(|\mathcal {Y}|\) channel matrix in which each entry C(x, y) corresponds to the probability of the channel producing output y when the input is x. Hence each row of C is a probability distribution over \(\mathcal {Y}\) (entries are non-negative and sum to 1). A channel is deterministic iff each row contains a single 1 identifying the only possible output for that input.
A distribution \(\pi {:}\mathbb {D}{\mathcal {X}}\) and a channel C from \(\mathcal {X}\) to \(\mathcal {Y}\) induce a joint distribution \(p(x,y) = \pi (x)C({x,y})\) on \(\mathcal {X}\times \mathcal {Y}\), producing joint random variables X, Y with marginal probabilities \(p(x) = \sum _{y} p(x,y)\) and \(p(y) = \sum _{x} p(x,y)\), and conditional probabilities  (if p(x) is non-zero) and
(if p(x) is non-zero) and  (if p(y) is non-zero). Note that \(p_{XY}\) is the unique joint distribution that recovers \(\pi \) and C, in that \(p(x) = \pi _{x}\) and \(p(y{\mid }x) = C({x,y})\) (if p(x) is non-zero).Footnote 1 For a given y (s.t. p(y) is non-zero), the conditional probabilities \(p(x{\mid }y)\) for each \(x \in \mathcal {X}\) form the posterior distribution \(p_{X \mid y}\).
(if p(y) is non-zero). Note that \(p_{XY}\) is the unique joint distribution that recovers \(\pi \) and C, in that \(p(x) = \pi _{x}\) and \(p(y{\mid }x) = C({x,y})\) (if p(x) is non-zero).Footnote 1 For a given y (s.t. p(y) is non-zero), the conditional probabilities \(p(x{\mid }y)\) for each \(x \in \mathcal {X}\) form the posterior distribution \(p_{X \mid y}\).
A channel C from a set \(\mathcal {X}\) of secret values to set \(\mathcal {Y}\) of observable values can be used to model computations on secrets. Assuming the adversary has prior knowledge \(\pi \) about the secret value, knows how a channel C works, and can observe the channel’s outputs, the effect of the channel is to update the adversary’s knowledge from \(\pi \) to a collection of posteriors \(p_{X \mid y}\), each occurring with probability p(y). Hence, following [12, 20], we view a channel as producing hyper-distribution.Footnote 2 We use \([\pi ,C]\) to denote the hyper obtained by the action of C on \(\pi \). We say that \([\pi ,C]\) is the result of pushing prior \(\pi \) through channel C.
Notation on expectations. We denote the expected value of some random variable \(F{:}\mathcal {X}{\rightarrow }R\) over a distribution \(\pi {:}\mathbb {D}{\mathcal {X}}\) by \( \mathbb {E}_{\pi }F \mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def}}}\mathbb {E}_{x \leftarrow \pi }F(x) \mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def}}}\sum _{x \in \mathcal {X}} \pi (x)F(x). \) Here, R is usually the reals \(\mathbb {R}\) but more generally can be a vector space. If \(\mathcal {X}\) itself is a vector space, then we abbreviate \(\mathbb {E}_{\pi }{(\text {id})}\) by just \(\mathbb {E}_{}{\pi }\), the “average” of the distribution \(\pi \) on \(\mathcal {X}\).
g-vulnerability. Recently, the g-vulnerability framework [19] proposed a family of vulnerability measures that capture various adversarial models. Its operational scenario is parameterized by a set \(\mathcal {W}\) of guesses (possibly infinite) that the adversary can make about the secret, and a gain function \(g{:}\mathcal {W}\times \mathcal {X}{\rightarrow }\mathbb {R}\). The gain g(w, x) expresses the adversary’s benefit for having made the guess w when the actual secret is x. Given a distribution \(\pi \), the g-vulnerability function measures the adversary’s success as the expected gain of an optimal guessing strategy:
The g-vulnerability of a hyper \(\mathsf {H}{:}\mathbb {D}^{2}{\mathcal {X}}\) is defined as
In particular, when \(\mathsf {H}\) is the result of pushing distribution \(\pi {:}\mathbb {D}{\mathcal {X}}\) through a channel C from \(\mathcal {X}\) to \(\mathcal {Y}\) we have \( V_{g}[\pi ,C] = \sum _{y \in \mathcal {Y}} \max _{w \in \mathcal {W}} \sum _{x \in \mathcal {X}} \pi (x) C({x,y}) g(w,x). \)
The set of g-vulnerabilities coincides with the set of all convex and continuous information measures, which recently have been shown to be precisely those to satisfy a set of basic axioms for information measures.Footnote 3
Theorem 1
(Expressiveness of g-vulnerabilities [21]). Any g-vulnerability \(V_{g}\) is a continuous and convex function on \(\mathbb {D}{\mathcal {X}}\). Moreover, given any continuous and convex function \(\mathbb {V}_{X}{:}\mathbb {D}{\mathcal {X}}{\rightarrow }\mathbb {R}^{+}\) there exists a gain function g with a countable set of guesses such that \(\mathbb {V}_{X}= V_{g}\).
In the remainder of this paper we will consider only vulnerabilities that are continuous and convex (although all of our results carry on for continuous and concave uncertainty measures). We may alternate between the notation \(\mathbb {V}_{X}\) and \(V_{g}\) for vulnerabilities depending on whether we want to emphasize the g-function associated with the measure via Theorem 1.
3 Adversarial Knowledge as Hyper-Distributions
This section shows how an adversary’s prior knowledge can be profitably represented as a hyper-distribution on secrets, rather than simply a distribution. We begin by presenting a basic system model for wherein secrets are not necessarily generated according to a single “strategy”, but rather an “environment”, which is a distribution on strategies. This change motivates an adversary who can learn about the strategy being used, and from that pose a higher threat to the secret. This notion, which we call “environmental vulnerability”, strictly generalizes the standard notion of vulnerability.
3.1 Strategies and Environments
Figure 1 illustrates our basic model. A system is a probabilistic mapping from secret inputs to public outputs, represented as a channel.Footnote 4 Secrets are produced according to a strategy chosen by a defender.
A strategy is modeled as a probability distribution on the set of secrets \(\mathcal {X}= \{x_{1}, x_{2}, \ldots , x_{n}\}\); i.e., the defender chooses the secret by sampling the distribution. The set \(\mathcal {S}\) of all possible strategies is thus \(\mathbb {D}{\mathcal {X}}\), but in this paper we shall assume that there is a set \(\mathcal {S}_{\mathcal {X}} = \{ \pi _{1}, \pi _{2}, \ldots , \pi _{m} \} \subset \mathbb {D}{\mathcal {X}}\) of strategies of interest.Footnote 5
In traditional QIF, this defender strategy is essentially synonymous with prior knowledge—we assume the adversary knows exactly the strategy being used. However, as motivated by the password example in the introduction, in reality a secret may be generated by a myriad of possible strategies, and each strategy may be more or less likely. We represent this idea in our model as an environment, which is a probabilistic rule used to choose the secret-generating strategy; it is represented as a probability distribution on the set \(\mathcal {S}_{\mathcal {X}}\) of strategies of interest. The set \(\mathbb {D}{\mathcal {S}_{\mathcal {X}}}\) of all possible environments is a subset of the set \(\mathbb {D}^{2}{\mathcal {X}}\) of all hypers on \(\mathcal {X}\). In case only one strategy \(\pi \) is possible, as in traditional models, the corresponding environment is the point-hyper \([\pi ]\). We will use letters like \(\mathsf {H}\), \(\mathsf {M}\), \(\mathsf {En}\) to denote hypers that are distributions on strategies of interest.
Example 1
Consider a password-checking system. There are various methods for choosing passwords, each of which can be represented as a different strategy; which strategy is used by a particular user is determined by an environment. The adversary is interested in identifying the password used for a particular user. For simplicity, we limit attention to two possible values for passwords, \(\mathcal {X}= \{x_{1}, x_{2}\}\).
Consider the set of possible strategies for generating secrets is \(\mathcal {S}_{\mathcal {X}} = \{\pi _{1}, \pi _{2}, \pi _{3}\}\), where \(\pi _{1} = [1, 0]\) always generates secret \(x_{1}\), \(\pi _{2} = [0, 1]\) always generates secret \(x_{2}\), and  generates either secret with equal probability. Consider also two possible environments for this system:
generates either secret with equal probability. Consider also two possible environments for this system:
-
 is the environment in which strategies \(\pi _{1}\) and \(\pi _{2}\) may be adopted with equal probability. This represents a scenario in which any user logging in has an equal probability of having generated his password either according to strategy \(\pi _{1}\) or according to strategy \(\pi _{2}\).
is the environment in which strategies \(\pi _{1}\) and \(\pi _{2}\) may be adopted with equal probability. This represents a scenario in which any user logging in has an equal probability of having generated his password either according to strategy \(\pi _{1}\) or according to strategy \(\pi _{2}\). -
\(\mathsf {En}_{2} = [0, \, 0, \, 1]\) is the environment in which strategy \(\pi _{3}\) is always adopted. This represents a scenario in which every user logging is assured to having generated his password using strategy \(\pi _{3}\).
We depict strategies and environments in Table 1. The columns list strategies; the first grouping of rows contains the definition of the strategy (i.e., the probability that it chooses a particular secret), and the next grouping of rows contains the definition of each environment, one per row, which gives the probability of each strategy. \(\square \)
3.2 Prior Knowledge as a Hyper, and Environmental Vulnerability
Given a model with an environment \(\mathsf {En}\), we can continue to represent the prior in the traditional manner, as a distribution on secrets \(\pi \). We call this prior the concise knowledge of the environment, and it is defined as the expectation of all strategies of \(\mathsf {En}\), i.e., \(\pi = \mathbb {E}_{}\,\mathsf {En}\). When this equation holds, we also say that \(\pi \) is consistent with \(\mathsf {En}\); when needed we may denote by \(\pi _{\mathsf {En}}\) the prior consistent with environment \(\mathsf {En}\). For instance, consistent, concise knowledge of users’ passwords in Example 1 would be the expectation of how a randomly picked user would generate their password: each user may potentially adopt a unique strategy for generating their password, and the prior captures the expected behavior of the population of users.
Alternatively, we can represent the prior as a hyper \(\mathsf {M}\), representing the adversary’s unabridged knowledge of the environment \(\mathsf {En}\). For now, we will assume an adversary knows the environment \(\mathsf {En}\) precisely, i.e., \(\mathsf {M}= \mathsf {En}\), just as, in traditional QIF, it is often assumed that the adversary precisely knows the defender’s single secret-generating strategy. Later, in Sect. 5, we will introduce the notion of a abstraction \(\mathsf {M}\), which is model consistent with an environment \(\mathsf {En}\), but that does not match it exactly; this allows us to model partial adversary knowledge.
Given this new notion of prior (i.e., unabridged knowledge), we must define a corresponding notion of the vulnerability of a secret. We call this notion environmental vulnerability.
Definition 1
(Environmental vulnerability). Given a vulnerability measure \(\mathbb {V}_{X}{:}\mathbb {D}{\mathcal {X}}{\rightarrow }\mathbb {R}\), the environmental vulnerability of the secret is a function \(\mathbb {V}^{en}_{X}{:}\mathbb {D}^{2}{\mathcal {X}}{\rightarrow }\mathbb {R}\) of the environment \(\mathsf {En}\) defined as
It is easy to show that if the environment \(\mathsf {En}\) is a point-hyper \([\pi ]\), environmental vulnerability \(\mathbb {V}^{en}_{X}(\mathsf {En})\) collapses into traditional prior vulnerability \(\mathbb {V}_{X}(\pi )\).
Proposition 1
For all environments \(\mathsf {En}\), if \(\mathsf {En}= [\pi _{}]\) then \(\mathbb {V}^{en}_{X}(\mathsf {En}) = \mathbb {V}_{X}(\pi _{})\).
The converse of Proposition 1, however, is not true, i.e., \(\mathbb {V}^{en}_{X}(\mathsf {En}) = \mathbb {V}_{X}(\pi )\) does not imply \(\mathsf {En}= [\pi ]\). We can also show that, in expectation, an adversary with unabridged knowledge \(\mathsf {En}\) can never be worse-off than an adversary with concise knowledge \(\pi _{\mathsf {En}}\).
Proposition 2
For any vulnerability \(\mathbb {V}_{X}\), \(\mathbb {V}^{en}_{X}(\mathsf {En}) \ge \mathbb {V}_{X}(\pi _{\mathsf {En}})\) for all environments \(\mathsf {En}\).
Proposition 2 shows that the modeling of adversarial knowledge as only a distribution on secrets overlooks how the adversary can exploit knowledge of the environment. Indeed, as the next example shows, secrets distributed according to a same prior may present drastically different environmental vulnerability.
Example 2
Consider the password system of Example 1. Both environments yield the same prior distribution  , so an adversary with only concise knowledge would obtain the same traditional prior vulnerability in both environments. E.g., for Bayes vulnerability, defined as
, so an adversary with only concise knowledge would obtain the same traditional prior vulnerability in both environments. E.g., for Bayes vulnerability, defined as
the adversary would obtain a traditional prior vulnerability of  .
.
However, an adversary with unabridged knowledge would obtain different values for the vulnerability of the secret in each environment. In \(\mathsf {En}_1\) environmental vulnerability is  , whereas in \(\mathsf {En}_2\) environmental vulnerability is
, whereas in \(\mathsf {En}_2\) environmental vulnerability is  (recall that higher is worse for the defender).
(recall that higher is worse for the defender).
Note that in \(\mathsf {En}_{2}\), the value for environmental vulnerability and traditional prior vulnerability is the same  so an adversary who learns the strategy being used is not expected to be more successful than an adversary who only knows the prior. \(\square \)
so an adversary who learns the strategy being used is not expected to be more successful than an adversary who only knows the prior. \(\square \)
4 Security by Aggregation and Security by Strategy
In this section we discuss further the advantage of using a hyper as the prior, showing how it can distinguish two types of security guarantees that are conflated when the prior is merely a distribution: security “by aggregation” and security “by strategy”. We also show that the traditional definition of prior vulnerability decomposes neatly into environmental vulnerability and “strategy vulnerability”, which measures the information the adversary has about the strategy used to generate secrets.
4.1 Dissecting the Security Guarantees of Traditional Prior Vulnerability
The final example in the last section provides some insights about the security guarantees implied by traditional prior vulnerability. First, security by aggregation occurs when environmental vulnerability (largely) exceeds traditional prior vulnerability: \(\mathbb {V}^{en}_{X}(\mathsf {En}) \gg \mathbb {V}_{X}(\pi _{\mathsf {En}})\). In this case the secret is protected by the adversary’s lack of knowledge of the strategy being used, and, if the adversary learns the strategy, the vulnerability of the secret can (significantly) increase. An example of security by aggregation is a scenario in which all users pick passwords with deterministic strategies, but the adversary does not know which user is generating the password. If there is a large number of users, and if their strategies are varied enough, the passwords may be considered “secure” only as long as the adversary cannot use knowledge about the environment to identify the strategy being used.
On the other hand, security by strategy occurs when environmental and prior vulnerabilities have similar values: \(\mathbb {V}^{en}_{X}(\mathsf {En}) \approx \mathbb {V}_{X}(\pi _{\mathsf {En}})\). In this case the secret is protected by the unpredictability (or uncertainty) within the strategies that generate the secret, so even if the strategy becomes known, the vulnerability of the secret will not increase significantly. An example of security by strategy is a bank system in which user PINs are chosen uniformly. Even if the algorithm is known to the adversary, the vulnerability of the secret is not increased.
In Sect. 4.3 we define measures of the two types of security discussed above, but for that we need first to formalize the concept of strategy vulnerability.
4.2 Strategy Vulnerability
We now turn our attention to how the knowledge of an environment reflects on the adversary’s knowledge about the strategy being used to generate secrets. For that we will define a measure \(\mathbb {V}^{st}_{S}{:}\mathbb {D}{\mathcal {S}}{\rightarrow }\mathbb {R}\) of strategy vulnerability.
Our measure should cover two key points. First, it should reflect how certain an adversary is about which strategy is being used to generate secrets, independently of whether the strategy itself is deterministic or random. In particular, it must distinguish between environments in which the adversary knows exactly the strategy being used, but that strategy happens to employ randomization (in which case strategy vulnerability should be high) from environments in which the adversary does not know what strategy is being used, even if all possible strategies are deterministic (in which case strategy vulnerability should be low).
Second, the measure should characterize environments that are “predictable” from the point of view of the adversary. The key insight is that \(\mathbb {V}^{st}_{S}(\mathsf {En})\) should consider the “similarity” among strategies in the support of \(\mathsf {En}\). From the point of view of the adversary, whose goal is to “guess the secret” (or, more precisely, to exploit his knowledge about the secret according to some information measure \(\mathbb {V}_{X}{:}\mathbb {D}{\mathcal {X}}{\rightarrow }\mathbb {R}\) of interest), two strategies should be considered “similar” if they yield “similar” vulnerabilities of the secret, as measured according to this \(\mathbb {V}_{X}\). The following example motivates this reasoning.
Example 3
Consider an extension from Example 1, adding a strategy \(\pi _4\) and environment \(\mathsf {En}_{3}\), depicted in Table 2. Intuitively, strategy vulnerability should be high in \(\mathsf {En}_2 = [\pi _{3}]\), since an adversary would know exactly the strategy being used. But what should be the strategy vulnerability in \(\mathsf {En}_1\) and in \(\mathsf {En}_3\)?
Suppose we simply considered the set \(\mathcal {S}_{\mathcal {X}}\) of strategies as our set of secrets, and defined \(\mathbb {V}^{st}_{S}\) as the Bayes vulnerability w.r.t. that set: \({\mathbb {V}^{st}_{S}}^{(*)}(\mathsf {En}) \mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {def?}}}\max _{\pi \in \mathcal {S}} \mathsf {En}(\pi ).\) As expected we would have \({\mathbb {V}^{st}_{S}}^{(*)}(\mathsf {En}_{2}) = 1\), but since in each environment \(\mathsf {En}_{1}\) and \(\mathsf {En}_{3}\) there are two possible strategies, each with probability  , we would then have
, we would then have  , and
, and  . But this seems wrong: we are assigning the same measure of vulnerability to both \(\mathsf {En}_{1}\) and \(\mathsf {En}_{3}\), but these two environments are very different. The possible strategies in \(\mathsf {En}_{1}\) never produce the same secret, whereas the strategies of \(\mathsf {En}_{3}\) produce secrets \(x_1\) and \(x_2\) with similar probabilities. \({\mathbb {V}^{st}_{S}}^{(*)}\) ascribes \(\mathsf {En}_{1}\) and \(\mathsf {En}_{3}\) the same measure even though the uncertainty about the strategy under knowledge of \(\mathsf {En}_{3}\) seems much lower than \(\mathsf {En}_{1}\). For instance, if the adversary is interested in guessing the secret correctly in one try, an adversary who knows \(\mathsf {En}_{3}\) would always guess the secret to be \(x_1\) and would be right most of the time, but an adversary who knows \(\mathsf {En}_{1}\) gains no advantage about which secret to guess. In short, for this type of adversary we want \(\mathbb {V}^{st}_{S}(\mathsf {En}_{2})> \mathbb {V}^{st}_{S}(\mathsf {En}_{3}) > \mathbb {V}^{st}_{S}(\mathsf {En}_{1})\), but \({\mathbb {V}^{st}_{S}}^{(*)}\) fails to satisfy this ordering. \(\square \)
. But this seems wrong: we are assigning the same measure of vulnerability to both \(\mathsf {En}_{1}\) and \(\mathsf {En}_{3}\), but these two environments are very different. The possible strategies in \(\mathsf {En}_{1}\) never produce the same secret, whereas the strategies of \(\mathsf {En}_{3}\) produce secrets \(x_1\) and \(x_2\) with similar probabilities. \({\mathbb {V}^{st}_{S}}^{(*)}\) ascribes \(\mathsf {En}_{1}\) and \(\mathsf {En}_{3}\) the same measure even though the uncertainty about the strategy under knowledge of \(\mathsf {En}_{3}\) seems much lower than \(\mathsf {En}_{1}\). For instance, if the adversary is interested in guessing the secret correctly in one try, an adversary who knows \(\mathsf {En}_{3}\) would always guess the secret to be \(x_1\) and would be right most of the time, but an adversary who knows \(\mathsf {En}_{1}\) gains no advantage about which secret to guess. In short, for this type of adversary we want \(\mathbb {V}^{st}_{S}(\mathsf {En}_{2})> \mathbb {V}^{st}_{S}(\mathsf {En}_{3}) > \mathbb {V}^{st}_{S}(\mathsf {En}_{1})\), but \({\mathbb {V}^{st}_{S}}^{(*)}\) fails to satisfy this ordering. \(\square \)
These observations lead us to define the vulnerability of a strategy in terms of the difference in accuracy, as measured by a choice of \(\mathbb {V}_{X}\), of an adversary acting according to its full knowledge of the environment \(\mathsf {En}\) and an adversary betting according to the expected behavior \(\pi _{\mathsf {En}} = \mathbb {E}_{}\mathsf {En}\) of the environment. The key intuition is that a strategy is, for practical purposes, known within an environment when \(\mathbb {V}_{X}(\pi _{\mathsf {En}}) \approx \mathbb {V}^{en}_{X}(\mathsf {En})\), or, equivalently, \(\mathbb {V}_{X}(\mathbb {E}_{}\mathsf {En}) \approx \mathbb {E}_{\mathsf {En}} \mathbb {V}_{X}\).
Definition 2
(Strategy vulnerability). Given a vulnerability \(\mathbb {V}_{X}\), the strategy vulnerability in environment \(\mathsf {En}\) is defined as the ratio
By Proposition 2, \(\mathbb {V}^{st}_{S}(\mathsf {En}) \le 1\), and it is maximum when \(\mathbb {V}_{X}(\pi _{\mathsf {En}}) = \mathbb {V}^{en}_{X}(\mathsf {En})\). As for a lower bound, it can be shown that strategy vulnerability is minimum when the adversary’s measure of interest is Bayes vulnerability.
Proposition 3
Given any vulnerability \(\mathbb {V}_{X}\), strategy vulnerability is bounded by  for all environments \(\mathsf {En}\).
for all environments \(\mathsf {En}\).
The following example illustrates how Definition 2 covers the two key points.
Example 4
Consider the scenario from Example 3, but assume an adversary A is only interested in the chances of correctly guessing the secret in one try, no matter what the secret is, whereas an adversary B also wants to guess the secret in one try, but considers secret \(x_{2}\) as 9.5 times more valuable than secret \(x_{1}\) (say, for instance, that secrets are passwords to bank accounts, and one of the accounts has 9.5 times more money than the other).
Mathematically, adversary A’s measure of success is represented by the vulnerability \(\mathbb {V}^{(A)}_{X}= \mathbb {V}^{(Bayes)}_{X}\) defined in Eq. (2). As for adversary B, the vulnerability \(\mathbb {V}^{(B)}_{X}\) can be defined as a g-vulnerability where the set \(\mathcal {W}\) of guesses of guesses is the same as the set \(\mathcal {X}\) of secrets, and the gain function g is such that \(g(x_{i},x_{j})\) equals 1 when \(i = j = 1\), equals 9.5 when \(i = j = 2\), and equals 0 when \(i \ne j\).
Table 3 shows the environmental, strategy, and traditional prior vulnerabilities for each adversary in each environment. Note that the calculated values substantiate the intuitions we argued for in Example 3. For both adversaries strategy vulnerability is maximum in environment \(\mathsf {En}_{2}\) (\(\mathbb {V}^{st(A)}_{S}(\mathsf {En}_{2}) = \mathbb {V}^{st(B)}_{S}(\mathsf {En}_{2}) = 1\)), and it is higher in environment \(\mathsf {En}_{3}\) than in environment \(\mathsf {En}_{1}\).
In particular for environment \(\mathsf {En}_{3}\), the obtained value \(\mathbb {V}^{st(A)}_{S}(\mathsf {En}_{3}) = 1\) meets our intuition that, for practical purposes, adversary A has little uncertainty about the strategy being used: if all he cares about is to guess the secret in one try, the differences between the possible strategies are too small to provoke any change in A’s behavior. On the other hand, the obtained value  reflects our intuition that in the same environment adversary B has more uncertainty about the strategy being used: the differences in each possible strategy are significant enough to induce changes in B’s behavior. \(\square \)
reflects our intuition that in the same environment adversary B has more uncertainty about the strategy being used: the differences in each possible strategy are significant enough to induce changes in B’s behavior. \(\square \)
4.3 Measures of Security by Aggregation and by Strategy
In this section we provide measures of the two types of security—by aggregation and by strategy—motivated in Sect. 4.1. The key idea is to observe that Definition 2 is consistent with the decomposition of traditional prior vulnerability into the product of strategy vulnerability and environmental vulnerability, and that these two factors are measures of security by aggregation and security by strategy, respectively:
Equation (3) states that any fixed amount of traditional prior vulnerability (i.e., perceived security) can be allocated among strategy and environmental vulnerability in different proportions, but in such a way that when one increases, the other must decrease to compensate for it. Environmental vulnerability is a meaningful measure of security by strategy because it quantifies the intrinsic uncertainty about how secrets are generated within each possible strategy. Indeed, when strategies are random, this uncertainty cannot be avoided. On the other hand, security by aggregation is a measure of the decrease in the adversary’s effectiveness caused by his lack of knowledge of the environment.
Example 5
Environments \(\mathsf {En}_{1}\) and \(\mathsf {En}_{2}\) from Example 4 yield the same perceived security for an adversary with concise knowledge; e.g., for adversary A,  . However, each environment allocates this perceived security differently. W.r.t. adversary A, \(\mathsf {En}_{1}\) has minimum security by strategy (
. However, each environment allocates this perceived security differently. W.r.t. adversary A, \(\mathsf {En}_{1}\) has minimum security by strategy ( ). Conversely, environment \(\mathsf {En}_{2}\) has maximum security by strategy (
). Conversely, environment \(\mathsf {En}_{2}\) has maximum security by strategy ( ), and minimum security by aggregation (\(\mathbb {V}^{st(A)}_{S}(\mathsf {En}_{1}) = 1\)). Note that this quantitative analysis precisely characterize intuitions for the distinction among the two types of security motivated in Example 2. \(\square \)
), and minimum security by aggregation (\(\mathbb {V}^{st(A)}_{S}(\mathsf {En}_{1}) = 1\)). Note that this quantitative analysis precisely characterize intuitions for the distinction among the two types of security motivated in Example 2. \(\square \)
A note on the chain rule for information measures. Equation (3) is not a trivial analogue of the chain-rule for information measures. For a start, most information measures do not follow any traditional form of the chain rule.Footnote 6 Even for Shannon entropy, which respects the chain rule, the decomposition of entropies of random variables S, X corresponding to strategies and secrets, respectively, would be \(H(X,S) = H(S) + H(X \mid S)\). But even if it is reasonable to equate \(H(X \mid S)\) to “environmental entropy” of the secret given the strategy is known, H(S) cannot be equated with “strategy entropy” if we want the sum of both values to be equal to H(X), which is the “entropy of the secret”. In other words, H(S) does not seem to be a reasonable measure of “strategy entropy” (in fact, H(S) would be a function on the distribution on strategies only, so it would fail to take into account the similarity among strategies). However, we can derive that \( H(X) = I(X;S) + H(X \mid S) \), which would suggest that an appropriate measure of “strategy entropy” is actually I(X; S). This is in line with our definition of strategy vulnerability as the amount of information the environment carries about the secret.
5 Models of Adversarial Partial Knowledge
Starting from Sect. 3.2 we assumed that prior knowledge represented as a hyper exactly matches the environment \(\mathsf {En}\). However, in real-world settings the adversary is likely only to know some features of the environment, but not its complete structure. As such, in this section we develop the notion of a “model” that is hyper on secrets representing an adversary’s partial knowledge of that environment. By employing “abstractions” of the environment as models, we are able to generalize prior, environmental, and strategy vulnerability, and to provide a stronger version of the “decomposition rule” for security of Eq. (3).
5.1 Models of Partial Knowledge as Abstractions of the Environment
A model of adversarial knowledge is a hyper \(\mathsf {M}{:}\mathbb {D}{\mathcal {S}_{\mathcal {X}}}\), representing the adversary’s knowledge about how secrets are generated. Each inner \(\pi _{j}\) in \(\mathsf {M}\) corresponds to a strategy the adversary can interpret as possibly generating a secret, and the corresponding outer probability \(\mathsf {M}(\pi _{j})\) represents the probability the adversary attributes to \(\pi _{j}\) being used.
Models can be used to represent states of knowledge of varied precision. In particular, the environment \(\mathsf {En}\) itself is a model of an adversary with unabridged knowledge, whereas the point hyper \([\pi _{\mathsf {En}}]\) is the model of an adversary with only concise knowledge. Here we are interested also in models of intermediate levels of adversarial knowledge lying in between these two extreme cases. In particular, as we show in the next example, a model’s strategies may not directly match those of the true environment, but rather abstract information in that environment in a consistent manner.
Example 6
Consider the password system from Example 1, but assume now that the environment \(\mathsf {En}\) of execution consists in six possible strategies, as depicted in Table 4a. The model of knowledge of an adversary who can always identify the user logging into the system is the environment \(\mathsf {En}\) itself. As for an adversary who can never identify the user logging in, the model of knowledge is the expected behavior of all users, represented by the point hyper \([\pi _{\mathsf {En}}]\) in Table 4c.
Consider now another adversary who cannot exactly identify the user logging into the system, but can determine from what state in the country the user is attempting to login (for instance, by observing the IP of the request). Assume also that users \(\pi _{1}\), \(\pi _{2}\) come from state A, users \(\pi _{3}\), \(\pi _{4}\) come from state B, and users \(\pi _{5}\), \(\pi _{6}\) come from state C. The model of knowledge for this adversary, depicted as hyper \(\mathsf {F}\) in Table 4b, consists in three strategies \(\pi _{A}\), \(\pi _{B}\) and \(\pi _{C}\) representing the expected pattern of password generation in states A, B and C, respectively. The difference in strategies \(\pi _{A}\), \(\pi _{B}\) and \(\pi _{C}\) can capture the different frequency of passwords from state to state (caused, e.g., by regional uses of slangs, names of cities, etc.). The probability assigned by the adversary to each strategy corresponding to a state is given by the probability of any given user coming from that state. For instance, the probability \(\mathsf {F}(\pi _{A})\) of strategy corresponding to state A is given by  and strategy \(\pi _{A}\) itself is obtained as the expectation of all strategies of users coming from that state:
and strategy \(\pi _{A}\) itself is obtained as the expectation of all strategies of users coming from that state:  . \(\square \)
. \(\square \)
Model \(\mathsf {F}\) of Example 6 can be conveniently represented using a matrix representation of hypers as follows. First, note that any hyper \(\mathsf {H}{:}\mathbb {D}{\mathcal {S}_{\mathcal {X}}}\) induces a joint probability distribution \(p^{\mathsf {H}}{:}\mathbb {D}{(\mathcal {X}\times \mathcal {S}_{\mathcal {X}})}\) on secrets and strategies, defined as \(p^{\mathsf {H}}(x_{i},\pi _{j}) = \mathsf {H}(\pi _{j}) \pi _{j}(x_{i})\). For a hyper \(\mathsf {H}\), we let \(\mathsf {H}^{joint}\) be the \(|\mathcal {X}| \times |\mathcal {S}_{X}|\) matrix in which \(\mathsf {H}^{joint}({i,j}) = p^{\mathsf {H}}(i,j)\). For instance, in Example 6 we have that

Conversely, using the usual concepts of marginalization and conditioning, given any joint distribution \(p^{\mathsf {H}}\) we can recover the corresponding hyper \(\mathsf {H}\). Because of that, we shall equate a hyper \(\mathsf {H}\) with its corresponding joint distribution \(p^{\mathsf {H}}\), and, equivalently, with its matrix representation \(\mathsf {H}^{joint}\).

Second, the adversary’s incapability of distinguishing users within a state can be modeled by the matrix \(A^{State}\) on the side, which maps each strategy corresponding to a user in the environment to a strategy corresponding to a state in the model. It can be easily verified that the hyper \(\mathsf {F}\) in its joint form can be recovered as the product of the environment \(\mathsf {En}\) in its joint form with \(A^{State}\), i.e., \( \mathsf {F}^{joint} = \mathsf {En}^{joint} \times A^{State}. \)
Although in Example 6 the adversary could only deterministically aggregate strategies together, in general models can be the result of an adversary probabilistically identifying a trait of the strategy used. Moreover, note that the adversary does not need to know the exact strategy from each user first, to only then aggregate them into the expected behavior of the state. He could, for instance, obtain the average behavior from the state directly from a log of passwords in which only the user’s state of origin is known.
Formally, let \(p(\mu \mid \pi )\) be the probability of the adversary modeling the context as strategy \( \mu {:}\mathcal {S}_{\mathcal {X}}\) when in reality it is strategy \(\pi {:}\mathcal {S}_{\mathcal {X}}\). A model \(\mathsf {M}\) for environment \(\mathsf {En}\) obtained using distribution \(p(\mu \mid \pi )\) assigns to each strategy \(\mu \) outer probability
The formulas in Eq. (4) are equivalent to the following characterization of the abstraction of a model into another in terms of “aggregation matrices”. An aggregation matrix A is a \(|\mathcal {S}_{\mathcal {X}}| \times |\mathcal {S}_{\mathcal {X}}|\) channel matrix in which each entry A(i, j) is the probability \(p(\pi \mid \mu )\) of the adversary mapping strategy \(\pi \) to strategy \( \mu \).
Definition 3
(Abstraction of a hyper). A hyper \(\mathsf {H}'\) is an abstraction of another hyper \(\mathsf {H}\), denoted by \(\mathsf {H}' \sqsubseteq \mathsf {H}\), iff \( \mathsf {H}' = \mathsf {H}{\cdot }A \) for some aggregation matrix A.
Definition 3 says that an abstraction \(\mathsf {M}\) can be obtained as the result of post-processing the environment \(\mathsf {En}\) with an aggregation matrix A that makes convex combinations of actual strategies. The matrix A can be seen as the adversary’s capability of correctly identifying the context of execution. In particular, when A is the identity matrix I, the resulting abstraction is the environment itself: \(\mathsf {En}= \mathsf {En}{\cdot }I\). When A is the non-interferent channel \(\overline{0}\), the resulting abstraction is the point-hyper \([\pi ] = \mathsf {En}{\cdot }\overline{0}\).Footnote 7 In particular, because in Example 6 the adversary can only group whole strategies together based on state, the aggregation matrix \(A^{State}\) is deterministic.
As a sanity check, the following result shows that the result of post-processing a hyper with a channel matrix is itself a hyper with same expectation, which implies that all abstractions are consistent with the prior distribution.
Proposition 4
If \(\mathsf {H}\) is a hyper of type \(\mathbb {D}^{2}{\mathcal {X}}\) and A is a channel matrix from \(\mathcal {X}\) to any domain \(\mathcal {Y}\), then \(\mathsf {H}{\cdot }A\) is also a hyper of type \(\mathbb {D}^{2}{\mathcal {X}}\). Moreover, if we call \(\mathsf {H}' = \mathsf {H}{\cdot }A\), then the priors from both hypers are the same: \(\pi _{\mathsf {H}} = \pi _{\mathsf {H}'}\).
5.2 Vulnerability of the Secret Given an Abstraction
We will now generalize the definition of environmental vulnerability of the secret (in which the adversary is assumed to have unabridged knowledge), to scenarios in which the adversary’s knowledge is an abstraction \(\mathsf {M}\) of the environment \(\mathsf {En}\).
The key insight of this measure is that, whereas the adversary’s actions are chosen depending on his modeling of the context as strategy \( \mu \) from \(\mathsf {M}\), his actual gain should be measured according to the real strategy \(\pi \) coming from the environment \(\mathsf {En}\). We formalize this below, recalling that, from Theorem 1 we know that every continuous and convex vulnerability \(\mathbb {V}_{X}\) can be written as a g-vulnerability \(V_{g}\) for some suitable g.
Definition 4
The vulnerability of the secret in an environment \(\mathsf {En}\) when the adversary’s model is abstraction \(\mathsf {M}\) is given by
where \( w_{\mu } = \mathop {\hbox {argmax} }\nolimits _{w} \sum _{x} \mu (x) g(w,x) \) is the adversary’s optimal guess if the secret were actually distributed according to strategy \(\mu \).
Note that Eq. (5) is defined only when \(p(\mu \mid \pi ) = A({\mu ,\pi })\) is well defined, that is, when there exists an aggregation matrix A making \(\mathsf {M}\sqsubseteq \mathsf {En}\).
The following result states that the vulnerability of the secret for an adversary who reasons according to an abstraction (as per Eq. (5)) is the same as environmental vulnerability in case this abstraction were the real environment.
Proposition 5
For any vulnerability \(\mathbb {V}_{X}\), environment \(\mathsf {En}\) and model \(\mathsf {M}\), if \(\mathsf {M}\sqsubseteq \mathsf {En}\) then \(\mathbb {V}^{md}_{X}(\mathsf {M} , \mathsf {En}) = \mathbb {V}^{en}_{X}(\mathsf {M})\).
Proposition 5 has a few interesting consequences. First, it implies that the definition of \(\mathbb {V}^{md}_{X}(\mathsf {M} , \mathsf {En})\) generalizes environmental and traditional prior vulnerabilities: when the adversary’s model is \(\mathsf {M}= \mathsf {En}\), we have that \(\mathbb {V}^{md}_{X}(\mathsf {M} , \mathsf {En}) = \mathbb {V}^{en}_{X}(\mathsf {En})\), and his model is \(\mathsf {M}= [\pi _{\mathsf {En}}]\), we have that \(\mathbb {V}^{md}_{X}([\pi ] , \mathsf {En}) = \mathbb {V}^{en}_{X}([\pi ]) = \mathbb {V}_{X}(\pi )\).
More importantly, though, Proposition 5 provides a precise information-theoretic characterization of our definition of abstractions for an environment. More precisely, it can be used to show that by using a more refined model an adversary can never be worse off than by using a less refined model.
Proposition 6
If \(\mathsf {M}', \mathsf {M}\) are abstractions for an environment \(\mathsf {En}\), then \(\mathsf {M}' \sqsubseteq \mathsf {M}\) iff \(\mathbb {V}^{md}_{X}(\mathsf {M}' , \mathsf {En}) \le \mathbb {V}^{md}_{X}(\mathsf {M} , \mathsf {En})\) for all vulnerabilities \(\mathbb {V}_{X}\).
5.3 Strategy Vulnerability Given an Abstraction
Next, we will generalize strategy vulnerability to the scenario in which the adversary reasons according to an abstraction \(\mathsf {M}\) of the environment \(\mathsf {En}\).
Our definition is analogous to that of strategy vulnerability, and it is based on the observation that a strategy is vulnerable given a model to the extent the average behavior of the model can be used to infer the strategy being used. In other words, the strategy is protected if knowledge about the model does not give information about what strategy is being used.
Definition 5
Given a vulnerability \(\mathbb {V}_{X}\), the corresponding strategy vulnerability given an abstraction \(\mathsf {M}\) within an environment \(\mathsf {En}\) is defined as
where the second equality stems from Proposition 5.
The next result shows that a more refined abstraction never yields smaller strategy vulnerability than a less refined abstraction for the same environment.
Proposition 7
Given two abstractions \(\mathsf {M}\) and \(\mathsf {M}'\) of an environment \(\mathsf {En}\), \({\mathsf {M}' \sqsubseteq \mathsf {M}}\) iff \(\mathbb {V}^{st}_{S}(\mathsf {M}' , \mathsf {En}) \le \mathbb {V}^{st}_{S}(\mathsf {M} , \mathsf {En})\) for all vulnerabilities \(\mathbb {V}_{X}\).
Proposition 7 implies bounds on strategy vulnerability given an abstraction.
Proposition 8
Given any vulnerability \(\mathbb {V}_{X}\), for any environment \(\mathsf {En}\) and any abstraction \(\mathsf {M}\sqsubseteq \mathsf {En}\), \(\mathbb {V}^{st}_{S}(\mathsf {En}) \le \mathbb {V}^{st}_{S}(\mathsf {M} , \mathsf {En}) \le 1\), with equality for the lower bound occurring when \(\mathsf {M}= [\pi _{\mathsf {En}}]\), and equality for the upper bound occurring when \(\mathsf {M}= \mathsf {En}\).
Finally, we note that Definition 5 naturally extends the decomposition rule of Eq. (3) and the definitions of different types of security as follows.

An interesting observation. The following observation means that the increase in accuracy given by a more refined abstraction \(\mathsf {M}\) over a less refined abstraction \(\mathsf {M}'\) is the same for secrets and for strategies. If \(\mathsf {M}' \sqsubseteq \mathsf {M}\sqsubseteq \mathsf {En}\) then
Making \(\mathsf {M}= \mathsf {En}\) in Eq. (6) we recover the definition of strategy vulnerability:  . Making \(\mathsf {M}' = [\pi _{\mathsf {En}}]\) in Eq. (6) we obtain that the increase in information about secrets and the increase in information about strategies provided by a model is the same:
. Making \(\mathsf {M}' = [\pi _{\mathsf {En}}]\) in Eq. (6) we obtain that the increase in information about secrets and the increase in information about strategies provided by a model is the same:  .
.
6 On the Expressiveness of Hypers
Hyper distributions play an essential role in this paper to generalize the modeling of secret-generation process and the adversary’s prior knowledge about it. Having gone from distributions over secrets to distributions over distributions over secrets, one might wonder whether further levels of distribution (i.e., “higher-order” hypers of type \(\mathbb {D}^{n}{\mathcal {X}}\), for \(n > 2\)) might be necessary to fully account for adversary knowledge. The simple answer is no.
The core idea is that a hyper corresponds to a joint distribution in \(\mathbb {D}(\mathcal {X}\times \mathcal {Y})\) for some set \(\mathcal {Y}\) of labels for distributions on \(\mathcal {X}\). Likewise, an object of type \(\mathbb {D}^{n+1}{\mathcal {X}}\) corresponds to a joint distribution in \(\mathbb {D}(\mathcal {X}\times \mathcal {Y}_1{\times }\cdots \times \mathcal {Y}_{n})\), which is itself equivalent to a joint distribution in \(\mathbb {D}(\mathcal {X}\times \mathcal {Y})\) where \(\mathcal {Y}= \mathcal {Y}_1 \times \cdots {\times }\mathcal {Y}_{n}\). But note that \(\mathbb {D}(\mathcal {X}\times \mathcal {Y})\) is equivalent to a hyper of type \(\mathbb {D}^2{\mathcal {X}}\). Hence, any “higher-order” hyper is equivalent to some regular hyper of type \(\mathbb {D}^{2}{\mathcal {X}}\) and, moreover, both objects preserve the same distribution on distributions on \(\mathcal {X}\). Since measures of the vulnerability of the secret are functions of distributions on \(\mathcal {X}\), the user of “higher-order” hypers is not necessary to measure vulnerability.
To make this idea precise, let \(\pi ^{n}\) range over objects of type \(\mathbb {D}^{n}\mathcal {X}\). If the adversary’s knowledge is represented by \(\pi ^{n}\) (for some \(n \ge 2\)), it is natural to define the vulnerability of the secret as the expectation of the vulnerabilities of hypers of lower order. A vulnerability of order n is a function \(\mathbb {V}^{n}{:}\mathbb {D}^{n}\mathcal {X}{\rightarrow }\mathbb {R}\) s.t. \(\mathbb {V}^{1}(\pi ^{1}) = \mathbb {V}_{X}(\pi ^{1})\), and \(\mathbb {V}^{n}(\pi ^{n}) = \mathbb {E}_{\pi ^{n}}\mathbb {V}^{n-1}\) for \(n \ge 2\). In particular, \(\mathbb {V}^{1}(\pi ^{1}) = \mathbb {V}_{X}(\pi ^{1})\) is the traditional vulnerability on secrets, and \(\mathbb {V}^{2}(\pi ^{2}) = \mathbb {E}_{\pi ^{2}}\mathbb {V}_{X}\) is environmental vulnerability. The next result shows that an adversary who reasons according to a model of type \(\mathbb {D}^{n}{\mathcal {X}}\) for some \(n \ge 2\) is only as well off as an adversary with an appropriate model of type \(\mathbb {D}^{2}{\mathcal {X}}\).
Proposition 9
For every \(\pi ^{n}{:}\mathbb {D}^{n}{\mathcal {X}}\), with \(n \ge 2\), \(\mathbb {V}^{n}(\pi ^{n}) = \mathbb {V}^{2}(\widehat{\pi }^{2})\), where \(\widehat{\pi }^{2}{:}\mathbb {D}^{2}{\mathcal {X}}\) is the hyper resulting from marginalizing the joint of \(\pi ^{n}\) w.r.t. \(Y_{2} \times Y_{3}\times \ldots \times Y_{n-1}\).
7 Case Study
To illustrate the utility of our model, we synthesize an environment based on the RockYou password dataset [22], which contains the un-hashed passwords of around 32 million users of the RockYou gaming site. We construct several abstractions for this environment, computing for each of them the corresponding vulnerability of the secret and strategy vulnerability, and show how they relate.
To synthesize the environment, we begin by reducing the 32 million passwords to the around 350 thousand passwords that contain a string suggesting the birth year of the password’s owner (the strings “1917” through “1995”). We assume that each of these passwords was generated by a distinct user, and construct a deterministic strategy for each of these users. The intention is that each strategy represents the user’s exact preference at the time they selected their password. The environment consists in these strategies distributed according to their relative frequency in the database.
To construct abstractions for this environment, we attribute to each user the birth year used in their password, as well as a randomly chosen gender. The first abstraction, called Omniscient, is the environment itself, and it represents an adversary with unabridged knowledge. Although this level of knowledge is beyond any realistic adversary, it will illustrate the limiting values of vulnerability.
To construct the Age abstraction, we partition users into blocks according to their birth year. From each block we derive a distribution on passwords representing the expected strategy for a person born in that year. This produces one strategy for each birth year from 1917 through 1995, and the probability of each strategy is determined by the relative frequency of each birth year.
The Gender abstraction aggregates users by gender, and contains one strategy representing the expected behavior of males and of females. Since we assigned genders to users uniformly at random, these two strategies each occur with equal probability (0.5) and are mostly similar.
Finally, the Prior abstraction has only one strategy in its support that aggregates all of the 350 thousand users, with each password’s probability being proportional to its relative frequency. This environment is equivalent to the point hyper \([\pi ]\) containing only the prior distribution on secrets.
Several strategies in the last three abstractions are visualized in Fig. 2. The “all” line shows the probability of various passwords being picked in the Prior environment, sorted by their rank (most probable first). The two gender aggregate strategies from the Gender environment are labeled “male” and “female” (note that “male”, “female” and “all” largely coincide). Finally, three example years from the Age environment are labeled “1930”, “1960”, and “1990”. The Bayes vulnerability of each strategy is the probability of the rank 1 password and min-entropy is negation of the base 2 exponent of that probability.
The decomposition of prior Bayes vulnerability as per Definition 2 is summarized in Table 5. Note that the vulnerability in the prior is around \(2^{-11.892}=2.632{\cdot }10^{-4}\). An adversary who can learn the user’s gender could achieve vulnerability of \(2^{-11.876} = 2.66084\cdot 10^{-4}\). The strategy vulnerability here shows negligible advantage over the prior as we synthesized the gender uniformly. On the other hand, an adversary reasoning according to the aggregation by age, the vulnerability of the secret is \( 2^{-7.442} = 57.526 \cdot 10^{-4} \), providing the equivalent of 4.450 bits of information over the prior when measured as min-entropy.
These measurements let us reach several conclusions. First, the (environmental) vulnerability of the prior forms a baseline level of security in the authentication system for the users in this experiment. The measurements for age and gender abstractions, on the other hand, gauge the effective security under the pessimistic assumption that users’ age or gender (respectively) can be discovered by an adversary. The complement (strategy vulnerability) of these measurements give the relative importance of keeping these demographics secret. In this case, gender is unimportant, while age encodes a significant amount of a password’s entropy. A system designer should be wary of displaying age on user profiles.
8 Related Work
Our work is mainly motivated by the questions raised by the model of Mardziel et al. [14] for dynamic secrets that evolve over time, and that may vary as the system interacts with its environment. Their model also considers secrets that are generated according to a strategy, and they give an example that an evolving secret subject to repeated observations, in some cases, can be learned faster if it is changed (and observed) more often. They suggest that this effect is related to the lack of randomness within the strategy for generating secrets, but they do not develop a formal measure of that randomness. In [23] the authors take a step further and distinguish between adversary’s and defender’s goals, but they still do not have results about the vulnerability of the strategy itself.
Hyper-distributions were introduced in [20] to model the adversary’s posterior knowledge about the secret (i.e., after an observation of the system is performed). The inners of the hyper are conditional distributions on secrets given each possible observable produced by the system, and the outer is a distribution on the observables. Several other models for QIF have used hypers in a similar way (e.g., [12, 21, 24]), but all of them still model prior knowledge as a single distribution on secrets. Our work models prior knowledge itself as a hyper-distribution, in which the inners are strategies for generating secrets, and the outer is a distribution on strategies.
Several models investigate systems in which secrets are correlated in interactive systems. Some approaches capture interactivity in systems by encoding it as a single “batch job” execution. Desharnais et al. [25], for instance, model the system as a channel matrix of conditional probabilities of whole output traces given whole input traces. O’Neill et al. [26], based on Wittbold and Johnson [27], improve on batch-job models by introducing strategies. The strategy functions of O’Neill et al. are deterministic, whereas ours are probabilistic.
Clark and Hunt [28], following O’Neill et al., investigate a hierarchy of strategies. Stream strategies, at the bottom of the hierarchy, are equivalent to having agents provide all their inputs before system execution as a stream of values. But probabilities are essential for information-theoretic quantification of information flow. Clark and Hunt do not address quantification, instead focusing on the more limited problem of noninterference.
The work of Shokri et al. [29] strives to quantify the privacy of users of location-based services using Markov models and various machine learning techniques for constructing and applying them. Shokri et al.’s work employs two phases, one for learning a model of how a principal’s location could change over time, and one for de-anonymizing subsequently observed, but obfuscated, location information using this model. Our work focuses on information theoretic characterizations of security in such applications, and allows for the quantification of how much information is learned about the strategies themselves.
9 Conclusion
In this paper we generalized the representation of the adversary’s prior knowledge about the secret from a single probability distribution on secrets to an environment, which is a distribution on strategies for generating secrets. This generalization allowed us to derive relevant extensions of the traditional approaches to QIF, including measures of environmental vulnerability, strategy vulnerability, and to disentangle security by strategy and security by aggregation, two concepts usually conflated in traditional approaches to QIF.
We are currently working on the extending the notion of strategies to model secrets that evolve over time, and on the corresponding quantification of strategy leakage when secrets are processed by a system.
Notes
- 1.
To avoid ambiguity, we may use subscripts on distributions, e.g., \(p_{XY}\), \(p_{Y}\) or \(p_{X \mid Y}\).
- 2.
Mappings of priors to hypers are called abstract channels in [12].
- 3.
More precisely, if the vulnerability of a hyper is defined as the expectation of the vulnerability of its inners (as for \(V_{g}\) in Eq. (1)), it respects the data-processing inequality and always yields non-negative leakage iff the vulnerability is convex.
- 4.
Prior systems often also permit public inputs and secret outputs; we leave such generalizations to future work.
- 5.
Given that \(\mathcal {X}\) is finite, we can make \(\mathcal {S}_{\mathcal {X}}\) finite via a discretization that defines an indivisible amount \(\mu \) of probability mass that strategies can allocate among secrets. Any precision in strategies can be achieved by making \(\mu \) as small as needed.
- 6.
In particular, Bayes vulnerability does not: in general \(V^{(Bayes)}(X,Y) \ne V^{(Bayes)}(X){\cdot }V^{(Bayes)}(Y \mid X)\). As an example, consider the joint distribution p on \(\mathcal {X}= \{x_{1},x_{2}\}\) and \(\mathcal {Y}= \{y_{1},y_{2}\}\) s.t.
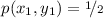 , \(p(x_{2},y_{1}) = 0\), and
, \(p(x_{2},y_{1}) = 0\), and  . Then
. Then 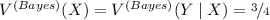 , but
, but 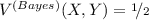 , and the chain rule is not respected.
, and the chain rule is not respected. - 7.
The non-interferent channel \(\overline{0}\) is a column-matrix in which all rows are identical, and for that reason it allows no flow of information from inputs to outputs.
References
Millen, J.K.: Covert channel capacity. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (1987)
McLean, J.: Security models, information flow. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (1990)
Gray III, J.W.: Toward a mathematical foundation for information flow security. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (1991)
Clark, D., Hunt, S., Malacaria, P.: Quantitative analysis of the leakage of confidential data. In: Workshop on Quantitative Aspects of Programming Languages (QAPL) (2001)
Boreale, M.: Quantifying information leakage in process calculi. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 119–131. Springer, Heidelberg (2006). doi:10.1007/11787006_11
Malacaria, P.: Assessing security threats of looping constructs. In: Proceedings of the ACM SIGPLAN Conference on Principles of Programming Languages (POPL) (2007)
Chatzikokolakis, K., Palamidessi, C., Panangaden, P.: Anonymity protocols as noisy channels. Inf. Comput. 206, 378–401 (2008)
Smith, G.: On the foundations of quantitative information flow. In: Alfaro, L. (ed.) FoSSaCS 2009. LNCS, vol. 5504, pp. 288–302. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00596-1_21
Köpf, B., Basin, D.: Automatically deriving information-theoretic bounds for adaptive side-channel attacks. J. Comput. Secur. 19(1), 1–31 (2011)
Boreale, M., Pampaloni, F., Paolini, M.: Asymptotic information leakage under one-try attacks. In: Hofmann, M. (ed.) FoSSaCS 2011. LNCS, vol. 6604, pp. 396–410. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19805-2_27
Alvim, M.S., Andrés, M.E., Palamidessi, C.: Quantitative information flow in interactive systems. J. Comput. Secur. 20(1), 3–50 (2012)
McIver, A., Morgan, C., Smith, G., Espinoza, B., Meinicke, L.: Abstract channels and their robust information-leakage ordering. In: Abadi, M., Kremer, S. (eds.) POST 2014. LNCS, vol. 8414, pp. 83–102. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54792-8_5
Clarkson, M.R., Schneider, F.B.: Quantication of integrity. Math. Struct. Comput. Sci. 25(2), 207–258 (2015)
Mardziel, P., Alvim, M.S., Hicks, M., Clarkson, M.: Quantifying information flow for dynamic secrets. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (2014)
Alvim, M.S., Mardziel, P., Hicks, M.: Quantifying vulnerability of secret generation using hyper-distributions (extended version) (2017). arXiv:1701.04174 [cs.CR]
Chatzikokolakis, K., Palamidessi, C., Panangaden, P.: On the Bayes risk in information-hiding protocols. J. Comput. Secur. 16(5), 531–571 (2008)
Shannon, C.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948)
Massey, J.L.: Guessing, entropy. In: Proceedings of the IEEE International Symposium on Information Theory (ISIT) (1994)
Alvim, M.S., Chatzikokolakis, K., Palamidessi, C., Smith, G.: Measuring information leakage using generalized gain functions. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2012)
McIver, A., Meinicke, L., Morgan, C.: Compositional closure for Bayes risk in probabilistic noninterference. In: Proceedings of the International Colloquium on Automata, Languages and Programming (ICALP) (2014)
Alvim, M.S., Chatzikokolakis, K., McIver, A., Morgan, C., Palamidessi, C., Smith, G.: Axioms for information leakage. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2016)
Vance, A.: If Your Password Is 123456, Just Make It HackMe. http://www.nytimes.com/2010/01/21/technology/21password.html. Accessed 16 Apr 2016
Mardziel, P., Alvim, M.S., Hicks, M.: Adversary gain vs defender loss in quantified information flow. In: Workshop on Foundations of Computer Security (FCS) (2014)
Alvim, M.S., Chatzikokolakis, K., McIver, A., Morgan, C., Palamidessi, C., Smith, G.: Additive, multiplicative notions of leakage, their capacities. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2014)
Desharnais, J., Jagadeesan, R., Gupta, V., Panangaden, P.: The metric analogue of weak bisimulation for probabilistic processes. In: Proceedings of the Conference on Logic in Computer Science (LICS) (2002)
O’Neill, K.R., Clarkson, M.R., Chong, S.: Information-flow security for interactive programs. In: Proceedings of the IEEE Computer Security Foundations Symposium (CSF) (2006)
Wittbold, J.T., Johnson, D.M.: Information flow in nondeterministic systems. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (1990)
Clark, D., Hunt, S.: Non-interference for deterministic interactive programs. In: Degano, P., Guttman, J., Martinelli, F. (eds.) FAST 2008. LNCS, vol. 5491, pp. 50–66. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01465-9_4
Shokri, R., Theodorakopoulos, G., Le Boudec, J.-Y., Hubaux, J.-P.: Quantifying location privacy. In: Proceedings of the IEEE Symposium on Security and Privacy (S&P) (2011)
Acknowledgments
This work was developed with the support of CNPq, CAPES, FAPEMIG, US National Science Foundation grant CNS-1314857, and DARPA and the Air Force Research Laboratory, under agreement numbers FA8750-16-C-0022, FA8750-15-2-0104, and FA8750-15-2-0277. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes not withstanding any copyright notation thereon. The views, opinions, and/or findings expressed are those of the author(s) and should not be interpreted as representing the official views or policies of DARPA, the Air Force Research Laboratory, or the U.S. Government.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Alvim, M.S., Mardziel, P., Hicks, M. (2017). Quantifying Vulnerability of Secret Generation Using Hyper-Distributions. In: Maffei, M., Ryan, M. (eds) Principles of Security and Trust. POST 2017. Lecture Notes in Computer Science(), vol 10204. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54455-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-662-54455-6_2
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54454-9
Online ISBN: 978-3-662-54455-6
eBook Packages: Computer ScienceComputer Science (R0)






 is the environment in which strategies
is the environment in which strategies 
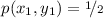 ,
,  . Then
. Then 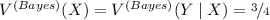 , but
, but 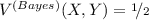 , and the chain rule is not respected.
, and the chain rule is not respected.