Abstract
We introduce AmiCo, a tool that extends a proof assistant, Isabelle/HOL, with flexible function definitions well beyond primitive corecursion. All definitions are certified by the assistant’s inference kernel to guard against inconsistencies. A central notion is that of friends: functions that preserve the productivity of their arguments and that are allowed in corecursive call contexts. As new friends are registered, corecursion benefits by becoming more expressive. We describe this process and its implementation, from the user’s specification to the synthesis of a higher-order definition to the registration of a friend. We show some substantial case studies where our approach makes a difference.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Codatatypes and corecursion are emerging as a major methodology for programming with infinite objects. Unlike in traditional lazy functional programming, codatatypes support total (co)programming [1, 8, 30, 68], where the defined functions have a simple set-theoretic semantics and productivity is guaranteed. The proof assistants Agda [19], Coq [12], and Matita [7] have been supporting this methodology for years.
By contrast, proof assistants based on higher-order logic (HOL), such as HOL4 [64], HOL Light [32], and Isabelle/HOL [56], have traditionally provided only datatypes. Isabelle/HOL is the first of these systems to also offer codatatypes. It took two years, and about 24 000 lines of Standard ML, to move from an understanding of the mathematics [18, 67] to an implementation that automates the process of checking high-level user specifications and producing the necessary corecursion and coinduction theorems [16].
There are important differences between Isabelle/HOL and type theory systems such as Coq in the way they handle corecursion. Consider the codatatype of streams given by

where  (written infix) is the constructor, and
(written infix) is the constructor, and  and
and  are the head and tail selectors, respectively. In Coq, a definition such as
are the head and tail selectors, respectively. In Coq, a definition such as

which introduces the function  , is accepted after a syntactic check that detects the
, is accepted after a syntactic check that detects the  -guardedness of the corecursive call. In Isabelle, this check is replaced by a deeper analysis. The
-guardedness of the corecursive call. In Isabelle, this check is replaced by a deeper analysis. The  command [16] transforms a user specification into a blueprint object: the coalgebra
command [16] transforms a user specification into a blueprint object: the coalgebra  . Then
. Then  is defined as
is defined as  , where
, where  is the fixed primitive corecursive combinator for
is the fixed primitive corecursive combinator for  . Finally, the user specification is derived as a theorem from the definition and the characteristic equation of the corecursor.
. Finally, the user specification is derived as a theorem from the definition and the characteristic equation of the corecursor.
Unlike in type theories, where (co)datatypes and (co)recursion are built-in, the HOL philosophy is to reduce every new construction to the core logic. This usually requires a lot of implementation work but guarantees that definitions introduce no inconsistencies. Since codatatypes and corecursion are derived concepts, there is no a priori restriction on the expressiveness of user specifications other than expressiveness of HOL itself.
Consider a variant of  , where the function
, where the function  adds 1 to each element of a stream:
adds 1 to each element of a stream:

Coq’s syntactic check fails on  . After all,
. After all,  could explore the tail of its argument before it produces a constructor, hence blocking productivity and leading to underspecification or inconsistency.
could explore the tail of its argument before it produces a constructor, hence blocking productivity and leading to underspecification or inconsistency.
Isabelle’s bookkeeping allows for more nuances. Suppose  has been defined as
has been defined as

When analyzing  ’s specification, the
’s specification, the  command synthesizes its definition as a blueprint
command synthesizes its definition as a blueprint  . This definition can then be proved to be friendly, hence acceptable in corecursive call contexts when defining other functions. Functions with friendly definitions are called friendly, or friends. These functions preserve productivity by consuming at most one constructor when producing one.
. This definition can then be proved to be friendly, hence acceptable in corecursive call contexts when defining other functions. Functions with friendly definitions are called friendly, or friends. These functions preserve productivity by consuming at most one constructor when producing one.
Our previous work [17] presented the category theory underlying friends, based on more expressive blueprints than the one shown above for primitive corecursion. We now introduce a tool, AmiCo, that automates the process of applying and incrementally improving corecursion.
To demonstrate AmiCo’s expressiveness and convenience, we used it to formalize eight case studies in Isabelle, featuring a variety of codatatypes and corecursion styles (Sect. 2). A few of these examples required ingenuity and suggest directions for future work. Most of the examples fall in the executable framework of Isabelle, which allows for code extraction to Haskell via Isabelle’s code generator. One of them pushes the boundary of executability, integrating friends in the quantitative world of probabilities.
At the low level, the corecursion state summarizes what the system knows at a given point, including the set of available friends and a corecursor up to friends (Sect. 3). Polymorphism complicates the picture, because some friends may be available only for specific instances of a polymorphic codatatype. To each corecursor corresponds a coinduction principle up to friends and a uniqueness theorem that can be used to reason about corecursive functions. All of the constructions and theorems are derived from first principles, without requiring new axioms or extensions of the logic. This foundational approach prevents the introduction of inconsistencies, such as those that have affected the termination and productivity checkers of Agda and Coq in recent years.
The user interacts with our tool via the following commands to the proof assistant (Sect. 4). The  command defines a function
command defines a function  by extracting a blueprint
by extracting a blueprint  from a user’s specification, defining
from a user’s specification, defining  using
using  and a corecursor, and deriving the original specification from the characteristic property of the corecursor. Moreover,
and a corecursor, and deriving the original specification from the characteristic property of the corecursor. Moreover,  supports mixed recursion–corecursion specifications, exploiting proof assistant infrastructure for terminating (well-founded) recursion. Semantic proof obligations, notably termination, are either discharged automatically or presented to the user. Specifying the
supports mixed recursion–corecursion specifications, exploiting proof assistant infrastructure for terminating (well-founded) recursion. Semantic proof obligations, notably termination, are either discharged automatically or presented to the user. Specifying the  option to
option to  additionally registers
additionally registers  as a friend, enriching the corecursor state. Another command,
as a friend, enriching the corecursor state. Another command,  , registers existing functions as friendly. Friendliness amounts to the relational parametricity [60, 69] of a selected part of the definition [17], which in this paper we call a surface. The tool synthesizes the surface, and the parametricity proof is again either discharged automatically or presented to the user.
, registers existing functions as friendly. Friendliness amounts to the relational parametricity [60, 69] of a selected part of the definition [17], which in this paper we call a surface. The tool synthesizes the surface, and the parametricity proof is again either discharged automatically or presented to the user.
AmiCo is a significant piece of engineering, at about 7 000 lines of Standard ML code (Sect. 5). It subsumes a crude prototype [17] based on a shell script and template files that automated the corecursor derivation but left the blueprint and surface synthesis problems to the user. Our tool is available as part of the official Isabelle2016-1 release. The formalized examples and case studies are provided in an archive [14].
The contributions of this paper are the following:
-
We describe our tool’s design, algorithms, and implementation as a foundational extension of Isabelle/HOL, taking the form of the
 ,
,  and
and  commands and the
commands and the  proof method.
proof method. -
We apply our tool to a wide range of case studies, most of which are either beyond the reach of competing systems or would require type annotations and additional proofs.
More details, including thorough descriptions and proofs of correctness for the surface synthesis algorithm and the mixed recursion–corecursion pipeline, are included in a technical report [15]. Although our tool works for Isabelle, the same methodology is immediately applicable to any prover in the HOL family (including HOL4, HOL Light, HOL Zero [6], and HOL-Omega [34]), whose users represent about half of the proof assistant community. Moreover, a similar methodology is in principle applicable to provers based on type theory, such as Agda, Coq, and Matita (Sect. 6).
Conventions. We recall the syntax relevant for this paper, relying on the standard set-theoretic interpretation of HOL [27].
We fix infinite sets of type variables  and term variables
and term variables  and a higher-order signature, consisting of a set of type constructors including
and a higher-order signature, consisting of a set of type constructors including  and the binary constructors for functions (
and the binary constructors for functions ( ), products (
), products ( ), and sums (+). Types
), and sums (+). Types  are defined using type variables and applying type constructors, normally written postfix. Isabelle /HOL supports Haskell-style type classes, with
are defined using type variables and applying type constructors, normally written postfix. Isabelle /HOL supports Haskell-style type classes, with  expressing class membership (e.g.,
expressing class membership (e.g.,  ).
).
Moreover, we assume a set of polymorphic constants  with declared types, including equality
with declared types, including equality  , left and right product projections
, left and right product projections  and
and  , and left and right sum embeddings
, and left and right sum embeddings  and
and  . Terms t are built from constants
. Terms t are built from constants  and variables x by means of typed
and variables x by means of typed  -abstraction and application. Polymorphic constants and terms will be freely used in contexts that require a less general type.
-abstraction and application. Polymorphic constants and terms will be freely used in contexts that require a less general type.
2 Motivating Examples
We apply AmiCo to eight case studies to demonstrate its benefits—in particular, the flexibility that friends provide and reasoning by uniqueness (of solutions to corecursive equations). The first four examples demonstrate the flexibility that friends provide. The third one also features reasoning by uniqueness. The fourth example crucially relies on a form of nested corecursion where the operator under definition must be recognized as a friend. The fifth through seventh examples mix recursion with corecursion and discuss the associated proof techniques. The last example, about a probabilistic process calculus, takes our tool to its limits: We discuss how to support corecursion through monadic sequencing and mix unbounded recursion with corecursion. All eight formalizations are available online [14], together with our earlier stream examples [17].
Since all examples are taken from the literature, we focus on the formalization with AmiCo. No detailed understanding is needed to see that they fit within the friends framework. Background information can be found in the referenced works.
Remarkably, none of the eight examples work with Coq’s or Matita’s standard mechanisms. Sized types in Agda [4] can cope with the first six but fail on the last two: In one case a function must inspect an infinite list unboundedly deeply, and in the other case the codatatype cannot even be defined in Agda. The Dafny verifier, which also provides codatatypes [46], supports only the seventh case study.
2.1 Coinductive Languages
Rutten [62] views formal languages as infinite tries, i.e., prefix trees branching over the alphabet with boolean labels at the nodes indicating whether the path from the root denotes a word in the language. The type  features corecursion through the right-hand side of the function arrow (
features corecursion through the right-hand side of the function arrow ( ).
).

Traytel [66] has formalized tries in Isabelle using a codatatype, defined regular operations on them as corecursive functions, and proved by coinduction that the defined operations form a Kleene algebra. Because Isabelle offered only primitive corecursion when this formalization was developed, the definition of concatenation, iteration, and shuffle product was tedious, spanning more than a hundred lines.
Corecursion up to friends eliminates this tedium. The following extract from an Isabelle formalization is all that is needed to define the main operations on languages:

Concatenation ( ) and shuffle product (
) and shuffle product ( ) are corecursive up to alternation (+), and iteration (
) are corecursive up to alternation (+), and iteration ( ) is corecursive up to concatenation (
) is corecursive up to concatenation ( ). All four definitions use an alternative
). All four definitions use an alternative  -based syntax for performing corecursion under the right-hand side of
-based syntax for performing corecursion under the right-hand side of  , instead of applying the functorial action
, instead of applying the functorial action  (composition) associated with
(composition) associated with  .
.
The  command is provided by AmiCo, whereas
command is provided by AmiCo, whereas  and
and  (Sect. 3.2) has been part of Isabelle since 2013. The
(Sect. 3.2) has been part of Isabelle since 2013. The  option registers the defined functions as friends and automatically discharges the emerging proof obligations, which ensure that friends consume at most one constructor to produce one constructor.
option registers the defined functions as friends and automatically discharges the emerging proof obligations, which ensure that friends consume at most one constructor to produce one constructor.
Proving equalities on tries conveniently works by coinduction up to congruence (Sect. 3.7). Already before  existence, Traytel was able to write automatic one-line proofs such as
existence, Traytel was able to write automatic one-line proofs such as

The  proof method [16] instantiates the bisimulation witness of the given coinduction rule before applying it backwards. Without
proof method [16] instantiates the bisimulation witness of the given coinduction rule before applying it backwards. Without  , the rule +.coinduct of coinduction up to congruence had to be stated and proved manually, including the manual inductive definition of the congruence closure under +.
, the rule +.coinduct of coinduction up to congruence had to be stated and proved manually, including the manual inductive definition of the congruence closure under +.
Overall, the usage of  compressed Traytel’s development from 750 to 600 lines of Isabelle text. In Agda, Abel [3] has formalized Traytel’s work up to proving the recursion equation
compressed Traytel’s development from 750 to 600 lines of Isabelle text. In Agda, Abel [3] has formalized Traytel’s work up to proving the recursion equation  for iteration (
for iteration ( ) in 219 lines of Agda text, which correspond to 125 lines in our version. His definitions are as concise as ours, but his proofs require more manual steps.
) in 219 lines of Agda text, which correspond to 125 lines in our version. His definitions are as concise as ours, but his proofs require more manual steps.
2.2 Knuth–Morris–Pratt String Matching
Building on the trie view of formal languages, van Laarhoven [44] discovered a concise formulation of the Knuth–Morris–Pratt algorithm [41] for finding one string in another:

Here, we overload the stream constructor  for finite lists;
for finite lists;  and
and  are the selectors. In our context,
are the selectors. In our context,  is the most interesting definition because it corecurses through
is the most interesting definition because it corecurses through  Since there is no constructor guard,
Since there is no constructor guard,  would appear not to be productive. However, the constructor is merely hidden in
would appear not to be productive. However, the constructor is merely hidden in  and can be pulled out by unrolling the definition of
and can be pulled out by unrolling the definition of  as follows.
as follows.
As the first step, we register  defined by
defined by  as a friend, using the
as a friend, using the  command provided by our tool. The registration of an existing function as a friend requires us to supply an equation with a constructor-guarded right-hand side and to prove the equation and the parametricity of the destructor-free part of the right-hand side, called the surface (Sect. 3.4). Then the definition of
command provided by our tool. The registration of an existing function as a friend requires us to supply an equation with a constructor-guarded right-hand side and to prove the equation and the parametricity of the destructor-free part of the right-hand side, called the surface (Sect. 3.4). Then the definition of  corecurses through
corecurses through  Finally, we derive the original specification by unrolling the definition. We can use the derived specification in the proofs, because proofs in HOL do not depend on the actual definition (unlike in type theory).
Finally, we derive the original specification by unrolling the definition. We can use the derived specification in the proofs, because proofs in HOL do not depend on the actual definition (unlike in type theory).

2.3 The Stern–Brocot Tree
The next application involves infinite trees of rational numbers. It is based on Hinze’s work on the Stern–Brocot and Bird trees [33] and the Isabelle formalization by Gammie and Lochbihler [25]. It illustrates reasoning by uniqueness (Sect. 3.7).
The Stern–Brocot tree contains all the rational numbers in their lowest terms. It is an infinite binary tree  of formal fractions
of formal fractions  Each node is labeled with the mediant of its rightmost and leftmost ancestors, where
Each node is labeled with the mediant of its rightmost and leftmost ancestors, where  Gammie and Lochbihler define the tree via an iterative helper function.
Gammie and Lochbihler define the tree via an iterative helper function.

Using AmiCo, we can directly formalize Hinze’s corecursive specification of the tree, where  and
and  The tree is corecursive up to the two friends
The tree is corecursive up to the two friends  and
and 

Without the iterative detour, the proofs, too, become more direct as the statements need not be generalized for the iterative helper function. For example, Hinze relies on the uniqueness principle to show that a loopless linearization  of the tree yields Dijkstra’s
of the tree yields Dijkstra’s  function [23] given by
function [23] given by

where all arithmetic operations are lifted to streams elementwise—e.g.,  zips two streams. We define
zips two streams. We define  and
and  as follows. To avoid the mutual corecursion, we inline
as follows. To avoid the mutual corecursion, we inline  in
in  for the definition with
for the definition with  after having registered the arithmetic operations as friends:
after having registered the arithmetic operations as friends:

Hinze proves that  equals
equals  by showing that both satisfy the corecursion equation
by showing that both satisfy the corecursion equation  where
where  This equation yields the loopless algorithm, because
This equation yields the loopless algorithm, because  satisfies it as well, where
satisfies it as well, where  is defined by
is defined by

Our tool generates a proof rule for uniqueness of solutions to the recursion equation (Sect. 3.7). We conduct the equivalence proofs using this rule.
For another example, all rational numbers also occur in the Bird tree given by

It satisfies  , where
, where  corecursively swaps all subtrees. Again, we prove this identity by showing that both sides satisfy the corecursion equation
corecursively swaps all subtrees. Again, we prove this identity by showing that both sides satisfy the corecursion equation  This equation does not correspond to any function defined with
This equation does not correspond to any function defined with  but we can derive its uniqueness principle using our proof method
but we can derive its uniqueness principle using our proof method  without defining the function. The Isabelle proof is quite concise:
without defining the function. The Isabelle proof is quite concise:

No coinduction is needed: The identities are proved by expanding the definitions a finite number of times (once each here). We also show that  by uniqueness, where
by uniqueness, where  swaps the subtrees only at levels of odd depth.
swaps the subtrees only at levels of odd depth.
Gammie and Lochbihler manually derive each uniqueness rule using a separate coinduction proof. For  alone, the proof requires 25 lines. With AmiCo’s
alone, the proof requires 25 lines. With AmiCo’s  proof method, such proofs are automatic.
proof method, such proofs are automatic.
2.4 Breadth-First Tree Labeling
Abel and Pientka [4] demonstrate the expressive power of sized types in Agda with the example of labeling the nodes of an infinite binary tree in breadth-first order, which they adapted from Jones and Gibbons [39]. The function  takes a stream of streams of labels as input and labels the nodes at depth i according to a prefix of the ith input stream. It also outputs the streams of unused labels. Then
takes a stream of streams of labels as input and labels the nodes at depth i according to a prefix of the ith input stream. It also outputs the streams of unused labels. Then  ties the knot by feeding the unused labels back into
ties the knot by feeding the unused labels back into 

Because  returns a pair, we define the two projections separately and derive the original specification for
returns a pair, we define the two projections separately and derive the original specification for  trivially from the definitions. One of the corecursive calls to
trivially from the definitions. One of the corecursive calls to  occurs in the context of
occurs in the context of  itself—it is “self-friendly” (Sect. 4.2).
itself—it is “self-friendly” (Sect. 4.2).

For comparison, Abel’s and Pientka’s formalization in Agda is of similar size, but the user must provide some size hints for the corecursive calls.
2.5 Stream Processors
Stream processors are a standard example of mixed fixpoints:

When defining functions on these objects, we previously had to break them into a recursive and a corecursive part, using Isabelle’s  command for the latter [16]. Since our tool supports mixed recursion–corecursion, we can now express functions on stream processors more directly.
command for the latter [16]. Since our tool supports mixed recursion–corecursion, we can now express functions on stream processors more directly.
We present two functions. The first one runs a stream processor:

The second function,  composes two stream processors:
composes two stream processors:

The selector  in the noncorecursive friend
in the noncorecursive friend  is legal, because
is legal, because  also adds a constructor. In both cases, the
also adds a constructor. In both cases, the  command emits a termination proof obligation, which we discharged in two lines, using the same techniques as when defining recursive functions. This command is equivalent to
command emits a termination proof obligation, which we discharged in two lines, using the same techniques as when defining recursive functions. This command is equivalent to  , except that it lets the user discharge proof obligations instead of applying some standard proof automation.
, except that it lets the user discharge proof obligations instead of applying some standard proof automation.
2.6 A Calculator
Next, we formalize a calculator example by Hur et al. [37]. The calculator inputs a number, computes the double of the sum of all inputs, and outputs the current value of the sum. When the input is 0, the calculator counts down to 0 and starts again. Hur et al. implement two versions,  and
and  in a programming language embedded deeply in Coq and prove that
in a programming language embedded deeply in Coq and prove that  simulates
simulates  using parameterized coinduction.
using parameterized coinduction.
We model the calculator in a shallow fashion as a function from the current sum to a stream processor for  s. Let
s. Let  abbreviate
abbreviate  We can write the program directly as a function and very closely to its specification [37, Fig. 2]. In
We can write the program directly as a function and very closely to its specification [37, Fig. 2]. In  and
and  the corecursion goes through the friends
the corecursion goes through the friends  and
and  and the constructor guard is hidden in the abbreviation
and the constructor guard is hidden in the abbreviation 

Our task is to prove that  simulates
simulates  In fact, the two can even be proved to be bisimilar. In our shallow embedding, bisimilarity coincides with equality. We can prove
In fact, the two can even be proved to be bisimilar. In our shallow embedding, bisimilarity coincides with equality. We can prove  by coinduction with the rule generated for the friends
by coinduction with the rule generated for the friends  and
and 
2.7 Lazy List Filtering
A classic example requiring a mix of recursion and corecursion is filtering on lazy lists. Given the polymorphic type of lazy lists

the task is to define the function  that retains only the elements that satisfy the given predicate. Paulson [58] defined
that retains only the elements that satisfy the given predicate. Paulson [58] defined  using an inductive search predicate. His development culminates in a proof of
using an inductive search predicate. His development culminates in a proof of

In Dafny, Leino [45] suggests a definition that mixes recursion and corecursion. We can easily replicate Leino’s definition in Isabelle, where  converts lazy lists to sets:
converts lazy lists to sets:

The nonexecutability of the infinite  quantifier in the ‘if’ condition is unproblematic in HOL, which has no built-in notion of computation. Lochbihler and Hölzl [48] define
quantifier in the ‘if’ condition is unproblematic in HOL, which has no built-in notion of computation. Lochbihler and Hölzl [48] define  as a least fixpoint in the prefix order on
as a least fixpoint in the prefix order on  Using five properties, they substantiate that fixpoint induction leads to shorter proofs than Paulson’s approach.
Using five properties, they substantiate that fixpoint induction leads to shorter proofs than Paulson’s approach.
We show how to prove three of their properties using our definition, namely (1) and


We start with (2). We prove the interesting direction,  , by induction on
, by induction on  where the inductive cases are solved automatically. For (3), the
where the inductive cases are solved automatically. For (3), the  direction is also a simple induction on
direction is also a simple induction on  The other direction requires two nested inductions: first on
The other direction requires two nested inductions: first on  and then a well-founded induction on the termination argument for the recursion in
and then a well-founded induction on the termination argument for the recursion in  Finally, we prove (1) using the uniqueness principle. We first derive the uniqueness rule for
Finally, we prove (1) using the uniqueness principle. We first derive the uniqueness rule for  by a coinduction with a nested induction; this approach reflects the mixed recursive-corecursive definition of
by a coinduction with a nested induction; this approach reflects the mixed recursive-corecursive definition of  which nests recursion inside corecursion.
which nests recursion inside corecursion.

(Our tool does not yet generate uniqueness rules for mixed recursive–corecursive definitions.) Then the proof of (1) is automatic:

Alternatively, we could have proved (1) by coinduction with a nested induction on the termination argument. The uniqueness principle works well because it incorporates both the coinduction and the induction. This underlines that uniqueness can be an elegant proof principle for mixed recursive–corecursive definitions, despite being much weaker than coinduction in the purely corecursive case. Compared with Lochbihler and Hölzl’s proofs by fixpoint induction, our proofs are roughly of the same length, but  eliminates the need for the lengthy setup for the domain theory.
eliminates the need for the lengthy setup for the domain theory.
2.8 Generative Probabilistic Values
Our final example relies on a codatatype that fully exploits Isabelle’s modular datatype architecture built on bounded natural functors (Sect. 3.1) and that cannot be defined easily, if at all, in other systems. This example is covered in more detail in the report [15].
Lochbihler [47] proposes generative probabilistic values (GPVs) as a semantic domain for probabilistic input–output systems. Conceptually, each GPV chooses probabilistically between failing, terminating with a result of type  and continuing by producing an output
and continuing by producing an output  and transitioning into a reactive probabilistic value (RPV), which waits for a response
and transitioning into a reactive probabilistic value (RPV), which waits for a response  of the environment before moving to the generative successor state. Lochbihler models GPVs as a codatatype
of the environment before moving to the generative successor state. Lochbihler models GPVs as a codatatype  He also defines a monadic language on GPVs similar to a coroutine monad and an operation
He also defines a monadic language on GPVs similar to a coroutine monad and an operation  for composing GPVs with environment converters. The definition of
for composing GPVs with environment converters. The definition of  poses two challenges. First, it corecurses through the monadic sequencing operation
poses two challenges. First, it corecurses through the monadic sequencing operation  Due to HOL restrictions, all type variables in a friend’s signature must show up in the resulting codatatype, which is not the case for
Due to HOL restrictions, all type variables in a friend’s signature must show up in the resulting codatatype, which is not the case for  To work around this, we define a copy
To work around this, we define a copy  with a phantom type parameter
with a phantom type parameter  register
register  as a friend, and define
as a friend, and define  in terms of its copy on
in terms of its copy on  Second,
Second,  recurses in a non-well-founded manner through the environment converter. Since our tool supports only mixing with well-founded recursion, we mimic the tool’s internal behavior using a least fixpoint operator.
recurses in a non-well-founded manner through the environment converter. Since our tool supports only mixing with well-founded recursion, we mimic the tool’s internal behavior using a least fixpoint operator.
Initially, Lochbihler had manually derived the coinduction rule up to  which our tool now generates. However, because of the copied type, our reformulation ended up roughly as complicated as the original. Moreover, we noted that coinduction up to congruence works only for equality; for user-defined predicates (e.g., typing judgments), the coinduction rule must still be derived manually. But even though this case study is not conclusive, it demonstrates the flexibility of the framework.
which our tool now generates. However, because of the copied type, our reformulation ended up roughly as complicated as the original. Moreover, we noted that coinduction up to congruence works only for equality; for user-defined predicates (e.g., typing judgments), the coinduction rule must still be derived manually. But even though this case study is not conclusive, it demonstrates the flexibility of the framework.
3 The Low Level: Corecursor States
Starting from the primitive corecursor provided by Isabelle [16], our tool derives corecursors up to larger and larger sets of friends. The corecursion state includes the set of friends  and the corecursor
and the corecursor  . Four operations manipulate states:
. Four operations manipulate states:
-
Base gives the first nonprimitive corecursor by registering the first friends—the constructors (Sect. 3.3);
-
Step incorporates a new friend into the corecursor (Sect. 3.4);
-
Merge combines two existing sets of friends (Sect. 3.5);
-
Instantiate specializes the corecursor type (Sect. 3.6).
The operations Base and Step have already been described in detail and with many examples in our previous paper [17]. Here, we give a brief, self-contained account of them. Merge and Instantiate are new operations whose need became apparent in the course of implementation.
3.1 Bounded Natural Functors
The mathematics behind our tool assumes that the considered type constructors are both functors and relators, that they include basic functors such as identity, constant, sum, and product, and that they are closed under least and greatest fixpoints (initial algebras and final coalgebras). The tool satisfies this requirement by employing Isabelle’s infrastructure for bounded natural functors (BNFs) [16, 67]. For example, the codatatype  is defined as the greatest solution to the fixpoint equation
is defined as the greatest solution to the fixpoint equation  , where both the right-hand side
, where both the right-hand side  and the resulting type
and the resulting type  are BNFs.
are BNFs.
BNFs have both a functor and a relator structure. If  is a unary type constructor, we assume the existence of polymorphic constants for the functorial action, or map function,
is a unary type constructor, we assume the existence of polymorphic constants for the functorial action, or map function,  and the relational action, or relator,
and the relational action, or relator,  , and similarly for n-ary type constructors. For finite lists,
, and similarly for n-ary type constructors. For finite lists,  is the familiar map function, and given a relation r,
is the familiar map function, and given a relation r,  relates two lists of the same length and with r-related elements positionwise. While the BNFs are functors on their covariant positions, the relator structure covers contravariant positions as well.
relates two lists of the same length and with r-related elements positionwise. While the BNFs are functors on their covariant positions, the relator structure covers contravariant positions as well.
We assume that some of the polymorphic constants are known to be (relationally) parametric in some type variables, in the standard sense [60]. For example, if  is a ternary relator and
is a ternary relator and  , then
, then  is parametric in
is parametric in  if
if  holds for all
holds for all  . In a slight departure from standard practice, if a term does not depend on a type variable
. In a slight departure from standard practice, if a term does not depend on a type variable  , we consider it parametric in
, we consider it parametric in  . The map function of a BNF is parametric in all its type variables. By contrast,
. The map function of a BNF is parametric in all its type variables. By contrast,  is not parametric in
is not parametric in  .
.
3.2 Codatatypes and Primitive Corecursion
We fix a codatatype  . In general,
. In general,  may depend on some type variables, but we leave this dependency implicit for now. While
may depend on some type variables, but we leave this dependency implicit for now. While  also may have multiple, curried constructors, it is viewed at the low level as a codatatype with a single constructor
also may have multiple, curried constructors, it is viewed at the low level as a codatatype with a single constructor  and a destructor
and a destructor  :
:

The mutually inverse constructor and destructor establish the isomorphism between  and
and  . For streams, we have
. For streams, we have  ,
,  , and
, and  . Low-level constructors and destructors combine several high-level constructors and destructors in one constant each. Internally, the
. Low-level constructors and destructors combine several high-level constructors and destructors in one constant each. Internally, the  command works on the low level, providing the high-level constructors as syntactic sugar [16].
command works on the low level, providing the high-level constructors as syntactic sugar [16].
In addition, the  command derives a primitive corecursor
command derives a primitive corecursor  characterized by the equation
characterized by the equation  . The
. The  command, provided by Isabelle, reduces a primitively corecursive specification to a plain, acyclic definition expressed using this corecursor.
command, provided by Isabelle, reduces a primitively corecursive specification to a plain, acyclic definition expressed using this corecursor.
3.3 Corecursion up to Constructors
We call blueprints the arguments passed to corecursors. When defining a corecursive function  , a blueprint for
, a blueprint for  is produced, and
is produced, and  is defined as the corecursor applied to the blueprint. The expressiveness of a corecursor is indicated by the codomain of its blueprint argument. The blueprint passed to the primitive corecursor must return an
is defined as the corecursor applied to the blueprint. The expressiveness of a corecursor is indicated by the codomain of its blueprint argument. The blueprint passed to the primitive corecursor must return an  value—e.g., a pair
value—e.g., a pair  for streams of natural numbers. The remaining corecursion structure is fixed: After producing m, we proceed corecursively with x. We cannot produce two numbers before proceeding corecursively—to do so, the blueprint would have to return
for streams of natural numbers. The remaining corecursion structure is fixed: After producing m, we proceed corecursively with x. We cannot produce two numbers before proceeding corecursively—to do so, the blueprint would have to return  .
.
Our first strengthening of the corecursor allows an arbitrary number of constructors before proceeding corecursively. This process takes a codatatype  and produces an initial corecursion state
and produces an initial corecursion state  , where
, where  is a set of known friends,
is a set of known friends,  is a BNF that incorporates the type signatures of known friends, and
is a BNF that incorporates the type signatures of known friends, and  is a corecursor. We omit the set-of-friends index whenever it is clear from the context. The initial state knows only one friend,
is a corecursor. We omit the set-of-friends index whenever it is clear from the context. The initial state knows only one friend,  .
.

Let us define the type  used for the corecursor. First, we let
used for the corecursor. First, we let  be the free monad of
be the free monad of  extended with
extended with  -constant leaves:
-constant leaves:

Inhabitants of  are (formal) expressions built from variable or constant leaf nodes (
are (formal) expressions built from variable or constant leaf nodes ( or
or  ) and a syntactic representation of the constants in
) and a syntactic representation of the constants in  . Writing
. Writing  for
for  , we can build expressions such as
, we can build expressions such as  and
and  . The type
. The type  , of guarded expressions, is similar to
, of guarded expressions, is similar to  , except that it requires at least one
, except that it requires at least one  guard on every path to a
guard on every path to a  . Formally,
. Formally,  is defined as
is defined as  , so that
, so that  marks the guards. To simplify notation, we will pretend that
marks the guards. To simplify notation, we will pretend that  .
.
Guarded variable leaves represent corecursive calls. Constant leaves allow us to stop the corecursion with an immediate result of type  . The polymorphism of
. The polymorphism of  is crucial. If we instantiate
is crucial. If we instantiate  to
to  , we can evaluate formal expressions with the function
, we can evaluate formal expressions with the function  given by
given by  ,
,  , and
, and  . We also write
. We also write  for other versions of the operator (e.g., for
for other versions of the operator (e.g., for  ).
).
The corecursor’s argument, the blueprint, returns guarded expressions consisting of one or more applications of  before proceeding corecursively. Proceeding corecursively means applying the corecursor to all variable leaves and evaluating the resulting expression. Formally:
before proceeding corecursively. Proceeding corecursively means applying the corecursor to all variable leaves and evaluating the resulting expression. Formally:

3.4 Adding New Friends
Corecursors can be strengthened to allow friendly functions to surround the context of the corecursive call. At the low level, we consider only uncurried functions.
A function  is friendly if it consumes at most one constructor before producing at least one constructor. Friendliness is captured by a mixture of two syntactic constraints and the semantic requirement of parametricity of a certain term, called the surface. The syntactic constraints amount to requiring that
is friendly if it consumes at most one constructor before producing at least one constructor. Friendliness is captured by a mixture of two syntactic constraints and the semantic requirement of parametricity of a certain term, called the surface. The syntactic constraints amount to requiring that  is expressible using
is expressible using  , irrespective of its actual definition.
, irrespective of its actual definition.
Specifically,  must be equal to
must be equal to  for some blueprint
for some blueprint  that has the guarding constructor at the outermost position, and this object must be decomposable as
that has the guarding constructor at the outermost position, and this object must be decomposable as  for some
for some  . The convolution operator
. The convolution operator  combines two functions
combines two functions  and
and  .
.
We call s the surface of  because it captures
because it captures  ’s superficial layer while abstracting the application of the destructor. The surface s is more polymorphic than needed by the equation it has to satisfy. Moreover, s must be parametric in
’s superficial layer while abstracting the application of the destructor. The surface s is more polymorphic than needed by the equation it has to satisfy. Moreover, s must be parametric in  . The decomposition, together with parametricity, ensures that friendly functions apply
. The decomposition, together with parametricity, ensures that friendly functions apply  at most once to their arguments and do not look any deeper—the “consumes at most one constructor” property.
at most once to their arguments and do not look any deeper—the “consumes at most one constructor” property.

The return type of blueprints corresponding to  is
is  , where
, where  extends
extends  with
with  . The type
. The type  allows all guarded expressions of the previous corecursor but may also refer to
allows all guarded expressions of the previous corecursor but may also refer to  . The syntactic representations
. The syntactic representations  of old friends
of old friends  must be lifted to the type
must be lifted to the type  , which is straightforward. In the sequel, we will reuse the notation
, which is straightforward. In the sequel, we will reuse the notation  for the lifted syntactic representations. In addition to
for the lifted syntactic representations. In addition to  , new expressions are allowed to freely use the syntactic representation
, new expressions are allowed to freely use the syntactic representation  of the new friend
of the new friend  , defined as
, defined as  . Like for
. Like for  , we have
, we have  . As before, we have
. As before, we have  .
.
Consider the corecursive specification of pointwise addition on streams of numbers, where  is
is  and
and  :
:

To make sense of this specification, we take  to be
to be  and define
and define  as
as  , where the blueprint
, where the blueprint  is
is

To register  as friendly, we must decompose
as friendly, we must decompose  as
as  . Expanding the definition of
. Expanding the definition of  , we get
, we get

It is easy to see that the following term is a suitable surface s:

In Sect. 4, we give more details on how the system synthesizes blueprints and surfaces.
3.5 Merging Corecursion States
Most formalizations are not linear. A module may import several other modules, giving rise to a directed acyclic graph of dependencies. We can reach a situation where the codatatype has been defined in module A; its corecursor has been extended with two different sets of friends  and
and  in modules B and C, each importing A; and finally module D, which imports B and C, requires a corecursor that mixes friends from
in modules B and C, each importing A; and finally module D, which imports B and C, requires a corecursor that mixes friends from  and
and  . To support this scenario, we need an operation that merges two corecursion states.
. To support this scenario, we need an operation that merges two corecursion states.

The return type of blueprints for  is
is  , where
, where  is the sum of the two input signatures
is the sum of the two input signatures  and
and  . By lifting the syntactic representations of old friends using overloading, we establish the invariant that for each
. By lifting the syntactic representations of old friends using overloading, we establish the invariant that for each  of a corecursor state, there is a syntactic representation
of a corecursor state, there is a syntactic representation  . The function
. The function  is then defined in the usual way and constitutes the main ingredient in the definition of
is then defined in the usual way and constitutes the main ingredient in the definition of  with the usual characteristic equation. For operations
with the usual characteristic equation. For operations  , two syntactic representations are available; we arbitrarily choose the one inherited from
, two syntactic representations are available; we arbitrarily choose the one inherited from 
3.6 Type Instantiation
We have so far ignored the potential polymorphism of  . Consider
. Consider  . The operations on corecursor states allow friends of type
. The operations on corecursor states allow friends of type  but not
but not  . To allow friends for
. To allow friends for  , we must keep track of specialized corecursors. First, we need an operation for instantiating corecursor states.
, we must keep track of specialized corecursors. First, we need an operation for instantiating corecursor states.

Once we have derived a specific corecursor for  , we can extend it with friends of type
, we can extend it with friends of type  . Such friends cannot be added to the polymorphic corecursor, but the other direction works: Any friend of a polymorphic corecursor is also a friend of a specialized corecursor. Accordingly, we maintain a Pareto optimal subset of corecursor state instances
. Such friends cannot be added to the polymorphic corecursor, but the other direction works: Any friend of a polymorphic corecursor is also a friend of a specialized corecursor. Accordingly, we maintain a Pareto optimal subset of corecursor state instances  , where
, where  denotes that the type
denotes that the type  can be obtained from the type
can be obtained from the type  by applying a type substitution.
by applying a type substitution.
More specific corecursors are stored only if they have more friends: For each pair of corecursor instances for  and
and  contained in the Pareto set, we have
contained in the Pareto set, we have  whenever
whenever  . All the corecursors in the Pareto set are kept up to date. If we add a friend to a corecursor instance for
. All the corecursors in the Pareto set are kept up to date. If we add a friend to a corecursor instance for  from the set via Step, it is also propagated to all instances
from the set via Step, it is also propagated to all instances  of
of  by applying Instantiate to the output of Step and combining the result with the existing corecursor state for
by applying Instantiate to the output of Step and combining the result with the existing corecursor state for  via Merge. When analyzing a user specification,
via Merge. When analyzing a user specification,  selects the most specific applicable corecursor.
selects the most specific applicable corecursor.
Eagerly computing the entire Pareto set is exponentially expensive. Consider a codatatype  and the friends
and the friends  for
for  ,
,  for
for  , and
, and  for
for  . The set would contain eight corecursors, each with a different subset of
. The set would contain eight corecursors, each with a different subset of  as friends. To avoid such an explosion, we settle for a lazy derivation strategy. In the above example, the corecursor for
as friends. To avoid such an explosion, we settle for a lazy derivation strategy. In the above example, the corecursor for  , with
, with  as friends, is derived only if a definition needs it.
as friends, is derived only if a definition needs it.
3.7 Reasoning Principles
The primary activity of a working formalizer is to develop proofs. To conveniently reason about nonprimitively corecursive functions,  provides two reasoning principles: coinduction up to congruence and a uniqueness theorem.
provides two reasoning principles: coinduction up to congruence and a uniqueness theorem.
Coinduction up to Congruence. Codatatypes are equipped with a coinduction principle. Coinduction reduces the task of proving equality between two inhabitants l and r of a codatatype to the task of exhibiting a relation R which relates l and r and is closed under application of destructors. A relation closed under destructors is called a bisimulation. The  command derives a plain coinduction rule. The rule for
command derives a plain coinduction rule. The rule for  follows:
follows:

To reason about functions that are corecursive up to a set of friends, a principle of coinduction up to congruence of friends is crucial. For a corecursor with friends  , our tool derives a rule that is identical to the standard rule except with
, our tool derives a rule that is identical to the standard rule except with  instead of
instead of  , where
, where  denotes the congruence closure of the relation R with respect to the friendly operations
denotes the congruence closure of the relation R with respect to the friendly operations  .
.
After registering a binary  on
on  as friendly, the introduction rules for the inductively defined congruence closure include
as friendly, the introduction rules for the inductively defined congruence closure include

Since the tool maintains a set of incomparable corecursors, there is also a set of coinduction principles and a set of sets of introduction rules. The  command orders the set of coinduction principles by increasing generality, which works well with Isabelle’s philosophy of applying the first rule that matches.
command orders the set of coinduction principles by increasing generality, which works well with Isabelle’s philosophy of applying the first rule that matches.
In some circumstances, it may be necessary to reason about the union of friends associated with several incomparable corecursors. To continue with the example from Sect. 3.6, suppose we want to prove a formula about  by coinduction up to
by coinduction up to  before the corresponding corecursor has been derived. Users can derive it and the associated coinduction principle by invoking a dedicated command:
before the corresponding corecursor has been derived. Users can derive it and the associated coinduction principle by invoking a dedicated command:

Uniqueness Principles. It is sometimes possible to achieve better automation by employing a more specialized proof method than coinduction. Uniqueness principles exploit the property that the corecursor is the unique solution to a fixpoint equation:

This rule can be seen as a less powerful version of coinduction, where the bisimulation relation has been preinstantiated. In category-theoretic terms, the existence and uniqueness of a solution means that we maintain on  a completely iterative algebra [51] (whose signature is gradually incremented with each additional friend).
a completely iterative algebra [51] (whose signature is gradually incremented with each additional friend).
For concrete functions defined with  , uniqueness rules can be made even more precise by instantiating the blueprint
, uniqueness rules can be made even more precise by instantiating the blueprint  . For example, the pointwise addition on streams from Sect. 3.4
. For example, the pointwise addition on streams from Sect. 3.4

yields the following uniqueness principle:

Reasoning by uniqueness is not restricted to functions defined with  . Suppose
. Suppose  is an arbitrary term depending on a list of free variables
is an arbitrary term depending on a list of free variables  . The
. The  proof method, also provided by our tool, transforms proof obligations of the form
proof method, also provided by our tool, transforms proof obligations of the form

into  . The higher-order functional H must be such that the equation
. The higher-order functional H must be such that the equation  would be a valid
would be a valid  specification (but without nested calls to h or unguarded calls). Internally,
specification (but without nested calls to h or unguarded calls). Internally,  extracts the blueprint
extracts the blueprint  from
from  as if it would define h with
as if it would define h with  and uses the uniqueness principle for
and uses the uniqueness principle for  instantiated with
instantiated with  to achieve the described transformation.
to achieve the described transformation.
4 The High Level: From Commands to Definitions
AmiCo’s two main commands  (Sect. 4.1) and
(Sect. 4.1) and  (Sect. 4.2) introduce corecursive functions and register friends. We describe synthesis algorithms for any codatatype as implemented in the tool. We also show how to capture the “consumes at most one constructor, produces at least one constructor” contract of friends.
(Sect. 4.2) introduce corecursive functions and register friends. We describe synthesis algorithms for any codatatype as implemented in the tool. We also show how to capture the “consumes at most one constructor, produces at least one constructor” contract of friends.
4.1 Defining Corecursive Functions
The  command reduces the user’s corecursive equation to non(co)recursive primitives, so as to guard against inconsistencies. To this end, the command engages in a chain of definitions and proofs. Recall the general context:
command reduces the user’s corecursive equation to non(co)recursive primitives, so as to guard against inconsistencies. To this end, the command engages in a chain of definitions and proofs. Recall the general context:
-
The codatatype
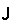 is defined as a fixpoint of a type constructor
is defined as a fixpoint of a type constructor 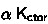 equipped with constructor
equipped with constructor 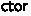 and destructor
and destructor  .
. -
The current set of friends
 contains
contains  and has a signature
and has a signature 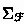 (or
(or 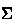 ). Each friend
). Each friend 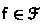 of type
of type 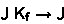 has a companion syntactic expression
has a companion syntactic expression 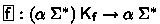 .
. -
The corecursor up to
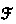 is
is  .
.
In general,  may be polymorphic and
may be polymorphic and  may take more than one argument, but these are minor orthogonal concerns here. As before, we write
may take more than one argument, but these are minor orthogonal concerns here. As before, we write  for the type of formal expressions built from
for the type of formal expressions built from  -leaves and friend symbols
-leaves and friend symbols  , and
, and  for
for  -guarded formal expressions. For
-guarded formal expressions. For  , we can evaluate the formal expressions into elements of
, we can evaluate the formal expressions into elements of  , by replacing each
, by replacing each  with
with  and omitting the
and omitting the  and
and  constructors. Finally, we write
constructors. Finally, we write  for the evaluation functions of various types of symbolic expressions to
for the evaluation functions of various types of symbolic expressions to  .
.
Consider the command

where  is a term that may refer to
is a term that may refer to  and x. The first task of
and x. The first task of  is to synthesize a blueprint object
is to synthesize a blueprint object  such that
such that

holds for all  . This equation states that the synthesized blueprint must produce, by evaluation, the concrete right-hand side of the user equation. The unknown function h represents corecursive calls, which will be instantiated to
. This equation states that the synthesized blueprint must produce, by evaluation, the concrete right-hand side of the user equation. The unknown function h represents corecursive calls, which will be instantiated to  once
once  is defined. To the occurrences of h in
is defined. To the occurrences of h in  correspond occurrences of
correspond occurrences of  in b.
in b.
Equipped with a blueprint, we define  and derive the user equation:
and derive the user equation:

Blueprint Synthesis. The blueprint synthesis proceeds by a straightforward syntactic analysis, similar to the one used for primitive corecursion [16]. We illustrate it with an example. Consider the definition of  from Sect. 3.4. Ignoring currying, the function has type
from Sect. 3.4. Ignoring currying, the function has type  , with
, with  . The term
. The term  is synthesized by processing the right-hand side of the corecursive equation for
is synthesized by processing the right-hand side of the corecursive equation for  . After removing the syntactic sugar, we obtain the following term, highlighting the corecursive call:
. After removing the syntactic sugar, we obtain the following term, highlighting the corecursive call:

The blueprint is derived from this term by replacing the constructor guard  and the friends with their syntactic counterparts and the corecursive call with a variable leaf:
and the friends with their syntactic counterparts and the corecursive call with a variable leaf:

Synthesis will fail if after the indicated replacements the result does not have the desired type (here,  ). If we omit ‘
). If we omit ‘ ’ in the definition, the type of b becomes
’ in the definition, the type of b becomes  , reflecting the lack of a guard. Another cause of failure is the presence of unfriendly operators in the call context. Once
, reflecting the lack of a guard. Another cause of failure is the presence of unfriendly operators in the call context. Once  has been produced,
has been produced,  proves that
proves that  satisfies the user equation we started with.
satisfies the user equation we started with.
Mixed Recursion–Corecursion. If a self-call is not guarded,  still gives it a chance, since it could be a terminating recursive call. As an example, the following definition computes all the odd numbers greater than 1 arising in the Collatz sequence:
still gives it a chance, since it could be a terminating recursive call. As an example, the following definition computes all the odd numbers greater than 1 arising in the Collatz sequence:

The highlighted call is not guarded. Yet, it will eventually lead to a guarded call, since repeatedly halving a positive even number must at some point yield an odd number. The unguarded call yields a recursive specification of the blueprint  , which is resolved automatically by the termination prover.
, which is resolved automatically by the termination prover.
By writing  instead of
instead of  , the user takes responsibility for proving termination. A manual proof was necessary for
, the user takes responsibility for proving termination. A manual proof was necessary for  in Sect. 2.7, whose blueprint satisfies the recursion
in Sect. 2.7, whose blueprint satisfies the recursion

Termination is shown by providing a suitable well-founded relation, which exists because  is closer than
is closer than  to the next element that satisfies the predicate P.
to the next element that satisfies the predicate P.
Like the corecursive calls, the recursive calls may be surrounded only by friendly operations (or by parametric operators such as ‘case’, ‘if’, and ‘let’). Thus, the following specification is rejected—and rightly so, since the unfriendly  cancels the corecursive guard that is reached when recursion terminates.
cancels the corecursive guard that is reached when recursion terminates.

4.2 Registering New Friendly Operations
The command

defines  and registers it as a friend. The domain is viewed abstractly as a type constructor
and registers it as a friend. The domain is viewed abstractly as a type constructor  applied to the codatatype
applied to the codatatype  .
.
The command first synthesizes the blueprint  , similarly to the case of plain corecursive definitions. However, this time the type \(\Sigma \) is not
, similarly to the case of plain corecursive definitions. However, this time the type \(\Sigma \) is not  , but
, but  . Thus,
. Thus,  mixes freely the type
mixes freely the type  with the components
with the components  of
of  , which caters for self-friendship (as in the
, which caters for self-friendship (as in the  example from Sect. 2.4):
example from Sect. 2.4):  can be defined making use of itself as a friend (in addition to the already registered friends).
can be defined making use of itself as a friend (in addition to the already registered friends).
The next step is to synthesize a surface s from the blueprint  . Recall from Sect. 3.4 that a corecursively defined operator is friendly if its blueprint
. Recall from Sect. 3.4 that a corecursively defined operator is friendly if its blueprint  can be decomposed as
can be decomposed as  , where
, where  is parametric in
is parametric in  .
.
Once the surface s has been synthesized, proved parametric, and proved to be in the desired relationship with b, the tool invokes the Step operation (Sect. 3.4), enriching the corecursion state with the function defined by  as a new friend, called
as a new friend, called  .
.
Alternatively, users can register arbitrary functions as friends:

The user must then prove the equation  . The command extracts a blueprint from it and proceeds with the surface synthesis in the same way as
. The command extracts a blueprint from it and proceeds with the surface synthesis in the same way as 

Surface Synthesis Algorithm. The synthesis of the surface from the blueprint proceeds by the context-dependent replacement of some constants with terms. AmiCo performs the replacements in a logical-relation fashion, guided by type inference.
We start with  and need to synthesize
and need to synthesize  such that s is parametric in
such that s is parametric in  and
and  . We traverse
. We traverse  recursively and collect context information about the appropriate replacements. The technical report describes the algorithm in detail. Here, we illustrate it on an example.
recursively and collect context information about the appropriate replacements. The technical report describes the algorithm in detail. Here, we illustrate it on an example.
Consider the definition of a function that interleaves a nonempty list of streams:

Here,  is the type of nonempty lists with head and tail selectors
is the type of nonempty lists with head and tail selectors  and
and  and
and  is defined such that
is defined such that  appends y to
appends y to  . We have
. We have  and
and  . The blueprint is
. The blueprint is

From this, the tool synthesizes the surface

When transforming the blueprint  into the surface
into the surface  , the selectors
, the selectors  and
and  are replaced by suitable compositions. One of the other constants,
are replaced by suitable compositions. One of the other constants,  , is composed with a mapping of
, is composed with a mapping of  . The treatment of constants is determined by their position relative to the input variables (here,
. The treatment of constants is determined by their position relative to the input variables (here,  ) and by whether the input is eventually consumed by a destructor-like operator on
) and by whether the input is eventually consumed by a destructor-like operator on  (here,
(here,  and
and  ). Bindings can also carry consumption information—from the outer context to within their scope—as in the following variant of
). Bindings can also carry consumption information—from the outer context to within their scope—as in the following variant of  :
:

The case expression is syntactic sugar for a  combinator. The desugared blueprint and surface constants are
combinator. The desugared blueprint and surface constants are

The case operator for streams is processed specially, because just like  and
and  it consumes the input. The expression in the scope of the inner
it consumes the input. The expression in the scope of the inner  of the blueprint contains two variables—
of the blueprint contains two variables— and
and  —that have
—that have  in their type. Due to the outer context, they must be treated differently:
in their type. Due to the outer context, they must be treated differently:  as an unconsumed input (which tells us to process the surrounding constant
as an unconsumed input (which tells us to process the surrounding constant  ) and
) and  as a consumed input (which tells us to leave the surrounding constant
as a consumed input (which tells us to leave the surrounding constant  unchanged). The selectors and case operators for
unchanged). The selectors and case operators for  can also be applied indirectly, via mapping (e.g.,
can also be applied indirectly, via mapping (e.g.,  ).
).
5 Implementation in Isabelle/HOL
The implementation of AmiCo followed the same general strategy as that of most other definitional mechanisms for Isabelle:
-
1.
We started from an abstract formalized example consisting of a manual construction of the Base and Step corecursors and the corresponding reasoning principles.
-
2.
We streamlined the formal developments, eliminating about 1000 lines of Isabelle definitions and proofs—to simplify the implementation and improve performance.
-
3.
We formalized the new Merge operation in the same style as Base and Step.
-
4.
We developed Standard ML functions to perform the corecursor state operations for arbitrary codatatypes and friendly functions.
-
5.
We implemented, also in Standard ML, the commands that process user specifications and interact with the corecursor state.
HOL’s type system cannot express quantification over arbitrary BNFs, thus the need for ML code to repeat the corecursor derivations for each new codatatype or friend. With the foundational approach, not only the corecursors and their characteristic theorems are produced but also all the intermediate objects and lemmas, to reach the highest level of trustworthiness. Assuming the proof assistant’s inference kernel is correct, bugs in our tool can lead at most to run-time failures, never to logical inconsistencies.
The code for step 4 essentially constructs the low-level types, terms, and lemma statements presented in Sect. 3 and proves the lemmas using dedicated tactics—ML programs that generalize the proofs from the formalization. In principle, the tactics always succeed. The code for step 5 analyses the user’s specification and synthesizes blueprints and surfaces, as exemplified in Sect. 4. It reuses  parsing combinators [16] for recognizing map functions and other syntactic conveniences, such as the use of
parsing combinators [16] for recognizing map functions and other syntactic conveniences, such as the use of  s as an alternative to
s as an alternative to  for corecursing under
for corecursing under  , as seen in Sect. 2.1.
, as seen in Sect. 2.1.
The archive accompanying this paper [14] contains instructions that explain where to find the code and the users’ manual and how to run the code.
6 Related Work and Discussion
This work combines the safety of foundational approaches to function definitions with an expressive flavor of corecursion and mixed recursion–corecursion. It continues a program of integrating category theory insight into proof assistant technology [16,17,18, 67]. There is a lot of related work on corecursion and productivity, both theoretical and applied to proof assistants and functional programming languages.
Theory of (Co)recursion. AmiCo incorporates category theory from many sources, notably Milius et al. [52] for corecursion up-to and Rot et al. [61] for coinduction up-to. Our earlier papers [17, 67] discuss further theoretical sources. AmiCo implements the first general, provably sound, and fully automatic method for mixing recursive and corecursive calls in function definitions. The idea of mixing recursion and corecursion appears in Bertot [11] for the stream filter, and a generalization is sketched in Bertot and Komendantskaya [13] for corecursion up to constructors. Leino’s Dafny tool [46] was the first to offer such a mixture for general codatatypes, which turned out to be unsound and was subsequently restricted to the sound but limited fragment of tail recursion.
Corecursion in Other Proof Assistants. Coq supports productivity by a syntactic guardedness check, based on the pioneering work of Giménez [26]. MiniAgda [2] and Agda implement a more flexible approach to productivity due to Abel et al. [3, 5], based on sized types and copatterns. Coq’s guardedness check allows, in our terminology, only the constructors as friends [21]. By contrast, Agda’s productivity checker is more expressive than AmiCo’s, because sized types can capture more precise contracts than the “consumes at most one constructor, produces at least one constructor” criterion. For example, a Fibonacci stream definition such as  can be made to work in Agda, but is rejected by AmiCo because
can be made to work in Agda, but is rejected by AmiCo because  is not a friend. As mentioned in Sect. 2.4, this flexibility comes at a price: The user must encode the productivity argument in the function’s type, leading to additional proof obligations.
is not a friend. As mentioned in Sect. 2.4, this flexibility comes at a price: The user must encode the productivity argument in the function’s type, leading to additional proof obligations.
CIRC [50] is a theorem prover designed for automating coinduction via sound circular reasoning. It bears similarity with both Coq’s Paco and our AmiCo. Its freezing operators are an antidote to what we would call the absence of friendship: Equality is no longer a congruence, hence equational reasoning is frozen at unfriendly locations.
Foundational Function Definitions. AmiCo’s commands and proof methods fill a gap in Isabelle/HOL’s coinductive offering. They complement 
 and
and  [16], allowing users to define nonprimitive corecursive and mixed recursive–corecursive functions. Being foundational, our work offers a strong protection against inconsistency by reducing circular fixpoint definitions issued by the user to low-level acyclic definitions in the core logic. This approach has a long tradition.
[16], allowing users to define nonprimitive corecursive and mixed recursive–corecursive functions. Being foundational, our work offers a strong protection against inconsistency by reducing circular fixpoint definitions issued by the user to low-level acyclic definitions in the core logic. This approach has a long tradition.
Most systems belonging to the HOL family include a counterpart to the  command of Isabelle, which synthesizes the argument to a primitive recursor. Isabelle/HOL is the only HOL system that also supports codatatypes and
command of Isabelle, which synthesizes the argument to a primitive recursor. Isabelle/HOL is the only HOL system that also supports codatatypes and  [16]. Isabelle/ZF, for Zermelo–Fraenkel set theory, provides
[16]. Isabelle/ZF, for Zermelo–Fraenkel set theory, provides  and
and  [57] commands, but no high-level mechanisms for defining corecursive functions.
[57] commands, but no high-level mechanisms for defining corecursive functions.
For nonprimitively recursive functions over datatypes, Slind’s TFL package for HOL4 and Isabelle/HOL [63] and Krauss’s  command for Isabelle/HOL [42] are the state of the art. Krauss developed the
command for Isabelle/HOL [42] are the state of the art. Krauss developed the  command for defining monadic functions [43]. Definitional mechanisms based on the Knaster–Tarski fixpoint theorems were also developed for (co)inductive predicates [31, 57]. HOLCF, a library for domain theory, offers a
command for defining monadic functions [43]. Definitional mechanisms based on the Knaster–Tarski fixpoint theorems were also developed for (co)inductive predicates [31, 57]. HOLCF, a library for domain theory, offers a  command for defining continuous functions [35].
command for defining continuous functions [35].
Our handling of friends can be seen as a round trip between a shallow and a deep embedding that resembles normalization by evaluation [9] (but starting from the shallow side). Initially, the user specification contains shallow (semantic) friends. For identifying the involved corecursion as sound, the tool reifies the friends into deep (syntactic) friends, which make up the blueprint. Then the deep friends are “reflected” back into their shallow versions by the evaluation function  . A similar technique is used by Myreen in HOL4 for verification and synthesis of functional programs [55].
. A similar technique is used by Myreen in HOL4 for verification and synthesis of functional programs [55].
In Agda, Coq, and Matita, the definitional mechanisms for (co)recursion are built into the system. In contrast, Lean axiomatizes only the recursor [54]. The distinguishing features of AmiCo are its dynamicity and high level of automation. The derived corecursors and coinduction principles are updated with new ones each time a friend is registered. This permits reuse both internally (resulting in lighter constructions) and at the user level (resulting in fewer proof obligations).
Code Extraction. Isabelle’s code generator [29] extracts Haskell code from an executable fragment of HOL, mapping HOL (co)datatypes to lazy Haskell datatypes and HOL functions to Haskell functions. Seven out of our eight case studies fall into this fragment; the extracted code is part of the archive [14]. Only the filter function on lazy lists is clearly not computable (Sect. 2.7). In particular, extraction works for Lochbihler’s probabilistic calculus (Sect. 2.8) which involves the type  of discrete subprobability distributions. Verified data refinement in the code generator makes it possible to implement such BNFs in terms of datatypes, e.g.,
of discrete subprobability distributions. Verified data refinement in the code generator makes it possible to implement such BNFs in terms of datatypes, e.g.,  as associative lists similar to Erwig’s and Kollmansberger’s PFP library [24]. Thus, we can extract code for GPVs and their operations like inlining. Lochbihler and Züst [49] used an earlier version of the calculus to implement a core of the Transport Layer Security (TLS) protocol in HOL.
as associative lists similar to Erwig’s and Kollmansberger’s PFP library [24]. Thus, we can extract code for GPVs and their operations like inlining. Lochbihler and Züst [49] used an earlier version of the calculus to implement a core of the Transport Layer Security (TLS) protocol in HOL.
Certified Lazy Programming. Our tool and the examples are a first step towards a framework for friendship-based certified programming: Programs are written in the executable fragment, verified in Isabelle, and extracted to Haskell. AmiCo ensures that corecursive definitions are productive and facilitates coinductive proofs by providing strong coinduction rules. Productivity and termination of the extracted code are guaranteed if the whole program is specified in HOL exclusively with datatypes, codatatypes, recursive functions with the  command, and corecursive functions with
command, and corecursive functions with  , and no custom congruence rules for higher-order operators have been used. The technical report [15, Sect. 6] explains why these restrictions are necessary.
, and no custom congruence rules for higher-order operators have been used. The technical report [15, Sect. 6] explains why these restrictions are necessary.
If the restrictions are met, the program clearly lies within the executable fragment and the code extracted from the definitions yields the higher-order rewrite system which the termination prover and AmiCo have checked. In particular, these restrictions exclude the noncomputable filter function on lazy lists (Sect. 2.7), with the test 
A challenge will be to extend these guarantees to Isabelle’s modular architecture. Having been designed with only partial correctness in mind, the code extractor can be customized to execute arbitrary (proved) equations—which can easily break productivity and termination. A similar issue occurs with  which cares only about semantic properties of the friend to be. For example, we can specify the identity function
which cares only about semantic properties of the friend to be. For example, we can specify the identity function  on streams by
on streams by  and register it as a friend with the derived equation
and register it as a friend with the derived equation  Consequently, AmiCo accepts the definition
Consequently, AmiCo accepts the definition  , but the extracted Haskell code diverges. To avoid these problems, we would have to (re)check productivity and termination on the equations used for extraction. In this scenario, AmiCo can be used to distinguish recursive from corecursive calls in a set of (co)recursive equations, and synthesize sufficient conditions for the function being productive and the recursion terminating, and automatically prove them (using Isabelle’s parametricity [36] and termination provers [20]).
, but the extracted Haskell code diverges. To avoid these problems, we would have to (re)check productivity and termination on the equations used for extraction. In this scenario, AmiCo can be used to distinguish recursive from corecursive calls in a set of (co)recursive equations, and synthesize sufficient conditions for the function being productive and the recursion terminating, and automatically prove them (using Isabelle’s parametricity [36] and termination provers [20]).
AmiCo Beyond Higher-Order Logic. The techniques implemented in our tool are applicable beyond Isabelle/HOL. In principle, nothing stands in the way of AgdamiCo, AmiCoq, or MatitamiCo. Danielsson [22] and Thibodeau et al. [65] showed that similar approaches work in type theory; what is missing is a tool design and implementation. AmiCo relies on parametricity, which is now understood for dependent types [10].
In Agda, parametricity could be encoded with sized types, and AgdamiCo could be a foundational tool that automatically adds suitable sized types for justifying the definition and erases them from the end product. Coq includes a parametricity-tracking tool [40] that could form the basis of AmiCoq. The Paco library by Hur et al. [37] facilitates coinductive proofs based on parameterized coinduction [53, 70]. Recent work by Pous [59] includes a framework to combine proofs by induction and coinduction. An AmiCoq would catch up on the corecursion definition front, going beyond what is possible with the  tactic [21]. On the proof front, AmiCoq would provide a substantial entry into Paco’s knowledge base: For any codatatype
tactic [21]. On the proof front, AmiCoq would provide a substantial entry into Paco’s knowledge base: For any codatatype  with destructor
with destructor  , all registered friends are, in Paco’s terminology, respectful up-to functions for the monotonic operator
, all registered friends are, in Paco’s terminology, respectful up-to functions for the monotonic operator  , whose greatest fixpoint is the equality on
, whose greatest fixpoint is the equality on  .
.
A more lightweight application of our methodology would be an AmiCo for Haskell or for more specialized languages such as CoCaml [38]. In these languages, parametricity is ensured by the computational model. An automatic tool that embodies AmiCo’s principles could analyze a Haskell program and prove it total. For CoCaml, which is total, a tool could offer more flexibility when writing corecursive programs.
Surface Synthesis Beyond Corecursion. The notion of extracting a parametric component with suitable properties can be useful in other contexts than corecursion. In the programming-by-examples paradigm [28], one needs to choose between several synthesized programs whose behavior matches a set of input–output instances. These criteria tend to prefer programs that are highly parametric. A notion of degree of parametricity does not exist in the literature but could be expressed as the size of a parametric surface, for a suitable notion of surface, where  is replaced by domain specific functions and
is replaced by domain specific functions and  by their left inverses.
by their left inverses.
References
Abbott, M., Altenkirch, T., Ghani, N.: Containers: constructing strictly positive types. Theor. Comput. Sci. 342(1), 3–27 (2005)
Abel, A.: MiniAgda: integrating sized and dependent types. In: Bove, A., Komendantskaya, E., Niqui, M. (eds.) PAR 2010. EPTCS, vol. 43, pp. 14–28 (2010)
Abel, A.: Compositional coinduction with sized types. In: Hasuo, I. (ed.) CMCS 2016. LNCS, vol. 9608, pp. 5–10. Springer, Heidelberg (2016). doi:10.1007/978-3-319-40370-0_2
Abel, A., Pientka, B.: Well-founded recursion with copatterns and sized types. J. Funct. Program. 26, e2 (2016)
Abel, A., Pientka, B., Thibodeau, D., Setzer, A.: Copatterns: programming infinite structures by observations. In: Giacobazzi, R., Cousot, R. (eds.) POPL 2013, pp. 27–38. ACM (2013)
Adams, M.: Introducing HOL Zero. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 142–143. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15582-6_25
Asperti, A., Ricciotti, W., Sacerdoti Coen, C., Tassi, E.: The Matita interactive theorem prover. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 64–69. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22438-6_7
Atkey, R., McBride, C.: Productive coprogramming with guarded recursion. In: Morrisett, G., Uustalu, T. (eds.) ICFP 2013, pp. 197–208. ACM (2013)
Berger, U., Schwichtenberg, H.: An inverse of the evaluation functional for typed lambda-calculus. In: LICS 1991, pp. 203–211. IEEE Computer Society (1991)
Bernardy, J.P., Jansson, P., Paterson, R.: Proofs for free: parametricity for dependent types. J. Funct. Program. 22(2), 107–152 (2012)
Bertot, Y.: Filters on coinductive streams, an application to Eratosthenes’ sieve. In: Urzyczyn, P. (ed.) TLCA 2005. LNCS, vol. 3461, pp. 102–115. Springer, Heidelberg (2005). doi:10.1007/11417170_9
Bertot, Y., Casteran, P.: Interactive Theorem Proving and Program Development–Coq’Art: The Calculus of Inductive Constructions. Texts in Theoretical Computer Science. Springer, Heidelberg (2004)
Bertot, Y., Komendantskaya, E.: Inductive and coinductive components of corecursive functions in Coq. Electr. Notes Theor. Comput. Sci. 203(5), 25–47 (2008)
Blanchette, J.C., Bouzy, A., Lochbihler, A., Popescu, A., Traytel, D.: Archive associated with this paper. http://matryoshka.gforge.inria.fr/pubs/amico_material.tar.gz
Blanchette, J.C., Bouzy, A., Lochbihler, A., Popescu, A., Traytel, D.: Friends with benefits: implementing corecursion in foundational proof assistants. Technical report (2017). http://matryoshka.gforge.inria.fr/pubs/amico_report.pdf
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (co)datatypes for Isabelle/HOL. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 93–110. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08970-6_7
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion: a proof assistant perspective. In: Fisher, K., Reppy, J.H. (eds.) ICFP 2015, pp. 192–204. ACM (2015)
Blanchette, J.C., Popescu, A., Traytel, D.: Witnessing (co)datatypes. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 359–382. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46669-8_15
Bove, A., Dybjer, P., Norell, U.: A brief overview of Agda – a functional language with dependent types. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 73–78. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_6
Bulwahn, L., Krauss, A., Nipkow, T.: Finding lexicographic orders for termination proofs in Isabelle/HOL. In: Schneider, K., Brandt, J. (eds.) TPHOLs 2007. LNCS, vol. 4732, pp. 38–53. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74591-4_5
Chlipala, A.: Certified Programming with Dependent Types—A Pragmatic Introduction to the Coq Proof Assistant. MIT Press, Cambridge (2013)
Danielsson, N.A.: Beating the productivity checker using embedded languages. In: Bove, A., Komendantskaya, E., Niqui, M. (eds.) PAR 2010. EPTCS, vol. 43, pp. 29–48 (2010)
Dijkstra, E.W.: An exercise for Dr. R. M. Burstall. In: Dijkstra, E.W. (ed.) Selected Writings on Computing: A Personal Perspective, pp. 215–216. Texts and Monographs in Computer Science. Springer, Heidelberg (1982)
Erwig, M., Kollmansberger, S.: Probabilistic functional programming in Haskell. J. Funct. Programm. 16(1), 21–34 (2006)
Gammie, P., Lochbihler, A.: The Stern-Brocot tree. Archive of Formal Proofs (2015). https://www.isa-afp.org/entries/Stern_Brocot.shtml
Giménez, E.: Codifying guarded definitions with recursive schemes. In: Dybjer, P., Nordström, B., Smith, J. (eds.) TYPES 1994. LNCS, vol. 996, pp. 39–59. Springer, Heidelberg (1995). doi:10.1007/3-540-60579-7_3
Gordon, M.J.C., Melham, T.F.: Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press, Cambridge (1993)
Gulwani, S.: Programming by examples—and its applications in data wrangling. In: Dependable Software Systems Engineering. NATO Science for Peace and Security Series D: Information and Communication Security, vol. 45, pp. 137–158. IOS Press (2016)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010). doi:10.1007/978-3-642-12251-4_9
Hagino, T.: A categorical programming language. Ph.D. thesis, University of Edinburgh (1987)
Harrison, J.: Inductive definitions: automation and application. In: Thomas Schubert, E., Windley, P.J., Alves-Foss, J. (eds.) TPHOLs 1995. LNCS, vol. 971, pp. 200–213. Springer, Heidelberg (1995). doi:10.1007/3-540-60275-5_66
Harrison, J.: HOL Light: an overview. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 60–66. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_4
Hinze, R.: The Bird tree. J. Func. Programm. 19(5), 491–508 (2009)
Homeier, P.V.: The HOL-Omega logic. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 244–259. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_18
Huffman, B.: HOLCF ’11: a definitional domain theory for verifying functional programs. Ph.D. thesis, Portland State University (2012)
Huffman, B., Kun\(\check{\rm c}\)ar, O.: Lifting and transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Heidelberg (2013). doi:10.1007/978-3-319-03545-1_9
Hur, C.K., Neis, G., Dreyer, D., Vafeiadis, V.: The power of parameterization in coinductive proof. In: Giacobazzi, R., Cousot, R. (eds.) POPL 2013, pp. 193–206. ACM (2013)
Jeannin, J.-B., Kozen, D., Silva, A.: Language constructs for non-well-founded computation. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 61–80. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37036-6_4
Jones, G., Gibbons, J.: Linear-time breadth-first tree algorithms: an exercise in the arithmetic of folds and zips. Technical report 71, Computer Science Department, University of Auckland (1993)
Keller, C., Lasson, M.: Parametricity in an impredicative sort. In: Cégielski, P., Durand, A. (eds.) CSL 2012. LIPIcs, vol. 16, pp. 381–395. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2012)
Knuth, D.E., Morris, J.H., Pratt, V.R.: Fast pattern matching in strings. SIAM J. Comput. 6(2), 323–350 (1977)
Krauss, A.: Partial recursive functions in higher-order logic. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 589–603. Springer, Heidelberg (2006). doi:10.1007/11814771_48
Krauss, A.: Recursive definitions of monadic functions. In: Bove, A., Komendantskaya, E., Niqui, M. (eds.) PAR 2010. EPTCS, vol. 43, pp. 1–13 (2010)
van Laarhoven, T.: Knuth-Morris-Pratt in Haskell (2007). http://www.twanvl.nl/blog/haskell/Knuth-Morris-Pratt-in-Haskell
Leino, K.R.M.: Automating theorem proving with SMT. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 2–16. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39634-2_2
Leino, K.R.M., Moskal, M.: Co-induction simply: automatic co-inductive proofs in a program verifier. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 382–398. Springer, Heidelberg (2014). doi:10.1007/978-3-319-06410-9_27
Lochbihler, A.: Probabilistic functions and cryptographic oracles in higher order logic. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 503–531. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49498-1_20
Lochbihler, A., Hölzl, J.: Recursive functions on lazy lists via domains and topologies. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 341–357. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08970-6_22
Lochbihler, A., Züst, M.: Programming TLS in Isabelle/HOL. Isabelle Workshop 2014 (2014). https://www.ethz.ch/content/dam/ethz/special-interest/infk/inst-infsec/information-security-group-dam/research/publications/pub2014/lochbihler14iw.pdf
Lucanu, D., Goriac, E.-I., Caltais, G., Roşu, G.: CIRC: a behavioral verification tool based on circular coinduction. In: Kurz, A., Lenisa, M., Tarlecki, A. (eds.) CALCO 2009. LNCS, vol. 5728, pp. 433–442. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03741-2_30
Milius, S.: Completely iterative algebras and completely iterative monads. Inf. Comput. 196(1), 1–41 (2005)
Milius, S., Moss, L.S., Schwencke, D.: Abstract GSOS rules and a modular treatment of recursive definitions. Log. Meth. Comput. Sci. 9(3:28), 1–52 (2013)
Moss, L.S.: Parametric corecursion. Theor. Comput. Sci. 260(1–2), 139–163 (2001)
de Moura, L., Kong, S., Avigad, J., van Doorn, F., von Raumer, J.: The Lean theorem prover (system description). In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 378–388. Springer, Heidelberg (2015). doi:10.1007/978-3-319-21401-6_26
Myreen, M.O.: Functional programs: conversions between deep and shallow embeddings. In: Beringer, L., Felty, A. (eds.) ITP 2012. LNCS, vol. 7406, pp. 412–417. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32347-8_29
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer, Heidelberg (2002)
Paulson, L.C.: A fixedpoint approach to implementing (co)inductive definitions. In: Bundy, A. (ed.) CADE 1994. LNCS, vol. 814, pp. 148–161. Springer, Heidelberg (1994). doi:10.1007/3-540-58156-1_11
Paulson, L.C.: Mechanizing coinduction and corecursion in higher-order logic. J. Log. Comput. 7(2), 175–204 (1997)
Pous, D.: Coinduction all the way up. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) LICS 2016, pp. 307–316. ACM (2016)
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: Mason, R.E.A. (ed.) IFIP 1983, pp. 513–523. North-Holland/IFIP (1983)
Rot, J., Bonsangue, M., Rutten, J.: Coalgebraic bisimulation-up-to. In: Emde Boas, P., Groen, F.C.A., Italiano, G.F., Nawrocki, J., Sack, H. (eds.) SOFSEM 2013. LNCS, vol. 7741, pp. 369–381. Springer, Heidelberg (2013). doi:10.1007/978-3-642-35843-2_32
Rutten, J.J.M.M.: Automata and coinduction (an exercise in coalgebra). In: Sangiorgi, D., Simone, R. (eds.) CONCUR 1998. LNCS, vol. 1466, pp. 194–218. Springer, Heidelberg (1998). doi:10.1007/BFb0055624
Slind, K.: Function definition in higher-order logic. In: Goos, G., Hartmanis, J., Leeuwen, J., Wright, J., Grundy, J., Harrison, J. (eds.) TPHOLs 1996. LNCS, vol. 1125, pp. 381–397. Springer, Heidelberg (1996). doi:10.1007/BFb0105417
Slind, K., Norrish, M.: A brief overview of HOL4. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 28–32. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71067-7_6
Thibodeau, D., Cave, A., Pientka, B.: Indexed codata types. In: Sumii, E. (ed.) ICFP 2016. ACM (2016)
Traytel, D.: Formal languages, formally and coinductively. In: Kesner, D., Pientka, B. (eds.) FSCD. LIPIcs, vol. 52, pp. 31:1–31:17. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2016)
Traytel, D., Popescu, A., Blanchette, J.C.: Foundational, compositional (co)datatypes for higher-order logic: category theory applied to theorem proving. In: LICS 2012, pp. 596–605. IEEE Computer Society (2012)
Turner, D.A.: Elementary strong functional programming. In: Hartel, P.H., Plasmeijer, R. (eds.) FPLE 1995. LNCS, vol. 1022, pp. 1–13. Springer, Heidelberg (1995). doi:10.1007/3-540-60675-0_35
Wadler, P.: Theorems for free! In: Stoy, J.E. (ed.) FPCA 1989, pp. 347–359. ACM (1989)
Winskel, G.: A note on model checking the modal \(\nu \)-calculus. Theor. Comput. Sci. 83(1), 157–167 (1991)
Acknowledgment
Martin Desharnais spent months extending Isabelle’s  command to generate a wealth of theorems, many of which were useful when implementing AmiCo. Lorenz Panny developed
command to generate a wealth of theorems, many of which were useful when implementing AmiCo. Lorenz Panny developed  whose code provided valuable building blocks. Mathias Fleury, Mark Summerfield, Daniel Wand, and the anonymous reviewers suggested many textual improvements. We thank them all. Blanchette is supported by the European Research Council (ERC) starting grant Matryoshka (713999). Lochbihler is supported by the Swiss National Science Foundation (SNSF) grant “Formalising Computational Soundness for Protocol Implementations” (153217). Popescu is supported by the UK Engineering and Physical Sciences Research Council (EPSRC) starting grant “VOWS: Verification of Web-based Systems” (EP/N019547/1). The authors are listed in alphabetical order.
whose code provided valuable building blocks. Mathias Fleury, Mark Summerfield, Daniel Wand, and the anonymous reviewers suggested many textual improvements. We thank them all. Blanchette is supported by the European Research Council (ERC) starting grant Matryoshka (713999). Lochbihler is supported by the Swiss National Science Foundation (SNSF) grant “Formalising Computational Soundness for Protocol Implementations” (153217). Popescu is supported by the UK Engineering and Physical Sciences Research Council (EPSRC) starting grant “VOWS: Verification of Web-based Systems” (EP/N019547/1). The authors are listed in alphabetical order.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Blanchette, J.C., Bouzy, A., Lochbihler, A., Popescu, A., Traytel, D. (2017). Friends with Benefits. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  and
and  commands and the
commands and the  proof method.
proof method. is defined as a fixpoint of a type constructor
is defined as a fixpoint of a type constructor 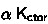 equipped with constructor
equipped with constructor  and destructor
and destructor  .
. contains
contains  and has a signature
and has a signature 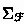 (or
(or  ). Each friend
). Each friend 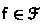 of type
of type 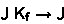 has a companion syntactic expression
has a companion syntactic expression 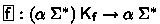 .
. is
is  .
.