Deniable Attribute Based Encryption for Branching Programs from LWE

Abstract

Deniable encryption (Canetti et al. CRYPTO ’97) is an intriguing primitive that provides a security guarantee against not only eavesdropping attacks as required by semantic security, but also stronger coercion attacks performed after the fact. The concept of deniability has later demonstrated useful and powerful in many other contexts, such as leakage resilience, adaptive security of protocols, and security against selective opening attacks. Despite its conceptual usefulness, our understanding of how to construct deniable primitives under standard assumptions is restricted.

In particular from standard lattice assumptions, i.e. Learning with Errors (LWE), we have only flexibly and non-negligible advantage deniable public-key encryption schemes, whereas with the much stronger assumption of indistinguishable obfuscation, we can obtain at least fully sender-deniable PKE and computation. How to achieve deniability for other more advanced encryption schemes under standard assumptions remains an interesting open question.

In this work, we construct a flexibly bi-deniable Attribute-Based Encryption (ABE) scheme for all polynomial-size Branching Programs from LWE. Our techniques involve new ways of manipulating Gaussian noise that may be of independent interest, and lead to a significantly sharper analysis of noise growth in Dual Regev type encryption schemes. We hope these ideas give insight into achieving deniability and related properties for further, advanced cryptographic systems from lattice assumptions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Deniable encryption, introduced by Canetti et al. [14] at CRYPTO 1997, is an intriguing primitive that allows Alice to privately communicate with Bob in a way that resists not only eavesdropping attacks as required by semantic security, but also stronger coercion attacks performed after the fact. An eavesdropper Eve stages a cocercion attack by additionally approaching Alice (or Bob, or both) after a ciphertext is transmitted and demanding to see all secret information: the plaintext, the random coins used by Alice for encryption, and any private keys held by Bob (or Alice) related to the ciphertext. In particular, Eve can use this information to “fully unroll” the exact transcript of some deterministic decryption procedure purportedly computed by Bob, as well as verify that the exact coins and decrypted plaintext in fact produce the coerced ciphertext. A secure deniable encryption scheme should maintain privacy of the sensitive data originally communicated between Alice and Bob under the coerced ciphertext (instead substituting a benign yet convincing plaintext in the view of Eve), even in the face of such a revealing attack and even if Alice and Bob may not interact during the coercion phase.

Historically, deniable encryption schemes have been challenging to construct. Under standard assumptions, Canetti et al. [14] constructed a sender-deniable¹ PKE where the distinguishing advantage between real and fake openings is an inverse polynomial depending on the public key size. But it was not until 2011 that O’Neill, Peikert, and Waters [35] proposed the first constructions of bi-deniable PKE with negligible deniability distinguishing advantage: from simulatable PKE generically, as well as from Learning with Errors ($\mathsf {LWE}$ [36]) directly.

Concurrently, Bendlin et al. [8] showed an inherent limitation: any non-interactive public-key encryption scheme may be receiver-deniable (resp. bi-deniable) only with non-negligible $\varOmega (1/\mathsf {size}(\mathsf {pk}))$ distinguishing advantage in the deniability experiment. Indeed, O’Neill et al. [35] bypass the impossibility result of [8] by working in the so-called flexible ² model of deniability. In the flexible of deniability, private keys $\mathsf {sk}$ are distributed by a central key authority. In the event that Bob is coerced to reveal a key $\mathsf {sk}$ that decrypts chosen ciphertext $\mathsf {ct}^*$, the key authority distributes a faking key $\mathsf {fk}$ to Bob, which Bob can use to generate a fake key $\mathsf {sk}^*$ (designed to behave identically to $\mathsf {sk}$ except on ciphertext $\mathsf {ct}^*$). If this step is allowed, then O’Neill et al. demonstrate that for their constructions, Eve has at most negligible advantage in distinguishing whether Bob revealed an honest $\mathsf {sk}$ or fake $\mathsf {sk}^*$.

A major breakthrough in deniable encryption arrived with the work of Sahai and Waters [38], who proposed the first sender-deniable PKE with negligible distinguishing advantage from indistinguishability obfuscation ($i\mathcal {O}$) for $\mathsf {P/poly}$ [22]. The concept of deniability has been demonstrated useful in the contexts of leakage resilience [20], adaptive security for protocols, and as well as deniable computation (or algorithms) [16, 19, 23]. In addition to coercion resistance, a bi-deniable encryption scheme is a non-committing encryption scheme [15], as well as a scheme secure under selective opening (SOA) attacks [7], which are of independent theoretical interest.

Very recently, De Caro, Iovino, and O’Neill [17] gave various constructions of deniable functional encryption. First, they show a generic transformation of any IND-secure FE scheme for circuits into a flexibly receiver-deniable FE for circuits. Second, they give a direct construction of receiver-deniable FE for Boolean formulae from bilinear maps. Further, in the stronger multi-distributional model of deniable functional encryption – where there are special “deniable” set-up and encryption algorithms in addition to the plain ones, and where under coercion, it may non-interactively be made to seem as only the normal algorithms were used – De Caro et al. [17] construct receiver-deniable FE for circuits under the additional (powerful) assumption of different-inputs obfuscation ($di\mathcal {O}$).

De Caro et al. [17] also show (loosely speaking) that any receiver-deniable FE implies SIM-secure FE for the same functionality. Following [17], we also emphasize that deniability for functional encryption is a strictly stronger property than SIM security, since fixed coerced ciphertexts must decrypt correctly and benignly in the real world. Finally, we mention that in concurrent work, Apon, Fan, and Liu, in an unpublished work [5], construct flexibly bi-deniable inner product encryption from standard lattice assumptions. This work generalizes and thus subsumes the prior results of [5].

Despite the apparent theoretical utility in understanding the extent to which cryptographic constructions are deniable, our current knowledge of constructing such schemes from standard lattice assumptions is still limited. From $\mathsf {LWE}$, we have only flexible and non-negligible advantage deniable encryption schemes (or IPE from [5]), whereas with the much more powerful assumption of indistinguishability obfuscation ($i\mathcal {O}$), we can obtain at least fully-secure sender-deniable PKE and computation [16, 19, 23], or as mentioned above even a multi-distributional receiver-deniable FE for all circuits from the even stronger assumption of $di\mathcal {O}.$

1.1 Our Contributions

In this work, we further narrow this gap by investigating a richer primitive – attribute-based encryption (ABE) [9, 28, 30, 31] – without the use of obfuscation as a black box primitive. We hope that the techniques developed in this work can further shed light on deniability for even richer schemes such as functional encryption [9, 12, 22, 29] under standard assumptions.

• Our main contribution is the construction of a flexibly bi-deniable ABE for poly-sized branching programs (which can compute $\mathsf {NC1}$ via Barrington’s theorem [6]) from the standard Learning with Errors assumption [36].

Theorem 1.1

Under the standard $\mathsf {LWE}$ assumption, there is a flexibly bi-deniable attribute-based encryption scheme for all poly-size branching programs.

Recall that in an attribute-based encryption (ABE) scheme for a family of functions $\mathcal {F} : \mathcal {X} \rightarrow \mathcal {Y}$, every secret key $\mathsf {sk}_{f}$ is associated with a predicate $f\in \mathcal {F}$, and every ciphertext $\mathsf {ct}_{\varvec{x}}$ is associated with an attribute $\varvec{x}\in \mathcal {X}$. A ciphertext $\mathsf {ct}_{\varvec{x}}$ can be decrypted by a given secret key $\mathsf {sk}_{f}$ to its payload message m only when $f(x) = 0\in \mathcal {Y}$. Informally, the typical security notion for an ABE scheme is collusion resistance, which means no collection of keys can provide information on a ciphertext’s message, if the individual keys are not authorized to decrypt the ciphertext in the first place. Intuitively, a bi-deniable ABE must provide both collusion and coercion resistance.

Other contributions of this work can be summarized as:

• A new form of the Extended Learning with Errors ($\mathsf {e}\mathsf {LWE}$) assumption [2, 13, 35], which is convenient in the context of Dual Regev type ABE/FE schemes that apply the Leftover Hash Lemma [21] in their security proofs.

• An explicit, tightened noise growth analysis for lattice-based ABE for branching programs. Prior work used the loose $l_\infty$ norm to give a rough upper bound, which is technically insufficient to achieve deniability using our proof techniques. (We require matching upper and lower bounds on post-evaluation noise sizes.)

The $\mathsf {e}\mathsf {LWE}$ assumption above is roughly the standard $\mathsf {LWE}$ assumption, but where the distinguisher also receives “hints” on the $\mathsf {LWE}$ sample’s noise vector $\varvec{e}$ in the form of inner products, i.e. distributions $\left\{ \mathbf{A}, \varvec{b} = \mathbf{A}^T\varvec{s}+\varvec{e}, \varvec{z}, \langle \varvec{z}, \varvec{e} \rangle \right\}$ where (intuitively) $\varvec{z}$ is a decryption key in the real system (which are denoted $\varvec{r}$ elsewhere). Our contribution here is a new reduction from the standard $\mathsf {LWE}$ assumption to our correlated variant of extended-$\mathsf {LWE}$, $\mathsf {e}\mathsf {LWE} ^+$, where the adversary requests arbitrary correlations (expressed as a matrix $\mathbf{R}$) between the hints, in the case of a prime poly-size modulus with noise-less hints. We show this by extending the $\mathsf {LWE}$ to $\mathsf {e}\mathsf {LWE}$ reduction of Alperin-Sheriff and Peikert [2] to our setting.

1.2 Our Approach

At a high level, our work begins with the ABE for branching programs of Gorbunov and Vinayagamurthy [30]. We will augment the basic ABE-BP = $(\mathsf {Setup}$, $\mathsf {Keygen}$, $\mathsf {Enc}$, $\mathsf {Dec})$ with an additional suite of algorithms $(\mathsf {Den} \mathsf {Setup}$, $\mathsf {Den} \mathsf {Enc}$, $\mathsf {SendFake}$, $\mathsf {RecFake})$ to form our flexibly bi-deniable ABE-BP. Doing so requires careful attention to the setting of parameters, as we explain in the sequel.

We remark now that – due to reasons related to the delicateness of our parameter setting – the ABE scheme of [30] is particularly suited to being made bi-deniable, as compared to similar schemes such as the ABE for arithmetic circuits of Boneh et al. [9]. We will explain this in what follows as well.

Intuition for Our New Deniability Mechanism. As in the work of O’Neill et al. [35], our approach to bi-deniability relies primarily on a curious property of Dual Regev type [24] secret keys: by correctness of any such scheme, each key $\varvec{r}$ is guaranteed to behave as intended for some $1-\mathsf {negl}(n)$ fraction of the possible random coins used to encrypt, but system parameters may be set so that each key is also guaranteed to be faulty (i.e. fail to decrypt) on some $\mathsf {negl}(n)$ fraction of the possible encryption randomness. More concretely, each secret key vector $\varvec{r}$ in lattice-based schemes is sampled from an m-dimensional Gaussian distribution, as is the error term $\varvec{e}$ (for $\mathsf {LWE}$ public key $\mathbf{A}\in \mathbb {Z}_q^{n\times m}$). For every fixed $\varvec{r}$, with overwhelming probability over the choice of $\varvec{e}$, the vectors $\varvec{r}, \varvec{e}\in \mathbb {Z}_q^m$ will point in highly uncorrelated directions in m-space. However, if the vector $\varvec{r}$ and $\varvec{e}$ happen to point in similar directions, the error magnitude will be (loosely) squared during decryption.

Our scheme is based around the idea that a receiver, coerced on honest key-ciphertext pair $(\varvec{r}, \mathsf {ct}^*)$, can use the key authority’s faking key $\mathsf {fk}$ to learn the precise error vector $\varvec{e}^*$ used to construct $\mathsf {ct}^*$. Given $\varvec{e}^*, \varvec{r}$, and $\mathsf {fk}$, the receiver re-samples a fresh secret key $\varvec{r}^*$ that is functionally-equivalent to the honest key $\varvec{r}$, except that $\varvec{r}^*$ is strongly correlated with the vector $\varvec{e}^*$ in $\mathsf {ct}^*$. When the coercer then attempts to decrypt the challenge ciphertext $\mathsf {ct}^*$ using $\varvec{r}^*$, the magnitude of decryption error will artificially grow and cause the decryption to output the value we want to deny to. Yet, when the coercer attempts to decrypt any other independently-sampled ciphertext $\mathsf {ct}$, decryption will succeed with overwhelming probability under $\varvec{r}^*$ if it would have under $\varvec{r}$.

We emphasize that to properly show coercion resistance (when extending this intuition to the case of Dual Regev ABE instead of Dual Regev PKE), this behavior of $\varvec{r}^*$ should hold even when $\mathsf {ct}$ and $\mathsf {ct}^*$ embed the same attribute $\varvec{x}$. (Indeed, the majority of our effort is devoted to ensuring this simple geometric intuition allows a valid instantiation of the denying algorithms $(\mathsf {Den} \mathsf {Setup}$, $\mathsf {Den} \mathsf {Enc}$, $\mathsf {SendFake}$, $\mathsf {RecFake})$ without “damaging” the basic operation of $(\mathsf {Setup}$, $\mathsf {Keygen}$, $\mathsf {Enc}$, $\mathsf {Dec})$ in the underlying ABE scheme.)

Then, given the ability to “artificially blow-up” the decryption procedure of a specific key on a ciphertext-by-ciphertext basis, we can employ an idea originally due to Canetti et al. [14] of translucent sets, but generalized to the setting of ABE instead of PKE, to construct our new, flexibly bi-deniable ABE-BP scheme out of the framework provided by the “plain” SIM-secure ABE-BP scheme of [30].

Highlights of the Gorbunov-Vinayagamurthy Scheme. In the ABE for (width 5) branching programs of [30], bits a are “$\mathsf {LWE}$-encoded” by the vector

$$\begin{aligned} \psi _{\mathbf {A}, \varvec{s}, a} = \varvec{s}^T(\mathbf {A} + a\cdot \mathbf {G})+\varvec{e}\in \mathbb {Z}_q^m \end{aligned}$$

where $\mathbf {G}$ is the gadget matrix [34].

The ciphertext $\mathsf {ct}$ encrypting message $\mu$ under $\mathsf {BP}$-input $\varvec{x}$ is given by

$$\begin{aligned} \mathsf {ct}= (\psi _0, \psi ^c, \{\psi _{i}\}_{i\in [\ell ]}, \{\psi _{0,i}\}_{i\in [5]}, c), \end{aligned}$$

and is composed of a Dual Regev $\mathsf {ct}$-pair of vectors $(\psi _0, c)$ encrypting the ciphertext’s message $\mu$, an encoding $\psi ^c$ representing the (freshly randomized) encoding of the constant 1, five encodings $\{\psi _{0,i}\}_{i\in [5]}$ representing a (freshly randomized) encoding of the initial state of a width-5, length-$\ell$ branching program $\mathsf {BP}$, and $\ell$ encodings $\{\psi _i\}_{i\in [\ell ]}$ – one for each step of the branching program’s evaluation, storing a constant-sized permutation matrix associated with the i-th level of $\mathsf {BP}$. Note that each “$\mathsf {LWE}$ encoding” $\psi$ is performed under a distinct public key matrix $\mathbf {A},$ $\mathbf {A}^c$, $\{\mathbf {A}_i\}$, or $\{\mathbf {A}_{0,i}\}$ respectively.

The (key-homomorphic) evaluation procedure takes as input a ciphertext $\mathsf {ct}= (\psi _0, \psi ^c, \{\psi _{i}\}, \{\psi _{0,i}\}, c)$ and the public key $\mathsf {pk} = (\mathbf {A}, \mathbf {A}^c, \{\mathbf {A}_i\}, \{\mathbf {A}_{0,i}\})$, as well as the cleartext branching program description $\mathsf {BP}$ and the $\mathsf {BP}$-input $\varvec{x}$. It produces the evaluated public key $\mathbf {V}_\mathsf {BP}$ and the evaluated encoding $\psi _{\mathsf {BP}(\varvec{x})}$. Given a short secret key vector $\varvec{r}\in \mathbb {Z}^{2m}$ matching (some public coset $\varvec{u}$ of) the lattice generated by $[\mathbf {A} | \mathbf {V}_\mathsf {BP}]\in \mathbb {Z}^{n\times 2m}$, the encoding vector $\psi _{\mathsf {BP}(\varvec{x})}$ (whose Dual Regev encoding-components $(\psi _0, c)$ also match coset $\varvec{u}$) can be decrypted to the message $\mu$ if and only if $\mathsf {BP}(\varvec{x}) = \mathsf {accept} = \varvec{0}$.

On the Necessity of Exact Noise Control. In order to push the intuition for our deniability mechanism through for an ABE of the above form, we must overcome a number of technical hurdles.

The major challenge is an implicit technical requirement to very tightly control the precise noise magnitude of evaluated ciphertexts. In previous functional (and homomorphic) encryption schemes from lattices, the emphasis is placed on upper bounding evaluated noise terms, to ensure that they do not grow too large and cause decryption to fail. Moreover, security (typically) holds for any ciphertext noise level at or above the starting ciphertexts’ noises. In short, noise growth during evaluation is nearly always undesirable.

As with previous schemes, we too must upper bound the noise growth of evaluated ciphertexts in order to ensure basic correctness of our ABE. But unlike previous schemes, we must take the step of also (carefully) lower bounding the noise growth during the branching program evaluation (which technically motivates deviating from the $l_\infty$ norm of prior analyses). This is due to the fact, highlighted above, that producing directional alignment between a key and error term can at most square the noise present during decryption. Since coercion resistance requires that it must always be possible to deny any ciphertext originally intended for any honest key, it must be that, with overwhelming probability, every honest key and every honest ciphertext produce evaluated error that is no less than the square root of the maximum noise threshold tolerated.

In a little more detail – as we will later demonstrate in Sect. 4 – in dimension m there is precisely an expected $\mathsf {poly}(m)$ gap in magnitude between the inner products of (i) two relatively orthogonal key/error vectors $\varvec{r}, \varvec{e}_{\mathsf {BP}(\varvec{x})}$, and (ii) two highly correlated key/error vectors $\varvec{r}^*, \varvec{e}_{\mathsf {BP}(\varvec{x})}$. The ability to deny is based around our ability to design $\varvec{r}^*$ that are statistically indistinguishable from $\varvec{r}$ in the attacker’s view, but where $\varvec{r}^*$ “punctures out” decryptions of ciphertexts with error vectors pointing in the direction of $\varvec{e}_{\mathsf {BP}(\varvec{x})}$ in m-space (error-vector directions are unique to each honest $\mathsf {ct}$ with overwhelming probability).

Crucially, this approach generically forces the use of a polynomial-sized modulus q in the scheme.³ In particular, when error vectors $\varvec{e}$ may (potentially) grow to be some superpolynomial magnitude in the dimension m of the public/secret keys, we totally lose any efficiently testable notion of “error vector orientation in m-space” for the purposes of Dual Regev type decryption.

Further, in order to “correctly trace and distinguish” different orientations throughout the computation of an arbitrary branching program $\mathsf {BP}$, we are required to make careful use of multi-dimensional Gaussian distributions. These are sampled using covariance matrices $\mathbf {Q}\in \mathbb {Z}^{m\times m}$ that allow us to succinctly describe the underlying, geometric randomized rotation action on error vector orientations in m-space with each arithmetic operation of the $\mathsf {BP}$ evaluation in the overall ABE-BP scheme. (We use the geometrically-inspired term “rotation matrix” to describe our low-norm matrices $\mathbf {R}$ for this reason.)

An additional subtlety in our new noise analysis is that we require the individual multiplications of the $\mathsf {ct}$ evaluation procedure to have independently sampled error vectors in each operand-encoding – and thus be “independently oriented” – in order for the overall analysis to go through correctly. (While there could in principle be some way around this technical obstacle in the analysis, we were unable to find one.) This appears to a priori exclude a straightforward denying procedure for all circuits [9], where a gate’s input wires’ preceding sub-circuits may have cross-wires between them. But it naturally permits denying branching program computations, where at the i-th time-step, an i-th independently generated $\mathsf {ct}$-component is merged into an accumulated $\mathsf {BP}$ state, as with [30].

Finally, we mention that an inherent limitation in the techniques of Apon et al. [5], used to construct (the weaker notion of) flexibly bi-deniable inner product encryption from $\mathsf {LWE}$, is bypassed in the current work at the cost of supporting only $\mathsf {BP}$ computations of an a-priori bounded length $\ell$. Namely, it was the case in [5] that the length $\ell$ of the attribute vector $\varvec{w}$ had to be “traded off” against the dimension m of the public/secret keys. We suppress the details, other than to point out that this issue can be resolved by artificially boosting the magnitude of the low-norm matrices used to generate error terms in fresh ciphertexts from $\{-1,1\}$ up to $\{-\varTheta (m\ell ), \varTheta (m\ell )\}$-valued matrices. This, of course, requires knowing the length $\ell$ of the branching program up front. (Intuitively, this technical change as compared to [5] allows for a sharp inductive lower bound on the minimum noise growth across all possible function-input pairs that might be evaluated in a given instance of our bi-deniable ABE-BP scheme.)

1.3 Future Directions

The next, most natural question is whether bi-deniable functional encryption can be built out of similar techniques (from only $\mathsf {LWE}$), perhaps by leveraging our bi-deniable ABE for $\mathsf {NC}1$ computations as a building block. We briefly sketch one possible approach and the obstacles encountered. Recall that Goldwasser et al. [27] show to transform the combination of (i) any ABE for a circuit family $\mathcal {C}$, (ii) fully homomorphic encryption, and (iii) a randomized encoding scheme (such as Yao’s garbled circuits) into a 1-key (resp. bounded collusion) SIM-secure functional encryption scheme for $\mathcal {C}$.

If we instantiate the Goldwasser et al. transformation with our deniable ABE, we get a functional encryption scheme for $\mathsf {NC}1$. We can then boost functional encryption for shallow circuits to functional encryption for all circuits using the “trojan method” of Ananth et al. [4]. As it turns out, it is easy to directly prove flexible receiver-deniability of the final scheme, independently of but matching the generic results of De Caro et al. [17] for receiver-deniable FE.

Unfortunately, we do not know how to prove (even, flexible) sender-deniability of this final scheme. Roughly speaking, the problem is that each ciphertext’s attribute in such a scheme contains an FHE ciphertext $\mathsf {ct}_{\mathsf {FHE}}$ for its attribute, and this attribute leaks to the attacker (resp. cocercer) on decryptions that succeed. In particular, there is nothing stopping the coercer from demanding that the sender also provide randomness $r_S$ that opens the attribute’s FHE ciphertext.

We speculate that a possible way around this obstacle would be to use an adaptively-secure homomorphic encryption scheme for $\mathsf {NC}1$ computations. Note that adaptively-secure FHE is known to be impossible for circuits with $\omega (\log (n))$ depth due to a counting argument lower bound by Katz, Thiruvengadam, and Zhou [32], but this leaves open the possibility of an $\mathsf {NC}1$-homomorphic encryption scheme with the necessary properties to re-obtain (flexible) sender deniability for lattice-based FE. We leave this as an intriguing open problem for future work.

2 Preliminaries

Notations. Let $\textsc {ppt}$ denote probabilistic polynomial time. We use bold uppercase letters to denote matrices, and bold lowercase letters to denote vectors, where vectors are by default column vectors throughout the paper. We let $\lambda$ be the security parameter, [n] denote the set $\{1,...,n\}$, and $|\varvec{t}|$ denote the number of bits in a string or vector $\varvec{t}$. We denote the i-th bit value of a string $\varvec{s}$ by $\varvec{s}[i]$. We use $[\cdot | \cdot ]$ to denote the concatenation of vectors or matrices, and $||\cdot ||$ to denote the norm of vectors or matrices respectively. We use the $\ell _2$ norm for all vectors unless explicitly stated otherwise.

We present necessary background knowledge of branching programs and lattices (such as the LWE assumption and lattice sampling algorithms) in full version.

Randomness Extraction. We will use the following lemma to argue the indistinghishability of two different distributions, which is a generalization of the leftover hash lemma proposed by Dodis et al. [21].

Lemma 2.1

([1]). Suppose that $m > (n + 1) \log q + w(\log n)$. Let $\mathbf {R} \in \{-1, 1\}^{m \times k}$ be chosen uniformly at random for some polynomial $k = k(n)$. Let $\mathbf {A}, \mathbf {B}$ be matrix chosen randomly from $\mathbb {Z}^{n \times m}_q, \mathbb {Z}^{n \times k}_q$ respectively. Then, for all vectors $\varvec{w} \in \mathbb {Z}^m$, the two following distributions are statistically close:

$$\begin{aligned} (\mathbf {A}, \mathbf {A} \mathbf {R}, \varvec{w}^T\mathbf {R}) \approx (\mathbf {A}, \mathbf {B}, \varvec{w}^T \mathbf {R}) \end{aligned}$$

Learning With Errors. The LWE problem was introduced by Regev [36], who showed that solving it on the average is as hard as (quantumly) solving several standard lattice problems in the worst case.

Definition 2.2

(LWE). For an integer $q = q(n) \ge 2$, and an error distribution $\chi = \chi (n)$ over $\mathbb {Z}_q$, the learning with errors problem $\mathsf {LWE} _{n, m, q, \chi }$ is to distinguish between the following pairs of distributions:

$$\begin{aligned} \{\mathbf {A}, \varvec{b} = \mathbf {A}^T\varvec{s} + \varvec{e}\} \ \text {and} \ \{\mathbf {A}, \varvec{u}\}\end{aligned}$$

where $\mathbf {A} \overset{\$}{\leftarrow }\mathbb {Z}^{n \times m}_q$, $\varvec{s} \overset{\$}{\leftarrow } \mathbb {Z}^n_q$, $\varvec{u} \overset{\$}{\leftarrow } \mathbb {Z}^m_q$, and $\varvec{e} \overset{\$}{\leftarrow } \chi ^m$.

Trapdoors and Sampling Algorithms. We will use the algorithms $\mathsf{TrapGen}, \mathsf{SampleLeft}, \mathsf{SampleRight}, \mathsf{ExtBasis}, \mathsf{Invert}$ first proposed in [1, 18, 24, 34] to sample short vectors from specified lattices. For details of these sampling algorithms, please refer to the full version.

3 New Definitions and Tools

In this section, we first describe our new notion of flexibly bi-deniable ABE, which is a natural generalization of the flexibly bi-deniable PKE of [35]. Then we define the notion of a flexibly attribute-based bi-translucent set (AB-BTS), which generalizes the idea of bi-translucent set (BTS) in the work [35]. Using a similar argument as in the work [35], we can show that an AB-BTS suffices to construct bi-deniable ABE. In the last part of this section, we define a new assumption called Extended LWE Plus, and show its hardness by giving a reduction from the standard LWE problem.

3.1 Flexibly Bi-Deniable ABE: Syntax and Deniability Definition

A flexibly bi-deniable key-policy attribute based encryption for a class of Boolean circuits $\mathcal {C}: \{0,1\}^{\ell } \rightarrow \{0,1\}$ consists a tuple of $\textsc {ppt}$ algorithms $\Pi = (\mathsf {Setup}, \mathsf {Keygen}, \mathsf {Enc}, \mathsf {Dec}, \mathsf {Den} \mathsf {Setup}, \mathsf {Den} \mathsf {Enc}, \mathsf {SendFake}, \mathsf {RecFake})$. We describe them in detail as follows:

 

$\mathsf {Setup} (1^\lambda )$::

On input the security parameter $\lambda$, the setup algorithm outputs public parameters $\mathsf {pp}$ and master secret key $\mathsf {msk}$.

$\mathsf {Keygen} (\mathsf {msk}, f)$::

On input the master secret key $\mathsf {msk}$ and a function $f \in \mathcal {C}$, it outputs a secret key $\mathsf {sk} _f$.

$\mathsf {Enc} (\mathsf {pp}, \varvec{x}, \mu ; r_S)$::

On input the public parameter $\mathsf {pp}$, an attribute/message pair $(\varvec{x}, \mu )$ and randomness $r_S$, it outputs a ciphertext $c_{\varvec{x}}$.

$\mathsf {Dec} (\mathsf {sk} _f, c_{\varvec{x}})$::

On input the secret key $\mathsf {sk} _f$ and a ciphertext $c_{\varvec{x}}$, it outputs the corresponding plaintext $\mu$ if $f(\varvec{x}) = 0$; otherwise, it outputs $\bot$.

$\mathsf {Den} \mathsf {Setup} (1^\lambda )$::

On input the security parameter $\lambda$, the deniable setup algorithm outputs pubic parameters $\mathsf {pp}$, master secret key $\mathsf {msk}$ and faking key $\mathsf {fk}$.

$\mathsf {Den} \mathsf {Enc} (\mathsf {pp}, \varvec{x}, \mu ; r_S)$::

On input the public parameter $\mathsf {pp}$, an attribute/message pair $(\varvec{x}, \mu )$ and randomness $r_S$, it outputs a ciphertext $c_{\varvec{x}}$.

$\mathsf {SendFake}(\mathsf {pp}, r_S, \mu , \mu ')$::

On input public parameters $\mathsf {pp}$, original random coins $r_S$, message $\mu$ of $\mathsf {Den} \mathsf {Enc}$ and desired message $\mu '$, it outputs a faked random coin $r'_S$.

$\mathsf {RecFake}(\mathsf {pp}, \mathsf {fk}, c_{\varvec{x}}, f, \mu ')$::

On input public parameters $\mathsf {pp}$, faking key $\mathsf {fk}$, a ciphertext $c_{\varvec{x}}$, a function $f \in \mathcal {C}$, and desired message $\mu '$, the receiver faking algorithm outputs a faked secret key $\mathsf {sk} '_f$.

 

Correctness. We say the flexibly bi-deniable ABE scheme described above is correct, if for any $(\mathsf {msk}, \mathsf {pp}) \leftarrow \mathsf {S}(1^\lambda )$, where $\mathsf {S} \in \{\mathsf {Setup}, \mathsf {Den} \mathsf {Setup} \}$, any message $\mu$, function $f \in \mathcal {C}$, and any attribute vector $\varvec{x}$ where $f(\varvec{x}) = 0$, we have $\mathsf {Dec} (\mathsf {sk} _f, c_{\varvec{x}}) = \mu$, where $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {msk}, f)$ and $c_{\varvec{x}} \leftarrow \mathsf {E}(\mathsf {pp}, \varvec{x}, \mu ; r_S)$ where $\mathsf {E} \in (\mathsf {Enc}, \mathsf {Den} \mathsf {Enc})$.

Bi-Deniability Definition. Let $\mu , \mu '$ be two arbitrary messages, not necessarily different. We propose the bi-deniability definition by describing real experiment $\mathbf {Expt} ^\mathsf{Real}_{\mathcal {A}, \mu , \mu '}(1^\lambda )$ and faking experiment $\mathbf {Expt} ^\mathsf{Fake}_{\mathcal {A}, \mu , \mu '}(1^\lambda )$ regarding adversary $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2, \mathcal {A}_3)$ as shown in Fig. 1:

where $\mathsf {KG} (\mathsf {msk},\varvec{x}^*,\cdot )$ returns a secret key $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {msk}, f)$ if $f(\varvec{x}^*) \ne 0$ and $\bot$ otherwise.

Fig. 1.

Security experiments for bi-deniable ABE

Definition 3.1

(Flexibly Bi-Deniable ABE). An ABE scheme $\Pi$ is bi-deniable if for any two messages $\mu , \mu '$, any probabilistic polynomial-time adversaries $\mathcal {A}$ where $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2, \mathcal {A}_3)$, there is a negligible function $\mathsf {negl} (\lambda )$ such that

$$\begin{aligned} \mathbf {Adv}_{\mathcal {A}, \mu , \mu '}^{\Pi }(1^\lambda ) = |\mathbf {Pr}[\mathbf {Expt} ^\mathsf{Real}_{\mathcal {A}, \mu , \mu '}(1^\lambda ) = 1] - \mathbf {Pr}[\mathbf {Expt} ^\mathsf{Fake}_{\mathcal {A}, \mu , \mu '}(1^\lambda ) = 1]| \le \mathsf {negl} (\lambda ) \end{aligned}$$

3.2 Attribute Based Bitranslucent Set Scheme

In this section, we define the notion of a Attribute Based Bitranslucent Set (AB-BTS), which is an extension of bitranslucent sets (BTS) as defined by O’Neill et al. in [35]. Our new notion permits a more fine-grained degree of access control, where pseudorandom samples and secret keys are associated with attributes $\varvec{x}$, and the testing algorithm can successfully distinguish a pseudorandom sample from a truly random one if and only if the attribute of the sample is accepted under a given secret key’s policy f – i.e. when $f(\varvec{x}) = \varvec{0}$. This concept is reminiscent of attribute-based encryption (ABE), and in fact, we will show in the sequel how to construct a flexibly bi-deniable ABE from an AB-BTS. This is analogous to the construction of a flexibly bi-deniable PKE from O’Neill et al.’s BTS. We present the formal definition below.

Let $\mathcal {F}$ be some family of functions. An attribute based bitranslucent set (AB-BTS) scheme for $\mathcal {F}$ consists of the following algorithms:

 

$\mathsf {Setup} (1^\lambda )$::

On input the security parameter, the normal setup algorithm outputs a public parameter $\mathsf {pp}$ and master secret key $\mathsf {msk}$.

$\mathsf {Den} \mathsf {Setup} (1^\lambda )$::

On input the security parameter, the deniable setup algorithm outputs a public parameter $\mathsf {pp}$, master secret key $\mathsf {msk}$ and faking key $\mathsf {fk}$.

$\mathsf {Keygen} (\mathsf {msk}, f)$::

On input the master secret key $\mathsf {msk}$ and a function $f \in \mathcal {F}$, the key generation algorithm outputs a secret key $\mathsf {sk} _f$.

P :

- and U-samplers $\mathsf {SampleP}(\mathsf {pp}, \varvec{x}; r_S)$ and $\mathsf {SampleU}(\mathsf {pp}, \varvec{x}; r_S)$ output some $\varvec{c}$.

$\mathsf {TestP}(\mathsf {sk} _f, \varvec{c}_{\varvec{x}})$::

On input a secret key $\mathsf {sk} _f$ and a ciphertext $\varvec{c}_{\varvec{x}}$, the P-tester algorithm outputs 1 (accepts) or 0 (rejects).

$\mathsf {FakeSCoins} (\mathsf {pp}, r_S)$::

On input a public parameters $\mathsf {pp}$ and randomness $r_S$, the sender-faker algorithm outputs randomness $r^*_S$.

$\mathsf {FakeRCoins} (\mathsf {pp}, \mathsf {fk}, \varvec{c}_{\varvec{x}},f)$::

On input a public parameters $\mathsf {pp}$, the faking key $\mathsf {fk}$, a ciphertext $\varvec{c}_{\varvec{x}}$ and a function $f \in \mathcal {F}$, the receiver-faker algorithm outputs a faked secret key $\mathsf {sk} '_f$.

 

Definition 3.2

(AB-BTS). We say a scheme $\Pi = (\mathsf {Setup}, \mathsf {Den} \mathsf {Setup}, \mathsf {Keygen}, \mathsf {SampleP}, \mathsf {SampleU}, \mathsf {TestP}, \mathsf {\mathsf {FakeSCoins}}, \mathsf {\mathsf {FakeRCoins}})$ is an AB-BTS scheme for a function family $\mathcal {F}$ if it satisfies:

• 1. (Correctness.) The following experiments accept or respectively reject with overwhelming probability over the randomness.

  • Let $(\mathsf {pp}, \mathsf {msk}) \leftarrow \mathsf {Setup} (1^\lambda )$, $f \in \mathcal {F}$, $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {msk}, f)$. If $f(\varvec{x}) = 0$ and $\varvec{c}_{\varvec{x}} \leftarrow \mathsf {SampleP}(\mathsf {pp}, \varvec{x}; r_S)$, then $\mathsf {TestP}(\mathsf {sk} _f, \varvec{c}_{\varvec{x}}) = 1$; otherwise, $\mathsf {TestP}(\mathsf {sk} _f, \varvec{c}_{\varvec{x}}) = 0$.

  • Let $(\mathsf {pp}, \mathsf {msk}) \leftarrow \mathsf {Setup} (1^\lambda )$, $f \in \mathcal {F}$, $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {msk}, f)$, $\varvec{c} \leftarrow \mathsf {SampleU}(\mathsf {pp}; r_S)$. Then $\mathsf {TestP}(\mathsf {sk} _f, \varvec{c}) = 0$.

• 2. (Indistinguishable public parameters.) The public parameters $\mathsf {pp}$ generated by the two setup algorithms $(\mathsf {pp}, \mathsf {msk}) \leftarrow \mathsf {Setup} (1^\lambda )$ and $(\mathsf {pp}, \mathsf {msk}, \mathsf {fk}) \leftarrow \mathsf {Den} \mathsf {Setup} (1^\lambda )$ should be indistinguishable.

• 3. (Selective bi-deniability.) Let $\mathcal {F}$ be a family of functions. We define the following two experiments: the real experiment $\mathbf {Expt} ^\mathsf{Real}_{\mathcal {A},\mathcal {F}}(1^\lambda )$ and the faking experiment $\mathbf {Expt} ^\mathsf{Fake}_{\mathcal {A},\mathcal {F}}(1^\lambda )$ regarding an adversary $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2, \mathcal {A}_3)$ as shown in Fig. 2:

  where $\mathsf {KG} (\mathsf {msk},\varvec{x}^*,\cdot )$ returns a secret key $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {msk}, f)$ if $f\in \mathcal {F}$ and $f(\varvec{x}^*) \ne 0$; it returns $\bot$ otherwise. We also require that $f^{*} \in \mathcal {F}$.

  We say the scheme is selectively bi-deniable for $\mathcal {F}$, if for any probabilistic polynomial-time adversaries $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2, \mathcal {A}_3)$, there is a negligible function $\mathsf {negl} (\lambda )$ such that

  $$\begin{aligned} \mathbf {Adv}_{\mathcal {A}}^{\Pi }(1^\lambda ) = |\mathbf {Pr}[\mathbf {Expt} ^\mathsf{Real}_{\mathcal {A},\mathcal {F}}(1^\lambda ) = 1] - \mathbf {Pr}[\mathbf {Expt} ^\mathsf{Fake}_{\mathcal {A},\mathcal {F}}(1^\lambda ) = 1]| \le \mathsf {negl} (\lambda ) \end{aligned}$$

Fig. 2.

Security experiments for AB-BTS

Remark 3.3

Correctness for the faking algorithms is implied by the bi-deniability property. In particular, with overwhelming probability over the overall randomness, the following holds: let $(\mathsf {pp}, \mathsf {msk}, \mathsf {fk}) \leftarrow \mathsf {Den} \mathsf {Setup} (1^\lambda )$, $f\in \mathcal {F}$, $\mathsf {sk} _{f}\leftarrow \mathsf {Keygen} (\mathsf {msk},f)$, $\varvec{x}$ be a string and $\varvec{c}_{\varvec{x}} \leftarrow \mathsf {SampleP}(\mathsf {pp},x ; r_S)$, then

• $\mathsf {SampleU}(\mathsf {pp}, \varvec{x};\mathsf {FakeSCoins} (\mathsf {pp},r_{S}) ) = \varvec{c}_{\varvec{x}}$,

• $\mathsf {TestP}( \mathsf {FakeRCoins} (\mathsf {pp}, \mathsf {fk}, \varvec{c}_{\varvec{x}}, f), \varvec{c}_{\varvec{x}}) = 0$

• For any other $x'$, let $\varvec{c}' \leftarrow \mathsf {SampleP}(\mathsf {pp},x' ; r_{S}')$, then (with overwhelming probability) we have

  $$\begin{aligned} \mathsf {TestP}\left( \mathsf {FakeRCoins} (\mathsf {pp}, \mathsf {fk}, \varvec{c}_{\varvec{x}}, f), \varvec{c}' \right) = \mathsf {TestP}(\mathsf {sk} _{f}, c' ). \end{aligned}$$

It is not hard to see that if one of these does not hold, then one can easily distinguish the real experiment from the faking experiment.

Remark 3.4

Canetti et al. [14] gave a simple encoding technique to construct a sender-deniable encryption scheme from a translucent set. O’Neill, Peikert, and Waters [35] used a similar method to construct a flexibly bi-deniable encryption from a bi-translucent set scheme. Here we further observe that the same method as well allows us to construct a flexibly bi-deniable ABE scheme from bi-deniable AB-BTS. We present the construction in Sect. 4.4.

3.3 Extended LWE and Our New Variant

O’Neill et al. [35] introduced the Extended LWE problem, which allows a “hint” on the error vector $\varvec{x}$ to leak in form of a noisy inner product. They observe a trivial “blurring” argument shows that $\mathsf {LWE}$ reduces to $\mathsf {e}\mathsf {LWE}$ when the hint-noise $\beta q$ is superpolynomially larger than the magnitude of samples from $\chi$, and also allows for unboundedly many independent hint vectors $\langle \varvec{z}, \varvec{x}_i\rangle$ while retaining $\mathsf {LWE}$-hardness.

Definition 3.5

(Extended LWE). For an integer $q = q(n) \ge 2$, and an error distribution $\chi = \chi (n)$ over $\mathbb {Z}_q$, the extended learning with errors problem $\mathsf {e}\mathsf {LWE} _{n, m, q, \chi , \beta }$ is to distinguish between the following pairs of distributions:

$$\begin{aligned} \{\mathbf {A}, \varvec{b} = \mathbf {A}^T\varvec{s} + \varvec{e}, \varvec{z}, \langle \varvec{z}, \varvec{b} - \varvec{e} \rangle + e'\} \ \text {and} \ \{\mathbf {A}, \varvec{u}, \varvec{z}, \langle \varvec{z}, \varvec{u} - \varvec{x} \rangle + e'\} \end{aligned}$$

where $\mathbf {A} \overset{\$}{\leftarrow }\mathbb {Z}^{n \times m}_q$, $\varvec{s} \overset{\$}{\leftarrow } \mathbb {Z}^n_q$, $\varvec{u} \overset{\$}{\leftarrow } \mathbb {Z}^m_q$, $\varvec{e, z} \overset{\$}{\leftarrow } \chi ^m$ and $e' \overset{\$}{\leftarrow } \mathcal {D}_{\beta q}$.

Further, Alperin-Sheriff and Peikert [2] show that $\mathsf {LWE}$ reduces to $\mathsf {e}\mathsf {LWE}$ with a polynomial modulus and no hint-noise (i.e. $\beta = 0$), even in the case of a bounded number of independent hints.

We introduce the following new form of extended-LWE, called $\mathsf {e}\mathsf {LWE} ^+$, which considers leaking a pair of correlated hints on the same noise vector. Our security proof of the AB-BTS construction relies on this new assumption.

Definition 3.6

(Extended LWE Plus). For integer $q = q(n) \ge 2, m = m(n)$, an error distribution $\chi = \chi (n)$ over $\mathbb {Z}_q$, and a matrix $\mathbf {R} \in \mathbb {Z}_q^{m\times m}$, the extended learning with errors problem $\mathsf {e}\mathsf {LWE} ^{+}_{n, m, q, \chi , \beta , \mathbf {R} }$ is to distinguish between the following pairs of distributions:

$$\begin{aligned} \{\mathbf {A}, \varvec{b} = \mathbf {A}^T\varvec{s} + \varvec{e}, \varvec{z}_{0}, \varvec{z}_{1}, \langle \varvec{z}_{0}, \varvec{b} - \varvec{e} \rangle + e, \langle \mathbf {R}\varvec{z}_{1}, \varvec{b} - \varvec{e} \rangle + e'\} \text { and} \end{aligned}$$

$$\begin{aligned} \{\mathbf {A}, \varvec{u}, \varvec{z}_{0}, \varvec{z}_{1}, \langle \varvec{z}_{0}, \varvec{u} - \varvec{e} \rangle + e,\langle \mathbf {R} \varvec{z}_{1}, \varvec{u} - \varvec{e} \rangle + e'\} \end{aligned}$$

where $\mathbf {A} \overset{\$}{\leftarrow }\mathbb {Z}^{n \times m}_q$, $\varvec{s} \overset{\$}{\leftarrow } \mathbb {Z}^n_q$, $\varvec{u} \overset{\$}{\leftarrow } \mathbb {Z}^m_q$, $\varvec{e}, \varvec{z}_{0},\varvec{z}_{1} \overset{\$}{\leftarrow } \chi ^m$ and $e, e' \overset{\$}{\leftarrow } \mathcal {D}_{\beta q}$.

Hardness of Extended-LWE $^+$. A simple observation, following prior work, is that when $\chi$ is $\mathsf {poly}(n)$-bounded and the hint noise $\beta q$ (and thus, modulus q) is superpolynomial in n, then $\mathsf {LWE} _{n, m, q, \chi }$ trivially reduces to $\mathsf {e}\mathsf {LWE} ^+_{n, m, q, \chi , \beta , \mathbf {R}}$ for every $\mathbf {R}\in \mathbb {Z}_q^{m\times m}$ so that $\mathbf {R}\mathbf {z}_1$ has $\mathsf {poly}(n)$-bounded norm. This is because, for any $r = \omega (\sqrt{\log {n}}), c\in \mathbb {Z}$, the statistical distance between $\mathcal {D}_{\mathbb {Z}, r}$ and $c + \mathcal {D}_{\mathbb {Z}, r}$ is at most O(|c| / r).

However, our cryptosystem will require a polynomial-size modulus q. So, we next consider the case of prime modulus q of $\mathsf {poly}(n)$ size and no noise on the hints (i.e. $\beta = 0$). Following [2]⁴, it will be convenient to swap to the “knapsack” form of $\mathsf {LWE}$, which is: given $\mathbf {H}\leftarrow \mathbb {Z}_q^{(m-n)\times m}$ and $\varvec{c}\in \mathbb {Z}_q^{m-n}$, where either $\mathbf {c} = \mathbf {H}\varvec{e}$ for $\varvec{e}\leftarrow \chi ^m$ or $\mathbf {c}$ uniformly random and independent of $\mathbf {H}$, determine which is the case (with non-negligible advantage). The “extended-plus” form of the knapsack problem also reveals a pair of hints $(\varvec{z}_0, \varvec{z}_1, \langle \varvec{z}_0, \varvec{e} \rangle , \langle \mathbf {R}\varvec{z}_1, \varvec{e}\rangle )$. Note the equivalence between $\mathsf {LWE}$ and knapsack-$\mathsf {LWE}$ is proven in [33] for $m\ge n + \omega (\log {n})$.

Theorem 3.7

For $m\ge n+\omega (\log {n})$, for every prime $q = \mathsf {poly}(n)$, for every $\mathbf {R}\in \mathbb {Z}_q^{m\times m}$, and for every $\beta \ge 0$, $\mathbf {Adv}_{\mathcal {B}^{\mathcal {A}}}^{\mathsf {LWE} _{n,m,q,\chi }}(1^\lambda ) \ge (1/q^2)\mathbf {Adv}_{\mathcal {A}}^{\mathsf {e}\mathsf {LWE} ^+_{n,m,q,\chi , \beta , \mathbf {R}}}(1^\lambda )$.

Proof

We construct an $\mathsf {LWE}$ to $\mathsf {e}\mathsf {LWE} ^+$ reduction $\mathcal {B}$ as follows. $\mathcal {B}$ receives a knapsack-$\mathsf {LWE}$ instance $\mathbf {H}\in \mathbb {Z}_q^{(m-n)\times m}, \varvec{c}\in \mathbb {Z}_q^{m-n}$. It samples $\varvec{e}', \varvec{z}_0, \varvec{z}_1\leftarrow \chi ^m$ and uniform $\varvec{v}_0, \varvec{v}_1\leftarrow \mathbb {Z}_q^{m-n}$. It chooses any $\mathbf {R}\in \mathbb {Z}_q^{m\times m}$, then sets

$$\begin{aligned} \begin{aligned} \mathbf {H}'&:= \mathbf {H} - \varvec{v}_0\varvec{z}_0^T - \varvec{v}_1\left( \mathbf {R}\varvec{z}_1\right) ^T \in \mathbb {Z}_q^{(m-n)\times m},\\ \varvec{c}'&:= \varvec{c} - \varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e}' \rangle - \varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e}' \rangle \in \mathbb {Z}_q^{m-n}. \end{aligned} \end{aligned}$$

It sends $\left( \mathbf {H}', \varvec{c}', \mathbf {z}_0, \mathbf {z}_1, \langle \varvec{z}_0, \varvec{e}' \rangle , \langle \mathbf {R}\varvec{z}_1, \varvec{e}' \rangle \right)$ to the knapsack-$\mathsf {e}\mathsf {LWE} ^+$ adversary $\mathcal {A}$, and outputs what $\mathcal {A}$ outputs.

Notice that when $\mathbf {H}, \varvec{c}$ are independent and uniform, so are $\mathbf {H}', \mathbf {c}'$, in which case $\mathcal {B}$’s simulation is perfect.

Now, consider the case when $\mathbf {H}, \mathbf {c}$ are drawn from the knapsack-$\mathsf {LWE}$ distribution, with $\mathbf {c} = \mathbf {H}\varvec{x}$ for $\varvec{e}\leftarrow \chi ^m$. In this case, $\mathbf {H}'$ is uniformly random over the choice of $\mathbf {H}$, and we have

$$\begin{aligned} \begin{aligned} \varvec{c}'&= \mathbf {H}\varvec{x} - \varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e}' \rangle - \varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e}' \rangle \\&= \left( \mathbf {H}' + \varvec{v}_0\varvec{z}_0^T + \varvec{v}_1\left( \mathbf {R}\varvec{z}_1\right) ^T\right) \varvec{e} - \varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e}' \rangle - \varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e}' \rangle \\&= \mathbf {H}'\varvec{e} + \varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e} - \varvec{e}' \rangle + \varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e} - \varvec{e}' \rangle . \end{aligned} \end{aligned}$$

Define the event $E = [E_0 \wedge E_1]$ as

$$\begin{aligned} \begin{aligned} E_0&\mathop {=}\limits ^\mathrm{def} \left[ \langle \varvec{z}_0, \varvec{e} \rangle = \langle \varvec{z}_0, \varvec{e}' \rangle \right] , \\ E_1&\mathop {=}\limits ^\mathrm{def} \left[ \langle \mathbf {R}\varvec{z}_1, \varvec{e} \rangle = \langle \mathbf {R}\varvec{z}_1, \varvec{e}' \rangle \right] . \end{aligned} \end{aligned}$$

If event E occurs, then the reduction $\mathcal {B}$ perfectly simulates a pseudorandom instance of knapsack-$\mathsf {e}\mathsf {LWE} ^+$ to $\mathcal {A}$, as then $\varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e} - \varvec{e}' \rangle + \varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e} - \varvec{e}' \rangle$ vanishes, leaving $\varvec{c}' = \mathbf {H}'\varvec{e}$ for $\mathbf {H}'\leftarrow \mathbb {Z}_q^{(m-n)\times m}$ and $\varvec{e}\leftarrow \chi ^m$ as required. Otherwise since q is prime, the reduction $\mathcal {B}$ (incorrectly) simulates an independent and uniform instance of knapsack-$\mathsf {e}\mathsf {LWE} ^+$ to $\mathcal {A}$, as then either one of $\varvec{v}_0\cdot \langle \varvec{z}_0, \varvec{e} - \varvec{e}' \rangle$ or $\varvec{v}_1\cdot \langle \mathbf {R}\varvec{z}_1, \varvec{e} - \varvec{e}' \rangle$ does not vanish, implying that $\varvec{c}'$ is uniform in $\mathbb {Z}_q^{m-n}$ over the choice of $\varvec{v}_0$ (resp. $\varvec{v}_1$) alone, independent of the choices of $\mathbf {H}'$ and $\varvec{x}$.

It remains to analyze the probability that event E occurs. Because $\varvec{e}$ and $\varvec{e}'$ are i.i.d., we may define the random variable $\mathcal {Z}_0$ that takes values $\langle \varvec{z}_0, \varvec{e}^* \rangle \in \mathbb {Z}_q$ and the random variable $\mathcal {Z}_1$ that takes values $\langle \mathbf {R}\varvec{z}_1, \varvec{e}^* \rangle \in \mathbb {Z}_q$ jointly over choice of $\varvec{e}^*\leftarrow \chi ^m$, and analyze their collision probabilities independently. Since the collision probability of any random variable $\mathcal {Z}$ is at least $1/|\mathsf {Supp}(\mathcal {Z})|$, we have that $\Pr [E] \ge \min CP[\mathcal {Z}_0] \cdot \min CP[\mathcal {Z}_1] = 1/q^2 = 1/\mathsf {poly}(n)$, and the theorem follows.   $\square$

4 Flexibly Bi-Deniable Attribute-Based Encryption (ABE) for Branching Programs

In this section, we present our flexibly bi-deniable ABE for bounded-length Branching Program. We organize our approach into the following three steps: (1) first, we recall the encoding scheme proposed in the SIM-secure ABE-BP of [30]; (2) Then, we present our flexibly bi-deniable attribute bi-translucent set (AB-BTS) scheme, as was defined in Definition 3.2. Our AB-BTS construction uses the ideas of Gorbunov and Vinayagamurthy [30], with essential modifications that allow us to tightly upper and lower bound evaluated noise terms. As discussed in the Introduction, this tighter analysis plays a key role in proving bi-deniability. (3) Finally, we show how to obtain the desired bi-deniable ABE scheme from our AB-BTS. As pointed out by Canetti et al. [14] and O’Neill et al. [35], a bitranslucent set scheme implies flexibly bi-deniable PKE. We observe that the same idea generalizes to the case of an AB-BTS scheme and flexibly bi-deniable ABE in a straightforward manner.

4.1 Encoding Schemes for Branching Programs

Basic Homomorphic Encoding. Before proceeding to the public key evaluation algorithm, we first described basic homomorphic addition and multiplication over public keys and encoded ciphertexts based on the techniques in [3, 9, 25].

Definition 4.1

(LWE Encoding). For any matrix $\mathbf {A} \leftarrow \mathbb {Z}_q^{n \times m}$, we define an LWE encoding of a bit $a \in \{0,1\}$ with respect to a public key $\mathbf {A}$ and randomness $\varvec{s} \leftarrow \mathbb {Z}_q^n$ as

$$\begin{aligned} \psi _{\mathbf {A}, \varvec{s}, a} = \varvec{s}^T(\mathbf {A} + a \cdot \mathbf {G}) + \varvec{e} \in \mathbb {Z}_q^m \end{aligned}$$

for error vector $\varvec{e} \leftarrow \chi ^m$ and the gadget matrix $\mathbf {G}\in \mathbb {Z}_q^{n \times m}$.

In our construction, all LWE encodings will be encoded using the same LWE secret $\varvec{s}$, thus for simplicity, we will simply refer to such an encoding as $\psi _{\mathbf {A}, a}$.

For homomorphic addition, the addition algorithm takes as input two encodings $\psi _{\mathbf {A}, a}, \psi _{\mathbf {A}', a'}$, and outputs the sum of them. Let $\mathbf {A}^+ = \mathbf {A} + \mathbf {A}'$ and $a^+ = a + a'$

$$\begin{aligned} \mathsf{Add} (\psi _{\mathbf {A}, a}, \psi _{\mathbf {A}', a'}) = \psi _{\mathbf {A}, a} + \psi _{\mathbf {A}', a'} = \psi _{\mathbf {A}^+, a^+} \end{aligned}$$

For homomorphic multiplication, the multiplication algorithm takes as input two encodings $\psi _{\mathbf {A}, a}, \psi _{\mathbf {A}', a}$, and outputs an encoding $\psi _{\mathbf {A}^\times , a^\times }$, where $\mathbf {A}^\times = -\mathbf {A} \mathbf {G}^{-1}(\mathbf {A}')$ and $a^\times = aa'$.

$$\begin{aligned} \mathsf {Mult}(\psi _{\mathbf {A}, a}, \psi _{\mathbf {A}', a'}) = - \psi \cdot \mathbf {G}^{-1}(\mathbf {A}') + a \cdot \psi ' = \psi _{\mathbf {A}^\times , a^\times } \end{aligned}$$

Public Key Evaluation Algorithm. Following the notation in [30], we define a public evaluation algorithm $\mathsf {Eval}_\mathsf {pk}$. The algorithm takes as input a description of the branching program $\mathsf {BP}$, a collection of public keys $\{\mathbf {A}_i\}_{i \in [\ell ]}$ (one for each attribute bit $x_i$), a collection of public keys $\mathbf {V}_{0, i}$ for initial state vector and an auxiliary matrix $\mathbf {A}^c$, and outputs an evaluated public key corresponding to the branching program $\mathsf {BP}$.

$$\begin{aligned} \mathbf {V}_\mathsf {BP}\leftarrow \mathsf {Eval}_\mathsf {pk} (\mathsf {BP}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c) \end{aligned}$$

where the auxiliary matrix $\mathbf {A}^c$ are used to encoded constant 1 for each input wire. We also define matrix $\mathbf {A}'_i = \mathbf {A}^c - \mathbf {A}_i$ as a public key used to encode $1 - x_i$. By the definition of branching programs, the output $\mathbf {V}_\mathsf {BP}\in \mathbb {Z}_q^{n \times m}$ is the homomorphically generated public key $\mathbf {V}_{L, 1}$ at position 1 of the state vector for the L-th step of the branching program evaluation.

Recall that in the definition of branching programs, $\mathsf {BP}$ is represented by the tuple $\{\mathsf {var}(t), \{\gamma _{t, i, 0}, \gamma _{t, i, 1}\}_{i \in [5]}\}$ for $t \in [L]$, and the initial state vector is set to be $\varvec{v}_0 = (1,0,0,0,0)$. Further, for $t \in [L]$, the computation is performed as $\varvec{v}_t[i] = \varvec{v}_{t - 1}[\gamma _{t, i, 0}](1 - x_{\mathsf {var}(t)}) + \varvec{v}_{t - 1}[\gamma _{t, i, 1}] \cdot x_{\mathsf {var}(t)}$. It is important for the security proof (among other reasons) that the evaluated state vector in each step is independent of the attribute vector.

Encoding Evaluation Algorithm. We define an encoding evaluation algorithm $\mathsf {Eval}_{\mathsf {ct}}$ that takes as input the description of a branching program $\mathsf {BP}$, an attribute vector $\varvec{x}$, a set of encodings for the attribute $\{\mathbf {A}_i, \psi _i := \psi _{\mathbf {A}_i, x_i}\}_{i \in [\ell ]}$, encodings of the initial state vector $\{\mathbf {V}_{0, i}, \psi _{0, i} := \psi _{\mathbf {V}_{0, i} \varvec{v}_0[i]}\}_{i \in [5]}$ and an encoding of a constant 1, i.e. $\psi ^c := \psi _{\mathbf {A}^c, 1}$. The algorithm $\mathsf {Eval}_{\mathsf {ct}}$ outputs an encoding of the result $y:= \mathsf {BP}(\varvec{x})$ with respect to the homomorphically derived public key $\mathbf {V}_\mathsf {BP}:= \mathbf {V}_{L, 1}$

$$\begin{aligned} \psi _\mathsf {BP}\leftarrow \mathsf {Eval}_{\mathsf {ct}}(\mathsf {BP}, \varvec{x}, \{\mathbf {A}_i, \psi _i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}, \psi _{0, i}\}_{i \in [5]}, \{\mathbf {A}^c, \psi ^c \}) \end{aligned}$$

As mentioned above, in branching program computation, for $t \in [L]$, we have for all $i \in [5]$

$$\begin{aligned} \varvec{v}_t[i] = \varvec{v}_{t - 1}[\gamma _{t, i, 0}](1 - x_{\mathsf {var}(t)}) + \varvec{v}_{t - 1}[\gamma _{t, i, 1}] \cdot x_{\mathsf {var}(t)} \end{aligned}$$

The evaluation algorithm proceeds inductively to update the encoding of the state vector for each step of the branching program. Next, we need to instantiate this inductive computation using the homomorphic operations described above, i.e. $\mathsf{Add}, \mathsf {Mult}$. Following the notation used in [30], we define $\psi '_i := \psi _{\mathbf {A}'_i, (1 - x_i)} = \varvec{s}^T (\mathbf {A}'_i + (1 - x_i) \mathbf {G}) + \varvec{e}'_i$, where $\mathbf {A}'_i = \mathbf {A}^c - \mathbf {A}_i$, to denote the encoding of $1 - x_i$. This encoding can be computed using $\mathsf{Add} (\psi _{\mathbf {A}_i^c, 1}, -\psi _{\mathbf {A}_i, x_i})$. Then assuming at time $t - 1 \in [L]$ we hold encodings of the state vector $\{\psi _{\mathbf {V}_{t - 1}, i, \varvec{v}_{t - 1}[i]}\}_{i \in [5]}$. For $i \in [5]$, we compute the encodings of new state values as

$$\begin{aligned} \psi _{i, t} = \mathsf{Add} (\mathsf {Mult}(\psi '_{\mathsf {var}(t)}, \psi _{t - 1, \gamma _0}), \mathsf {Mult}(\psi _{\mathsf {var}(t)}, \psi _{t - 1, \gamma _1})) \end{aligned}$$

where $\gamma _0 := \gamma _{t, i, 0}$ and $\gamma _1 := \gamma _{t, i, 1}$. We omit the correctness proof of the encoding here, which is presented in [30].

The above algorithms suffice for us to describe our construction. To analyze the scheme, we need to encode a simulated public key and evaluate the simulated key. Due to lack of space, we present details on these simulated encodings and evaluations, plus some useful lemmas to bound the norm of errors in the simulation, in full version. As mentioned in the Introduction, these new bounds play a critical, technical role in our formal proof of flexible bi-deniability.

4.2 Construction of Flexibly Bi-Deniable ABE for Branching Programs

In this part, we present our flexibly bi-deniable AB-BTS scheme for bounded- length Branching Programs. We use a semantically-secure public key encryption $\Pi = (\mathsf {Gen}', \mathsf {Enc} ', \mathsf {Dec} ')$ with message space $\mathcal {M}_{\Pi } \!\!=\!\! \mathbb {Z}_q^{m \times m}$ and ciphertext space $\mathcal {C}_{\Pi }$. For a family of branching programs of length bounded by L and input space $\{0,1\}^\ell$, the description of $\mathsf {BiDenAB\text {-}BTS}$ = $(\mathsf {Setup}, \mathsf {Den} \mathsf {Setup}, \mathsf {Keygen}, \mathsf {SampleP},\mathsf {SampleU},\mathsf {TestP}, \mathsf {FakeRCoins}, \mathsf {FakeSCoins})$ are as follows:

• $\mathsf {Setup} (1^\lambda , 1^L, 1^\ell )$: On input the security parameter $\lambda$, the length of the branching program L and length of the attribute vector $\ell$,

  • 1. Set the LWE dimension be $n = n(\lambda )$, modulus $q = q(n, L)$. Choose Gaussian distribution parameter $s = s(n)$. Let $\mathsf {params}= (n, q, m, s)$.

  • 2. Sample one random matrix associated with its trapdoor as

    $$\begin{aligned} (\mathbf {A}, \mathbf {T}_{\mathbf {A}}) \leftarrow \mathsf{TrapGen}(q, n, m) \end{aligned}$$

  • 3. Choose $\ell + 6$ random matrices $\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c$ from $\mathbb {Z}_q^{n \times m}$.

  • 4. Choose a random vector $\varvec{u} \in \mathbb {Z}_q^n$.

  • 5. Compute a public/secret key pair $(\mathsf {pk} ', \mathsf {sk} ')$ for a semantically secure public key encryption $(\mathsf {pk} ', \mathsf {sk} ') \leftarrow \mathsf {Gen}'(1^\lambda )$

  • 6. Output the public parameter $\mathsf {pp}$ and master secret key $\mathsf {msk}$ as

    $$\begin{aligned} \mathsf {pp} = (\mathsf {params}, \mathbf {A}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c, \varvec{u}, \mathsf {pk} '), \quad \mathsf {msk} = (\mathbf {T}_{\mathbf {A}}, \mathsf {sk} ') \end{aligned}$$

• $\mathsf {Den} \mathsf {Setup} (1^\lambda , 1^L, 1^\ell )$: On input the security parameter $\lambda$, the length of branching program L and length of attribute vector $\ell$, the deniable setup algorithm runs the same computation as setup algorithm, and outputs

  $$\begin{aligned} \mathsf {pp} = (\mathsf {params}, \mathbf {A}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c, \varvec{u}, \mathsf {pk} '), \quad \mathsf {msk} =(\mathbf {T}_{\mathbf {A}}, \mathsf {sk} ') \quad \mathsf {fk} = (\mathbf {T}_{\mathbf {A}}, \mathsf {sk} ') \end{aligned}$$

• $\mathsf {Keygen} (\mathsf {msk}, \mathsf {BP})$: On input the master secret key $\mathsf {msk}$ and the description of a branching program $\mathsf {BP}$, $\mathsf {BP}= (\varvec{v}_0, \{\mathsf {var}(t), \{\gamma _{t, i, 0}, \gamma _{t, i, 1}\}_{i \in [5]}\}_{t \in [L]})$.

  • 1. Homomorphically compute a public matrix with respect to the branching program $\mathsf {BP}$: $\mathbf {V}_\mathsf {BP}\leftarrow \mathsf {Eval}_\mathsf {pk} (\mathsf {BP}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c)$.

  • 2. Sample a low norm vector $\varvec{r}_\mathsf {BP}\in \mathbb {Z}_q^{2m}$, using

    $$\begin{aligned} \varvec{r}_\mathsf {BP}\leftarrow \mathsf{SampleLeft}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, (\mathbf {V}_\mathsf {BP}+ \mathbf {G}), \varvec{u}, sq) \end{aligned}$$

    such that $\varvec{r}_\mathsf {BP}^T \cdot [\mathbf {A} | \mathbf {V}_\mathsf {BP}+ \mathbf {G}] = \varvec{u}$.

  • 3. Output the secret key $\mathsf {sk} _\mathsf {BP}$ for branching program as $\mathsf {sk} _\mathsf {BP}= (\varvec{r}_\mathsf {BP}, \mathsf {BP})$.

• $\mathsf {SampleP}(\mathsf {pp}, \varvec{x})$: On input public parameters $\mathsf {pp}$ and attribute $\varvec{x}$,

  • 1. Choose an LWE secret $\varvec{s} \in \mathbb {Z}_q^n$ uniformly at random.

  • 2. Choose noise vector $\varvec{e} \leftarrow \mathcal {D}_{\mathbb {Z}_q^m, \alpha }$, and compute $\psi _0 = \varvec{s}^T \mathbf {A} + \varvec{e}$.

  • 3. Choose one random matrices $\mathbf {R}^c \leftarrow \{-1, 1\}^{m \times m}$, and let $\varvec{e}^c = \varvec{e}^T \mathbf {R}^c$. Compute an encoding of constant 1: $\psi ^c = \varvec{s}^T (\mathbf {A}^c + \mathbf {G}) + \varvec{e}^c$.

  • 4. Encode each bit $i \in [\ell ]$ of the attribute vector:

    • (a) Choose a random matrix $\mathbf {R}_i \leftarrow \{-1, 1\}^{m \times m}$, and let $\varvec{e}_i = \varvec{e}^T \mathbf {R}_i$.

    • (b) Compute $\psi _i = \varvec{s}^T(\mathbf {A}_i + x_i \mathbf {G}) + \varvec{e}_i$.

  • 5. Encode the initial state vector $\varvec{v}_0 = (1,0,0,0,0)$, for $i \in [5]$

    • (a) Choose a random matrix $\mathbf {R}'_{0, i} \leftarrow \{-1, 1\}^{m \times m}$, and let 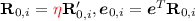, where the noise scaling parameter 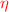is set in Sect. 4.3.

    • (b) Compute $\psi _{0, i} = \varvec{s}^T(\mathbf {V}_{0, i} + \varvec{v}_0[i] \mathbf {G}) + \varvec{e}_{0, i}$.

  • 6. Compute $c = \varvec{s}^T \varvec{u} + e$, where $e \leftarrow \mathcal {D}_{\mathbb {Z}_q, s}$

  • 7. Use PKE to encrypt randomly chosen matrices $\mathbf {R}^c, \{\mathbf {R}_i\}_{i \in [\ell ]}$ and $\{\mathbf {R}_{0, i}\}_{i \in [5]}$:

    $$\begin{aligned} \mathbf {T}_i \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}_i), \mathbf {T}^c \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}^c), \mathbf {T}_{0, i} \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}_{0, i}) \end{aligned}$$

  • 8. Output the ciphertext

    $$\begin{aligned} \mathsf {ct}_{\varvec{x}} = (\varvec{x}, \psi _0, \{\psi _i\}_{i \in [\ell ]}, \psi ^c, \{\psi _{0, i}\}_{i \in [5]}, c, \{\mathbf {T}_i\}_{i \in [\ell ]}, \mathbf {T}^c, \{\mathbf {T}_{0, i}\}_{i \in [5]}) \end{aligned}$$

• $\mathsf {SampleU}(\mathsf {pp}, \varvec{x})$: Output a uniformly random vector $\mathsf {ct}\in \mathbb {Z}_q^m \times \mathbb {Z}_q^{\ell m} \times \mathbb {Z}_q^{\ell m} \times \mathbb {Z}_q^{5m} \times \mathbb {Z}_q \times \mathcal {C}_{\Pi }^\ell \times \mathcal {C}_{\Pi } \times \mathcal {C}_{\Pi }^5$.

• $\mathsf {TestP}(\mathsf {sk} _\mathsf {BP}, \mathsf {ct}_{\varvec{x}})$: On input the secret key $\mathsf {sk} _\mathsf {BP}$ for a branching program $\mathsf {BP}$ and a ciphertext associated with attribute $\varvec{x}$, if $\mathsf {BP}(\varvec{x}) = 0$, output $\bot$, otherwise,

  • 1. Homomorphically compute the evaluated ciphertext of result $\mathsf {BP}(\varvec{x})$

    $$\begin{aligned} \psi _\mathsf {BP}\leftarrow \mathsf {Eval}_{\mathsf {ct}}(\mathsf {BP}, \varvec{x}, \{\mathbf {A}_i, \psi _i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}, \psi _{0, i}\}_{i \in [5]}, \{\mathbf {A}^c_i, \psi _i^c \}_{i \in [\ell ]}) \end{aligned}$$

  • 2. Then compute $\phi = [\psi _0 | \psi _\mathsf {BP}]^T \cdot \varvec{r}_\mathsf {BP}$. Accept $\mathsf {ct}_{\varvec{x}}$ as a P-sample if $|c - \phi | < 1 / 4$, otherwise reject.

• $\mathsf {FakeSCoins} (r_S)$: Simply output the P-sample $\mathbf{c}$ as the randomness $r^*_S$ that would cause $\mathsf {SampleU}$ to output $\varvec{c}_{\varvec{x}}$.

• $\mathsf {FakeRCoins} (\mathsf {pp}, \mathsf {fk}, \mathsf {ct}_{\varvec{x}}, \mathsf {BP})$: On input the public parameters $\mathsf {pp}$, the faking key $\mathsf {fk}$, a ciphertext $\mathsf {ct}_{\varvec{x}}$ and description of a branching program $\mathsf {BP}$

  • 1. If $\mathsf {BP}(\varvec{x}) \ne 0$, then output $\mathsf {sk} _f \leftarrow \mathsf {Keygen} (\mathsf {fk}, \mathsf {BP})$.

  • 2. Otherwise, parse ciphertext $\mathsf {ct}_{\varvec{x}}$ as

    $$\begin{aligned} \mathsf {ct}_{\varvec{x}} = (\varvec{x}, \psi _0, \{\psi _i\}_{i \in [\ell ]}, \psi ^c, \{\psi _{0, i}\}_{i \in [5]}, c, \{\mathbf {T}_i\}_{i \in [\ell ]}, \mathbf {T}^c, \{\mathbf {T}_{0, i}\}_{i \in [5]}) \end{aligned}$$

    Compute $\varvec{e} \leftarrow \mathsf {Invert}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, \psi _0)$. Then decrypt $(\{\mathbf {T}_i\}_{i \in [\ell ]}, \mathbf {T}^c, \{\mathbf {T}_{0, i}\}_{i \in [5]})$ respectively using $\mathsf {Dec} (\mathsf {sk} ', \cdot )$ to obtain $\{\mathbf {R}_i \}_{i \in [\ell ]}, \mathbf {R}^c, \{\mathbf {R}_{0, i}\}_{i \in [5]}$. Compute evaluated error

    $$\begin{aligned} \varvec{e}_{\mathsf {BP}} \leftarrow \mathsf {Eval}_{\mathsf {ct}}(\mathsf {BP}, \varvec{x}, \{\mathbf {A}_i, \varvec{e}^T \mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}, \varvec{e}^T \mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c, \varvec{e}^T \mathbf {R}^c \}) \end{aligned}$$

    such that $\varvec{e}_\mathsf {BP}= \varvec{e}^T \mathbf {R}_{\mathsf {BP}}$.

  • 3. Homomorphically compute a public matrix with respect to the branching program $\mathsf {BP}$: $\mathbf {V}_\mathsf {BP}\leftarrow \mathsf {Eval}_\mathsf {pk} (\mathsf {BP}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c_i\}_{i \in [\ell ]})$. Then sample a properly distributed secret key $\varvec{r}_\mathsf {BP}\in \mathbb {Z}_q^{2m}$, using

    $$\begin{aligned} \varvec{r}_\mathsf {BP}\leftarrow \mathsf{SampleLeft}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, (\mathbf {V}_\mathsf {BP}+ \mathbf {G}), \varvec{u}, s) \end{aligned}$$

  • 4. Sample correlation vector $\mathbf {y}_0 \leftarrow \mathcal {D}_{\mathbb {Z}_q^{m}, \beta ^2 q^2 \mathbf {I}_{m \times m}}$. Then sample correlation coefficient $\mu \leftarrow \mathcal {D}_{\gamma }$, and set vector $\varvec{y}_1 = (\mu \varvec{e}_\mathsf {BP}+ \mathcal {D}_{\mathbf {Z}^m, \mathbf {Q}}) q$, where

    $$\begin{aligned} \mathbf {Q} = \beta ^2 \mathbf {I}_{m \times m} - \gamma ^2 \alpha ^2 \mathbf {R}_\mathsf {BP}^T \mathbf {R}_\mathsf {BP}\end{aligned}$$

    (1)

  • 5. Let $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1)$, then sample and output the faked secret key $\mathsf {sk} ^*_\mathsf {BP}= \mathbf {r}^*_\mathsf {BP}$ as $\mathbf {r}^*_\mathsf {BP}\leftarrow \varvec{y} + \mathcal {D}_{\Lambda + \varvec{r}_\mathsf {BP}- \varvec{y}, \sqrt{s^2 - \beta ^2}}$, using $\mathsf{SampleD}(\mathsf{ExtBasis}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, \mathbf {V}_\mathsf {BP}+ \mathbf {G}), \varvec{r}_\mathsf {BP}- \varvec{y}, \sqrt{s^2 - \beta ^2})$, where $\Lambda = \Lambda ^\bot ([\mathbf {A} | \mathbf {V}_\mathsf {BP}+ \mathbf {G}])$.

The SampleP algorithm is similar to the ABE ciphertexts in the work [30], except that we add another scaling factor $\eta$ to the rotation matrices $\mathbf {R}_{0, i}$’s. This allows us to both upper and lower bound the noise growth, which is essential to achieve bi-deniability. Detailed analysis can be found in full version. As we discussed in the introduction, the FakeRCoins embeds the evaluated noise into the secret key, so that it will change the decrypted value of the targeted ciphertext, but not others. Next we present the theorem we achieve and a high level ideas of the proof. We defer the formal analysis after the proof intuition.

Theorem 4.2

Assuming the hardness of extended-$\mathsf {LWE} _{q, \beta '}$, the above algorithms form a secure attribute-based bitranslucent set schemem, as in Definition 3.2.

Overview of Our Security Proof. At a high level, our security proof begins at the $\mathsf {Fake}$ experiment (cf. Definition 3.1 for a formal description), where first a ciphertext $\mathsf {ct}^*$ and its associated noise terms $\varvec{e}^*$ are sampled, then a fake key $\varvec{r}^*$ is generated that “artificially” fails to decrypt any ciphertext with noise vector (oriented close to) $\varvec{e}^*$. In the end, we will arrive at the $\mathsf {Real}$ experiment, where an honest key $\varvec{r}$ is generated that “genuinely” fails to decrypt the honestly generated, coerced ciphertext $\mathsf {ct}^*$. (Multi-$\mathsf {ct}$ coercion security follows by a standard hybrid argument that repeatedly modifies respective $\varvec{r}^*$ to $\varvec{r}$ for each coerced $\mathsf {ct}^*$ in order.) In order to transition from $\mathsf {Fake}$ to $\mathsf {Real}$, we move through a sequence of computationally- or statistically-indistinguishable hybrid experiments.

The first set of intermediate experiments (represented by $\mathsf {H}_1$ and $\mathsf {H}_2$ in our formal proof) embeds the attribute $\varvec{x}$ of the challenge ciphertext $\mathsf {ct}^*$ in the public parameters, in a similar fashion to the beginning of every SIM-secure proof of lattice-based ABE. Indistinguishability follows via the Leftover Hash Lemma [21]. (Note that the additional hybrid in our proof is used to ensure that the random rotation matrices $\mathbf {R}$ employed by the LHL for public key embedding of $\varvec{x}$ are the exact same matrices $\mathbf {R}$ as used to generate the noise terms of the coerced $\mathsf {ct}^*$, and uses the security of any semantically-secure PKE for computational indistinguishability.)

The next set of intermediate experiments (given by $\mathsf {H}_3, \mathsf {H}_4,$ and $\mathsf {H}_5$ in our formal proof) perform the “main, new work” of our security proof. Specifically, they “swap the order” of the generation of the $\mathsf {pk}$ matrices $\{\mathbf {A}\}$, the public coset $\varvec{u}$ (in the public parameters and in the coerced ciphertext), and the error vector(s) $\varvec{e}$ in the coerced ciphertext components. (An additional hybrid is used to toggle the order of a “correlation vector” $\varvec{y}$ – a random, planted vector used to allow for a more modular analysis of these steps.) In each case, we give a statistical argument that the adversary’s view in adjacent hybrids is indistinguishable or identical, using elementary properties of multi-dimensional Gaussians.

In the next step (given by $\mathsf {H}_6$), we apply the $\mathsf {e}\mathsf {LWE} ^+$ assumption to (roughly) change every component of the coerced ciphertext $\mathsf {ct}^*$ to uniform – except for the final $c^*$ component used to blind the message $\mu$.

In the final step (given by $\mathsf {H}_7$), we transition to the $\mathsf {Real}$ experiment by changing the $c^*$ component to uniform (in the presence of Dual Regev decryption under honest $\varvec{z}$), using our sharper noise analysis as described above to show statistical indistinguishability of the final decryption output of $\varvec{z}$ on $\mathsf {ct}^*$.

Lemma 4.3

For parameters set in Sect. 4.3, the AB-BTS defined above satisfies the correctness property in Definition 3.2.

Proof

As we mentioned in Remark 3.3, the correctness of faking algorithms is implied by the bi-deniability property. Therefore, we only need to prove the correctness of normal decryption algorithm. For branching program $\mathsf {BP}$ and input $\varvec{x}$, such that $\mathsf {BP}(\varvec{x}) = 1$, we compute $\psi _{t, i}$ for $t \in [\ell ]$ as

$$\begin{aligned} \psi _{t, i}&= \mathsf{Add} (\mathsf {Mult}(\psi '_{\mathsf {var}(t)}, \psi _{t - 1, \gamma _0}), \mathsf {Mult}(\psi _{\mathsf {var}(t)}, \psi _{t - 1, \gamma _1})) \\&= \mathsf{Add} \bigg ([\varvec{s}^T(-\mathbf {A}'_{\mathsf {var}(t)} \mathbf {G}^{-1}(\mathbf {V}_{t - 1, \gamma _0}) + (\varvec{v}_t[\gamma _0] \cdot (1 - x_{\mathsf {var}(t)})) \cdot \mathbf {G}) + \varvec{e}_1], \\&\qquad ([\varvec{s}^T(-\mathbf {A}'_{\mathsf {var}(t)} \mathbf {G}^{-1}(\mathbf {V}_{t - 1, \gamma _1}) + (\varvec{v}_t[\gamma _1] \cdot x_{\mathsf {var}(t)}) \cdot \mathbf {G}) + \varvec{e}_2] \bigg ) \\&= \varvec{s}^T \bigg [ \underbrace{\big (-\mathbf {A}'_{\mathsf {var}(t)} \mathbf {G}^{-1}(\mathbf {V}_{t - 1, \gamma _0}) - \mathbf {A}'_{\mathsf {var}(t)} \mathbf {G}^{-1}(\mathbf {V}_{t - 1, \gamma _1}) \big )}_{\mathbf {V}_{t, i}} \\&\qquad + \underbrace{\big ( \varvec{v}_t[\gamma _0] \cdot (1 - x_{\mathsf {var}(t)}) + \varvec{v}_t[\gamma _1] \cdot x_{\mathsf {var}(t)}\big )}_{\varvec{v}_t[i]} \cdot \mathbf {G}\bigg ] + \varvec{e}_{t, i} \end{aligned}$$

At the end of the ciphertext evaluation, since $\mathsf {BP}(\varvec{x}) = 1$, we can obtain $\psi _{\mathsf {BP}} = \varvec{s}^T(\mathbf {V}_{\mathsf {BP}} + \mathbf {G}) + \varvec{e}_{\mathsf {BP}}$, where $\varvec{e}_\mathsf {BP}= \varvec{e}^T \mathbf {R}_{\mathsf {BP}}$. Recall that the secret key $\mathsf {sk} = \varvec{r}_\mathsf {BP}$ satisfying $[\mathbf {A} | \mathbf {V}_{\mathsf {BP}} + \mathbf {G}] \cdot \varvec{r}_\mathsf {BP}= \varvec{u}$. Then for $c - [\psi _0 | \psi _\mathsf {BP}] \cdot \varvec{r}_\mathsf {BP}$, it holds that

$$\begin{aligned} c - [\psi _0 | \psi _\mathsf {BP}]^T \cdot \varvec{r}_\mathsf {BP}= e - \varvec{e}^T \mathbf {R}_{\mathsf {BP}} \cdot \varvec{r}_\mathsf {BP}\end{aligned}$$

Now we need to compute a bound for the final noise term. By applying analysis of norm in full version, we obtain that

$$\begin{aligned} ||\varvec{e}^T|| \cdot ||\mathbf {R}_{\mathsf {BP}} || + 2m^{1.5} \ell ||e|| \le (2m^{1.5} \ell + \eta \sqrt{m}) ||\varvec{e}|| \le \alpha \sqrt{m}(2m^{1.5} \ell + \eta \sqrt{m}) \cdot sq \sqrt{m} \le \frac{1}{4} \end{aligned}$$

So by setting the parameters appropriately, as in Sect. 4.3, we have that

$$\begin{aligned} |c - [\psi _0 | \psi _\mathsf {BP}]^T \cdot \varvec{r}_\mathsf {BP}| \le 1 / 4 \end{aligned}$$

and the lemma follows.   $\square$

Lemma 4.4

Assuming the hardness of extended-$\mathsf {LWE} _{q, \beta '}$, the AB-BTS scheme described above is bi-deniable as defined in Definition 3.2.

Proof

First, we notice that because $\mathsf {SampleU}$ simply outputs its random coins as a uniformly random $\mathsf {ct}$, we can use $\mathsf {ct}$ itself as the coins.

We prove the bi-deniability property by a sequence of hybrids $\mathsf {H}_i$ with details as follows:  

Hybrid $\mathsf {H}_0$::

Hybrid $\mathsf {H}_0$ is the same as the view of adversary $\mathcal {A}$ in the right-hand faking experiment in the definition of bi-deniability. We use the fact that algorithm $\mathsf{Invert}$ successfully recovers $\varvec{e}$ from $\mathsf {ct}$ with overwhelming probability over all randomness in the experiment.

Hybrid $\mathsf {H}_1$::

In hybrid $\mathsf {H}_2$, we switch the encryptions of matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \mathbf {R}^c)$ in the ciphertext to encryptions of zero. Recall that in hybrid $\mathsf {H}_0$, we encrypt the randomness matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \mathbf {R}^c)$ using semantically secure PKE $\Pi$, i.e.

$$\begin{aligned} \mathbf {T}_i \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}_i), \quad \mathbf {T}^c \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}^c), \quad \mathbf {T}_{0, i} \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {R}_{0, i}) \end{aligned}$$

In hybrid $\mathsf {H}_1$, we just set

$$\begin{aligned} \mathbf {T}_i \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {0}), \quad \mathbf {T}^c \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {0}), \quad \mathbf {T}_{0, i} \leftarrow \mathsf {Enc} '(\mathsf {pk} ', \mathbf {0}) \end{aligned}$$

to be encryptions of $\mathbf {0}\in \mathbb {Z}^{m \times m}$ to replace encryptions of matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \mathbf {R}^c)$.

Hybrid $\mathsf {H}_2$::

In hybrid $\mathsf {H}_2$, we embed random matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \mathbf {R}^c)$ and challenge attribute $\varvec{x}^*$ in the public parameters $\mathsf {pp}$. Recall that in hybrid $\mathsf {H}_1$ the matrices $(\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c)$ are sampled at random. In hybrid $\mathsf {H}_2$, we slightly change how these matrices are generated. Let $\varvec{x}^* = (x^*_1,..., x^*_\ell )$ be the challenge attribute that the adversary $\mathcal {A}$ intends to attack. We sample matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}'_{0, i}\}_{i \in [5]}, \mathbf {R}^c)$ uniformly random from $\{-1, 1\}^{m \times m}$ and set $\mathbf {R}_{0, i} = \eta \mathbf {R}'_{0, i}$, which would be used both in the generation of public parameters and challenge ciphertext. We set $(\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c)$ respectively as

$$\begin{aligned} \mathbf {A}_i = \mathbf {A}\mathbf {R}_i - x^*_i \mathbf {G}, \quad \mathbf {V}_{0, i} = \mathbf {A} \mathbf {R}_{0, i} - \varvec{v}_0[i] \mathbf {G}, \quad \mathbf {A}^c = \mathbf {A} \mathbf {R}^c - \mathbf {G}\end{aligned}$$

where $\varvec{v}_0 = [1,0,0,0,0]$. The rest of the hybrid remains unchanged.

Hybrid $\mathsf {H}_3$::

In hybrid $\mathsf {H}_3$, we change the generation of matrix $\mathbf {A}$ and vector $\varvec{u}$ in public parameters $\mathsf {pp}$.

Let $\mathbf {A}$ be a random matrix in $\mathbb {Z}_q^{n \times m}$. The construction of matrices $(\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c)$ remains the same, as in hybrid $\mathsf {H}_2$. Sample error vectors $\varvec{e}$ that would be used in algorithm $\mathsf {SampleP}$ later. Then compute the error vector

$$\begin{aligned} \varvec{e}_{\mathsf {BP}^*} \leftarrow \mathsf {Eval}_{\mathsf {ct}}(\mathsf {BP}, \varvec{x}, \{\mathbf {A}_i, \varvec{e}^T \mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}, \varvec{e}^T \mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c, \varvec{e}^T \mathbf {R}^c\}) \end{aligned}$$

and choose a correlation coefficient $\mu \leftarrow \mathcal {D}_{\gamma }$, and set vector $\varvec{y}_1 = (\mu \varvec{e}_{\mathsf {BP}^*} + \mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}})q$, where

$$\begin{aligned} \mathbf {Q} = \beta ^2 \mathbf {I}_{m \times m} - \gamma ^2 \alpha ^2 \mathbf {R}_{\mathsf {BP}^*}^T \mathbf {R}_{\mathsf {BP}^*} \end{aligned}$$

Then let $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1)$, where $\varvec{y}_0 \leftarrow \mathcal {D}_{\mathbf {Z}_q^{m}, \beta ^2 q^2 \mathbf {I}_{m \times m}}$. Sample vector $\mathbf {r}_{\mathsf {BP}^*} \leftarrow \varvec{y} +\mathcal {D}_{\mathbb {Z}^{2m} - \varvec{y}, (s^2 - \beta ^2)q^2 \mathbf {I}_{2m \times 2m}}$, and compute matrix

$$\begin{aligned} \mathbf {V}_{\mathsf {BP}^*} \leftarrow \mathsf {Eval}_\mathsf {pk} (\mathsf {BP}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \mathbf {A}^c) \end{aligned}$$

Set vector $\varvec{u}$ in public parameters $\mathsf {pp}$ as $\mathbf {u} = [\mathbf {A} | \mathbf {V}_{\mathsf {BP}^*}] \cdot \mathbf {r}_{\mathsf {BP}^*}$. Since $\mathbf {A}$ is a random matrix without trapdoor $\mathbf {T}_{\mathbf {A}}$ to answer key queries, we will use trapdoor $\mathbf {T}_\mathbf {G}$ to answer queries as follows. Consider a secret key query for branching program $\mathsf {BP}$ such that $\mathsf {BP}(\varvec{x}^*) = 0$. To respond, we do the following computations:

1.:

First, we compute

$$\begin{aligned} \mathbf {R}_\mathsf {BP}\leftarrow \mathsf {Eval}_\mathsf {Sim} (\mathsf {BP}, \varvec{x}, \{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \mathbf {R}^c, \mathbf {A}) \end{aligned}$$

to obtain a low-norm matrix $\mathbf {R}_\mathsf {BP}\in \mathbb {Z}_q^{m \times m}$ satisfying $\mathbf {A}\mathbf {R}_\mathsf {BP}- \mathsf {BP}(\varvec{x}^*) \mathbf {G}= \mathbf {V}_\mathsf {BP}$.

2.:

Then, we sample $\varvec{r}_\mathsf {BP}$ using

$$\begin{aligned} \varvec{r}_\mathsf {BP}\leftarrow \mathsf{SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}_\mathsf {BP}, \mathbf {T}_{\mathbf {G}}, \varvec{u}, sq) \end{aligned}$$

such that

$$\begin{aligned} \varvec{r}_\mathsf {BP}^T \cdot [\mathbf {A} | \mathbf {V}_\mathsf {BP}+ \mathbf {G}] = \varvec{u} \end{aligned}$$

By property of algorithm $\mathsf{SampleRight}$, vector $\varvec{r}_\mathsf {BP}$ is distributed as required.

The computation of answering P-sampler query, $\mathsf {SampleP}$ is the same as hybrid $\mathsf {H}_1$ with error vectors $\varvec{e}$, For faking receiver coins, $\mathsf {FakeRCoins}$, simply output the vector $\varvec{r}_{\mathsf {BP}^*}$ pre-sampled in the generation of vector $\varvec{u}$ before.

Hybrid $\mathsf {H}_4$::

In hybrid $\mathsf {H}_4$, we change the generation order of vector $\varvec{y}$ and error vector $\varvec{e}$. First sample vector $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1) \leftarrow \mathcal {D}_{\mathbb {Z}^{2m}, \beta ^2 q^2 \mathbf {I}_{2m \times 2m}}$ and compute $\varvec{r}_{\mathsf {BP}^*}$ from $\varvec{y}$ as in previous hybrid. Next, we compute error term $\varvec{e}$ as $\varvec{e} = \nu \varvec{y}_1^T \mathbf {R}_{\mathsf {BP}^*} / q + \mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}'}$, where $\nu \leftarrow \mathcal {D}_\tau , \tau = \gamma \alpha ^2 / \beta ^2$, and $\mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}'}$ is sampled as $\mathbf {L}' \mathcal {D}_{\mathbf {Z}_1^m, \mathbf {I}_{m \times m}}$ for

$$\begin{aligned} \mathbf {Q}' = \mathbf {L}' \mathbf {L}'^T = \alpha ^2 \mathbf {I} - \tau ^2 \beta ^2 \mathbf {R}_{\mathsf {BP}^*}^T \mathbf {R}_{\mathsf {BP}^*} \end{aligned}$$

(2)

Additionally, we modify the challenge ciphertext to be

$$\begin{aligned} \psi ^*_0 = \varvec{s}^T \mathbf {A} / q + \varvec{e}, \quad \psi ^*_i = \psi ^{*T}_0 \mathbf {R}_i / q, \quad \psi ^*_{0, i} = \psi ^{*T}_0 \mathbf {R}_{0, i} / q, \quad \psi ^{*c} = \psi ^{*T}_0 \mathbf {R}^c / q \end{aligned}$$

and $c^*= \varvec{s}^T \varvec{u} + \mathcal {D}_{\mathbf {Z}^m, \alpha \mathbf {I}_{m \times m }}$.

Hybrid $\mathsf {H}_5$::

In hybrid $\mathsf {H}_5$, we change the generation order of secret key $\varvec{r}_{\mathsf {BP}^*}$ and vector $\varvec{y}$.

We first sample matrix $\varvec{r}_{\mathsf {BP}^*}$ from discrete Gaussian distribution $\mathcal {D}_{\mathbb {Z}^{2m}, s^2 q^2 \mathbf {I}_{2m \times 2m}}$, and set vector $\varvec{u}$ in public parameters $\mathsf {pp}$ to be $\varvec{u} = [\mathbf {A} | \mathbf {V}_{\mathsf {BP}^*}] \cdot \varvec{r}_{\mathsf {BP}^*}$, where

$$\begin{aligned} \mathbf {V}_{\mathsf {BP}^*} \leftarrow \mathsf {Eval}_\mathsf {pk} (\mathsf {BP}, \{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c_i\}_{i \in [\ell ]}) \end{aligned}$$

Then set $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1) = \varvec{r}_{\mathsf {BP}^*} / 2+ \mathcal {D}_{\mathbb {Z}^{2m}, (\beta ^2 - s^2 / 4)q^2 \mathbf {I}_{2m \times 2m}}$. The remainder of the hybrid remains roughly the same. In particular, the challenge ciphertext $\mathsf {ct}^*$ is generated in the same manner as Hybrid $\mathsf {H}_4$. We break the noise term $\varvec{e}$ into two terms $\varvec{e} = \varvec{e}_0^{(1)} + \varvec{e}_0^{(2)} + \nu \varvec{y}_1^T \mathbf {R}_{\mathsf {BP}^*} / q$, where $\varvec{e}_0^{(1)} \leftarrow \mathcal {D}_{\mathbb {Z}^m, \beta '\mathbf {I}_{m \times m}}, \varvec{e}_0^{(2)} \leftarrow \mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}' - \beta '^2 \mathbf {I}_{m \times m}}$ and $\beta ' = \alpha / 2$.

Hybrid $\mathsf {H}_6$::

In hybrid $\mathsf {H}_6$, we change how the challenge ciphertext is generated by using the Extended-LWE$^+$ instance. First sample uniformly random vector $\varvec{b} \in \mathbb {Z}^m$ and set the challenge ciphertext as

$$\begin{aligned} \psi ^*_0 = \varvec{b} / q + \varvec{e}_0^{(2)}, \quad \psi ^*_i = \psi ^{*T}_0 \mathbf {R}_i / q, \quad \psi ^*_{0, i} = \psi ^{*T}_0 \mathbf {R}_{0, i} / q, \quad \psi ^{*c} = \psi ^{*T}_0 \mathbf {R}^c / q\end{aligned}$$

and $c^*=\varvec{r}^T_{\mathsf {BP}^*} [\mathbf {I}_{m \times m} | \mathbf {R}_{\mathsf {BP}^*}] (\varvec{b} / q - \varvec{e}_0^{(1)}) + \mathcal {D}_{\mathbb {Z}^m, \alpha \mathbf {I}_{m \times m}}$.

Hybrid $\mathsf {H}_7$::

In hybrid $\mathsf {H}_7$, we change the challenge ciphertext to be uniformly random. In algorithm $\mathsf {SampleP}$, sample uniformly random vectors $\mathsf {ct}\in \mathbb {Z}_q^m \times \mathbb {Z}_q^{\ell m} \times \mathbb {Z}_q^{ m} \times \mathbb {Z}_q^{5m} \times \mathbb {Z}_q$ and outputs $\mathsf {ct}$.

 

Claim 4.5

Assuming the semantic security of PKE $\Pi = (\mathsf {Gen}', \mathsf {Enc} ', \mathsf {Dec} ')$, hybrid $\mathsf {H}_0$ and $\mathsf {H}_1$ are computationally indistinguishable.

Proof

Observe there is only one difference between hybrids $\mathsf {H}_0$ and $\mathsf {H}_1$ occurs in the challenge ciphertext, i.e. the encryption (under PKE $\Pi$) of the random matrices $\mathbf {S}_i$ are replaced by encryption of 0. If a $\textsc {ppt}$ adversary $\mathcal {A}$ distinguishes between the $\mathsf {H}_0$-encryptions of $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {R}^c\})$ and the $\mathsf {H}_1$-encryptions of $\mathbf {0}$ with non-negligible probability, then we can construct an efficient reduction $\mathcal {B}$ that uses $\mathcal {A}$ to break the semantic security of PKE $\Pi$ with similar probability.    $\square$

Claim 4.6

Hybrids $\mathsf {H}_1$ and $\mathsf {H}_2$ are statistically indistinguishable.

Proof

Observe the only difference between hybrids $\mathsf {H}_1$ and $\mathsf {H}_2$ is the generation of matrices

$$\begin{aligned} (\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c_i\}_{i \in [\ell ]}) \end{aligned}$$

The random matrices $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {R}^c_i\}_{i \in [\ell ]})$ are used in the generation of public parameters $\mathsf {pp}$:

$$\begin{aligned} \mathbf {A}_i = \mathbf {A}\mathbf {R}_i - x^*_i \mathbf {G}, \quad \mathbf {V}_{0, i} = \mathbf {A} \mathbf {R}_{0, i} - \varvec{v}_0[i] \mathbf {G}, \quad \mathbf {A}^c = \mathbf {A} \mathbf {R}^c - \mathbf {G}\end{aligned}$$

and the construction of errors in challenge ciphertext

$$\begin{aligned} \varvec{e}_i = \varvec{e}^T \mathbf {R}_i, \quad \varvec{e}^c = \varvec{e}^T \mathbf {R}^c, \quad \varvec{e}_{0, i} = \varvec{e}^T \mathbf {R}_{0, i} \end{aligned}$$

Then by Leftover Hash Lemma 2.1, the following two distributions are statistically indistinguishable

$$\begin{aligned} (\mathbf {A}, \{\mathbf {A} \mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {A} \mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {A}\mathbf {R}^c\}, \widetilde{\varvec{e}}) \approx (\mathbf {A},\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c\}, \widetilde{\varvec{e}}) \end{aligned}$$

where $\widetilde{\varvec{e}} = (\{\varvec{e}_i\}_{i \in [\ell ]}, \{\varvec{e}_{0, i}\}_{i \in [5]}, \{\varvec{e}^c\})$. Hence, hybrid $\mathsf {H}_0$ and $\mathsf {H}_1$ are statistically indistinguishable.    $\square$

Claim 4.7

Hybrids $\mathsf {H}_2$ and $\mathsf {H}_3$ are statistically indistinguishable.

Proof

Observe there are three differences between hybrid $\mathsf {H}_2$ and $\mathsf {H}_3$: The generation of matrix $\mathbf {A}$ and vector $\varvec{u}$ in $\mathsf {pp}$, challenge secret key $\mathsf {sk} _{\mathsf {BP}^*}$ and the computation methods to answer secret key queries. By the property of algorithm $\mathsf{TrapGen}(q, n, m)$, the distribution of matrix $\mathbf {A}$ in hybrid $\mathsf {H}_2$ is statistically close to uniform distribution, from which matrix $\mathbf {A}$ in hybrid $\mathsf {H}_3$ is sampled.

For secret key queries regarding branching program $\mathsf {BP}$, in hybrid $\mathsf {H}_2$, we sample vector $\varvec{r}_\mathsf {BP}$, using

$$\begin{aligned} \varvec{r}_\mathsf {BP}\leftarrow \mathsf{SampleLeft}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, (\mathbf {V}_\mathsf {BP}+ \mathbf {G}), \varvec{u}, s) \end{aligned}$$

While in hybrid $\mathsf {H}_3$, we sample vector $\varvec{r}_\mathsf {BP}$, using

$$\begin{aligned} \varvec{r}_\mathsf {BP}\leftarrow \mathsf{SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}_\mathsf {BP}, \mathbf {T}_{\mathbf {G}}, \varvec{u}, sq) \end{aligned}$$

By setting the parameters appropriately as specified in Sect. 4.3, and the properties of algorithms $\mathsf{SampleLeft}$ and $\mathsf{SampleRight}$, the answers to secret key queries are statistically close.

By Leftover Hash Lemma 2.1, the distribution $([\mathbf {A} | \mathbf {V}_{\mathsf {BP}^*}], [\mathbf {A} | \mathbf {V}_{\mathsf {BP}^*}] \cdot \varvec{r}_{\mathsf {BP}^*})$ and $([\mathbf {A} | \mathbf {V}_{\mathsf {BP}^*}], \varvec{u})$ are statistically close. Hence, hybrid $\mathsf {H}_2$ and $\mathsf {H}_3$ are statistically indistinguishable.    $\square$

Claim 4.8

Hybrids $\mathsf {H}_3$ and $\mathsf {H}_4$ are statistically indistinguishable.

Proof

The only difference between the two experiments is in the choice of $\varvec{y}$ and $\varvec{e}$, specifically, the choice of the $\varvec{y}_1$ component of $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1)$. We will show that the joint distribution of $(\varvec{e}, \varvec{y}_1)$ is identically distributed in these two hybrids:

In hybrid $\mathsf {H}_3$, $\varvec{y}_1$ is set as $\varvec{y}_1 = (\mu \varvec{e}_{\mathsf {BP}^*} + \mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}})q$, where $\mathbf {Q} = \beta ^2 \mathbf {I}_{m \times m} - \gamma ^2 \alpha ^2 \mathbf {R}_{\mathsf {BP}^*}^T \mathbf {R}_{\mathsf {BP}^*}$ with $\varvec{e} \leftarrow \mathcal {D}_{\mathbb {Z}^m, \alpha ^2 \mathbf {I}_{m \times m}}$ and

$$\begin{aligned} \varvec{e}_{\mathsf {BP}^*} \leftarrow \mathsf {Eval}_{\mathsf {ct}}(\mathsf {BP}, \varvec{x}, \{\mathbf {A}_i, \varvec{e}^T \mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}, \varvec{e}^T \mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c, \varvec{e}^T \mathbf {R}^c \}) \end{aligned}$$

Therefore, in hybrid $\mathsf {H}_3$, we may write the joint distribution of $(\varvec{e}, \varvec{y}_1)$ as $\mathbf {T}_1 \cdot \mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}}$, where $\mathbf {T}_1 \mathop {=}\limits ^\mathrm{def} \left( \begin{array}{cc} \alpha \mathbf {I}_{m\times m} &{} \mathbf {0}_{m\times m} \\ \gamma \alpha q \mathbf {R}_{\mathsf {BP}^*}^{T} &{} q\mathbf {L} \end{array}\right)$ for $\mathbf {Q} = \mathbf {L}\mathbf {L}^T \in \mathbb {Z}^{m\times m}$ via the Cholesky decomposition Lemma in full version.

In hybrid $\mathsf {H}_4$, vector $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1)$ is sampled as $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1) \leftarrow \mathcal {D}_{\mathbb {Z}^{2m}, \beta ^2 q^2 \mathbf {I}_{2m \times 2m}}$. Then $\varvec{e}$ is computed as $\varvec{e} = \nu \varvec{y}_1^T \mathbf {R}_{\mathsf {BP}^*} / q + \mathcal {D}_{\mathbb {Z}^m, \mathbf {Q}'}$, where $\nu \leftarrow \mathcal {D}_\tau , \tau = \gamma \alpha ^2 / \beta ^2$, and $\mathbf {Q}' = \alpha ^2 \mathbf {I} - \tau ^2 \beta ^2 \mathbf {R}_{\mathsf {BP}^*}^T \mathbf {R}_{\mathsf {BP}^*}$. Then in hybrid $\mathsf {H}_4$, we may write the joint distribution of $(\varvec{e}, \varvec{y}_1)$ as $\mathbf {T}_2 \cdot \mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}}$, where $\mathbf {T}_2 \mathop {=}\limits ^\mathrm{def} \left( \begin{array}{cc} \mathbf {L}' &{} \tau \beta \mathbf {R}_{\mathsf {BP}^*} \\ \mathbf {0}_{m\times m} &{} \beta q \mathbf {I}_{m\times m} \end{array}\right)$ for $\mathbf {Q}' = \mathbf {L}'\mathbf {L}'^T \in \mathbb {Z}^{m\times m}$ via the Cholesky decomposition Lemma in full version.

We claim equality of the following systems of equations:

$$\begin{aligned} \mathbf {T}_1\mathbf {T}_1^T&= \left( \begin{array}{cc} \alpha ^2\mathbf {I}_{m\times m} &{} \gamma \alpha ^2 q \mathbf {R}_{\mathsf {BP}^*} \\ \gamma \alpha ^2 q \mathbf {R}_{\mathsf {BP}^*}^{T} &{} \gamma ^2\alpha ^2 q^2 \mathbf {R}_{\mathsf {BP}^*}^{T}\mathbf {R}_{\mathsf {BP}^*} + q^2 \mathbf {L}\mathbf {L}^T \end{array}\right) \\&= \left( \begin{array}{cc} \mathbf {L}'\mathbf {L}'^T+\tau ^2\beta ^2\mathbf {R}_{\mathsf {BP}^*}\mathbf {R}_{\mathsf {BP}^*}^{T} &{} \tau \beta ^2 q \mathbf {R}_{\mathsf {BP}^*}\\ \tau \beta ^2 q \mathbf {R}_{\mathsf {BP}^*}^{T} &{} \beta ^2 q^2 \mathbf {I}_{m\times m} \end{array}\right) = \mathbf {T}_2\mathbf {T}_2^T. \end{aligned}$$

This fact may be seen quadrant-wise by our choice of $\tau = \gamma \alpha ^2/\beta ^2$ and the settings of $\mathbf {Q} = \mathbf {L}\mathbf {L}^T$ and $\mathbf {Q}' = \mathbf {L}'\mathbf {L}'^T$ in Eqs. (1) and (2). It then follows that $(\mathbf {T}_2^{-1}\mathbf {T}_1)(\mathbf {T}_2^{-1}\mathbf {T}_1)^{T} = \mathbf {I}_{2m\times 2m},$ implying $\mathbf {T}_1 = \mathbf {T}_2 \mathbf {Q}^*$ for some orthogonal matrix $\mathbf {Q}^*$. Because the spherical Gaussian $\mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}}$ is invariant under rigid transformations, we have $\mathbf {T}_1\cdot \mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}} = \mathbf {T}_2\mathbf {Q}^*\cdot \mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}} = \mathbf {T}_2\cdot \mathcal {D}_{\mathbb {Z}^{2m}, \mathbf {I}_{2m \times 2m}},$ and the claim follows.   $\square$

Claim 4.9

Hybrids $\mathsf {H}_4$ and $\mathsf {H}_5$ are statistically indistinguishable.

Proof

Observe the main difference between hybrids $\mathsf {H}_4$ and $\mathsf {H}_5$ is the order of generation of vectors $\varvec{y}$ and $\varvec{r}_{\mathsf {BP}^*}$: In hybrid $\mathsf {H}_4$, we first sample $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1) \leftarrow \mathcal {D}_{\mathbb {Z}^{2m}, \beta ^2 q^2 \mathbf {I}_{2m \times 2m}}$ and set $\varvec{r}_{\mathsf {BP}^*} \leftarrow \varvec{y} + \mathcal {D}_{\mathbb {Z}^{2m} - \varvec{y}, q^2 (s^2 - \beta ^2) \mathbf {I}_{2m \times 2m}}$, while in hybrid $\mathsf {H}_5$, we first sample $\varvec{r}_{\mathsf {BP}^*} \leftarrow \mathcal {D}_{\mathbb {Z}^{2m}, s^2 q^2 \mathbf {I}_{2m \times 2m}}$ and set $\varvec{y} = (\varvec{y}_0 | \varvec{y}_1) \leftarrow \varvec{r}_{\mathsf {BP}^*} / 2 + \mathcal {D}_{\mathbb {Z}^{2m}, (\beta ^2 - s^2 / 4)q^2 \mathbf {I}_{2m \times 2m}}$. By setting parameters appropriately as in Sect. 4.3, these two distributions are statistically close.   $\square$

Claim 4.10

Assuming the hardness of extended-$\mathsf {LWE} ^+ _{n,m,q, D_{\mathbb {Z}^m, \beta '},\mathbf {R}}$ for any adversarially chosen distribution over matrices $\mathbf {R}\in \mathbb {Z}_q^{m\times m},$ then hybrids $\mathsf {H}_5$ and $\mathsf {H}_6$ are computationally indistinguishable.

Proof

Suppose $\mathcal {A}$ has non-negligible advantage in distinguishing hybrid $\mathsf {H}_5$ and $\mathsf {H}_6,$ then we use $\mathcal {A}$ to construct an extended-LWE$^+$ algorithm $\mathcal {B}$ as follows:  

Invocation. :

$\mathcal {B}$ invokes adversary $\mathcal {A}$ to commit to a challenge attribute vector $\varvec{x}^* = (x^*_1,...,x^*_\ell )$ and challenge branching program $\mathsf {BP}^*$. Then $\mathcal {B}$ generates $\mathbf {R}_{\mathsf {BP}^*}$ by first sampling $(\{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {R}^c\})$ as in the hybrid, and computes

$$\begin{aligned} \mathbf {R}_\mathsf {BP}\leftarrow \mathsf {Eval}_\mathsf {Sim} (\mathsf {BP}, \varvec{x}, \{\mathbf {R}_i\}_{i \in [\ell ]}, \{\mathbf {R}_{0, i}\}_{i \in [5]}, \{\mathbf {R}^c\}, \mathbf {A}) \end{aligned}$$

Then it receives an extended-LWE$^+$ instance for the matrix $\mathbf {R} = \mathbf {R}_{\mathsf {BP}^*}$ as follows:

$$\begin{aligned} \{\mathbf {A}, \varvec{b} = \varvec{s}^T \mathbf {A} + \varvec{e}, \varvec{z}_{0}, \varvec{z}_{1}, \langle \varvec{z}_{0}, \varvec{b} - \varvec{e} \rangle + e, \langle \varvec{z}_{1}^T\mathbf {R}, \varvec{b} - \varvec{e} \rangle + e'\} \end{aligned}$$

where $\mathbf {A} \overset{\$}{\leftarrow }\mathbb {Z}^{n \times m}_q,$ $\varvec{s} \overset{\$}{\leftarrow } \mathbb {Z}^n_q,$ $\varvec{u} \overset{\$}{\leftarrow } \mathbb {Z}^m_q,$ $\varvec{e}, \varvec{z}_{0},\varvec{z}_{1} \overset{\$}{\leftarrow } \chi ^n$ and $e, e' \overset{\$}{\leftarrow } \chi$. Algorithm $\mathcal {B}$ aims to leverage adversary $\mathcal {A}$’s output to solve the extended-LWE$^+$ assumption.

Setup. :

$\mathcal {B}$ generates matrices $(\{\mathbf {A}_i\}_{i \in [\ell ]}, \{\mathbf {V}_{0, i}\}_{i \in [5]}, \{\mathbf {A}^c\})$ as specified in hybrid $\mathsf {H}_1$. Then, $\mathcal {B}$ sets challenge secret key $\mathsf {sk} _{\mathsf {BP}^*} = \varvec{r}_{\mathsf {BP}^*} = (\varvec{r}^*_0 | \varvec{r}^*_1) = (\varvec{z}_0 | \varvec{z}_1)$ from extended-LWE$^+$ instance and computes vector $\varvec{u}$ as in hybrid $\mathsf {H}_5$.

Secret key queries. :

$\mathcal {B}$ answers adversary $\mathcal {A}$’s secret key queries as in hybrid $\mathsf {H}_2$.

Challenge ciphertext. :

$\mathcal {B}$ answers adversary $\mathcal {A}$’s P-sample query by setting

$$\begin{aligned} \psi ^*_0 = \varvec{b} / q + \varvec{e}_0^{(2)} + \nu \varvec{y}_1^T \mathbf {R}_{\mathsf {BP}^*} / q, \quad \psi ^*_i = \psi ^{*T}_0 \mathbf {R}_i / q, \quad \psi ^*_{0, i} = \psi ^{*T}_0 \mathbf {R}_{0, i} / q, \quad \psi ^{*c} = \psi ^{*T}_0 \mathbf {R}^c / q \end{aligned}$$

and $c^*=\varvec{r}^T_{\mathsf {BP}^*} [\mathbf {I}_{m \times m} | \mathbf {R}_{\mathsf {BP}^*}] (\varvec{b} / q - \varvec{e}^{(1)}) + \mathcal {D}_{\mathbb {Z}^m, \alpha \mathbf {I}_{m \times m}}$.

Faking receiver coin query. :

$\mathcal {B}$ answers adversary $\mathcal {A}$’s faking receiver coin query by outputting the extended-LWE instance’s vector $\mathsf {sk} _{\mathsf {BP}^*} = \varvec{r}_{\mathsf {BP}^*}$.

Output. :

$\mathcal {B}$ outputs whatever $\mathcal {A}$ outputs.

 

We can rewrite the expression of $c^{*'}$ to be

We can see that if the $\mathsf {e}\mathsf {LWE} ^+$ instance’s vector $\varvec{b}$ is pseudorandom, then the distribution simulated by $\mathcal {B}$ is exactly the same as $H_{5}$. If $\varvec{b}$ is truly random and independent, then the distribution simulated by $\mathcal {B}$ is exactly the same as $H_{6}$. Therefore, if $\mathcal {A}$ can distinguish $H_{5}$ from $H_{6}$ with non-negligible probability, then $\mathcal {B}$ can break the $\mathsf {e}\mathsf {LWE} ^+_{n,m,q,\mathcal {D}_{(\alpha /2) q}, \alpha ', \mathbf {S}_{f^*}}$ problem for some $\alpha ' \ge 0$ with non-negligible probability.    $\square$

Claim 4.11

Hybrids $\mathsf {H}_6$ and $\mathsf {H}_7$ are statistically indistinguishable.

Proof

Recall the only difference between hybrids $\mathsf {H}_6$ and $\mathsf {H}_7$ is the generation of challenge ciphertext. In hybrid $\mathsf {H}_7$, we observe if $\psi ^*_0$ is chosen from uniform distribution, then by Leftover Hash Lemma 2.1, it holds

$$\begin{aligned} \psi ^*_i = \psi ^{*T}_0 \mathbf {R}_i / q, \quad \psi ^*_{0, i} = \psi ^{*T}_0 \mathbf {R}_{0, i} / q, \quad \psi ^{*c} = \psi ^{*T}_0 \mathbf {R}^c / q \end{aligned}$$

is also uniformly random (in their marginal distribution). Therefore, it remains to show that $c^*$ is still uniformly random even conditioned on fixed samples of $(\psi ^*_0, \{\psi ^*_i\}_i, \{\psi ^*_{0, i}\}_i, \{\psi ^c\})$.

As calculated above, we can unfold the expression of $c^*$ as

$$\begin{aligned} c^* = \langle \varvec{z}_0, \varvec{b} / q - \varvec{x}^{(1)} \rangle + \langle \varvec{z}_1^T \mathbf {R}_{\mathsf {BP}^*}, \varvec{b} / q - \varvec{x}^{(1)} \rangle + \mathcal {D}_{\mathbb {Z}_1, \alpha } \end{aligned}$$

We note that $\varvec{b} / q - \varvec{x}^{(1)} = \psi ^*_0 - \varvec{x}^{(1)} - \varvec{x}^{(2)} - \nu \mathbf {R}_{\mathsf {BP}^*} \varvec{y}_1 / q$, thus if we show that

$$\begin{aligned} \langle \mathbf {R}_{\mathsf {BP}^*} \varvec{z}_1, \nu \mathbf {R}_{\mathsf {BP}^*} \varvec{y}_1 / q \rangle \end{aligned}$$

is close to uniform distribution (modulo 1), then $c^*$ will also be close to the uniform distribution (modulo 1), as $c^*$ is masked by this uniformly random number. Recall in hybrids, we set $\varvec{y}_1 = \varvec{z}_1 / 2 + \text {(shift)}$, so it is sufficient to analyze

$$\begin{aligned} \langle \mathbf {R}_{\mathsf {BP}^*} \varvec{z}_1, \nu \mathbf {R}_{\mathsf {BP}^*} \varvec{y}_1 / q \rangle = \nu \langle \mathbf {R}_{\mathsf {BP}^*} \varvec{z}_1, \mathbf {R}_{\mathsf {BP}^*} \varvec{z}_1 / q \rangle = \nu ||\mathbf {R}^*_{\mathsf {BP}^*} \varvec{z}_1||^2 / q \end{aligned}$$

By applying analysis of norm inductively on matrix $\mathbf {R}_{\mathsf {BP}^*}$, we can obtain that

$$\begin{aligned} ||\mathbf {R}^*_{\mathsf {BP}^*} \varvec{z}_1||^2 / q \ge \frac{(||\mathbf {R}_{0, j} \varvec{z}_1 || - \varTheta (m^{1.5}) \ell ||\varvec{z}_1||)^2}{q} \end{aligned}$$

where $\mathbf {R}_{0, j} \in \{-1, 1\}^{m \times m}$. Since vector $\varvec{z}_1$ is sampled from Gaussian with width sq, so its two-norm is at least $\sqrt{m}(sq)$ with overwhelming probability. Then by analysis of norm, the distribution $\nu ||\mathbf {R}^*_{\mathsf {BP}^*} \varvec{z}_1||^2 / q$ is a Gaussian distribution with width at least

$$\begin{aligned} d = \tau \frac{(\eta sqm - \varTheta (m^2 \ell ) sq)^2}{q} = \frac{\gamma \alpha ^2 (\eta sqm - \varTheta (m^2 \ell ) sq)^2}{\beta ^2 q} \end{aligned}$$

We recall again that $\nu$ was sampled from a Gaussian with parameter $\tau = \gamma \alpha ^2 / \beta ^2$. By our setting of parameters, we have $d/\omega (\log (n)) \ge 1$. A Gaussian with such width is statistically close to uniform in the domain $\mathbb {Z}_1$. This completes the proof of Lemma 4.4. Further, Theorem 4.2 follows from Lemmas 4.3 and 4.4. A (flexibly) bi-deniable ABE from LWE then follows.   $\square$

4.3 Parameter Setting

The parameters in Table 1 are selected in order to satisfy the following constraints:

Table 1. Parameter description and simple example setting

• To ensure correctness in Lemma 4.3, we have $\alpha sqm(\eta \sqrt{m} + 2m^{1.5}\ell )\le 1 / 4$.

• To ensure deniability in Hybrid $\mathsf {H}_7,$ we have $d/\omega (\log (n))> \frac{\gamma \alpha ^2 (\eta sqm - \varTheta (m^2 \ell sq))^2}{\beta ^2 q \omega (\log (n))} > 1$.

• To ensure large enough $\mathsf {LWE}$ noise, we need $\alpha \ge (\sqrt{n}\log ^{1+\delta }{n})/q$.

• To apply the leftover hash lemma, we need $m \ge 2n\log (q)$.

• To ensure that the matrix $\mathbf {Q}$ in $\mathsf {FakeRCoins}$ is positive definite, we have $\beta \ge \alpha \gamma \sqrt{\eta \sqrt{m} + 2m^{1.5} \ell }$; To ensure that the matrix $\mathbf {Q}'$ in the security proof is positive definite, we have $\alpha \ge \tau \beta \sqrt{\eta \sqrt{m} + 2m^{1.5} \ell }$. This constraint will also imply that in the security proof, both $\mathbf {Q}'$ and $\mathbf {Q}' - \beta ' \mathbf {I}_{m \times m}$ are positive definite (note $\beta ' = \alpha / 2$).

• To ensure hybrids $\mathsf {H}_3$ and $\mathsf {H}_5$ are well-defined, we have $s > \beta$ and $\beta > s / 2$. Let $s := (3/2)\beta$.

Regev [36] showed that for $q > \sqrt{m} / \beta ',$ an efficient algorithm for $\mathsf {LWE} _{n,m,q,\chi }$ for $\chi = \mathcal {D}_{\beta ' q}$ (and $\beta ' q \ge \sqrt{n}\omega (\log (n))$) implies an efficient quantum algorithm for approximating the $\mathsf {SIVP}$ and $\mathsf {GapSVP}$ problems, to within $\tilde{O}(n / \beta ')$ approximation factors in the worst case. Our example parameter setting yields a bi-deniable AB-BTS based on the (quantum) hardness of solving $\mathsf {SIVP}_{\widetilde{O}(n^{9.5})},$ respectively $\mathsf {GapSVP}_{\widetilde{O}(n^{9.5})}$. (We write this term to additionally absorb the $(1/q^2)$ loss from our $\mathsf {LWE}$ to $\mathsf {e}\mathsf {LWE} ^+$ reduction.) We leave further optimizing the lattice problem approximation factor to future work.

4.4 From AB-BTS to Flexible Bi-Deniable ABE

We present the instantiation of a flexible bi-deniable ABE using our AB-BTS scheme described above. We let $\varSigma ' = (\mathsf {Setup} ', \mathsf {Den} \mathsf {Setup} ', \mathsf {Keygen} ', \mathsf {SampleP}',\mathsf {SampleU}',$ $\mathsf {TestP}', \mathsf {FakeRCoins} ', \mathsf {FakeSCoins} ')$ be an AB-BTS scheme. Then the flexible bi-deniable ABE $\varSigma = (\mathsf {Setup}, \mathsf {Den} \mathsf {Setup}, \mathsf {Keygen}, \mathsf {Enc}, \mathsf {Den} \mathsf {Enc}, \mathsf {Dec}, \mathsf {SendFake}, \mathsf {RecFake})$ is:

• $\mathsf {Setup} (1^\lambda )$: Run algorithm $(\mathsf {pp} ', \mathsf {msk} ') \leftarrow \mathsf {Setup} '(1^\lambda )$ in AB-BTS and set $\mathsf {pp} = \mathsf {pp} ', \mathsf {msk} = \mathsf {msk} '$.

• $\mathsf {Den} \mathsf {Setup} (1^\lambda )$: Run algorithm $(\mathsf {pp} ', \mathsf {msk} ', \mathsf {fk} ') \leftarrow \mathsf {Den} \mathsf {Setup} '(1^\lambda )$ in AB-BTS and set $\mathsf {pp} = \mathsf {pp} ', \mathsf {msk} = \mathsf {msk} ', \mathsf {fk} = (\mathsf {fk} ' , \mathsf {msk} ')$.

• $\mathsf {Keygen} (\mathsf {msk}, f)$: Run algorithm $\mathsf {sk} '_f \leftarrow \mathsf {Keygen} '(\mathsf {msk}, f)$ in AB-BTS and set $\mathsf {sk} _f = \mathsf {sk} '_f$.

• $\mathsf {Enc} (\mathsf {pp}, \varvec{x}, \mu ; (r_S^{(1)}, r_S^{(2)}))$: On input the message $\mu \in \{0,1\}$, if $\mu = 0$, then run $c_i \leftarrow \mathsf {SampleU}'(\mathsf {pp}, \varvec{x}; r_S^{(i)})$ for $i = 1, 2$, otherwise, $\mu = 1$, run $c_1 \leftarrow \mathsf {SampleU}'(\mathsf {pp}, \varvec{x}; r_S^{(1)})$ and $c_2 \leftarrow \mathsf {SampleP}'(\mathsf {pp}, \varvec{x}; r_S^{(2)})$. Output $\mathsf {ct}_{\varvec{x}} = (c_1, c_2)$.

• $\mathsf {Den} \mathsf {Enc} (\mathsf {pp}, \varvec{x}, \mu ; (r_S^{(1)}, r_S^{(2)}))$: On input the message $\mu \in \{0,1\}$, then run $c_i \leftarrow \mathsf {SampleP}'(\mathsf {pp}, \varvec{x}; r_S^{(i)})$ for $i = 1, 2$, otherwise, $\mu = 1$, run $c_1 \leftarrow \mathsf {SampleU}'(\mathsf {pp}, \varvec{x}; r_S^{(1)})$ and $c_2 \leftarrow \mathsf {SampleP}'(\mathsf {pp}, \varvec{x}; r_S^{(2)})$. Output $\mathsf {ct}_{\varvec{x}} = (c_1, c_2)$.

• $\mathsf {Dec} (\mathsf {ct}_{\varvec{x}}, \mathsf {sk} _f)$: If $f(\varvec{x}) \ne 0$, then output $\bot$. Otherwise, parse $\mathsf {ct}_{\varvec{x}} = (c_1, c_2)$ and run $b_i \leftarrow \mathsf {TestP}'(\mathsf {sk} _f, c_i)$ for $i = 1, 2$. Output 0 if the $b_1= b_2$ and 1 if $b_1 \ne b_2$.

• $\mathsf {SendFake}(\mathsf {pp}, r_S, \mu , \mu ')$: If $\mu =\mu '$, return $r_{S}$. If $(\mu ,\mu ') = (0,1)$, then run $r_S^{*(2)}\leftarrow \mathsf {FakeSCoins} '(\mathsf {pp}, r_S^{(2)})$ and return $(r_{S}^{(1)}, r_{S}^{*(2)})$. Else if $(\mu , \mu ') = (1,0)$, run $r_S^{*(1)} \leftarrow \mathsf {FakeSCoins} '(\mathsf {pp}, r_S^{(1)})$ and return $(r_{S}^{*(1)}, r_{S}^{(2)})$.

• $\mathsf {RecFake}(\mathsf {pp}, \mathsf {fk}, \mathsf {ct}_{\varvec{x}}, f, \mu ')$: Parse $\mathsf {ct}_{\varvec{x}} = (c_1, c_2)$ and use $\mathsf {fk}$ to decrypt the ciphertext $\mathsf {ct}_{\varvec{x}}$ then obtain the plaintext $\mu$. If $\mu = \mu '$, then run the honest key generation of the BTS scheme, i.e. $\mathsf {sk} '_{f} \leftarrow \mathsf {Keygen} '(\mathsf {msk} ', f)$. Otherwise, run $\mathsf {sk} '_f \leftarrow \mathsf {FakeRCoins} '(\mathsf {pp}, \mathsf {fk}, c_{\mu +1}, f)$. Return $\mathsf {sk} '_{f}$.

Similar to the work by Canetti et al. [14] and O’Neil et al. [35], the following, desired theorem can be proven in a straightforward manner.

Theorem 4.12

Assume that $\varSigma '$ is a flexible bi-deniable AB-BTS, as in Definition 3.2. Then $\varSigma$ is a flexibly bi-deniable ABE, as in Definition 3.1.