Integrals Go Statistical: Cryptanalysis of Full Skipjack Variants

Abstract

Integral attacks form a powerful class of cryptanalytic techniques that have been widely used in the security analysis of block ciphers. The integral distinguishers are based on balanced properties holding with probability one. To obtain a distinguisher covering more rounds, an attacker will normally increase the data complexity by iterating through more plaintexts with a given structure under the strict limitation of the full codebook. On the other hand, an integral property can only be deterministically verified if the plaintexts cover all possible values of a bit selection. These circumstances have somehow restrained the applications of integral cryptanalysis.

In this paper, we aim to address these limitations and propose a novel statistical integral distinguisher where only a part of value sets for these input bit selections are taken into consideration instead of all possible values. This enables us to achieve significantly lower data complexities for our statistical integral distinguisher as compared to those of traditional integral distinguisher. As an illustration, we successfully attack the full-round Skipjack-BABABABA for the first time, which is the variant of NSA’s Skipjack block cipher.

1 Introduction

Integral attack is an important cryptanalytic technique for symmetric-key ciphers, which was originally proposed by Knudsen as a dedicated attack against Square cipher [7]. Later, Knudsen and Wagner unified it as integral attack [11]. The integral distinguisher of this attack makes use of the balanced property where one fixes a part of plaintext bits and takes all possible values for the other plaintext bits such that a specific part of the corresponding ciphertext gets balanced, i.e., each possible partial value for the ciphertext occurs exactly the same number of times. If one additional linear layer after this distinguisher is considered, the property will be that the XOR of all possible values of the specific part of ciphertext becomes zero, referred to as zero-sum property [1] throughout this paper¹. Being variants of the original integral distinguisher, saturation distinguisher [15] and multiset distinguisher [3] also use the same balanced property or zero-sum property with probability one as integral distinguisher.

Statistical saturation attack is different from integral attack, as proposed by Collard and Standaert in [6]. Here by choosing a plaintext set with some bits fixed while the others vary randomly, the statistical saturation distinguisher tracks the evolution of a non-uniform plaintext distribution through the cipher instead of observing the evolution of the plaintext bits in the integral distinguisher. In other words, the statistical saturation distinguisher requires the same inputs as the integral distinguisher, but uses the different property on the output side to distinguish between the right or wrong key guesses. As Leander showed that the statistical saturation distinguisher is identical to multidimensional linear distinguisher on average in [13], the statistical saturation distinguisher makes use of the advantage (bias or capacity) while the balanced property used in the integral distinguisher has no bias. The first publication of statistical saturation distinguisher came without a method to estimate its complexity. However, this complexity was demonstrated to be inverse proportional to the capacity or square of the capacity for the output under the chosen input set [4, 13]. Block ciphers such as PRESENT and PUFFIN are natural targets for such statistical saturation attacks as well as linear cryptanalysis, but the integral cryptanalysis has not been proven efficient for them [21, 22]. This highlights the difference between the integral distinguisher and statistical saturation distinguisher.

Integral attack has been widely used for many other block ciphers. In order to reduce the time complexity of integral attack, Moriai et al. gave a method to improve the time complexity against low degree round function for higher order differential attacks including integral attacks in [16]. Ferguson et al. proposed the partial-sum technique in [8]. Sasaki and Wang presented the meet-in-the-middle technique for integral attack on Feistel ciphers in [17].

So far the data complexity for a given integral has been determined by taking all values of a bit selection at the input of the balanced property. However, there are cases where it is possible or even desirable to shift the tradeoff from data towards time. Often it is the data requirements that exceeds the restriction while the time complexity budget of an attack is far from being exhausted. Therefore, in these cases, it is of paramount importance to reduce the data complexity of an attack to make it applicable. An interesting example of this behaviour is constituted by NSA’s Skipjack variant Skipjack-BABABABA studied at ASIACRYPT’12 [5]. It has been attacked for 31 rounds with an integral distinguisher, whereas the data complexity prohibits the attack to apply to the full 32 rounds. In this paper, we aim to remove this restriction by proposing a novel type of integral distinguisher that features a lower data complexity with non-balanced output bits that are still distinguishable from random.

1.1 Our Contributions

Integrals Go Statistical. We propose a new statistical integral distinguisher that consists in applying a statistical technique on top of the original integral distinguisher with the balanced property. The proposed statistical integral distinguisher requires less data than the original integral distinguisher. Although the balanced property does not strictly hold in the statistical integral distinguisher, we prove that the distribution of output values for a cipher can be distinguished from the distribution of output values which originate from a random permutation. This allows us to distinguish between the two distributions and to construct our statistical integral distinguisher. To quantify the advantage, let s be the number of input bits that take all possible values at some bits of the input while the other input bits are fixed. Furthermore, let t be the number of the output bits that are balanced. Then, for the original integral distinguisher, the data complexity is $\mathcal {O}(2^s).$ At the same time, by deploying our new statistical integral distinguisher, the data complexity is reduced to $\mathcal {O}(2^{s-\frac{t}{2}}).$

In summary, statistical integral attacks we propose have lower data complexity than traditional integral attacks. From [5, 19], the traditional integral distinguisher with the balanced property can be converted to a zero-correlation integral distinguisher, so our proposed statistical integral attacks can be regarded as chosen-plaintext multidimensional zero-correlation attacks.

Note that the statistical integral attack is different from the statistical saturation attack as they use different distinguishers and the statistical integral attack is efficient for word-wise ciphers but the statistical saturation attack seems to be valid for bitwise ciphers.

The effectiveness of our proposed statistical integral distinguisher is well presented with the key-recovery attack the full-round Skipjack-BABABABA.

Key Recovery Attack on Full-Round Skipjack’s Variants. Using the statistical integral cryptanalysis, we propose a first-time cryptanalysis on the full-round Skipjack-BABABABA — a variant of Skipjack suggested by Knudsen et al. [10, 12] to strengthen its resistance against impossible differential attacks. Skipjack-BABABABA has been shown to withstand truncated differentials (which implies that the impossible differentials are also thwarted). At ASIACRYPT’12, Bogdanov et al. [5] attacked 31-round Skipjack-BABABABA by utilizing a 30-round integral distinguisher. Built upon their work, we achieves the full-round attack of Skipjack-BABABABA by taking advantage of the statistical integral technique. To the best of our knowledge, this is the first full-round cryptanalysis against Skipjack-BABABABA. Moreover, we improved the previous attack on 31-round Skipjack-BABABABA in [5] with the new statistical integral distinguisher. The results are summarized in Table 1.

Table 1. Summary of attacks on Skipjack-BABABABA

Outline. The new statistical integral distinguisher is established in Sect. 2. Section 3 presents the attack on the full-round Skipjack-BABABABA and the improved attack on 31-round Skipjack-BABABABA. Finally the paper is concluded in Sect. 4.

2 Statistical Integral Distinguisher

2.1 Integral Distinguisher

In this section, we give some notions and results about the integral distinguisher with balanced property, following the description in [5]. Assume that $H:\mathbb {F}_2^n\rightarrow \mathbb {F}_2^n$ is a part of a block cipher. To be convenient and without loss of generality, we split the inputs and outputs into two parts each.

$$ H:\mathbb {F}_2^r \times \mathbb {F}_2^{s} \rightarrow \mathbb {F}_2^{t} \times \mathbb {F}_2^{u},\ H(x,y)=\left( \begin{array}{c} H_1(x,y) \\ H_2(x,y)\end{array}\right) . $$

Then we use $T_\lambda$ to denote the function H where the first r bits of its input are fixed to the value $\lambda$ and only the first t bits of the output are considered:

$$T_\lambda :\mathbb {F}_2^s\rightarrow \mathbb {F}_2^t,\ T_\lambda (y)=H_1(\lambda ,y).$$

For an integral distinguisher, if y in the above notation iterates all possible values of $\mathbb {F}_2^s$, then the output value $T_\lambda (y)$ is uniformly distributed where $n > s\ge t$ to ensure the balanced property on the t-bit. However, this uniform distribution cannot be obtained if the attacker chooses some random values (other than iterating all possible values) for y. The good side is that when considerable quantity of values of y are chosen, the distribution of $T_\lambda (y)$ can be distinguished from a random variable’s distribution. In this case, $T_\lambda (y)$ obeys multivariate hypergeometric distribution while t-bit value chosen randomly from an uniform distribution obeys multinomial distribution. These two distributions can be distinguishable from each other as they have different parameters for large number of input-output pairs N.

2.2 Statistical Integral Distinguisher

Assume that we need N different values of y to distinguish the above two distributions. A t-bit value $T_\lambda (y)\in \mathbb {F}_2^t$ is computed for each y and we allocate a counter vector $V[T_\lambda (y)],T_\lambda (y)\in \mathbb {F}_2^t$ and initialize these counters to zero. These counters are used to keep track of the number of each value $T_\lambda (y)$. Usually t is far from block size n.

It is easy to construct a simple distinguisher which can be described as follows:

• If there is one or more values of $T_{\lambda }[y]$ satisfying $V[T_{\lambda }(y)]>2^{s-t}$, then output random permutation.

• If there is no value of $T_{\lambda }[y]$ satisfying $V[T_{\lambda }(y)]>2^{s-t}$, then output actual cipher.

However, for a random permutation, the probability satisfying $V[T_{\lambda }(y)]>2^{s-t}$ is too low to distinguish from the cipher. For example, if $s=16$, $t=8$ and $N=2^{12}$ values of y are involved. For some fixed z, $0\le z \le 2^{t}-1$, the probability that $T_{\lambda }(y)=z$ is $p=2^{-8}$. Then V[z] follows a binomial distribution,

$$\begin{aligned} V[z]\sim B(N,p), \end{aligned}$$

which approximately follows a normal distribution $\phi (Np, Np(1-p))$. The probability that $V[z] >2^{s-t}=2^8$ for some fixed z is computed as follows,

$$\begin{aligned} 1-\varPhi (\frac{2^{s-t}-Np}{\sqrt{Np(1-p)}})\approx 1-\varPhi (60.12)\approx 1.1\times 10^{-787}. \end{aligned}$$

As a result, the probability that any V[z] is greater than $2^8$ is upper bounded by $256\times 1.1\times 10^{-787}$, which is too low to be detected. Thus such a distinguisher only using single counter value is invalid.

Now we will construct an efficient distinguisher by investigating the distribution of the following statistic

$$\begin{aligned} C=\sum _{T_\lambda (y)=0}^{2^t-1}\frac{(V[T_\lambda (y)]-N\cdot 2^{-t})^2}{N\cdot 2^{-t}}. \end{aligned}$$

(1)

This statistic is widely used in probability theory. It was also used in [20] for the $\chi ^{2}$ cryptanalysis on DES.

This statistic C follows different distributions determined by whether we are dealing with an actual cipher (right key guess) or a random permutation (wrong key guess).

Proposition 1

For sufficiently large N and t, the statistic $\frac{2^s-1}{2^s-N}C_{cipher}$ ($C_{cipher}$ is the statistic C for cipher) follows a $\chi ^2$-distribution with degree of freedom $2^t-1$, which means that $C_{cipher}$ approximately follows a normal distribution with mean and variance

$$\begin{aligned} \mu _0=Exp(C_{cipher})=(2^t-1)\frac{2^s-N}{2^s-1}\ {and} \ \sigma _0^2=Var(C_{cipher})=2(2^t-1)(\frac{2^s-N}{2^s-1})^2. \end{aligned}$$

The statistic $C_{random}$ ($C_{random}$ is the statistic C for randomly drawn permutation) follows a $\chi ^2$-distribution with degree of freedom $2^t-1$, which means that $C_{random}$ approximately follows a normal distribution with mean and variance

$$\begin{aligned} \mu _1=Exp(C_{random})=2^t-1\ {and}\ \sigma _1^2=Var(C_{random})=2(2^t-1). \end{aligned}$$

Proof

For a randomly drawn permutation, the values of $V[T_\lambda (y)]$ are obtained by counting the occurrences of $T_\lambda (y)$ when the values are chosen uniformly at random, which follows the multinomial distribution with parameter N and $\varvec{p}=(p_0, \ldots , p_{2^t-1})$, $p_i=2^{-t}$ $(0 \le i= T_\lambda (y)< 2^t)$.

The well-known Pearson’s $\chi ^2$ statistical result is that $\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}$ follows a $\chi ^{2}$-distribution with degree of freedom $k-1$, where the vector $X = (X_1, \ldots , X_k)$ follows a multinomial distribution with parameters n and $\varvec{p}$, where $\varvec{p} = (p_1, \ldots , p_k)$. We give a short proof for Pearson’s $\chi ^2$ statistic in Appendix A.1 based on [9, 14].

Thus we get the statistic for the randomly drawn permutation

$$\begin{aligned} C_{random}=\sum _{i=T_\lambda (y)=0}^{2^t-1}\frac{(V[T_\lambda (y)]-Np_i)^2}{Np_i}=\sum _{i=T_\lambda (y)=0}^{2^t-1}\frac{(V[T_\lambda (y)]-N\cdot 2^{-t})^2}{N\cdot 2^{-t}}, \end{aligned}$$

which follows a $\chi ^2$-distribution with degrees of freedom $2^t-1$. Then for sufficiently large N and t, $C_{random}$ approximately follows a normal distribution with the expected value and variance:

$$\begin{aligned} Exp(C_{random})=2^t-1\ \text {and}\ Var(C_{random})=2(2^t-1). \end{aligned}$$

For the cipher, the values of $V[T_\lambda (y)]$ follows a multivariate hypergeometric distribution with parameters $(\varvec{K},2^s,N)$, where $\varvec{K}=(2^{s-t},\ldots , 2^{s-t})$.

If the vector $X = (X_1, \ldots , X_k)$ follows a multivariate hypergeometric distribution with parameters $(\varvec{K},m,n)$, where $\varvec{K}=(K_1,\ldots , K_k)$ with $\sum _{i=1}^k K_i=m$, the statistic $\frac{m-1}{m-n}\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}$ follows a $\chi ^{2}$-distribution with degree of freedom $k-1$, which is proved in Appendix A.2.

So the statistic for the cipher

$$\begin{aligned} \frac{2^s-1}{2^s-N}\sum _{T_\lambda (y)=0}^{2^t-1}\frac{(V[T_\lambda (y)]-N \cdot 2^{-t})^{2}}{N\cdot 2^{-t}}=\frac{2^s-1}{2^s-N}C_{cipher} \end{aligned}$$

follows a $\chi ^2$-distribution with degrees of freedom $2^t-1$. For sufficiently large N and t, we get $C_{cipher}$ approximately follows a normal distribution with the expected value and variance:

$$\begin{aligned} Exp(C_{cipher})=(2^t-1)\frac{2^s-N}{2^s-1}\ \text {and} \ Var(C_{cipher})=2(2^t-1)(\frac{2^s-N}{2^s-1})^2. \end{aligned}$$

   $\square$

To distinguish these two normal distributions with different means and variances, one can compute the data complexity required as follows, given error probabilities.

Corollary 1

(Data Complexity). Under the assumption of Proposition 1, for type-I error probability $\alpha _0$ (the probability to wrongfully discard the cipher), type-II error probability $\alpha _1$ (the probability to wrongfully accept a randomly chosen permutation as the cipher), to distinguish a cipher and a randomly chosen permutation based on t-bit outputs when fixing r-bit inputs and randomly choosing values for s-bit inputs, the data complexity can be approximated by

$$\begin{aligned} N=\frac{(2^s-1)(q_{1-\alpha _0}+q_{1-\alpha _1})}{\sqrt{(2^t-1)/2}+q_{1-\alpha _0}}+1, \end{aligned}$$

(2)

where $q_{1-\alpha _0}$ and $q_{1-\alpha _1}$ are the respective quantiles of the standard normal distribution.

Note that this statistic test is based on the decision threshold $\tau =\mu _0+\sigma _0q_{1-\alpha _0}=\mu _1-\sigma _1q_{1-\alpha _1}$: if $C\le \tau$, the test outputs ‘cipher’. Otherwise, if the statistic $C>\tau$, the test outputs ‘random’.

As the integral distinguisher with the balanced property is equivalent to the multidimensional zero-correlation distinguisher [5], the statistical integral attacks can be regarded as the chosen-plaintext multidimensional zero-correlation attacks which require lower data complexity than the known-plaintext multidimensional zero-correlation attacks.

2.3 Experiment Results

In order to verify the theoretical model of statistical integral distinguisher, we implement a distinguishing attack on a mini variant of AES with the block size 64-bit denoted as AES* here. The round function of AES* is similar to that of AES, including four operations, i.e., SB, SR, MC and AK. 64-bit block is partitioned into 16 nibbles and SB uses S-box $S_0$ in LBlock. SR is similar as that of AES, and the matrix used in MC is

$$ M=\begin{pmatrix} 1&{}1&{}4&{}9\\ 9&{}1&{}1&{}4\\ 4&{}9&{}1&{}1\\ 1&{}4&{}9&{}1 \end{pmatrix}, $$

which is defined over $GF(2^4)$. For the multiplication, each nibble and value in M are considered as a polynomial over GF(2) and then the nibble is multiplied modulo $x^4+x+1$ by the value in M. The addition is simply XOR operation. The subkeys are XORed with the nibbles in AK operation.

Fig. 1.

Integral property for 4-round AES* (The MC operation in the last round is omitted.)

The distinguisher is shown in Fig. 1, where $(A^i_1,A^i_2,A^i_3,A^i_4), i=1,2,3,4$ denotes that these special 16 bits are balanced in the integral. Note that the state after SB operation in round 3 takes all $2^{16}$ values in each row, and $2^{4}$ values in each column. However, after SR operation the state takes all $2^{16}$ values in each column. We consider the distributions of the 8-bit values of the output including the first nibble in the first row and the last nibble in the second row, which are colored in red in Fig. 1, so $s=16, t=8$ here. If we set $\alpha _0=0.2$ and different values for N, $\alpha _1$ and $\tau$ can be computed using Eq. (2), thus we proceed the experiment to compute the statistic C for AES* and random permutations. With 1000 times of experiment, we can obtain the empirical error probabilities $\hat{\alpha _0}$ and $\hat{\alpha _1}$. The experiment results for $\hat{\alpha _0}$ and $\hat{\alpha _1}$ are compared with the theoretical values $\alpha _0$ and $\alpha _1$ in Fig. 2, which shows that the test results for the error probabilities are in good accordance with those for theoretical model.

Fig. 2.

Experimental results for AES* considering four input nibbles

3 Statistical Integral Attack on Skipjack-BABABABA

3.1 Skipjack and Its Variant Skipjack-BABABABA

Before SIMON and SPECK were proposed in 2013, Skipjack [18] was the only block cipher known to be designed by NSA (declassified in 1998). Skipjack is a 64-bit block cipher with 80-bit key adopting an unbalanced Feistel network with 32 rounds of two types, namely Rule A and Rule B. The 64-bit block of Skipjack is divided into four 16-bit words and each round is described in the form of a linear feedback shift register with additional non-linear keyed G permutation. The keyed G permutation $G:\mathbb {F}_2^{32}\times \mathbb {F}_2^{16}\rightarrow \mathbb {F}_2^{16}$ consists of a 4-round Feistel structure whose internal function $F:\mathbb {F}_2^{8}\rightarrow \mathbb {F}_2^8$ is an $8\times 8$ S-box. Skipjack applies eight rounds of Rule A, followed by eight rounds of Rule B and once again eight rounds of Rule A and finally eight rounds of Rule B. The key schedule of Skipjack takes 10 bytes secret key and uses four bytes at a time to key each G permutation, thus Skipjack’s key schedule has a periodicity of five rounds. In this section, we use $k_0, k_1, \ldots , k_9$ to denote the ten bytes secret key. This original Skipjack is often referred to as Skipjack-AABBAABB, where A denotes 4-round Rule A and B denotes 4-round Rule B. A variant of Skipjack, namely Skipjack-BABABABA consisting of four iterations of four-round Rule B followed by four-round Rule A, is also discussed. This variant has the same number of rounds and key schedule as Skipjack-AABBAABB.

Since its declassification, Skipjack-AABBAABB has sparked numerous security analysis. Among which, the best known cryptanalytic result against Skipjack-AABBAABB was reported more than one decade ago by Biham et al. [2] at EUROCRYPT’99, where a 24-round impossible differential was revealed and with which an attack against 31-round Skipjack-AABBAABB was mounted. Besides the considerable security analysis, Skipjack’s structure was also studied to discuss variants of Skipjack to improve its strength. In [10, 12], Knudsen et al. suggested that putting Rule B before Rule A, for example, the earlier mentioned Skipjack-BABABABA, might facilitate the resistance to truncated differential attacks. Till now, the only security analysis against Skipjack-BABABABA was reported by Bogdanov et al. [5] at ASIACRYPT’12, where an integral distinguisher over 30-round Skipjack-BABABABA was utilized to attack a 31-round version.

3.2 Integral Distinguisher of Skipjack-BABABABA

To attack full-round Skipjack-BABABABA, we are going to use the 30-round integral distinguisher proposed at ASIACRYPT’12 [5]. The 30-round integral distinguisher can be described as: when we take all $2^{48}$ possible values for the input of round 2 $(\alpha ^2,\beta ^2,\gamma ^2,\delta ^2)$ with $\delta ^2=\alpha ^2$, the set of all corresponding values for the output of round 31 $\beta ^{32}\oplus \gamma ^{32}$ is balanced.

3.3 Key Recovery Attack on 32-Round Skipjack-BABABABA

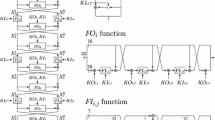
As the integral distinguisher starts at the input of round 2 and ends at the output of round 31, to attack full-round Skipjack-BABABABA we add one round (Rule B) before and append one round (Rule A) after the distinguisher, illustrated in Fig. 3. Note that in Fig. 3, the internal details of the keyed G permutation are also illustrated. To be more clear, several 8-bit variables a, b, c, d are employed in the attack procedure, see Fig. 3.

Fig. 3.

Key recovery attack on full-round Skipjack-BABABABA

We consider only the integral property of the right 8 bits of $\beta ^{32} \oplus \gamma ^{32}$, namely $\beta ^{32}_R \oplus \gamma ^{32}_R$, making $t=8$ in Eq. (2). And according to the 30-round integral distinguisher, to guarantee the integral property with probability one, we need to iterate through all possible values of $(\alpha ^2,\beta ^2,\gamma ^2,\delta ^2=\alpha ^2)$. In other words, s in Eq. (2) is 48. Set $\alpha _0=2^{-2.7}$ and $\alpha _1=2^{-4}$ (the values of $\alpha _0$ and $\alpha _1$ can be chosen appropriately to balance the data complexity, success rate and time complexity in exhaustive phase), we have $q_{1-\alpha _0}\approx 1.02$ and $q_{1-\alpha _1}\approx 1.53$. Thus we need about $2^{45.7}$ values of $(\alpha ^2,\beta ^2,\gamma ^2,\delta ^2=\alpha ^2)$ and the threshold value $\tau \approx 221.6$. We can traverse through all possible values of $\alpha ^1$ and $\beta ^1$ and randomly choose $2^{13.7}$ values for $\gamma ^1$ and guess the value of $k_0,k_1,k_2,k_3$ to compute $\alpha ^2, \beta ^2, \gamma ^2$ and set $\delta ^2=\alpha ^2$. In this way, $2^{45.7}$ values of $(\alpha ^2, \beta ^2, \gamma ^2, \delta ^2=\alpha ^2)$ could be produced under any key value of $(k_0,k_1,k_2,k_3)$. The key can be recovered following Algorithm 1, where $\beta ^{33}_R$ and $\beta ^{33}_L$ denote the right 8-bit and left 8-bit of $\beta ^{33}$ respectively, and so as $\gamma ^{33}_R$.

Complexity Estimation. In Step 8 and Step 9, the time complexity is $2^{61.7} \cdot 2=2^{62.7}$ memory accesses which is equivalent to $2^{62.7}$ encryptions. Next, Step 15 needs about $2^{32}\cdot 2^{16}=2^{48}$ times of G computation equivalent to $2^{48}\cdot \frac{1}{32}=2^{43}$ encryptions. Suppose that one memory access to an array of size $2^{24}$ and of size $2^{61.7}$ are equivalent to one round encryption and full cipher encryption respectively, then Step 17 and 18 need about $2^{32}\cdot 2^{16}\cdot 2^{16}\cdot 2^{13.7} \cdot (1+\frac{1}{32})\approx 2^{77.7}$ encryptions. The operations done in Step 23 and Step 24 are comparable to half-round encryption, which are about $2^{32}\cdot 2^{16}\cdot 2^{24}\cdot \frac{1}{2}\cdot \frac{1}{32}=2^{66}$ encryptions. In the same way, we regard the operations in Step 29 and Step 30 also as half-round encryption, then the time complexity of these two steps is about $2^{32}\cdot 2^{16}\cdot 2^{8}\cdot 2^{16}\cdot \frac{1}{2}\cdot \frac{1}{32}=2^{66}$ encryptions. As we set the wrong key guess filteration ratio as $\alpha _1=2^{-4}$, thus in Step 33, we need to exhaustively search about $2^{80-4}=2^{76}$ key values to find the right key. To summarize, the time complexity of our key recovery attack on full-round Skipjack-BABABABA is about $2^{62.7}+2^{43}+2^{77.7}+2^{66}+2^{66}+2^{76}\approx 2^{78.1}$ encryptions. About the data complexity, in Step 6, all possible values of $\delta ^1$ will be iterated through. Thus our attack needs about $2^{61.7}$ chosen plaintexts. The dominant memory requirements occur to store the plaintext/ciphertext pairs in Step 1, which needs about $2\times 2^{61.7}\times 8 =2^{65.7}$ bytes.

3.4 Improved Integral Attack on 31-Round Skipjack

With the statistical integral model, we can improve the integral attack on 31-round Skipjack [5] by appending one round after the 30-round distinguisher above, too. In Fig. 3, we attack from the second round to the 32nd round. In order to reduce the time complexity, we consider the statistical integral property of $\beta ^{32}_R \oplus \gamma ^{32}_R$ and $\beta ^{32}_L \oplus \gamma ^{32}_L$ respectively, so $t=8$ in Eq. (2). According to the 30-round integral distinguisher, to guarantee the integral property to hold with probability one, we should iterate through all possible values of $(\alpha ^2,\beta ^2,\gamma ^2,\delta ^2=\alpha ^2)$. In other words, s in Eq. (2) is 48. Set $\alpha _0=2^{-3.7}$ and $\alpha _1=2^{-16}$, we have $q_{1-\alpha _0}\approx 1.43$ and $q_{1-\alpha _1}\approx 4.17$. Thus we need about $2^{46.8}$ values of $(\alpha ^2,\beta ^2,\gamma ^2,\delta ^2=\alpha ^2)$ and the threshold value $\tau \approx 160.84$. The key recovery attack is described in Algorithm 2.

Complexity Estimation. Assume that one memory access is equivalent to one round encryption, Step 3 and 4 need about $2^{46.8}\times \frac{1}{31}\approx 2^{41.8}$ encryptions. Then the operations in Step 9 and 10 are about $2^{16}\times 2^{24}\times \frac{1}{2}\times \frac{1}{31}\approx 2^{34.0}$ encryptions. Step 15 and 16 need about $2^{16}\times 2^8 \times 2^{16}\times \frac{1}{2}\times \frac{1}{31}\approx 2^{34.0}$ encryptions. As we set the wrong key guess filteration ratio as $2^{-16}$, the numbers of remained key $(k_5, k_6, k_7)$ are about $2^{24-16}=2^8$ in Step 19. Until now, we exploit the integral property of $\beta ^{32}_R \oplus \gamma ^{32}_R$ to filter most wrong keys. Next, we use the integral property of $\beta ^{32}_L \oplus \gamma ^{32}_L$ to filter all wrong keys of $(k_4, k_5, k_6, k_7)$. Step 25 needs about $2^{8}\times 2^8 \times 2^{24}\times \frac{1}{31}\approx 2^{35.0}$ encryptions. Finally, by setting $\alpha _1=2^{-16}$ we need to exhaustively search about $2^{80-16-16}=2^{48}$ key values in Step 28 to find the right key. In total the time complexity is about $2^{41.8}+2^{34.0}+2^{34.0}+2^{35.0}+2^{48}\approx 2^{48}$ encryptions. The dominant memory complexity is required in Step 1 which is about $2 \times 2^{24}\times 3 \approx 2^{27.6}$ bytes which happen.

4 Conclusion

In this paper, we propose the statistical integral attack where we use the statistic technique to deal with the original integral distinguisher with balanced property. The new integral attack has the lower data complexity than that of the original one. Our experiment for mini version of AES shows that the experimental results are in good accordance with the theoretic results. What’ more, with this new distinguisher we can improve the previous integral attack on 31-round Skipjack-BABABABA and achieve the full-round attack of Skipjack-BABABABA. In the future, we will apply the statistical integral model to many other block ciphers which are vulnerable to integral attack.

A Appendix

1.1 A.1 Pearson’s $\chi ^{2}$ Statistic from the Multinomial Distribution

In this subsection, we describe Pearson’s $\chi ^2$ statistic deduced from multinomial distribution and provide a short proof based on [9, 14] the asymptotic distribution of the $\chi ^2$ expression.

A fundamental result about Pearson’s $\chi ^2$ statistic is that the following expression follows a $\chi ^{2}$-distribution with degree of freedom $k-1$

$$\begin{aligned} \sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}, \end{aligned}$$

where the random vector $\varvec{X} = (X_1, \ldots , X_k)$ follows a multinomial distribution with parameters n and $\varvec{p}$, where $\varvec{p} = (p_1, \ldots , p_k)$ with $\sum _{i=1}^k p_i=1$.

Now we will give a short proof based on [9, 14] in the following.

In probability theory, the multinomial distribution is a generalization of the binomial distribution. For n independent trials each of which leads to a success for exact one of k categories, with each category i $(1\le i\le k)$ having a given fixed success probability $p_{i}$ satisfying $\sum _{i=1}^k p_i=1$. Then if the random variable $X_i$ indicates that the number of times outcome number i is observed over the n trials, the vector $\varvec{X} = (X_1, \ldots , X_k)$ follows a multinomial distribution with parameters n and $\varvec{p} = (p_1, \ldots , p_k)$. Note that while the trials are independent, k outcomes are dependent because they must be summed to n.

Since the variance of $X_j$ is $np_j(1-p_j)$ and $Cov(X_j, X_l)=-np_jp_l, j\ne l$, the random vector $\varvec{X}$ with $(k-1)$ dimensions has covariance matrix

$$ \varSigma = \left( \begin{array}{cccc} np_{1}(1-p_1) &{} -np_1p_2 &{} \ldots &{} -np_1p_{k-1} \\ -np_1p_2 &{} np_{2}(1-p_{2}) &{} \ldots &{} -np_2p_{k-1} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ -np_1p_{k-1} &{} -np_2p_{k-1} &{} \ldots &{} np_{k-1}(1-p_{k-1}) \\ \end{array} \right) . $$

So we can denote $\varSigma$ as follows,

$$\begin{aligned} \varSigma = n(D-\varvec{p'}\varvec{p}), \end{aligned}$$

where $\varvec{p}=(p_{1}, p_{2}, \ldots , p_{k-1})$ and $\varvec{p'}$ is its transposition, D is a $(k-1)\times (k-1)$ diagonal matrix and

$$ D = \left( \begin{array}{cccc} p_{1} &{} \ &{} \ &{}\ \\ \ &{} p_{2} &{} \ &{} \ \\ \ &{} \ &{} \ddots &{} \ \\ \ &{} \ &{} \ &{} p_{k-1} \\ \end{array} \right) . $$

Thus, one can show

$$\begin{aligned} \varSigma ^{-1}= & {} \frac{1}{n} \left( D^{-1} + \frac{D^{-1}\varvec{p'}\varvec{p}D^{-1}}{1-\varvec{p}D^{-1}\varvec{p'}}\right) = \frac{1}{n} \left( D^{-1} + \frac{E}{p_{k}}\right) , \end{aligned}$$

where E is a $(k-1) \times (k-1)$ matrix where all entries are equal to one.

We only consider $k-1$ dimensions here, since using all k dimensions would make the variance singular. The first $k-1$ dimensions have all of the information needed anyway, so there’s no problem in doing this.

There is a fact: for any d-dimensional normal $\varvec{X}$ with nonsingular covariance matrix, the statistic $(\varvec{X} - \varvec{\mu })'\varSigma ^{-1}(\varvec{X} - \varvec{\mu })$ follows a $\chi ^{2}$-distribution with degree of freedom d.

Thus, in the above case we concern $(k-1)$-dimensional normal $\varvec{X}$:

$$\begin{aligned} (\varvec{X} - \varvec{\mu })'\varSigma ^{-1}(\varvec{X} - \varvec{\mu })= & {} (\varvec{X}-n\varvec{p})'\left( \frac{1}{n} \left( D^{-1} + \frac{E}{p_{k}}\right) \right) (\varvec{X}-n\varvec{p})\\= & {} \frac{1}{n}(\varvec{X}-n\varvec{p})'D^{-1}(\varvec{X}-n\varvec{p}) + \frac{1}{np_{k}}(\varvec{X}-n\varvec{p})'E(\varvec{X}-n\varvec{p})\\= & {} \sum _{i=1}^{k-1}\frac{(X_{i}-np_{i})^{2}}{np_{i}}+\frac{1}{np_{k}}\left( \sum _{i=1}^{k-1}(X_{i}-np_{i})\right) ^{2}\\= & {} \sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}+\frac{1}{np_{k}}\left( (n-x_k) -n(1-p_k)\right) ^2 \\= & {} \sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}. \end{aligned}$$

That is, $\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}$ has an approximation to $\chi ^{2}$-distribution with degree of freedom $k-1$ for large enough n.

1.2 A.2 Extend Pearson’s $\chi ^{2}$ Statistic to Multivariate Hypergeometric Distribution

In this subsection, we will extend Pearson’s $\chi ^2$ statistic to multivariate hypergeometric distribution based on the proof of the above subsection and prove that the following expression follows a $\chi ^{2}$-distribution with degree of freedom $k-1$

$$\begin{aligned} \frac{m-1}{m-n}\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}, \end{aligned}$$

where the random vector $\varvec{X} = (X_1, \ldots , X_k)$ follows a multivariate hypergeometric distribution with parameters $(\varvec{K},m,n)$ where $\varvec{K}={K_1,\ldots , K_k}$ with $\sum _{i=1}^k K_i=m$.

The multivariate hypergeometric distribution is a generalization of the hypergeometric distribution. For n dependent trials each of which leads to a success for exact one of k categories, with each category i $(1 \le i \le k)$ having a given fixed success probability $(p_{1}, p_{2}, \ldots , p_{k})$. The multivariate hypergeometric distribution gives the probability of any particular combination of numbers of successes for the various categories.

Then if the random variables $X_i$ indicates that the number of times outcome number i is observed over the n trials, the vector $\varvec{X} = (X_1, \ldots , X_k)$ follows a multivariate hypergeometric distribution with parameters $(\varvec{K},m,n)$.

As the mean for $X_j$ is $np_j$ and the variance of $X_j$ is $np_j(1-p_j)\frac{m-n}{m-1}$ and since $Cov(X_j, X_l)=-np_jp_l\frac{m-n}{m-1}, j\ne l$, the random vector $\varvec{X}$ with $k-1$ dimension has covariance matrix

$$\begin{aligned} \varUpsilon = n\frac{m-n}{m-1}(D-\varvec{p'}\varvec{p}) \end{aligned}$$

and

$$\begin{aligned} \varUpsilon ^{-1} = \frac{1}{n} \frac{m-1}{m-n} \left( D^{-1} + \frac{D^{-1}\varvec{p'}\varvec{p}D^{-1}}{1-\varvec{p}D^{-1}\varvec{p'}}\right) = \frac{1}{n} \frac{m-1}{m-n} \left( D^{-1} + \frac{E}{p_{k}}\right) . \end{aligned}$$

With the similar trick as the above subsection, for the $(k-1)$-dimensional normal $\varvec{X}$, it is easy to show that

$$\begin{aligned} (\varvec{X} - \varvec{\mu })'\varUpsilon ^{-1}(\varvec{X} - \varvec{\mu })= & {} (\varvec{X}-n\varvec{p})'\left( \frac{1}{n} \frac{m-1}{m-n} \left( D^{-1} + \frac{E}{p_{k}}\right) \right) (\varvec{X}-n\varvec{p})\\= & {} \frac{m-1}{m-n}\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}, \end{aligned}$$

which means that $\frac{m-1}{m-n}\sum _{i=1}^{k}\frac{(X_{i}-np_{i})^{2}}{np_{i}}$ has an approximation to $\chi ^{2}$-distribution with degree of freedom $k-1$ for large enough n.