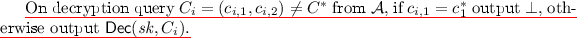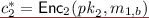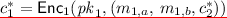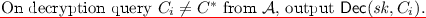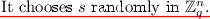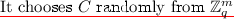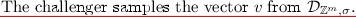New Circular Security Counterexamples from Decision Linear and Learning with Errors

Abstract

We investigate new constructions of n-circular counterexamples with a focus on the case of $n=2$. We have a particular interest in what qualities a cryptosystem must have to be able to separate such circular security from IND-CPA or IND-CCA security. To start, we ask whether there is something special about the asymmetry in bilinear groups that is inherent in the works of [1, 18] or whether it is actually the bilinearity that matters. As a further question, we explore whether such counterexamples are derivable from other assumptions such as the Learning with Errors (LWE) problem. If it were difficult to find such counterexamples, this might bolster our confidence in using 2-circular encryption as a method of bootstrapping Fully Homomorphic Encryption systems that are based on lattice assumptions.

The results of this paper broadly expand the class of assumptions under which we can build 2-circular counterexamples. We first show for any constant $k \ge 2$ how to build counterexamples from a bilinear group under the decision k-linear assumption. Recall that the decision k-linear assumption becomes progressively weaker as k becomes larger. This means that we can instantiate counterexamples from symmetric bilinear groups and shows that asymmetric groups do not have any inherently special property needed for this problem. We then show how to create 2-circular counterexamples from the Learning with Errors problem. This extends the reach of these systems beyond bilinear groups and obfuscation.

A. Bishop — Supported by NSF CNS 1413971 and NSF CCF 1423306.

S. Hohenberger — Supported by NSF CNS-1228443 and CNS-1414023, the Office of Naval Research under contract N00014-14-1-0333, and a Microsoft Faculty Fellowship.

B. Waters — Supported by NSF CNS-1228599 and CNS-1414082, DARPA SafeWare, a Google Faculty Research Award, the Alfred P. Sloan Fellowship, Microsoft Faculty Fellowship, and Packard Foundation Fellowship.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The notion of key dependent message security [12] moves beyond our classical notion of encryption security [22]. It demands a system remain secure even if an attacker gains access to ciphertexts that encrypt messages that are, or depend on, the very private keys of the system it is trying to attack. As a concrete example, consider a special case of key-dependent security called n-circular security. Here an encryption scheme is said to be n-circular secure, if an adversary is unable to distinguish $\mathsf {Enc}( pk _1, sk _2), \mathsf {Enc}( pk _2, sk _3), \ldots , \mathsf {Enc}( pk _n, sk _1)$ from corresponding zero encryptions.

While the notion of key dependent or circular security might first appear to be just a technical exercise, this very problem arises in multiple contexts. Camenisch and Lysyanskaya [17] applied circular secure encryption to build an anonymous credentials scheme with certain properties. Other works used circular security in formal methods to prove the soundness of symbolic protocols [2, 26]. Perhaps the most compelling example comes from Gentry [20], who showed that a fully homomorphic scheme for limited depth can be “bootstrapped” to work for arbitrary depth circuits if the original system is sufficient to compute its own decryption circuit and is 1-circular secure.

The first positive examples of key-dependent message security were given in the random oracle model by Black et al. [12] and Camenisch and Lysyanskaya [17]. It was a significant time later when Boneh, Hamburg, Halevi and Ostrovsky [14] gave an elegant construction of an n-circular secure encryption in the standard model under the decision Diffie-Hellman assumption. Subsequently, a sequence of further works [5, 7–9, 15, 16] gave standard model constructions of key dependent security for functions that could be arbitrary circuits on the private key(s).

All the above constructions and proofs were based on encryption schemes with specific properties. A natural question is whether key-dependent message security is implied by IND-CPA (or IND-CCA) security. If this were true, we would get it for free, without needing such specific properties of the encryption scheme.

A cursory examination of the problem shows that in the broadest sense the answer is no. One can derive a simple counterexample for 1-circular security (i.e., a system that encrypts its own private key) by slightly modifying a public key encryption system. To do so, simply augment a standard private key K with a randomly chosen $K ' \in \{0,1\}^\lambda$ and append $y=f(K')$ to the public key where f is a one way function. When encrypting a message $m=(m_1,m_2)$ the system will give out the message in the clear if $f(m_2)=y)$ and encrypt normally otherwise. Clearly, an encryption of the private key will be detectable. Yet, if the function f is one way and the original system is IND-CPA secure, the resulting system will still be IND-CPA secure.

While it can be trivially shown (by the argument above) that IND-CPA security does not imply 1-circular security, the case for $n \ge 2$ becomes significantly more challenging. Intuitively, when multiple public keys are thrown into the mix, we need a system that is powerful enough to allow for different ciphertexts to “talk” to each other in a manner that allows for cycle detection, but does not compromise IND-CPA security. So far there have been two approaches to this. For the case of $n=2$, Acar et al. [1] and Cash, Green and Hohenberger [18] showed how to construct a counterexample from a certain class of asymmetric bilinear groups.¹ Here there must exist a bilinear map $e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T$ where the decision Diffie-Hellman problem is believed to remain hard respectively within $\mathbb {G}_1$ and within $\mathbb {G}_2$ (this is called the SXDH assumption). A second approach by Koppula, Ramchen and Waters [25] showed a counterexample under the assumption of indistinguishability obfuscation for poly-sized circuits. Independently and concurrently, Marcedone and Orlandi [27] showed this under the stronger assumption of virtual black box obfuscation.

Our Goals and Results. In this work, we investigate new constructions of n-circular counterexamples with a focus on the case of $n=2$. We have a particular interest in what qualities a cryptosystem must have to be able to separate circular security from IND-CPA and IND-CCA security.

To start, we ask whether there is something special about the asymmetry in bilinear groups that is inherent in the works of [1, 18, 34] or whether it is actually more the bilinearity that matters. As a further question, we explore how to derive such counterexamples from other assumptions such as the Learning with Errors (LWE) problem. If it were difficult to find such counterexamples, this might bolster are confidence in using 2-circular encryption as a method of bootstrapping [20] fully homomorphic encryption systems that are based on lattice assumptions.

The results of this paper broadly expand the class of assumptions from which we can build 2-circular counterexamples. We first show for any constant $k \ge 2$ how to build 2-circular counterexamples from a bilinear group under the decision k-linear assumption. Recall that the decision k-linear assumption becomes progressively weaker as k becomes larger. This means that we can instantiate counterexamples from symmetric bilinear groups and shows that asymmetric groups do not have any inherently special property needed for this problem. We then show how to create 2-circular counterexamples from the Learning with Error (LWE) problem. This extends the reach of these systems beyond bilinear groups and obfuscation, giving us a much broader understanding of circular security and its challenges.

Our Approach. We begin by introducing a new abstraction called an n-Cycle Tester that will simplify the process of finding and describing counterexamples by focusing on the core problem. A cycle tester consists of four algorithms $(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Test})$. The algorithms of $\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}$ behave as in a normal encryption scheme with a common trusted setup algorithm, while the $\mathsf {Test}$ algorithm will take in an n-tuple of public keys and ciphertexts and detect (with some non-negligible probability) the presence of a cycle. Notably absent is the inclusion of a decryption algorithm. Thus, a tester does not require that ciphertexts be decryptable in the traditional sense — it only matters that the $\mathsf {Test}$ algorithm work with some non-negligible probability. We found that relieving the responsibility of providing a system with decryption simplifies our constructions and allows us to focus on the main ideas. The security property required is IND-CPA security (recall that the basic IND-CPA game does not involve a decryption algorithm).

Of course, to obtain a full-fledged counterexample of an encryption system we actually do need to provide an encryption system that decrypts. We show how to generically derive such a counterexample for n-circular encryption by combining a standard IND-CPA secure cryptosystem (of sufficient message length) with a n-cycle tester. The idea is fairly straightforward. The setup algorithm of the counterexample will run the respective setup algorithms of the encryption and cycle tester schemes. The public key is the pair of these public keys and the secret key is the pair of secret keys. To encrypt a message $m=(m_1,m_2)$, first encrypt $m=(m_1,m_2)$ under the regular encryption system, then encrypt just $m_2$ under the cycle tester. We can now see that: (1) the cycle tester will allow for any key cycle to be detected and (2) the standard encryption scheme can be used for decryption. A simple hybrid argument shows that the IND-CPA security of the standard encryption scheme and cycle tester imply IND-CPA security of the derived counterexample system.

We also show that it is possible to extend this transformation idea to chosen ciphertext security, where we can combine any IND-CCA secure encryption system (of appropriate message length) with the same IND-CPA secure cycle tester to get an encryption system that is IND-CCA secure, but where encryption of key cycles can be detected.

Again, the usefulness of this framework is its modularity. We show these basic transformations once in Sect. 4, and then for each construction we only need to focus on the basic cycle tester abstraction.

A Cycle Tester from Asymmetric Bilinear Groups. As a baseline for our exploration (see [11] for the full details), we first create a 2-cycle tester from asymmetric groups using the SXDH assumption. Our construction is extracted from Cash et al. [18] (also similar to [1, 34]), but simpler in that we only aim for the tester abstraction.

In our construction, the $\mathsf {Setup}$ algorithm creates an asymmetric pairing description $\mathrm {PP}= (p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T,e)$ of prime order p. It also produces generators $g \in \mathbb {G}_1$ and $h \in \mathbb {G}_2$. The message space will be $\mathbb {Z}_p^*$.

A key can be of one of two types. The cycle detection algorithm $\mathsf {Test}$ will work on any cycle of keys of two different types. The key generation algorithm $\mathsf {KeyGen}$ will first flip a coin $\beta \in \{0,1\}$ to determine its type. It then picks a random key $s \in \mathbb {Z}_p^*$. If $\beta =0$, it sets its public key to be $K = g^s \in \mathbb {G}_1$; otherwise, its public key is $K = h^s \in \mathbb {G}_2$.

The encryption algorithm will choose a random exponent $t \in \mathbb {Z}_p$ and if the key is of type $\beta =0$, it produces the ciphertext as $(C_1= K^{tm} = g^{stm}, C_2= g^{t}) \in \mathbb {G}_1^2$; otherwise if $\beta =1$, it produces the ciphertext as $(C_1= K^{tm} = h^{stm}, ~~C_2= h^{t}) \in \mathbb {G}_2^2$. With ciphertexts of this form, the test algorithm follows straightforwardly. Suppose we had a pair of ciphertexts $\mathbf {y}=(C=(C_{1}, C_{2}), C'=(C'_1, C'_2))$ that encrypted a cycle for keys of different types. The algorithm can test this by simply computing $e(C_1, C'_2) \mathop {=}\limits ^{?} e(C_2, C'_1)$. Plugging in $s,s'$ as the respective keys, $t,t'$ as the encryption randomness, and $m,m'$ as the messages, we see that the test computes:

$$e(g^{stm}, h^{t'}) \mathop {=}\limits ^{?} e(g^t, h^{s't'm'}). $$

This equality holds if $m=s'$ and $m'=s$ and will not hold with high probability for a message independent of the private key.

One thing we emphasize here is that IND-CPA is clearly broken if the SXDH assumption does not hold. Consider an encryption $(C_1= K^{tm} = g^{stm}, ~~C_2= g^{t}) \in \mathbb {G}_1^2$ for the message m. The group elements $g, (g^s)^m= g^{sm}, C_2=g^t, C_1= g^{stm}$ clearly form a DDH tuple. So if DDH is easy in $\mathbb {G}_1$, any $\beta =0$ type key is susceptible to attack. An analogous statement holds in $\mathbb {G}_2$ for any $\beta =1$ key. This potential attack demonstrates that the above construction relies strongly on properties of asymmetric groups. We next show how to remove that reliance.

A Cycle Tester from the Decision k -Linear Assumption. We next move to constructing a cycle tester from the decision k-linear assumption for any constant $k \ge 2$. Recall that the k-linear assumption [24, 35] is a parameterized family of assumptions on the source elements of bilinear groups. The assumption class becomes progressively weaker for larger values of k. Importantly, by moving to the decision k-linear assumption we remove our dependence on asymmetric groups.² See [11] for a review.

In our construction, the setup algorithm first generates a bilinear source group $\mathbb {G}$ of prime order p with generator g. Then it chooses a random invertible (rank k) matrix $\mathbf {A} \in \mathbb {Z}_p^{k \times k}$ and computes $g^{ \mathbf {A} }$, which along with the group description forms the common public parameters. (We use the notation $g^{\mathbf {M}}$ as shorthand for the set of group elements resulting from raising g to each matrix entry in $\mathbf {M}$.) The message and key spaces are defined to be the set of rank k matrices in $\mathbb {Z}_p^{k \times k}$.³

Once again the key generation algorithm will flip a coin $\beta$ to determine its type. Next it chooses a random $\mathbf {W}$ from the set of invertible matrices in $\mathbb {Z}_p^{k \times k}$. If $\beta =0$ the key is $g^{ \mathbf {AW}}$; otherwise it is $g^{ \mathbf {WA}}$.

The encryption algorithm takes as input a message $\mathbf {M} \in \mathbb {Z}_p^{k \times k}$ and then computes its inverse $\mathbf {M}^{-1}$. (Recall the message space is the set of invertible matrices.) If the type bit $\beta =0$, the algorithm chooses a random row vector $\mathbf {r}$ of length k in $\mathbb {Z}_p$ (i.e. a random matrix of dimension $1 \times k$). The ciphertext is computed and output as $C_1 = g^{ \mathbf {r} \mathbf {AW}} , \quad C_2 = g^{ \mathbf {r} \mathbf {A} \mathbf {M}^{-1} }$. Thus, the ciphertext will consist of two row vectors in the exponent. We observe all terms are computable from the public keys and public parameters. If the type bit $\beta =1$ the algorithm chooses a random column vector $\mathbf {r}$ of length k in $\mathbb {Z}_p$ (i.e., a random matrix of dimension $k \times 1$). The ciphertext is computed and output as $C_1 = g^{ \mathbf {WA} \mathbf {r} } , \quad C_2 = g^{ \mathbf {M}^{-1} \mathbf {A} \mathbf {r} }$.

Now suppose we have two ciphertexts $\mathbf {y}=(C=(C_{1}, C_{2}), \ C'=(C'_1, C'_2))$ of different types (with the first being of $\beta =0$). We can then test for a cycle by testing if $e(C_1, C'_2) \mathop {=}\limits ^{?} e(C'_1, C_2)$. To see why, suppose we had a cycle, so we have that $\mathbf {M}'^{-1} = \mathbf {W}^{-1}$ and $\mathbf {M}^{-1} = \mathbf {W}'^{-1}$. Then, in the exponent, it follows that:

$$ \begin{array}{rcl} \mathbf {r} \mathbf {AW} \mathbf {M}'^{-1} \mathbf {A} \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A} \mathbf {M}^{-1} \mathbf {W}' \mathbf {A} \mathbf {r}' \\ \mathbf {r} \mathbf {A} \mathbf {I} \mathbf {A} \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A} \mathbf {I} \mathbf {A} \mathbf {r}' \\ \mathbf {r} \mathbf {A}^2 \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A}^2 \mathbf {r}' . \\ \end{array} $$

So if there is a cycle, the test will output 1. In contrast, if the messages encrypted are independent of the key, the test will output 0 with high probability.

Finally, we can give a simple proof of IND-CPA security from the decision k-linear assumption. More specifically, we will use the matrix k-linear assumption, introduced by Naor and Segev [29], that was shown to be equivalent to the decision k-linear assumption. Informally, the assumption says that it is hard to distinguish $g^\mathbf {X}$ and $g^\mathbf {Y}$ where $\mathbf {X}$ is a random matrix of rank $i >k$ and $\mathbf {Y}$ is a random matrix (of the same dimension) of rank $j>k$. I.e., the rank of matrices in the exponent cannot be determined as long as it is greater than k. For our purposes, we will be interested in using the difficulty of distinguishing between rank k and rank $k+1$ matrices.

Let us examine IND-CPA security for an encryption under a type $\beta =0$ key. (The argument for $\beta =1$ will follow analogously.) We will devise a reduction algorithm that receives a matrix k-linear assumption challenge $g^{\mathbf {M}}$, where $\mathbf {M}$ is selected as either a random rank k matrix or rank $k+1$ matrix. In the case where it is a rank k matrix, our reduction algorithm will use it to derive the key and ciphertext values of

$$\begin{aligned} g^{ \mathbf {A} }, g^{\mathbf {AW}}, g^{ \mathbf {rAW}} , g^{ \mathbf {rA}}. \end{aligned}$$

These can be used to generate a well-formed ciphertext of a given message. However, if the reduction algorithm receives a random matrix of rank $k+1$, it will create key and ciphertext values distributed as

$$\begin{aligned} g^{ \mathbf {A} }, g^{\mathbf {AW}}, g^{ \mathbf {rAW}} , g^{ \mathbf {uA}}. \end{aligned}$$

In this case the fact that $\mathbf {u}$ is fresh randomness will information-theoretically hide the message from the attacker. It then follows that any attacker with non-negligible advantage against our system must break the matrix k-linear assumption.

In the full version [11], we present a different 2-cycle tester from the Decision Linear assumption in symmetric pairing groups. This construction can be viewed as closer to an extension of the SXDH one (sketched above and detailed in [11]) to symmetric groups where new variables and equations are introduced to prevent the use of pairings to disrupt IND-CPA security. However, it does not seem to generalize to a system that is secure using the decision k-linear assumption for $k>2$ or help move toward a Learning with Errors Assumption. At the same time, when compared to our more general construction just given for the $k=2$ (decision linear assumption) case, it achieves smaller public keys. Public keys here are two group elements as opposed to four. Our techniques for this construction might be of future interest for other applications of transforming constructions proved under asymmetric group assumptions to those that do not rely on them. We defer further details of these techniques to the full version [11].

A Cycle Tester from Learning with Errors Assumption. While there are now many known examples of cryptographic functionalities that can be achieved in both the bilinear and lattice settings, it is not at all clear how to imitate the pairings-based approach above to obtain a cycle tester from the LWE assumption. Typically, encryption schemes proven secure under LWE have ciphertexts that are large, noisy vectors in $\mathbb Z_q^m$ and secret keys that are short vectors in $\mathbb Z^m$, with decryption computing a dot product and then removing the small effect of the noise multiplied by the short key vector. It seems unlikely that we could build a cycle tester using only this kind of structure, as the cycle effect would be obscured by the interactions of large ciphertext vectors with the embedded noise.

Intuitively, we then expect that a cycle tester may use ciphertexts that have two parts: a noisy vector and a short vector. The large, noisy vectors will help us prove IND-CPA security from LWE, while the short vectors will help us perform the cycle test. Naturally, the main challenge is designing the relationship between the noisy and short vectors such that the short vectors do not break security when there is no cycle.

The secret key for our scheme will generate a matrix B and a corresponding short trapdoor basis $T_B$. For IND-CPA security, it is important that B is hidden, so one should ignore the notational collision and not think of this as corresponding to the public matrix A in an LWE challenge, but rather the columns of B will play the role of different hidden s vectors in typical LWE notation. The public key will be formed by choosing several random vectors $c_1, \ldots , c_\ell$ and publishing noisy versions of $c_1 B, \ldots , c_\ell B$ as well as the (non-noisy) vectors $c_1, \ldots , c_\ell$ (so these $c_i$’s can be thought of as playing the role of the public matrix A in an LWE challenge).

To encrypt a message, the message will first be used to generate a matrix Z and a corresponding short trapdoor basis $T_Z$. The encryptor will mimic typical LWE-style encryption by forming a noisy version of sB for some vector s, but since it does not know B, it will form s as a linear combination of $c_1, \ldots , c_\ell$ with coefficients chosen randomly from $\{-1,1\}$. Note that the encryptor can then compute both s (without noise) and a noisy version of sB. The noisy version of sB becomes the noisy part of the ciphertext, and the other part of the ciphertext is a short vector v such that Zv equals the transpose of s. Note that such a vector v can be sampled appropriately using the trapdoor basis $T_Z$.

For full details of how the cycle test works, see Sect. 6. The main idea is that when there is a 2-cycle, the secret key matrix B for one ciphertext is the same as the message matrix Z for the other ciphertext and vice versa. This leads to a common relationship between the short vector of one ciphertext and the noisy vector of the other, while when the B, Z matrices of each are fresh and unrelated, this relationship does not appear. One convenient feature of this scheme as compared to the bilinear schemes is that there is no need for different types of ciphertexts. Intuitively, the pairing relationship has been replaced by a dot product relationship between a short vector and a noisy one.

Proving IND-CPA security for this scheme can be accomplished in a few steps. First, since B is hidden and its columns act like the hidden vector s in a typical LWE challenge and the $c_i$’s act like rows of the public matrix A, we can argue that LWE implies the noisy public versions of $c_i B$ can be replaced by uniformly random vectors, independent of the $c_i$’s and B. Next, using a convenient variant of the left over hash lemma from [3], we argue that the random coefficients in $\{-1,1\}$ that form s from the $c_i$’s and the noisy ciphertext vector from the public noisy vectors supply sufficient entropy to replace both of these with fresh uniformly random vectors as well. We are then left with an encryption that samples a uniformly random s (now independent of the noisy part of the ciphertext) and samples the short part of the ciphertext as a short vector v such that Zv is the transpose of s. Here we can argue that the distribution of such a v is statistically close to a distribution that is independent of Z: this follows from a result in [21] that ensures us that the image of a short, Gaussian distributed vector v under multiplication by Z is uniformly distributed in $\mathbb Z_q^n$. Thus, by employing LWE followed by a sequence of statistical arguments, we can arrive at a point where the ciphertext is independent of the message, and this implies IND-CPA security.

Other Related Work. Haitner and Holenstein [23] show black box impossibility results for proving key-dependent message security from different cryptographic assumptions. Their goal deviates from ours in two important ways. First, their work focuses on impossibility results for ciphertext encrypting functions of its own private keys, whereas we are concerned with the circular case where there is a cycle over multiple private keys. Second, we are interested in concrete counterexamples. In particular, it may be possible that IND-CPA security implies certain key-dependent security properties even if there does not exist any black box reduction. In contrast our counterexamples will show that this is impossible if certain specific number theoretic assumptions hold.

2 Preliminaries

Background on pairings can be found in the full version [11].

2.1 The k-LIN Assumption

Decision Linear and the k -LIN Family ( k -LIN). We now present a family of assumptions called the k-LIN assumptions (where $k=1$ is the standard DDH assumption and $k=2$ is called Decision Linear [13]) [10, 24]. Let $\mathbb {G}$ be a group of prime order $p \in \Theta (2^\lambda )$. For all p.p.t. adversaries $\mathcal {A}$ and $k \ge 1$, the following probability is 1 / 2 plus an amount negligible in $\lambda$:

$$\begin{aligned} \Pr [g, g_1, \dots , g_k \leftarrow \mathbb {G}; r_1, \dots , r_k \leftarrow \mathbb {Z}_p; T_0 = g^{(r_1+ \dots + r_k)}; T_1 \leftarrow \mathbb {G}; d \leftarrow \{0,1\}; \\ d' \leftarrow \mathcal {A}(g,g_1, \dots , g_k, g_1^{r_1}, \dots , g_k^{r_k}, T_d): d = d']. \end{aligned}$$

In the generic group model, these k-LIN assumptions become progressively weaker for increasing k.

In our proof of security in Sect. 5 we will use a theorem due to Naor and Segev [29] that shows that under the decision k-linear assumption no attacker can distinguish between a random rank i matrix and a random rank j matrix (in the exponent and of the same dimensions) for $i,j \ge k$.

2.2 Lattices and LWE

We let q, n, and m denote positive integers. Given a matrix $A \in \mathbb Z_q^{n \times m}$, we let $\Lambda _q^\perp (A)$ denote the lattice $\{x \in \mathbb Z^m \; : \; Ax = 0 \mod q\}$. For $u \in \mathbb Z_q^n$, we let $\Lambda _q^u(A)$ denote the set $\{x \in \mathbb Z^m \; : \; Ax = u \mod q\}$.

For a matrix $A \in \mathbb Z^{n \times m}$, we let ||A|| denote the $\ell _2$ length of the longest column of A, and we let $||A||_{GS}$ denote $||\widetilde{A}||$, where $\widetilde{A}$ is the Gram-Schmidt orthogonalization of the columns of A. We let $A^t$ denote the transpose of the matrix A.

Learning with Errors (LWE). Given integers n, m, a prime q, and a noise distribution $\chi$ over $\mathbb Z$, the $(n,m,q, \chi )$-LWE problem is to distinguish the distributions $(A, A^t s + e)$ and (A, u), where A is chosen uniformly from $\mathbb Z_q^{n \times m}$, s is chosen uniformly from $\mathbb Z_q^n$, e is chosen from $\chi ^m$, and u is chosen uniformly from $\mathbb Z_q^m$.

Under a quantum reduction, Regev [33] showed that for certain noise distributions, the LWE problem is as hard as the worst-case SIVP and GapSVP. Peikert [31] gave a reduction in the classical setting. Our construction will admit a range of parameters where solving the LWE problem is as hard as approximating the worst-case GapSVP to polynomial (in n) factors, which is believed to be computationally hard.

Trapdoor Generation. We will rely on the polynomial time algorithm TrapGen$(1^n$, $1^m,q)$ (developed in [4, 6, 28]). This is a randomized algorithm that when given $m = \Theta (n \log q)$, outputs a full rank matrix $A \in \mathbb Z_q^{n \times m}$ and an accompanying basis $T_A \in \mathbb Z^{m \times m}$ for $\Lambda _q^\perp (A)$ such that the distribution of A is negligibly close (in n) to uniform over $\mathbb Z_q^{n \times m}$ and $||T_A||_{GS} = \mathcal {O}(\sqrt{n \log q})$ with all but negligible probability (as a function of n).

Discrete Gaussian Distributions. We employ the discrete Gaussian distribution $\mathcal {D}_\sigma (\Gamma _q^u(A))$ on $\Gamma _q^u(A)$, parameterized by $\sigma >0$ (as defined e.g. in [33]). The salient fact we will use about this distribution is that for a random matrix $A \in Z_q^{n \times m}$ and $\sigma = \tilde{\Omega }(\sqrt{n})$, a vector sampled from $\mathcal {D}_\sigma (\Lambda _q^u(A))$ has $\ell _2$ norm less than $\sigma \sqrt{m}$ with probability at least 1 minus a quantity that is negligible in m.

We will rely on a polynomial time algorithm SampleD$(A, T_A, u, \sigma )$ [21]. This is a randomized algorithm that when $\sigma = ||T_A||_{GS} \cdot \omega (\sqrt{\log m})$, produces a random vector x from a distribution that is statistically close to $\mathcal {D}_\sigma (\Lambda _q^u(A))$.

We also employ the following result from [21] (appears as Corollary 5.4 in that work):

Lemma 1

Let n and q be positive integers with q prime, and let $m \ge 2n \log q$. Then for all but a $2q^{-n}$ fraction of all $A \in \mathbb Z_q^{n \times m}$ and for any $\sigma \ge \omega (\sqrt{\log m})$, the distribution of the syndrome $u = A e \mod q$ is statistically close to uniform over $\mathbb Z_q^n$, where e is distributed according to $\mathcal {D}_{\mathbb Z^m, \sigma }$.

Randomness Extraction. We will use the leftover hash lemma (see [3] e.g. for an even stronger statement):

Lemma 2

Suppose that $\ell > (j+1) \log q + \omega (\log j)$ and $q>2$ is prime (for integers $q,j, \ell$). Let R be an $\ell \times 1$ vector chosen uniformly in $\{1, -1\}^{\ell } \mod q$. Let A and B be matrices chosen uniformly in $\mathbb Z_q^{j\times \ell }$ and $\mathbb Z_q^{j \times 1}$ respectively. Then, the distribution (A, AR) is statistically close to the distribution (A, B).

3 Security Definitions

In this work, we will focus on public key encryption schemes that admit a global setup algorithm.

Definition 1

(Public Key Encryption). A public key encryption scheme $\varPi =(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ for a message space M and secret key space S ⁴ is a tuple of algorithms specified as follows:

• $\mathsf {Setup}(1^\lambda ) \rightarrow \mathrm {PP}$. The Setup algorithm takes as input the security parameter $\lambda$ and outputs common public parameters $\mathrm {PP}$.

• $\mathsf {KeyGen}(\mathrm {PP}) \rightarrow ( pk , sk )$. The Key Generation algorithm takes as input the public parameters $\mathrm {PP}$ and outputs a public $pk$ and secret key $sk \in S$.

• $\mathsf {Enc}( pk ,m \in M) \rightarrow C$. The Encryption algorithm takes as input a public key $pk$ and a message $m \in M$ and outputs a ciphertext C.

• $\mathsf {Dec}( sk ,C) \rightarrow m$. The Decryption algorithm takes as input a secret key $sk$ and a ciphertext C and outputs either an error message $\perp$ or a value $m \in M$.

By $\mathsf {negl}(k)$ we denote some negligible function, i.e., one such that, for all $c > 0$ and all sufficiently large k, $\mathsf {negl}(k) < 1/k^c$. We abbreviate probabilistic polynomial time as PPT.

Perfect Correctness. An encryption scheme $\varPi =(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ for message space M is said to be perfectly correct if for all $\lambda \in \mathbb {N}$, $m \in M$, and $( pk , sk ) \in \mathsf {KeyGen}(\mathsf {Setup}(1^\lambda ))$, it holds that $\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m)) = m$.

Security. We recall the notion of indistinguishability of encryptions under a chosen-plaintext attack [22].

Definition 2

( ${\mathsf{IND}\text {-}\mathsf{CPA}}$ Security). Let $\varPi =(\mathsf {Setup}, \mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})$ be a public-key encryption scheme. For scheme $\varPi$, adversary $\mathcal {A}$, and $\lambda \in \mathbb {N}$, let the random variable ${\mathsf{IND}\text {-}\mathsf{CPA}}(\varPi ,\mathcal {A},\lambda )$ be defined by the probabilistic algorithm described on the left side of Fig. 1. We denote the ${\mathsf{IND}\text {-}\mathsf{CPA}}$ advantage of $\mathcal {A}$ by $\mathsf {Adv}^{\mathsf {cpa}}_{\varPi ,\mathcal {A}}(\lambda ) = 2\cdot \Pr [{\mathsf{IND}\text {-}\mathsf{CPA}}(\varPi ,\mathcal {A},\lambda ) = 1] - 1$. We say that $\varPi$ is ${\mathsf{IND}\text {-}\mathsf{CPA}}$ secure if $\mathsf {Adv}^{\mathsf {cpa}}_{\varPi ,\mathcal {A}}(\lambda )$ is negligible for all PPT $\mathcal {A}$.

We also consider the indistinguishability of encryptions under a chosen-ciphertext attack [19, 30, 32].

Definition 3

( ${\mathsf{IND}\text {-}\mathsf{CCA}}$ Security). Let $\varPi =(\mathsf {Setup}, \mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})$ be a public-key encryption scheme. Let the random variable ${\mathsf{IND}\text {-}\mathsf{CCA}}(\varPi ,\mathcal {A},\lambda )$ be defined by an algorithm identical to ${\mathsf{IND}\text {-}\mathsf{CPA}}(\varPi ,\mathcal {A},\lambda )$ above, except that $\mathcal {A}$ has access to an oracle $\mathsf {Dec}( sk ,\cdot )$ that returns the output of the decryption algorithm and $\mathcal {A}$ cannot query this oracle on input y. We denote the ${\mathsf{IND}\text {-}\mathsf{CCA}}$ advantage of $\mathcal {A}$ by $\mathsf {Adv}^{\mathsf {cca}}_{\varPi ,\mathcal {A}}(\lambda ) = 2\cdot \Pr [{\mathsf{IND}\text {-}\mathsf{CCA}}(\varPi ,\mathcal {A},\lambda ) = 1] - 1$. We say that $\varPi$ is ${\mathsf{IND}\text {-}\mathsf{CCA}}$ secure if $\mathsf {Adv}^{\mathsf {cca}}_{\varPi ,\mathcal {A}}(\lambda )$ is negligible for all PPT $\mathcal {A}$.

3.1 Circular Security

We next define circular security of public-key encryption. This definition is derived from the Key-Dependent Message (KDM) security notion of Black et al. [12]. We follow prior counterexample definitions [1, 18] which restrict the adversary’s power (e.g., cannot ask for any affine function of the secret keys). The adversary is asked to distinguish between an encryption cycle or encryptions of zero as in [14, 18]. The bit string zero is not actually in the message spaces we consider, but this value can be encoded to be in the space; equivalently, one can follow the approach of Acar et al. [1] which instead of zero, encrypts a fresh random message.

Fig. 1.

Experiments for Definitions 2 and 4, each for a message space M, and we assume that $m_0,m_1, sk _i \in M$. We write $\mathbf {pk}$, $\mathbf {sk}$, and $\mathbf {y}$ for $( pk _1,\ldots , pk _n)$, $( sk _1,\ldots , sk _n)$ and $(y_1,\ldots ,y_n)$ respectively.

Definition 4

( ${\mathsf{IND}\text {-}\mathsf{CIRC\text {-}CPA}}^n$ ). Let $\varPi =(\mathsf {Setup}, \mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})$ be a public-key encryption scheme. For integer $n>0$, scheme $\varPi$, adversary $\mathcal {A}$ and $\lambda \in \mathbb {N}$, let the random variable ${\mathsf{IND}\text {-}\mathsf{CIRC\text {-}CPA}}^n(\varPi ,\mathcal {A},\lambda )$ be defined by the probabilistic algorithm in the middle of Fig. 1. We denote the ${\mathsf{IND}\text {-}\mathsf{CIRC\text {-}CPA}}^n$ advantage of $\mathcal {A}$ by

$$\mathsf {Adv}^{{n}{\text {-}}\mathsf {circ{\text {-}}cpa}}_{\varPi ,\mathcal {A}}(\lambda ) = 2\cdot \Pr [{\mathsf{IND}\text {-}\mathsf{CIRC\text {-}CPA}}^n(\varPi ,\mathcal {A},\lambda ) = 1] - 1.$$

We say that $\varPi$ is ${\mathsf{IND}\text {-}\mathsf{CIRC\text {-}CPA}}^n$ secure if $\mathsf {Adv}^{{n}{\text {-}}\mathsf {circ{\text {-}}cpa}}_{\varPi ,\mathcal {A}}(\lambda )$ is negligible for all PPT $\mathcal {A}$.

Discussion. Cash et al. [18] made a distinction between whether an adversary could distinguish an encryption cycle from encryptions of zero (as in the standard game above), or whether an adversary could actually recover the secret keys (and provided the latter type of counterexample). Recently, Koppula et al. [25] showed that if there exists (an IND-CPA secure) scheme with a PPT adversary that can distinguish an encryption cycle (in the standard game), then it can be transformed into another scheme with a corresponding adversary that can extract the secret keys from the cycle. Thus, in this work, we can focus exclusively on the standard definition.

4 A Framework for Generating Circular Counterexamples

We now present a general framework for creating circular security counterexamples, which we will instantiate under a variety of different assumptions in the subsequent sections. At the center of our framework is an abstraction called a “cycle tester”. Like an encryption scheme, a cycle tester must be able to encode a message in an IND-CPA secure manner. However, unlike an encryption scheme, the cycle tester need not support a decryption operation, instead it must support a testing operation which can detect the presence of an encryption cycle.

After formalizing this abstraction, we provide two results that use it. First, we show how our tester can be combined with any IND-CPA encryption scheme (of appropriate message length) to provide a full blown counterexample. Second, we extend this idea to show how to combine any tester with any IND-CCA encryption scheme to get an IND-CCA counterexample.

In addition to letting us focus on a narrower primitive for our counterexample, this separation avoids duplication of work and minimizes assumptions. In particular, we can design a single tester and then both the IND-CPA and IND-CCA counterexamples follow. Most prior works did not address IND-CCA counterexamples. While Cash et al. [18] did, their IND-CCA counterexample required the use of NIZKs, which is a stronger assumption than simply assuming the existence of IND-CCA encryption schemes as we do here. Our abstraction and transformation essentially show that designing IND-CCA counterexamples is no harder than designing IND-CPA ones.

We remark that Koppula et al. [25] have a IND-CPA counterexample with structure similar to our general transformation, however, no generic or IND-CCA theorems are proven.

Definition 5

( n -Cycle Tester). A cycle tester $\Gamma = (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Test})$ for message space M and secret key space S is a tuple of algorithms specified as follows:

• $\mathsf {Setup}(1^\lambda ) \rightarrow \mathrm {PP}$. The Setup algorithm takes as input the security parameter $\lambda$ and outputs common public parameters $\mathrm {PP}$.

• $\mathsf {KeyGen}(\mathrm {PP}) \rightarrow ( pk , sk )$. The Key Generation algorithm takes as input the public parameters $\mathrm {PP}$ and outputs a public key $pk$ and secret key $sk \in S$.

• $\mathsf {Enc}( pk ,m \in M) \rightarrow C$. The Encryption algorithm takes as input a public key $pk$ and a message $m \in M$ and outputs a ciphertext C.

• $\mathsf {Test}(\mathbf {pk},\mathbf {y}) \rightarrow \{0,1\}$. On input $\mathbf {pk}= ( pk _1,\dots , pk _n)$ and $\mathbf {y}= (C_1,\dots ,C_n)$, the Testing algorithm outputs a bit in $\{0,1\}$.

It also must possess the following properties. Let $\varPi = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\cdot )$ be an encryption scheme formed from the first three algorithms of the tester with an empty decryption algorithm. Then, it must hold that:

• 1. (IND-CPA security) $\varPi$ is IND-CPA secure according to Definition 2.

• 2. (Testing Correctness) the Testing algorithm’s advantage in distinguishing encryption cycles, denoted $\mathsf {Adv}^{{n}{\text {-}}\mathsf {circ{\text {-}}cpa}}_{\varPi ,\mathsf {Test}}(\lambda )$ from Definition 4, is non-negligible.

We now prove two theorems.

Theorem 1

(CPA Counterexample from Cycle Testers). If there exists an IND-CPA-secure encryption scheme $\varPi$ for message space $M = (M_1 \times M_2)$ and secret key space $S_1 \subseteq M_1$ and an n-cycle tester $\Gamma$ for message space $M_2$ and secret key space $S_2 \subseteq M_2$, then there exists an IND-CPA-secure encryption scheme $\varPi '$ for message space $M = (M_1 \times M_2)$ and secret key space $S = (S_1 \times S_2)$ that is n-circular insecure.

Proof

Let $\varPi =(\mathsf {Setup}_1, \mathsf {KeyGen}_1,\mathsf {Enc}_1,\mathsf {Dec}_1)$ and $\Gamma =(\mathsf {Setup}_{2}, \mathsf {KeyGen}_{2},\mathsf {Enc}_{2}$, $\mathsf {Test}_{2})$. We construct an IND-CPA $\varPi ' = (\mathsf {Setup}, \mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})$, together with its IND-CIRC-CPA$^2$ test algorithm $\mathsf {Test}$, as follows.

• $\mathsf {Setup}(1^\lambda )$: On input $1^{\lambda }$, run $\mathrm {PP}_1 \leftarrow \mathsf {Setup}_1(1^\lambda )$ and $\mathrm {PP}_2 \leftarrow \mathsf {Setup}_{2}(1^\lambda )$. Output $\mathrm {PP}= (\mathrm {PP}_1, \mathrm {PP}_2)$.

• $\mathsf {KeyGen}(\mathrm {PP})$: On input $\mathrm {PP}=(\mathrm {PP}_1, \mathrm {PP}_2)$, run $( pk _1, sk _1) \leftarrow \mathsf {KeyGen}_1(\mathrm {PP}_1)$ and $( pk _2, sk _2) \leftarrow \mathsf {KeyGen}_{2}(\mathrm {PP}_2)$. Output $pk = ( pk _1, pk _2)$ and $sk =( sk _1, sk _2)$.

• $\mathsf {Enc}( pk ,m)$: On input $pk =( pk _1, pk _2)$ and $m=(m_1,m_2) \in M$, run $c_1 \leftarrow \mathsf {Enc}_1( pk _1,(m_1, m_2))$ and $c_2 \leftarrow \mathsf {Enc}_{2}( pk _2, m_2)$. Output $C = (c_1,c_2).$

• $\mathsf {Dec}( sk ,C)$: On input $sk =( sk _1, sk _2)$ and $C=(c_1,c_2)$, output $\mathsf {Dec}_1( sk _1,c_1)$.

• $\mathsf {Test}(\mathbf {pk},\mathbf {y})$: On input $\mathbf {pk}= ( pk _1,\dots , pk _n)$ and $\mathbf {y}= (C_1,\dots ,C_n)$, parse $pk _i = (a_i,b_i)$ and $C_i = (c_i,d_i)$ and output the bit $\mathsf {Test}_{2}((b_1,\dots ,b_n),(d_1,\dots ,d_n))$.

The correctness of $\mathsf {Test}$ follows directly from that of $\mathsf {Test}_{2}$. If $(\mathbf {pk},\mathbf {y})$ contains an encryption cycle (or encryptions of zero, respectively), then so will $((b_1,\dots ,b_n),(d_1,\dots ,d_n))$, and thus by definition of the cycle tester, the test will distinguish between these cases with non-negligible advantage.

It remains to argue that $\varPi '$ is an IND-CPA secure encryption scheme. This follows by a simple hybrid argument based on the fact that an encryption in $\varPi '$ is a pair of encryptions from two different IND-CPA-secure schemes, $\Gamma$ and $\varPi$. We omit this proof as it is a simplified version of the IND-CCA proof that we provide next.

Theorem 2

(CCA Counterexample from Cycle Testers). Let $k,\ell$ be security parameters and $p(\cdot )$ be a polynomial. If there exists an IND-CCA-secure encryption scheme $\varPi$ (with k-bit secret keys and $(p(\ell )+2k)$-bit messages) and an n-cycle tester $\Gamma$ (with k-bit secret keys, k-bit messages, and $p(\ell )$-bit ciphertexts), then there exists an IND-CCA-secure encryption scheme $\varPi '$ for 2k-bit messages that is n-circular insecure.

Proof

Let $\varPi =(\mathsf {Setup}_1,\mathsf {KeyGen}_1,\mathsf {Enc}_1,\mathsf {Dec}_1)$ and $\Gamma =(\mathsf {Setup}_2,\mathsf {KeyGen}_2,\mathsf {Enc}_2$, $\mathsf {Test}_2)$ with the length constraints above. We construct an IND-CCA $\varPi ' = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})$, together with its IND-CIRC-CPA$^2$ test algorithm $\mathsf {Test}$, as follows. We can no longer simply append the cycle-tester encryption to the regular encryption, because changes to the cycle-testing portion might be leveraged to obtain a decryption of a portion of the challenge ciphertext. Instead, we encrypt this cycle-testing portion using the regular CCA-secure scheme.

• $\mathsf {Setup}(1^\lambda )$: On input $1^{\lambda }$, run $\mathrm {PP}_1 \leftarrow \mathsf {Setup}_1(1^\lambda )$ and $\mathrm {PP}_2 \leftarrow \mathsf {Setup}_{2}(1^\lambda )$. Output $\mathrm {PP}= (\mathrm {PP}_1, \mathrm {PP}_2)$.

• $\mathsf {KeyGen}(\mathrm {PP})$: On input $\mathrm {PP}=(\mathrm {PP}_1, \mathrm {PP}_2)$, run $( pk _1, sk _1) \leftarrow \mathsf {KeyGen}_1(\mathrm {PP}_1)$ and $( pk _2, sk _2) \leftarrow \mathsf {KeyGen}_{2}(\mathrm {PP}_2)$. Output $pk = ( pk _1, pk _2)$ and $sk =( sk _1, sk _2)$.

• $\mathsf {Enc}( pk ,(m_a,m_b))$: On input $pk =( pk _1, pk _2)$ and message $(m_a, m_b) \in \{0,1\}^k \times \{0,1\}^k$, run $c_2 \leftarrow \mathsf {Enc}_{2}( pk _2, m_b)$ and $c_1 \leftarrow \mathsf {Enc}_1( pk _1,(m_a,m_b,c_2))$. Output $C = (c_1,c_2).$

• $\mathsf {Dec}( sk ,C)$: On input $sk =( sk _1, sk _2)$ and $C=(c_1,c_2)$, run $\mathsf {Dec}_1( sk _1,c_1)$. If it does not return a message of the form $(m_a,m_b,m_c) \in \{0,1\}^k \times \{0,1\}^k \times \{0,1\}^{p(\lambda )}$ or if $m_c \ne c_2$, then output $\perp$ (invalid ciphertext). Otherwise, output the message $(m_a,m_b) \in \{0,1\}^k \times \{0,1\}^k$.

• $\mathsf {Test}(\mathbf {pk},\mathbf {y})$: On input $\mathbf {pk}= ( pk _1,\dots , pk _n)$ and $\mathbf {y}= (C_1,\dots ,C_n)$, parse $pk _i = (a_i,b_i)$ and $C_i = (c_i,d_i)$ and output the bit $\mathsf {Test}_{2}((b_1,\dots ,b_n),(d_1,\dots ,d_n))$. Same as before.

As before, the correctness of $\mathsf {Test}$ follows directly from that of $\mathsf {Test}_{2}$. If $(\mathbf {pk},\mathbf {y})$ contains an encryption cycle (or encryptions of zero, respectively), then so will $((b_1,\dots ,b_n),(d_1,\dots ,d_n))$, and thus by definition of the cycle tester, the test will distinguish between these cases with non-negligible advantage.

4.1 Proving IND-CCA Security via a Sequence of Games

It remains to argue that $\varPi '$ is an IND-CCA secure encryption scheme. This proof is significantly more involved than the IND-CPA case. We prove this using a sequence of games from an encryption of a message $M_0$ to an encryption of $M_1$ (where these messages come from the IND-CCA game). The public and secret keys are always distributed as in the real scheme, but the structure of the challenge ciphertext changes in each hybrid. We underline these changes for the reader. Let the challenge messages be described as $M_0 = (m_{0,a}, m_{0, b})$ and $M_1 = (m_{1, a}, m_{1, b})$. Then the hybrids are as follows:

Game 1

This corresponds to the original security game ${\mathsf{IND}\text {-}\mathsf{CCA}}(\varPi ',\mathcal{A},\lambda )$ in which the challenger interacts with adversary $\mathcal{A}$, except that the challenge ciphertext is always an encryption of message $M_0$.

• 1. Run $\mathsf {Setup}(1^\lambda )$ to produce $\mathrm {PP}$ and then $\mathsf {KeyGen}(\mathrm {PP})$ to produce $( pk , sk )$.

• 2. On decryption query $C_i$ from $\mathcal {A}$, output $\mathsf {Dec}( sk , C_i)$.

• 3. Provide the challenge ciphertext as $C^* =(c_1^*, c_2^*)$, where $c_1^* = \mathsf {Enc}_1( pk _1,(m_{0,a}$, $m_{0,b}, c_2^*))$ and $c_2^* = \mathsf {Enc}_2( pk _2,m_{0,b})$. This is a valid encryption of $M_0$.

• 4. On decryption query $C_i \ne C^*$ from $\mathcal {A}$, output $\mathsf {Dec}( sk ,C_i)$.

Game 2

This is the same as Game 1, except that we change how the second decryption queries to reject all requests where the first portion of the query matches the first portion of the challenge.

• 1. Run $\mathsf {Setup}(1^\lambda )$ to produce $\mathrm {PP}$ and then $\mathsf {KeyGen}(\mathrm {PP})$ to produce $( pk , sk )$.

• 2. On decryption query $C_i$ from $\mathcal {A}$, output $\mathsf {Dec}( sk , C_i)$.

• 3. Provide the challenge ciphertext as $C^* =(c_1^*, c_2^*)$, where $c_1^* = \mathsf {Enc}_1( pk _1,(m_{0,a}$, $m_{0,b}, c_2^*))$ and $c_2^* = \mathsf {Enc}_2( pk _2,m_{0,b})$. This is a valid encryption of $M_0$.

• 4.

  

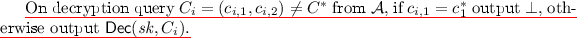
Game 3

This is the same as Game 2, except that we now encrypt $M_1$ in the cycle tester portion and continue to encrypt $M_0$ in the regular encryption portion. We continue to reject all decryption queries where the regular encryption portion matches the challenge.

• 1. Run $\mathsf {Setup}(1^\lambda )$ to produce $\mathrm {PP}$ and then $\mathsf {KeyGen}(\mathrm {PP})$ to produce $( pk , sk )$.

• 2. On decryption query $C_i$ from $\mathcal {A}$, output $\mathsf {Dec}( sk , C_i)$.

• 3. Provide the challenge ciphertext as $C^* =(c_1^*, c_2^*)$, where $c_1^* = \mathsf {Enc}_1( pk _1,(m_{0,a}$, $m_{0,b}, c_2^*))$ and

  

  .

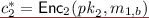
• 4. On decryption query $C_i=(c_{i,1}, c_{i,2}) \ne C^*$ from $\mathcal {A}$, if $c_{i,1} = c_1^*$ output $\perp$, otherwise output $\mathsf {Dec}( sk ,C_i)$.

Game 4

This is the same as Game 3, except that now the entire challenge ciphertext is an encryption of $M_1$. As before, we continue to reject all decryption queries where the regular encryption portion matches the challenge.

• 1. Run $\mathsf {Setup}(1^\lambda )$ to produce $\mathrm {PP}$ and then $\mathsf {KeyGen}(\mathrm {PP})$ to produce $( pk , sk )$.

• 2. On decryption query $C_i$ from $\mathcal {A}$, output $\mathsf {Dec}( sk , C_i)$.

• 3. Provide the challenge ciphertext as $C^* =(c_1^*, c_2^*)$, where

  

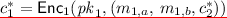
  and $c_2^* = \mathsf {Enc}_2( pk _2,m_{1,b})$.

• 4. On decryption query $C_i=(c_{i,1}, c_{i,2}) \ne C^*$ from $\mathcal {A}$, if $c_{i,1} = c_1^*$ output $\perp$, otherwise output $\mathsf {Dec}( sk ,C_i)$.

Game 5

This is the same as Game 4, except now all decryption queries are answered as normal. The challenge ciphertext always contains an encryption of $M_1$.

• 1. Run $\mathsf {Setup}(1^\lambda )$ to produce $\mathrm {PP}$ and then $\mathsf {KeyGen}(\mathrm {PP})$ to produce $( pk , sk )$.

• 2. On decryption query $C_i$ from $\mathcal {A}$, output $\mathsf {Dec}( sk , C_i)$.

• 3. Provide the challenge ciphertext as $C^* =(c_1^*, c_2^*)$, where $c_1^* = \mathsf {Enc}_1( pk _1,(m_{1,a}$, $m_{1,b}, c_2^*))$ and $c_2^* = \mathsf {Enc}_2( pk _2,m_{1,b})$.

• 4.

  

4.2 Adversary’s Probability of Outputting 1 in These Games

Let $\mathsf {Prob}^{i}_{\mathcal {A}}$ denote the probability that adversary $\mathcal {A}$ outputs a 1 in Game i. We will now show, by a series of steps, that for any adversary $\mathcal {A}$ the difference in its probability of outputting 1 between Game 1 (encryption of $M_0$) and Game 5 (encryption of $M_1$) is negligible. Thus, it cannot distinguish between these two games.

Claim

For any adversary $\mathcal {A}$, $\mathsf {Prob}^{2}_{\mathcal {A}} = \mathsf {Prob}^{1}_{\mathcal {A}}$.

Proof

These games are identical except that in Game 1 all decryption queries $C_i = C^*$ are rejected whereas in Game 2 all decryption queries $C_i=(c_{i,1}, c_{i,2})$ such that $c_{i,1} = c_1^*$ for $C^* = (c_1^*,c_2^*)$ are rejected. This results, however, in identical behavior on the decryption queries. Whenever $c_{i,1} \ne c_1^*$, both games answer the queries normally. Whenever $C_i = C^*$, neither game answers this illegal challenge query. On $c_{i,1} = c_1^*$ but $c_{i,2} \ne c_2^*$, Game 2 will output $\perp$. However, Game 1’s response is also to reject this query with the message $\perp$ for being a non-valid ciphertext, since the decryption of $c_1^*$ results in an intermediate tuple of the form $(m_{0,a},m_{0,b},c_2^*)$ and the decryption algorithm checks that $c_2^* = c_{i,2}$, which won’t be true in this case. Thus, the adversary gets identical responses to its decryption queries (and everything else) in both games. Since the games are identical, from the adversary’s viewpoint, it will output 1 with the same probability.

Claim

If $\Gamma$ is an IND-CPA-secure n-cycle tester with security parameter $\lambda$, then for any adversary $\mathcal {A}$, $\mathsf {Prob}^{3}_{\mathcal {A}} - \mathsf {Prob}^{2}_{\mathcal {A}} \le \mathsf {negl}(\lambda )$.

Proof

We show that an attacker’s probability of outputting 1 cannot be non-negligibly different in Games 2 and 3, because that would imply an attack on the IND-CPA security of the cycle tester. More formally, suppose there exists an adversary $\mathcal {A}$ such that $\mathsf {Prob}^{3}_{\mathcal {A}} - \mathsf {Prob}^{2}_{\mathcal {A}} = \epsilon$. Then we can construct an adversary $\mathcal {B}$ that uses $\mathcal {A}$ to show that $\Gamma$ is not an IND-CPA-secure n-cycle tester. $\mathcal {B}$ works as follows:

• 1. $\mathcal {B}$ runs $\mathsf {Setup}_1(1^\lambda ) \rightarrow \mathrm {PP}_1$ and $\mathsf {KeyGen}_1(\mathrm {PP}_1) \rightarrow ( pk _1, sk _1)$.

• 2. $\mathcal {B}$ obtains the public key $pk _2$ from the IND-CPA encryption challenger.

• 3. $\mathcal {B}$ sends $pk =( pk _1, pk _2)$ to $\mathcal {A}$.

• 4. $\mathcal {A}$ returns two messages $M_0 = (m_{0,a}, m_{0,b})$ and $M_1 = (m_{1,a},m_{1,b})$.

• 5. $\mathcal {B}$ sends $(m_{0,b}, m_{1,b})$ to the cycle tester encryption challenger and obtains the challenge $c_2^*$.

• 6. $\mathcal {B}$ forms the challenge ciphertext by computing $c_1^* = \mathsf {Enc}_1( pk _1,(m_{0,a}, m_{0,b}, c_2^*))$ and sending $C^* = (c_1^*, c_2^*)$ to $\mathcal {A}$.

• 7. Eventually, $\mathcal {A}$ returns a bit $\hat{b}$ and $\mathcal {B}$ outputs $\hat{b}$ to its challenger.

In the above, $\mathcal {B}$ perfectly simulates Game 2 for adversary $\mathcal {A}$ if the challenge ciphertext $c_2^*$ contains an encryption of $m_{0,b}$ and, in the other case, $\mathcal {B}$ perfectly simulates Game 3 for adversary $\mathcal {A}$ when the challenge ciphertext $c_2^*$ contains an encryption of $m_{1,b}$. Moreover, $\mathcal {B}$ succeeds if and only if $\mathcal {A}$ succeeds. Thus, if $\mathsf {Prob}^{3}_{\mathcal {A}} - \mathsf {Prob}^{2}_{\mathcal {A}} = \epsilon$, then we have $\Pr [\mathcal {B}$ is correct] = $\frac{1}{2}\Pr [\mathcal {B}$ is correct | IND-CPA challenger chose 0] + $\frac{1}{2}\Pr [\mathcal {B}$ is correct | IND-CPA challenger chose 1] = $\frac{1}{2}\Pr [\mathcal {A}$ is correct | Game 2] + $\frac{1}{2}\Pr [\mathcal {A}$ is correct | Game 3] = $\frac{1}{2}(1 - \mathsf {Prob}^{2}_{\mathcal {A}}) + \frac{1}{2}(\mathsf {Prob}^{3}_{\mathcal {A}})$ = $\frac{1}{2}(1 - \mathsf {Prob}^{2}_{\mathcal {A}}) + \frac{1}{2}(\mathsf {Prob}^{2}_{\mathcal {A}} + \epsilon )$ = $\frac{1}{2} + \frac{\epsilon }{2}$. Since we assumed the cycle tester was IND-CPA secure, it must hold that $\epsilon \le \mathsf {negl}(\lambda )$.

Claim

If $\varPi$ is an IND-CCA-secure encryption scheme with security parameter $\lambda$, then for any adversary $\mathcal {A}$, $\mathsf {Prob}^{4}_{\mathcal {A}} - \mathsf {Prob}^{3}_{\mathcal {A}} \le \mathsf {negl}(\lambda )$.

Proof

Suppose there exists an adversary $\mathcal {A}$ such that $\mathsf {Prob}^{4}_{\mathcal {A}} - \mathsf {Prob}^{3}_{\mathcal {A}} = \epsilon$. Then we can construct an adversary $\mathcal {B}$ that uses $\mathcal {A}$ to show that $\varPi$ is not an IND-CCA-secure encryption scheme. $\mathcal {B}$ works as follows:

• 1. $\mathcal {B}$ obtains the public key $pk _1$ from the IND-CCA encryption challenger.

• 2. $\mathcal {B}$ runs $\mathsf {Setup}_2(1^\lambda ) \rightarrow \mathrm {PP}_2$ and $\mathsf {KeyGen}_2(\mathrm {PP}_2) \rightarrow ( pk _2, sk _2)$.

• 3. $\mathcal {B}$ sends $pk =( pk _1, pk _2)$ to $\mathcal {A}$.

• 4. On receiving a decryption query for ciphertext $C_i = (c_{i,1},c_{i,2})$ from $\mathcal {A}$, $\mathcal {B}$ sends $c_{i,1}$ to its IND-CCA encryption challenger to obtain a message M. $\mathcal {B}$ returns M to $\mathcal {A}$.

• 5. $\mathcal {A}$ returns two messages $M_0 = (m_{0,a}, m_{0,b})$ and $M_1 = (m_{1,a},m_{1,b})$.

• 6. $\mathcal {B}$ computes $c_2^* = \mathsf {Enc}_2( pk _2,m_{1,b})$ and sends $M'_0 = (M_0,c_2^*)$ and $M'_1=(M_1,c_2^*)$ to the IND-CCA challenger and obtains the challenge $c_1^*$.

• 7. $\mathcal {B}$ sends the challenge ciphertext $C^* = (c_1^*, c_2^*)$ to $\mathcal {A}$.

• 8. On receiving a decryption query for ciphertext $C_i = (c_{i,1},c_{i,2})$ where $c_{i,1} \ne c_1^*$ from $\mathcal {A}$, $\mathcal {B}$ sends $c_{i,1}$ to its IND-CCA encryption challenger to obtain a message M. $\mathcal {B}$ returns M to $\mathcal {A}$

• 9. Eventually, $\mathcal {A}$ returns a bit $\hat{b}$ and $\mathcal {B}$ outputs $\hat{b}$ to its challenger.

In the above, $\mathcal {B}$ perfectly simulates Game 3 for adversary $\mathcal {A}$ if the challenge ciphertext $c_1^*$ contains an encryption of $M'_0$ and, in the other case, $\mathcal {B}$ perfectly simulates Game 4 for adversary $\mathcal {A}$ when the challenge ciphertext $c_1^*$ contains an encryption of $M'_1$. Moreover, $\mathcal {B}$ succeeds if and only if $\mathcal {A}$ succeeds. Thus, if $\mathsf {Prob}^{4}_{\mathcal {A}} - \mathsf {Prob}^{3}_{\mathcal {A}} = \epsilon$, then $\mathcal {B}$’s probability of success in the IND-CCA security game is $\Pr [\mathcal {B}$ is correct] = $\frac{1}{2}\Pr [\mathcal {B}$ is correct | IND-CCA challenger chose 0] + $\frac{1}{2}\Pr [\mathcal {B}$ is correct | IND-CCA challenger chose 1] = $\frac{1}{2}\Pr [\mathcal {A}$ is correct | Game 3] + $\frac{1}{2}\Pr [\mathcal {A}$ is correct | Game 4] = $\frac{1}{2}(1 - \mathsf {Prob}^{3}_{\mathcal {A}}) + \frac{1}{2}(\mathsf {Prob}^{4}_{\mathcal {A}})$ = $\frac{1}{2}(1 - \mathsf {Prob}^{3}_{\mathcal {A}}) + \frac{1}{2}(\mathsf {Prob}^{3}_{\mathcal {A}} + \epsilon )$ = $\frac{1}{2} + \frac{\epsilon }{2}$. Since we assumed that $\varPi$ was IND-CCA secure, it must hold that $\epsilon \le \mathsf {negl}(\lambda )$.

Claim

For any adversary $\mathcal {A}$, $\mathsf {Prob}^{5}_{\mathcal {A}} = \mathsf {Prob}^{4}_{\mathcal {A}}$.

Proof

These games are identical except that in Game 4 all decryption queries $C_i=(c_{i,1}, c_{i,2})$ such that $c_{i,1} = c_1^*$ for $C^* = (c_1^*,c_2^*)$ are rejected in Game 5 whereas all decryption queries $C_i = C^*$ are rejected. This results, however, in identical behavior on the decryption queries. This case is the mirror image of the argument in the proof of Claim 4.2.

Conclusion of the Proof of Theorem 2. Given the above claims, we can conclude that if $\Gamma$ is an IND-CPA-secure n-cycle tester and $\varPi$ is an IND-CCA-secure encryption scheme (with the appropriate length constraints), then for any adversary $\mathcal {A}$, it holds that $\mathsf {Prob}^{5}_{\mathcal {A}} - \mathsf {Prob}^{1}_{\mathcal {A}}$ is negligible, implying that $\varPi '$ is an IND-CCA-secure encryption scheme.

5 A 2-Cycle Tester from the k-DLIN Assumption

We now present a 2-cycle tester from the decision k-Linear assumption in pairing groups for any constant k (where this assumption is believed to hold for $k \ge 2$ in this bilinear setting and the assumption grows weaker as k increases). We will use a message space of $\{0,1\}^\lambda$. In our exposition we will use boldface to denote a matrix such as $\mathbf {M}$. We also use $g^{\mathbf {M}}$ as shorthand to denote the group elements corresponding to the raising g to each individual element of $\mathbf {M}$.

$\mathsf {Setup}(1^\lambda )\rightarrow \mathrm {PP}$. The setup algorithm first runs $\mathcal {G}(1^\lambda )$ to generate a (Type-1) group $\mathbb {G}$ of prime order p with generator g. Next it defines a pseudorandom generator $\mathrm {PRG}: \{0,1\}^\lambda \rightarrow \mathbb {Z}_p^{k \times k}$, which maps strings from $\{0,1\}^\lambda$ to invertible $k \times k$ matrices over $\mathbb {Z}_p$. Finally, it chooses a random invertible matrix $\mathbf {A} \in \mathbb {Z}_p^{k \times k}$ and computes $g^{ \mathbf {A} }$. The public parameters, $\mathrm {PP}$ consist of the group description $\mathbb {G}$, the description of $\mathrm {PRG}$ and $g^{ \mathbf {A}}$.

$\mathsf {KeyGen}(\mathrm {PP})\rightarrow ( pk , sk )$. The key generation algorithm first chooses random $w \in \{0,1\}^\lambda$. The secret key $sk =w$. Next, it computes $\mathrm {PRG}(w) \rightarrow \mathbf {W} \in \mathbb {Z}_p^{k \times k}$ and chooses a bit $\beta \in \{0,1\}$. Finally, in addition to implicitly including $\mathrm {PP}$, it defines the public key as

$$\begin{aligned} pk = {\left\{ \begin{array}{ll} (0, K= g^{ \mathbf {AW}} ) \in \{0,1\} \times \mathbb {G}^{k \times k} &{} \text {if } \beta = 0 ;\\ (1, K=g^{ \mathbf {WA}} ) \in \{0,1\} \times \mathbb {G}^{k \times k} &{}\text {if } \beta = 1. \end{array}\right. } \end{aligned}$$

$\mathsf {Enc}( pk = (\beta , K), m \in \{0,1\}^\lambda )\rightarrow ct$.

The encryption algorithm first computes computes $\mathrm {PRG}(m) \rightarrow \mathbf {M} \in \mathbb {Z}_p^{k \times k}$ and then computes $\mathbf {M}^{-1}$. Note that since $\mathrm {PRG}$ maps to invertible matrices, $\mathbf {M}$ will have an inverse.

If the type bit $\beta =0$ the key $K= g^{ \mathbf {AW}}$ for some $\mathbf {W}$. The algorithm chooses $\mathbf {r}$ as a random row vector of length k in $\mathbb {Z}_p$ (i.e. a random matrix of dimension $1 \times k$). The ciphertext is computed and output as

$$ C_1 = g^{ \mathbf {r} \mathbf {AW}} , \quad C_2 = g^{ \mathbf {r} \mathbf {A} \mathbf {M}^{-1} } . $$

Thus, the ciphertext will consist of two row vectors in the exponent. We observe all terms are computable from the public keys and public parameters.

If the type bit $\beta =1$ the key $K= g^{ \mathbf {WA}}$ for some $\mathbf {W}$. The algorithm chooses $\mathbf {r}$ as a random column vector of length k in $\mathbb {Z}_p$ (i.e. a random matrix of dimension $k \times 1$). The ciphertext $ct$ is computed and output as

$$ C_1 = g^{ \mathbf {WA} \mathbf {r} } , \quad C_2 = g^{ \mathbf {M}^{-1} \mathbf {A} \mathbf {r} } . $$

$\mathsf {Test}( \mathbf {pk}, \mathbf {y})\rightarrow \{0,1\}$. Since we are testing for 2-cycles, parse $\mathbf {y}=(C=(C_{1}, C_{2}),$ $C'=(C'_1, C'_2))$. If the key types are identical i.e. $\beta = \beta '$ then just output a random bit as a guess.

Otherwise, presume that $\beta =0, \beta '=1$ (if it is the other way around just flip the order). Then compute $e(C_1, C'_2) \mathop {=}\limits ^{?} e(C'_1, C_2)$ and output the result. Note here we overload notation so that the pairing operator e is over a matrix of group elements and means matrix multiplication in the exponent. (Or in this case a dot product in the exponent.)

Analysis of Test Algorithm. We analyze the correctness of the test algorithm. Let’s consider two secret keys $w,w'$ where $\mathrm {PRG}(w)=\mathbf {W}$ and $\mathrm {PRG}(w')=\mathbf {W}'$. Again, presume that $\beta =0, \beta '=1$. The corresponding public keys will be $pk = g^{ \mathbf {AW} }$ and $pk = g^{ \mathbf {W}' \mathbf {A} }$. Now consider an encryption of m under $pk$ and $m'$ under $pk '$ where $\mathrm {PRG}(m)=\mathbf {M}$ and $\mathrm {PRG}(M')=\mathbf {M}'$. Let $\mathbf {r}$ and $\mathbf {r}'$ be the respective randomness used for each encryption.

The test equations outputs 1 iff $e(C_1, C'_2) \mathop {=}\limits ^{?} e(C'_1, C_2)$ this is equivalent to testing

$$\begin{aligned} \mathbf {r} \mathbf {AW} \mathbf {M}'^{-1} \mathbf {A} \mathbf {r}' \mathop {=}\limits ^{?} \mathbf {r} \mathbf {A} \mathbf {M}^{-1} \mathbf {W}' \mathbf {A} \mathbf {r}' . \end{aligned}$$

(1)

Let’s first consider the case where we have an encryption of a cycle. This means that $m'=w$ and $m = w'$ so we have that $\mathbf {M}'^{-1} = \mathbf {W}^{-1}$ and $\mathbf {M}^{-1} = \mathbf {W}'^{-1}$. Substituting these in we see that

$$ \begin{array}{rcl} \mathbf {r} \mathbf {AW} \mathbf {M}'^{-1} \mathbf {A} \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A} \mathbf {M}^{-1} \mathbf {W}' \mathbf {A} \mathbf {r}' \\ \mathbf {r} \mathbf {A} \mathbf {I} \mathbf {A} \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A} \mathbf {I} \mathbf {A} \mathbf {r}' \\ \mathbf {r} \mathbf {A}^2 \mathbf {r}' &{} \mathop {=}\limits ^{?} &{} \mathbf {r} \mathbf {A}^2 \mathbf {r}' . \\ \end{array} $$

Thus, on a cycle the test will output 1.

We now turn to the case of showing that an encryption of 0’s will output 0 (when the keys have different $\beta$ types) with all but negligible probability.

First, we first let $\mathbf {Z} = \mathrm {PRG}(0^\lambda )^{-1}$ which is the matrix used to encrypt the all 0’s string. Second, we consider the probability of the tester outputting 1, when $\mathbf {W}$ and $\mathbf {W}'$ are chosen uniformly at random (and independently from $\mathbf {Z}$) from the set of full rank matrices, as opposed to being the output of a pseudorandom generator. If there, was more than a negligible difference of the test in outputting 1 in these two cases, it would lead to an attack on the security of the pseudorandom generator.

We can now observe that the matrices $\mathbf {X}= \mathbf {AW} \mathbf {Z} \mathbf {A}$ and $\mathbf {X}'= \mathbf {A} \mathbf {Z} \mathbf {W}' \mathbf {A}$ are distributed independently and uniformly random from full rank matrices. Note we substituted $\mathbf {Z}$ for both $\mathbf {M}'^{-1}$ and $\mathbf {M}^{-1}$ in Eq. 1. Then $\mathbf {u} = \mathbf {r} \mathbf {X}$ and $\mathbf {u}' = \mathbf {r} \mathbf {X}'$ are independently distributed as uniformly at random row vectors of length k. Finally, it follows that the probability that

$$ \mathbf {u} \mathbf {r}' \mathop {=}\limits ^{?} \mathbf {u}' \mathbf {r}' $$

is negligible in the security parameter. Thus, with probability negligibly close to 1 the test algorithm will output 0 when given an encryption of all 0’s.

IND-CPA Security of the Tester

Theorem 3

The above encryption scheme $\varPi =(\mathsf {KeyGen},\mathsf {Enc}, \mathsf {Test})$ (where the decryption algorithm is ignored) is ${\mathsf{IND}\text {-}\mathsf{CPA}}$-secure under the k-Linear Assumption in $\mathbb {G}$.

The proof of this theorem can be found in the full version [11].

6 A 2-Cycle Tester from Learning with Errors

We now present a 2-Cycle Tester whose ${\mathsf{IND}\text {-}\mathsf{CPA}}$ security follows from the Learning with Errors Assumption. We note that our construction is similar to multi-bit Regev encryption.

6.1 Construction

$\mathsf {Setup}(1^n)\rightarrow \mathrm {PP}$. The setup algorithm chooses $m, q, \ell , \sigma , r,\alpha$. These parameters are chosen to satisfy the following constraints: $m\ge 2n \log q$, $\sigma \ge L \omega (\sqrt{\log m})$, $q \ge 5\sigma (m+1)$, $\ell > (n+m+1)\log q + \omega (\log (n+m))$, $r:= \sigma \ell$, $\alpha \le 1/(r \sqrt{m+1} \cdot \omega (\sqrt{\log n}))$, and $q>2$ is prime. Here, L is defined as follows. We let z denote the number of uniform random bits employed by TrapGen to generate a matrix B in $\mathbb Z_q^{n \times m}$ along with a trapdoor basis $T_B$. L is a bound such that $||T_B||_{GS} \le L$ with overwhelming probability. (We note that this range of parameters allows us to set $\alpha$ so that $n/\alpha$ is polynomial, and LWE is believed to be hard in this parameter regime.) The public parameters are $\mathrm {PP}= (m,q,\ell ,\sigma ,r,\alpha ,z)$.

$\mathsf {KeyGen}(\mathrm {PP})\rightarrow ( pk , sk )$. The key generation algorithm chooses a uniformly random secret key $sk$ in $\{0,1\}^z$ and runs TrapGen($sk$) to produce a matrix $B \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_B$. It then chooses independent and uniformly random vectors $c_1, \ldots , c_\ell \in \mathbb Z_q^n$ and noise vectors $\gamma _1, \ldots , \gamma _\ell$ from $\chi ^m$, where $\chi$ is distributed as $\lfloor q \varPsi _\alpha \rfloor \mod q$, where $\varPsi _\alpha$ is a distribution on $\mathbb {T}$ of a normal variable with mean 0 and standard deviation $\alpha /\sqrt{2\pi }$ reduced modulo 1. (We think of these vectors as row vectors.) In addition to implicitly including the $\mathrm {PP}$, it sets

$$\begin{aligned} pk = \{ c_1, \ldots , c_\ell , y_1 := c_1 B + \gamma _1, \ldots , y_\ell := c_\ell B+ \gamma _\ell \}. \end{aligned}$$

$\mathsf {Enc}( pk , m \in \{0,1\}^z) \rightarrow ct$. The encryption algorithm runs TrapGen(m) to produce a matrix $Z \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_Z$. It chooses random signs $r_1, \ldots , r_\ell \in \{-1,1\}$ and computes $s := \sum _{i=1}^\ell r_i c_i$. It then uses $T_Z$ to sample a short (column) vector v such that $Z v = s^t$, by calling the algorithm SampleD. It computes $C = \sum _{i=1}^\ell r_i y_i,$ and sets the ciphertext as $ct = (C, v)$.

$\mathsf {Test}(( pk _0, pk _1),((C_0, v_0),(C_1,v_1)))\rightarrow \{0,1\}$. The cycle test algorithm compares $C_0 v_1$ to $C_1 v_0$ and checks if there are close modulo q (if their distance is $\le 2q/5$). If so, it outputs 1. If not, it outputs 0.

Analysis of Test Algorithm. We let $B_0, Z_0, s_0$ be the B, Z and s values corresponding to ciphertext $(C_0, v_0)$ and $B_1, Z_1, s_1$ be the analogous values for $(C_1, v_1)$. When there is a cycle, we then have $Z_0 = B_1$ and $Z_1 = B_0$. We then have $B_0 v_1 = s^t_1$ and $B_1 v_0 = s^t_0$. Noting that $C_0 = s_0 B_0 + \psi _0$ for some small vector $\psi _0$, we see that

$$\begin{aligned} C_0 v_1 = s_0 B_0 v_1 + \psi _0 v_1 = s_0 s^t_1 + \psi _0 v_1. \end{aligned}$$

Similarly, $C_1 = s_1 B_1 + \psi _1$ for some small vector $\psi _1$, so we have that

$$\begin{aligned} C_1 v_0 = s_1 B_1 v_0 + \psi _1 v_0 = s_1 s^t_0 + \psi _1 v_0. \end{aligned}$$

We consider the size of $\psi _0 v_1 - \psi _1 v_0$ modulo q. First, $|\psi _0 v_1|$ is at most $\ell$ times the maximal size of $|\gamma _j v_1|$. Using the same analysis as in the proof of Lemma 8.2 of [21], each of these is $\le \frac{q}{5\ell }$ with high probability. Thus, $|\psi _0 v_1 - \psi _1 v_0| \le \frac{2q}{5}$ with high probability.

Since all of $v_0, v_1, \psi _0, \psi _1$ are short, this will cause these values to be close modulo q, so the cycle test will output 1 with high probability.

When there is no cycle, the matrices $B_0$ and $B_1$ are (statistically close) to independent, uniformly random matrices. Thus the probability that $s_0B_0v_1$ and $s_1B_1v_0$ will be within $\frac{2}{5}q$ modulo q is negligibly close to $\frac{2}{5}$. Thus the cycle test wins the distinguishing game with probability negligibly close to $\frac{1}{2} + \frac{1}{2} \cdot \frac{3}{5} = \frac{4}{5}$.

6.2 IND-CPA Security of the Tester

To prove that this construction satisfies IND-CPA, we define a sequence of security games.

Game $_0$ This is the regular ${\mathsf{IND}\text {-}\mathsf{CPA}}$ security game for our construction:

• 1. The challenger runs $\mathsf {Setup}(1^n) \rightarrow \mathrm {PP}= (m,q,\ell ,\sigma ,r,\alpha ,z)$.

• 2. The challenger chooses a uniformly random secret key $sk$ in $\{0,1\}^z$ and runs TrapGen($sk$) to produce a matrix $B \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_B$. It then chooses independent and uniformly random vectors $c_1, \ldots , c_\ell \in \mathbb Z_q^n$ and noise vectors $\gamma _1, \ldots , \gamma _\ell$ from $\chi ^m$. It sets

  $$\begin{aligned} pk = \{ c_1, \ldots , c_\ell , y_1 := c_1 B + \gamma _1, \ldots , y_\ell := c_\ell B+ \gamma _\ell \}. \end{aligned}$$

  The challenger gives the parameters $\mathrm {PP}$ and key $pk$ to the attacker.

• 3. $\mathcal {A}$ The attacker submits two messages $m_0, m_1$ to the challenger.

• 4. The challenger flips a coin $b \in \{0,1\}$. It runs TrapGen$(m_b)$ to produce a matrix $Z \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_Z$. It chooses random signs $r_1, \ldots , r_\ell \in \{-1,1\}$ and computes $s := \sum _{i=1}^\ell r_i c_i$. It then uses $T_Z$ to sample a short (column) vector v such that $Z v = s^t$, by calling the algorithm SampleD. It computes $C = \sum _{i=1}^\ell r_i y_i,$ and sets the ciphertext as (C, v).

• 5. The attacker receives the challenge ciphertext. It then outputs a guess $b'$ and wins if $b'=b$.

Game $_1$

• 2. The challenger chooses a uniformly random secret key $sk$ in $\{0,1\}^z$ and runs TrapGen($sk$) to produce a matrix $B \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_B$. It then chooses independent and uniformly random vectors $c_1, \ldots , c_\ell \in \mathbb Z_q^n$ and

  

  . It sets $pk = \{ c_1, \ldots , c_\ell , y_1, \ldots , y_\ell \}.$

Game $_2$

• 4. The challenger flips a coin $b \in \{0,1\}$. It runs TrapGen$(m_b)$ to produce a matrix $Z \in \mathbb Z_q^{n \times m}$ and a corresponding trapdoor basis $T_Z$.

  

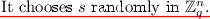
  It then uses $T_Z$ to sample a short (column) vector v such that $Z v = s^t$, by calling the algorithm SampleD.

  

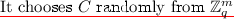
  and sets the ciphertext as (C, v).

Game $_3$

• 4.

  

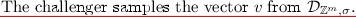
  It chooses C randomly from $\mathbb Z_q^m$ and sets the ciphertext as (C, v).

At this point, the distribution of the ciphertext is independent of the message, and it is clear that no PPT adversary can obtain a non-zero advantage.

Lemma 3

Under the LWE assumption for the noise distribution $\chi$, no PPT attacker can obtain a non-negligible difference in advantage between Game$_0$ and Game$_1$.

Proof

We can collect the column vectors $c^t_1, \ldots , c^t_\ell$ into a $n\times \ell$ matrix we call D. We can collect the row vectors $y_1, \ldots , y_m$ into a $\ell \times m$ matrix we call Y and the row vectors $\gamma _1, \ldots , \gamma _\ell$ into a $\ell \times m$ matrix we call $\Gamma$. We can then write the public key as $D, D^t B + \Gamma$. Since B is never published, each column of B is a fresh, uniform vector in $\mathbb Z_q^n$, and therefore each column of $D^t B+ \Gamma$ is distributed as an LWE sample with D playing the role of the $n \times m$ matrix A and the column of B playing the role of the random vector s. By a hybrid argument over the columns, we can thus rely on LWE to change each $y_i$ to be uniformly distributed in $\mathbb Z_q^m$.

Lemma 4

No PPT attacker can obtain a non-negligible difference in advantage between Game$_1$ and Game$_2$.

Proof

For this, we will argue that the distributions of s, C in Game$_1$ and Game$_2$ are statistically close. This is a direct application of Lemma 2 with j set to be $n+m$. To see this, we consider the random signs $r_1, \ldots , r_\ell \in \{-1,1\}$ as a column vector R of length $\ell$. We then consider the (vertical) concatenation of $s^t$ and $C^t$ into a $n+m$ length column vector. In Game$_1$, this is produced as MR, where M is a $(n+m)\times \ell$ matrix formed by vertically concatenating D and $Y^t$ as defined in the proof of the previous lemma. Since the matrices D, Y are now uniformly chosen, replacing MR by a uniformly random $(n+m)\times 1$ matrix (as in Game$_2$) is a statistically close distribution by Lemma 2.

Lemma 5

No PPT attacker can obtain a non-negligible difference in advantage between Game$_2$ and Game$_3$.

Proof

We will argue that the distributions of v in Game$_2$ and Game$_3$ are statistically close. We first observe that in Game$_2$, v is chosen so that $Zv = s^t$ for a uniformly random s that is now independent of the rest of the ciphertext. The distribution of v here produced by SampleD is statistically close to $\mathcal {D}_{\Lambda ^s_q(Z),\sigma }$. Now by Lemma 1, if we consider the distribution $\mathcal {D}_{\mathbb Z^m,\sigma }$, the probability mass on the preimages of $s^t$ under the mapping $Zv = s^t$ is (up to a negligible statistical distance) the same for each s. Thus, the distribution of v in both Game$_2$ and in Game$_3$ is statistically close to $\mathcal {D}_{\mathbb Z^m, \sigma }$.