Abstract
Feistel Networks (FN) are now being used massively to encrypt credit card numbers through format-preserving encryption. In our work, we focus on FN with two branches, entirely unknown round functions, modular additions (or other group operations), and when the domain size of a branch (called  ) is small. We investigate round-function-recovery attacks.
) is small. We investigate round-function-recovery attacks.
The best known attack so far is an improvement of Meet-In-The-Middle (MITM) attack by Isobe and Shibutani from ASIACRYPT 2013 with optimal data complexity  and time complexity
and time complexity  , where
, where  is the round number in FN. We construct an algorithm with a surprisingly better complexity when
is the round number in FN. We construct an algorithm with a surprisingly better complexity when  is too low, based on partial exhaustive search. When the data complexity varies from the optimal to the one of a codebook attack
is too low, based on partial exhaustive search. When the data complexity varies from the optimal to the one of a codebook attack  , our time complexity can reach
, our time complexity can reach  . It crosses the complexity of the improved MITM for
. It crosses the complexity of the improved MITM for  .
.
We also estimate the lowest secure number of rounds depending on  and the security goal. We show that the format-preserving-encryption schemes FF1 and FF3 standardized by NIST and ANSI cannot offer 128-bit security (as they are supposed to) for
and the security goal. We show that the format-preserving-encryption schemes FF1 and FF3 standardized by NIST and ANSI cannot offer 128-bit security (as they are supposed to) for  and
and  , respectively (the NIST standard only requires
, respectively (the NIST standard only requires  ), and we improve the results by Durak and Vaudenay from CRYPTO 2017.
), and we improve the results by Durak and Vaudenay from CRYPTO 2017.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Feistel Networks (FN) have been used in constructing many block ciphers such as DES [1]. In the classical FN, we construct a permutation from  bits to
bits to  bits with round functions from
bits with round functions from  bits to
bits to  bits. We call it as balanced Feistel network. Figure 1 represents a 4-round FN with modular addition (modulo the size of the domain for a branch). Other well known types of Feistel networks are unbalanced FN, alternating between contracting and expanding round functions.
bits. We call it as balanced Feistel network. Figure 1 represents a 4-round FN with modular addition (modulo the size of the domain for a branch). Other well known types of Feistel networks are unbalanced FN, alternating between contracting and expanding round functions.
Although block ciphers only encrypt blocks of a fixed format (typically: a binary string of length 128), there are many applications requiring to encrypt data of another format (such as a decimal string of a given length) and to have encrypted data in the same format. For example, Credit Card Numbers (CCN) consist of 16 decimal numbers, whose 6 digits must be kept confidential. For this reason, these 6 digits are typically encrypted in digital transactions using a Format-Preserving Encryption (FPE). Recently, FPE based on FN [5, 6, 9] have been standardized [2, 3]. As an example, the FPE solution of the terminal manufacturer company Verifone encrypts about 30M credit card transactions per day in the United States alone.
In this work, we are specifically interested in FN with two branches (not necessarily balanced) with secret round functions and modular addition operation. Moreover, we are interested in small domain size over larger key space. We investigate the security when the round function is entirely unknown instead of a publicly known round function that mixes the input with a secret key (i.e. round function is  , where
, where  is the round key in
is the round key in  round). We do not assume that round functions are bijective. This applies to FF1 [6] by Bellare et al. and FF3 [9] by Brier et al. which have been standardized by The National Institute of Standards an Technology (NIST) published in March, 2016 [2]. This standard aims at a 128-bit security for any
round). We do not assume that round functions are bijective. This applies to FF1 [6] by Bellare et al. and FF3 [9] by Brier et al. which have been standardized by The National Institute of Standards an Technology (NIST) published in March, 2016 [2]. This standard aims at a 128-bit security for any  . FF3 was broken and repaired by Durak and Vaudenay [15]. Herein, we denote by FF3
. FF3 was broken and repaired by Durak and Vaudenay [15]. Herein, we denote by FF3 the repaired scheme.
the repaired scheme.
Since their invention, Feistel networks and their security analysis have been studied. Many cryptanalysis studies have been done to give key-recovery, message-recovery, round-function-recovery, and differential attacks on different types of Feistel networks [7, 12, 16, 18, 21, 24]. We summarize the best function recovery attacks in Table 1.Footnote 1 The complexities are given in terms of number of encryptions. In Appendix, we present a brief survey of existing attacks. So far, the best generic attack was a variant of Meet-In-The-Middle (MITM) attack.
 -round FN with domain branch size
-round FN with domain branch size  . (All
. (All  are different constants such that
are different constants such that  .)
.)The most famous security result dates back to late 80’s given by Luby-Rackoff [20]. In their seminal paper, Luby and Rackoff first showed that a three round Feistel construction is a secure pseudorandom permutation from  bits to
bits to  bits. Moreover, they showed that for more than three rounds FN, all generic chosen-plaintext attacks on Feistel schemes require
bits. Moreover, they showed that for more than three rounds FN, all generic chosen-plaintext attacks on Feistel schemes require  queries where
queries where  is the input/output size to the round function. Information theoretically, the number
is the input/output size to the round function. Information theoretically, the number  of queries provides
of queries provides  bits of information. For
bits of information. For  -round FN, we need
-round FN, we need  bits of information to recover the round functions (each round function can be represented with a string of size
bits of information to recover the round functions (each round function can be represented with a string of size  ). Therefore,
). Therefore,  is enough to reconstruct the round function, in theory. Patarin [23] further showed that for
is enough to reconstruct the round function, in theory. Patarin [23] further showed that for  , four rounds are secure against known-plaintext attacks (the advantage would be bounded by
, four rounds are secure against known-plaintext attacks (the advantage would be bounded by  for
for  ), five rounds are secure against chosen-plaintext attacks (the advantage would be bounded by
), five rounds are secure against chosen-plaintext attacks (the advantage would be bounded by  for
for  ) and six rounds are secure against chosen-plaintext and ciphertext attacks (the advantage would be bounded by
) and six rounds are secure against chosen-plaintext and ciphertext attacks (the advantage would be bounded by  for
for  ).
).
As we will not necessarily assume messages in binary, we use the notation  as the domain size of the round functions. We introduce some known attacks on Feistel networks with our focused properties: two branches with domain size
as the domain size of the round functions. We introduce some known attacks on Feistel networks with our focused properties: two branches with domain size  and
and  , with modular addition modulo
, with modular addition modulo  and
and  , secret random round functions which are balanced (
, secret random round functions which are balanced ( ) or unbalanced but with
) or unbalanced but with  .
.
Our Contributions. In this work, we propose the best known generic exhaustive search attack on Feistel networks with two branches and random functions with arbitrary number  of rounds. We compare it with MITM. It is better for some parameters. When the data complexity varies in between the optimal (based on information theory) and the one of the codebook attack, our best time complexity goes from
of rounds. We compare it with MITM. It is better for some parameters. When the data complexity varies in between the optimal (based on information theory) and the one of the codebook attack, our best time complexity goes from  (MITM-based, see Eq. (2) for
(MITM-based, see Eq. (2) for  even) to
even) to  (based on partial exhaustive search, see Eq. (8)), where
(based on partial exhaustive search, see Eq. (8)), where  is the domain size of the branch. More precisely, the optimal data complexity is
is the domain size of the branch. More precisely, the optimal data complexity is  . MITM works with the optimal data complexity and with time complexity
. MITM works with the optimal data complexity and with time complexity  (see Eq. (2)). Our partial exhaustive search attack can use any data complexity from the optimal to the one of a codebook
(see Eq. (2)). Our partial exhaustive search attack can use any data complexity from the optimal to the one of a codebook  , but it is better than MITM for
, but it is better than MITM for  . It reaches the time complexity (called
. It reaches the time complexity (called  )
)  for some constant
for some constant  (see Eq. (8)) using
(see Eq. (8)) using  chosen plaintexts.
chosen plaintexts.
We plot in Fig. 2 the  parameters for which we have
parameters for which we have  . As we can see, for any constant
. As we can see, for any constant  and a low
and a low  (including
(including  and
and  as the NIST standards suggest),
as the NIST standards suggest),  is the best attack. The same figure includes two curves that correspond to the 128-bit and 256-bit security parameters
is the best attack. The same figure includes two curves that correspond to the 128-bit and 256-bit security parameters  . The curves are computed with the minimum between
. The curves are computed with the minimum between  and
and  . It can be read that an intended 128-bit security level in FF3
. It can be read that an intended 128-bit security level in FF3 with
with  ,
,  and in FF1 with
and in FF1 with  ,
,  has not been satisfied.Footnote 2 E.g., for 6-bit messages and 2-digit messages.Footnote 3
has not been satisfied.Footnote 2 E.g., for 6-bit messages and 2-digit messages.Footnote 3
Another application could be to reverse engineer an S-box based on FN [8].
Structure of Our Paper. In Sect. 2, we review the symmetries in the set of tuples of round functions which define the same FN and we describe the MITM attacks. Our algorithm is described and analyzed in Sect. 3. Section 4 applies our results to format preserving encryption standards. Finally, we conclude.Footnote 4
2 Preliminaries
In this section, we present known techniques to recover the  -tuple of round functions in FN. Note that we actually recover an equivalent tuple of round functions. Indeed, we can see that round functions differing by constants can define the actual same cipher [13, 15]. Concretely, let
-tuple of round functions in FN. Note that we actually recover an equivalent tuple of round functions. Indeed, we can see that round functions differing by constants can define the actual same cipher [13, 15]. Concretely, let  be a tuple defining a cipher
be a tuple defining a cipher  . For every
. For every  ,
,  such that
such that  and
and  , we can define
, we can define  by
by  . We obtain a tuple defining the same cipher
. We obtain a tuple defining the same cipher  . Therefore, we can fix arbitrarily one point of
. Therefore, we can fix arbitrarily one point of  and we are ensured to find an equivalent tuple of functions including those points.
and we are ensured to find an equivalent tuple of functions including those points.
2.1 Meet-In-The-Middle (MITM) Attack
The MITM attack was introduced by Diffie and Hellman [10]. It is a generic known-plaintext attack. Briefly, consider an  round encryption
round encryption  and corresponding
and corresponding  decryption algorithms. We assume each algorithm uses a
decryption algorithms. We assume each algorithm uses a  -bit key and we denote the keys by
-bit key and we denote the keys by  . Let
. Let  be the plaintexts and
be the plaintexts and  be the corresponding ciphertexts. Let the intermediate values entering to round
be the corresponding ciphertexts. Let the intermediate values entering to round  be
be  for
for  . The adversary enumerates each possible combination of the keys
. The adversary enumerates each possible combination of the keys  for the first
for the first  rounds and it computes the intermediate values for each plaintexts as
rounds and it computes the intermediate values for each plaintexts as  until round
until round  . Then, these values along with their possible keys are stored in a table (The memory complexity is
. Then, these values along with their possible keys are stored in a table (The memory complexity is  messages). Then, the adversary partially decrypts the ciphertext
messages). Then, the adversary partially decrypts the ciphertext  for each value of the keys
for each value of the keys  backward. Finally, the adversary looks for a match between the partially decrypted values and the rows of the stored table. Each match suggests keys for
backward. Finally, the adversary looks for a match between the partially decrypted values and the rows of the stored table. Each match suggests keys for  and the adversary recovers all the keys. The time complexity of the MITM attack is
and the adversary recovers all the keys. The time complexity of the MITM attack is  and memory complexity is
and memory complexity is  .Footnote 5
.Footnote 5
We can apply the MITM attack to the Feistel networks with  rounds and
rounds and  known plaintext/ciphertext pairs. In our setting,
known plaintext/ciphertext pairs. In our setting,  is quite small, thus we can focus on a generic FN with functions specified by tables. This is equivalent to using a key of
is quite small, thus we can focus on a generic FN with functions specified by tables. This is equivalent to using a key of  bits. Therefore, the standard MITM attack has a time complexity of
bits. Therefore, the standard MITM attack has a time complexity of  with same memory complexity. We label the time complexity as follows:
with same memory complexity. We label the time complexity as follows:

with  known plaintexts. The pseudocode is given in Algorithm 1.
known plaintexts. The pseudocode is given in Algorithm 1.

2.2 Improved MITM
In this section, we elaborate and extend the attack mentioned briefly in [11, 12] on  -round FN. The same attack appears in [17, 18] with
-round FN. The same attack appears in [17, 18] with  . We are only adapting the algorithm to our settings. We take
. We are only adapting the algorithm to our settings. We take  and
and  so that
so that  and
and  . Consider the FN in Fig. 3 for
. Consider the FN in Fig. 3 for  even (When
even (When  is odd, we can set
is odd, we can set  so that
so that  ). We can split the
). We can split the  - round FN in 4 parts: starting with a single round
- round FN in 4 parts: starting with a single round  ; a
; a  -round Feistel Network called
-round Feistel Network called  , the
, the  round with function
round with function  , and finally another
, and finally another  -round Feistel Network called
-round Feistel Network called  .
.
An intuitive attack works as follows. Fix a value  and consider all possible
and consider all possible  so that we obtain
so that we obtain  plaintexts. We do it
plaintexts. We do it  times to obtain
times to obtain  plaintexts. Hence, we have
plaintexts. Hence, we have  values for
values for  . We set the output of
. We set the output of  for one value of
for one value of  arbitrarily. For all the plaintexts, we query
arbitrarily. For all the plaintexts, we query  and obtain
and obtain 
 values. We enumerate all the functions of
values. We enumerate all the functions of  , and compute
, and compute  from
from  by decrypting. We set
by decrypting. We set  if
if  is even and set
is even and set  if
if  is odd. We store each
is odd. We store each  in a hash table. We then enumerate all the functions of
in a hash table. We then enumerate all the functions of  , and compute
, and compute  from
from  . For each computed values of
. For each computed values of  (for
(for  even) or
even) or  (for
(for  odd), we look for a match in the hash table storing
odd), we look for a match in the hash table storing  values (since they have to be equal). The time complexity of this approach consists of enumerating many values and functions with memory complexity
values (since they have to be equal). The time complexity of this approach consists of enumerating many values and functions with memory complexity  to store the hash table. Enumerating
to store the hash table. Enumerating  and
and  gives
gives  tuples which are filtered by
tuples which are filtered by  . We obtain
. We obtain  tuples. Thus, for each filtered tuple, we can deduce input/output values for
tuples. Thus, for each filtered tuple, we can deduce input/output values for  and rule out inconsistent tables to isolate the solutions
and rule out inconsistent tables to isolate the solutions  . This post-filtering has a complexity
. This post-filtering has a complexity  . We will see that it is lower than the complexity of the rest of the algorithm. Thus, it disappears in the big-
. We will see that it is lower than the complexity of the rest of the algorithm. Thus, it disappears in the big- . The pseudocode is given in Algorithm 2.
. The pseudocode is given in Algorithm 2.

In this attack, we have to guess  values for
values for  ,
,  values (we have
values (we have  instead of
instead of  because one value per round is free to select) for enumerating
because one value per round is free to select) for enumerating  (we guess
(we guess  values in total). And, we guess
values in total). And, we guess  values for enumerating
values for enumerating  (we guess
(we guess  in total). Therefore, the complexity is
in total). Therefore, the complexity is  for
for  is even and
is even and  for
for  is odd. We label the time complexity for described attack as:
is odd. We label the time complexity for described attack as:

with  chosen plaintexts.
chosen plaintexts.
3 Round-Function-Recovery by Partial Exhaustive Search
We consider exhaustive search algorithms dealing with partial functions. Normally, a function  is defined by its set of all possible
is defined by its set of all possible  pairs. We call a table as partial table if it is a subset of its table. It is a set of pairs such that
pairs. We call a table as partial table if it is a subset of its table. It is a set of pairs such that

If  , we say that
, we say that  is defined and we denote
is defined and we denote  . The density of a partial table is the ratio
. The density of a partial table is the ratio  of its cardinality by
of its cardinality by  . For example,
. For example,  corresponds to a partial table defined on a single point
corresponds to a partial table defined on a single point  and
and  corresponds to the full table. Our aim is to enumerate possible partial tables of increasing density by exhaustive search. So, we will “extend” partial functions. A partial table is an extension of another partial table if the former is a superset of the latter.
corresponds to the full table. Our aim is to enumerate possible partial tables of increasing density by exhaustive search. So, we will “extend” partial functions. A partial table is an extension of another partial table if the former is a superset of the latter.
We deal with partial tables for each round function. We define  -tuples
-tuples  of partial tables in which
of partial tables in which  denotes the partial table of
denotes the partial table of  in
in  .Footnote 6 We say that
.Footnote 6 We say that  is homogeneous with density
is homogeneous with density  if for all
if for all  ,
,  has density
has density  . Similarly, a tuple
. Similarly, a tuple  is an extension of
is an extension of  if for each
if for each  ,
,  is an extension of
is an extension of  . An elementary tuple is a homogeneous tuple of density
. An elementary tuple is a homogeneous tuple of density  . This means that each of its partial functions are defined on a single point.
. This means that each of its partial functions are defined on a single point.
Again, our aim is to start with an elementary tuple and to list all extensions, as long as they are compatible (as defined below) with the collected pairs of plaintexts and ciphertexts  . We say that a tuple
. We say that a tuple  encrypts a plaintext
encrypts a plaintext  into a ciphertext
into a ciphertext  (or decrypts
(or decrypts  into
into  or even that
or even that  encrypts the pair
encrypts the pair  ) if we can evaluate the FN on
) if we can evaluate the FN on  with the partial information we have about the round functions and if it gives
with the partial information we have about the round functions and if it gives  . We say that a pair
. We say that a pair  is computable except for r’ rounds for a tuple
is computable except for r’ rounds for a tuple  if there exists a round number
if there exists a round number  such that the partial functions are enough to encrypt
such that the partial functions are enough to encrypt  for up to
for up to  rounds and to decrypt
rounds and to decrypt  for up to
for up to  rounds.
rounds.
We want to define what it means for a tuple to be compatible with  . Roughly, it is compatible if for each
. Roughly, it is compatible if for each  , there exists an extension encrypting
, there exists an extension encrypting  into
into  . (However, it does not mean there exists an extension encrypting each
. (However, it does not mean there exists an extension encrypting each  to
to  .) More precisely, we say that a tuple
.) More precisely, we say that a tuple  of partial tables is compatible with
of partial tables is compatible with  if for each
if for each  , at least one of the following conditions is satisfied:
, at least one of the following conditions is satisfied:
-
(i)
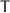 encrypts
encrypts 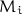 into
into 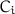 (in this case, there is no need to extend
(in this case, there is no need to extend  );
); -
(ii)
 is computable except for two rounds or more (indeed, if two rounds are undetermined, we know that we can extend
is computable except for two rounds or more (indeed, if two rounds are undetermined, we know that we can extend  to encrypt
to encrypt  to
to 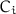 );
); -
(iii)
 is computable except for one round (numbered
is computable except for one round (numbered  below) and their is a match in the value skipping the missing round: more precisely, their exists
below) and their is a match in the value skipping the missing round: more precisely, their exists  and one
and one  pair such that if
pair such that if 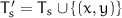 , the tuple
, the tuple 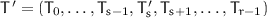 encrypts
encrypts  to
to 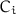 (indeed, we know we can extend the missing round with
(indeed, we know we can extend the missing round with  ).
).
Clearly, if no condition is satisfied for  , then no extension of
, then no extension of  can encrypt
can encrypt  into
into  , so we can prune an exhaustive search.
, so we can prune an exhaustive search.
3.1  : Iterative Partial Exhaustive Search
: Iterative Partial Exhaustive Search
Assume that  plaintext/ciphertext pairs
plaintext/ciphertext pairs  are known to the adversary. Due to the symmetries in the set of tuples which are compatible with the codebook, we can focus on the tuples which are extensions of an arbitrarily fixed elementary tuple
are known to the adversary. Due to the symmetries in the set of tuples which are compatible with the codebook, we can focus on the tuples which are extensions of an arbitrarily fixed elementary tuple  which encrypts the pair
which encrypts the pair  . So, we define
. So, we define  as the set of all extensions
as the set of all extensions  of
of  encrypting the pairs
encrypting the pairs  , which are compatible with all other pairs, and which are minimal (in the sense that removing any entry in the partial tables of
, which are compatible with all other pairs, and which are minimal (in the sense that removing any entry in the partial tables of  makes at least one
makes at least one  pair not computable, for
pair not computable, for  ).
).

We iteratively construct  . For that, we take all possible minimal extensions of tuples from
. For that, we take all possible minimal extensions of tuples from  which encrypt the
which encrypt the  pair and remain compatible with all others. We proceed as defined by Algorithm 3.
pair and remain compatible with all others. We proceed as defined by Algorithm 3.
With an appropriate data structure, we can avoid to retry to encrypt  or decrypt
or decrypt  and directly go to the next computable round (if any) in every pair. For each tuple
and directly go to the next computable round (if any) in every pair. For each tuple  in
in  , we maintain a hash table
, we maintain a hash table  in which
in which  is a list of pairs of the form
is a list of pairs of the form  or
or  with
with  . If
. If  is in
is in  , this means that
, this means that  encrypts
encrypts  up to round
up to round  and that the input to
and that the input to  (the output of which is unknown) is
(the output of which is unknown) is  . If
. If  is in
is in  , this means that
, this means that  decrypts
decrypts  up to round
up to round  and that the input to
and that the input to  is
is  . Concretely, this means that
. Concretely, this means that  lists the indices of
lists the indices of  pairs who need the value of
pairs who need the value of  to encrypt/decrypt one more round. With this type algorithmic trick, we save the inner loop and the complexity is expected to be close to the total size of the pools:
to encrypt/decrypt one more round. With this type algorithmic trick, we save the inner loop and the complexity is expected to be close to the total size of the pools:  .
.
3.2 A Heuristic Complexity Analysis of 
We heuristically estimate  . First, we recall that
. First, we recall that  is the subset of all minimal extensions of the elementary tuple
is the subset of all minimal extensions of the elementary tuple  which encrypt the first
which encrypt the first  plaintext/ciphertext pairs, restricted to the ones which are compatible with all others.
plaintext/ciphertext pairs, restricted to the ones which are compatible with all others.
We approximate  by
by  where
where  is the number of entries in the partial tables (i.e. the number of defined points throughout all rounds) and
is the number of entries in the partial tables (i.e. the number of defined points throughout all rounds) and  is the number of independent equations modulo
is the number of independent equations modulo  which a tuple must satisfy to be compatible. So,
which a tuple must satisfy to be compatible. So,  is the probability for a tuple to satisfy the conditions in
is the probability for a tuple to satisfy the conditions in  . In other words, the
. In other words, the  possible tuples are decimated by a factor
possible tuples are decimated by a factor  . To treat the fact that we start with only
. To treat the fact that we start with only  in
in  , we decrease
, we decrease  by
by  (it means that entries defined in
(it means that entries defined in  do not have to be enumerated as they are fixed) and we decrease
do not have to be enumerated as they are fixed) and we decrease  by 2 (i.e., we consider that the
by 2 (i.e., we consider that the  pair never decimates tuples as it is always compatible by the choice of
pair never decimates tuples as it is always compatible by the choice of  ).
).
Although it would be inefficient to proceed this way, we could see  as follows. For all sets
as follows. For all sets  of elementary tuples in which
of elementary tuples in which  encrypts the
encrypts the  pair, we check if
pair, we check if  are non-conflicting, and check if merging them defines partial tables which are compatible with the
are non-conflicting, and check if merging them defines partial tables which are compatible with the  other pairs. We consider that picking an elementary tuple
other pairs. We consider that picking an elementary tuple  encrypting the
encrypting the  th plaintext (irrespective of the ciphertext) corresponds to picking one random input in each of the
th plaintext (irrespective of the ciphertext) corresponds to picking one random input in each of the  round functions. We call this a trial. An input to one round function corresponds to a ball with a number from
round functions. We call this a trial. An input to one round function corresponds to a ball with a number from  to
to  . A round function is a bag of
. A round function is a bag of  balls. So, we have
balls. So, we have  bags of balls and a trial consists of picking one ball in each bag. Balls are replaced in their respective bags after picking them. Each
bags of balls and a trial consists of picking one ball in each bag. Balls are replaced in their respective bags after picking them. Each  makes one trial. Consequently, we have
makes one trial. Consequently, we have  trials. The balls which are picked during these
trials. The balls which are picked during these  trials are called good balls. Then, checking compatibility with the remaining
trials are called good balls. Then, checking compatibility with the remaining  pairs corresponds to making
pairs corresponds to making  additional trials. In those additional trials, we simply look at the number of good balls to see how many rounds can be processed for encryption/decryption.
additional trials. In those additional trials, we simply look at the number of good balls to see how many rounds can be processed for encryption/decryption.
We estimate the random variable  as the total number of good balls (to which we subtract the
as the total number of good balls (to which we subtract the  balls corresponding to the trial of
balls corresponding to the trial of  ). Conditioned to a density of good balls of
). Conditioned to a density of good balls of  in round
in round  , we have
, we have  . All
. All  are random, independent, and with expected value
are random, independent, and with expected value  . So,
. So,  .
.
The random variable  is set to
is set to  . The variable
. The variable  counts the number of modulo
counts the number of modulo  equations so that the encryption of the first
equations so that the encryption of the first  plaintexts match the corresponding ciphertext. So,
plaintexts match the corresponding ciphertext. So,  (the first pair
(the first pair  is satisfied by default, and each of the
is satisfied by default, and each of the  other ones define two equations due to the two halves of the ciphertexts). The variable
other ones define two equations due to the two halves of the ciphertexts). The variable  counts the number of equations coming from pairs encrypted for all but one round. So,
counts the number of equations coming from pairs encrypted for all but one round. So,  counts the number of trials (out of the last
counts the number of trials (out of the last  ones) picking exactly
ones) picking exactly  good balls, as they encrypt for all but one round so they define a single equation. The variable
good balls, as they encrypt for all but one round so they define a single equation. The variable  counts the number of equations coming from pairs in
counts the number of equations coming from pairs in  which are fully encrypted. So,
which are fully encrypted. So,  is twice the number of trials (out of the last
is twice the number of trials (out of the last  ones) with
ones) with  good balls, as they fully encrypt their corresponding pair and thus define two equations each. Conditioned to a density of good balls of
good balls, as they fully encrypt their corresponding pair and thus define two equations each. Conditioned to a density of good balls of  in round
in round  , we have
, we have

All  are random and independent, with expected value
are random and independent, with expected value  . Thus,
. Thus,

We obtain  where
where  is adjusted such that
is adjusted such that  . Hence,
. Hence,

with  such that
such that  .
.
To estimate  , we look at how it grows compared to
, we look at how it grows compared to  . During the
. During the  trial, with probability
trial, with probability  a picked ball is already good (so the density remains the same), and with probability
a picked ball is already good (so the density remains the same), and with probability  , picking a ball defines an additional good one (so the density increases by
, picking a ball defines an additional good one (so the density increases by  ).Footnote 7 Therefore, on average we have
).Footnote 7 Therefore, on average we have

As  , we deduce
, we deduce  .
.
Assuming that the above model fits well with  , the expected value of
, the expected value of  should match Eq. (3). However, Eq. (3) cannot represent well the expected value of
should match Eq. (3). However, Eq. (3) cannot represent well the expected value of  as exponential with bigger exponents will have a huge impact on the average. This motivates an abort strategy when the pool becomes too big. The abort strategy has known and influenced many works [19]. The way we use this strategy will be discussed in Sect. 3.5.
as exponential with bigger exponents will have a huge impact on the average. This motivates an abort strategy when the pool becomes too big. The abort strategy has known and influenced many works [19]. The way we use this strategy will be discussed in Sect. 3.5.
Finally, the heuristic complexity is computed by

3.3 Approximation of the Complexity
For  , we can write
, we can write  . By neglecting
. By neglecting  against
against  , the complexity is approximated by the maximum of
, the complexity is approximated by the maximum of  . We can easily show that the maximum is reached by
. We can easily show that the maximum is reached by  with
with

We obtain the complexity

with  known plaintexts. We will see later that (5) approximates well (4).
known plaintexts. We will see later that (5) approximates well (4).
The best complexity is reached with the full codebook  with
with

which is  for some
for some  .
.
3.4  : A Chosen Plaintext Extension to
: A Chosen Plaintext Extension to 
Finally, if  is not too close to
is not too close to  , a chosen plaintext attack variant consists of fixing the right half of the plaintext as much as possible, then guessing
, a chosen plaintext attack variant consists of fixing the right half of the plaintext as much as possible, then guessing  on these points and run the known-plaintext attack on
on these points and run the known-plaintext attack on  rounds to obtain
rounds to obtain

with  chosen plaintexts such that
chosen plaintexts such that  .
.
Discussion. For  , we have
, we have  and that means
and that means  . Therefore, our
. Therefore, our  algorithm becomes better than
algorithm becomes better than  . Also, for
. Also, for  , we have
, we have  so
so  is faster than exhaustive search on a single round function.
is faster than exhaustive search on a single round function.
Optimization with Larger  . We easily obtain that
. We easily obtain that  in (7) is optimal with
in (7) is optimal with

for

chosen plaintexts.
3.5 Variants of  and
and 
Optimized Algorithm. We can speed up the algorithm by adding more points in the tuples as soon as we can compute them. Concretely, if one plaintext/ciphertext pair can be “computed” except in one or two rounds, we can deduce the values in the missing rounds and define them in the tuple. Adding  points reduce the number of iterations to define the next pool by
points reduce the number of iterations to define the next pool by  .
.
Abort Strategy. Our complexity is not an average complexity but its logarithm is an average logarithmic complexity. To avoid having a too high average complexity, we may change the algorithm to make it abort if the pool exceeds a threshold to be defined. For instance, if our theoretical formula predicts a complexity  , to make sure that the worst case complexity does not exceed
, to make sure that the worst case complexity does not exceed  , we set this to the threshold value. This will affect the success probability, which is
, we set this to the threshold value. This will affect the success probability, which is  without the abort strategy, but may be lower for any real number
without the abort strategy, but may be lower for any real number  .
.
Other Improvements. We believe that we could improve our algorithms in many ways. For instance, we could take the  pairs in an optimized order so that we do not have too many new values appearing in the first and last round functions. This would decrease the number of tuples to consider.
pairs in an optimized order so that we do not have too many new values appearing in the first and last round functions. This would decrease the number of tuples to consider.
3.6 Experimental Results
We implemented Algorithm 3 with known plaintext,  ,
,  ,
,  . Our algorithm always ended with a pool limited to a correct set of full tables.
. Our algorithm always ended with a pool limited to a correct set of full tables.
With these parameters, Eq. (3) estimates  to be the largest, and estimates
to be the largest, and estimates  . We checked over 100 executions, that
. We checked over 100 executions, that  has an average of
has an average of  and a standard deviation of
and a standard deviation of  . This is a bad news as it is quite larger than what is predicted. More precisely, each partial function in
. This is a bad news as it is quite larger than what is predicted. More precisely, each partial function in  has on average
has on average  defined entries, which is slightly more than the
defined entries, which is slightly more than the  which is predicted.Footnote 8 But adjusting
which is predicted.Footnote 8 But adjusting  to
to  in Eq. (3) gives
in Eq. (3) gives  , which is not enough to explain the high
, which is not enough to explain the high  which is observed. So, our model for the random variable
which is observed. So, our model for the random variable  may be correct but
may be correct but  may be overestimated:
may be overestimated:  decimates less than expected. Although we thought
decimates less than expected. Although we thought  would be the largest from our theory, the largest observed pool during our experiment were
would be the largest from our theory, the largest observed pool during our experiment were  with logarithmic size with average
with logarithmic size with average  . This indicates that our model for
. This indicates that our model for  is not accurate.
is not accurate.
All these problems find several explanations. First of all, our parameter  is so small that a tiny variation of number of defined entries (supposed to be
is so small that a tiny variation of number of defined entries (supposed to be  ) in each round has a dramatic impact on the number of tuples. Second, our approach takes the
) in each round has a dramatic impact on the number of tuples. Second, our approach takes the  as uniform in all rounds and runs although there are variations. Some rounds have more than
as uniform in all rounds and runs although there are variations. Some rounds have more than  entries and some others have less. The function we analyze is not linear in
entries and some others have less. The function we analyze is not linear in  . It is exponential. So, any round with more than
. It is exponential. So, any round with more than  defined entries increase the complexity quite a lot.
defined entries increase the complexity quite a lot.
The good news is that using our optimized variant reduced the gap substantially. The largest  becomes
becomes  . Using the abort strategy with
. Using the abort strategy with  gives a success rate of
gives a success rate of  and
and  . So, we believe that our anticipated complexities are achievable with a good success probability. However, finding a good model for decimation and for the improved algorithm remains an open question.
. So, we believe that our anticipated complexities are achievable with a good success probability. However, finding a good model for decimation and for the improved algorithm remains an open question.
We summarize our experiments in the Table 2. For the  column is the average (logarithmically) of the largest observed pool. The logarithm is the maximum over each iteration of the average over the runs of the logarithm of the pool size. The computed average only includes successful runs, as unsuccessful ones are all on the abort threshold.
column is the average (logarithmically) of the largest observed pool. The logarithm is the maximum over each iteration of the average over the runs of the logarithm of the pool size. The computed average only includes successful runs, as unsuccessful ones are all on the abort threshold.
 ,
,  , and
, and  and with parameters
and with parameters  ,
,  , and
, and  . The
. The  column reports
column reports  : the average (logarithmically) of the largest observed pool. It is compared with
: the average (logarithmically) of the largest observed pool. It is compared with  which is derived as the largest theoretical pool size by our theory. The column
which is derived as the largest theoretical pool size by our theory. The column  shows whether we used the optimization trick. The
shows whether we used the optimization trick. The  column indicates when we used the abort strategy, and with which bound.
column indicates when we used the abort strategy, and with which bound.4 Applications
In the standards, the supported domain size of messages in FF1 and FF3 is greater than 100 (i.e.
is greater than 100 (i.e.  ). For FF1 and FF3
). For FF1 and FF3 , the best attack is roughly
, the best attack is roughly  for very low
for very low  , then
, then  for larger
for larger  . More precisely, we achieve the results shown in Table 3.Footnote 9
. More precisely, we achieve the results shown in Table 3.Footnote 9
 (
( ) and
) and  (
( ) with query complexity
) with query complexity  for various values of
for various values of  and
and  or
or  . Computations for
. Computations for  were done without using approximations.
were done without using approximations.For a better precision, we did the computation without approximations, i.e. by using Eq. (4) instead of Eq. (5) in Eq. (7). In any case, we have checked that the figures with approximation do not differ much. They are reported in the Table 4.
 (
( ) and
) and  (
( ) with query complexity
) with query complexity  for various values of
for various values of  and
and  or
or  . Computations for
. Computations for  were done using approximations.
were done using approximations.As an example, for FF3 with
with  (i.e., messages have 6 bits),
(i.e., messages have 6 bits),  uses
uses  pairs (half of the codebook) and search on three points for
pairs (half of the codebook) and search on three points for  , the entire (but one point)
, the entire (but one point)  and
and  , one bit of
, one bit of  in the encryption direction, and the entire (but one point)
in the encryption direction, and the entire (but one point)  and
and  and one bit of
and one bit of  in the decryption direction. This is
in the decryption direction. This is  . With
. With  , we also use
, we also use  and the pool reaches its critical density for
and the pool reaches its critical density for  . The complexity is
. The complexity is  .
.
We may wonder for which  the ciphers offer a 128-bit security. Durak and Vaudenay [15] showed that this is not the case for FF3
the ciphers offer a 128-bit security. Durak and Vaudenay [15] showed that this is not the case for FF3 with
with  and FF1 with
and FF1 with  . By doing computations for
. By doing computations for  , we extend this to show that FF3* does not offer a 128-bit security for
, we extend this to show that FF3* does not offer a 128-bit security for  , and FF1 does not offer a 128-bit security for
, and FF1 does not offer a 128-bit security for  .
.
Genuinely, we can compute in Table 5 the minimum  of the number of rounds for which
of the number of rounds for which  depending on
depending on  and
and  . Again, we computed without using our approximations. For
. Again, we computed without using our approximations. For  and
and  , we fetch the following table.Footnote 10
, we fetch the following table.Footnote 10
 of rounds for various
of rounds for various  in order to have complexities at least
in order to have complexities at least  or
or  . Computations for
. Computations for  were done without using approximations.
were done without using approximations.Even by adding a safety margin, this shows that we do not need many rounds to safely encrypt a byte (that is,  ) with respect to our best attacks. However, with low
) with respect to our best attacks. However, with low  , we should care about other attacks as in Table 1. Indeed, for
, we should care about other attacks as in Table 1. Indeed, for  -FN, we recommend never to take
-FN, we recommend never to take  due to the yo-yo attack [7]. For other FN, we recommend never to take
due to the yo-yo attack [7]. For other FN, we recommend never to take  .
.
In Fig. 4, we plot complexities for  or
or  and various ranges of
and various ranges of  . The regions for
. The regions for  we plot have a minimum for the optimal
we plot have a minimum for the optimal  and a maximum for
and a maximum for  . The region corresponds to all complexities for
. The region corresponds to all complexities for  .
.
Time complexity of attacks against generic 8-round and 10-round FN for  with
with  minimal or
minimal or  making the complexity optimal, for
making the complexity optimal, for  [15], and
[15], and  .
.
5 Conclusion
Standard Feistel Networks and its variations have created an active research area since their invention and have been used in constructions of many cryptographic systems to a wide extent. The security of FN has been studied for many decades resulting in many interesting results for cryptanalysis purpose. In this work, we analyze the security of a very specific type of FN with two branches, secure random round functions, and modular addition to analyze its security. Additionally, we consider small domains. The best attack was believed to be MITM. However, we show that partial exhaustive search can be better. Concretely, we show that the number of rounds recommended by NIST is insufficient in FF1 and FF3* for very small  .
.
This specific FN with the described properties has been used to build Format-Preserving Encryption and perhaps will inspire many other constructions. However, the security of FN with various properties is not clear (regardless of the significant security analyses mentioned in the introduction) and has to be investigated more. Our work shows only that a caution should be taken in order to meet the desired security level in the systems.
We proposed a new algorithm based on partial exhaustive search. We observed a gap between our heuristic complexity and experiments and suggested possible explanations. However, the problem to reduce this gap is left as an open problem.
Notes
- 1.
- 2.
It was shown by Durak and Vaudenay [15] that 128-bit security was not reached by FF3
 and FF1 for
and FF1 for  and
and 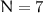 , respectively.
, respectively. - 3.
Note that the NIST standard [2] requires
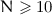 .
. - 4.
The full version of our paper [14] includes appendices with: a description of the message recovery attacks from Bellare et al. [4], the generic round-function-recovery attack from Durak and Vaudenay [13, 15], an attack exploiting the bias in the modulo-
 reduction inspired by Bleichenbacher (as described by Vaudenay [25]), and the generic round-function-recovery attacks by Biryukov et al. [7].
reduction inspired by Bleichenbacher (as described by Vaudenay [25]), and the generic round-function-recovery attacks by Biryukov et al. [7]. - 5.
In order to improve the memory complexity of MITM attack, a new technique called dissection attack has been introduced by Dinur et al. in [11].
- 6.
We denote an
 -tuple with capital letter
-tuple with capital letter  . Each tuple
. Each tuple  consists of
consists of  tables, i.e.
tables, i.e. 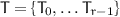 . When we have multiple
. When we have multiple  -tuples, we denote different tuples indexed with a superscript
-tuples, we denote different tuples indexed with a superscript  .
. - 7.
It would increase with a probability a bit larger than
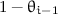 , namely
, namely 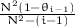 if the messages are not independent but conditioned to being pairwise different.
if the messages are not independent but conditioned to being pairwise different. - 8.
This is partially explained by the fact that plaintexts are pairwise different.
- 9.
Note that the standard requires
 . Hence, the first three rows are not relevant in practice.
. Hence, the first three rows are not relevant in practice. - 10.
In this table, we computed the value of
 suggested by our formulas but rounded in the
suggested by our formulas but rounded in the  interval.
interval.
References
Data Encryption Standard, National Bureau of Standards, NBS FIPS PUB 46, January 1977. National Bureau of Standards. U.S, Department of Commerce (1977)
Recommendation for Block Cipher Modes of Operation: Methods for Format Preserving Encryption, NIST Special Publication (SP) 800-38G, 29 March 2016. National Institute of Standards and Technology
Retail Financial Services - Requirements for Protection of Sensitive Payment Card Data - Part 1: Using Encryption Method. American National Standards Institute (2016)
Bellare, M., Hoang, V.T., Tessaro, S.: Message-recovery attacks on Feistel-based format-preserving encryption. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS 2016, pp. 444–455. ACM, New York (2016)
Bellare, M., Ristenpart, T., Rogaway, P., Stegers, T.: Format-preserving encryption. In: Jacobson, M.J., Rijmen, V., Safavi-Naini, R. (eds.) SAC 2009. LNCS, vol. 5867, pp. 295–312. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-05445-7_19
Bellare, M., Rogaway, P., Spies, T.: The FFX Mode of Operation for Format-Preserving Encryption. draft 1.1. Submission to NIST, February 2010. http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/ffx/ffx-spec.pdf
Biryukov, A., Leurent, G., Perrin, L.: Cryptanalysis of feistel networks with secret round functions. In: Dunkelman, O., Keliher, L. (eds.) SAC 2015. LNCS, vol. 9566, pp. 102–121. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31301-6_6
Biryukov, A., Perrin, L.: On reverse-engineering S-boxes with hidden design criteria or structure. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 116–140. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_6
Brier, E., Peyrin, T., Stern, J.: BPS: A Format-Preserving Encryption Proposal. http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/bps/bps-spec.pdf
Diffie, W., Hellman, M.E.: Special feature exhaustive cryptanalysis of the NBS data encryption standard. Computer 10(6), 74–84 (1977)
Dinur, I., Dunkelman, O., Keller, N., Shamir, A.: Efficient dissection of composite problems, with applications to cryptanalysis, knapsacks, and combinatorial search problems. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 719–740. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_42
Dinur, I., Dunkelman, O., Keller, N., Shamir, A.: New attacks on feistel structures with improved memory complexities. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 433–454. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_21
Durak, F.B., Vaudenay, S.: Breaking the FF3 format-preserving encryption. In: Proceedings of ESC 2017. https://www.cryptolux.org/mediawiki-esc2017/images/8/83/Proceedings_esc2017.pdf
Durak, F.B., Vaudenay, S.: Generic Round-Function-Recovery attacks for Feistel Networks over Small Domains. https://eprint.iacr.org/2018/108.pdf
Durak, F.B., Vaudenay, S.: Breaking the FF3 format-preserving encryption standard over small domains. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 679–707. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_23
Hoang, V.T., Rogaway, P.: On generalized Feistel networks. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 613–630. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_33
Isobe, T., Shibutani, K.: All subkeys recovery attack on block ciphers: extending meet-in-the-middle approach. In: Knudsen, L.R., Wu, H. (eds.) SAC 2012. LNCS, vol. 7707, pp. 202–221. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35999-6_14
Isobe, T., Shibutani, K.: Generic key recovery attack on Feistel scheme. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 464–485. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_24
Lu, J., Kim, J., Keller, N., Dunkelman, O.: Improving the efficiency of impossible differential cryptanalysis of reduced Camellia and MISTY1. In: Malkin, T. (ed.) CT-RSA 2008. LNCS, vol. 4964, pp. 370–386. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79263-5_24
Luby, M., Rackoff, C.: How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Comput. 17(2), 373–386 (1988)
Nachef, V., Volte, E., Patarin, J.: Differential attacks on generalized Feistel schemes. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 1–19. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-02937-5_1
Patarin, J.: Generic attacks on Feistel schemes (2008). http://eprint.iacr.org/2008/036
Patarin, J.: Security of Balanced and Unbalanced Feistel Schemes with Non-linear Equalities (2010). http://eprint.iacr.org/2010/293
Patarin, J., Nachef, V., Berbain, C.: Generic attacks on unbalanced Feistel schemes with contracting functions. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 396–411. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_26
Vaudenay, S.: The security of DSA and ECDSA. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 309–323. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_23
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Durak, F.B., Vaudenay, S. (2018). Generic Round-Function-Recovery Attacks for Feistel Networks over Small Domains. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_23
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)






 for
for  and parameters to meet a 128-bit and a 256-bit security level.
and parameters to meet a 128-bit and a 256-bit security level.
 even on the picture)
even on the picture) encrypts
encrypts 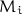 into
into 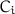 (in this case, there is no need to extend
(in this case, there is no need to extend  );
); is computable except for two rounds or more (indeed, if two rounds are undetermined, we know that we can extend
is computable except for two rounds or more (indeed, if two rounds are undetermined, we know that we can extend  to encrypt
to encrypt  to
to 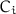 );
); is computable except for one round (numbered
is computable except for one round (numbered  below) and their is a match in the value skipping the missing round: more precisely, their exists
below) and their is a match in the value skipping the missing round: more precisely, their exists  and one
and one  pair such that if
pair such that if 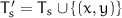 , the tuple
, the tuple 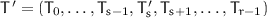 encrypts
encrypts  to
to 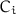 (indeed, we know we can extend the missing round with
(indeed, we know we can extend the missing round with  ).
). : Iterative Partial Exhaustive Search
: Iterative Partial Exhaustive Search
 : A Chosen Plaintext Extension to
: A Chosen Plaintext Extension to 
 and
and 

 (instead of
(instead of  ). It does not include distinguishers such as the ones from Patarin [
). It does not include distinguishers such as the ones from Patarin [ and FF1 for
and FF1 for  and
and  , respectively.
, respectively.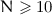 .
.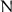 reduction inspired by Bleichenbacher (as described by Vaudenay [
reduction inspired by Bleichenbacher (as described by Vaudenay [ -tuple with capital letter
-tuple with capital letter  . Each tuple
. Each tuple  consists of
consists of  tables, i.e.
tables, i.e. 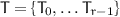 . When we have multiple
. When we have multiple  -tuples, we denote different tuples indexed with a superscript
-tuples, we denote different tuples indexed with a superscript  .
.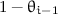 , namely
, namely 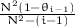 if the messages are not independent but conditioned to being pairwise different.
if the messages are not independent but conditioned to being pairwise different. . Hence, the first three rows are not relevant in practice.
. Hence, the first three rows are not relevant in practice. suggested by our formulas but rounded in the
suggested by our formulas but rounded in the  interval.
interval.