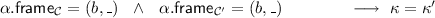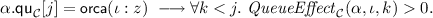Correctness of a Concurrent Object Collector for Actor Languages

Abstract

ORCA is a garbage collection protocol for actor-based programs. Multiple actors may mutate the heap while the collector is running without any dedicated synchronisation. ORCA is applicable to any actor language whose type system prevents data races and which supports causal message delivery. We present a model of ORCA which is parametric to the host language and its type system. We describe the interplay between the host language and the collector. We give invariants preserved by ORCA, and prove its soundness and completeness.

1 Introduction

Actor-based systems are massively parallel programs in which individual actors communicate by exchanging messages. In such systems it is essential to be able to manage data automatically with as little synchronisation as possible. In previous work [9, 12], we introduced the ORCA protocol for garbage collection in actor-based systems. ORCA is language-agnostic, and it allows for concurrent collection of objects in actor-based programs with no additional locking or synchronisation, no copying on message passing and no stop-the-world steps. ORCA can be implemented in any actor-based system or language that has a type system which prevents data races and that supports causal message delivery. There are currently two instantiations of ORCA, one is for Pony [8, 11] and the other for Encore [5]. We hypothesise that ORCA could be applied to other actor-based systems that use static types to enforce isolation [7, 21, 28, 36]. For libraries, such as Akka, which provide actor-like facilities, pluggable type systems could be used to enforce isolation [20].

This paper develops a formal model of ORCA. More specifically, the paper contributions are:

• 1. Identification of the requirements that the host language must statically guarantee;

• 2. Description and model of ORCA at a language-agnostic level;

• 3. Identification of invariants that ensure global consistency without synchronisation;

• 4. Proofs of soundness, i.e. live objects will not be collected, and proofs of completeness, i.e. all garbage will be identified as such.

A formal model facilitates the understanding of how ORCA can be applied to different languages. It also allows us to explore extensions such as shared mutable state across actors [40], reduction of tracing of immutable references [12], or incorporation of borrowing [4]. Alternative implementations of ORCA that rely on deep copying (e.g., to reduce type system complexity) across actors on different machines can also be explored through our formalism.

Developing a formal model of ORCA presents challenges:

• Can the model be parametric in the host language? We achieved parametricity by concentrating on the effects rather than the mechanisms of the language. We do not model language features, instead, we model actor behaviour through non-deterministic choice between heap mutation and object creation. All other actions, such as method call, conditionals, loops etc., are irrelevant.

• Can the model be parametric in the host type system? We achieved parametricity by concentrating on the guarantees rather than the mechanism afforded by the type system. We do not define judgments, but instead, assume the existence of judgements which determines whether a path is readable or writeable from a given actor. Through an (uninterpreted) precondition to any heap mutation, we require that no aliasing lets an object writeable from an actor be readable/writeable from any other actor.

• How to relax atomicity? ORCA relies on a global invariant that relates the number of references to any data object and the number of messages with a path to that object. This invariant only holds if actors execute atomically. Since we desire actors to run in parallel, we developed a more subtle, and weaker, definition of the invariant.

The full proofs and omitted definitions are available in appendix [16].

2 Host Language Requirements

ORCA makes some assumptions about its host language, we describe them here.

2.1 Actors and Objects

Actors are active entities with a thread of control, while objects are data structures. Both actors and objects may have fields and methods. Method calls on objects are synchronous, whereas method calls on actors amount to asynchronous message sends—they all called behaviours. Messages are stored in a FIFO queue. When idle, an actor processes the top message from its queue. At any given point of time an actor may be either idle, executing a behaviour, or collecting garbage.

Fig. 1.

Actors and objects. Full arrows are references, grey arrows are overwritten references: references that no longer exist.

Figure 1 shows actors $\alpha _1$ and $\alpha _2$, objects $\omega _1$ to $\omega _4$. In [16] we show how to create this object graph in Pony. In Fig. 1(a), actor $\alpha _1$ points to object $\omega _1$ through field $f_1$ to $\omega _2$ through field $f_3$, and object $\omega _1$ points to $\omega _3$ through field $f_5$. In Fig. 1(b), actor $\alpha _1$ creates $\omega _4$ and assigns it to $\textsf {this}.f_1.f_5$. In Fig. 1(c), $\alpha _1$ has given up its reference to $\omega _1$ and sent it to $act_2$ which stored it in field $f_6$. Note that the process of sending sent not only $\omega _1$ but also implicitily $\omega _4$.

2.2 Mutation, Transfer and Accessibility

Message passing is the only way to share objects. This falls out of the capability system. If an actor shares an object with another actor, then either it gives up the object or neither actor has a write capability to that object. For example, after $\alpha _1$ sends $\omega _1$ to $\alpha _2$, it cannot mutate $\omega _1$. As a consequence, heap mutation only decreases accessibility, while message sends can transfer accessibility from sender to receiver. When sending immutable data the sender does not need to transfer accessibility. However, when it sends a mutable object it cannot keep the ability to read or to write the object. Thus, upon message send of a mutable object, the actor must consume, or destroy, its reference to that object.

2.3 Capabilities and Accessibility

ORCA assumes that a host language’s type system assigns access rights to paths. A path is a sequence of field names. We call these access rights capabilities.

Fig. 2.

Capabilities. Heap mutation may modify what object is reachable through a path, but not the path’s capability.

We expect the following three capabilities; read, write, tag. The first two allow reading and writing an object’s fields respectively. The tag capability only allows identity comparison and sending the object in a message. The type system must ensure that actors have no read-write races. This is natural for actor languages [5, 7, 11, 21].

Figure 2 shows capabilities assigned to the paths in Fig. 1: $\alpha _1.f_1.f_5$ has capability write, thus $\alpha _1$ can read and write to the object reachable from that path. Note that capapabilities assigned to paths are immutable, while the contents of those paths may change. For example, in Fig. 1(a), $\alpha _1$ can write to $\omega _3$ through path $f_1.f_5$, while in Fig. 1(b) it can write to $\omega _4$ through the same path. In Fig. 1(a) and (b), $\alpha _2$ can use the address of $\omega _1$ but cannot read or write it, due to the tag capability, and therefore cannot access $\omega _3$ (in Fig. 1(a)) nor $\omega _4$ (in Fig. 1(b)). However, in Fig. 1(c) the situation reverses: $\alpha _2$, which received $\omega _1$ with write capability is now able to reach it through field $f_6$, and therefore $\omega _4$. Notice that the existence of a path from an actor to an object does not imply that the object is accessible to the actor: In Fig. 1(a), there is a path from $\alpha _2$ to $\omega _3$, but $\alpha _2$ cannot access $\omega _3$. Capabilities protect against data races by ensuring that if an object can be mutated by an actor, then no other actor can access its fields.

2.4 Causality

ORCA uses messages to deliver protocol-related information, it thus requires causal delivery. Messages must be delivered after any and all messages that caused them. Causality is the smallest transitive relation, such that if a message $m'$ is sent by some actor after it received or sent m, then m is a cause of $m'$. Causal delivery entails that $m'$ be delivered after m.

For example, if actor $\alpha _1$ sends $m_1$ to actor $\alpha _2$, then sends $m_2$ to actor $\alpha _3$, and $\alpha _3$ receives $m_2$ and sends $m_3$ to $\alpha _2$, then $m_1$ is a cause of $m_2$, and $m_2$ is a cause of $m_3$. Causal delivery requires that $\alpha _2$ receive $m_1$ before receiving $m_3$. No requirements are made on the order of delivery to different actors.

3 Overview of ORCA

We introduce ORCA and discuss how to localise the necessary information to guarantee safe deallocation of objects in the presence of sharing. Every actor has a local heap in which it allocates objects. An actor owns the objects it has allocated, and ownership is fixed for an object’s life-time, but actors are free to reference objects that they do not own. Actors are obligated to collect their own objects once these are no longer needed. While collecting, an actor must be able to determine whether an object can be deallocated using only local information. This allows all other actors to make progress at any point.

3.1 Mutation and Collection

ORCA relies on capabilities for actors to reference objects owned by other actors and to support concurrent mutation to parts of the heap that are not being concurrently collected. Capabilities avoid the need for barriers.

 

$\mathbf {I_1}$ :

An object accessible with write capability from an actor is not accessible with read or write capability from any other actor.

 

This invariant ensures an actor, while executing garbage collection, can safely trace any object to which it has read or write access without the need to protect against concurrent mutation from other actors.

3.2 Local Collection

An actor can collect its objects based on local information without consulting other actors. For this to be safe, the actor must know that an owned, locally inaccessible, object is also globally inaccessible (i.e., inaccessible from any other actors or messages)¹. Shared objects are reference counted by their owner to ensure:  

$\mathbf {I_2}$ :

An object accessible from a message queue or from a non-owning actor has reference count larger than zero in the owning actor.

 

Thus, a locally inaccessible object with a reference count of 0 can be collected.

3.3 Messages and Collection

$\mathbf {I_1}$ and $\mathbf {I_2}$ are sufficient to ensure that local collection is safe. Maintaining $\mathbf {I_2}$ is not trivial as accessibility is affected by message sends. Moreover, it is possible for an actor to share a read object with another actor through a message. What if that actor drops its reference to the object? The object’s owner should be informed so it can decrease its reference count. What happens when an actor receives an object in a message? The object’s owner should be infomed, so that it can increase its reference count. To reduce message traffic, ORCA uses distributed, weighted, deferred reference counts. Each actor maintains reference counts that tracks the sharing of its objects. It also maintains counts for “foreign objects”, tracking references to objects owned by other actors. This reference count for non-owning actors is what allows sending/receiving objects without having to inform their owner while maintaining $\mathbf {I_2}$. For any object or actor $\iota$, we denote with $\mathrm {LRC} (\iota )$ the reference count for $\iota$ in $\iota$’s owner, and with $\mathrm {FRC} (\iota )$ we denote the sum of the reference counts for $\iota$ in all other actors. The counts do not reflect the number of references, rather the existence of references:

 

$\mathbf {I_3}$ :

If a non-owning actor can access an object through a path from its fields or call stack, its reference count for this object is greater than 0.

 

An object is globally accessible if it is accessible from any actor or from a message in some queue. Messages include reference increment or decrement messages—these are ORCA-level messages and they are not visible to applications. We introduce two logical counters: $\mathrm {AMC}_{}(\iota )$ to account for the number of application messages with paths to $\iota$, and $\mathrm {OMC}_{}(\iota )$ to account for ORCA-level messages with reference count increment and decrement requests. These counters are not present at run-time, but they will be handy for reasoning about ORCA. The owner’s view of an object is described by the $\mathrm {LRC}$ and the $\mathrm {OMC}$, while the foreign view is described by the $\mathrm {FRC}$ and the $\mathrm {AMC}$. These two views must agree:

 

$\mathbf {I_4}$ :

      $\forall ~\iota$. $\mathrm {LRC} (\iota ) + \mathrm {OMC} (\iota ) = \mathrm {AMC} (\iota ) + \mathrm {FRC} (\iota )$

 

$\mathbf {I_2}$, $\mathbf {I_3}$ and $\mathbf {I_4}$ imply that a locally inaccessible object with $\mathrm {LRC} =0$ can be reclaimed.

3.4 Example

Consider actors $\mathsf {Andy}$, $\mathsf {Bart}$ and $\mathsf {Catalin}$, and steps from Fig. 3.

Fig. 3.

Black arrows are references, numbered in creation order. Blue solid arrows are application messages and blue dashed arrows ORCA-level message. (Color figure online)

Initial State. Let $\omega$ be a newly allocated object. As it is only accessible to its owning actor, $\mathsf {Andy}$, there is no entry for it in any $\mathrm {RC}$.

Sharing $\omega$. When $\mathsf {Andy}$ shares $\omega$ with $\mathsf {Bart}$, $\omega$ is placed on $\mathsf {Bart}$ ’s message queue, meaning that $\mathrm {AMC} (\omega )\!=\!1$. This is reflected by setting $\mathrm {RC} _\mathsf {Andy} (\omega )$ to 1. This preserves $\mathbf {I_4}$ and the other invariants. When $\mathsf {Bart}$ takes the message with $\omega$ from his queue, $\mathrm {AMC} (\omega )$ becomes zero, and $\mathsf {Bart}$ sets his foreign reference count for $\omega$ to 1, that is, $\mathrm {RC} _\mathsf {Bart} (\omega ) = 1$. When $\mathsf {Bart}$ shares $\omega$ with $\mathsf {Catalin}$, we get $\mathrm {AMC} (\omega ) = 1$. To preserve $\mathbf {I_4}$, $\mathsf {Bart}$ could set $\mathrm {RC} _{\mathsf {Bart}}(\omega )$ to 0, but this would break $\mathbf {I_3}$. Instead, $\mathsf {Bart}$ sends an ORCA-level message to $\mathsf {Andy}$, asking him to increment his (local) reference count by some n, and sets his own $\mathrm {RC} _{\mathsf {Bart}}(\omega )$ to n.² This preserves $\mathbf {I_4}$ and the other invariants. When $\mathsf {Catalin}$ receives the message later on, she will behave similarly to $\mathsf {Bart}$ in step 2, and set $\mathrm {RC} _\mathsf {Catalin} (\omega )\!=\!1$.

The general rule is that when an actor sends one of its objects, it increments the corresponding (local) $\mathrm {RC}$ by 1 (reflecting the increasing number of foreign references) but when it sends a non-owned object, it decrements the corresponding (foreign) $\mathrm {RC}$ (reflecting a transfer of some of its stake in the object). Special care needs to be taken when the sender’s $\mathrm {RC}$ is 1.

Further note that if $\mathsf {Andy}$, the owner of $\omega$, received $\omega$, he would decrease his counter for $\omega$ rather than increase it, as his reference count denotes foreign references to $\omega$. When an actor receives one of its owned objects, it decrements the corresponding (local) $\mathrm {RC}$ by 1 but when it receives a non-owned object, it increments the corresponding (foreign) $\mathrm {RC}$ by 1.

Dropping References to $\omega$. Subsequent to sharing $\omega$ with $\mathsf {Catalin}$, $\mathsf {Bart}$ performs GC, and traces his heap without reaching $\omega$ (maybe because it did not store $\omega$ in a field). This means that $\mathsf {Bart}$ has given up his stake in $\omega$. This is reflected by sending a message to $\mathsf {Andy}$ to decrease his $\mathrm {RC}$  for $\omega$ by n, and setting $\mathsf {Bart}$ ’s $\mathrm {RC}$  for $\omega$ to 0. $\mathsf {Andy}$ ’s local count of the foreign references to $\omega$ are decreased piecemeal like this, until $\mathrm {LRC} (\omega )$ reaches zero. At this point, tracing $\mathsf {Andy}$ ’s local heap can determine if $\omega$ should be collected.

Further Aspects. We briefly outline further aspects which play a role in ORCA.  

Concurrency.:

Actors execute concurrently. For example, sharing of $\omega$ by $\mathsf {Bart}$ and $\mathsf {Catalin}$ can happen in parallel. As long as $\mathsf {Bart}$ and $\mathsf {Catalin}$ have foreign references to $\omega$, they may separately, and in parallel cause manipulation of the global number of references to $\omega$. These manipulations will be captured locally at each site through $\mathrm {FRC}$, and through increment and decrement messages to $\mathsf {Andy}$ ($\mathrm {OMC}$).

Causality.:

Increment and decrement messages may arrive in any order. $\mathsf {Andy}$ ’s queue will serialise them, i.e. concurrent asynchronous reference count manipulations will be ordered and executed sequentially. Causality is key here, as it prevents ORCA-level messages to be overtaken by application messages which cause $\mathrm {RC}$ s to be decremented; thus causality keeps counters non-negative.

Composite Objects.:

Objects message must be traced to find the transitive closure of accessible data. For example, when passing $\omega _1$ in a message in Fig. 1(c), objects accessible through it, e.g., $\omega _4$ will be traced. This is mandated by $\mathbf {I_3}$ and $\mathbf {I_4}$.

 

Finally, we reflect on the nature of reference counts: they are distributed, in the sense that an object’s owner and every actor referencing it keep separate counts; weighted, in that they do not reflect the number of aliases; and deferred, in that they are not manipulated immediately on alias creation or destruction, and that non-local increments/decrements are handled asynchronously.

4 The ORCA Protocol

We assume enumerable, disjoint sets and , for addresses of actors and objects. The union of the two is the set of addresses including null. We require a mapping $\mathcal {C}\!\textit{lass}$ that gives the name of the class of each actor in a given configuration, and a mapping $\mathcal {O}$ that returns the owner of an address

such that the owner of an actor is the actor itself, i.e., .

Definition 1 describes run-time configurations, $\mathcal {C}$. They consist of a heap, $\chi$, which maps addresses and field identifiers to addresses,³ and an actor map, $as$, from actor addresses to actors. Actors consist of a frame, a queue, a reference count table, a state, a working set, marks, and a program counter. Frames are either empty, or consist of the identifier for the currently executing behaviour, and a mapping from variables to addresses. Queues are sequences of messages. A message is either an application message of the form $\textsf {app} (\phi )$ denoting a high-level language message with the frame $\phi$, or an ORCA message, of the form $\textsf {orca} (\iota \!:\!z)$, denoting an in-flight request for a reference count change for $\iota$ by z. The state distinguishes whether the actor is idle, or executing some behaviour, or performing garbage collection. We discuss states, working sets, marks, and program counters in Sect. 4.3. We use naming conventions: ; ; ; $z\!\in \!\mathbb {Z}$; $n\!\in \!\mathbb {N}$; ; ; ; and $\iota s$ for a sequence of addresses $\iota _1...\iota _n$. We write $\mathcal {C}.\textsf {heap}$ for $\mathcal {C}$’s heap; and $\alpha .\textsf {qu} _\mathcal {C}$, or $\alpha .\textsf {rc} _\mathcal {C}$, or $\alpha .\textsf {frame} _\mathcal {C}$, or $\alpha .\textsf {st} _\mathcal {C}$ for the queue, reference count table, frame or state of actor $\alpha$ in configuration $\mathcal {C}$, respectively.

Definition 1

(Runtime entities and notation)

, , , and described in Definition 7.

Fig. 4.

Configuration $\mathcal {C} _0$. $\omega _1$ is absent in the ref. counts, it has not been shared.

Example:

Figure 4 shows $\mathcal {C} _0$, our running example for a runtime configuration. It has three actors: $\alpha _1$–$\alpha _3$, represented by light grey boxes, and eight objects, $\omega _1$–$\omega _8$, represented by circles. We show ownership by placing the objects in square boxes, e.g. $\mathcal {O}(\omega _7)=\alpha _1$. We show references through arrows, e.g. $\omega _6$ references $\omega _8$ through field $f_7$, that is, $\mathcal {C} _0.{\textsf {heap}}(\omega _6,f_7)=\omega _8$. The frame of $\alpha _2$ contains behaviour identifier $b'$, and maps $x'$ to $\omega _8$. All other frames are empty. The message queue of $\alpha _1$ contains an application message for behaviour $b$ and argument $\omega _5$ for x, the queue of $\alpha _2$ is empty, and the queue of $\alpha _3$ an ORCA message for $\omega _7$. The bottom part shows reference count tables: $\alpha _1.\textsf {rc} _{\mathcal {C} _0}(\alpha _1)=21$, and $\alpha _1.\textsf {rc} _{\mathcal {C} _0}(\omega _7)=50$. Entries of owned addresses are shaded. Since $\alpha _2$ owns $\alpha _2$ and $\omega _2$, the entries for $\alpha _2.\textsf {rc} _{\mathcal {C} _0}(\alpha _2)$ and $\alpha _2.\textsf {rc} _{\mathcal {C} _0}(\omega _2)$ are shaded. Note that $\alpha _1$ has a non-zero entry for $\omega _7$, even though there is no path from $\alpha _1$ to $\omega _7$. There is no entry for $\omega _1$; no such entry is needed, because no actor except for its owner has a path to it. The 0 values indicate potentially non-existent entries in the corresponding tables; for example, the reference count table for actor $\alpha _3$ needs only to contain entries for $\alpha _1$, $\alpha _3$, $\omega _3$, and $\omega _4$. Ownership does not restrict access to an address: e.g. actor $\alpha _1$ does not own object $\omega _3$, yet may access it through the path $\textsf {this}.f_1.f_2.f_3$, may read its field through $\textsf {this}.f_1.f_2.f_3.f_4$, and may mutate it, e.g. by $\textsf {this}.f_1.f_2.f_3=\textsf {this}.f_1$.

Lookup of fields in a configuration is defined in the obvious way, i.e.

Definition 2

$\mathcal {C} (\iota .f)\equiv \mathcal {C}.\textsf {heap} (\iota ,f)$, and $\mathcal {C} (\iota .\overline{f}.f')\equiv \mathcal {C}.\textsf {heap} (\mathcal {C} (\iota .\overline{f},f'))$

4.1 Capabilities and Accessibility

ORCA considers three capabilities:

where read allows reading, write allows reading and writing, and tag forbids both read and write, but allows the use of an object’s address. To describe the capability at which objects are visible from actors we use the concepts of static and dynamic paths.

Static paths consist of the keyword $\textsf {this}$ (indicating a path starting at the current actor), or the name of a behaviour, b, and a variable, x, (indicating a path starting at local variable x from a frame of b), followed by any number of fields, f.

The host language must assign these capabilities to static paths. Thus, we assume it provides a static judgement of the form

meaning that a static path $sp$ has capability capability when “seen” from a class A. We highlight .

We expect the type system to guarantee that read and write access rights are “deep”, meaning that all paths to a $\textsf {read}$ capability must go through other $\textsf {read}$ or $\textsf {write}$ capabilities (A1), and all paths to a $\textsf {write}$ capability must go through $\textsf {write}$ capabilities (A2).

Such requirements are satisfied by many type systems with read-only references or immutability (e.g. [7, 11, 18, 23, 29, 33, 37, 41]). An implication of A1 and A2 is that capabilities degrade with growing paths, i.e., the prefix of a path has more rights than its extensions. More precisely: $A \vdash sp : \kappa$ and $A \vdash sp .f : \kappa '$ imply that $\kappa \le \kappa '$, where we define $\textsf {write}< \textsf {read} < \textsf {tag}$, and $\kappa \le \kappa '$ iff $\kappa = \kappa '$ or $\kappa < \kappa '$.

Example:

Table 1 shows capabilities for some paths from Fig. 4. Thus, $A_1 \vdash \textsf {this}.f_1: \textsf {write}$, and $A_2 \vdash b'.x' : \textsf {write}$, and $A_2 \vdash \textsf {this}.f_8 : \textsf {tag}$. The latter, together with A1 gives that $A_2 \not \vdash \textsf {this}.f_8.f : \kappa$ for all $\kappa$ and f.

As we shall see later, the existence of a path does not imply that the path may be navigated. For example, $\mathcal {C} _0(\alpha _2.f_8.f_4) =\omega _4$, but actor $\alpha _2$ cannot access $\omega _4$ because of $A_2\vdash \textsf {this}.f_8:\textsf {tag}$.

Moreover, it is possible for a path to have a capability, while not being defined. For example, Table 1 shows $A_1 \vdash \textsf {this}.f_1.f_2: \textsf {write}$ and it would be possible to have $\mathcal {C} _i(\alpha _1.f_1) = \textsf {null}$, for some configuration $\mathcal {C} _i$ that derives from $\mathcal {C} _0$.

Table 1. Capabilities for paths, where $A_1 = \mathcal {C}lass(\alpha _1)$ and $A_2 = \mathcal {C}lass(\alpha _2)$.

Dynamic paths (in short paths p) start at the actor’s fields, or frame, or at some pending message in an actor’s queue (the latter cannot be navigated yet, but will be able to be navigated later on when the message is taken off the queue). Dynamic paths may be local paths (lp) or message paths. Local paths consist of $\textsf {this}$ or a variable x followed by any number of fields f. In such paths, $\textsf {this}$ is the current actor, and x is a local variable from the current frame. Message paths consist of k.x followed by a sequence of fields. If $k\ge 0$, then k.x indicates the local variable x from the k-th message from the queue; $k=-1$ indicates variables from either (a) a message that has been popped from the queue, but whose frame has not yet been pushed onto the stack, or (b) a message whose frame has been created but not yet been pushed onto the queue. Thus, $k=-1$ indicates that either (a) a frame will be pushed onto the stack, during message receiving, or (b) a message will be pushed onto the queue during message sending.

We define accessibility as the lookup of a path provided that the capability for this path is defined. The partial function $\mathcal {A}$ returns a pair: the address accessible from actor $\alpha$ following path $p$, and the capability of $\alpha$ on $p$. A path of the form $p .\textsf {owner}$ returns the owner of the object accessible though $p$ and capability tag.

Definition 3

(accessibility). The partial function

We use $\mathcal {A}_{\mathcal {C}}(\alpha , p)=\iota$ as shorthand for $\exists \kappa .\, \mathcal {A}_{\mathcal {C}}(\alpha , p)\!=\!(\iota , \kappa )$. The second and third case above ensure that the capability of a message path is the same as when the message has been taken off the queue and placed on the frame.

Example:

We obtain that $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, \textsf {this}.f_1.f_2.f_3) = (\omega _3, \textsf {write})$, from the fact that Fig. 4 says that $\mathcal {C} _0(\alpha _1.f_1.f_2.f_3) = \omega _3$ and from the fact that Table 1 says that $A_1 \vdash \textsf {this}.f_1.f_2.f_3:\textsf {write}$. Similarly, $\mathcal {A}_{\mathcal {C} _0}(\alpha _2, \textsf {this}.f_8) = (\omega _3, \textsf {tag})$, and $\mathcal {A}_{\mathcal {C} _0}(\alpha _2, x') = (\omega _8, \textsf {write})$, and $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, 0.x.f_5.f_7) = (\omega _8, \textsf {tag})$.

Both $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, \textsf {this}.f_1.f_2.f_3)$, and $\mathcal {A}_{\mathcal {C} _0}(\alpha _2, \textsf {this}.f_8)$ describe paths from actors’ fields, while $\mathcal {A}_{\mathcal {C} _0}(\alpha _2, x')$ describes a path from the actor’s frame, and finally $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, 0.x.f_5.f_7)$ is a path from the message queue.

Accessibility describes what may be read or written to: $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, \textsf {this}.f_1.f_2.f_3) = (\omega _3, \textsf {write})$, therefore actor $\alpha _1$ may mutate object $\omega _3$. However, this mutation is not visible by $\alpha _2$, even though $\mathcal {C} _0(\alpha _2.f_8)= \omega _3$, because $\mathcal {A}_{\mathcal {C} _0}(\alpha _2, \textsf {this}.f_8)=(\omega _3, \textsf {tag})$, which means that actor $\alpha _2$ has only opaque access to $\omega _3$.

Accessibility plays a role in collection: If the reference $f_3$ were to be dropped it would be safe to collect $\omega _4$; even though there exists a path from $\alpha _2$ to $\omega _4$; object $\omega _4$ is not accessible to $\alpha _2$: the path $\textsf {this}.f_8.f_4$ leads to $\omega _4$ but will never be navigated ($\mathcal {A}_{\mathcal {C} _0}(\alpha _2, \textsf {this}.f_8.f_4)$ is undefined). Also, $\mathcal {A}_{\mathcal {C}}(\alpha _2, \textsf {this}.f_8.\textsf {owner}) = (\alpha _3, \textsf {tag})$; thus, as long as $\omega _4$ is accessible from some actor, e.g. through ${\mathcal {C}}({\alpha _2.f_8}) = \omega _4$, actor $\alpha _3$ will not be collected.

Because the class of an actor as well as the capability attached to a static path are constant throughout program execution, the capabilities of paths starting from an actor’s fields or from the same frame are also constant.

Lemma 1

For actor $\alpha$, fields $\overline{f}$, behaviour $b$, variable $x$, fields $\overline{ f }$, capabilities $\kappa$, $\kappa '$, configurations $\mathcal {C}$ and $\mathcal {C} '$, such that $\mathcal {C}$ reduces to $\mathcal {C}$ ’ in one or more steps:

• $\mathcal {A}_{\mathcal {C}}(\alpha , \textsf {this}.\overline{f})= (\iota , \kappa ) \ \ \wedge \ \ \mathcal {A}_{\mathcal {C} '}(\alpha , \textsf {this}.\overline{f})= (\iota ', \kappa ') ~~\!\longrightarrow ~~ \kappa = \kappa '$

• $\mathcal {A}_{\mathcal {C}}(\alpha , x.\overline{f})= (\iota , \kappa ) \ \ \wedge \ \ \mathcal {A}_{\mathcal {C} '}(\alpha , x.\overline{f}) = (\iota ', \kappa ') \ \ \wedge \ \$

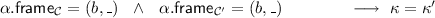
4.2 Well-Formed Configurations

We characterise data-race free configurations ($\vDash \mathcal {C}\ \diamondsuit$):

This definition captures invariant $\mathbf {I_1}$. The remaining invariants depend on the four derived counters introduced in Sect. 3. Here we define $\mathrm {LRC}$ and $\mathrm {FRC}$, and give a preliminary definition of $\mathrm {AMC}$ and $\mathrm {OMC}$.

Definition 5

(Derived counters—preliminary for $\mathrm {AMC}$  andss $\mathrm {OMC}$)

where $\#$ denotes cardinality.

For the time being, we will be reading this preliminary definition as if ... stood for 0. This works under the assumption the procedures are atomic. However Sect. 5.3, when we consider fine-grained concurrency, will refine the definition of $\mathrm {AMC}$ and $\mathrm {OMC}$ so as to also consider whether an actor is currently in the process of sending or receiving a message from which the address is accessible. For the time being, we continue with the preliminary reading.

Example:

Assuming that in $\mathcal {C} _0$ none of the actors is sending or receiving, we have $\mathrm {LRC}_{\mathcal {C} _0}(\omega _3) = 160$, and $\mathrm {FRC}_{\mathcal {C} _0}(\omega _3) = 160$, and $\mathrm {OMC}_{\mathcal {C} _0}(\omega _3) = 0$, and $\mathrm {AMC}_{\mathcal {C} _0}(\omega _3) = 0$. Moreover, $\mathrm {AMC}_{\mathcal {C} _0}(\omega _6) = \mathrm {AMC}_{\mathcal {C} _0}(\alpha _2) = 1$: neither $\omega _6$ nor $\alpha _2$ are arguments in application messages, but they are indirectly reachable through the first message on $\alpha _1$’s queue.

A well-formed configuration requires: $\mathbf {I_1}$–$\mathbf {I_4}$: introduced in Sect. 3; $\mathbf {I_5}$: the $\mathrm {RC}$’s are non-negative; $\mathbf {I_6}$: accessible paths are not dangling; $\mathbf {I_7}$: processing message queues will not turn $\mathrm {RC}$’s negative; $\mathbf {I_8}$: actors’ contents is in accordance with their state. The latter two will be described in Definition 14.

Definition 6

(Well-formed configurations—preliminary). $\vDash \mathcal {C}$, iff for all $\alpha$, $\alpha _{o}$, $\iota$, $\iota '$, $p$, lp, and mp, such that $\alpha _{o} = \mathcal {O}(\iota ) \ne \alpha$:

 

$\mathbf {I_1}$ :

$\vDash \mathcal {C}\ \diamondsuit$

$\mathbf {I_2}$ :

$[\ \ \mathcal {A}_{\mathcal {C}}(\alpha , p)\!=\!\iota \ \ \vee \mathcal {A}_{\mathcal {C}}(\alpha _{o}, mp)\!=\!\iota \ \ ] \longrightarrow \ \mathrm {LRC}_{\mathcal {C}}(\iota )\!>\!0$

$\mathbf {I_3}$ :

$\mathcal {A}_{\mathcal {C}}(\alpha , lp) = \iota \longrightarrow \alpha .\textsf {rc} _{\mathcal {C}}(\iota ) > 0$

$\mathbf {I_4}$ :

$\mathrm {LRC}_{\mathcal {C}}(\iota ) + \mathrm {OMC}_{\mathcal {C}}(\iota ) = \mathrm {FRC}_{\mathcal {C}}(\iota ) + \mathrm {AMC}_{\mathcal {C}}(\iota )$

$\mathbf {I_5}$ :

$\alpha .\textsf {rc} _{\mathcal {C}}(\iota ') \ge 0$

$\mathbf {I_6}$ :

$\mathcal {A}_{\mathcal {C}}(\alpha , p)\!=\!\iota \longrightarrow \mathcal {C}.\textsf {heap} (\iota ) \ne \perp$

$\mathbf {I_7}$, $\mathbf {I_8}$:

description in Definition 14.

 

For ease of notation, we take $\mathbf {I_5}$ to mean that if $\alpha .\textsf {rc} _{\mathcal {C}}(\iota ')$ is defined, then it is positive. And we take any undefined entry of $\alpha .\textsf {rc} _{\mathcal {C}}(\iota )$ to be 0.

4.3 Actor States

We now complete the definition of runtime entities (Definition 1), and describe the states of an actor, the worksets, the marks, and program counters. (Definition 7). We distinguish the following states: idle (), collecting (), receiving (), sending a message (), or executing the synchronous part of a behaviour (). We discuss these states in more detail next.

Except for the idle state, , all states use auxiliary data structures: work-sets, denoted by $\textsf {ws}$, which stores a set of addresses; marks maps, denoted by $\textsf {ms}$, from addresses to $\textsf {R}$ (reachable) or $\textsf {U}$ (unreachable), and program counters. Frames are relevant when in states , or , and otherwise are assumed to be empty. Worksets are used to store all addresses traced from a message or from the actor itself, and are relevant when in states , or , or , and otherwise are empty. Marks are used to calculate reachability and are used in state , and are ignored otherwise. The program counters record the instruction an actor will execute next; they range between $\mathsf{{4}}$ and $\mathsf{{27}}$ and are ghost state, i.e. only used in the proofs.

Definition 7

(Actor States, Working sets, and Marks)

We write $\alpha .\textsf {st} _\mathcal {C}$, or $\alpha .\textsf {ws} _\mathcal {C}$, or $\alpha .\textsf {ms} _\mathcal {C}$, or $\alpha .\mathsf{{pc}}_\mathcal {C}$ for the state, working set, marks, or the program counter of $\alpha$ in $\mathcal {C}$, respectively.

Actors may transition between states. The state transitions are depicted in Fig. 5. For example, an actor in the idle state () may receive an orca message (remaining in the same state), receive an $\textsf {app}$ message (moving to the state), or start garbage collection (moving to the state).

Fig. 5.

State transitions diagram for an actor.

In the following sections we describe the actions an actor may perform. Following the style of [17, 26, 27] we describe actors’ actions through pseudo-code procedures, which have the form:

We let $\alpha$ denote the executing actor, and the left-hand side of the arrow describes the condition that must be satisfied in order to execute the instructions on the arrow’s right-hand side. Any actor may execute concurrently with other actors. To simplify notation, we assume an implicit, globally accessible configuration $\mathcal {C}$. Thus, instruction $\alpha$.state := is short for updating the state of $\alpha$ in $\mathcal {C}$ to be . We elide configurations when obvious, e.g. $\alpha$.frame = $\phi$ is short for requiring that in $\mathcal {C}$ the frame of $\alpha$ is $\phi$, but we mention them when necessary—e.g. $\vDash \mathcal {C} [\iota _1,f\mapsto \iota _2]\ \diamondsuit$ expresses that the configuration that results from updating field f in $\iota _1$ is data-race free.

Tracing Function. Both garbage collection, and application message sending/receiving need to find all objects accessible from the current actor and/or from the message arguments. We define two functions: $\mathsf{{trace\_this}}$ finds all addresses which are accessible from the current actor, and $\mathsf{{trace\_frame}}$ finds all addresses which are accessible through a stack frame (but not from the current actor, $\mathrm {this}$).

Definition 8

(Tracing). We define the functions

4.4 Garbage Collection

We describe garbage collection in Fig. 6. An idle, or an executing actor (precondition on line 2) may start collecting at any time. Then, it sets its state to (line 5), and initialises the marks, ms, to empty (line 6).

Fig. 6.

Pseudo-code for garbage collection.

The main idea of ORCA collection is that the requirement for global unreachability of owned objects can be weakened to the local requirement to local unreachability and a $LRC = 0$. Therefore, the actor marks all owned objects, and all addresses with a $\mathrm {RC} >0$ as $\textsf {\small U}$ (line 9). After that, it traces the actor’s fields, and also the actor’s frame if it happens not to be empty (as we shall see later, idle actors have empty frames) and marks all accessible addresses as R (line 12). Then, the actor marks all owned objects with $\mathrm {RC} \!>\!0$ as $\textsf {\small R}$ (line 15). Thus we expect that: (*) Any $\iota$ with $\textsf {ms} (\iota )\!=\!\textsf {\small U}$ is locally unreachable, and if owned by the current actor, then its $\mathrm {LRC}$ is 0. For each address with $\textsf {ms} (\iota )\!=\!\textsf {\small U}$, if the actor owns $\iota$, then it collects it (line 20)—this is sound because of $\mathbf {I_2}$, $\mathbf {I_3}$, $\mathbf {I_4}$ and (*). If the actor does not own $\iota$, then it asks $\iota$’s owner to decrement its reference count by the current actor’s reference count, and deletes its own reference count to it (thus becoming 0) (line 24)—this preserves $\mathbf {I_2}$, $\mathbf {I_3}$ and $\mathbf {I_4}$.

There is no need for special provision for cycles across actor boundaries. Rather, the corresponding objects will be collected by each actor separately, when it is the particular actor’s turn to perform GC.

Example:

Look at the cycle $\omega _5$–$\omega _6$, and assume that the message $\textsf {\small app} (b,\omega _5)$ had finished execution without any heap mutation, and that $\alpha _1.\textsf {rc} _{\mathcal {C}}(\omega _5) = \alpha _1.\textsf {rc} _{\mathcal {C}}(\omega _6) = 1 = \alpha _2.\textsf {rc} _{\mathcal {C}}(\omega _5) = \alpha _2.\textsf {rc} _{\mathcal {C}}(\omega _6)$—this will be the outcome of the example in Sect. 4.5. Now, the objects $\omega _5$ and $\omega _6$ are globally unreachable. Assume that $\alpha _1$ performs GC: it will not be able to collect any of these objects, but it will send a $\textsf {orca} (\omega _6:\!-1)$ to $\alpha _2$. Some time later, $\alpha _2$ will pop this message, and some time later it will enter a GC cycle: it will collect $\omega _6$, and send a $\textsf {orca} (\omega _5:\!-1)$ to $\alpha _1$. When, later on, $\alpha _1$ pops this message, and later enters a GC cycle, it will collect $\omega _5$.

At the end of the GC cycle, the actor sets is state back to what it was before (line 26). If the frame is empty, then the actor had been , otherwise it had been in state .

4.5 Receiving and Sending Messages

Through message send or receive, actors share addresses with other actors. This changes accessibility. Therefore, action is needed to re-establish $\mathbf {I_3}$ and $\mathbf {I_4}$ for all the objects accessible from the message’s arguments.

Receiving application messages is described by in Fig. 7. It requires that the actor $\alpha$ is in the state and has an application message on top of its queue. The actor sets its state to (line 5), traces from the message arguments and stores all accessible addresses into (line 7). Since accessibility is not affected by other actors’ actions, c.f., last paragraph in Sect. 4.6 it is legitimate to consider the calculation of $\mathsf{{trace\_frame}}$ as one single step. It then pops the message from its queue (line 8), and thus the $\mathrm {AMC}$ for all the addresses in will decrease by 1. To preserve $\mathbf {I_4}$, for each $\iota$ in its , the actor:

• if it is $\iota$’s owner, then it decrements its reference count for $\iota$ by 1, thus decreasing $\mathrm {LRC}_{\mathcal {C}}(\iota )$ (line 12).

• if it is not $\iota$’s owner, then it increments its reference count for $\iota$ by 1, thus increasing $\mathrm {FRC}_{\mathcal {C}}(\iota )$ (line 14).

After that, the actor sets its frame to that from the message (line 17), and goes to the state (line 18).

Fig. 7.

Receiving application and ORCA messages.

Example:

Actor $\alpha _1$ has an application message in its queue. Assuming that it is , it may execute : It will trace $\omega _5$ and as a result store $\{ \omega _5, \omega _6, \omega _8, \alpha _1, \alpha _2 \}$ in its . It will then decrement its reference count for $\omega _5$ and $\alpha _1$ (the owned addresses) and increment it for the others. It will then pop the message from its queue, create the appropriate frame, and go to state .

Receiving ORCA messages is described in Fig. 7. An actor in the state with an ORCA message at the top, pops the message from its queue, and adds the value z to the reference count for $\iota$, and stays in the state.

Sending application messages is described in Fig. 8. The actor must be in the state for some behaviour b and must have local variables which can be split into $\psi$ and $\psi '$—the latter will form part of the message to be sent. As the $\mathrm {AMC}$ for all the addresses reachable through the message increases by 1, in order to preserve $\mathbf {I_4}$ for each address $\iota$ in , the actor:

Fig. 8.

Pseudo-code for message sending.

• increments its reference count for $\iota$ by 1, if it owns it (line 14);

• decrements its reference count for $\iota$ if it does not own it (line 16). But special care is needed if the actor’s (foreign) reference count for $\iota$ is 1, because then a simple decrement would break $\mathbf {I_5}$. Instead, the actor set its reference count for $\iota$ by 256 (line 18) and sends an ORCA message to $\iota$’s owner with 256 as argument.

After this, it removes $\psi '$ from its frame (line 22), pushes the message $\textsf {\small app} (b',\psi ')$ onto $\alpha '$’s queue, and transitions to the state.

We now discuss the preconditions. These ensure that sending the message $\textsf {\small app} (b,\psi ')$ will not introduce data races: Line 4 ensures that there are no data races between paths starting at $\psi$ and paths starting at $\psi '$, while Line 5 ensures that the sender, $\alpha$, and the receiver, $\alpha '$ see all the paths sent, i.e. those starting from $(b',\psi ')$, at the same capability. We express our expectation that the source language compiler produces code only if it satisfies this property by adding this static requirement as a precondition. These static requirements imply that after the message has been sent, there will be no races between paths starting at the sender’s frame and those starting at the last message in the receiver’s queue. In more detail, after the sender’s frame has been reduced to $(b,\psi )$, and $app(b',\psi ')$ has been added to the receiver’s queue (at location k), we will have a new configuration . In this new configuration lines 4 and 5 ensure that $\mathcal {A}_{\mathcal {C} '}(\alpha , x.\overline{f})\!=\!(\iota ,\kappa ) \wedge \mathcal {A}_{\mathcal {C} '}(\alpha ', k.x'.\overline{f'})\!=\!(\iota ,\kappa ') \ \longrightarrow \ \kappa ' \sim \kappa$, which means that if there were no data races in $\mathcal {C}$, there will be no data races in $\mathcal {C} '$ either. Formally: $\vDash \mathcal {C}\ \diamondsuit \ \longrightarrow \ \vDash \mathcal {C} '\ \diamondsuit$.

We can now complete Definition 3 for the receiving and the sending cases, to take into account paths that do not exist yet, but which will exist when the message receipt or message sending has been completed.

Definition 9

(accessibility—receiving and sending). Completing Definition 3:

Example:

When actor $\alpha _1$ executes , and its program counter is between 9 and 18, then $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, -1.x.f_5)=(\omega _6,\textsf {write})$, even though x is not yet on the stack frame. As soon as the frame is pushed on the stack, and we reach program counter 20, then t $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, -1.x.f_5)$ is undefined, but $\mathcal {A}_{\mathcal {C} _0}(\alpha _1, x.f_5)=(\omega _6,\textsf {write})$.

4.6 Actor Behaviour

As our model is parametric with the host language, we do not aim to describe any of the actions performed while executing behaviours, such as synchronous method calls and pushing frames onto stacks, conditionnals, loops etc. Instead, we concentrate on how behaviour execution may affect GC; this happens only when the heap is mutated either by object creation or by mutation of objects’ fields (since this affects accessibility). In particular, our model does not accommodate for recursive calls; we claim that the result from the current model would easily be extended to a model with recursion in synchronous behaviour, but would require a considerable notation overhead.

Figure 9 shows the actions of an actor $\alpha$ while in the state, i.e. while it executes behaviours synchronously. The description is nondeterministic: the procedures , or , or , may execute when the corresponding preconditions hold. Thus, we do not describe the execution of a given program, rather we describe all possible executions for any program. In , the actor $\alpha$ simply passes from the execution state to the idle state; the only condition is that its state is (line 2). It deletes the frame, and sets the actor’s state to (line 4). creates a new object, initialises its fields to null, and stores its address into local variable x.

Fig. 9.

Pseudo-code for synchronous operations.

The most interesting procedure is field assignment, . line 8 modifies the object at address $\iota _1$, reachable through local path lp1, and stores in its field f the address $\iota _2$ which was reachable through local path lp2. We require that the type system makes the following two guarantees: line 2, second conjunct, requires that , while line 3 requires that . Line 4 and line 5 requite that : any address that is accessible with a capability $\kappa$ after the field update was accessible with the same or more permissive capability $\kappa '$ before the field update. This requirment guarantees preservation of data race freedom, i.e. that $\vDash \mathcal {C}\ \diamondsuit$ implies $\vDash \mathcal {C} [\iota _1,f~\mapsto ~\iota _2]\ \diamondsuit$.

Heap Mutation Does not Affect Accessibility in Other Actors. Heap mutation either creates new objects, which will not be accessible to other actors, or modifies objects to which the current actor has write access. By $\vDash \mathcal {C}\ \diamondsuit$ all other actors have only tag access to the modified object. Therefore, because of capabilities’ degradation with growing paths (as in A1 and A2), no other actor will be able to access objects reachable through paths that go through the modified object.

5 Soundness and Completeness

In this section we show soundness and completeness of ORCA.

5.1 $\mathbf {I_1}$ and $\mathbf {I_2}$ Support Safe Local GC

As we said earlier, $\mathbf {I_1}$ and $\mathbf {I_2}$ support safe local GC. Namely, $\mathbf {I_1}$ guarantees that as long as GC only traces objects to which the actor has $\textsf {read}$ or $\textsf {write}$ access, there will be no data races with other actors’ behaviour or GC. And $\mathbf {I_2}$ guarantees that collection can take place based on local information only:

Definition 10

For a configuration $\mathcal {C}$, and object address $\omega$ we say that

• $\omega$ is globally inaccessible in $\mathcal {C}$, iff $\forall \alpha , p. \, \mathcal {A}_{\mathcal {C}}(\alpha , p)\ne \omega$

• $\omega$ is collectable, iff $\mathrm {LRC}_{\mathcal {C}}(\omega ) = 0$, and $\forall lp.\ \mathcal {A}_{\mathcal {C}}(\mathcal {O}(\omega ), lp) \ne \omega$.

Lemma 2

If $\mathbf {I_2}$ holds, then every collectable object is globally inaccessible.

5.2 Completeness

In [16] we show that globally inaccessible objects remain so, and that for any globally inaccessible object there exists a sequence of steps which will collect it.

Theorem 1

(Inaccessibility is monotonic). For any configurations $\mathcal {C}$, and $\mathcal {C} '$, if $\mathcal {C} '$ is the outcome of the execution of any single line of code from any of the procedures from Figs. 6, 7, 8 and 9, and $\omega$ is globally inaccessible in $\mathcal {C}$, then $\omega$ is globally inaccessible in $\mathcal {C} '$.

Theorem 2

(Completeness of ORCA). For any configuration $\mathcal {C}$, and object address $\omega$ which is globally inaccessible in $\mathcal {C}$, there exists a finite sequence of steps which lead to $\mathcal {C} '$ in which $\omega \notin dom(\mathcal {C} ')$.

5.3 Dealing with Fine-Grained Concurrency

So far, we have discussed actions under an assumption atomicity. However, ORCA needs to work under fine-grained concurrency, whereby several actors may be executing concurrently, each of them executing a behaviour, or sending or receiving a message, or collecting garbage. With fine-grained concurrency, and with the preliminary definitions of $\mathrm {AMC}$  and $\mathrm {OMC}$, the invariants are no longer preserved. In fact, they need never hold!

Example:

Consider Fig. 4, and assume that actor $\alpha _1$ was executing . Then, at line 7 and before popping the message off the queue, we have $\mathrm {LRC}_{ }(\omega _5)= 2$, $\mathrm {FRC}_{ }(\omega _5)=1$, $\mathrm {AMC}_{ }^p(\omega _5)= 1$, where $\mathrm {AMC}_{}^p(\_)$ stands for the preliminary definition of $\mathrm {AMC}$; thus $\mathbf {I_4}$ holds. After popping and before updating the RC for $\omega _5$, i.e. between lines 9 and 11, we have $\mathrm {AMC}_{ }^p(\omega _5)= 0$—thus $\mathbf {I_4}$ is broken. At first sight, this might not seem a big problem, because the update of RC at line 12 will set $\mathrm {LRC}_{ }(\omega _5)= 1$, and thus restore $\mathbf {I_4}$. However, if there was another message containing $\omega _5$ in $\alpha _2$’s queue, and consider a snapshot where $\alpha _2$ had just finished line 8 and $\alpha _1$ had just finished line 12, then the update of $\alpha _1$’s RC will not restore $\mathbf {I_4}$.

The reason for this problem is, that with the preliminary definition $\mathrm {AMC}_{}^p(\_)$, upon popping at line 8, the $\mathrm {AMC}$ is decremented in one atomic step for all objects accessible from the message, while the RC is updated later on (at line 12 or line 14), and one object at a time. In other words, the updates to $\mathrm {AMC}$ and $\mathrm {LRC}$ are not in sync. Instead, we give the full definition of $\mathrm {AMC}$ so, that $\mathrm {AMC}$ is in sync $\mathrm {LRC}$; namely it is not affected by popping the message, and is reduced one object at a time once we reach program counter line 15. Similarly, because updating the $\mathrm {RC}$’s takes place in a separate step from the removal of the ORCA-message from its queue, we refine the definition of $\mathrm {OMC}$:

Definition 11

(Auxiliary Counters for $\mathrm {AMC}$, and $\mathrm {OMC}$)

In the above $\alpha .\textsf {ws}$ refers to the contents of the variable $\textsf {ws}$ while the actor $\alpha$ is executing the pseudocode from , and $\iota _{10}$ refers to the contents of the variable $\iota$ arbitrarily chosen in line 10 of the code.

We define , , and similarly in [16].

The counters and are zero except for actors which are in the process of receiving or sending application messages. Also, the counters and are zero except for actors which are in the process of receiving or sending ORCA-messages. All these counters are always $\ge 0$. We can now complete the definition of $\mathrm {AMC}$ and $\mathrm {OMC}$:

Definition 12

($\mathrm {AMC}$ and $\mathrm {OMC}$ – full definition)

where $\#$ denotes cardinality.

Example:

Let us again consider that $\alpha _1$ was executing . Then, at line 10 we have $\textsf {ws} = \{ \iota _5, \iota _6 \}$ and $\mathrm {AMC}_{ }(\omega _5)= 1=\mathrm {AMC}_{ }(\omega _6)$. Assume at the first iteration, at line 10 we chose $\iota _5$, then right before reaching line 15 we have $\mathrm {AMC}_{ }(\omega _5)= 0$ and $\mathrm {AMC}_{ }(\omega _6)=1$. At the second iteration, at line 10 we will chose $\iota _6$, and then right before reaching 15 we have $\mathrm {AMC}_{ }(\omega _6)= 0$.

5.4 Soundness

To complete the definition of well-formed configurations, we need to define what it means for an actor or a queue to be well-formed.

Well-Formed Queues - $\mathbf {I_7}$. The owner’s reference count for any live address (i.e. any address reachable from a message path, or foreign actor, or in an ORCA message) should be greater than 0 at the current configuration, as well as, at all configurations which arise from receiving pending, but no new, messages from the owner’s queue. Thus, in order to ensure that ORCA decrement messages do not make the local reference count negative, $\mathbf {I_7}$ requires that the effect of any prefix of the message queue leaves the reference count for any object positive. To formulate $\mathbf {I_7}$ we use the concept of $QueueEffect _\mathcal {C} (\alpha ,\iota ,n)$, which describes the contents of LRC after the actor $\alpha$ has consumed and reacted to the first n messages in its queue—i.e. is about “looking into the future”. Thus, for actor $\alpha$, address $\iota$, and number n we define the effect of the n-prefix of the queue on the reference count as follows:

$QueueEffect _\mathcal {C} (\alpha ,\iota ,n) \ \equiv \ \mathrm {LRC}_{\mathcal {C}}(\iota ) -z + \sum _{j\!=\!0}^n Weight _\mathcal {C} (\alpha ,\iota ,j)$

where $z = k$, if $\alpha$ is in the process of executing , and $\alpha$.$\mathrm {pc}$$_\mathcal {C} =6$, and $\alpha$.qu.top = orca ($\iota : k$), and otherwise $z=0$.

And where,

$\mathbf {I_7}$ makes the following four guarantees: [a] The effect of any prefix of the message queue leaves the LRC non-negative. [b] If $\iota$ is accessible from the j-th message in its owner’s queue, then the LRC for $\iota$ will remain ${>}0$ during execution of the current message queue up to, and including, the j-th message. [c] If $\iota$ is accessible from an ORCA-message, then the LRC will remain ${>}0$ during execution of the current message queue, up to and excluding execution of the ORCA-message itself. [d] If $\iota$ is globally accessible (i.e. reachable from a local path or from a message in a non-owning actor) then $LRC(\iota )$ is currently ${>}0$, and will remain so after during popping of all the entries in the current queue.

Definition 13

($\mathbf {I_7}$).  $\models _{{Queues}} \mathcal {C}$, iff for all $j\in \mathbb {N}$, for all addresses $\iota$, actors $\alpha$, $\alpha '$, where $\mathcal {O}(\iota )=\alpha \ne \alpha '$, the following conditions hold:

 

a:

$~~\forall n.~ QueueEffect _\mathcal {C} (\alpha ,\iota ,n) \ge 0$

b:

$~~\exists x.~\exists \overline{f}.~\mathcal {A}_{\mathcal {C}}(\alpha , j.x.\overline{f}) = \iota \longrightarrow \forall k\le j. \ QueueEffect _\mathcal {C} (\alpha ,\iota ,k) > 0.$

c:

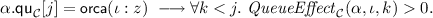
d:

$~~\exists p.\mathcal {A}_{\mathcal {C}}(\alpha ', p) = \iota \longrightarrow \forall k\in \mathbb {N}.~ QueueEffect _\mathcal {C} (\alpha ,\iota ,k) > 0.$

 

For example, in a configuration with $LRC(\iota )=2$, and a queue with is illegal by $\mathbf {I_7}$.[a]. Similarly, in a configuration with $LRC(\iota )=2$, and a queue with , the owning actor could collect $\iota$ before popping the message from its queue. Such a configuration is also deemed illegal by $\mathbf {I_7}$.[c].

$\mathbf {I_8}$-Well-Formed Actor. In [16] we define well-formedness of an actor $\alpha$ through the judgement $\mathcal {C},\alpha \vdash \textsf {st}$. This judgement depends on $\alpha$’s current state st, and requires, among other things, that the contents of the local variables , are consistent with the contents of the and . Remember also, that because and modify the or send ORCA-messages before updating the frame or sending the application message, in the definition of $\mathrm {AMC}$ and $\mathrm {OMC}$ we took into account the internal state of actors executing such procedures.

Well-Formed Configuration. The following completes Definition 6 from Sect. 4.2.

Definition 14

(Well-formed configurations—full). A configuration $\mathcal {C}$ is well-formed, $\vDash \mathcal {C}$, iff $\mathbf {I_1}$–$\mathbf {I_6}$ (Definition 6) for $\mathcal {C}$, if its queues are well-formed ($\models _{{Queues}} \mathcal {C}$, $\mathbf {I_7}$), as well as, all its actors ($\mathcal {C},\alpha \vdash \alpha .\textsf {st} _\mathcal {C}$, $\mathbf {I_8}$).

In [16] we consider the execution of each line in the codes from Sect. 4, and prove:

Theorem 3

(Soundness of ORCA). For any configurations $\mathcal {C}$ and $\mathcal {C} '$: If $\vDash \mathcal {C}$, and $\mathcal {C} '$ is the outcome of the execution of any single line of code from any of the procedures from Figs. 6, 7, 8 and 9, then $\vDash \mathcal {C} '$.

This theorem together with $\mathbf {I_6}$ implies that ORCA never leaves accessible paths dangling. Note that the theorem is stated so as to be applicable for a fine interleaving of the execution. Even though we expressed ORCA through procedures, in our proof we cater for an execution where one line of any of these procedures is executed interleaved with any other procedures in the other actors.

6 Related Work

The challenges faced when developing and debugging concurrent garbage collectors have motivated the development of formal models and proofs of correctness [6, 13, 19, 30, 35]. However, most work considers a global heap where mutator and collector threads race for objects and relies on synchronisation mechanisms (or atomic reduction steps), such as read or write barriers, in contrast to ORCA which considers many local heaps, no atomicity or synchronization, and relies on the properties of the type system. McCreight et al. [25] introduced a framework to reason about and build certified garbage collectors, verifying independently both mutator and collector threads. Their work focuses mainly on garbage collectors similar to those that run on Java programs, such as STW mark-and-sweep, STW copying and incremental copying. Vechev et al. [39] specified concurrent mark-and-sweep collectors with write barriers for synchronisation. The authors also present a parametric garbage collector from which other collectors can be derived. Hawblitzel and Petrank [22] mechanized proofs of two real-world collectors (copying and mark-and-sweep) and their respective allocators. The assembly code was instrumented with pre- and post-conditions, invariants and assertions, which were then verified using Z3 and Boogie. Ugawa et al. [38] extended a copying, on-the-fly, concurrent garbage collector to process reference types. The authors model-checked their algorithm using a model that limited the number of objects and threads. Gamie et al. [17] machine-checked a state-of-the-art, on-the-fly, concurrent, mark-and-sweep garbage collector [32]. They modelled one collector thread and many mutator threads. ORCA does not limit the number of actors running concurrently.

Local heaps have been used in the context of garbage collection to reduce the amount of synchronisation required before [1,2,3, 13, 15, 24, 31, 34], where different threads have their own heap and share a global heap. However, only two of these have been proved correct. Doligez and Gonthier [13] proved a collector [14] which splits the heap into many local heaps and one global heap, and uses mark-and-sweep for individual collection of local heaps. The algorithm imposes restrictions on the object graph, that is, a thread cannot access objects in other threads’ local heaps. ORCA allows for references across heaps. Raghunathan et al. [34] proved correct a hierarchical model of local heaps for functional programming languages. The work restricted objects graphs and prevented mutation.

As for collectors that rely on message passing, Moreau et al. [26] revisited the Birrell’s reference listing algorithm, which also uses message passing to update reference counts in a distributed system, and presented its formalisation and proofs or soundness and completeness. Moreover, Clebsch and Drossopoulou [10] proved correct MAC, a concurrent collector for actors.

7 Conclusions

We have shown the soundness and completeness of the ORCA actor memory reclamation protocol. The ORCA model is not tied to a particular programming language and is parametric in the host language. Instead it relies on a number of invariants and properties which can be met by a combination of language and static checks. The central property that is required is the absence of data races on objects shared between actors.

We developed a formal model of ORCA and identified requirements for the host language, its type system, or associated tooling. We described ORCA at a language-agnostic level and identified eight invariants that capture how global consistency is obtained in the absence of synchronisation. We proved that ORCA will not prematurely collect objects (soundness) and that all garbage will be identified as such (completeness).