Abstract
We revisit the notion of proxy re-encryption (\(\mathsf {PRE}\)), an enhanced public-key encryption primitive envisioned by Blaze et al. (Eurocrypt’98) and formalized by Ateniese et al. (NDSS’05) for delegating decryption rights from a delegator to a delegatee using a semi-trusted proxy. \(\mathsf {PRE}\) notably allows to craft re-encryption keys in order to equip the proxy with the power of transforming ciphertexts under a delegator’s public key to ciphertexts under a delegatee’s public key, while not learning anything about the underlying plaintexts.
We study an attractive cryptographic property for \(\mathsf {PRE}\), namely that of forward secrecy. In our forward-secret \(\mathsf {PRE}\) (fs-\(\mathsf {PRE}\)) definition, the proxy periodically evolves the re-encryption keys and permanently erases old versions while he delegator’s public key is kept constant. As a consequence, ciphertexts for old periods are no longer re-encryptable and, in particular, cannot be decrypted anymore at the delegatee’s end. Moreover, delegators evolve their secret keys too, and, thus, not even they can decrypt old ciphertexts once their key material from past periods has been deleted. This, as we will discuss, directly has application in short-term data/message-sharing scenarios.
Technically, we formalize fs-\(\mathsf {PRE}\). Thereby, we identify a subtle but significant gap in the well-established security model for conventional \(\mathsf {PRE}\) and close it with our formalization (which we dub fs-\(\mathsf {PRE} ^+\)). We present the first provably secure and efficient constructions of fs-\(\mathsf {PRE}\) as well as \(\mathsf {PRE}\) (implied by the former) satisfying the strong fs-\(\mathsf {PRE} ^+\) and \(\mathsf {PRE} ^+\) notions, respectively. All our constructions are instantiable in the standard model under standard assumptions and our central building block are hierarchical identity-based encryption (\(\mathsf {HIBE}\)) schemes that only need to be selectively secure.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The security of cryptosystems essentially relies on the secrecy of the respective secret key. For example, if for an encryption scheme a secret key is (accidentally) leaked, the confidentiality of all the data encrypted with respect to this key so far is immediately destroyed. One simple mitigation strategy for such a secret-key leakage is to frequently change secret keys such that leaking a secret key only affects a small amount of data. Implementing this in a naïve way, for instance in context of public-key encryption, means that one either has to securely and interactively distribute copies of new public keys frequently or to have huge public keysFootnote 1, which is rather inconvenient in practice. Consequently, cryptographic research focused on the design of cryptosystems that inherently provide such a property, being denoted as forward secrecy (or, forward security) [28]. The goal hereby is that key leakage at some point in time does not affect the data which was encrypted before the key leakage, while mitigating the drawbacks of the naïve solution discussed before. That is, one aims at efficient non-interactive solutions that have fixed sublinear-size public keys in the number of key switches/time periods. Those (strong) properties are the minimal requirements in the de-facto standard notion of forward secrecy in the cryptographic literature.
Within the last two decades, forward secrecy has been identified as an important property of various different cryptographic primitives such as digital signatures [6], identification schemes [1], public-key encryption [15], and private-key cryptography [7]. Only recently, another huge step forward has been made by Green and Miers [27] as well as Günther et al. [29] to bring forward secrecy to important practical applications in the context of asynchronous messaging and zero round-trip time (0-RTT) key exchange. Given revelations and leaks about large-scale surveillance activities of security agencies within the last years, it is of utmost importance to further develop and deploy cryptosystems that inherently provide forward secrecy. We aim at advancing the research on forward secrecy with respect to other practically important public-key primitives, ideally, to ones with slightly more functionality.
Proxy re-encryption. Proxy re-encryption (\(\mathsf {PRE}\)), envisoned by Blaze et al. [9] and formalized by Ateniese et al. [4, 5], is a cryptographic primitive that can be seen as an extension of public-key encryption. A central feature of \(\mathsf {PRE}\) is that senders can craft so-called re-encryption keys, which are usually created using only public information of the designated delegatee and the delegators’ key material. Those re-encryption keys have the power to transform ciphertexts under a delegator’s public key to ciphertexts under the delegatees’ public keys. Within \(\mathsf {PRE}\), this transformation is done by a semi-trustedFootnote 2 proxy. The widely accepted model for \(\mathsf {PRE}\) security (i.e., the conventional or plain \(\mathsf {PRE}\) model) [4] requires that the proxy does not learn anything about the plaintexts which underlie the ciphertexts to be transformed.Footnote 3
Proxy re-encryption is considered very useful in applications such as encrypted e-mail forwarding or access control in secure file systems, which was already discussed heavily in earlier work, e.g., in [4]. Furthermore, \(\mathsf {PRE}\) has been object of significant research for almost two decades now, be it in a conventional setting [4, 5, 9], \(\mathsf {PRE}\) with temporary delegation [4, 5, 34], identity-based \(\mathsf {PRE}\) [26, 37], extensions to the chosen-ciphertext setting [16, 34], type-based/conditional \(\mathsf {PRE}\) [39, 41], anonymous (or key-private) \(\mathsf {PRE}\) [3], traceable \(\mathsf {PRE}\) [32], or \(\mathsf {PRE}\) from lattice-based assumptions [18, 36]. Generic constructions of \(\mathsf {PRE}\) schemes from fully-homomorphic encryption [24] and from non-standard building blocks such as resplittable-threshold public key encryption as proposed in [30] are known, where different constructions of secure obfuscators for the re-encryption functionality have been given [18, 19, 31]. Despite \(\mathsf {PRE}\) being an object of such significant research, forward-secret constructions remain unknown.Footnote 4
On modeling forward-secret proxy re-encryption. Forward secrecy in the context of \(\mathsf {PRE}\) is more complex than in standard public-key primitives, as \(\mathsf {PRE}\) involves multiple different parties (i.e., delegator, proxy, and delegatees), where delegator and delegatees all have their own secret-key material and the proxy additionally holds all the re-encryption keys. One may observe that the proxy needs to be considered as a semi-trusted (central) party being always online, and, thus, it is reasonable to assume that this party is most valuable to attack. Consequently, we model forward secrecy in the sense that the re-encryption-key material can be evolved by the proxy to new periods while past-period re-encryption keys are securely erased. Hence, ciphertexts under the delegator’s public key with respect to past-periods can no longer be re-encrypted. In addition, we model forward secrecy for the delegator’s key material in a way that it is consistent with the evolution of the re-encryption material at the proxy.
For now, we do not consider forward secrecy at the delegatee, who can be seen as a passive party and does not need to take any further interaction with the delegator during the life-time of the system, except providing her public key once after set-up (e.g., via e-mail or public key server). It also does not have to be online when ciphertexts are re-encrypted for her by the proxy. Nevertheless, we leave it as a path for future research to cover the third dimension, i.e., model forward secrecy for the delegator and proxy as well as forward secrecy for the delegatee with efficient non-trivial constructions. However, it seems highly non-trivial to achieve efficient constructions that support forward secrecy for the delegatee additionally. In particular, we believe that the difficulty of achieving such strong type of forward secrecy is due to the circumstance that one has to carefully integrate three dimension of evolving key-material, one at the delegator, one at the proxy, and one at the delegatee. All dimensions seem to interfere with each other.Footnote 5 As it will be confirmed by our application, covering the two dimensions already yields an interesting tool.
Moreover, to achieve forward secrecy for delegator and proxy key material, we face the following obstacles. First, it has to be guaranteed that the honest proxy must not be able to gain any information from the ciphertexts while at the same time being able to transform such ciphertexts and to update re-encryption key material consistently to newer time periods without any interaction with the delegator. Secondly, any delegatee must not be able to decrypt past-period ciphertexts. In this work, we give an affirmative answer to overcome those obstacles.
A practical application of forward-secret PRE. We believe that forward secrecy is an essential topic nowadays for any application. Also \(\mathsf {PRE}\) is increasingly popular, be it in applied cryptographic literature [10, 14, 35, 36, 42], working groups such as the CFRG of the IRTFFootnote 6, large-scale EU-funded projectsFootnote 7, and meanwhile also companiesFootnote 8 that foster transition of such technologies into applications.
A practical application for forward-secret \(\mathsf {PRE}\) is disappearing 1-to-n messaging. Here, a user encrypts a message under his public key and sends it to the proxy server that is responsible for distributing the encrypted messages to all pre-determined n receivers (note that receivers do not have to be online at the time the encrypted message is sent and an initial public-key exchange has to be done only in the beginning, but no more interactivity is needed). During setup time, the user has equipped the server with re-encryption keys (one for each receiver) while new keys can be added any time once a new receiver is present. Furthermore, the user does not need to manage a potentially huge list of public keys for each message to be sent. After a period, the data gets deleted by the proxy server, the re-encryption keys get evolved to a new period (without any interactions), and old-period re-encryption keys get deleted. The security of forward-secret \(\mathsf {PRE}\) then guarantees that the proxy server does not learn the sensitive messages, neither can the two types of parties access disappeared messages later on. Once period-i re-encryption keys leak from the proxy server, only present and future encrypted messages (from period i onward) are compromised, while period-\((i-1)\) messages stay confidential. More generally, we believe that forward-secret \(\mathsf {PRE}\) can be beneficially used in all kinds of settings that require access revocation, e.g., in outsourced encrypted data storage.
We also stress that within our forward-secret \(\mathsf {PRE}\) instantiations, each user is only required to manage her own public and secret keys on her device and not a list of recipient public keys (or, identities). This deviates significantly from other primitives such as broadcast encryption (BE) [12, 22, 38], which could also be suitable in such scenarios. However, practical BE schemes, e.g., [13], need large public keys and are computationally expensive.
1.1 Contribution
In this paper, we investigate forward secrecy in the field of proxy re-encryption (\(\mathsf {PRE}\)) and term it fs-\(\mathsf {PRE}\). More precisely, our contributions are as follows:
-
We first port the security model of \(\mathsf {PRE}\) to the forward-secret setting (fs-\(\mathsf {PRE} ^-\)). Thereby, we observe a subtle but significant gap in existing (plain) security models for conventional \(\mathsf {PRE}\) with regard to the granularity of delegations of decryption rights. In particular, existing models allow that a recipient, who has once decrypted a re-encrypted ciphertext, can potentially decrypt all re-encryptable ciphertexts of the same sender without further involvement of the proxy. In the forward-secret setting, it would essentially require to trust the delegatees to delete their re-encrypted ciphertexts whenever the period is switched, which is a problematic trust assumption.Footnote 9
-
We close this gap by introducing an additional security notion which inherently requires the involvement of a proxy in every re-encryption and in particular consider this notion in the forward-secret setting (fs-\(\mathsf {PRE} ^+\)). We also note that, when considering only a single time interval, this implicitly closes the aforementioned gap in the conventional PRE setting.Footnote 10 We also provide an explicit separation of the weaker fs-\(\mathsf {PRE} ^-\) notion (resembling existing \(\mathsf {PRE}\) models) and our stronger notion fs-\(\mathsf {PRE} ^+\).
-
We then continue by constructing the first forward-secret \(\mathsf {PRE}\) schemes (in the weaker as well as our stronger model) that are secure in the standard model under standard assumptions. On a technical side, only few approaches to forward secrecy are known. Exemplary, in the public-key-encryption (\(\mathsf {PKE}\)) setting, we essentially have two ways to construct forward secrecy, i.e., the Canetti-Halevi-Katz (CHK) framework [15] from selectively secure hierarchical identity-based encryption (\(\mathsf {HIBE}\)) [25] schemes and the more abstract puncturable-encryption (PE) approaches by [27, 29] (where both works either explicitly or implicitly use the CHK techniques). Particularly, we are not aware of any framework to achieve forward secrecy for \(\mathsf {PKE}\) schemes based on “less-complex” primitives in comparison to selectively secure \(\mathsf {HIBE}\) schemes. Consequently, we also base our constructions on selectively secure \(\mathsf {HIBE}\) schemes [25], which we combine with linearly homomorphic encryption schemes, e.g., (linear) ElGamal.
-
As a side result, we generalize the recent work of PE [17, 21, 27, 29] to what we call fully puncturable encryption (\(\mathsf {FuPE}\)) in the full version of this paper and show how we can use \(\mathsf {FuPE}\) to construct fs-\(\mathsf {PRE}\).
1.2 Intuition and Construction Overview
To obtain more general results and potentially also more efficient instantiations, we use a relaxation of HIBEs denoted as binary-tree encryption (\(\mathsf {BTE}\)) which was introduced by Canetti, Halevi, and Katz (CHK) in [15]. As an intermediate step, we introduce the notion of a forward-secret delegatable public-key encryption (fs-\(\mathsf {DPKE}\)) scheme and present one instantiation which we obtain by combining the results of CHK with a suitable homomorphic public-key encryption (\(\mathsf {HPKE}\)) scheme. Loosely speaking, a fs-\(\mathsf {DPKE}\) scheme allows to delegate the decryption functionality of ciphertexts computed with respect to the public key of some user A to the public key of some other user B. Therefore, A provides a public delegation key to B. B then uses the delegation key together with the secret key corresponding to B’s public key to decrypt any ciphertext that has been produced for A. A fs-\(\mathsf {DPKE}\) scheme moreover incorporates forward secrecy in a sense that the originator A can evolve it’s secret key and the scheme additionally allows to publicly evolve delegation keys accordingly. Interestingly, such a scheme is already sufficient to construct a fs-\(\mathsf {PRE} ^-\)-secure \(\mathsf {PRE}\) scheme. Finally, we demonstrate how to strengthen this construction to a fs-\(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme, by solely relying on a certain type of key-homomorphism of the underlying fs-\(\mathsf {DPKE}\) scheme. The intermediate step of introducing fs-\(\mathsf {DPKE}\) is straightforward yet interesting, since we believe fs-\(\mathsf {DPKE}\) is the “next natural step” to lift \(\mathsf {PKE}\) to a setting which allows for controlled delegation of decryption rights.
Instantiation. In Table 1, we present an instantiation including the resulting key and ciphertext sizes. Thereby, we only look at fs-\(\mathsf {PRE}\) instantiations that are fs-\(\mathsf {PRE} ^+\)-secure and note that the asymptotic sizes for fs-\(\mathsf {PRE} ^-\)-secure fs-\(\mathsf {PRE}\) schemes are identical. For our instantiation, we use the \(\mathsf {BTE}\) (or any selectively secure \(\mathsf {HIBE}\)) from [15] and the linear encryption scheme from [11] as \(\mathsf {HPKE}\) scheme under the Bilinear Decisional Diffie-Hellman (BDDH) and decision linear (DLIN) assumption respectively.
A note on a side result. Additionally, in the full version, we include the definition and a construction of a so called fully puncturable encryption (\(\mathsf {FuPE}\)) scheme which is inspired by techniques known from HIBEs and the recent PE schemes in [27, 29]. We then show that \(\mathsf {FuPE}\) schemes closely capture the essence which is required to construct fs-\(\mathsf {PRE} ^+\)-secure schemes by presenting a construction of a fs-\(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme from \(\mathsf {FuPE}\) and \(\mathsf {HPKE}\).
1.3 Related Work and Outline
Work related to forward-secret PRE. Tang et al. [39, 41] introduced type-based/conditional \(\mathsf {PRE}\), which allows re-encryption of ciphertexts at the proxy only if a specific condition (e.g., a time period) is satisfied by the ciphertext. Furthermore, \(\mathsf {PRE}\) with temporary delegations was proposed by Ateniese et al. [4, 5] and improved by Libert and Vernaud (LV) [34]. All those approaches yield a weak form of forward secrecy. Notably, the LV schemes provide fixed public parameters and non-interactivity with the delegatee as well. However, in contrast to our approach, LV and Tang et al. require at least to update the re-encryption keys for each time period with the help of the delegator (i.e., one message per time period from the delegator to the proxy) and also do not allow for exponentially many time periods, which do not suit our (stronger) forward-secret scenario.
Concurrent work on PRE. There is a considerable amount of very recent independent and concurrent work on different aspects of \(\mathsf {PRE}\) and its applications [8, 20, 23, 35]. The works in [8, 23, 35] are only related in that they also deal with various aspects of \(\mathsf {PRE}\), but not fs-\(\mathsf {PRE}\). Those aspects are however unrelated to the work presented in this paper. In contrast, the work presented in [20] is related to one aspect of our work. It formalizes a security property for conventional \(\mathsf {PRE}\), which can be seen as a special case of our fs-\(\mathsf {PRE} ^+\) notion which we introduce in context of fs-\(\mathsf {PRE}\). More precisely, our notion generalizes the notion of [20] and implies it if we fix the numbers of time periods to \(n=1\).
Outline. After discussing preliminaries in Section 2, we define fs-\(\mathsf {PRE}\) in Section 3, discuss the gap in previous models and also briefly discuss its consequences to conventional \(\mathsf {PRE}\). We then give the first construction of a fs-\(\mathsf {PRE}\) scheme from binary tree encryption in Section 4. We also show a separation result for the weaker fs-\(\mathsf {PRE} ^-\) (resembling existing \(\mathsf {PRE}\) models) and our stronger notion fs-\(\mathsf {PRE} ^+\).
2 Preliminaries
For \(n\in \mathbb {N} \), let \([n]:=\{1,\ldots ,n\}\) and let \(k \in \mathbb {N} \) be the security parameter. For an algorithm \(A \), let \(y\leftarrow A (1^k,x)\) be the process of running \(A \), on input \(1^k \) and x, with access to uniformly random coins and assigning the result to y. We assume that all algorithms take \(1^k \) as input and we will sometimes not make this explicit in the following. To make the random coins r explicit, we write \(A (1^k,x;r)\). An algorithm \(A \) is probabilistic polynomial time (PPT) if its running time is polynomially bounded in \(k\). A function f is negligible if \(\forall c\exists k _0\forall k \ge k _0:|f(k)|\le 1/k ^c\). For binary trees, we denote the root node with \(\varepsilon \) and all other nodes are encoded as binary strings, i.e., for a node w we denote child nodes as w0 and w1.
Homomorphic public-key encryption. A \(\mathcal F\)-homomorphic public key encryption (\(\mathsf {HPKE}\)) scheme is a public-key encryption (\(\mathsf {PKE}\)) scheme that is homomorphic with respect to a class of functions \(\mathcal F\), i.e., given a sequence of ciphertexts to messages \((M _i)_{i \in [n]}\) one can evaluate a function \(f:\mathcal {M} ^n\rightarrow \mathcal {M} \in \mathcal F\) on the ciphertexts such that the resulting ciphertext decrypts to \(f(M _1, \ldots , M _n)\).
Definition 1
(( \(\mathbf {\mathcal {F}}\) -) \(\mathbf {\mathsf {HPKE}}\) ). A \(\mathcal {F}\)-homomorphic public key encryption (\(\mathcal {F}\)-\(\mathsf {HPKE}\) or \(\mathsf {HPKE}\) for short) scheme with message space \(\mathcal {M}\), ciphertext space \(\mathcal {C}\) and a function family \(\mathcal {F}\) consists of the PPT algorithms \((\mathsf {Gen},\mathsf {Enc},\mathsf {Dec},\mathsf {Eval})\):
- \(\mathsf {Gen} (1^k)\! :\) :
-
On input security parameter \(k\), outputs public and secret keys \((\mathsf {pk},\mathsf {sk})\).
- \(\mathsf {Enc} (\mathsf {pk},M)\! :\) :
-
On input a public key \(\mathsf {pk}\), and a message \(M \in \mathcal {M} \), outputs a ciphertext \(C \in \mathcal {C} \).
- \(\mathsf {Dec} (\mathsf {sk},C)\! :\) :
-
On input a secret key \(\mathsf {sk}\), and ciphertext \(C\), outputs \(M \in \mathcal {M} \cup \{\bot \}\).
- \(\mathsf {Eval} (f, (C _i)_{i \in [n]})\! :\) :
-
On input a function \(f : \mathcal {M} ^n \rightarrow \mathcal {M} \in \mathcal {F}\), a sequence of ciphertexts \((C _i)_{i\in [n]}\) encrypted under the same public key, outputs \(C \).
In addition to the standard and folklore correctness definition for public-key encryption (\(\mathsf {PKE}\)), we further require for \(\mathsf {HPKE}\) that for all security parameters \(k \in \mathbb {N} \), all key pairs \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {Gen} (1^k)\), all functions \(f : \mathcal {M} ^n \rightarrow \mathcal {M} \in \mathcal {F}\), all message sequences \((M _i)_{i \in [n]}\) it holds that \(\mathsf {Dec} (\mathsf {sk}, \mathsf {Eval} (f, (\mathsf {Enc} (\mathsf {pk}, M _i))_{i \in [n]})) = f(M _1, \ldots , M _n)\). We are particularly interested in the case where \(\mathcal {M} \) is a group and \(\mathcal {F}\) is the set of all linear functions on products of \(\mathcal {M} \). In that case, we call the \(\mathsf {HPKE}\) scheme linearly homomorphic. For a \(\mathsf {HPKE}\), we require conventional IND-CPA security as with \(\mathsf {PKE}\) schemes and recall an efficient instantiation of a linearly homomorphic scheme, i.e., linear ElGamal [11], in the full version.
Proxy re-encryption. Subsequently, we define proxy re-encryption and defer a formal treatment of security to Sect. 3.
Definition 2
 A proxy re-encryption (\(\mathsf {PRE}\)) scheme with message space \(\mathcal {M}\) consists of the PPT algorithms \((\mathsf {Setup}, \mathsf {Gen}, \mathbf {\mathsf {Enc}}, \mathbf {\mathsf {Dec}},\mathsf {ReGen},\mathsf {ReEnc})\) where \(\mathbf {\mathsf {Enc}}= (\mathsf {Enc} ^{(j)})_{j \in [2]}\) and \(\mathbf {\mathsf {Dec}}= (\mathsf {Dec} ^{(j)})_{j \in [2]}\). For \(j \in [2]\), they are defined as follows.
A proxy re-encryption (\(\mathsf {PRE}\)) scheme with message space \(\mathcal {M}\) consists of the PPT algorithms \((\mathsf {Setup}, \mathsf {Gen}, \mathbf {\mathsf {Enc}}, \mathbf {\mathsf {Dec}},\mathsf {ReGen},\mathsf {ReEnc})\) where \(\mathbf {\mathsf {Enc}}= (\mathsf {Enc} ^{(j)})_{j \in [2]}\) and \(\mathbf {\mathsf {Dec}}= (\mathsf {Dec} ^{(j)})_{j \in [2]}\). For \(j \in [2]\), they are defined as follows.
- \(\mathsf {Setup} (1^k)\! :\) :
-
On input security parameter \(k\), outputs public parameters \(\mathsf {pp}\).
- \(\mathsf {Gen} (\mathsf {pp})\! :\) :
-
On input public parameters \(\mathsf {pp}\), outputs public and secret keys \((\mathsf {pk},\mathsf {sk})\).
- \(\mathsf {Enc} ^{(j)}(\mathsf {pk},M)\! :\) :
-
On input a public key \(\mathsf {pk}\), and a message \(M \in \mathcal {M} \) outputs a level j ciphertext \(C\).
- \(\mathsf {Dec} ^{(j)}(\mathsf {sk},C)\! :\) :
-
On input a secret key \(\mathsf {sk} \), and level j ciphertext \(C\), outputs \(M \in \mathcal {M} \cup \{\bot \}\).
- \(\mathsf {ReGen} (\mathsf {sk} _{A}, \mathsf {pk} _B)\! :\) :
-
On input a secret key \(\mathsf {sk} _{A}\) and a public key \(\mathsf {pk} _B\) for B, outputs a re-encryption \(\mathsf {rk} _{A \rightarrow B}\).
- \(\mathsf {ReEnc} (\mathsf {rk} _{A \rightarrow B}, C _A)\! :\) :
-
On input a re-encryption key \(\mathsf {rk} _{A \rightarrow B}\), and a ciphertext \(C _A\) for user A, outputs a ciphertext \(C _B\) for user B.
Binary tree encryption. Binary tree encryption (\(\mathsf {BTE}\)) [15] is a relaxed version of hierarchical identity-based encryption (\(\mathsf {HIBE}\)) [25]. Similar to a \(\mathsf {HIBE}\) scheme, a \(\mathsf {BTE}\) scheme has a (master) public key associated to a binary tree where each node in the tree has a corresponding secret key. To encrypt a message for some node, one uses both the public key and the name of the target node. Using the node’s secret key, the resulting ciphertext can then be decrypted. Additionally, the secret key of a node can be used to derive the secret keys of its child nodes.
In contrast to \(\mathsf {BTE}\) defined in [15], we make the part of the secret key used to perform the key derivation explicit, i.e., we will have secret keys for the decryption and derivation keys to derive secret keys. In case, an instantiation does not support a clear distinction, it is always possible to assume that the derivation key is empty and everything is contained in the secret key.
Definition 3
A binary tree encryption (\(\mathsf {BTE}\)) scheme with message space \(\mathcal {M}\) consists of the PPT algorithms \((\mathsf {Gen},\mathsf {Evo},\mathsf {Enc},\mathsf {Dec})\) as follows:
- \(\mathsf {Gen} (1^k, \ell )\! :\) :
-
On input security parameter \(k\) and depth of the tree \(\ell \), outputs public, secret, and derivation keys \((\mathsf {pk}, \mathsf {sk} ^{(\varepsilon )}, \mathsf {dk} ^{(\varepsilon )})\).
- \(\mathsf {Der} (\mathsf {sk} ^{(w)}, \mathsf {dk} ^{(w)})\! :\) :
-
On input secret key \(\mathsf {sk} ^{(w)}\) and derivation key \(\mathsf {dk} ^{(w)}\), for node \(w\in \{ 0, 1 \}^{< \ell }\), outputs secret keys \(\mathsf {sk} ^{(w0)}, \mathsf {sk} ^{(w1)}\) and derivation keys \(\mathsf {dk} ^{(w0)},\mathsf {dk} ^{(w1)}\) for the two children of w.
- \(\mathsf {Enc} (\mathsf {pk},M,w)\! :\) :
-
On input a public key \(\mathsf {pk}\), a message \(M \in \mathcal {M} \), and node \(w \in \{0, 1\}^{\le \ell }\), outputs a ciphertext \(C\).
- \(\mathsf {Dec} (\mathsf {sk} ^{(w)},C)\! :\) :
-
On input a secret key \(\mathsf {sk} ^{(w)}\), for node \(w\in \{0,1\}^{\le \ell }\), and ciphertext \(C\), outputs \(M \in \mathcal {M} \cup \{\bot \}\).
For correctness, we require that for all security parameters \(k \in \mathbb {N} \), all depths \(\ell \in \mathbb {N} \), all key pairs \((\mathsf {pk},(\mathsf {sk} ^{(\varepsilon )}, \mathsf {ek} ^{(\varepsilon )}))\) generated by \(\mathsf {Gen} (1^k, \ell )\), any node \(w \in \{ 0, 1 \}^{\le \ell }\), any derived key \(\mathsf {sk} ^{(w)}\) derived using \(\mathsf {Der} \) from \((\mathsf {sk} ^{(\varepsilon )}, \mathsf {dk} ^{(\varepsilon )})\), and all messages \(M \in \mathcal {M} \), it holds that \( \mathsf {Dec} (\mathsf {sk} ^{(w)}, \mathsf {Enc} (\mathsf {pk}, M, w)) = M. \)
The indistinguishability against selective node, chosen plaintext attacks (IND-SN-CPA) is a generalization of the standard IND-CPA security notion of \(\mathsf {PKE}\) schemes. Essentially, the security notion requires the adversary to commit to the node to be attacked in advance. The adversary gets access to all secret keys except the secret keys for all nodes that are on the path from the root node to the targeted node.

Definition 4
(IND-SN-CPA). For a polynomially bounded function \(\ell \), a PPT adversary \(A\), we define the advantage function in the sense of IND-SN-CPA as
If for all \(\ell \), and any \(A \) there exists a negligible function \(\varepsilon \) such that \(\mathsf {Adv}^{\mathsf {ind-sn-cpa}}_{\mathsf {BTE},A}(1^k,\ell (k)) < \varepsilon (k)\), then a \(\mathsf {BTE}\) scheme is IND-SN-CPA secure.
The CHK Compiler. The technique of Canetti et al. [15] can be summarized as follows. To build a forward-secret \(\mathsf {PKE}\) scheme with n periods, one uses a \(\mathsf {BTE}\) of depth \(\ell \) such that \(n < 2^{\ell + 1}\). Associate each period with a node of the tree and write \(w^i\) to denote the node for period i. The node for period 0 is the root node, i.e. \(w^0 = \varepsilon \). If \(w^i\) is an internal node, then set \(w^{i+1} = w^i 0\). Otherwise, if \(w^i\) is a leaf node and \(i < N - 1\), then set \(w^{i+1} = w'1\) where \(w'\) is the longest string such that \(w'0\) is a prefix of \(w^i\). The public key is simply the public key of the \(\mathsf {BTE}\) scheme. The secret key for period i consists of the secret key for node \(w^i\).
3 Security of (Forward-Secret) Proxy Re-encryption
Proxy re-encryption (\(\mathsf {PRE}\)) schemes can exhibit several important properties. In the following, we focus on the most common \(\mathsf {PRE}\) properties in the cryptographic literature, i.e., uni-directionality (Alice is able to delegate decryption rights to Bob but not from Bob to Alice), non-interactivity (Alice can generate delegation key material without interacting with Bob), and collusion-safeness (even if Bob and other delegatees are colluding with the proxy, they cannot extract Alice’ full secret key). Moreover, we consider \(\mathsf {PRE}\) schemes that only allow a single hop, i.e., a ciphertext can be re-encrypted only a single time in contrast to multiple times in a row (multi-hop). Latter can be problematic due to unwanted transitivity.
In this work, we examine a further property of \(\mathsf {PRE}\) schemes, namely the property of forward secrecy and propose the first uni-directional, non-interactive, collusion-safe, single hop, and forward-secret \(\mathsf {PRE}\) scheme (dubbed fs-\(\mathsf {PRE}\)) in the standard model from generic assumptions. Subsequently, in Sect. 3.1, we present the formal model for fs-\(\mathsf {PRE}\), while in Sect. 3.3 we discuss the relation and application of our stronger model to the conventional (i.e., plain) \(\mathsf {PRE}\) security model.
3.1 Syntax of Forward-Secret Proxy Re-encryption
To realize forward-secure \(\mathsf {PRE}\) (fs-\(\mathsf {PRE}\)), we lift the definitions and security models of uni-directional, single-hop, non-interactive, and collusion-safe \(\mathsf {PRE}\) to a setting where we can have several periods. Thereby, we allow re-encryptions in every period such that re-encryption keys—in the same way as secret keys—are bound to a period. Furthermore, we align our \(\mathsf {PRE}\) definitions with Ateniese et al. as well as Libert and Vergnaud [4, 5, 33] such that if we only have a single period, then they are equivalent to the definitions for plain \(\mathsf {PRE}\) in [5, 33].Footnote 11
Definition 5
 A forward-secure proxy re-encryption (fs-\(\mathsf {PRE}\)) scheme with message space \(\mathcal {M}\) consists of the PPT algorithms \((\mathsf {Setup}, \mathsf {Gen},\mathsf {Evo}, \mathbf {\mathsf {Enc}}, \mathbf {\mathsf {Dec}},\mathsf {ReGen},\mathsf {ReEvo},\mathsf {ReEnc})\) where \(\mathbf {\mathsf {Enc}}= (\mathsf {Enc} ^{(j)})_{j \in [2]}\) and \(\mathbf {\mathsf {Dec}}= (\mathsf {Dec} ^{(j)})_{j \in [2]}\) for levels \(j \in [2]\). We denote level-2 ciphertext as re-encryptable ciphertexts, whereas level-1 ciphertexts are not re-encryptable.
A forward-secure proxy re-encryption (fs-\(\mathsf {PRE}\)) scheme with message space \(\mathcal {M}\) consists of the PPT algorithms \((\mathsf {Setup}, \mathsf {Gen},\mathsf {Evo}, \mathbf {\mathsf {Enc}}, \mathbf {\mathsf {Dec}},\mathsf {ReGen},\mathsf {ReEvo},\mathsf {ReEnc})\) where \(\mathbf {\mathsf {Enc}}= (\mathsf {Enc} ^{(j)})_{j \in [2]}\) and \(\mathbf {\mathsf {Dec}}= (\mathsf {Dec} ^{(j)})_{j \in [2]}\) for levels \(j \in [2]\). We denote level-2 ciphertext as re-encryptable ciphertexts, whereas level-1 ciphertexts are not re-encryptable.
- \(\mathsf {Setup} (1^k)\! :\) :
-
On input security parameter \(k\), outputs public parameters \(\mathsf {pp}\).
- \(\mathsf {Gen} (\mathsf {pp}, n)\! :\) :
-
On input public parameters \(\mathsf {pp}\), and number of periods \(n \in \mathbb {N} \), outputs public and secret keys \((\mathsf {pk},(\mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}))\).
- \(\mathsf {Evo} (\mathsf {sk} ^{(i)}, \mathsf {ek} ^{(i)})\! :\) :
-
On input secret key \(\mathsf {sk} ^{(i)}\) and evolution key \(\mathsf {ek} ^{(i)}\) for period \(i\in \{0,\ldots ,n-2\}\), outputs a secret key \(\mathsf {sk} ^{(i+1)}\) and evolution key \(\mathsf {ek} ^{(i+1)}\) for period \(i+1\).
- \(\mathsf {Enc} ^{(j)}(\mathsf {pk},M,i)\! :\) :
-
On input a public key \(\mathsf {pk}\), a message \(M \in \mathcal {M} \), and period \(i\in \{0,\ldots ,n-1\}\), outputs a level-j ciphertext \(C\).
- \(\mathsf {Dec} ^{(j)}(\mathsf {sk} ^{(i)},C)\! :\) :
-
On input a secret key \(\mathsf {sk} ^{(i)}\), for period \(i\in \{0,\ldots ,n-1\}\), and level-j ciphertext \(C\), outputs \(M \in \mathcal {M} \cup \{\bot \}\).
- \(\mathsf {ReGen} (\mathsf {sk} _{A}^{(i)}, \mathsf {ek} _{A}^{(i)}, \mathsf {pk} _B)\! :\) :
-
On input a secret key \(\mathsf {sk} _{A}^{(i)}\) and a evolution key \(\mathsf {ek} _{A}^{(i)}\) (or \(\bot \)) for A and period \(i\in \{0,\ldots ,n-1\}\), and a public key \(\mathsf {pk} _B\) for B, outputs a re-encryption \(\mathsf {rk} _{A \rightarrow B}^{(i)}\) and re-encryption-evolution key \(\mathsf {rek} _{A \rightarrow B}^{(i)}\) (or \(\bot \)).
- \(\mathsf {ReEvo} (\mathsf {rk} _{A \rightarrow B}^{(i)}, \mathsf {rek} _{A \rightarrow B}^{(i)})\! :\) :
-
On input a re-encryption key \(\mathsf {rk} _{A \rightarrow B}^{(i)}\), and a re-encryption-evolution key \(\mathsf {rek} _{A \rightarrow B}^{(i)}\) for period \(i\in \{0,\ldots ,n-2\}\), outputs a re-encryption key \(\mathsf {rk} _{A \rightarrow B}^{(i+1)}\) and re-encryption evolution key \(\mathsf {rek} _{A \rightarrow B}^{(i+1)}\) for the period \(i+1\).
- \(\mathsf {ReEnc} (\mathsf {rk} _{A \rightarrow B}^{(i)}, C _A)\! :\) :
-
On input a re-encryption key \(\mathsf {rk} _{A \rightarrow B}^{(i)}\), and a (level-2) ciphertext \(C _A\) for user A, outputs a (level-1) ciphertext \(C _B\) for user B.
Correctness. For correctness, we basically require on the one hand that every ciphertext encrypted for some period i can be decrypted with the respective secret key from period i. On the other hand—when also considering re-encryptable and re-encrypted ciphertexts—we require that level-2 ciphertexts encrypted for period i can be re-encrypted with a suitable re-encryption key for the same period and then decrypted using the (delegatee’s) respective secret key for period i. More formally, for all security parameters \(k \in \mathbb {N} \), all public parameters \(\mathsf {pp} \leftarrow \mathsf {Setup} (1^k)\), any number of periods \(n \in \mathbb {N} \) and users \(U\in \mathbb {N} \), all key tuples \((\mathsf {pk} _u,\mathsf {sk} _{u}^{(0)}, \mathsf {ek} _{u}^{(0)})_{u \in [U]}\) generated by \(\mathsf {Gen} (1^k, n)\), any period \(i \in \{0,\ldots ,n-1\}\), for any \(u \in [U]\), any evolved key \(\mathsf {sk} _{u}^{(i+1)}\) generated by \(\mathsf {Evo} (\mathsf {sk} _{u}^{(i)})\), for all \(u' \in [U], u \ne u'\), any (potentially evolved) re-encryption and re-encryption-evolution keys \(\mathsf {rk} _{u \rightarrow u'}^{(i)}\) and \(\mathsf {rek} _{u \rightarrow u'}^{(i)}\), respectively, for period i generated using \(\mathsf {ReGen} \) from (potentially evolved) secret and evolution keys as well as the target public key, and all messages \(M \in \mathcal {M} \), it holds that
3.2 Security of Forward-Secret Proxy Re-encryption
The security notions for fs-\(\mathsf {PRE}\) are heavily inspired by the security notions of (plain) \(\mathsf {PRE}\) [4, 5, 33] and forward-secret \(\mathsf {PKE}\) [15]. We will discuss multiple notions, combine them carefully, and introduce forward-secret indistinguishably under chosen-plaintext attacks for level-1 and level-2 ciphertexts (termed fs-IND-CPA-1 and fs-IND-CPA-2, respectively) which we argue to be reasonable notions in our setting. Additionally, we define a new (stronger) variant of indistinguishably-under-chosen-plaintext-attacks security for fs-\(\mathsf {PRE}\) (dubbed fs-RIND-CPA) that focuses on malicious users in the face of honest proxies. In particular, the latter strengthen the folklore \(\mathsf {PRE}\) security notion.
For all experiments defined in this section, the environment keeps initially empty lists of dishonest (\(\mathtt {DU} \)) and honest users (\(\mathtt {HU} \)). The oracles are defined as follows:
- \(\mathsf {Gen} ^{(h)}(\mathsf {pp}, n)\! :\) :
-
Run \((\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \leftarrow \mathsf {Gen} (\mathsf {pp}, n)\), set \(\mathtt {HU} \leftarrow \mathtt {HU} \cup \{ (\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \}\), and return \(\mathsf {pk} \).
- \(\mathsf {Gen} ^{(d)}(\mathsf {pp}, n)\! :\) :
-
Run \((\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \leftarrow \mathsf {Gen} (\mathsf {pp}, n)\), set \(\mathtt {DU} \leftarrow \mathtt {DU} \cup \{ (\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \}\), and return \((\mathsf {pk}, \mathsf {sk}, \mathsf {ek})\).
- \(\mathsf {ReGen} ^{(h)}(j, \mathsf {pk} _u, \mathsf {pk})\! :\) :
-
On input a period j, a public key \(\mathsf {pk} _u\) and a public key \(\mathsf {pk} \), abort if \((\mathsf {pk} _u,\cdot ,\cdot ) \not \in \mathtt {HU} \). Otherwise, look up \(\mathsf {sk} _u^{(0)}\) and \(\mathsf {ek} _u^{(0)}\) corresponding to \(\mathsf {pk} _u\) from \(\mathtt {HU}\). If \(j>0\) set \((\mathsf {sk} _u^{(i)}, \mathsf {ek} _u^{(i)}) \leftarrow \mathsf {Evo} (\mathsf {sk} _u^{(i-1)}, \mathsf {ek} _u^{(i-1)})\) for \(i \in [j]\). Return \(\mathsf {ReGen} (\mathsf {sk} _u^{(j)}, \mathsf {ek} _u^{(j)}, \mathsf {pk})\).
- \(\mathsf {ReGen} ^{(h')}(j, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}, \mathsf {pk} _u)\! :\) :
-
On input a period j, secret key \(\mathsf {sk} ^{(0)}\), evolution key \(\mathsf {ek} ^{(0)}\), and a public key \(\mathsf {pk} _u\), abort if \((\mathsf {pk} _u,\cdot ,\cdot ) \not \in \mathtt {HU} \). Otherwise, if \(j>0\) set \((\mathsf {sk} ^{(i)}, \mathsf {ek} ^{(i)}) \leftarrow \mathsf {Evo} (\mathsf {sk} ^{(i-1)}, \mathsf {ek} ^{(i-1)})\) for \(i \in [j]\). Return \(\mathsf {ReGen} (\mathsf {sk} ^{(j)}, \mathsf {ek} ^{(j)}, \mathsf {pk} _u)\).
- \(\mathsf {ReGen} ^{(d)}(j, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}, \mathsf {pk} _d)\! :\) :
-
On input a period j, secret key \(\mathsf {sk} ^{(0)}\), evolution key \(\mathsf {ek} ^{(0)}\), and a public key \(\mathsf {pk} _d\), abort if \((\mathsf {pk} _d,\cdot ,\cdot ) \not \in \mathtt {DU} \). Otherwise, if \(j>0\) set \((\mathsf {sk} ^{(i)}, \mathsf {ek} ^{(i)}) \leftarrow \mathsf {Evo} (\mathsf {sk} ^{(i-1)}, \mathsf {ek} ^{(i-1)})\) for \(i \in [j]\). Return \(\mathsf {ReGen} (\mathsf {sk} ^{(j)}, \mathsf {ek} ^{(j)}, \mathsf {pk} _d)\).
fs-IND-CPA-i security. We start with the definition of fs-IND-CPA-1 and fs-IND-CPA-2 security for fs-\(\mathsf {PRE}\). Inspired by the work on forward secrecy due to Canetti et al. [15], our experiments lift standard \(\mathsf {PRE}\) security notions as defined in Ateniese et al. [4] (AFGH) to the forward-secrecy setting. More concretely, after the selection of a target period \(j^*\) by the adversary A, A gets access to the secret and the evolution key (\(\mathsf {sk} ^{(j^*)},\mathsf {ek} ^{(j^*)}\)) of the target period \(j^*\), while the challenge ciphertext for A-chosen message \(M _b\) is generated for period \(j^*-1\), for uniform \(b\leftarrow \{0,1\}\). Eventually, A outputs a guess on b. We say A is valid if A only outputs equal-length messages \(|M _0|=|M _1|\) and \(1\le j^*\le n\).
Furthermore, we adapted the AFGH security experiment such that A has access to re-encryption and re-encryption-evolution keys for period \(j^*-1\). Analogously to previous work on \(\mathsf {PRE}\), we present two separate notions for level-1 and level-2 ciphertexts. The corresponding security experiments are given in Experiment 2 and Experiment 3. The only difference in Experiment 2 is that for level-1 ciphertexts, i.e., the ones which can no longer be re-encrypted, the adversary gets access to more re-encryption and re-encryption-evolution keys (obviously, the challenge ciphertext in that experiment is a level-1 ciphertext).


Definition 6
(fs-IND-CPA-i). For a polynomially bounded function \(n(\cdot )>1\), a PPT adversary \(A\), we define the advantage function for \(A\) in the sense of fs-IND-CPA-i for level-i ciphertexts as
A fs-\(\mathsf {PRE}\) scheme is fs-IND-CPA-i secure if for all polynomially bounded \(n(\cdot )>1\) and any valid PPT \(A\) there exists a negligible function \(\varepsilon \) such that \(\mathsf {Adv}^{\mathsf {fs-ind-cpa-i}}_{fs-\mathsf {PRE},A}(1^k, n(k)) < \varepsilon (k)\), where \(\mathsf {Exp}^{\mathsf {fs-ind-cpa-i}}_{fs-\mathsf {PRE},A}\), for all \(i\in [2]\), are defined in Experiment 2 and Experiment 3, respectively.
Master-secret security. As discussed in [33], the security notion for level-1 (i.e., non re-encryptable) ciphertexts already implies classical master-secret security notion for \(\mathsf {PRE}\) [4].Footnote 12 However, this must not be the case in the forward-secret setting. To formally close this gap, we give a trivial lemma (cf. Lemma 1) which states that fs-IND-CPA-1 implies master-secret security in the sense of Experiment 4 in the forward-secrecy setting. Essentially, master-secret security ensures collusion safeness such that re-encryption keys in period j do not leak the secret key corresponding to level-1 ciphertexts which can not be re-encrypted in period \(j-1\). In Experiment 4, we lift master-secret security in the classical \(\mathsf {PRE}\) sense to the forward-secret setting. In the experiment, the adversary A selects an target period \(j^*\) and receives the secret and evolution keys \((\mathsf {sk} ^{(j^*)},\mathsf {ek} ^{(j^*)})\) for the target period in return. Within the experiment, A has access to several oracles, e.g., to obtain re-encryption and re-encryption-evolution keys for period \(j^*\). Eventually, A outputs secret and evolutions keys \((\mathsf {sk} ^*,\mathsf {ek} ^*)\) and the experiment returns 1 (i.e., A wins) if \((\mathsf {sk} ^*,\mathsf {ek} ^*)=(\mathsf {sk} ^{(j^*-1)},\mathsf {ek} ^{(j^*-1)})\). We say A is valid if A only outputs \(1\le j^*\le n\).

Definition 7
(fs-master-secret security). For a polynomially bounded function \(n(\cdot )>1\) and a PPT adversary \(A\), we define the advantage function for \(A\) in the sense of fs-master-secret security as
A fs-\(\mathsf {PRE}\) scheme is fs-master-secret secure if for all polynomially bounded \(n(\cdot )>1\) and any valid PPT \(A\) there exists a negligible function \(\varepsilon \) such that \(\mathsf {Adv}^{\mathsf {fs-msk}}_{fs-\mathsf {PRE},A}(1^k, n(k)) < \varepsilon (k)\), where \(\mathsf {Exp}^{\mathsf {fs-msk}}_{fs-\mathsf {PRE},A}\) is defined in Experiment 4.
We now show that this notion in the sense of Definition 7 is trivially implied by fs-IND-CPA-1 security for fs-\(\mathsf {PRE}\) in the sense of Definition 6.
Lemma 1
If a fs-\(\mathsf {PRE}\) scheme is fs-IND-CPA-1 secure in the sense of Definition 6, then the same fs-\(\mathsf {PRE}\) scheme is fs-master-secret secure in the sense of Definition 7.
Proof sketch
It is trivial to see that any successful PPT adversary on the fs-master-secret security of a fs-\(\mathsf {PRE}\) scheme can be transformed into a PPT adversary on the fs-IND-CPA-1 security of that fs-\(\mathsf {PRE}\) scheme. (Essentially, any PPT adversary that is able to gain access to the secret key of the prior period can trivially distinguish ciphertexts for the same period.)
 A problem with the notion of standard (i.e., IND-CPA and master secret) security for (plain) \(\mathsf {PRE}\) and also our fs-\(\mathsf {PRE}\) notions so far is that the secret keys used for level-1 (i.e., non re-encryptable) and level-2 (i.e., re-encryptable) ciphertexts can be independent. Consequently, although ciphertexts on both levels can be shown to be indistinguishable, this does not rule out the possibility that ciphertexts on level-2 reveal the respective level-2 secret key of the sender to an legitimate receiver. This is exactly the reason for the gap in the plain \(\mathsf {PRE}\) model which allows to leak a “level-2 secret key” once a re-encryption has been performed while all security properties are still satisfied (we provide an example for such a scheme in Sect. 4.4). In particular, this allows the receiver to potentially decrypt any level-2 ciphertext. We provide a solution in form of a stronger security notion which we term fs-RIND-CPA security in the following.
A problem with the notion of standard (i.e., IND-CPA and master secret) security for (plain) \(\mathsf {PRE}\) and also our fs-\(\mathsf {PRE}\) notions so far is that the secret keys used for level-1 (i.e., non re-encryptable) and level-2 (i.e., re-encryptable) ciphertexts can be independent. Consequently, although ciphertexts on both levels can be shown to be indistinguishable, this does not rule out the possibility that ciphertexts on level-2 reveal the respective level-2 secret key of the sender to an legitimate receiver. This is exactly the reason for the gap in the plain \(\mathsf {PRE}\) model which allows to leak a “level-2 secret key” once a re-encryption has been performed while all security properties are still satisfied (we provide an example for such a scheme in Sect. 4.4). In particular, this allows the receiver to potentially decrypt any level-2 ciphertext. We provide a solution in form of a stronger security notion which we term fs-RIND-CPA security in the following.
fs-RIND-CPA security. We observe that existing \(\mathsf {PRE}\) notions only consider that (1) as long as the users are honest, the proxy learns nothing about any plaintext, and (2) if proxies and users collude they do not learn anything about the ciphertexts which are not intended to be re-encrypted. We go a step further and consider malicious users in the face of an honest proxy in the forward-secret and, hence, also in the plain \(\mathsf {PRE}\) sense. That is, we want to enforce that a malicious user can only read the ciphertexts which were actually re-encrypted by the proxy and can not tell anything about the ciphertexts which can potentially be re-encrypted. We capture this via the notion of fs-RIND-CPA security. In this scenario, an adversary receives re-encrypted ciphertexts generated by an honest proxy, that it is able to decrypt. Nevertheless, for all other level-2 ciphertexts, the adversary should still be unable to recover the plaintext. In Experiment 5, we model this notion where the adversary gets access to a \(\mathsf {ReEnc} \)-oracle which is in possession of the re-encryption key from the target user to the adversary. We say A is valid if A only outputs \(1\le j^*\le n\) and equal length messages \(|M _0|=|M _1|\).

Definition 8
(fs-RIND-CPA). For a polynomially bounded function \(n(\cdot )\) and a PPT adversary \(A\), we define the advantage function for \(A\) in the sense of fs-RIND-CPA as
A fs-\(\mathsf {PRE}\) scheme is fs-RIND-CPA if for all polynomially bounded \(n(\cdot )\) and any valid PPT \(A\) there exists a negligible function \(\varepsilon \) such that \(\mathsf {Adv}^{\mathsf {fs-rind-cpa}}_{fs-\mathsf {PRE},A} (1^k, n(k)) < \varepsilon (k)\), where \(\mathsf {Exp}^{\mathsf {fs-rind-cpa}}_{fs-\mathsf {PRE},A}\) is defined in Experiment 5.
We distinguish fs-\(\mathsf {PRE}\) schemes based on this last notion:
Definition 9
(fs- \({\mathsf {PRE} ^{-}}\) -security). If a fs-\(\mathsf {PRE}\) scheme is fs-IND-CPA-1 and fs-IND-CPA-2 secure, then we say this fs-\(\mathsf {PRE}\) scheme is fs-\(\mathsf {PRE} ^{-}\)-secure.
Definition 10
(fs- \({\mathsf {PRE} ^{+}}\) -security). If a fs-\(\mathsf {PRE}\) scheme is fs-IND-CPA-1, fs-IND-CPA-2, and fs-RIND-CPA secure, then we say this fs-\(\mathsf {PRE}\) scheme is fs-\(\mathsf {PRE} ^{+}\)-secure.
3.3 Stronger Security for Proxy Re-encryption
To conclude the discussion of the security model of fs-\(\mathsf {PRE}\) schemes, we first observe that it is interesting to consider the notion of fs-RIND-CPA security in the classical setting for \(\mathsf {PRE}\), i.e., Experiment 5 with fixed \(n = 1\) and no call to the \(\mathsf Evo\) algorithm. The notion again ensures involvement of the proxy for the re-encryption of every ciphertext, and can, thus, enforce that malicious users cannot learn anything beyond the explicitly re-encrypted ciphertexts. This immediately leads to a stronger security model for classical \(\mathsf {PRE}\) (given in the full version), which we denote as \(\mathsf {PRE} ^+\). In particular, it extends the classical model [4], dubbed \(\mathsf {PRE} ^-\), which covers standard (IND-CPA) and master-secret security definitions, by our fs-RIND-CPA security notion ported to the \(\mathsf {PRE}\) setting. As our fs-IND-CPA-i notions for fs-\(\mathsf {PRE}\) are generalizations of the established standard security notions of \(\mathsf {PRE}\) as defined in [4], we consequently obtain a \(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme from any fs-\(\mathsf {PRE} ^+\)-secure fs-\(\mathsf {PRE}\) scheme. We formalize this observation via Lemma 2.
Lemma 2
Any fs-\(\mathsf {PRE} ^+\)-secure fs-\(\mathsf {PRE}\) scheme yields a \(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme.
In the full version, we formally prove this lemma. This immediately gives us a construction for a \(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme.
Corollary 1
Scheme 3 when limited to a single time period, i.e., setting \(n=1\), represents a \(\mathsf {PRE} ^+\)-secure \(\mathsf {PRE}\) scheme.
4 Constructing Fs-\(\mathsf {PRE}\) from Binary Tree Encryption
In this section we present our construction of fs-\(\mathsf {PRE} \) which is based on \(\mathsf {BTE} \)s. Along the way, we introduce the notion of forward-secret delegatable \(\mathsf {PKE}\) (fs-\(\mathsf {DPKE} \)) as intermediate step. Such a fs-\(\mathsf {DPKE} \) scheme then directly gives us a first fs-\(\mathsf {PRE} \) satisfying fs-\(\mathsf {PRE} ^-\) security. To extend our construction to satisfy the stronger fs-\(\mathsf {PRE} ^+\) notion generically, we require a relatively mild homomorphic property of the fs-\(\mathsf {DPKE} \). This property is in particular satisfied by our fs-\(\mathsf {DPKE} \) instantiation, which yields the first fs-\(\mathsf {PRE} \) scheme with strong security.
4.1 Forward-Secret Delegatable Public-Key Encryption
We now formalize fs-\(\mathsf {DPKE} \). In such a scheme decryption rights within a public-key encryption scheme can be delegated from a delegator to a delegatee and secret keys of delegators can be evolved so that a secret key for some period \(e_i\) is no longer useful to decrypt ciphertexts of prior periods \(e_j\) with \(j<i\).
Definition 11
 A forward-secret delegatable \(\mathsf {PKE}\) (fs-\(\mathsf {DPKE} \)) scheme with message space \(\mathcal {M} \) consists of the PPT algorithms \((\mathsf {Setup},\mathsf {Gen},\mathsf {Evo},\mathsf {Del},\mathsf {Enc},\mathsf {Dec},\mathsf {DelEvo},\mathsf {DelDec})\) as follows:
A forward-secret delegatable \(\mathsf {PKE}\) (fs-\(\mathsf {DPKE} \)) scheme with message space \(\mathcal {M} \) consists of the PPT algorithms \((\mathsf {Setup},\mathsf {Gen},\mathsf {Evo},\mathsf {Del},\mathsf {Enc},\mathsf {Dec},\mathsf {DelEvo},\mathsf {DelDec})\) as follows:
- \(\mathsf {Setup} (1^k)\! :\) :
-
On input security parameter \(k\), outputs public parameters \(\mathsf {pp}\).
- \(\mathsf {Gen} (\mathsf {pp}, n)\! :\) :
-
On input public parameters \(\mathsf {pp}\), and maximum number of periods n, outputs public, secret and evolution keys \((\mathsf {pk}, \mathsf {sk} ^{(0)},\mathsf {ek} ^{(0)})\).
- \(\mathsf {Evo} (\mathsf {sk} ^{(i)}, \mathsf {ek} ^{(i)})\! :\) :
-
On input secret key \(\mathsf {sk} ^{(i)}\), and evolution key \(\mathsf {ek} ^{(i)}\) for period \(i\in \{0,\ldots ,n-2\}\), outputs secret key \(\mathsf {sk} ^{(i+1)}\) and evolution key \(\mathsf {ek} ^{(i+1)}\) for period \(i+1\).
- \(\mathsf {Del} ( \mathsf {sk} _A^{(i)}, \mathsf {ek} _A^{(i)}, \mathsf {pk} _B)\! :\) :
-
On input secret key \(\mathsf {sk} _A^{(i)}\) and evolution key \(\mathsf {ek} _A^{(i)}\) (or \(\bot \)) for A and period \(i\in \{0,\ldots ,n-1\}\), and public key \(\mathsf {pk} _B\) for B, outputs delegated key \(\mathsf {dk} ^{(i)}\) and delegated evolution key \(\mathsf {dek} ^{(i)}\) (or \(\bot \)) for period i.
- \(\mathsf {Enc} (\mathsf {pk},M,i)\! :\) :
-
On input a public key \(\mathsf {pk}\), a message \(M \in \mathcal {M} \), and period \(i\in \{0,\ldots ,n-1\}\), outputs a ciphertext \(C\).
- \(\mathsf {Dec} (\mathsf {sk} ^{(i)},C)\! :\) :
-
On input a secret key \(\mathsf {sk} ^{(i)}\), for period \(i\in \{0,\ldots ,n-1\}\), and ciphertext \(C\), outputs \(M \in \mathcal {M} \cup \{\bot \}\).
- \(\mathsf {DelEvo} (\mathsf {dk} ^{(i)}, \mathsf {dek} ^{(i)})\! :\) :
-
On input a delegation key \(\mathsf {dk} ^{(i)}\) and delegated evolution key \(\mathsf {dek} ^{(i)}\) for period \(i\in \{0,\ldots ,n-2\}\), output delegation key \(\mathsf {dk} ^{(i+1)}\) and delegated evolution key \(\mathsf {dek} ^{(i+1)}\) for period \(i+1\).
- \(\mathsf {DelDec} (\mathsf {sk} _B^{(i)}, \mathsf {dk} _{A \rightarrow B}^{(i)}, C _A)\! :\) :
-
On input secret key \(\mathsf {sk} _B^{(i)}\) for B and period \(i\in \{0,\ldots ,n-1\}\), delegation key \(\mathsf {dk} _{A\rightarrow B}^{(i)}\) from A for B and period i, and ciphertext \(C _A\) for A, outputs \(M \in \mathcal {M} \cup \{ \bot \}\).
We note that the existence of the \(\mathsf {DelEvo}\) algorithm is entirely optional. If provided, it allows the user in possession of a delegation key to evolve it for later periods without additional interaction with the delegator.
Correctness. For correctness we require that period i ciphertexts encrypted for user u can be decrypted if one is in possession of the secret key of u evolved to that period or one possess a delegation key of u to another user \(u'\) and the secret key for \(u'\) for that period. More formally, we require that for all security parameters \(k \in \mathbb {N} \), all public parameters \(\mathsf {pp}\) generated by \(\mathsf {Setup} (1^k)\), all number of periods \(n\in \mathbb {N} \), all users \(U\in \mathbb {N} \), all key tuples \((\mathsf {pk} _u,\mathsf {sk} _{u}^{(0)}, \mathsf {ek} _{u}^{(0)})_{u \in [U]}\) generated by \(\mathsf {Gen} (\mathsf {pp}, n)\), any period \(i\in \{0,\ldots ,n-1\}\), for any \(u \in [U]\), any evolved keys \((\mathsf {sk} _{u}^{(i)}, \mathsf {ek} _{u}^{(i)})\) generated by \(\mathsf {Evo} \) from \((\mathsf {sk} _{u}^{(0)}, \mathsf {ek} _{u}^{(0)})\), for all \(u' \in [U], u \ne u'\), any (potentially evolved) delegation key \(\mathsf {dk} _{u \rightarrow u'}^{(i)}\) for period i generated using \(\mathsf {Del} \) from a (potentially evolved) secret key and the target public key, and all messages \(M \in \mathcal {M} \) it holds that
Security notions. The forward-secret IND-CPA notion is a straight-forward extension of the typical IND-CPA notion: the adversary selects a target period and gets access to secret and evolution keys of the targeted user for the selected period and is able to request delegation keys with honest and dishonest users for that period. The adversary then engages with an IND-CPA style challenge for the previous period. For the experiment, which is depicted in Experiment 6, the environment keeps a list of an initial empty list of honest users \(\mathtt {HU} \).
- \(\mathsf {Gen} ^{(h)}(\mathsf {pp}, n)\! :\) :
-
Run \((\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \leftarrow \mathsf {Gen} (\mathsf {pp}, n)\), set \(\mathtt {HU} \leftarrow \mathtt {HU} \cup \{ (\mathsf {pk}, \mathsf {sk}, \mathsf {ek}) \}\), and return \(\mathsf {pk} \).
- \(\mathsf {Del} ^{(h)}(j, \mathsf {pk} _u, \mathsf {pk})\! :\) :
-
On input a period j, a public key \(\mathsf {pk} _u\) and a public key \(\mathsf {pk} \), abort if \((\mathsf {pk} _u, \cdot ) \not \in \mathtt {HU} \). Otherwise, look up \(\mathsf {sk} _u^{(0)}, \mathsf {ek} _u^{(0)}\) corresponding to \(\mathsf {pk} _u\) from \(\mathtt {HU}\), set \((\mathsf {sk} _u^{(i)}, \mathsf {ek} _u^{(i)}) \leftarrow \mathsf {Evo} (\mathsf {sk} _u^{(i-1)}, \mathsf {ek} _u^{(i-1)})\) for \(i \in [j]\) if \(j>0\), and return \(\mathsf {Del} (\mathsf {sk} _u^{(j)}, \mathsf {ek} _u^{(j)}, \mathsf {pk})\).
- \(\mathsf {Del} ^{(h')}(j, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}, \mathsf {pk} _u)\! :\) :
-
On input a period j, a secret key \(\mathsf {sk} ^{(0)}\), a evolution key \(\mathsf {ek} ^{(0)}\), and a public key \(\mathsf {pk} _u\), abort if \((\mathsf {pk} _u, \cdot ) \not \in \mathtt {HU} \). Otherwise, set \((\mathsf {sk} ^{(i)}, \mathsf {ek} ^{(i)}) \leftarrow \mathsf {Evo} (\mathsf {sk} ^{(i-1)}, \mathsf {ek} ^{(i-1)})\) for \(i \in [j]\) if \(j>0\), and return \(\mathsf {Del} (\mathsf {sk} ^{(j)}, \mathsf {ek} ^{(j)}, \mathsf {pk} _u)\).

Definition 12
(fs-IND-CPA). For a polynomially bounded function \(n(\cdot )>1\), a PPT adversary \(A\), we define the advantage function in the sense of fs-IND-CPA as
If for all \(n(\cdot )>1\), and any \(A\) there exists a negligible function \(\varepsilon \) such that \({fs-\mathsf {DPKE},A}(1^k,n(k)) < \varepsilon (k)\), then a fs-\(\mathsf {DPKE}\) scheme is fs-IND-CPA secure.
4.2 Constructing fs-\(\mathsf {DPKE}\) from \(\mathsf {BTE}\)
Now we construct a fs-\(\mathsf {DPKE} \) scheme from a \(\mathsf {BTE} \) scheme by applying the \(\mathsf CHK\) compiler to a \(\mathsf {BTE} \) and combining it with an \(\mathcal {F}\)-\(\mathsf {HPKE} \) scheme for handling the delegation keys, i.e., the fs-\(\mathsf {DPKE} \) key contains a \(\mathsf {BTE} \) and an \(\mathcal {F}\)-\(\mathsf {HPKE} \) key. The evolution key contains the secret and derivation keys for all right siblings on the path from the root node to \(w^i\) as well as the evolution key for \(w^i\). The evolution algorithms traverse the tree in a depth-first manner, hence the evolution keys are viewed as stack and when visiting a node, the derived secret and derivation keys are pushed onto the stack. To simplify the presentation of the scheme, we define an algorithm \(\mathsf {DFEval}\) that performs the stack manipulation on a stack of pairs:
-
\(\mathsf {DFEval} (s_1^{(w^i)}, s, \mathsf {Eval})\! :\) On input the stack s and first element \(s_1^{(w^i)}\) of the pair for node \(w^i\), an algorithm \(\mathsf {Eval} \), perform the following steps:
-
Pop the topmost element, \((\bot , s_2^{(w^i)})\), from the stack s.
-
If \(w^i\) is an internal node, set \(s^{(w^i0)}, s^{(w^i1)} \leftarrow \mathsf {Eval} (s_1^{(w^i)}, s_2^{(w^i)})\) and push \(s^{(w^i1)}, s^{(w^i0)}\) onto s.
-
Replace the topmost element, \((s_1^{(w^{i+1})}, s_2^{(w^{i+1})})\), with \((\bot , s_2^{(w^{i+1})})\).
-
Return \(s_1^{(w^{i+1})}\) and the new stack s.
-
The overall idea is now to encrypt the \(\mathsf {BTE} \) secret key of the current period using the \(\mathcal {F}\)-\(\mathsf {HPKE}\) scheme’s public key of the target user. Using the homomorphic property of the encryption scheme, we are able to evolve the delegation keys in the same way as the secret keys of the nodes. In particular, we will require that the key derivation algorithm of the \(\mathsf {BTE}\) can be represented by functions in \(\mathcal {F}\), i.e., \(\mathsf {Der} _{\mathsf {BTE}} = (f_i)_{i \in [m]}\). For notional simplicity, we will write \(\mathsf {Eval} _{\mathsf {HPKE}}(\mathsf {Der} _{\mathsf {BTE}}, \cdot )\) instead of repeating it for each \(f_i\) that represents \(\mathsf {Der} _{\mathsf {BTE}}\).
For our fs-\(\mathsf {DPKE}\) scheme we need keys of different users to live in compatible key spaces. To that end, we introduce \(\mathsf {Setup} \) algorithms for both schemes that fix the key spaces and we change the key generation algorithms to take the public parameters instead of the security parameter as argument. Note that when using the \(\mathsf {BTE}\) from [15], linear ElGamal [11] as \(\mathcal {F}\)-\(\mathsf {HPKE}\) to encrypt the \(\mathsf {BTE}\) keys suffices for our needs.
Our construction. The fs-\(\mathsf {DPKE} \) scheme is detailed in Scheme 1. We note that only the definition of \(\mathsf {DelEvo} \) relies on the homomorphic properties of the \(\mathsf {HPKE}\) scheme. So to obtain a fs-\(\mathsf {DPKE}\) scheme without \(\mathsf {DelEvo} \) algorithm, a compatible \(\mathsf {PKE}\) scheme is sufficient. Yet, we will require the homomorphic properties later to achieve a suitable notion of adaptability regardless of the availability of \(\mathsf {DelEvo} \).
Similar to Canetti et al.’s construction, our fs-\(\mathsf {DPKE}\) scheme inherits the fs-IND-CPA security from the \(\mathsf {BTE}\) ’s IND-SN-CPA security.
Theorem 1
If instantiated with an IND-SN-CPA secure \(\mathsf {BTE}\) scheme and a IND-CPA secure \(\mathsf {HPKE}\) scheme, then Scheme 1 is a fs-IND-CPA secure fs-\(\mathsf {DPKE}\).
Proof
We prove the theorem using a sequence of games. We denote by W all the relevant nodes in the binary tree for period j. We note that the size of W is bounded by \(\log _2(n)\). We index W as \(w_i\) for \(i \in [|W|]\).
-
Game 0: The original game.
-
Game \(1_{i,j}\) (\(1 \le i \le q_{\mathsf {Del} ^h}, 1 \le j \le 2 |W|)\) : As the previous game, but we replace all \(\mathsf {HPKE} \) ciphertexts up to the j-th one in the i-th query with ciphertexts encrypting random plaintexts. That is, we modify the \(\mathsf {Del} ^{h'}\) in the i-th query as follows:
-
\(\mathsf {Del} ^{h'}(j, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}, \mathsf {pk} _i)\) : Up to the j-th call to \(\mathsf {Enc} _{\mathsf {HPKE}}\), encrypt a uniformly random value.
-
-
Transition \(^{0 \rightarrow 1_{1,1}}\), Transition \(^{1_{i,j} \rightarrow 1_{i,j+1}}\), Transition \(^{1_{i,2W|} \rightarrow 1_{i+1,1}}\) : A distinguisher \(\mathcal {D}^{0 \rightarrow 1_{1,1}}\) (respectively \(\mathcal {D}^{1_{i,j} \rightarrow 1_{i,j+1}}\) or \(\mathcal {D}^{1_{i,2 |W|} \rightarrow 1_{i+1,1}}\)) is an IND-CPA adversary against the \(\mathsf {HPKE}\) scheme. We construct a reduction where we let \(\mathcal {C}\) be a IND-CPA challenger. We modify \(\mathsf {Del} ^{h'}\) in the i-th query in the following way:
-
\(\mathsf {Del} ^{h'}(j, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}, \mathsf {pk} _{i'})\) : Simulate everything honestly, but on the j-th query choose
 uniformly at random and run
uniformly at random and run 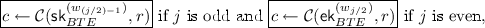
where \(c \leftarrow \mathcal {C}(m_0, m_b)\) denotes a challenge ciphertext with respect to \(m_0\) and \(m_1\).
Now, the bit b chosen by \(\mathcal {C}\) switches between the distributions of the Games.
-
In Game \(1_{q_{\mathsf {Del} ^h}, 2 |W|}\) all ciphertexts obtainable from \(\mathsf {Del} ^{h'}\) are with respect to random values. Now, an adversary \(B\) winning Game \(1_{q_{\mathsf {Del} ^h}, 2 |W|}\) can be transformed into a IND-SN-CPA adversary \(A\) against the underlying \(\mathsf {BTE}\) scheme:
-
1.
When \(A\) is first started on \(1^k, \ell \), choose
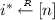 and output \(w^{(i^*-1)}\).
and output \(w^{(i^*-1)}\). -
2.
When \(A\) is started on \(\mathsf {pk} _{\mathsf {BTE}}, (\mathsf {sk} ^{(w)},\mathsf {dk} ^{(w)})_{w \in W}\), compute \((\mathsf {pk} _{\mathsf {HPKE}}, \mathsf {sk} _{\mathsf {HPKE}}) \leftarrow \mathsf {Gen} _{\mathsf {HPKE}}(1^k)\). The secret key \(\mathsf {sk} _{\mathsf {HPKE}}\) is stored in the state st and we extend the public key to \(\mathsf {pk} \leftarrow (\mathsf {pk} _{\mathsf {BTE}},\mathsf {pk} _{\mathsf {HPKE}})\). Now start \(B\) on the extended public key, i.e. \((j^*, \mathsf {st}) \leftarrow {B}(1^k, n, \mathsf {pk})\). If \(i^* \ne j^*\), output a random bit and halt. Otherwise we have the secret-derivation key pairs of all nodes that are right siblings on the path from the root node to \(w^{(j^* - 1)}\) and (if they exist) all child nodes of \(w^{(j^* -1)}\), hence we are able to simulate all oracle queries from \(B\) honestly. Similarly, we can compute \((\mathsf {sk} ^{(j^*)}, \mathsf {dk} ^{(j^*)})\) from the given keys. Thus we run \(B ^{\mathcal {O}}(\mathsf {st}, \mathsf {sk} ^{(j^*)}, \mathsf {dk} ^{(j^*)})\) and forward its result.
-
3.
When \(A\) is finally started on the challenge ciphertext, the ciphertext is simply forwarded to \(B\) and when \(B\) outputs the bit b, \(A\) returns b and halts.
When \(B\) is running within \(A\) and \(j^* = i^*\), \(B\) has exactly the same view as in Game \(1_{q_{\mathsf {Gen} ^h}, 2 |W|}\). In this case the probability of \(A \) to win is exactly the same as the winning probability of \(B \), and Game \(1_{q_{\mathsf {Gen} ^h}, 2 |W|}\) is computationally indistinguishable from the initial game. The random guess of \(i^*\) so that \(i^* = j^*\) induces a loss of \(\frac{1}{n}\), which is however bounded by a polynomial in the security parameter. \(\square \)
4.3 Constructing fs-\(\mathsf {PRE}\) from fs-\(\mathsf {DPKE}\)
Now we present a construction of a fs-\(\mathsf {PRE} ^+\)-secure fs-\(\mathsf {PRE}\) scheme from a fs-\(\mathsf {DPKE} \) scheme. Therefore, we define additional properties of fs-\(\mathsf {DPKE}\) and show that a fs-\(\mathsf {PRE} \) can be directly obtained from a fs-\(\mathsf {DPKE} \). For our transformation to work, we need to define an additional algorithm that allows us to homomorphically shift ciphertexts and delegation keys. That is, ciphertexts and delegation keys are modified in such a way that the delegation keys look like randomly distributed fresh keys, which are only useful to decrypt ciphertexts adapted to this key. Formally, we introduce an algorithm \(\mathsf {Adapt} \) that enables this adaption:
- \(\mathsf {Adapt} (\mathsf {dk}, C)\! :\) :
-
On input a delegation key \(\mathsf {dk}\), a ciphertext \(C\), outputs an adapted delegation key \(\mathsf {dk} '\) and ciphertext \(C '\).
Since the delegation keys in our construction are encrypted \(\mathsf {BTE}\) secret keys, we essentially adapt secret keys and ciphertexts from a \(\mathsf {BTE}\). We will see that this adaption is possible as long as the \(\mathsf {HPKE}\) scheme used to encrypt the \(\mathsf {BTE}\) keys provides a suitable homomorphism on the message space.
To adapt ciphertexts and delegation keys we extend correctness to additionally require that for any message \(M \) encrypted under the public key of A, any delegation key \(\mathsf {dk} ^{(i)}_{A \rightarrow B}\), and any adapted delegation key-ciphertext pairs \((\mathsf {dk} ', C ') \leftarrow \mathsf {Adapt} (\mathsf {dk} ^{(i)}_{A \rightarrow B}, C _A)\), it holds that \(M = \mathsf {DelDec} _{\mathsf {DPKE}}(sk_B^{(i)}, \mathsf {dk} ', C ')\).
As security notion we introduce the fs-ADAP-IND-CPA notion, where the adversary may see multiple adapted delegation keys and ciphertexts, but the adversary should be unable to win an IND-CPA game for non-adapted ciphertexts. We give the formal definition of the security experiment in Experiment 7. This notion gives the delegator more control over the ciphertexts that should be readable for the delegatee. If given the delegation key, the delegatee can always decrypt all ciphertexts, but if just given an adapted delegation key, only a selected subset of ciphertexts is decryptable.

Definition 13
(fs-ADAP-IND-CPA). For a polynomially bounded function \(n(\cdot )>1\), a PPT adversary \(A\), we define the advantage function in the sense of fs-IND-CPA as
If for all \(n(\cdot )>1\), and any \(A \) there exists a negligible function \(\varepsilon \) such that \(\mathsf {Adv}^{\mathsf {fs-adap-ind-cpa}}_{fs-\mathsf {DPKE},A}(1^k,n(k)) < \varepsilon (k)\), then a fs-\(\mathsf {DPKE}\) scheme is fs-ADAP-IND-CPA secure.
For Scheme 1, this adaption can be achieved solely from key-homomorphic properties of the \(\mathsf {BTE}\) and homomorphic properties of the \(\mathsf {HPKE}\), respectively. Subsequently, we define the required homomorphisms. Our definitions are inspired by [2, 40]. We focus on schemes where the secret/derived key pairs, and public keys live in groups \((\mathbb {G}, +)\), and \((\mathbb {H}, \cdot )\), respectively. We will require two different properties: first, the public key is the image of the secret key under a group homomorphism, and second, given two secret keys with a known difference, we can map the binary tree of derived keys from one key to the other key. In other words, the difference in the keys propagates to the derived keys.
Definition 14
Let \(\varOmega \) be a \(\mathsf {BTE}\) scheme with secret/derived key space \((\mathbb {G}, +)\) and public key space \((\mathbb {H}, \cdot )\).
-
1.
The scheme \(\varOmega \) provides a secret-key-to-public-key homomorphism, if there exists an efficiently computable group homomorphism \(\mu : \mathbb {G} \rightarrow \mathbb {H} \) such that for all \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Gen} \), it holds that \(\mathsf {pk} = \mu (\mathsf {sk})\).
-
2.
The scheme \(\varOmega \) provides a derived-key homomorphism, if there exists a family of efficiently computable group homomorphisms \(\nu ^{(w)} : \mathbb {G} \rightarrow \mathbb {G} ^2\) such that for all \((\mathsf {pk}, \mathsf {sk} ^{(\varepsilon )}) \leftarrow \mathsf {Gen} \), all nodes w it holds that \((\mathsf {sk} ^{(w0)}, \mathsf {sk} ^{(w1)}) = \nu ^{(w)}(\mathsf {sk} ^{(w)})\) and for all messages \(M \) it holds that \(\mathsf {Dec} (\mathsf {sk} ^{(w)}, \mathsf {Enc} (\mathsf {pk}, M, w)) = M \).
We denote by \(\varPhi ^+\) the set of all possible secret key differences in \(\mathbb {G} \). Alternatively, it is possible to view \(\varPhi ^+\) as set of functions representing all linear shifts in \(\mathbb {G} \) and we simply identify each shift by an element \(\varDelta \in \mathbb {G} \).
Definition 15
A \(\mathsf {BTE}\) scheme \(\varOmega \) is called \(\varPhi ^+\)-key-homomorphic, if it provides both a secret-key-to-public-key homomorphism and a derived key homomorphism and an additional PPT algorithm \(\mathsf {Adapt} \), defined as:
- \(\mathsf {Adapt} (\mathsf {pk}, C, \varDelta )\! :\) :
-
On input a delegation key \(\mathsf {dk}\), a ciphertext \(C\) and a secret key difference \(\varDelta \), outputs a public key \(\mathsf {pk} '\) and a ciphertext \(C '\).
such that for all \(\varDelta \in \varPhi ^+\), and all \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Gen} (\ldots )\), all message \(M \), and all \(C \leftarrow \mathsf {Enc} (\mathsf {pk}, M)\), and \((\mathsf {pk} ', C ') \leftarrow \mathsf {Adapt} (\mathsf {pk}, C, \varDelta )\) it holds that \(\mathsf {pk} ' = \mathsf {pk} \cdot \mu (\varDelta )\) and \(\mathsf {Dec} (\mathsf {sk} ^{(w)} + \nu ^{(w)}(\varDelta ), C ') = M \).
Definition 16
(Adaptability of ciphertexts). A \(\varPhi ^+\)-key-homomorphic \(\mathsf {BTE}\) scheme provides adaptability of ciphertexts, if for every security parameter \(k \in \mathbb {N} \), any public parameters \(\mathsf {pp} \leftarrow \mathsf {Setup} (1^k)\), every message \(M \) and every period j, it holds that \(\mathsf {Adapt} (\mathsf {pk}, \mathsf {Enc} (\mathsf {pk}, M, j), \varDelta )\) and \((\mathsf {pk} \cdot \mu (\varDelta ), \mathsf {Enc} (\mathsf {pk} \cdot \mu (\varDelta ), M, j))\) as well as \((\mathsf {sk}, \mathsf {pk})\) and \((\mathsf {sk} ', \mu (\mathsf {sk} '))\) are identically distributed, where \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Gen} (\mathsf {pp}, n)\),  and \(\varDelta \leftarrow \varPhi ^+\).
and \(\varDelta \leftarrow \varPhi ^+\).
Next, we discuss the \(\mathsf {BTE}\) from [15] with respect to our notion of ciphertext adaptability. We first recall the \(\mathsf {BTE}\) scheme in Scheme 2 where \(\mathsf {BGGen} \) is a bilinear group generator. By [15, Proposition 1] this scheme is IND-SN-CPA secure if the decisional BDH assumption holds relative to \(\mathsf {BGGen}\).
BTE scheme from [15]
Now we show that Scheme 2 also provides adaptability of ciphertexts:
Lemma 3
Scheme 2 provides adaptability of ciphertexts under shared H.
Proof
We show the existence of the homomorphisms and give the \(\mathsf {Adapt}\) algorithm. Note that the master secret key can easily be viewed as containing \(\alpha \), hence, the secret-to-public-key homomorphism is simply \(\mu : \alpha \mapsto \alpha P\). As the \(\mathsf {Der}\) algorithm simply computes sums, the existence of the homomorphism is clear.
We now show the existence of \(\mathsf {Adapt}\):
- \(\mathsf {Adapt} (\mathsf {pk},C,\varDelta )\! :\) :
-
Parse \(\mathsf {pk} \) as \((Q, \ell , H)\) and \(C \) as \((U_0, \ldots , U_t, V)\). Let \(Q' \leftarrow Q + \varDelta \cdot P\) and set \(\mathsf {pk} ' \leftarrow (Q', \ell , H)\). Let \(V' \leftarrow V e(U_0, \varDelta \cdot H(\varepsilon ))\) and set \(C ' \leftarrow (U_0, \ldots , U_t, V')\) and return \((\mathsf {pk} ', C ')\).
The adapted \(C '\) ciphertext is an encryption of the original message under the public key \(Q' = Q + \varDelta \cdot P\). \(\square \)
Now, given any \(\varPhi ^+\)-key-homomorphic \(\mathsf {BTE}\) scheme, it can be turned into an adaptable fs-\(\mathsf {DPKE}\) by defining \(\mathsf {Adapt}\) in a publicly computable way as follows:
- \(\mathsf {Adapt} (\mathsf {dk} _{A \rightarrow B}^{(i)}, C)\! :\) :
-
Sample
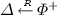 and compute \(\mathsf {dk} _\varDelta \leftarrow \mathsf {Enc} _{\mathsf {HPKE}}(\mathsf {pk} _B, \nu ^{(w^i)}(\varDelta ))\), and then \(\mathsf {dk} ' \leftarrow \mathsf {Eval} _{\mathsf {HPKE}}(+, \mathsf {dk} _{A \rightarrow B}^{(i)}, \mathsf {dk} _{\varDelta })\). Set \((\cdot , C ') \leftarrow \mathsf {Adapt} _\mathsf {BTE} (\mathsf {pk} _A,C, \varDelta )\). Return \((\mathsf {dk} ', C ')\).
and compute \(\mathsf {dk} _\varDelta \leftarrow \mathsf {Enc} _{\mathsf {HPKE}}(\mathsf {pk} _B, \nu ^{(w^i)}(\varDelta ))\), and then \(\mathsf {dk} ' \leftarrow \mathsf {Eval} _{\mathsf {HPKE}}(+, \mathsf {dk} _{A \rightarrow B}^{(i)}, \mathsf {dk} _{\varDelta })\). Set \((\cdot , C ') \leftarrow \mathsf {Adapt} _\mathsf {BTE} (\mathsf {pk} _A,C, \varDelta )\). Return \((\mathsf {dk} ', C ')\).
Theorem 2
If in addition to the premise in Theorem 1 the \(\mathsf {BTE}\) scheme also provides adaptability of ciphertexts, then Scheme 1 is a fs-ADAP-IND-CPA secure fs-\(\mathsf {DPKE}\) scheme.
Proof
We prove this theorem with a sequence of games.
- Game 0::
-
The original game.
- Game 1::
-
We modify the simulation of the \(\mathsf {Adapt} \) oracle as follows, where we denote the modified oracle by \(\mathsf {Adapt} '\):
-
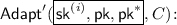 :
: -
Parse \(\mathsf {sk} ^{(i)}\) as \((\mathsf {sk} ^{(w^i)}_\mathsf {BTE}, \cdot )\), \(\mathsf {pk} \) as \((\mathsf {pk} _{\mathsf {BTE}}, \cdot )\), and \(\mathsf {pk} ^*\) as \((\cdot , \mathsf {pk} ^*_\mathsf {HPKE})\). Choose \(\varDelta \leftarrow \varPhi ^+\), run
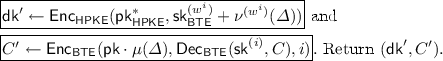
-
- Transition\(^{0 \rightarrow 1}\)::
-
The distributions of Game 0 and Game 1 are indistinguishable under the \(\mathsf {BTE}\) ’s adaptability of ciphertexts.
- Game 2::
-
We further modify the simulation of \(\mathsf {Adapt} '\) as follows:
-
 :
: -
Parse \(\mathsf {sk} ^{(i)}\) as \((\mathsf {sk} ^{(w^i)}_\mathsf {BTE}, \cdot )\), \(\mathsf {pk} \) as \((\mathsf {pk} _{\mathsf {BTE}}, \cdot )\), and \(\mathsf {pk} ^*\) as \((\cdot , \mathsf {pk} ^*_\mathsf {HPKE})\). Choose
 and evolve the secret key to period i, run
and evolve the secret key to period i, run 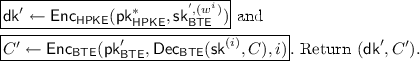
-
- Transition\(^{1 \rightarrow 2}\)::
-
The change is conceptual.
In Game 2 all the secret \(\mathsf {BTE}\) keys the adversary gets are chosen independently from the challenge key. Hence, Game 2 is a standard IND-CPA game and thus the success probability of Game 2 is negligible by Theorem 1. \(\square \)
Now, given an adaptable fs-\(\mathsf {DPKE}\) scheme, we use the \(\mathsf {Adapt}\) algorithm to obtain a fs-\(\mathsf {PRE} ^+\) secure fs-\(\mathsf {PRE}\) scheme. While the algorithms \(\mathsf {Setup}\), \(\mathsf {Gen}\), \(\mathsf {Evo}\), \(\mathsf {Enc} ^{(i)}\), and \(\mathsf {Dec} ^{(i)}\) can simply be lifted from the fs-\(\mathsf {DPKE}\) scheme, we note that for each period j in the fs-\(\mathsf {PRE}\) scheme, we use two periods, i.e., \(2j - 1\) and 2j, of the fs-\(\mathsf {DPKE}\) scheme. The period \(2j -1\) is used for level 1 ciphertexts whereas the period 2j is used for level 2 ciphertextsFootnote 13. We use \(\mathsf {Del} _\mathsf {DPKE} \) and \(\mathsf {DelEvo} _\mathsf {DPKE} \) for \(\mathsf {ReGen}\) and \(\mathsf {ReEvo}\), respectively. For the re-encryption algorithm \(\mathsf {ReEnc} \), we apply \(\mathsf {Adapt}\). \(\mathsf {Dec} ^{(1)}\) for re-encrypted ciphertexts then decrypts the ciphertext by running \(\mathsf {DelDec} _\mathsf {DPKE} \) on the adapted delegation key and ciphertext. The full scheme is presented in Scheme 3.
We prove that our scheme is both fs-IND-CPA-1 and fs-IND-CPA-2 secure. Both security notions follow from the fs-IND-CPA security of the underlying fs-\(\mathsf {DPKE}\) scheme. In contrast, to achieve fs-RIND-CPA, we require an fs-ADAP-IND-CPA fs-\(\mathsf {DPKE}\) scheme.
Theorem 3
If instantiated with a fs-IND-CPA and fs-ADAP-IND-CPA secure fs-\(\mathsf {DPKE}\) scheme, Scheme 3 is a fs-\(\mathsf {PRE} ^+\)-secure fs-\(\mathsf {PRE}\) scheme.
Proof
Informally speaking, the security experiment for fs-IND-CPA-2 with a fixed period \(j^*\) corresponds to the fs-IND-CPA experiment for fs-\(\mathsf {DPKE}\) for period \(2j^*\). We can build a straightforward reduction from an adversary against fs-IND-CPA-2, \(A _2\) to fs-IND-CPA for fs-\(\mathsf {DPKE}\):
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), run \((j^*, \mathsf {st}) \leftarrow A _2(\mathsf {pp}, \lceil \tfrac{n}{2} + 1 \rceil , \mathsf {pk})\). Set \(j' \leftarrow 2 j^*\) and return \((j', \mathsf {st})\).
-
When started on \(\mathsf {st}, \mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\), we simulate the \(\mathsf {ReGen} ^{(h)}\) and \(\mathsf {ReGen} ^{(h')}\) oracles using \(\mathsf {Del} ^{(h)}\) and \(\mathsf {Del} ^{(h')}\). Indeed, \(\mathsf {Del} ^{(h)}\) and \(\mathsf {Del} ^{(h')}\) return delegation keys for period \(j' - 1 = 2 j^*-1\), which are re-encryption keys for period \(j^*-1\). Using \(\mathsf {Evo} \) we evolve \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to period \(j'+1\). Set \((\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)}) \leftarrow ((\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {sk} _{\mathsf {DPKE}}^{(j'+1)}), (\mathsf {ek} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j'+1)}))\) and start \(A _2\) on \(\mathsf {st}, (\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)})\) and simply forward the result.
-
Finally, when started on st and \(C _{j' - 1}\), \(C _{j'-1}\) is a level 2 ciphertext for \(j^*-1\). Hence we start \(A _2\) on the ciphertext and return its’ result.
To show fs-IND-CPA-1 security, we perform a similar reduction:
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), run \((j^*, \mathsf {st}) \leftarrow A _1(\mathsf {pp}, \lceil \tfrac{n}{2} + 1 \rceil , \mathsf {pk})\). Set \(j' \leftarrow 2 j^*-1\) and return \((j', \mathsf {st})\).
-
When started on \(\mathsf {st}, \mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\), we simulate the \(\mathsf {ReGen} ^{(h)}\) and \(\mathsf {ReGen} ^{(h')}\) oracles using \(\mathsf {Del} ^{(h)}\) and \(\mathsf {Del} ^{(h')}\) and by running \(\mathsf {DelEvo} \) on the result. Indeed, \(\mathsf {Del} ^{(h)}\) and \(\mathsf {Del} ^{(h')}\) return delegation keys for period \(j' - 1 = 2 j^*-2\), hence after applying \(\mathsf {DelEvo} \) we obtain re-encryption keys for period \(j^*-1\). \(\mathsf {ReGen} ^{(d)}\) is simulated honestly by delegating \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to a dishonest user. Using \(\mathsf {Evo} \) we evolve \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to period \(j'+2\). Set \((\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)}) \leftarrow ((\mathsf {sk} _{\mathsf {DPKE}}^{(j'+1)}, \mathsf {sk} _{\mathsf {DPKE}}^{(j'+2)}), (\mathsf {ek} _{\mathsf {DPKE}}^{(j'+1)}, \mathsf {ek} _{\mathsf {DPKE}}^{(j'+2)}))\) and start \(A _1\) on \(\mathsf {st}, (\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)})\) and simply forward the result.
-
Finally, when started on st and \(C _{j' - 1}\), \(C _{j'-1}\) is a level 1 ciphertext for \(j^*-1\). Hence we start \(A _1\) on the ciphertext and return its’ result.
To show receiver-IND-CPA security we build an fs-ADAP-IND-CPA adversary against the fs-\(\mathsf {DPKE}\) scheme. The fs-RIND-CPA adversary is denoted as \(A _r\).
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), run \((j^*, \mathsf {st}) \leftarrow A _r(\mathsf {pp}, \lceil \tfrac{n}{2} + 1 \rceil , \mathsf {pk})\). Set \(j' \leftarrow 2 j^*+1\) and return \((j', \mathsf {st})\).
-
When started on st, we can simulate \(\mathsf {ReEnc} \) honestly using \(\mathsf {Adapt} \).
-
Wen started on st and \(C \), the ciphertext is a level 2 ciphertext for period \(j*\), hence we return \(A _r(\mathsf {st}, C)\).
Note that all values are consistently distributed in all three reductions. \(\square \)
4.4 Separating fs-PRE\(^-\) from fs-PRE\(^+\)
To expand on the gap between fs-\(\mathsf {PRE} ^{+}\) and fs-\(\mathsf {PRE} ^{-}\) schemes and to provide an explicit separation, we construct a counterexample. In particular, it is clear that every scheme that satisfies fs-\(\mathsf {PRE} ^+\) also satisfies fs-\(\mathsf {PRE} ^-\). For our separation we now present a scheme that is fs-\(\mathsf {PRE} ^-\) but trivially violates fs-\(\mathsf {PRE} ^+\). The scheme is also built from a fs-\(\mathsf {DPKE}\) scheme and presented in Scheme 4. In this scheme however, \(\mathsf {ReEnc} \) simply embeds the delegation key in the re-encrypted ciphertext. The shortcomings of this construction compared to Scheme 3 are obvious: once the receiver is presented with one valid re-encrypted ciphertext, it can recover the delegation key from that ciphertext and can decrypt all level 2 ciphertexts for this period.
In the following Theorem, we first show that Scheme 4 is indeed fs-\(\mathsf {PRE} ^-\) secure, i.e., satisfies fs-IND-CPA-1 and fs-IND-CPA-2 security, but trivially does not satisfy fs-RIND-CPA security and thus is not fs-\(\mathsf {PRE} ^+\) secure.
Theorem 4
Scheme 4 when instantiated with a fs-IND-CPA secure fs-\(\mathsf {DPKE}\) scheme satisfies fs-IND-CPA-1 and fs-IND-CPA-2 security, but not fs-RIND-CPA security.
Proof
We follow the same strategy as for Theorem 3 to show fs-IND-CPA-2.
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), run \((j^*, \mathsf {st}) \leftarrow A _2(\mathsf {pp}, \lceil \tfrac{n}{2} + 1 \rceil , \mathsf {pk})\). Set \(j' \leftarrow 2 j^*\) and return \((j', \mathsf {st})\).
-
When started on \(\mathsf {st}, \mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\), we simulate the \(\mathsf {ReGen} ^h\) and \(\mathsf {ReGen} ^{h'}\) oracles using \(\mathsf {Del} ^h\) and \(\mathsf {Del} ^{h'}\). Indeed, \(\mathsf {Del} ^h\) and \(\mathsf {Del} ^{h'}\) return delegation keys for period \(j' - 1 = 2 j^*-1\), which are re-encryption keys for period \(j^*-1\). Using \(\mathsf {Evo} \) we evolve \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to period \(j'+1\). Set \((\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)}) \leftarrow ((\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {sk} _{\mathsf {DPKE}}^{(j'+1)}), (\mathsf {ek} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j'+1)}))\) and start \(A _2\) on \(\mathsf {st}, (\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)})\) and simply forward the result.
-
Finally, when started on st and \(C _{j' - 1}\), \(C _{j'-1}\) is a level 2 ciphertext for \(j^*-1\). Hence we start \(A _2\) on the ciphertext and return its’ result.
To show fs-IND-CPA-1 security, we perform a similar reduction:
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), run \((j^*, \mathsf {st}) \leftarrow A _1(\mathsf {pp}, \lceil \tfrac{n}{2} + 1 \rceil , \mathsf {pk})\). Set \(j' \leftarrow 2 j^*-1\) and return \((j', \mathsf {st})\).
-
When started on \(\mathsf {st}, \mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\), we simulate the \(\mathsf {ReGen} ^h\) and \(\mathsf {ReGen} ^{h'}\) oracles using \(\mathsf {Del} ^h\) and \(\mathsf {Del} ^{h'}\) and by running \(\mathsf {DelEvo} \) on the result. Indeed, \(\mathsf {Del} ^h\) and \(\mathsf {Del} ^{h'}\) return delegation keys for period \(j' - 1 = 2 j^*-2\), hence after applying \(\mathsf {DelEvo} \) we obtain re-encryption keys for period \(j^*-1\). \(\mathsf {ReGen} ^d\) is simulated honestly by delegating \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to a dishonest user. Using \(\mathsf {Evo} \) we evolve \(\mathsf {sk} _{\mathsf {DPKE}}^{(j')}, \mathsf {ek} _{\mathsf {DPKE}}^{(j')}\) to period \(j'+2\). Set \((\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)}) \leftarrow ((\mathsf {sk} _{\mathsf {DPKE}}^{(j'+1)}, \mathsf {sk} _{\mathsf {DPKE}}^{(j'+2)}), (\mathsf {ek} _{\mathsf {DPKE}}^{(j'+1)}, \mathsf {ek} _{\mathsf {DPKE}}^{(j'+2)}))\) and start \(A _1\) on \(\mathsf {st}, (\mathsf {sk} ^{(j^*)}, \mathsf {ek} ^{(j^*)})\) and simply forward the result.
-
Finally, when started on st and \(C _{j' - 1}\), \(C _{j'-1}\) is a level 1 ciphertext for \(j^*-1\). Hence we start \(A _1\) on the ciphertext and return its’ result.
Following the initial observation on the recoverability of delegation keys, an receiver-IND-CPA adversary is straightforward to define:
-
When started on \(\mathsf {pp} \), n and \(\mathsf {pk} \), honestly generate a key \((\mathsf {pk} ^*, \mathsf {sk} ^{(0)}, \mathsf {ek} ^{(0)}) \leftarrow \mathsf {Gen} (\mathsf {pp}, n)\) and store it in st. Choose
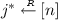 and store it together with \(\mathsf {pk} \) in st, and return \((j^*, \mathsf {pk} ^*, \textsf {st})\).
and store it together with \(\mathsf {pk} \) in st, and return \((j^*, \mathsf {pk} ^*, \textsf {st})\). -
When started on st to output the challenge messages, choose
 . Invoke the \(\mathsf {ReEnc} \) oracle as \((\cdot , \mathsf {dk}) \leftarrow \mathsf {ReEnc} (\mathsf {rk}, \mathsf {Enc} ^{(2)}(\mathsf {pk}, M _2, j^*))\) and store \(M _0, M _1, \mathsf {dk} \) in st. Return \(M _0, M _1, {\textsf {st}}\).
. Invoke the \(\mathsf {ReEnc} \) oracle as \((\cdot , \mathsf {dk}) \leftarrow \mathsf {ReEnc} (\mathsf {rk}, \mathsf {Enc} ^{(2)}(\mathsf {pk}, M _2, j^*))\) and store \(M _0, M _1, \mathsf {dk} \) in st. Return \(M _0, M _1, {\textsf {st}}\). -
Now when started on st and the challenge ciphertext \(C \), use \(\mathsf {dk} \) stored in st and obtain \(M \leftarrow \mathsf {DelDec} _{\mathsf {DPKE}}(\mathsf {sk} ^{(2j^* + 1)}, \mathsf {dk}, C)\). Check for which \(i \in \{ 0, 1 \}\) \(M = M _i\) and return i.
Regardless of the chosen period the adversary always wins, rendering the scheme insecure with respect to the fs-RIND-CPA notion. \(\square \)
From this theorem we obtain the following corollary:
Corollary 2
fs-PRE\(^+\) is a strictly stronger notion than fs-PRE\(^-\).
Note that this also shows that for conventional \(\mathsf {PRE}\) scheme there is a separation between the classical security notion of \(\mathsf {PRE}\) (\(\mathsf {PRE} ^-\)) as defined by Ateniese et al. and the \(\mathsf {PRE} ^+\) notion.
Notes
- 1.
With size O(n) for n key switches/time periods.
- 2.
A semi-trusted proxy honestly follows the protocols, i.e., stores consistent re-encryption keys and re-encrypts correctly.
- 3.
The well-established security notions for \(\mathsf {PRE}\) leave a potentially critical gap open. To look ahead, our proposed security model for forward-secret \(\mathsf {PRE}\) closes this gap (implicitly also for plain \(\mathsf {PRE}\)) and goes even beyond.
- 4.
We stress that we only aim at efficient non-trivial (non-interactive) forward-secret \(\mathsf {PRE}\) constructions that have sublinear-size public and re-encryption keys in the number of time periods.
- 5.
It is currently unknown to us how to solve the problem with efficient cryptographic tools, e.g., in the bilinear-maps setting. For efficiency reasons, multilinear maps and obfuscation are out of focus.
- 6.
- 7.
- 8.
- 9.
Clearly, we still have to trust that the proxy deletes past-period re-encryption key material.
- 10.
In the conventional \(\mathsf {PRE}\) setting, this gap was very recently independently addressed by Cohen [20].
- 11.
Observe that for a single period, i.e., \(n=1\), \(\mathsf {Evo} \) and \(\mathsf {ReEvo} \) in Definition 5 are not defined. Dropping these algorithms and the corresponding evolution keys \(\mathsf {ek} \) and \(\mathsf {rek} \) yields a plain \(\mathsf {PRE} \) scheme.
- 12.
As we will discuss below, this notion seems to suggest false guarantees and leaves a critical gap in the security model open.
- 13.
One can see the keys for period 2j as weak keys in the sense of [4, Third Attempt] whereas the keys for period \(2j-1\) constitute the master secret keys.
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_28
Applebaum, B., Harnik, D., Ishai, Y.: Semantic security under related-key attacks and applications. In: ICS (2011)
Ateniese, G., Benson, K., Hohenberger, S.: Key-private proxy re-encryption. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 279–294. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_19
Ateniese, G., Fu, K., Green, M., Hohenberger, S.: Improved proxy re-encryption schemes with applications to secure distributed storage. In: NDSS (2005)
Ateniese, G., Fu, K., Green, M., Hohenberger, S.: Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. 9(1), 1–30 (2006)
Bellare, M., Miner, S.K.: A forward-secure digital signature scheme. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 431–448. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_28
Bellare, M., Yee, B.: Forward-security in private-key cryptography. In: Joye, M. (ed.) CT-RSA 2003. LNCS, vol. 2612, pp. 1–18. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36563-X_1
Berners-Lee, E.: Improved security notions for proxy re-encryption to enforce access control. In: Latincrypt (2017)
Blaze, M., Bleumer, G., Strauss, M.: Divertible protocols and atomic proxy cryptography. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 127–144. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054122
Blazy, O., Bultel, X., Lafourcade, P.: Two secure anonymous proxy-based data storages. In: SECRYPT (2016)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Boneh, D., Gentry, C., Waters, B.: Collusion resistant broadcast encryption with short ciphertexts and private keys. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 258–275. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_16
Boneh, D., Waters, B.: A fully collusion resistant broadcast, trace, and revoke system. In: CCS (2006)
Borceaa, C., Guptaa, A.B.D., Polyakova, Y., Rohloffa, K., Ryana, G.: PICADOR: end-to-end encrypted publish-subscribe information distribution with proxy re-encryption. Future Gener. Comput. Syst. 71, 177–191 (2016)
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 255–271. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_16
Canetti, R., Hohenberger, S.: Chosen-ciphertext secure proxy re-encryption. In: CCS (2007)
Canetti, R., Raghuraman, S., Richelson, S., Vaikuntanathan, V.: Chosen-ciphertext secure fully homomorphic encryption. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 213–240. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_8
Chandran, N., Chase, M., Liu, F.-H., Nishimaki, R., Xagawa, K.: Re-encryption, functional re-encryption, and multi-hop re-encryption: a framework for achieving obfuscation-based security and instantiations from lattices. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 95–112. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_6
Chandran, N., Chase, M., Vaikuntanathan, V.: Functional re-encryption and collusion-resistant obfuscation. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 404–421. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_23
Cohen, A.: What about Bob? The inadequacy of CPA security for proxy re-encryption. Cryptology ePrint Archive, Report 2017/785 (2017)
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. In: STOC (2016)
Delerablée, C.: Identity-based broadcast encryption with constant size ciphertexts and private keys. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 200–215. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_12
Fan, X., Liu, F.H.: Proxy re-encryption and re-signatures from lattices. Cryptology ePrint Archive, Report 2017/456 (2017)
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC (2009)
Gentry, C., Silverberg, A.: Hierarchical ID-based cryptography. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 548–566. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_34
Green, M., Ateniese, G.: Identity-based proxy re-encryption. In: Katz, J., Yung, M. (eds.) ACNS 2007. LNCS, vol. 4521, pp. 288–306. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72738-5_19
Green, M.D., Miers, I.: Forward secure asynchronous messaging from puncturable encryption. In: IEEE S&P (2015)
Günther, C.G.: An identity-based key-exchange protocol. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 29–37. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_5
Günther, F., Hale, B., Jager, T., Lauer, S.: 0-RTT key exchange with full forward secrecy. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 519–548. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_18
Hanaoka, G., Kawai, Y., Kunihiro, N., Matsuda, T., Weng, J., Zhang, R., Zhao, Y.: Generic construction of chosen ciphertext secure proxy re-encryption. In: Dunkelman, O. (ed.) CT-RSA 2012. LNCS, vol. 7178, pp. 349–364. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27954-6_22
Hohenberger, S., Rothblum, G.N., Shelat, A., Vaikuntanathan, V.: Securely obfuscating re-encryption. J. Cryptol. 24, 694–719 (2011)
Libert, B., Vergnaud, D.: Tracing malicious proxies in proxy re-encryption. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 332–353. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_22
Libert, B., Vergnaud, D.: Unidirectional chosen-ciphertext secure proxy re-encryption. In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 360–379. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_21
Libert, B., Vergnaud, D.: Unidirectional chosen-ciphertext secure proxy re-encryption. IEEE Trans. Inf. Theory 57, 1786–1802 (2011)
Myers, S., Shull, A.: Efficient hybrid proxy re-encryption for practical revocation and key rotation. Cryptology ePrint Archive, Report 2017/833 (2017)
Polyakov, Y., Rohloff, K., Sahu, G., Vaikuntanathan, V.: Fast proxy re-encryption for publish/subscribe systems. ACM Trans. Priv. Secur. 20(4), 14 (2017)
Ren, Y., Gu, D., Wang, S., Zhang, X.: Hierarchical identity-based proxy re-encryption without random oracles. Int. J. Found. Comput. Sci. 21(6), 1049–1063 (2010)
Sakai, R., Furukawa, J.: Identity-based broadcast encryption. IACR Cryptology ePrint Archive (2007)
Tang, Q.: Type-based proxy re-encryption and its construction. In: Chowdhury, D.R., Rijmen, V., Das, A. (eds.) INDOCRYPT 2008. LNCS, vol. 5365, pp. 130–144. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89754-5_11
Tessaro, S., Wilson, D.A.: Bounded-collusion identity-based encryption from semantically-secure public-key encryption: generic constructions with short ciphertexts. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 257–274. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_15
Weng, J., Yang, Y., Tang, Q., Deng, R.H., Bao, F.: Efficient conditional proxy re-encryption with chosen-ciphertext security. In: Samarati, P., Yung, M., Martinelli, F., Ardagna, C.A. (eds.) ISC 2009. LNCS, vol. 5735, pp. 151–166. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04474-8_13
Xu, P., Xu, J., Wang, W., Jin, H., Susilo, W., Zou, D.: Generally hybrid proxy re-encryption: a secure data sharing among cryptographic clouds. In: AsiaCCS (2016)
Acknowledgments
Supported by H2020 project Prismacloud, grant agreement n\(\circ \)644962 and by H2020 project Credential, grant agreement n\(\circ \)653454. We thank all anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Derler, D., Krenn, S., Lorünser, T., Ramacher, S., Slamanig, D., Striecks, C. (2018). Revisiting Proxy Re-encryption: Forward Secrecy, Improved Security, and Applications. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10769. Springer, Cham. https://doi.org/10.1007/978-3-319-76578-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-76578-5_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76577-8
Online ISBN: 978-3-319-76578-5
eBook Packages: Computer ScienceComputer Science (R0)






 uniformly at random and run
uniformly at random and run 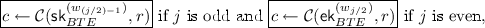
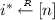 and output
and output 
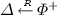 and compute
and compute 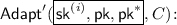 :
: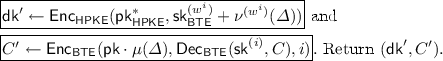
 :
: and evolve the secret key to period i, run
and evolve the secret key to period i, run 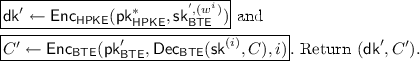


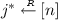 and store it together with
and store it together with  . Invoke the
. Invoke the 