Abstract
This paper contributes to understanding the interplay of security notions for PKE, KEMs, and DEMs, in settings with multiple users, challenges, and instances. We start analytically by first studying (a) the tightness aspects of the standard hybrid KEM+DEM encryption paradigm, (b) the inherent weak security properties of all deterministic DEMs due to generic key-collision attacks in the multi-instance setting, and (c) the negative effect of deterministic DEMs on the security of hybrid encryption.
We then switch to the constructive side by (d) introducing the concept of an augmented data encapsulation mechanism (ADEM) that promises robustness against multi-instance attacks, (e) proposing a variant of hybrid encryption that uses an ADEM instead of a DEM to alleviate the problems of the standard KEM+DEM composition, and (f) constructing practical ADEMs that are secure in the multi-instance setting.
The full version can be found in the IACR eprint archive as article 2017/843 (https://eprint.iacr.org/2017/843).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Hybrid encryption and its security. Public-key encryption (PKE) is typically implemented following a hybrid paradigm: To encrypt a message, first a randomized key encapsulation mechanism (KEM) is used to establish—independently of the message—a fresh session key that the receiver is able to recover using its secret key; then a deterministic data encapsulation mechanism (DEM) is used with the session key to encrypt the message. Both KEM and DEM output individual ciphertexts, and the overall PKE ciphertext is just their concatenation. Benefits obtained from deconstructing PKE into the two named components include easier implementation, deployment, and analysis. An independent reason that, in many cases, makes separating asymmetric from symmetric techniques actually necessary is that asymmetric cryptographic components can typically deal only with messages of limited length (e.g., 2048 bit messages in RSA-based systems) or of specific structure (e.g., points on an elliptic curve). The paradigm of hybrid encryption, where the message-processing components are strictly separated from the asymmetric ones, side-steps these disadvantages.
Hybrid encryption was first studied on a formal basis in [11]. (Implicitly the concept emerged much earlier, for instance in PGP email encryption.) The central result on the security of this paradigm is that combining a secure KEM with a secure DEM yields a secure PKE scheme. Various configurations of sufficient definitions of ‘secure’ for the three components have been proposed [11, 16, 18], with the common property that the corresponding security reductions are tight.
Multi-user security of PKE and KEMs. Classic security definitions for PKE, like IND-CPA and IND-CCA, formalize notions of confidentiality of a single message encrypted to a single user. (For public-key primitives, we identify (receiving) users with public keys.) This does not well-reflect real-world requirements where, in principle, billions of senders might use the same encryption algorithm to send, concurrently and independently of each other, related or unrelated messages to billions of receivers. Correspondingly, for adequately capturing security aspects of PKE that is deployed at large scale, generalizations of IND-CPA/CCA have been proposed that formalize indistinguishability in the face of multiple users and multiple challenge queries [4] (the goal of the adversary is to break confidentiality of one message, not necessarily of all messages). On the one hand, fortunately, these generalized notions turn out to be equivalent to the single-user single-challenge case [4] (thus supporting the relevance of the latter). On the other hand, and unfortunately, all known proofs of this statement use reductions that are not tight, losing a factor of \(n\cdot {q_e}\) where \(n\) is the number of users and \({q_e}\) the allowed number of challenge queries per user. Of course this does not mean that PKE schemes with tightly equivalent single- and multi-user security cannot exist, and indeed [1, 4, 12, 15, 17, 19, 20] expose examples of schemes with tight reductions between the two worlds.
The situation for KEMs is the same as for PKE: While the standard security definitions [11, 16] consider exclusively the single-user single-challenge case, natural multi-user multi-challenge variants have been considered and can be proven—up to a security loss with factor \(n\cdot {q_e}\)—equivalent to the standard notions.
Multi-instance security of DEMs. Besides scaled versions of security notions for PKE and KEMs, we also consider similarly generalized variants of DEM security. More specifically, we formalize a newFootnote 1 security notion for DEMs that assumes multiple independently generated instances and allows for one challenge encapsulation per instance. (For secret key primitives, we identify instances with secret keys.) The single-challenge restriction is due to the fact that overall we are interested in KEM+DEM composition and, akin to the single-instance case [11], a one-time notion for the DEM is sufficient (and, as we show, necessary) for proving security of the hybrid. As for PKE and KEMs, the multi-instance security of a DEM is closely coupled to its single-instance security; however, generically, if \(N\) is the number of instances, the corresponding reduction loses a factor of \(N\).
A couple of works [8, 22] observe that DEMs that possess a specific technical propertyFootnote 2 indeed have a lower security in the multi-instance setting than in the single-instance case. This is shown via attacks that assume a number of instances that is so large that, with considerable probability, different instances use the same encapsulation key; such key collisions can be detected, and message contents can be recovered. Note that, strictly speaking, the mentioned type of attack does not imply that the reduction of multi-instance to single-instance security is necessarily untight, as the attacks crucially depend on the DEM key size which is a parameter that does not appear in above tightness bounds. We finally point out that the attacks described in [8, 22] are not general but target only specific DEMs. In this paper we show that the security of any (deterministic) DEM degrades as the number of considered instances increases.
1.1 Our Contributions
This paper contributes to understanding the interplay of security notions for PKE, KEMs, and DEMs, in settings with multiple users, challenges, and instances. We start analytically by first studying (a) the tightness aspects of the standard hybrid KEM+DEM encryption paradigm, (b) the inherent weak security properties of deterministic DEMs in the multi-instance setting, and (c) the negative effect of deterministic DEMs on the security of hybrid encryption. We then switch to the constructive side by (d) introducing the concept of an augmented data encapsulation mechanism (ADEM) that promises robustness against multi-instance attacks, (e) proposing a variant of hybrid encryption that uses an ADEM instead of a DEM to alleviate the problems of the standard KEM+DEM composition, and (f) constructing secure practical ADEMs. We proceed with discussing some of these results in more detail, in the order in which they appear in the paper.
Standard KEM+DEM Hybrid Encryption. In Sect. 3 we define syntax and security properties of PKE, KEMs, and DEMs; we also recall hybrid encryption. Besides unifying the notation of algorithms and security definitions, the main contribution of this section is to provide a new multi-instance security notion for DEMs that matches the requirements of KEM+DEM hybrid encryption in the multi-user multi-challenge setting. That is, hybrid encryption is secure, tightly, if KEM and DEM are simultaneously secure (in our sense). We further show that any attack on the multi-instance security of the DEM tightly implies an attack on the multi-user multi-challenge security of the hybrid scheme. This implication is particularly relevant in the light of the results of Sect. 4, discussed next.
Generic Key-Collision Attacks on Deterministic DEMs. In Sect. 4 we study two attacks that target arbitrary (deterministic) DEMs, leveraging on the multi-instance setting and exploiting the tightness gap between single-instance and multi-instance security. Concretely, inspired by the key-collision attacks (also known as birthday-bound attacks) from [7, 8, 22], in Sects. 4.1 and 4.2 we describe two attacks against arbitrary DEMs that break indistinguishability or even recover encryption keys with success probability \({N^2}{/}{\left|\mathcal {K} \right|}\), where \(N\) is the number of instances and \(\mathcal {K}\) is the DEM’s key space. (The reason for specifying two attacks instead of just one is that deciding which one is preferable may depend on the particular DEM.) As mentioned above, in hybrid encryption these attacks carry over to the overall PKE.
What are the options to thwart the described attacks on DEMs? One way to avoid key-collision attacks in practice is of course to increase the key length of the DEM. This requires the extra burden of also changing the KEM (it has to output longer keys) and hence might not be a viable option. (Observe that leaving the KEM as-is but expanding its key to, say, double length using a PRG is not going to work as our generic DEM attacks would immediately kick in against that construction as well.) Another way to go would be to randomize the DEM. Drawbacks of this approach are that randomness might be a scarce resource (in particular on embedded systems, but also on desktop computers there is a price to pay for requesting randomnessFootnote 3), and that randomized schemes necessarily have longer ciphertexts than deterministic ones. In Sects. 5 to 7 we explore an alternative technique to overcome key-collision attacks in hybrid encryption without requiring further randomness and without requiring changing the KEM. We describe our approach in the following.
KEM+ADEM Hybrid Encryption. In Sect. 5 we introduce the concept of an augmented data encapsulation mechanism (ADEM). It is a variant of a DEM that takes an additional input: the tag. The intuition is that ADEMs are safer to use for hybrid encryption than regular DEMs, in particular in the presence of session-key collisions: Even if two keys collide, security is preserved if the corresponding tags are different. Importantly, the two generic DEM attacks from Sect. 4 do not apply to ADEMs. In Sect. 5 we further consider augmented hybrid encryption, which constructs PKE from a KEM and an ADEM by using the KEM ciphertext as ADEM tag. The corresponding security reduction is tight.
Practical ADEM Constructions. Sections 6 and 7 are dedicated to the construction of practical ADEMs. The two constructions in Sect. 6 are based on the well-known counter mode encryption, instantiated with an ideal random function and using the tag as initial counter value. We prove tight, beyond-birthday security bounds of the form \({N}{/}{\left|\mathcal {K} \right|}\) for the multi-instance security of our ADEMs. That is, our constructions provably do not fall prey to key collision attacks, in particular not the ones from [8, 22] and Sect. 4. Unfortunately, as they are based on counter mode, the two schemes per se are not secure against active adversaries. This is remedied in Sect. 7 where we show that an augmented message authentication code Footnote 4 (AMAC) can be used to generically strengthen a passively-secure ADEM to become secure against active adversaries. (We define AMACs and give a tightly secure construction in the same section.)
2 Notation
If S is a finite set,  denotes the operation of picking an element of S uniformly at random and assigning the result to variable s. For a randomized algorithm \(\mathsf {A}\) we write
denotes the operation of picking an element of S uniformly at random and assigning the result to variable s. For a randomized algorithm \(\mathsf {A}\) we write  to denote the operation of running \(\mathsf {A}\) with inputs \(x_1, x_2, \ldots \) and assigning the output to variable y. Further, we write \([\mathsf {A}(x_1, x_2, \ldots )]\) for the set of values that \(\mathsf {A}\) outputs with positive probability. We denote the concatenation of strings with \(\Vert \) and the XOR of same-length strings with \(\oplus \). If \(a\le b\) are natural numbers, we write
to denote the operation of running \(\mathsf {A}\) with inputs \(x_1, x_2, \ldots \) and assigning the output to variable y. Further, we write \([\mathsf {A}(x_1, x_2, \ldots )]\) for the set of values that \(\mathsf {A}\) outputs with positive probability. We denote the concatenation of strings with \(\Vert \) and the XOR of same-length strings with \(\oplus \). If \(a\le b\) are natural numbers, we write  for the range \(\{a,\ldots ,b\}\).
for the range \(\{a,\ldots ,b\}\).
We say a sequence \(v_1,\ldots ,v_n\) has a (two-)collision if there are indices \(1\le i<j\le n\) such that \(v_i=v_j\). More generally, the sequence has a k-collision if there exist \(1\le i_1<\ldots <i_k\le n\) such that \(v_{i_1}=\ldots =v_{i_k}\). We use predicate \(\mathbf {Coll}_{k}[\,]\) to indicate k-collisions. For instance, \(\mathbf {Coll}_{2}[1,2,3,2]\) evaluates to \( true \) and \(\mathbf {Coll}_{3}[1,2,3,2]\) evaluates to \( false \).
Let \(\mathcal {L}\) be a finite set of cardinality \(L=\left|\mathcal {L} \right|\). Sometimes we want to refer to the elements of \(\mathcal {L}\) in an arbitrary but circular way, i.e., such that indices x and \(x+L\) resolve to the same element. We do this by fixing an arbitrary bijection \(\llbracket \cdot \rrbracket _L:\mathbb {Z}/L\mathbb {Z}\rightarrow \mathcal {L}\) and extending the domain of \(\llbracket \cdot \rrbracket _L\) to the set \(\mathbb {Z}\) in the natural way. This makes expressions like \(\llbracket a+b \rrbracket _L\), for \(a,b\in \mathbb {N}\), well-defined. We use the shortcut notation \(\llbracket a \twoheadrightarrow l \rrbracket _{L}\) to refer to the span \(\{\llbracket a+1 \rrbracket _L,\ldots ,\llbracket a+l \rrbracket _L\}\) of length l. In particular we have \(\llbracket a \twoheadrightarrow 1 \rrbracket _{L}=\{\llbracket a+1 \rrbracket _L\}\).
Our security definitions are based on games played between a challenger and an adversary. These games are expressed using program code and terminate when the main code block executes ‘ ’; the argument of the latter is the output of the game. We write \(\Pr [G\Rightarrow 1]\) or \(\Pr [G\Rightarrow true ]\) or just \(\Pr [G]\) for the probability that game G terminates by executing a ‘
’; the argument of the latter is the output of the game. We write \(\Pr [G\Rightarrow 1]\) or \(\Pr [G\Rightarrow true ]\) or just \(\Pr [G]\) for the probability that game G terminates by executing a ‘ ’ instruction with a value interpreted as true. Further, if E is some game-internal event, we write \(\Pr [E]\) for the probability this event occurs. (Note the game is implicit in this notation.)
’ instruction with a value interpreted as true. Further, if E is some game-internal event, we write \(\Pr [E]\) for the probability this event occurs. (Note the game is implicit in this notation.)
3 Traditional KEM/DEM Composition and Its Weakness
We define PKE, KEMs, and DEMs, and give security definitions that consider multi-user, multi-challenge, and multi-instance attacks. Using the techniques from [4] we show that the multi notions are equivalent to their single counterparts, up to a huge tightness loss. We show that hybrid encryption enjoys tight security also in the multi settings. We finally show how (multi-instance) attacks on the DEM can be leveraged to attacks on the PKE.
3.1 Syntax and Security of PKE, KEMs, and DEMs
Public-key encryption. A public-key encryption scheme \({\mathsf {PKE}}= ({\mathsf {P\!{.}gen}},{\mathsf {P\!{.}enc}},{\mathsf {P\!{.}dec}})\) is a triple of algorithms together with a message space \(\mathcal {M}\) and a ciphertext space \(\mathcal {C}\). The randomized key-generation algorithm \({\mathsf {P\!{.}gen}}\) returns a pair \(( pk , sk )\) consisting of a public key and a secret key. The randomized encryption algorithm \({\mathsf {P\!{.}enc}}\) takes a public key \( pk \) and a message \(m \in \mathcal {M}\) to produce a ciphertext \(c\in \mathcal {C}\). Finally, the deterministic decryption algorithm \({\mathsf {P\!{.}dec}}\) takes a secret key \( sk \) and a ciphertext \(c\in \mathcal {C}\), and outputs either a message \(m\in \mathcal {M}\) or the special symbol \(\bot \notin \mathcal {M}\) to indicate rejection. The correctness requirement is that for all \(( pk , sk )\in [{\mathsf {P\!{.}gen}}]\), \(m \in \mathcal {M}\), and \(c\in [{\mathsf {P\!{.}enc}}( pk ,m)]\), we have \({\mathsf {P\!{.}dec}}( sk , c) = m\).
We adapt results from [4] to our notation, giving a game-based security definition for public-key encryption that formalizes multi-user multi-challenge indistinguishability: For a scheme \({\mathsf {PKE}}\), to any adversary \(\mathsf {A}\) and any number of users \(n\) we associate the distinguishing advantage  , where the two games are specified in Fig. 1. Note that if \({q_e}\) resp. \(q_d\) specify upper bounds on the number of \({\mathsf {Oenc}}\) and \({\mathsf {Odec}}\) queries per user, then the single-user configurations \((n,{q_e},q_d)=(1,1,0)\) and \((n,{q_e},q_d)=(1,1,\infty )\) correspond to standard definitions of IND-CPA and IND-CCA security for PKE.
, where the two games are specified in Fig. 1. Note that if \({q_e}\) resp. \(q_d\) specify upper bounds on the number of \({\mathsf {Oenc}}\) and \({\mathsf {Odec}}\) queries per user, then the single-user configurations \((n,{q_e},q_d)=(1,1,0)\) and \((n,{q_e},q_d)=(1,1,\infty )\) correspond to standard definitions of IND-CPA and IND-CCA security for PKE.
The following states that the multi-user multi-challenge notion is equivalent to the traditional single-user single-challenge case—up to a tightness loss linear in both the number of users and the number of challenges. The proof is in [4].
Lemma 1
[4]. For any public-key encryption scheme \({\mathsf {PKE}}\), any number of users \(n\), and any adversary \(\mathsf {A}\) that poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, there exists an adversary \(\mathsf {B}\) such that  , where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(n{q_e}\)-many \({\mathsf {P\!{.}enc}}\) operations and \(nq_d\)-many \({\mathsf {P\!{.}dec}}\) operations.
, where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(n{q_e}\)-many \({\mathsf {P\!{.}enc}}\) operations and \(nq_d\)-many \({\mathsf {P\!{.}dec}}\) operations.
Key encapsulation. A key-encapsulation mechanism \({\mathsf {KEM}}= ({\mathsf {K{.}gen}},{\mathsf {K{.}enc}},{\mathsf {K{.}dec}})\) for a finite session-key space \(\mathcal {K}\) is a triple of algorithms together with a ciphertext space \(\mathcal {C}\). The randomized key-generation algorithm \({\mathsf {K{.}gen}}\) returns a pair \(( pk , sk )\) consisting of a public key and a secret key. The randomized encapsulation algorithm \({\mathsf {K{.}enc}}\) takes a public key \( pk \) to produce a session key \(K\in \mathcal {K}\) and a ciphertext \(c\in \mathcal {C}\). Finally, the deterministic decapsulation algorithm \({\mathsf {K{.}dec}}\) takes a secret key \( sk \) and a ciphertext \(c\in \mathcal {C}\), and outputs either a session key \(K\in \mathcal {K}\) or the special symbol \(\bot \notin \mathcal {K}\) to indicate rejection. The correctness requirement is that for all \(( pk , sk )\in [{\mathsf {K{.}gen}}]\) and \((K,c)\in [{\mathsf {K{.}enc}}( pk )]\) we have \({\mathsf {K{.}dec}}( sk ,c) = K\).
Like for PKE schemes we give a security definition for KEMs that formalizes multi-user multi-challenge indistinguishability: For a scheme \({\mathsf {KEM}}\), to any adversary \(\mathsf {A}\) and any number of users \(n\) we associate the distinguishing advantage  , where the two games are specified in Fig. 2. Note that if \({q_e}\) resp. \(q_d\) specify upper bounds on the number of \({\mathsf {Oenc}}\) and \({\mathsf {Odec}}\) queries per user, then the single-user configurations \((n,{q_e},q_d)=(1,1,0)\) and \((n,{q_e},q_d)=(1,1,\infty )\) correspond precisely to standard definitions of IND-CPA and IND-CCA security for KEMs.
, where the two games are specified in Fig. 2. Note that if \({q_e}\) resp. \(q_d\) specify upper bounds on the number of \({\mathsf {Oenc}}\) and \({\mathsf {Odec}}\) queries per user, then the single-user configurations \((n,{q_e},q_d)=(1,1,0)\) and \((n,{q_e},q_d)=(1,1,\infty )\) correspond precisely to standard definitions of IND-CPA and IND-CCA security for KEMs.
Akin to the PKE case, our KEM multi-user multi-challenge notion is equivalent to its single-user single-challenge relative—again up to a tightness loss linear in the number of users and challenges. The proof can be found in the full version [14].
Lemma 2
For any key-encapsulation mechanism \({\mathsf {KEM}}\), any number of users \(n\), and any adversary \(\mathsf {A}\) that poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, there exists an adversary \(\mathsf {B}\) such that  , where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(n{q_e}\)-many \({\mathsf {K{.}enc}}\) operations and \(nq_d\)-many \({\mathsf {K{.}dec}}\) operations.
, where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(n{q_e}\)-many \({\mathsf {K{.}enc}}\) operations and \(nq_d\)-many \({\mathsf {K{.}dec}}\) operations.
Data encapsulation. A data-encapsulation mechanism \({\mathsf {DEM}}=({\mathsf {D{.}enc}},{\mathsf {D{.}dec}})\) for a message space \(\mathcal {M}\) is a pair of deterministic algorithms associated with a finite key space \(\mathcal {K}\) and a ciphertext space \(\mathcal {C}\). The encapsulation algorithm \({\mathsf {D{.}enc}}\) takes a key \(K\in \mathcal {K}\) and a message \(m \in \mathcal {M}\), and outputs a ciphertext \(c\in \mathcal {C}\). The decapsulation algorithm \({\mathsf {D{.}dec}}\) takes a key \(K\in \mathcal {K}\) and a ciphertext \(c\in \mathcal {C}\), and outputs either a message \(m\in \mathcal {M}\) or the special symbol \(\bot \notin \mathcal {M}\) to indicate rejection. The correctness requirement is that for all \(K\in \mathcal {K}\) and \(m\in \mathcal {M}\) we have \({\mathsf {D{.}dec}}(K,{\mathsf {D{.}enc}}(K,m))=m\).
As a security requirement for DEMs we formalize a multi-instance variant of the standard one-time indistinguishability notion: In our model the adversary can request one challenge encapsulation for each of a total of \(N\) independent keys; decapsulation queries are not restricted and can be asked multiple times for the same key. The corresponding games are in Fig. 3. Note that lines 05 and 09 ensure that the adversary cannot ask for decapsulations with respect to a key before having a challenge message encapsulated with it. (This matches the typical situation as it emerges in a KEM/DEM hybrid.) For a scheme \({\mathsf {DEM}}\), to any adversary \(\mathsf {A}\) and any number of instances \(N\) we associate the distinguishing advantage  . Note that if \(Q_d\) specifies a global upper bound on the number of \({\mathsf {Odec}}\) queries, then the single-instance configurations \((N,Q_d)=(1,0)\) and \((N,Q_d)=(1,\infty )\) correspond to standard definitions of OT-IND-CPA and OT-IND-CCA security for DEMs.
. Note that if \(Q_d\) specifies a global upper bound on the number of \({\mathsf {Odec}}\) queries, then the single-instance configurations \((N,Q_d)=(1,0)\) and \((N,Q_d)=(1,\infty )\) correspond to standard definitions of OT-IND-CPA and OT-IND-CCA security for DEMs.
Similarly to the cases of PKE and KEMs, our multi-instance notion for DEMs is equivalent to its single-instance counterpart, with a tightness loss of \(N\). The proof can be found in the full version [14].
Lemma 3
For any data-encapsulation mechanism \({\mathsf {DEM}}\), any number of instances \(N\), and any adversary \(\mathsf {A}\) that poses at most \(Q_d\)-many \({\mathsf {Odec}}\) queries in total, there exists an adversary \(\mathsf {B}\) such that  , where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(Q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(N\)-many \({\mathsf {D{.}enc}}\) operations and \(Q_d\)-many \({\mathsf {D{.}dec}}\) operations.
, where \(\mathsf {B}\) poses at most one \({\mathsf {Oenc}}\) and \(Q_d\)-many \({\mathsf {Odec}}\) queries. Further, the running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time needed to perform \(N\)-many \({\mathsf {D{.}enc}}\) operations and \(Q_d\)-many \({\mathsf {D{.}dec}}\) operations.
3.2 Hybrid Encryption
The main application of KEMs and DEMs is the construction of public key encryption: To obtain a (hybrid) PKE scheme, a KEM is used to establish a session key and a DEM is used with this key to protect the confidentiality of the message [11]. The details of this construction are in Fig. 4. It requires that the session key space of the KEM and the key space of the DEM coincide.
The central composability result for hybrid encryption [11] says that if the KEM and DEM components are strong enough then also their combination is secure, with tight reduction. In Theorem 1 we give a generalized version of this claim: it considers multiple users and challenges, and implies the result from [11] as a corollary. Note that also our generalization allows for a tight reduction. The proof can be found in the full version [14].
Theorem 1
Let \({\mathsf {PKE}}\) be the hybrid public-key encryption scheme constructed from a key-encapsulation mechanism \({\mathsf {KEM}}\) and a data-encapsulation mechanism \({\mathsf {DEM}}\) as in Fig. 4. Then for any number of users \(n\) and any PKE adversary \(\mathsf {A}\) that poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, there exist a KEM adversary \(\mathsf {B}\) and a DEM adversary \(\mathsf {C}\) such that

The running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time required to run \(n{q_e}\) DEM encapsulations and \(n{q_e}\) DEM decapsulations. The running time of \(\mathsf {C}\) is similar to the running time of \(\mathsf {A}\) plus the time required to run \(n{q_e}\) KEM encapsulations, \(n{q_e}\) KEM decapsulations, and \(n{q_e}\) DEM decapsulations. \(\mathsf {B}\) poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, and \(\mathsf {C}\) poses at most \(n{q_e}\)-many \({\mathsf {Oenc}}\) and \(nq_d\)-many \({\mathsf {Odec}}\) queries in total.
Theorem 1 bounds the distinguishing advantage of adversaries against hybrid PKE conditioned on its KEM and DEM components being secure. Note that from this result it cannot be deduced that deploying an insecure DEM (potentially in combination with a secure KEM) necessarily leads to insecure PKE. We show in Theorem 2 that also the latter implication holds. To ease the analysis, instead of requiring  -like properties of the KEM, we rather assume that it has uniformly distributed session keys. Formally this means that for all public keys \( pk \) the distribution of [
-like properties of the KEM, we rather assume that it has uniformly distributed session keys. Formally this means that for all public keys \( pk \) the distribution of [ ; output K] is identical with the uniform distribution on key space \(\mathcal {K}\). The proof can be found in the full version [14].
; output K] is identical with the uniform distribution on key space \(\mathcal {K}\). The proof can be found in the full version [14].
Theorem 2
For a key-encapsulation mechanism \({\mathsf {KEM}}\) and a data-encapsulation mechanism \({\mathsf {DEM}}\) let \({\mathsf {PKE}}\) be the corresponding hybrid encryption scheme. If \({\mathsf {KEM}}\) has uniform keys in \(\mathcal {K}\), any attack on \({\mathsf {DEM}}\) can be converted to an attack on \({\mathsf {PKE}}\). More precisely, for any \(n,{q_e}\) and any DEM adversary \(\mathsf {A}\) that poses in total at most \(n{q_e}\)-many \({\mathsf {Odec}}\) queries, there exists an adversary \(\mathsf {B}\) such that

The running time of \(\mathsf {B}\) is about that of \(\mathsf {A}\), and \(\mathsf {B}\) poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) queries per user and \(Q_d\)-many \({\mathsf {Odec}}\) queries in total.
4 Deterministic DEMs and Their Multi-instance Security
We give two generic key-collision attacks on the multi-instance security of (deterministic) DEMs. They have different attack goals (indistinguishability vs. key recovery) and succeed with slightly different probabilities. More precisely, in both cases the leading term of the success probability comes from the birthday bound and evaluates to roughly \({N^2}{/}{\left|\mathcal {K} \right|}\), and is thus much larger than the \({N}{/}{\left|\mathcal {K} \right|}\) that intuition might expect. By Theorem 2 the attacks can directly be lifted to ones targeting the multi-user multi-challenge security of a corresponding hybrid encryption scheme, achieving the same advantage.
4.1 A Passive Multi-instance Distinguishing Attack on DEMs
We describe an attack against multi-instance indistinguishability that applies generically to all DEMs. Notably, the attack is fully passive, i.e., the adversary does not pose any query to its \({\mathsf {Odec}}\) oracle. As technical requirements we assume a finite message space and a number of instances such that the inequalities \(N^2\le 2\left|\mathcal {K} \right|\) and \(\left|\mathcal {M} \right| \ge 3\left|\mathcal {K} \right|+N-1\) are fulfilled. We consider these conditions extremely mild, since in practice \(\mathcal {M}\) is very large and the value \(N\) can be chosen arbitrarily low by simply discarding some inputs.
For any value \(N\in \mathbb {N}\) the details of our adversary \(\mathsf {A}=\mathsf {A}_N\) are in Fig. 5a. It works as follows: It starts by picking uniformly at random messages \(m_0,m_1^1,\ldots ,m_1^N\in \mathcal {M}\) such that \(m_1^1,\ldots ,m_1^N\) are pairwise distinct. (Note the corresponding requirement \(N\le \left|\mathcal {M} \right|\) follows from above condition.) The adversary then asks for encapsulations of these messages in a way such that it obtains either \(N\) encapsulations of \(m_0\) (if executed in game  ), or one encapsulation of each message \(m_1^j\) (if executed in game
), or one encapsulation of each message \(m_1^j\) (if executed in game  ). If any two of the received ciphertexts collide, the adversary outputs 1; otherwise it outputs 0. The following theorem makes statements about advantage and running time of this adversary.
). If any two of the received ciphertexts collide, the adversary outputs 1; otherwise it outputs 0. The following theorem makes statements about advantage and running time of this adversary.
Theorem 3
For a finite message space \(\mathcal {M}\), let \({\mathsf {DEM}}\) be a DEM with key space \(\mathcal {K}\). Suppose that \(N^2\le 2\left|\mathcal {K} \right|\) and \(\left|\mathcal {M} \right| \ge 3\left|\mathcal {K} \right|+N-1\). Then adversary \(\mathsf {A}\) from Fig. 5a breaks the \(N\)-instance indistinguishability of \({\mathsf {DEM}}\), achieving the advantage

Its running time is \(\mathcal {O}(N\log N)\), and it poses \(N\)-many \({\mathsf {Oenc}}\) and no \({\mathsf {Odec}}\) queries.
We remark that, more generally, the bound on \(\left|\mathcal {M} \right|\) can be relaxed to \(\left|\mathcal {M} \right| \ge 2\,\left|\mathcal {K} \right|\,(1+\delta )+N-1\) for some \(\delta \ge 0\) to obtain  .
.
Proof
The task of collecting \(N\) ciphertexts and checking for the occurrence of a collision can be completed in \(\mathcal {O}(N\log N)\) operations. In the following we first assess the performance of the adversary when executed in games  and
and  ; then we combine the results.
; then we combine the results.
Case  . Adversary \(\mathsf {A}\) receives \(N\) encapsulations of the same message \(m_0\), created with \(N\) independent keys \(K_1,\ldots ,K_N\). If two of these keys collide then the corresponding (deterministic) encapsulations collide as well and \(\mathsf {A}\) returns 1. Since \(N(N-1)<N^2\le 2\left|\mathcal {K} \right|\) by the birthday bound we obtain
. Adversary \(\mathsf {A}\) receives \(N\) encapsulations of the same message \(m_0\), created with \(N\) independent keys \(K_1,\ldots ,K_N\). If two of these keys collide then the corresponding (deterministic) encapsulations collide as well and \(\mathsf {A}\) returns 1. Since \(N(N-1)<N^2\le 2\left|\mathcal {K} \right|\) by the birthday bound we obtain

Case  . Adversary \(\mathsf {A}\) receives encapsulations \(c^1,\ldots ,c^N\) of uniformly distributed (but distinct) messages \(m_1^1,\ldots ,m_1^N\). Denote with \(K_j\) the key used to compute \(c^j\), let
. Adversary \(\mathsf {A}\) receives encapsulations \(c^1,\ldots ,c^N\) of uniformly distributed (but distinct) messages \(m_1^1,\ldots ,m_1^N\). Denote with \(K_j\) the key used to compute \(c^j\), let  , and let further
, and let further  denote the image of \(\mathcal {M}_j\) under (injective) function \({\mathsf {D{.}enc}}(K_j,\cdot )\). Observe this setup implies \(\left|\mathcal {C}_j \right|=\left|\mathcal {M}_j \right|\) and \(\left|\mathcal {C}_1 \right|>\ldots >\left|\mathcal {C}_N \right|\). If further follows that each ciphertext \(c^j\) is uniformly distributed in set \(\mathcal {C}_j\).
denote the image of \(\mathcal {M}_j\) under (injective) function \({\mathsf {D{.}enc}}(K_j,\cdot )\). Observe this setup implies \(\left|\mathcal {C}_j \right|=\left|\mathcal {M}_j \right|\) and \(\left|\mathcal {C}_1 \right|>\ldots >\left|\mathcal {C}_N \right|\). If further follows that each ciphertext \(c^j\) is uniformly distributed in set \(\mathcal {C}_j\).
We aim at establishing an upper-bound on the collision probability of ciphertexts \(c^1,\ldots ,c^N\). The maximum collision probability is attained in the worst-case \(\mathcal {C}_1 \supset \ldots \supset \mathcal {C}_N\), in which it is bounded by the collision probability of choosing \(N\) values uniformly from a set of cardinality \(\left|\mathcal {C}_N \right|=\left|\mathcal {M} \right|-N+1\). Using again the birthday bound and \(\left|\mathcal {M} \right| \ge 3\left|\mathcal {K} \right|+N-1\) we obtain

Combining the two bounds yields the equation in our statement.
4.2 A Passive Multi-instance Key-Recovery Attack on DEMs
We give a generic attack on DEMs that aims at recovering keys rather than distinguishing encapsulations. Like in Sect. 4.1 the attack is passive. It is inspired by work of Zaverucha [22] and Chatterjee et al. [8]. However, our results are more general than theirs for not restricted to one specific DEM.
To formalize the notion of resilience against key recovery we correspondingly adapt the  game from Fig. 3 and obtain the
game from Fig. 3 and obtain the  game specified in Fig. 6. The \(N\)-instance advantage of an adversary \(\mathsf {A}\) is then defined as
game specified in Fig. 6. The \(N\)-instance advantage of an adversary \(\mathsf {A}\) is then defined as  . The following theorem shows that for virtually all practical DEMs (including those based on CBC mode, CTR mode, OCB, etc., and even one-time pad encryption) there exist adversaries achieving a considerable key recovery advantage, conditioned on the DEM key space being small enough. Concretely, the adversaries we propose encapsulate \(2N\) times the same message (\(N\) times with random but known keys, and \(N\) times with random but unknown keys) and detect collisions of ciphertexts.Footnote 5 As any ciphertext collision stems (in practice) from a collision of keys, this method allows for key recovery.Footnote 6
. The following theorem shows that for virtually all practical DEMs (including those based on CBC mode, CTR mode, OCB, etc., and even one-time pad encryption) there exist adversaries achieving a considerable key recovery advantage, conditioned on the DEM key space being small enough. Concretely, the adversaries we propose encapsulate \(2N\) times the same message (\(N\) times with random but known keys, and \(N\) times with random but unknown keys) and detect collisions of ciphertexts.Footnote 5 As any ciphertext collision stems (in practice) from a collision of keys, this method allows for key recovery.Footnote 6
Theorem 4
Fix a DEM and denote its key space with \(\mathcal {K}\) and its message space with \(\mathcal {M}\). Let \(m_0\in \mathcal {M}\) be any fixed message. Fixing \(N\in \mathbb {N}\) as a parameter, consider the adversary \(\mathsf {A}=\mathsf {A}_{N}\) specified in Fig. 5b. We then have

where \(p(m_0)\) denotes the collision probability

Its running time is \(\mathcal {O}(N\log N)\), and it poses \(N\)-many \({\mathsf {Oenc}}\) and no \({\mathsf {Odec}}\) queries.
We further prove that in the case of DEMs based on one-time pad encryption we have \(p(m_0)=1\) for any \(m_0\). Further, in the case of CBC-based encapsulation there exists a message \(m_0\) such that \( p(m_0)=\left|\mathcal {B} \right|/(\left|\mathcal {B} \right|+\left|\mathcal {K} \right|-1) \), where \(\mathcal {B}\) is the block space of the blockcipher and the latter is modeled as an ideal cipher.
Note that the performance of our attack crucially depends on the choice of message \(m_0\), and that there does not seem to be a general technique for identifying good candidates. In particular, (artificial) DEMs can be constructed where \(p(m_0)\) is small for some \(m_0\) but large for others, or where \(p(m_0)\) is small even for very long messages \(m_0\). However, in many practical schemes the choice of \(m_0\) is not determinant. After the proof we consider two concrete examples.
Proof
The running time of \(\mathsf {A}\) is upper bounded by the search for collisions in line 05, since all other operations require at most linear time in \(N\). We estimate the time bound: The list \(c_1,\ldots ,c_N\) is sorted, requiring time \(\mathcal {O}(N\log N)\). Searching an element in the ordered list requires \(\mathcal {O}(\log N)\) time. Repeating for all \(N\) searches requires \(\mathcal {O}(N\log N)\). Combining these observations yields our statement.
We claim that the probability that the adversary does not output \(\bot \) (in symbols, \(\mathsf {A}_{N}\nRightarrow \bot \)) is lower bounded by:
Since the DEM is deterministic, the probability to find any collision in line 05 is larger than the probability that any of the distinct \(N\) keys generated in lines 00–02 collides with one of the \(N\) keys \(\tilde{K}_1,\ldots ,\tilde{K}_N\) used by the  game to encapsulate. We compute the latter probability. Let \(K\in \{\tilde{K}_1,\ldots ,\tilde{K}_N\}\). We know that K is uniform in \(\mathcal {K}\). Since \(K_1,\ldots ,K_N\) are distinct and independently chosen we can write: \( \Pr _{}\mathopen {}[K\in \{K_1,\ldots ,K_N\}]\mathclose {} = {N}/{\left|\mathcal {K} \right|}. \) Moreover, since the keys \(\tilde{K}_1,\ldots ,\tilde{K}_N\) are generated independently of each other, Eq. (1) follows.
game to encapsulate. We compute the latter probability. Let \(K\in \{\tilde{K}_1,\ldots ,\tilde{K}_N\}\). We know that K is uniform in \(\mathcal {K}\). Since \(K_1,\ldots ,K_N\) are distinct and independently chosen we can write: \( \Pr _{}\mathopen {}[K\in \{K_1,\ldots ,K_N\}]\mathclose {} = {N}/{\left|\mathcal {K} \right|}. \) Moreover, since the keys \(\tilde{K}_1,\ldots ,\tilde{K}_N\) are generated independently of each other, Eq. (1) follows.
Let now (i, j) be the indices for which the condition in line 05 is triggered, i.e., \(c_i=c^\prime _j\) and \(\mathsf {A}_{N}\) outputs \(K_i\). We can write:

Applying known inequalities to the previous formula we obtain:

We compute \(p(m_0)\) for two specific DEMs (one-time pad and CBC mode) and choices of \(m_0\). We formalize the argument for CBC by considering single-block messages. We note that one can apply the same argument to other modes of operation, e.g., CTR. For notational simplicity we omit the description of the probability space, that is, uniform choice of \(K_1,K_2\in \mathcal {K}\).
- One-time pad. :
-
The one-time pad DEM encapsulation is given by combining a key \(K\in \mathcal {K}=\{0,1\}^k\) with a message \(m\in \mathcal {M}=\{0,1\}^k\) using the XOR operation. In this case, if two ciphertexts for the same message collide, the same key must have been used to encapsulate. Thus \(p(m_0)=1\) for all \(m_0\).
- CBC with an ideal cipher. :
-
CBC-based DEM encapsulation consists of encrypting the message using a blockcipher in CBC mode with the zero initialization vector (IV). In the following analysis we assume an idealized blockcipher (ideal cipher model) represented by \({\mathsf {E}}\). Note that since the IV is zero, encapsulating a single-block message \(m_0\) under the key K is equivalent to enciphering \(m_0\) with \({\mathsf {E}}_K\). Let \(\mathcal {B}\) be the block space. First we observe that for any single-block message \(m_0\) we have
$$\begin{aligned} {=}&\Pr [{\mathsf {E}}_{K_1}(m_0)={\mathsf {E}}_{K_2}(m_0)]\\&= \Pr [K_1=K_2]+\Pr [K_1\ne K_2]\Pr [{\mathsf {E}}_{K_1}(m_0)={\mathsf {E}}_{K_2}(m_0)\mid K_1\ne K_2] \\&= \left|\mathcal {K} \right|^{-1}+(1-\left|\mathcal {K} \right|^{-1})\left|\mathcal {B} \right|^{-1}. \end{aligned}$$We then use the previous equality to compute \(p(m_0)\) from its definition:
$$\begin{aligned} p(m_0)&= \frac{\Pr [K_1=K_2]}{\Pr [{\mathsf {E}}_{K_1}(m_0)={\mathsf {E}}_{K_2}(m_0)]}\\&= \frac{\left|\mathcal {K} \right|^{-1}}{\left|\mathcal {K} \right|^{-1}+(1-\left|\mathcal {K} \right|^{-1})\left|\mathcal {B} \right|^{-1}} = \frac{\left|\mathcal {B} \right|}{\left|\mathcal {B} \right|+\left|\mathcal {K} \right|-1}. \end{aligned}$$As an example, if \(\left|\mathcal {B} \right|\ge \left|\mathcal {K} \right|\) then \(p(m_0)> 1/2\) for any single-block message \(m_0\).
5 Augmented Data Encapsulation
In the previous sections we showed that all deterministic DEMs, including those that are widely used in practice, might be less secure than expected in the face of multi-instance attacks. We further showed that, in the setting of hybrid encryption, attacks on DEMs can be leveraged to attacks on the overall PKE. Given that the KEM+DEM paradigm is so important in practice, we next address the question of how this situation can be remedied. One option would of course be to increase the DEM key size (recall that good success probabilities in Theorems 3 and 4 are achieved only for not too large key spaces); however, increasing key sizes might not be a viable option in practical systems. (Potential reasons for this include that blockciphers like AES are slower with long keys than with short keys, and that ciphers like 3DES do not support key lengths that have a comfortable ‘multi-instance security margin’ in the first place.) A second option would be to augment the input given to the DEM encapsulation routine by an additional value. This idea was already considered in [22, p. 16] where, with the intuition of increasing the ‘entropy’ available to the DEM, it was proposed to use a KEM ciphertext as an initialization vector (IV) of a symmetric encryption mode. However, [22] does not contain any formalization or security analysis of this idea, and so it cannot be taken as granted that this strategy actually works. (And indeed, we show in Sect. 6.3 that deriving the starting value of blockcipher-based counter mode encryption from a KEM ciphertext is not ameliorating the situation for attacks based on indistinguishability.)
We formally explore the additional-input proposal for the DEM in this section. More precisely, we study two approaches of defining an augmented data encapsulation mechanism (ADEM), where we call the additional input the tag. The syntax is the same in both cases, but the security properties differ: either (a) the DEM encapsulator receives as the tag an auxiliary random (but public) string, or (b) the encapsulator receives as additional input a nonce (a ‘number used once’). In both cases the decapsulation oracle operates with respect to the tag also used for encapsulation. After formalizing this we prove the following results: First, if the tag space is large enough, ADEMs that expect a nonce can safely replace ADEMs that expect a uniform tag. Second, ADEMs that expect a uniform tag can be constructed from ADEMs that expect a nonce by applying a random oracle to the latter. Our third result is that the augmented variant of hybrid encryption remains (tightly) secure.
Augmented data encapsulation. An augmented data encapsulation mechanism \({\mathsf {ADEM}}=({\mathsf {A{.}enc}},{\mathsf {A{.}dec}})\) for a message space \(\mathcal {M}\) is a pair of deterministic algorithms associated with a finite key space \(\mathcal {K}\), a tag space \({\mathcal {T}}\), and a ciphertext space \(\mathcal {C}\). The encapsulation algorithm \({\mathsf {A{.}enc}}\) takes a key \(K\in \mathcal {K}\), a tag \(t\in {\mathcal {T}}\), and a message \(m \in \mathcal {M}\), and outputs a ciphertext \(c\in \mathcal {C}\). The decapsulation algorithm \({\mathsf {A{.}dec}}\) takes a key \(K\in \mathcal {K}\), a tag \(t\in {\mathcal {T}}\), and a ciphertext \(c\in \mathcal {C}\), and outputs either a message \(m\in \mathcal {M}\) or the special symbol \(\bot \notin \mathcal {M}\) to indicate rejection. The correctness requirement is that for all \(K\in \mathcal {K}\) and \(t\in {\mathcal {T}}\) and \(m\in \mathcal {M}\) we have \({\mathsf {A{.}dec}}(K,t,{\mathsf {A{.}enc}}(K,t,m))=m\).
Augmented data encapsulation with uniform tags. The first security notion we formalize assumes that each encapsulation operation uses a fresh and uniformly picked tag (note this imposes the technical requirement that the tag space be finite). More precisely, while the tag may become public after the encapsulation operation has completed, it may not be disclosed to the adversary before fixing the message to be encapsulated. We formalize this notion of uniform-tag multi-instance one-time indistinguishability for ADEMs via the games specified in Fig. 7. For a scheme \({\mathsf {ADEM}}\), to any adversary \(\mathsf {A}\) and any number of instances \(N\) we associate the distinguishing advantage  .
.
Augmented data encapsulation with nonces. Our second security notion for ADEMs requires the tag provided to each encapsulation operation to be unique (across all instances). The tag can be generated using any possible method (e.g., using some global type of counter). We formalize the corresponding security notion of nonce-based multi-instance one-time indistinguishability for ADEMs via the games specified in Fig. 8. For a scheme \({\mathsf {ADEM}}\), to any adversary \(\mathsf {A}\) and any number of instances \(N\) we associate the distinguishing advantage  .
.
5.1 Relations Between ADEMs with Uniform and Nonce Tags
The two types of ADEMs we consider here can be constructed from each other. More concretely, the following lemma shows that if the tag space is large enough, ADEMs that expect a nonce can safely replace ADEMs that expect a uniform tag. The proof can be found in the full version [14].
Lemma 4
Let \({\mathsf {ADEM}}\) be an augmented data encapsulation mechanism. If the cardinality of its tag space \({\mathcal {T}}\) is large enough and \({\mathsf {ADEM}}\) is secure with non-repeating tags, then it is also secure with random tags. More precisely, for any number of instances \(N\) and any adversary \(\mathsf {A}\) there exist an adversary \(\mathsf {B}\) that makes the same amount of queries such that  . The running time of the two adversaries is similar.
. The running time of the two adversaries is similar.
The following simple lemma shows that ADEMs that expect a nonce can be constructed from ADEMs that expect a uniform tag by using each nonce to obtain a uniform, independent value from a random oracle. The proof is immediate since all queries to the random oracle have different input, thus the corresponding output is uniformly random and independently generated.
Lemma 5
Let \({\mathsf {ADEM}}=({\mathsf {A{.}enc}},{\mathsf {A{.}dec}})\) be an augmented data encapsulation mechanism with tag space \({\mathcal {T}}\). Let \(H:{\mathcal {T}}'\rightarrow {\mathcal {T}}\) denote a hash function, where \({\mathcal {T}}'\) is another tag space. Define \({\mathsf {ADEM}}'=({\mathsf {A{.}enc}}',{\mathsf {A{.}dec}}')\) such that  and
and  . Then if H is modeled as a random oracle and if \({\mathsf {ADEM}}\) is secure with random tags in \({\mathcal {T}}\), then \({\mathsf {ADEM}}'\) is secure with non-repeating tags in \({\mathcal {T}}'\). Formally, for any number of instances \(N\) and any adversary \(\mathsf {A}\) there exists an adversary \(\mathsf {B}\) with
. Then if H is modeled as a random oracle and if \({\mathsf {ADEM}}\) is secure with random tags in \({\mathcal {T}}\), then \({\mathsf {ADEM}}'\) is secure with non-repeating tags in \({\mathcal {T}}'\). Formally, for any number of instances \(N\) and any adversary \(\mathsf {A}\) there exists an adversary \(\mathsf {B}\) with  .
.
5.2 Augmented Hybrid Encryption
A KEM and an ADEM can be combined to obtain a PKE scheme: the KEM establishes a session key and a first ciphertext component, and the ADEM is used on input the session key and the first ciphertext component (as tag) to protect the confidentiality of the message, creating a second ciphertext component. Figure 9 details this augmented hybrid encryption. It requires that the session key space of the KEM and the key space of the ADEM coincide. Further, the ciphertext space of the KEM needs to be a subset of the tag space of the ADEM.
The claim is that augmented hybrid encryption is more robust against attacks involving multiple users and challenges than standard hybrid encryption (see Fig. 4). The security condition posed on the ADEM requires that it be secure when operated with nonces, and the security property posed on the KEM requires that it be both indistinguishable and have non-repeating ciphertexts (i.e., invoking the encapsulation twice on any public keys does virtually never result in colliding ciphertexts). Technically, the latter property is implied by indistinguishability. However, to obtain better bounds, we formalize it as a statistical condition: To any scheme \({\mathsf {KEM}}\) we assign the maximum ciphertext-collision probability

where the maximum is over all pairs \( pk _1, pk _2\) of (potentially coinciding) public keys. Note that practical KEMs (ElGamal, RSA-based, Cramer–Shoup, ...) have much larger ciphertexts than session keysFootnote 7, so that the ciphertext-collision probability will always be negligible in practice. We proceed with a security claim for augmented hybrid encryption. The proof can be found in the full version [14].
Lemma 6
Let \({\mathsf {PKE}}\) be the hybrid public-key encryption scheme constructed from a key-encapsulation mechanism \({\mathsf {KEM}}\) and an augmented data-encapsulation mechanism \({\mathsf {ADEM}}\) as in Fig. 9. Let p be the maximum ciphertext-collision probability of \({\mathsf {KEM}}\) over all possible public keys. Then for any \(n\) and any PKE adversary \(\mathsf {A}\) that poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, there exist a KEM adversary \(\mathsf {B}\) and an ADEM adversary \(\mathsf {C}\) such that

where \(N=n{q_e}\). The running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time required to run \(n{q_e}\) ADEM encapsulations and \(n{q_e}\) ADEM decapsulations. The running time of \(\mathsf {C}\) is similar to that of \(\mathsf {A}\) plus the time required to run \(n{q_e}\) KEM encapsulations, \(n{q_e}\) KEM decapsulations, and \(n{q_e}\) ADEM decapsulations. \(\mathsf {B}\) poses at most \({q_e}\)-many \({\mathsf {Oenc}}\) and \(q_d\)-many \({\mathsf {Odec}}\) queries per user, and \(\mathsf {C}\) poses at most \(n{q_e}\)-many \({\mathsf {Oenc}}\) and \(nq_d\)-many \({\mathsf {Odec}}\) queries in total.
6 Constructions of Augmented Data Encapsulation
We construct two augmented data-encapsulation mechanisms and analyze their security. The schemes are based on operating a function in counter mode. If the function is instantiated with an ideal random function then the ADEMs are secure beyond the birthday bound. (We also show that if the function is instead instantiated with an idealized blockcipher, i.e., a random permutation, the schemes’ security may degrade.) Practical candidates for instantiating the ideal random function are for instance the compression functions of standardized Merkle–Damgård hash functions, e.g., of SHA2.Footnote 8 \(^{,}\) Footnote 9 Another possibility is deriving the random function from an ideal cipher as in [21].
6.1 Counter-Mode Encryption
Many practical DEMs are based on operating a blockcipher E in counter mode (CTR). Here, in brief, the encapsulation key is used as the blockcipher key, a sequence of message-independent input blocks is enciphered under that key, and the output blocks are XOR-ed into the message. More concretely, if under some key K a message m shall be encapsulated that, without requiring padding, evenly splits into blocks \(v_1\Vert \ldots \Vert v_l\), then the DEM ciphertext is the concatenation \(w_1\Vert \ldots \Vert w_l\) where \(w_i=v_i\oplus E_K(i)\).
In the context of this paper, three properties of this construction are worth pointing out: (a) the ‘counting’ component of CTR mode serves a single purpose: preventing that two inputs to the blockcipher coincide; (b) any ‘starting value’ for the counter can be used; (c) security analyses of CTR mode typically model E as a pseudorandom function (as opposed to a pseudorandom permutation)Footnote 10.
In Fig. 10 we detail three ways of turning the principles of CTR mode into a DEM encapsulation routine. In all cases the underlying primitive is, syntactically, a function \(F:\mathcal {K}\times \mathcal {B}\rightarrow \mathcal {D}\) that takes a key \(K\in \mathcal {K}\) and maps some finite input space \(\mathcal {B}\) into some finite group \((\mathcal {D},\oplus )\). (Intuitively, \(\mathcal {B}\) serves as a space of input blocks derived from a counter, and \(\mathcal {D}\) as a space of pads that can be XORed into message blocks; note that if F is instantiated with a blockcipher we have \(\mathcal {B}=\mathcal {D}\), but we explicitly allow other instantiations.) The most basic encapsulation routine based on CTR mode that we consider, and the one closest to our sketch above, is \({\mathsf {CTR0enc}}\). Note that this DEM further assumes a bijection \(\llbracket \cdot \rrbracket _L:\mathbb {Z}/L\mathbb {Z}\rightarrow \mathcal {L}\) with \(\mathcal {L}=\mathcal {B}\). (Intuitively, this bijection turns a counter that is cyclic with period length L into input blocks for F; see Sect. 2 for notation.) We finally point out that all three variants of CTR mode that we formalize exclusively work with fixed-length multi-block messages (i.e., \(\mathcal {M}=\mathcal {D}^l\)). This choice, that we made for simplicity of exposition, is not really a restriction as ‘any-length’ CTR mode encryption can be simulated from ‘block-wise’ CTR mode encryption.
Encapsulation algorithms of the \({\mathsf {CTR0}}\) DEM, the \({\mathsf {CTR}}\)+ ADEM, and the \({\mathsf {CTR\Vert }}\) ADEM, for multi-block messages. In \({\mathsf {CTR0enc}}\) and \({\mathsf {CTR}}{+}{\mathsf {enc}}\) we assume \(\llbracket \cdot \rrbracket _L:\mathbb {Z}/L\mathbb {Z}\rightarrow \mathcal {L}\) with \(\mathcal {L}=\mathcal {B}\), and in \({\mathsf {CTR\Vert enc}}\) we assume \(\llbracket \cdot \rrbracket _L:\mathbb {Z}/L\mathbb {Z}\rightarrow \mathcal {L}\) and \({\mathcal {T}}\) such that \(\mathcal {B}={\mathcal {T}}\times \mathcal {L}\). The corresponding decapsulation routines is immediate.
The two remaining procedures in Fig. 10 are ADEM encapsulation routines. The first one, \({\mathsf {CTR}}{+}{\mathsf {enc}}\), is the natural variant of \({\mathsf {CTR0enc}}\) where the tag space is  and the tag specifies the starting value of the counter. The second, \({\mathsf {CTR\Vert enc}}\), concatenates tag and counter. Here, the tag space \({\mathcal {T}}\) and parameter space \(\mathcal {L}\) have to be arranged such that \(\mathcal {B}={\mathcal {T}}\times \mathcal {L}\).
and the tag specifies the starting value of the counter. The second, \({\mathsf {CTR\Vert enc}}\), concatenates tag and counter. Here, the tag space \({\mathcal {T}}\) and parameter space \(\mathcal {L}\) have to be arranged such that \(\mathcal {B}={\mathcal {T}}\times \mathcal {L}\).
We analyze the security of \({\mathsf {CTR}}\)+ and \({\mathsf {CTR\Vert }}\) in the upcoming sections. Scheme \({\mathsf {CTR0}}\) is not an ADEM and falls prey to our earlier attacks.
6.2 Security of Function-Based Counter Mode
We establish upper bounds on the advantage of  adversaries against the \({\mathsf {CTR}}\)+ and \({\mathsf {CTR\Vert }}\) ADEMs.
adversaries against the \({\mathsf {CTR}}\)+ and \({\mathsf {CTR\Vert }}\) ADEMs.
Counter Mode with Tag-Controlled Starting Value. We limit the maximum amount of blocks in an encapsulation query to a fixed value \(\ell \). Prerequisites to our statement on \({\mathsf {CTR}}\)+ are two conditions on the number of instances relative to \(\mathcal {K}\) and  . The bound is namely \(N\le \min \big \{\left|\mathcal {K} \right|^{1/2},(\left|{\mathcal {T}} \right|/(2\ell ))^{1/(1+\delta )}\big \}\), for some arbitrary constant \(\delta \) such that \(1/N\le \delta \le 1\). Despite this restriction we consider our statement to be reflecting real-world applications: As an extreme example we see that the values \(\left|\mathcal {K} \right|=\left|{\mathcal {T}} \right|=2^{128}\), \(N=2^{56}\), \(\ell =2^{56}\), \(q=2^{64}\) and \(\delta =2/7\) fit above condition, yielding a maximum advantage of around \(2^{-61}\).
. The bound is namely \(N\le \min \big \{\left|\mathcal {K} \right|^{1/2},(\left|{\mathcal {T}} \right|/(2\ell ))^{1/(1+\delta )}\big \}\), for some arbitrary constant \(\delta \) such that \(1/N\le \delta \le 1\). Despite this restriction we consider our statement to be reflecting real-world applications: As an extreme example we see that the values \(\left|\mathcal {K} \right|=\left|{\mathcal {T}} \right|=2^{128}\), \(N=2^{56}\), \(\ell =2^{56}\), \(q=2^{64}\) and \(\delta =2/7\) fit above condition, yielding a maximum advantage of around \(2^{-61}\).
Theorem 5
Suppose \(N\le \min \big \{\left|\mathcal {K} \right|^{1/2},(\left|{\mathcal {T}} \right|/(2\ell ))^{1/(1+\delta )}\big \}\), for some \(1/N\le \delta \le 1\), and suppose that F is modeled as a random oracle (using oracle \({\mathsf {F}}\)). Then for any adversary \(\mathsf {A}\) against \(N\)-instance uniform-tag indistinguishability of \({\mathsf {CTR}}\)+ that poses at most \(q\) queries to \({\mathsf {F}}\), no decapsulation queries, and encapsulates messages of length at most \(\ell \) blocks we have:

The core of the proof exploits that the outputs of (random oracle) F that are used to encapsulate are uniformly distributed in \(\mathcal {D}\) and independent of each other. This requires forcing the inputs to be distinct in \(\mathcal {L}\). We give further insight on some non-standard techniques the we use in the analysis in the proof.
Proof
(of Theorem 5
). The definition of the games  ,
,  ,
,  and
and  are found in Fig. 11. Except for some bookkeeping, game
are found in Fig. 11. Except for some bookkeeping, game  is equivalent to game
is equivalent to game  , where \(b\in \{0,1\}\). For
, where \(b\in \{0,1\}\). For  we define \(T_j=\llbracket t_j \twoheadrightarrow \ell \rrbracket _{L}\).
we define \(T_j=\llbracket t_j \twoheadrightarrow \ell \rrbracket _{L}\).
- Game \(\mathsf {G}^{1}\).:
-
In game
 we implicitly generate pairs of colliding keys. We loop over all pairs \((j_1,j_2)\) such that \(1\le j_1 < j_2\le N\). If both indices were not previously paired (\({\mathsf {matched}}[j_1]={\mathsf {matched}}[j_2]= false \)) and the corresponding keys collide (\(K_{j_1}=K_{j_2}\)) then the two indices are marked as paired. Moreover, if the corresponding tag ranges collide (\(T_{j_1}\cap T_{j_2}\ne \emptyset \)) the flag \(\mathrm {bad}_1\) in line 10 is raised and the game aborts. We claim that
we implicitly generate pairs of colliding keys. We loop over all pairs \((j_1,j_2)\) such that \(1\le j_1 < j_2\le N\). If both indices were not previously paired (\({\mathsf {matched}}[j_1]={\mathsf {matched}}[j_2]= false \)) and the corresponding keys collide (\(K_{j_1}=K_{j_2}\)) then the two indices are marked as paired. Moreover, if the corresponding tag ranges collide (\(T_{j_1}\cap T_{j_2}\ne \emptyset \)) the flag \(\mathrm {bad}_1\) in line 10 is raised and the game aborts. We claim that  (2)
(2)To prove (2), we want to compute the probability \(\Pr _{}\mathopen {}[\mathrm {bad}_1]\mathclose {}\). Let \(m_\text {pairs}\) be the number of colliding key pairs in game
 , i.e., \(2 m_\text {pairs}\) entries of flag \({\mathsf {matched}}\) are set to 1 at the end of the game. Then, for every \(0 \le i \le \left\lfloor N/2 \right\rfloor \), \(\Pr [\mathrm {bad}_1 \mid m_\text {pairs}=i] \le (2\ell -1)i/\left|{\mathcal {T}} \right|\). This follows from the independent choices of the values \(K_j,t_j\) for each instance
, i.e., \(2 m_\text {pairs}\) entries of flag \({\mathsf {matched}}\) are set to 1 at the end of the game. Then, for every \(0 \le i \le \left\lfloor N/2 \right\rfloor \), \(\Pr [\mathrm {bad}_1 \mid m_\text {pairs}=i] \le (2\ell -1)i/\left|{\mathcal {T}} \right|\). This follows from the independent choices of the values \(K_j,t_j\) for each instance 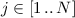 , and because for each pair of indices
, and because for each pair of indices  and for any choice of \(t_{j_1}\) there are exactly \(2\ell -1\) possible values of \(t_{j_2}\) such that \(T_{j_1}\cap T_{j_2}\ne \emptyset \). The sets \(\{m_\text {pairs}=i\}\), \(i\in {0,\ldots ,\left\lfloor N/2 \right\rfloor }\), partition the probability space, thus: $$\begin{aligned} \Pr [\mathrm {bad}_1] =&\sum _{i=0}^{\left\lfloor N/2 \right\rfloor }\Pr _{}\mathopen {}[\mathrm {bad}_1\mid m_\text {pairs}=i]\mathclose {}\Pr _{}\mathopen {}[m_\text {pairs}=i]\mathclose {} \nonumber \\ \le&\frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=0}^{\left\lfloor N/2 \right\rfloor }i\Pr _{}\mathopen {}[m_\text {pairs}= i]\mathclose {}=\frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=1}^{\left\lfloor N/2 \right\rfloor }\Pr _{}\mathopen {}[m_\text {pairs}\ge i]\mathclose {}. \end{aligned}$$(3)
and for any choice of \(t_{j_1}\) there are exactly \(2\ell -1\) possible values of \(t_{j_2}\) such that \(T_{j_1}\cap T_{j_2}\ne \emptyset \). The sets \(\{m_\text {pairs}=i\}\), \(i\in {0,\ldots ,\left\lfloor N/2 \right\rfloor }\), partition the probability space, thus: $$\begin{aligned} \Pr [\mathrm {bad}_1] =&\sum _{i=0}^{\left\lfloor N/2 \right\rfloor }\Pr _{}\mathopen {}[\mathrm {bad}_1\mid m_\text {pairs}=i]\mathclose {}\Pr _{}\mathopen {}[m_\text {pairs}=i]\mathclose {} \nonumber \\ \le&\frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=0}^{\left\lfloor N/2 \right\rfloor }i\Pr _{}\mathopen {}[m_\text {pairs}= i]\mathclose {}=\frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=1}^{\left\lfloor N/2 \right\rfloor }\Pr _{}\mathopen {}[m_\text {pairs}\ge i]\mathclose {}. \end{aligned}$$(3)The last equality follows since the expected value of any random variable m with values in \(\mathbb {N}\) can be written as \(\sum _{i=0}^\infty i\Pr _{}\mathopen {}[m=i]\mathclose {}=\sum _{i=1}^\infty \Pr _{}\mathopen {}[m\ge i]\mathclose {}\). We show by induction that the terms of the sum are:
 (4)
(4)To prove (4), we consider a slightly different event. We say that key \(K_i\) is bad if \(K_j = K_i\) for some \(1 \le i < j\). Let \(m_{\mathrm {badkeys}}\) be the random variable counting the number of bad keys. Since every colliding key pair implies at least one bad key, then it can be shown that \(\Pr _{}\mathopen {}[m_\text {pairs}\ge i]\mathclose {} \le \Pr _{}\mathopen {}[m_{\mathrm {badkeys}}\ge i]\mathclose {} \le ({N^2}/{2\left|\mathcal {K} \right|})^i \). For more details we refer to the full version [14].
Finally we prove (2) by combining (3) and (4), and by observing that from our hypothesis \(N^2/\left|\mathcal {K} \right|\le 1\):
$$\begin{aligned} \Pr [\mathrm {bad}_1] \le \frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=1}^{\left\lfloor N/2 \right\rfloor }\bigg (\frac{N^2}{2\left|\mathcal {K} \right|}\bigg )^i \le \frac{2\ell -1}{\left|{\mathcal {T}} \right|}\sum _{i=1}^{\infty }\frac{1}{2^{i}} = \frac{2\ell -1}{\left|{\mathcal {T}} \right|}. \end{aligned}$$(5) -
Game
 .:
.: -
Game
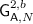 is equivalent to
is equivalent to 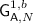 , with the exception that it raises flag \(\mathrm {bad}_2\) in line 12 and aborts if any three keys collide. By the generalized birthday bound, and since \(N^2/\left|\mathcal {K} \right|\le 1\), we obtain
, with the exception that it raises flag \(\mathrm {bad}_2\) in line 12 and aborts if any three keys collide. By the generalized birthday bound, and since \(N^2/\left|\mathcal {K} \right|\le 1\), we obtain  (6)
(6) - Game \(\mathsf {G}^{3}\).:
-
Game
 is equivalent to
is equivalent to  , with the exception that the game raises flag \(\mathrm {bad}_3\) in line 23 and aborts if \(\mathsf {A}\) makes a query \((K,v)\) to \({\mathsf {F}}\) for which there exists an index
, with the exception that the game raises flag \(\mathrm {bad}_3\) in line 23 and aborts if \(\mathsf {A}\) makes a query \((K,v)\) to \({\mathsf {F}}\) for which there exists an index 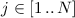 such that \(K=K_j\) and \(v\in T_j\). In the following we fix \(m_\text {inters}\) to be the random variable that counts the maximum number of sets \(T_1,\ldots ,T_N\) whose intersection is non-empty.
such that \(K=K_j\) and \(v\in T_j\). In the following we fix \(m_\text {inters}\) to be the random variable that counts the maximum number of sets \(T_1,\ldots ,T_N\) whose intersection is non-empty.Fix a query \((K,v)\) to \({\mathsf {F}}\). For each
 we have
we have 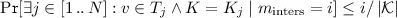 , because in the worst case \(v\) belongs to exactly \(m_\text {inters}\) of the sets \(T_1,\ldots ,T_N\). This bound yields
, because in the worst case \(v\) belongs to exactly \(m_\text {inters}\) of the sets \(T_1,\ldots ,T_N\). This bound yields 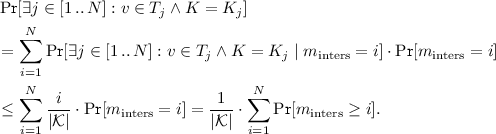 (7)
(7)Some probabilistic considerations allow us to write \(\Pr [m_\text {inters}\ge i+1] \le N^{i+1}\ell ^{i}/\left|{\mathcal {T}} \right|^{i}\) (details in the full version [14]). For all \(i\ge 1/\delta \) we can write \( \frac{N^{i+1}\ell ^{i}}{\left|{\mathcal {T}} \right|^{i}} \le \left( \frac{N^{1+\delta }\ell }{\left|{\mathcal {T}} \right|}\right) ^{i} \le \frac{1}{2^{i}} \). Thus we can split the sum (7) into
$$\begin{aligned} \frac{1}{\left|\mathcal {K} \right|} \cdot \sum _{i=1}^N\Pr [m_\text {inters}\ge i]&\le \frac{1}{\left|\mathcal {K} \right|} \bigg (\sum _{i=1}^{\left\lfloor {1}/{\delta } \right\rfloor } \Pr [m_\text {inters}\ge i]+\sum _{i=\left\lfloor 1/\delta \right\rfloor +1}^\infty \frac{1}{2^{i-1}}\bigg )\\&\le \frac{1}{\left|\mathcal {K} \right|} \bigg (\frac{1}{\delta }+1\bigg ). \end{aligned}$$Since \(m_\text {inters}\) is constant for all \(q\) queries to \({\mathsf {F}}\), a union bound gives us
 (8)
(8)
The theorem follows by combining the bounds in (2), (6), (8) for both \(b=0\) and \(b=1\) and the fact that game  is independent of the bit b.
is independent of the bit b.
Counter Mode with Tag Prefix. We have the following security statement on \({\mathsf {CTR\Vert }}\). Note it is slightly better than the one for \({\mathsf {CTR}}\)+.
Theorem 6
Suppose \(N\le \min \big \{ \left|\mathcal {K} \right|^{1/2},(\left|{\mathcal {T}} \right|/2)^{1/(1+\delta )} \big \}\), for some \(1/N\le \delta \le 1\), and suppose that F is modeled as a random oracle (using oracle \({\mathsf {F}}\)). Then for any adversary \(\mathsf {A}\) against \(N\)-instance uniform-tag indistinguishability of \({\mathsf {CTR\Vert }}\) that poses at most \(q\) queries to \({\mathsf {F}}\) and no decapsulation queries we have:

Proof
We refer to Fig. 12 for the definition of the games  ,
,  ,
,  and
and  . Except for some bookkeeping, game
. Except for some bookkeeping, game  is equivalent to the security game
is equivalent to the security game  , with \(b\in \{0,1\}\).
, with \(b\in \{0,1\}\).
- Game \(\mathsf {G}^{1}\).:
-
Game
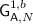 is equivalent to
is equivalent to 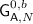 , except when any three keys collide. By the generalized birthday bound, and since \({N^2}{/}{\left|\mathcal {K} \right|}\le 1\), we obtain
, except when any three keys collide. By the generalized birthday bound, and since \({N^2}{/}{\left|\mathcal {K} \right|}\le 1\), we obtain 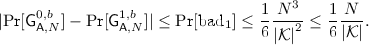 (9)
(9) - Game \(\mathsf {G}^{2}\).:
-
In game
 we abort when two events occur simultaneously: a key 2-collision and collision of the corresponding tags. The probability to abort is by the generalized birthday bound, the independence of the two events, and the condition \({N^2}{/}{\left|\mathcal {K} \right|}\le 1\):
we abort when two events occur simultaneously: a key 2-collision and collision of the corresponding tags. The probability to abort is by the generalized birthday bound, the independence of the two events, and the condition \({N^2}{/}{\left|\mathcal {K} \right|}\le 1\): 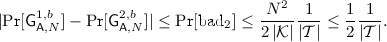 (10)
(10) -
Game
 .:
.: -
Game
 is equivalent to
is equivalent to 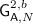 , with the exception that the game raises flag \(\mathrm {bad}_3\) in line 16 if some specific condition is met. To get an upper bound on the probability to distinguish
, with the exception that the game raises flag \(\mathrm {bad}_3\) in line 16 if some specific condition is met. To get an upper bound on the probability to distinguish  and
and 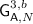 we compute the probability that the adversary explicitly queries \({\mathsf {F}}\) for an input \((K,v\Vert \llbracket i \rrbracket _L)\) such that for some
we compute the probability that the adversary explicitly queries \({\mathsf {F}}\) for an input \((K,v\Vert \llbracket i \rrbracket _L)\) such that for some  , \(K=K_j\) and \(v=t_j\). This leads to the equation:
, \(K=K_j\) and \(v=t_j\). This leads to the equation:  (11)
(11)Fix a query \((K,v\Vert \llbracket i \rrbracket _L)\) to \({\mathsf {F}}\). Since the adversary knows all possible values of \(v\) used by \({\mathsf {Oenc}}\) after each call, the adversary must only guess the key. Assume that there are at most \(m_\text {coll}\) keys that use the same tag value \(v\). Then the probability that flag \(\mathrm {bad}_3\) is triggered during this query is in the worst case \(m_\text {coll}/\left|{\mathcal {T}} \right|\). We compute the probability of this event as follows.
 (12)
(12)The last equality follows since the expected value of any random variable m with values in \(\mathbb {N}\) can be written as \(\sum _{i=0}^\infty i\Pr _{}\mathopen {}[m=i]\mathclose {}=\sum _{i=1}^\infty \Pr _{}\mathopen {}[m\ge i]\mathclose {}\). Now we estimate the probability \(\Pr _{}\mathopen {}[m_\text {coll}\le i]\mathclose {}\). Assume that \(i\ge 1/\delta \). Then from the generalized birthday bound and the condition \(N\le (\left|{\mathcal {T}} \right|/2)^{1/(1+\delta )}\) we can write:
$$ \Pr _{}\mathopen {}[m_\text {coll}\ge i+1]\mathclose {} \le \frac{N^{i+1}}{(i+1)!\left|{\mathcal {T}} \right|^i} \le \left( \frac{N^{1+\delta }}{\left|{\mathcal {T}} \right|}\right) ^{i} \le \frac{1}{2^{i}} \;. $$Considering this observation we split the sum in Eq. (12) into
$$\begin{aligned} \frac{1}{\left|\mathcal {K} \right|} \cdot \sum _{i=1}^N\Pr [m_\text {coll}\ge i]&\le \frac{1}{\left|\mathcal {K} \right|} \bigg (\sum _{i=1}^{\left\lfloor {1}/{\delta } \right\rfloor } \Pr [m_\text {coll}\ge i]+\sum _{i=\left\lfloor 1/\delta \right\rfloor +1}^\infty \frac{1}{2^{i-1}}\bigg )\\&\le \frac{1}{\left|\mathcal {K} \right|} \bigg (\frac{1}{\delta }+1\bigg ). \end{aligned}$$Since \(m_\text {coll}\) is constant for all queries to \({\mathsf {F}}\), a union bound yields our claim:
$$\begin{aligned} \Pr [\mathrm {bad}_3] \le \frac{q}{\left|\mathcal {K} \right|} \bigg (\frac{1}{\delta }+1\bigg ). \end{aligned}$$
The theorem follows by combining the bounds in (9), (10), (11) for both \(b=0\) and \(b=1\) and the fact that game  is independent of b.
is independent of b.
6.3 On the Security of Permutation-Based Counter Mode
In above Theorem 5 we assessed the security of the \({\mathsf {CTR}}\)+ ADEM, defined with respect to a function \(F:\mathcal {K}\times \mathcal {B}\rightarrow \mathcal {D}\). The analysis modeled F as an ideal random function and showed that using sets \(\mathcal {K}\) and \(\mathcal {B}\) of moderate size (e.g., of cardinality \(2^{128}\)) is sufficient to let \({\mathsf {CTR}}\)+ achieve security. We next show that if F is instead instantiated with a blockcipher and modeled as an ideal family of permutations, then the minimum cardinality of \(\mathcal {B}=\mathcal {D}\) for achieving security is considerably increased (e.g., to values around \(2^{256}\)).
Our argument involves the analysis of a  adversary \(\mathsf {A}\) that is specified in Fig. 13. Effectively, the idea of the attack is exploiting the tightness gap of the PRP/PRF switching lemma [5] via the multi-instance setting. More concretely, the adversary repeats the following multiple times (once for each instance): It asks either for the encapsulation of a message comprised of identical blocks, or for the encapsulation of a message consisting of uniformly-generated blocks. The adversary outputs 1 if any two blocks that form the ciphertext collide. If the ciphertext is the encapsulation of the identical-block message then the adversary does not find a collision, since \(F(K,\cdot )\) is a permutation for each key \(K\in \mathcal {K}\) and is evaluated on distinct input values. Otherwise the ciphertext blocks are random, and one can thus find a collision.
adversary \(\mathsf {A}\) that is specified in Fig. 13. Effectively, the idea of the attack is exploiting the tightness gap of the PRP/PRF switching lemma [5] via the multi-instance setting. More concretely, the adversary repeats the following multiple times (once for each instance): It asks either for the encapsulation of a message comprised of identical blocks, or for the encapsulation of a message consisting of uniformly-generated blocks. The adversary outputs 1 if any two blocks that form the ciphertext collide. If the ciphertext is the encapsulation of the identical-block message then the adversary does not find a collision, since \(F(K,\cdot )\) is a permutation for each key \(K\in \mathcal {K}\) and is evaluated on distinct input values. Otherwise the ciphertext blocks are random, and one can thus find a collision.
The theorem uses the technical condition that \(N\ell (\ell -1)/\left|{\mathcal {T}} \right|\le 4\), where \(\ell \) is a parameter that determines the length of the encapsulated messages, measured in blocks. Note that adversaries that could process values \(N,\ell \) that are too large to fulfill this bound will reach at least the same advantage as adversaries considered by the theorem, simply by refraining from posing queries. The stated lower-bound is roughly \(N\ell ^2/\left|{\mathcal {T}} \right|\) and effectively induced by \(N\) applications of the PRP/PRF switching lemma. Note that if the above condition is met with equality, the adversary’s advantage is at least 1/2. Further, if \(\left|{\mathcal {T}} \right|=\left|\mathcal {B} \right|=2^{128}\), \(\ell =2^{40}\) (this corresponds to a message length of 16 terabytes) and we have \(N=2^{48}\) instances, the success probability of \(\mathsf {A}\) is about 1/8, or larger.
Theorem 7
Consider \({\mathsf {CTR}}\)+ instantiated with a family of permutations \(F(K,\cdot )\) over \(\mathcal {B}\), and let \(N\ge 2\). Assume moreover that \(N\ell (\ell -1)\le 4\cdot \left|{\mathcal {T}} \right|\). Then for the adversary \(\mathsf {A}\) in Fig. 13 it holds:

The adversary has a running time of \(\mathcal {O}(N\ell \log \ell )\), makes \(N\) queries to \({\mathsf {Oenc}}\) for messages of length at most \(\ell \) and makes no \({\mathsf {Odec}}\) queries.
Proof
We start with the analysis of the running time of \(\mathsf {A}\): It is predominantly determined by the search for collisions among \(\ell \) blocks for each of the \(N\) iterations of the main loop, hence the bound of \(\mathcal {O}(N\ell \log \ell )\) on the time. We now compute the probability that the adversary outputs 1 depending on the game bit b.
Case  . For each instance
. For each instance  the adversary obtains an encapsulation of a sequence of identical blocks. All blocks composing \(c^j\) must be distinct, since for each key K, function \(F(K,\cdot )\) is a permutation over \(\mathcal {B}\). Therefore the output of this game is always 0 and we have
the adversary obtains an encapsulation of a sequence of identical blocks. All blocks composing \(c^j\) must be distinct, since for each key K, function \(F(K,\cdot )\) is a permutation over \(\mathcal {B}\). Therefore the output of this game is always 0 and we have  .
.
Case  . Let p be the probability that there is a collision between \(\ell \) random variables that are uniformly distributed in the set \(\mathcal {B}\). We show that for each
. Let p be the probability that there is a collision between \(\ell \) random variables that are uniformly distributed in the set \(\mathcal {B}\). We show that for each  the probability of \(\mathsf {A}\) to output 1 when running the j-th iteration of the loop is p. From the definition of \({\mathsf {Oenc}}\) we can write \(w_i^j=v_i^j\oplus F(K_j,\llbracket t_j+i \rrbracket _L)\) for each
the probability of \(\mathsf {A}\) to output 1 when running the j-th iteration of the loop is p. From the definition of \({\mathsf {Oenc}}\) we can write \(w_i^j=v_i^j\oplus F(K_j,\llbracket t_j+i \rrbracket _L)\) for each  , where \(K_j\) and \(t_j\) are the key-tag pairs generated by the game
, where \(K_j\) and \(t_j\) are the key-tag pairs generated by the game  . The elements \(v_1^j,\ldots ,v_\ell ^j\) are generated uniformly in \(\mathcal {B}\) and independently of \(K_j\), \(t_j\), their index, and from each other. Hence the elements \(w_1^j,\ldots ,w_\ell ^j\) are also uniformly distributed in \(\mathcal {B}\) and mutually independent, even in the presence of colliding keys among \(K_1,\ldots ,K_N\). Since all blocks \(v_i^j\) with
. The elements \(v_1^j,\ldots ,v_\ell ^j\) are generated uniformly in \(\mathcal {B}\) and independently of \(K_j\), \(t_j\), their index, and from each other. Hence the elements \(w_1^j,\ldots ,w_\ell ^j\) are also uniformly distributed in \(\mathcal {B}\) and mutually independent, even in the presence of colliding keys among \(K_1,\ldots ,K_N\). Since all blocks \(v_i^j\) with  and
and  are independently random, the probability that the adversary outputs 1 is:
are independently random, the probability that the adversary outputs 1 is:

Since \(\ell (\ell -1)\le 2\left|\mathcal {B} \right|=2\left|{\mathcal {T}} \right|\) by our hypotheses we can use the birthday bound to bound the probability p as \(p\ge \ell (\ell -1)/(4\cdot \left|\mathcal {B} \right|).\) With some simple algebra, and since \(N\ell (\ell -1)\le 4\left|{\mathcal {T}} \right|=4\left|\mathcal {B} \right|\), we can bound Eq. 13 as:

7 ADEMs Secure Against Active Adversaries
In the preceding section we proposed two ADEMs and proved them multi-instance secure against passive adversaries. However, the constructions are based on counter mode encryption and obviously vulnerable in settings with active adversaries that manipulate ciphertexts on the wire. In this section we alleviate the situation by constructing ADEMs that remain secure in the presence of active attacks. Concretely, in line with the encrypt-then-MAC approach [6], we show that an ADEM that is secure against active adversaries can be built from one that is secure against passive adversaries by tamper-protecting its ciphertexts using a message authentication code (MAC). More precisely, with the goal of tightly achieving multi-instance security, we use an augmented message authentication code (see footnote 4) (AMAC) where the generation and verification algorithms depend on an auxiliary input: the tag. In the combined construction, the same tag is used for both ADEM and AMAC. As before, using KEM ciphertexts as tags is a reasonable choice. We conclude the section by constructing a (tightly) secure AMAC based on a hash function.
7.1 Augmented Message Authentication
Augmented message authentication. An augmented message authentication code \({\mathsf {AMAC}}=({\mathsf {M{.}mac}},{\mathsf {M{.}vrf}})\) for a message space \(\mathcal {M}\) is a pair of deterministic algorithms associated with a finite key space \(\mathcal {K}\), a tag space \({\mathcal {T}}\), and a code space \(\mathcal {C}\). The algorithm \({\mathsf {M{.}mac}}\) takes a key \(K\in \mathcal {K}\), a tag \(t\in {\mathcal {T}}\), and a message \(m \in \mathcal {M}\), and outputs a code \(c \in \mathcal {C}\). The verification algorithm \({\mathsf {M{.}vrf}}\) takes a key \(K\in \mathcal {K}\), a tag \(t\in {\mathcal {T}}\), a message \(m\in \mathcal {M}\), and a code \(c \in \mathcal {C}\), and outputs either \( true \) or \( false \). The correctness requirement is that for all \(K\in \mathcal {K}\), \(t\in {\mathcal {T}}\), \(m\in \mathcal {M}\) and \(c \in [{\mathsf {M{.}mac}}(K,t,m)]\) we have \({\mathsf {M{.}vrf}}(K,t,m,c )= true \).
Augmented message authentication with nonces. We give a game-based authenticity model for AMACs.Footnote 11 In our model, for each of a total of \(N\) independent keys the adversary can request one MAC code computation but many verifications. The restriction is that for each key the MAC query has to precede all verification queries, and that always the same tag is used. Further, in line with the definition of nonce-based security for ADEMs, we require the tag provided in each MAC computation request to be unique (across all instances). We formalize the corresponding security notion of (strong) nonce-based multi-instance one-time unforgeability for AMACs via the game specified in Fig. 14. For a scheme \({\mathsf {AMAC}}\), to any adversary \(\mathsf {A}\) and any number of instances \(N\) we associate the advantage  .
.
7.2 The ADEM-Then-AMAC Construction
Let \({\mathsf {ADEM}}\) and \({\mathsf {AMAC}}\) be an ADEM and an AMAC, respectively. Following the generic encrypt-then-MAC [6] composition technique, and assuming \({\mathsf {ADEM}}\) is secure against passive adversaries, we combine the two schemes to obtain the augmented data-encapsulation mechanism \({\mathsf {ADEM}}'\), which we prove secure against active adversaries. More formally, if \({\mathsf {ADEM}}=({\mathsf {A{.}enc}},{\mathsf {A{.}dec}})\) and \({\mathsf {AMAC}}=({\mathsf {M{.}mac}},{\mathsf {M{.}vrf}})\) have key spaces \(\mathcal {K}_{\mathsf {dem}}\) and \(\mathcal {K}_{\mathsf {mac}}\), respectively, then the key space of \({\mathsf {ADEM}}'\) is \(\mathcal {K}_{\mathsf {dem}}\times \mathcal {K}_{\mathsf {mac}}\), and its algorithms are as in Fig. 15. Note that the tag space is the same for all three schemes (and that the message spaces have to be sufficiently compatible to each other).
The proof of the following theorem can be found in the full version [14].
Theorem 8
Let \({\mathsf {ADEM}}'\) be constructed from \({\mathsf {ADEM}}\) and \({\mathsf {AMAC}}\) as described. Then for any number of instances \(N\) and any ADEM adversary \(\mathsf {A}\) that poses at most \(Q_d\)-many \({\mathsf {Odec}}\) queries, there exist an AMAC adversary \(\mathsf {B}\) and an ADEM adversary \(\mathsf {C}\) such that

The running time of \(\mathsf {B}\) is at most that of \(\mathsf {A}\) plus the time required to run \(N\)-many \({\mathsf {ADEM}}\) encapsulations and \(Q_d\)-many \({\mathsf {ADEM}}\) decapsulations. The running time of \(\mathsf {C}\) is the same as the running time of \(\mathsf {A}\). Moreover, \(\mathsf {B}\) poses at most \(Q_d\)-many \({\mathsf {Ovrf}}\) queries, and \(\mathsf {C}\) poses no \({\mathsf {Odec}}\) query.
7.3 A Multi-instance Secure AMAC
A random oracle directly implies a multi-instance secure AMAC, with a straight-forward construction: the MAC code of a message is computed by concatenating key, tag, and message, and hashing the result. We formalize this as follows. Let \({\mathcal {T}}\) be a tag space and \(\mathcal {M}\) a message space. Let \(\mathcal {K}\) and \(\mathcal {C}\) be arbitrary finite sets. Let \(H:\mathcal {K}\times {\mathcal {T}}\times \mathcal {M}\rightarrow \mathcal {C}\) be a hash function. Define function \({\mathsf {M{.}mac}}\) and a predicate \({\mathsf {M{.}vrf}}\) such that for all K, t, m, c we have \({\mathsf {M{.}mac}}(K,t,m)=H(K,t,m)\), and \({\mathsf {M{.}vrf}}(K,t,m,c)= true \) iff \(H(K,t,m)=c\). Let finally \({\mathsf {AMAC}}=({\mathsf {M{.}mac}},{\mathsf {M{.}vrf}})\).
Note that hash functions based on the Merkle–Damgård design, like SHA256, do not serve directly as random oracles due to generic length-extension attacks [10], and indeed the \({\mathsf {ADEM}}'\) scheme from Fig. 15 is not secure if its \({\mathsf {AMAC}}\) is derived from such a function. Fortunately, Merkle–Damgård hashing can be modified to achieve indifferentiability from a random oracle [10]. Further, more recent hash functions like SHA3 are naturally resilient against length-extension attacks.
The proof of the following theorem can be found in the full version [14].
Theorem 9
Let \(\mathcal {K},{\mathcal {T}},\mathcal {M},\mathcal {C}\) and \({\mathsf {AMAC}}=({\mathsf {M{.}mac}},{\mathsf {M{.}vrf}})\) be as above. If H behaves like a (non-programmable) random oracle, for any number of instances \(N\) and any adversary \(\mathsf {A}\) we obtain

where \(q\) is the number of direct calls to the random oracle by the adversary, and \(Q_v\) is the number of calls to the oracle \({\mathsf {Ovrf}}\). Note that the bound does not depend on the number of \({\mathsf {Omac}}\) queries.
Notes
- 1.
- 2.
The cited work is not too clear about this property; loosely speaking the condition seems to be that colliding ciphertexts of the same message under random keys can be used as evidence that also the keys are colliding. One example for a DEM with this property is CBC encryption.
- 3.
Obtaining entropy from a modern operating system kernel involves either file access or system calls; both options are considerably more costly than, say, doing an AES computation. While some modern CPUs have built-in randomness generators, the quality of the latter is difficult to assess and relying exclusively on them thus discouraged (see https://plus.google.com/+TheodoreTso/posts/SDcoemc9V3J).
- 4.
The notion of an augmented MAC appeared recently in an unrelated context: An AMAC according to [3] is effectively keyed Merkle–Damgård hashing with an unkeyed output transform applied at the end. Importantly, while the notion of [3] follows the classic MAC syntax, ours does not (for having a separate tag input).
- 5.
While our setup is formally meaningful, in practice it would correspond to \(N\) parties, for a huge number \(N\), encapsulating the same message \(m_0\). This might feel rather unrealistic. However, we argue that a close variant of the attack might very well have the potential for practicality: All widely deployed DEMs are online, i.e., compute ciphertexts ‘left-to-right’. For such DEMs, for our attack to be successful, it suffices that the \(N\) parties encapsulate (different) messages that have a common prefix, for instance a standard protocol header.
- 6.
The efficiency of this attack can likely be improved, on a heuristic basis, by deploying dedicated data structures like rainbow tables.
- 7.
This is no coincidence but caused by generic attacks against cyclic groups, RSA, etc.
- 8.
- 9.
The idea to construct a DEM from a hash function’s compression function already appeared in the OMD schemes from [9].
- 10.
Technically, the PRP/PRF switching lemma [5] measures the price one has to pay for pursuing this modeling approach.
- 11.
In principle we could give two security definitions: one using uniform tags and one using nonce tags. In this paper we formalize only the latter, not the former, for mainly two reasons: (a) the nonce-based notion is not required for our results; (b) in the nonce setting it is not clear how to prove a result similar to the one of Theorem 8. The reason for (b) is that to simulate an encapsulation query for a
 adversary using an AMAC oracle one must specify the tag that is also used to generate the DEM ciphertext, but this is only given as an output of the AMAC oracle.
adversary using an AMAC oracle one must specify the tag that is also used to generate the DEM ciphertext, but this is only given as an output of the AMAC oracle.
References
Attrapadung, N., Hanaoka, G., Yamada, S.: A framework for identity-based encryption with almost tight security. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015 Part I. LNCS, vol. 9452, pp. 521–549. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_22
Bellare, M.: New proofs for NMAC and HMAC: security without collision resistance. J. Cryptol. 28(4), 844–878 (2015)
Bellare, M., Bernstein, D.J., Tessaro, S.: Hash-function based PRFs: AMAC and its multi-user security. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016 Part I. LNCS, vol. 9665, pp. 566–595. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_22
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Kilian, J., Rogaway, P.: The security of cipher block chaining. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 341–358. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_32
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_41
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016 Part I. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Chatterjee, S., Koblitz, N., Menezes, A., Sarkar, P.: Another look at tightness II: practical issues in cryptography. Cryptology ePrint Archive, Report 2016/360 (2016)
Cogliani, S., Maimuţ, D.Ş., Naccache, D., do Canto, R.P., Reyhanitabar, R., Vaudenay, S., Vizár, D.: OMD: a compression function mode of operation for authenticated encryption. In: Joux, A., Youssef, A. (eds.) SAC 2014. LNCS, vol. 8781, pp. 112–128. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-13051-4_7
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_26
Cramer, R., Shoup, V.: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. SIAM J. Comput. 33(1), 167–226 (2003)
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016 Part I. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_1
Gaži, P., Pietrzak, K., Tessaro, S.: Generic security of NMAC and HMAC with input whitening. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015 Part II. LNCS, vol. 9453, pp. 85–109. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_4
Giacon, F., Kiltz, E., Poettering, B.: Hybrid encryption in a multi-user setting, revisited. Cryptology ePrint Archive, Report 2017/843 (2017)
Gong, J., Chen, J., Dong, X., Cao, Z., Tang, S.: Extended nested dual system groups, revisited. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016 Part I. LNCS, vol. 9614, pp. 133–163. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_6
Herranz, J., Hofheinz, D., Kiltz, E.: Some (in)sufficient conditions for secure hybrid encryption. Inf. Comput. 208(11), 1243–1257 (2010)
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 553–571. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_31
Libert, B., Joye, M., Yung, M., Peters, T.: Concise multi-challenge CCA-secure encryption and signatures with almost tight security. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014 Part II. LNCS, vol. 8874, pp. 1–21. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_1
Libert, B., Peters, T., Joye, M., Yung, M.: Compactly hiding linear spans. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015 Part I. LNCS, vol. 9452, pp. 681–707. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_28
Patarin, J.: Security in \(O(2^n)\) for the xor of two random permutations–proof with the standard \(H\) technique. Cryptology ePrint Archive, Report 2013/368 (2013)
Zaverucha, G.: Hybrid encryption in the multi-user setting. Cryptology ePrint Archive, Report 2012/159 (2012)
Acknowledgments
We are grateful to Krzysztof Pietrzak and the anonymous reviewers for their valuable comments. The authors were partially supported by ERC Project ERCC (FP7/615074) and by DFG SPP 1736 Big Data.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Giacon, F., Kiltz, E., Poettering, B. (2018). Hybrid Encryption in a Multi-user Setting, Revisited. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10769. Springer, Cham. https://doi.org/10.1007/978-3-319-76578-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-76578-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76577-8
Online ISBN: 978-3-319-76578-5
eBook Packages: Computer ScienceComputer Science (R0)



 ,
, 
 ,
, 
 ,
, 


 modeling resilience against key recovery, for
modeling resilience against key recovery, for 
 ,
, 
 ,
, 

 we implicitly generate pairs of colliding keys. We loop over all pairs
we implicitly generate pairs of colliding keys. We loop over all pairs 
 , i.e.,
, i.e., 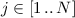 , and because for each pair of indices
, and because for each pair of indices  and for any choice of
and for any choice of 
 .:
.: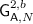 is equivalent to
is equivalent to 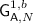 , with the exception that it raises flag
, with the exception that it raises flag 
 is equivalent to
is equivalent to  , with the exception that the game raises flag
, with the exception that the game raises flag 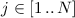 such that
such that  we have
we have 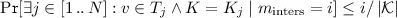 , because in the worst case
, because in the worst case 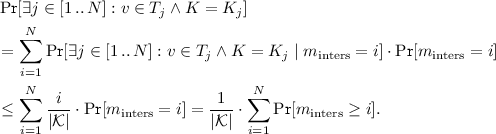


 for
for  ,
,  , and
, and  . Adversary
. Adversary  is equivalent to
is equivalent to  , except when any three keys collide. By the generalized birthday bound, and since
, except when any three keys collide. By the generalized birthday bound, and since 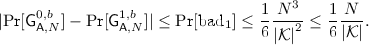
 we abort when two events occur simultaneously: a key 2-collision and collision of the corresponding tags. The probability to abort is by the generalized birthday bound, the independence of the two events, and the condition
we abort when two events occur simultaneously: a key 2-collision and collision of the corresponding tags. The probability to abort is by the generalized birthday bound, the independence of the two events, and the condition 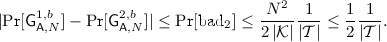
 .:
.: is equivalent to
is equivalent to 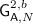 , with the exception that the game raises flag
, with the exception that the game raises flag  and
and 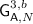 we compute the probability that the adversary explicitly queries
we compute the probability that the adversary explicitly queries  ,
, 


 for
for  ,
,  , and
, and  . Adversary
. Adversary 
 security of
security of 
 , modeling nonce-based multi-instance one-time unforgeability for
, modeling nonce-based multi-instance one-time unforgeability for 
 adversary using an AMAC oracle one must specify the tag that is also used to generate the DEM ciphertext, but this is only given as an output of the AMAC oracle.
adversary using an AMAC oracle one must specify the tag that is also used to generate the DEM ciphertext, but this is only given as an output of the AMAC oracle.