Ordered Level Planarity, Geodesic Planarity and Bi-Monotonicity

Abstract

We introduce and study the problem Ordered Level Planarity which asks for a planar drawing of a graph such that vertices are placed at prescribed positions in the plane and such that every edge is realized as a y-monotone curve. This can be interpreted as a variant of Level Planarity in which the vertices on each level appear in a prescribed total order. We establish a complexity dichotomy with respect to both the maximum degree and the level-width, that is, the maximum number of vertices that share a level. Our study of Ordered Level Planarity is motivated by connections to several other graph drawing problems.

Geodesic Planarity asks for a planar drawing of a graph such that vertices are placed at prescribed positions in the plane and such that every edge e is realized as a polygonal path p composed of line segments with two adjacent directions from a given set S of directions symmetric with respect to the origin. Our results on Ordered Level Planarity imply $\mathcal {NP}$-hardness for any S with $|S|\ge 4$ even if the given graph is a matching. Katz, Krug, Rutter and Wolff claimed that for matchings Manhattan Geodesic Planarity, the case where S contains precisely the horizontal and vertical directions, can be solved in polynomial time [GD 2009]. Our results imply that this is incorrect unless $\mathcal P=\mathcal NP$. Our reduction extends to settle the complexity of the Bi-Monotonicity problem, which was proposed by Fulek, Pelsmajer, Schaefer and Štefankovič.

Ordered Level Planarity turns out to be a special case of T-Level Planarity, Clustered Level Planarity and Constrained Level Planarity. Thus, our results strengthen previous hardness results. In particular, our reduction to Clustered Level Planarity generates instances with only two non-trivial clusters. This answers a question posed by Angelini, Da Lozzo, Di Battista, Frati and Roselli.

Due to space constraints, some proofs in this manuscript are only sketched or omitted entirely. Full proofs of all claims can be found in the appendix of the preprint [17].

1 Introduction

In this paper we introduce Ordered Level Planarity and study its complexity. We establish connections to several other graph drawing problems, which we survey in this first section. We proceed from general problems to more and more constrained ones.

Upward Planarity: An upward planar drawing of a directed graph is a plane drawing where every edge $e=(u,v)$ is realized as a y-monotone curve that goes upward from u to v. Such drawings provide a natural way of visualizing a partial order on a set of items. The problem Upward Planarity of testing whether a directed graph has an upward planar drawing is $\mathcal {NP}$-complete [10]. However, if the y-coordinate of each vertex is prescribed, the problem can be solved in polynomial time [15]. This is captured by the notion of level graphs.

Level Planarity: A level graph $\mathcal G=(G,\gamma )$ is a directed graph $G=(V,E)$ together with a level assignment $\gamma :V\rightarrow \lbrace 0,\dots ,h\rbrace$ where $\gamma$ is a surjective map with $\gamma (u)<\gamma (v)$ for every edge $(u,v)\in E$. Value h is the height of $\mathcal G$. The vertex set $V_i=\lbrace v\mid \gamma (v)=i\rbrace$ is called the i-th level of $\mathcal G$ and $\lambda _i=|V_i|$ is its width. The level-width $\lambda$ of $\mathcal G$ is the maximum width of any level in $\mathcal G$. A level planar drawing of $\mathcal G$ is an upward planar drawing of G where the y-coordinate of each vertex v is $\gamma (v)$. The horizontal line with y-coordinate i is denoted by $L_i$. The problem Level Planarity asks whether a given level graph has a level planar drawing. The study of the complexity of Level Planarity has a long history [7, 9, 13,14,15], culminating in a linear-time approach [15]. Level Planarity has been extended to drawings of level graphs on surfaces different from the plane such as standing cylinder, a rolling cylinder or a torus [1, 3, 4].

An important special case are proper level graphs, that is, level graphs in which $\gamma (v)=\gamma (u)+1$ for every edge $(u,v)\in E$. Instances of Level Planarity can be assumed to be proper without loss of generality by subdividing long edges [7, 15]. However, in variations of Level Planarity where we impose additional constraints, the assumption that instances are proper can have a strong impact on the complexity of the respective problems [2].

Level Planarity with Various Constraints: Clustered Level Planarity is a combination of Cluster Planarity and Level Planarity. The task is to find a level planar drawing while simultaneously visualizing a given cluster hierarchy according to the rules of Cluster Planarity. The problem is $\mathcal {NP}$-complete in general [2], but efficiently solvable for proper instances [2, 8].

T-Level Planarity is a consecutivity-constrained version of Level Planarity: every level $V_i$ is equipped with a tree $T_i$ whose set of leaves is $V_i$. For every inner node u of $T_i$ the leaves of the subtree rooted at u have to appear consecutively along $L_i$. The problem is $\mathcal {NP}$-complete in general [2], but efficiently solvable for proper instances [2, 18]. The precise definitions of both problems and a longer discussion about the related work can be found in [17].

Very recently, Brückner and Rutter [6] explored a variant of Level Planarity in which the left-to-right order of the vertices on each level has to be a linear extension of a given partial order. They refer to this problem as Constrained Level Planarity and they provide an efficient algorithm for single-source graphs and show $\mathcal {NP}$-completeness of the general case.

A Common Special Case - Ordered Level Planarity: We introduce a natural variant of Level Planarity that specifies a total order for the vertices on each level. An ordered level graph $\mathcal G$ is a triple $(G=(V,E),\gamma ,\chi )$ where $(G,\gamma )$ is a level graph and $\chi :V\rightarrow \lbrace 0,\dots ,\lambda -1\rbrace$ is a level ordering for G. We require that $\chi$ restricted to domain $V_i$ bijectively maps to $\lbrace 0,\dots , \lambda _i-1\rbrace$. An ordered level planar drawing of an ordered level graph $\mathcal G$ is a level planar drawing of $(G,\gamma )$ where for every $v\in V$ the x-coordinate of v is $\chi (v)$. Thus, the position of every vertex is fixed. The problem Ordered Level Planarity asks whether a given ordered level graph has an ordered level planar drawing.

In the above definitions, the x- and y-coordinates assigned via $\chi$ and $\gamma$ merely act as a convenient way to encode total and partial orders respectively. In terms of realizability, the problems are equivalent to generalized versions where $\chi$ and $\gamma$ map to the reals. In other words, the fixed vertex positions can be any points in the plane. All reductions and algorithms in this paper carry over to these generalized versions, if we pay the cost for presorting the vertices according to their coordinates. Ordered Level Planarity is also equivalent to a relaxed version where we only require that the vertices of each level $V_i$ appear along $L_i$ according to the given total order without insisting on specific coordinates. We make use of this equivalence in many of our figures for the sake of visual clarity.

Geodesic Planarity: Let $S\subset \mathbb Q^2$ be a finite set of directions symmetric with respect to the origin, i.e. for each direction $s\in S$, the reverse direction $-s$ is also contained in S. A plane drawing of a graph is geodesic with respect to S if every edge is realized as a polygonal path p composed of line segments with two adjacent directions from S. Two directions of S are adjacent if they appear consecutively in the projection of S to the unit circle. Such a path p is a geodesic with respect to some polygonal norm that corresponds to S. An instance of the decision problem Geodesic Planarity is a 4-tuple $\mathcal G=(G=(V,E),x,y,S)$ where G is a graph, x and y map from V to the reals and S is a set of directions as stated above. The task is to decide whether $\mathcal G$ has a geodesic drawing, that is, G has a geodesic drawing with respect to S in which every vertex $v\in V$ is placed at (x(v), y(v)).

Katz et al. [16] study Manhattan Geodesic Planarity, which is the special case of Geodesic Planarity where the set S consists of the two horizontal and the two vertical directions. Geodesic drawings with respect to this set of direction are also referred to as orthogeodesic drawings [11, 12]. Katz et al. [16] show that a variant of Manhattan Geodesic Planarity in which the drawings are restricted to the integer grid is $\mathcal {NP}$-hard even if G is a perfect matching. The proof is by reduction from 3-Partition and makes use of the fact the number of edges that can pass between two vertices on a grid line is bounded. In contrast, they claim that the standard version of Manhattan Geodesic Planarity is polynomial-time solvable for perfect matchings [16, Theorem 5]. To this end, they sketch a plane sweep algorithm that maintains a linear order among the edges that cross the sweep line. When a new edge is encountered it is inserted as low as possible subject to the constraints implied by the prescribed vertex positions. When we asked the authors for more details, they informed us that they are no longer convinced of the correctness of their approach. Theorem 2 of our paper implies that the approach is indeed incorrect unless $\mathcal P=\mathcal {NP}$.

Bi-Monotonicity: Fulek et al. [9] present a Hanani-Tutte theorem for y-monotone drawings, that is, upward drawings in which all vertices have distinct y-coordinates. They accompany their result with a simple and efficient algorithm for Y-Monotonicity, which is equivalent to Level Planarity restricted to instances with level-width $\lambda =1$. They propose the problem Bi-Monotonicity and leave its complexity as an open problem. The input of Bi-Monotonicity is a triple $\mathcal G=(G=(V,E),x,y)$ where G is a graph and x and y injectively map from V to the reals. The task is to decide whether $\mathcal G$ has a bi-monotone drawing, that is, a plane drawing in which edges are realized as curves that are both y-monotone and x-monotone and in which every vertex $v\in V$ is placed at (x(v), y(v)).

Main Results: In Sect. 3 we study the complexity of Ordered Level Planarity. While Upward Planarity is $\mathcal {NP}$-complete [10] in general but becomes polynomial-time solvable [15] for prescribed y-coordinates, we show that prescribing both x-coordinates and y-coordinates renders the problem $\mathcal {NP}$-complete. We complement our result with efficient approaches for some special cases of ordered level graphs and, thereby, establish a complexity dichotomy with respect to the level-width and the maximum degree.

Theorem 1

Ordered Level Planarity is $\mathcal {NP}$-complete, even for maximum degree $\varDelta =2$ and level-width $\lambda =2$. For level-width $\lambda =1$ or $\varDelta ^+=\varDelta ^-=1$ or proper instances Ordered Level Planarity can be solved in linear time, where $\varDelta ^+$ and $\varDelta ^-$ are the maximum in-degree and out-degree respectively.

Ordered Level Planarity restricted to instances with $\lambda =2$ and $\varDelta =2$ is an elementary problem. We expect that it may serve as a suitable basis for future reductions. As a proof of concept, the remainder of this paper is devoted to establishing connections between Ordered Level Planarity and several other graph drawing problems. Theorem 1 serves as our key tool for settling their complexity. In Sect. 2 we study Geodesic Planarity and obtain:

Theorem 2

Geodesic Planarity is $\mathcal {NP}$-hard for any set of directions S with $|S|\ge 4$ even for perfect matchings in general position.

Observe the aforementioned discrepancy between Theorem 2 and the claim by Katz et al. [16] that Manhattan Geodesic Planarity for perfect matchings is in $\mathcal P$. Bi-Monotonicity is closely related to a special case of Manhattan Geodesic Planarity. With a simple corollary we settle the complexity of Bi-Monotonicity and, thus, answer the open question by Fulek et al. [9].

Theorem 3

Bi-Monotonicity is $\mathcal {NP}$-hard even for perfect matchings.

Ordered Level Planarity is an immediate and very constrained special case of Constrained Planarity. Further, we establish Ordered Level Planarity as a special case of both Clustered Level Planarity and T-Level Planarity by providing the following reductions.

Theorem 4

Ordered Level Planarity with maximum degree $\varDelta =2$ and level-width $\lambda =2$ reduces in linear time to T-Level Planarity with maximum degree $\varDelta ' =2$ and level-width $\lambda ' =4$.

Theorem 5

Ordered Level Planarity with maximum degree $\varDelta =2$ and level-width $\lambda =2$ reduces in quadratic time to Clustered Level Planarity with maximum degree $\varDelta ' =2$, level-width $\lambda ' =2$ and $\kappa '=3$ clusters.

Angelini et al. [2] propose the complexity of Clustered Level Planarity for clustered level graphs with a flat cluster hierarchy as an open question. Theorem 5 answers this question by showing that $\mathcal {NP}$-hardness holds for instances with only two non-trivial clusters.

2 Geodesic Planarity and Bi-Monotonicity

In this section we establish that deciding whether an instance $\mathcal G=(G,x,y,S)$ of Geodesic Planarity has a geodesic drawing is $\mathcal {NP}$-hard even if G is a perfect matching and even if the coordinates assigned via x and y are in general position, that is, no two vertices lie on a line with a direction from S. The $\mathcal {NP}$-hardness of Bi-Monotonicity for perfect matchings follows as a simple corollary. Our results are obtained via a reduction from Ordered Level Planarity.

Lemma 1

Let $S\subset \mathbb Q^2$ with $|S|\ge 4$ be a finite set of directions symmetric with respect to the origin. Ordered Level Planarity with maximum degree $\varDelta =2$ and level-width $\lambda =2$ reduces to Geodesic Planarity such that the resulting instances are in general position and consist of a perfect matching and direction set S. The reduction can be carried out using a linear number of arithmetic operations.

Proof Sketch

In this sketch, we prove our claim only for the classical case that S contains exactly the four horizontal and vertical directions. Our reduction is carried out in two steps. Let $\mathcal G_o=(G_o=(V,E),\gamma ,\chi )$ be an Ordered Level Planarity instance with maximum degree $\varDelta =2$ and level-width $\lambda =2$. In Step (i) we turn $\mathcal G_o$ into an equivalent Geodesic Planarity instance $\mathcal G_g'=(G_o,x',\gamma ,S)$. In Step (ii) we transform $\mathcal G_g'$ into an equivalent Geodesic Planarity instance $\mathcal G_g=(G_g,x,y,S)$ where $G_g$ is a perfect matching and the vertex positions assigned via x and y are in general position.

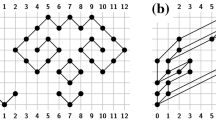
Step (i): In order to transform $\mathcal G_o$ into $\mathcal G_g'$ we apply a shearing transformation. We translate the vertices of each level $V_i$ by 3i units to the right, see Fig. 1(a) and (b). Clearly, every geodesic drawing of $\mathcal G_g'$ can be turned into an ordered level planar drawing of $\mathcal G_o$. On the other hand, consider an ordered level planar drawing $\varGamma _o$ of $\mathcal G_o$. Without loss of generality we can assume that in $\varGamma _o$ all edges are realized as polygonal paths in which bend points occur only on the horizontal lines $L_i$ through the levels $V_i$ where $0\le i\le h$. Further, we may assume that all bend points have x-coordinates in the open interval $(-1,2)$. We shear $\varGamma _o$ by translating the bend points and vertices of level $V_i$ by 3i units to the right for $0\le i\le h$, see Fig. 1(b). In the resulting drawing $\varGamma _o'$, the vertex positions match those of $\mathcal G_g'$. Furthermore, all edge-segments have a positive slope. Thus, since the maximum degree is $\varDelta =2$ we can replace all edge-segments with $L_1$-geodesic rectilinear paths that closely trace the segments and we obtain a geodesic drawing $\varGamma _g'$ of $\mathcal G_g'$, see Fig. 1(c).

Fig. 1.

(a), (b) and (c): Illustrations of Step (i). (d) The two gadget squares of each level. Grid cells have size $1/48\times 1/48$. (e) Illustration of Step (ii). Turning a drawing of $\mathcal G_g$ into a drawing of $\mathcal G_g'$ (f) and vice versa (g).

Step (ii): In order to turn $\mathcal G_g'=(G_o=(V,E),x',\gamma ,S)$ into the equivalent instance $\mathcal G_g=(G_g,x,y,S)$ we transform $G_o$ into a perfect matching. To this end, we split each vertex $v\in V$ by replacing it with a small gadget that fits inside a square $r_v$ centered on the position $p_v=(x'(v),\gamma (v))$ of v, see Fig. 1(e). We call $r_v$ the square of v and use $p_v^{tr}$, $p_v^{tl}$, $p_v^{br}$ and $p_v^{bl}$ to denote the top-right, top-left, bottom-right and bottom-left corner of $r_v$, respectively. We use two different sizes to ensure general position. The size of the gadget square is $1/4\times 1/4$ if $\chi (v)=0$ and it is $1/8\times 1/8$ if $\chi (v)=1$. The gadget contains a degree-1 vertex for every edge incident to v. In the following we explain the gadget construction in detail, for an illustration see Fig. 1(d). Let $\lbrace v,u\rbrace$ be an edge incident to v. We create an edge $\lbrace v_1,u\rbrace$ where $v_1$ is a new vertex which is placed at $p_v^{tr}-(1/48,1/48)$ if u is located to the top-right of v and it is placed at $p_v^{bl}+(1/48,1/48)$ if u is located to the bottom-left of v. Similarly, if v is incident to a second edge $\lbrace v,u'\rbrace$, we create an edge $\lbrace v_2,u'\rbrace$ where $v_2$ is placed at $p_v^{tr}-(1/24,1/24)$ or $p_v^{bl}+(1/24,1/24)$ depending on the position of $u'$. Finally, we create a blocking edge $\lbrace v_{tl},v_{br}\rbrace$ where $v_{tl}$ is placed at $p_v^{tl}$ and $v_{br}$ is placed at $p_v^{br}$. The thereby assigned coordinates are in general position and the construction can be carried out in linear time.

Assume that $\mathcal G_g$ has a geodesic drawing $\varGamma _g$. By construction, all blocking edges have a top-left and a bottom-right endpoint. On the other hand, all other edges have a bottom-left and a top-right endpoint. As a result, a non-blocking edge $e=\lbrace u,v\rbrace$ can not pass through any gadget square $r_w$, except the squares $r_u$ or $r_v$ since e would have to cross the blocking edge of $r_w$. Accordingly, it is straight-forward to obtain a geodesic drawing of $\varGamma _g'$: We remove the blocking edges, reinsert the vertices of V according to the mappings $x'$ and $\gamma$ and connect them to the vertices of their respective gadgets in a geodesic fashion. This can always be done without crossings. Figure 1(f) shows one possibility. If the edge from $v_2$ passes to the left of $v_1$, we may have to choose a reflected version. Finally, we remove the vertices $v_1$ and $v_2$ which now act as subdivision vertices.

On the other hand, let $\varGamma _g'$ be a geodesic planar drawing of $\mathcal G_g'$. Without loss of generality, we can assume that each edge $\lbrace u,v\rbrace$ passes only through the squares of u and v. Furthermore, for each $v\in V$ we can assume that its incident edges intersect the boundary of $r_v$ only to the top-right of $p_v^{tr}-(1/48,1/48)$ or to the bottom-left of $p_v^{bl}+(1/48,1/48)$, see Fig. 1(g). Thus, we can simply remove the parts of the edges in the interior of the gadget squares and connect the gadget vertices to the intersection points of the edges with the gadget squares in a geodesic fashion.    $\square$

The bit size of the numbers involved in the calculations of our reduction is linearly bounded in the bit size of the directions of S. Together with Theorem 1 we obtain the proof of Theorem 2. The instances generated by Lemma 1 are in general position. In particular, this means that the mappings x and y are injective. We obtain an immediate reduction to Bi-Monotonicity. The correctness follows from the fact that every $L_1$-geodesic rectilinear path can be transformed into a bi-monotone curve and vice versa. Thus, we obtain Theorem 3.

3 Ordered Level Planarity

To show $\mathcal {NP}$-hardness of Ordered Level Planarity we reduce from a 3-Satisfiability variant described in this paragraph. A monotone 3-Satisfiability formula is a Boolean 3-Satisfiability formula in which each clause is either positive or negative, that is, each clause contains either exclusively positive or exclusively negative literals respectively. A planar 3SAT formula $\varphi =(\mathcal U,\mathcal C)$ is a Boolean 3-Satisfiability formula with a set $\mathcal {U}$ of variables and a set $\mathcal {C}$ of clauses such that its variable-clause graph $G_\varphi = (\mathcal {U}\uplus \mathcal {C}, E)$ is planar. The graph $G_\varphi$ is bipartite, i.e. every edge in E is incident to both a clause vertex from $\mathcal C$ and a variable vertex from $\mathcal U$. Furthermore, edge $\lbrace c,u\rbrace \in E$ if and only if a literal of variable $u\in \mathcal U$ occurs in $c\in \mathcal C$. Planar Monotone 3-Satisfiability is a special case of 3-Satisfiability where we are given a planar and monotone 3-Satisfiability formula $\varphi$ and a monotone rectilinear representation $\mathcal R$ of the variable-clause graph of $\varphi$. The representation $\mathcal R$ is a contact representation on an integer grid in which the variables are represented by horizontal line segments arranged on a line $\ell$. The clauses are represented by E-shapes turned by $90^\circ$ such that all positive clauses are placed above $\ell$ and all negative clauses are placed below $\ell$, see Fig. 2a. Planar Monotone 3-Satisfiability is $\mathcal {NP}$-complete [5]. We are now equipped to prove the core lemma of this section.

Lemma 2

Planar Monotone 3-Satisfiability reduces in polynomial time to Ordered Level Planarity. The resulting instances have maximum degree $\varDelta =2$ and all vertices on levels with width at least 3 have out-degree at most 1 and in-degree at most 1.

Fig. 2.

(a) Representation $\mathcal R$ of $\varphi$ with negative clauses $(\overline{u}_1\vee \overline{u}_4 \vee \overline{u}_5)$, $(\overline{u}_1 \vee \overline{u}_3 \vee \overline{u}_4)$ and $(\overline{u}_1 \vee \overline{u}_2 \vee \overline{u}_3)$ and positive clauses $(u_1 \vee u_4 \vee u_5)$ and $(u_1 \vee u_2 \vee u_3 )$ and (b) its modified version $\mathcal R'$ in Lemma 2. (c) Tier $\mathcal T_0$.

Proof Sketch

We perform a polynomial-time reduction from Planar Monotone 3-Satisfiability. Let $\mathcal \varphi =(\mathcal U,\mathcal C)$ be a planar and monotone 3-Satisfiability formula with $\mathcal C=\lbrace c_1,\dots ,c_{|\mathcal C|}\rbrace$. Let $G_\varphi$ the variable-clause graph of $\varphi$. Let $\mathcal R$ be a monotone rectilinear representation of $G_\varphi$. We construct an ordered level graph $\mathcal G=(G,\gamma ,\chi )$ such that $\mathcal G$ has an ordered level planar drawing if and only if $\varphi$ is satisfiable. In this proof sketch we omit some technical details such as precise level assignments and level orderings.

Overview: The ordered level graph $\mathcal G$ has $l_3+1$ levels which are partitioned into four tiers $\mathcal T_0=\lbrace 0,\dots ,l_0\rbrace$, $\mathcal T_1=\lbrace l_0+1,\dots ,l_1\rbrace$, $\mathcal T_2=\lbrace l_1+1,\dots ,l_2\rbrace$ and $\mathcal T_3=\lbrace l_2+1,\dots ,l_3\rbrace$. Each clause $c_i\in \mathcal C$ is associated with a clause edge $e_i=(c_i^s,c_i^t)$ starting with $c_i^s$ in tier $\mathcal T_0$ and ending with $c_i^t$ in tier $\mathcal T_2$. The clause edges have to be drawn in a system of tunnels that encodes the 3-Satisfiability formula $\varphi$. In $\mathcal T_0$ the layout of the tunnels corresponds directly to the rectilinear representation $\mathcal R$, see Fig. 2c. For each E-shape there are three tunnels corresponding to the three literals of the associated clause. The bottom vertex $c_i^s$ of each clause edge $e_i$ is placed such that $e_i$ has to be drawn inside one of the three tunnels of the E-shape corresponding to $c_i$. This corresponds to the fact that in a satisfying truth assignment every clause has at least one satisfied literal. In tier $\mathcal T_1$ we merge all the tunnels corresponding to the same literal. We create variable gadgets that ensure that for each variable u edges of clauses containing u can be drawn in the tunnel associated with either the negative or the positive literal of u but not both. This corresponds to the fact that every variable is set to either true or false. Tiers $\mathcal T_2$ and $\mathcal T_3$ have a technical purpose.

We proceed by describing the different tiers in detail. Recall that in terms of realizability, Ordered Level Planarity is equivalent to the generalized version where $\gamma$ and $\chi$ map to the reals. For the sake of convenience we will begin by designing $\mathcal G$ in this generalized setting. It is easy to transform $\mathcal G$ such that it satisfies the standard definition in a polynomial-time post processing step.

Fig. 3.

(a) The E-shape and (b) the clause gadget of clause $c_i$. The thick gray lines represent the gates of $c_i$.

Tier 0 and 2, Clause Gadgets: The clause edges $e_i=(c_i^s,c_i^t)$ end in tier $\mathcal T_2$. It is composed of $l_2-l_1=|\mathcal C|$ levels each of which contains precisely one vertex. We assign $\gamma (c_i^t)=l_1+i$. Observe that this imposes no constraint on the order in which the edges enter $\mathcal T_2$.

Tier $\mathcal T_0$ consists of a system of tunnels that resembles the monotone rectilinear representation $\mathcal R$ of $G_\varphi = (\mathcal {U}\uplus \mathcal {C}, E)$, see Fig. 2c. Intuitively it is constructed as follows: We take the top part of $\mathcal R$, rotate it by $180^\circ$ and place it to the left of the bottom part such that the variables’ line segments align, see Fig. 2b. We call the resulting representation $\mathcal R'$. For each E-shape in $\mathcal R'$ we create a clause gadget, which is a subgraph composed of 11 vertices that are placed on a grid close to the E-shape, see Fig. 3. The red vertex at the bottom is the lower vertex $c_i^s$ of the clause edge $e_i$ of the clause $c_i$ corresponding to the E-shape. Without loss of generality we assume the grid to be fine enough such that the resulting ordered level graph can be drawn as in Fig. 2c without crossings. Further, we assume that the y-coordinates of every pair of horizontal segments belonging to distinct E-shapes differ by at least 3. This ensures that all vertices on levels with width at least 3 have out-degree at most 1 and in-degree at most 1 as stated in the lemma.

The clause gadget (without the clause edge) has a unique ordered level planar drawing in the sense that for every level $V_i$ the left-to-right sequence of vertices and edges intersected by the horizontal line $L_i$ through $V_i$ is identical in every ordered level planar drawing. This is due to the fact that the order of the top-most vertices $v_1'$, $v_6$, $v_2'$, $v_7$, $v_3'$ and $v_8$ is fixed. We call the line segments $v_1'v_6$, $v_2'v_7$ and $v_3'v_8$ the gates of $c_i$. Note that the clause edge $e_i$ has to intersect one of the gates of $c_i$. This corresponds to the fact the at least one literal of every clause has to be satisfied.

The subgraph $G_0$ induced by $\mathcal T_0$ (without the clause edges) has a unique ordered level planar drawing. In tier $\mathcal T_1$ we bundle all gates that belong to one literal together by creating two long paths for each literal. These two paths form the tunnel of the corresponding literal. All clause edges intersecting a gate of some literal have to be drawn inside the literal’s tunnel, see Fig. 2c. To this end, for $j=1,\dots ,|\mathcal U|$ we use $N_j^0$ ($n_j^0$) to refer to the left-most (right-most) vertex of a negative clause gadget placed on a line segment of $\mathcal R'$ representing $u_j\in \mathcal U$. The vertices $N_j^0$ and $n_j^0$ are the first vertices of the paths forming the negative tunnel $T_j^n$ of the negative literal of variable $u_j$. Analogously, we use $P_j^0$ ($p_j^0$) to refer to the left-most (right-most) vertex of a positive clause gadget placed on a line segment of $\mathcal R'$ representing $u_j$. The vertices $P_j^0$ and $p_j^0$ are the first vertices of the paths forming the positive tunnel $T_j^p$ of the positive literal of variable $u_j$. If for some j the variable $u_j$ is not contained both in negative and positive clauses, we artificially add two vertices $N_j^0$ and $n_j^0$ or $P_j^0$ and $p_j^0$ on the corresponding line segments in order to avoid having to treat special cases in the remainder of the construction.

Fig. 4.

(a) The variable gadget of $u_j$ in (b) positive and (c) negative state.

Tier 1 and 3, Variable Gadgets: Recall that every clause edge has to pass through a gate that is associated with some literal of the clause, and, thus, every edge is drawn in the tunnel of some literal. We need to ensure that it is not possible to use tunnels associated with the positive, as well as the negative literal of some variable simultaneously. To this end, we create a variable gadget with vertices in tier $\mathcal T_1$ and tier $T_3$ for each variable. The variable gadget of variable $u_j$ is illustrated in Fig. 4a. The variable gadgets are nested in the sense that they start in $\mathcal T_1$ in the order $u_1,u_2,...,u_{|\mathcal U |}$, from bottom to top and they end in the reverse order in $\mathcal T_3$, see Fig. 5. We force all tunnels with index at least j to be drawn between the vertices $u_j^a$ and $u_j^b$. This is done by subdividing the tunnel edges on this level, see Fig. 4b. The long edge $(u_j^s,u_j^t)$ has to be drawn to the left or right of $u_j^c$ in $\mathcal T_3$. Accordingly, it is drawn to the left of $u_j^a$ or to the right of $u_j^b$ in $\mathcal T_1$. Thus, it is drawn either to the right (Fig. 4b) of all the tunnels or to the left (Fig. 4c) of all the tunnels. As a consequence, the blocking edge $(u_j^s,u_j^p)$ is also drawn either to the right or the left of all the tunnels. Together with the edge $(u_j^q,u_j^p)$ it prevents clause edges from being drawn either in the positive tunnel $T_j^p$ or negative tunnel $T_j^n$ of variable $u_j$ which end at level $\gamma (u_j^q)$ because they can not reach their endpoints in $\mathcal T_2$ without crossings. We say $T_j^p$ or $T_j^n$ are blocked respectively.

The construction of the ordered level graph $\mathcal G$ can be carried out in polynomial time. Note that maximum degree is $\varDelta =2$ and that all vertices on levels with width at least 3 have out-degree at most 1 and in-degree at most 1 as claimed in the lemma.

Fig. 5.

Nesting structure of the variable gadgets.

Correctness: It remains to show that $\mathcal G$ has an ordered level planar drawing if and only if $\varphi$ is satisfiable. Assume that $\mathcal G$ has an ordered level planar drawing $\varGamma$. We create a satisfying truth assignment for $\varphi$. If $T_j^n$ is blocked we set $u_j$ to true, otherwise we set $u_j$ to false for $j\in 1,\dots ,|\mathcal U|$. Recall that the subgraph $G_0$ induced by the vertices in tier $\mathcal T_0$ has a unique ordered level planar drawing. Consider a clause $c_i$ and let f, g, j be the indices of the variables whose literals are contained in $c_i$. Clause edge $e_i=(e_i^s,e_i^t)$ has to pass level $l_0$ through one of the gates of $c_i$. More precisely, it has to be drawn between either $N_f^0$ and $n_f^0$, $N_g^0$ and $n_g^0$ or $N_j^0$ and $n_j^0$ if $c_i$ is negative or between either $P_f^0$ and $p_f^0$, $P_g^0$ and $p_g^0$ or $P_j^0$ and $p_j^0$ if $c_i$ is positive, see Fig. 2c. First, assume that $c_i$ is negative and assume without loss of generality that it traverses $l_0$ between $N_j^0$ and $n_j^0$. In this case clause edge $e_i$ has to be drawn in $T_j^n$. Recall that this is only possible if $T_j^n$ is not blocked, which is the case if $u_j$ is false, see Fig. 4c. Analogously, if $c_i$ is positive and $e_i$ traverses w.l.o.g. between $p_j^P$ and $p_j^p$, then $u_j$ is true, Fig. 4b. Thus, we have established that one literal of each clause in $\mathcal C$ evaluates to true for our truth assignment and, hence, formula $\varphi$ is satisfiable.

Now assume that $\varphi$ is satisfiable and consider a satisfying truth assignment. We create an ordered level planar drawing $\varGamma$ of $\mathcal G$. It is clear how to create the unique subdrawing of $G_0$. The variable gadgets are drawn in a nested fashion, see Fig. 5. For $j=1,\dots ,|\mathcal U|-1$ we draw edge $(u_j^a,u_j^c)$ to left of $u_{j+1}^a$ and $u_{j+1}^s$ and edge $(u_j^b,u_j^c)$ to right of $u_{j+1}^b$ and $u_{j+1}^s$. In other words, the pair $((u_j^a,u_j^c),(u_j^b,u_j^c))$ is drawn between all such pairs with index smaller than j. Recall that the vertices $u_j^a$, $u_j^b$, $u_j^s$, $u_j^p$ and $u_j^q$ are located on higher levels than the according vertices of variables with index smaller than j and that $u_j^t$ and $u_j^c$ are located on lower levels than the according vertices of variables with index smaller than j.

For $j=1,\dots ,|\mathcal U|$ if $u_j$ is positive we draw the long edge $(u_j^s,u_j^t)$ to the right of $u_j^b$ and $u_j^c$ and, accordingly, we have to draw all tunnels left of $u_j^s$ and $u_j^q$ (except for $T_j^n$, which has to be drawn to the left of $u_j^s$ and end to the right of $u_j^q$), see Fig. 4b. If $u_j$ is negative we draw the long edge $(u_j^s,u_j^t)$ to the left of $u_j^b$ and $u_j^c$ and, accordingly, we have to draw all tunnels right of $u_j^s$ and $u_j^q$ (except for $T_j^p$, which has to be drawn to the right of $u_j^s$ and end to the left of $u_j^q$), see Fig. 4c. We have to draw the blocking edge $(u_j^s,u_j^p)$ to the right of $n_j^{j+1}$ if $u_j$ is positive and to the left of $P_j^{j+1}$ if $u_j$ is negative.

It remains to describe how to draw the clause edges. Let $c_i$ be a clause. There is at least one true literal in $c_i$. Let k be the index of the corresponding variable. We describe the drawing of clause edge $e_i=(c_i^s,c_i^t)$ from bottom to top. We start by drawing $e_i$ in the tunnel $T_k^p$ ($T_k^n$) if $c_i$ is positive (negative). After the variable gadget of $u_k$ the edge $e_i$ leaves its tunnel and is drawn to the left (right) of all gadgets of variables with higher index, see Fig. 5.    $\square$

We obtain $\mathcal {NP}$-hardness for instances with maximum degree $\varDelta =2$. In fact, we can restrict our attention to instances level-width $\lambda =2$. To this end, we split levels with width $\lambda _i>2$ into $\lambda _i-1$ levels containing exactly two vertices each.

Lemma 3

An instance $\mathcal G=(G=(V,E),\gamma ,\chi )$ of Ordered Level Planarity with maximum degree $\varDelta \le 2$ can be transformed in linear time into an equivalent instance $\mathcal G'=(G'=(V',E'),\gamma ',\chi ')$ of Ordered Level Planarity with level-width $\lambda ' \le 2$ and maximum degree $\varDelta '$. If in $\mathcal G$ all vertices on levels with width at least 3 have out-degree at most 1 and in-degree at most 1, then $\varDelta '\le 2$. Otherwise, $\varDelta '\le \varDelta +1$.

The reduction in Lemma 2 requires degree-2 vertices. With $\varDelta =1$, the problem becomes polynomial-time solvable. In fact, even if $\varDelta =2$ one can easily solve it as long as the maximum in-degree and the maximum out-degree are both bounded by 1. Such instances consists of a set P of y-monotone paths.

We write $p \prec q$, meaning that $p\in P$ must be drawn to the left of $q\in P$, if p and q have vertices $v_p$ and $v_q$ that lie adjacent on a common level. If $\prec$ is acyclic, we can draw $\mathcal G$ according to a linear extension of $\prec$, otherwise there exists no solution.

Lemma 4

Ordered Level Planarity restricted to instances with maximum in-degree $\varDelta ^-=1$ and maximum out-degree $\varDelta ^+=1$ can be solved in linear time.

For $\lambda =1$ Ordered Level Planarity is solvable in linear time since Level Planarity can be solved in linear time [15]. Proper instances can be solved in linear-time via a sweep through every level. The problem is obviously contained in $\mathcal {NP}$. The results of this section establish Theorem 1.