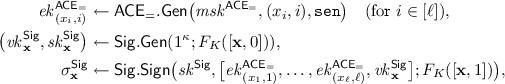Strengthening Access Control Encryption

Abstract

Access control encryption (ACE) was proposed by Damgård et al. to enable the control of information flow between several parties according to a given policy specifying which parties are, or are not, allowed to communicate. By involving a special party, called the sanitizer, policy-compliant communication is enabled while policy-violating communication is prevented, even if sender and receiver are dishonest. To allow outsourcing of the sanitizer, the secrecy of the message contents and the anonymity of the involved communication partners is guaranteed.

This paper shows that in order to be resilient against realistic attacks, the security definition of ACE must be considerably strengthened in several ways. A new, substantially stronger security definition is proposed, and an ACE scheme is constructed which provably satisfies the strong definition under standard assumptions.

Three aspects in which the security of ACE is strengthened are as follows. First, CCA security (rather than only CPA security) is guaranteed, which is important since senders can be dishonest in the considered setting. Second, the revealing of an (unsanitized) ciphertext (e.g., by a faulty sanitizer) cannot be exploited to communicate more in a policy-violating manner than the information contained in the ciphertext. We illustrate that this is not only a definitional subtlety by showing how in known ACE schemes, a single leaked unsanitized ciphertext allows for an arbitrary amount of policy-violating communication. Third, it is enforced that parties specified to receive a message according to the policy cannot be excluded from receiving it, even by a dishonest sender.

The full version of this paper is available at https://eprint.iacr.org/2017/429.

1 Introduction

1.1 Access Control Encryption—Model and Security Requirements

The concept of access control encryption (ACE) was proposed by Damgård et al. [6] in order to enforce information flow using cryptographic tools rather than a standard access control mechanism (e.g., a reference monitor) within an information system. If the encryption scheme provides certain operations (e.g., ciphertext sanitization) and satisfies an adequate security definition, then the reference monitor can be outsourced, as a component called the sanitizer, to an only partially trusted service provider. The goal of ACE is that the sanitizer learns nothing not intrinsically necessary. Security must also be guaranteed against dishonest users, whether senders or receivers of information, and against certain types of sanitizer misbehavior.

The information flow problem addressed by ACE is defined in a context with a set $\mathcal {R}$ of roles corresponding, for example, to different security clearances. Each user in a system can be assigned several roles. For example the users are employees of a company collaborating on a sensitive project, and they need to collaborate and exchange information by sending messages. Since the information is sensitive, which information a party can see must be restricted (hence the term access control), even if some parties are dishonest. In the most general form, the specification of which role may send to which other role corresponds to a relation (a subset of $\mathcal {R}\times \mathcal {R}$) or, equivalently, to a predicate $P:\mathcal {R}\times \mathcal {R}\rightarrow \{0,1\}$, where $s \in \mathcal {R}$ is allowed to communicate to $r \in \mathcal {R}$ if and only if $P(s, r) = 1$. The predicate $P$ is called the (security) policy. Typical examples of such policies arise from the Bell-LaPadula [2] model where roles are (partially) ordered, and the so-called “no-write-down” rule specifies that it is forbidden for a user to send information to another user with a lower role. Note that for this specific example, the relation is transitive, but ACE also allows to capture non-transitive security policies.

ACE was designed to work in the following setting. Users can communicate anonymously with a sanitizer. If a user wants to send a message, it is encrypted under a key corresponding to the sender’s role. Then the ciphertext is sent (anonymously) to the sanitizer who applies a certain sanitization operation and writes the sanitized ciphertext on a publicly readable bulletin board providing anonymous read-access to the users (receivers). Users who are supposed to receive the message according to the policy (and only those users) can decrypt the sanitized ciphertext.

To ensure security in the described setting, the ACE scheme must at least provide the following guarantees:

• 1. The encryption must assure privacy and anonymity against dishonest receivers as well as the sanitizer, i.e., neither the sanitizer nor dishonest receivers without access allowed by the policy should be able to obtain information about messages or the sender’s role.

• 2. A dishonest sender must be unable to communicate with a (potentially dishonest) receiver, unless this is allowed according to the policy. In other words, the system must not provide covert channels allowing for policy-violating communication.

As usual in a context with dishonest senders, the first goal requires security against chosen-ciphertext attacks (CCA) because dishonest users can send a ciphertext for which they do not know the contained message and by observing the effects the received message has on the environment, potentially obtain information about the message. This corresponds to the availability of a decryption oracle, as in the CCA-security definition.

Note that the second goal is only achievable if users cannot directly write to the repository or communicate by other means bypassing the sanitizer, and if the sanitizer is not actively dishonest because a dishonest sanitizer can directly write any information received from a dishonest sender to the repository. The assumption that a user cannot bypass the sanitizer and communicate to another party outside of the system can for example be justified by assuming that users, even if dishonest, want to avoid being caught communicating illegitimately, or if only a user’s system (not the user) is corrupted, and the system can technically only send message to the sanitizer.

Since the sanitizer is not fully trusted in our setting, one should consider the possibility that an unsanitized ciphertext is leaked (intentionally or unintentionally) to a dishonest party. This scenario can be called (unsanitized) ciphertext-revealing attack. Obviously, all information contained in this ciphertext gets leaked to that party. While this cannot be avoided, such an attack should not enable dishonest parties to violate the security requirements beyond that.

We point out that previously proposed encryption techniques (before ACE), such as attribute-based encryption [11, 17] and functional encryption [4], enable the design of schemes where a sender can encrypt messages such that only designated receivers (who possess the required key) can read the message. This captures the access control aspects of read permissions, but it does not allow to capture the control of write/send permissions. In other words, such schemes only achieve the first goal listed above, not the second one.

1.2 Contributions of this Paper

While the proposal of the ACE-concept and of efficient ACE-schemes were important first steps toward outsourcing access control, the existing security definition turns out to be insufficient for several realistic attack scenarios. The main contributions of this paper consist of uncovering issues with existing definitions and schemes, fixing these issues by proposing stronger security notions, and constructing a scheme satisfying our stronger notions.

Issues with existing definitions and schemes. As argued above, chosen-ciphertext attacks should be considered since the use case for ACE includes dishonest senders. Existing definitions, however, do not take this into account, i.e., the adversary does not have access to a decryption oracle in the security games.

Furthermore, existing notions do not consider ciphertext-revealing attacks. Technically speaking, the security game that is supposed to prevent dishonest senders from transmitting information to dishonest receivers (called no-write game), gives the adversary only access to an encryption oracle that sanitizes ciphertexts before returning them. This means that the adversary has no access to unsanitized ciphertexts. This is not only a definitional subtlety, but can completely break down any security guarantees. We demonstrate that existing ACE schemes allow the following attack: Assume there are three users A, M, and E in the system, where A is honest and by the policy allowed to send information to E, and M and E are dishonest and not allowed to communicate. If A sends an (innocent) message to E and the corresponding unsanitized ciphertext is leaked to M, malleability of the ciphertext can be exploited by M to subsequently communicate an arbitrary number of arbitrary messages chosen by M to E. Note that while this attack crucially exploits malleability of ciphertexts, it is not excluded by CCA security for two reasons: first, CCA security does not prevent an adversary from producing valid ciphertexts for unrelated messages, and second, the integrity should still hold if the adversary has the decryption key (but not the encryption key).

Finally, existing security definitions focus on preventing dishonest parties from communicating if disallowed by the policy, but they do not enforce information flow. For example, if user A only has a role such that according to the policy, users B and C can read what A sends, existing schemes do not prevent A from sending a message that can be read by B but not by C, or sending a message such that B and C receive different messages. This is not as problematic as the two issues above, and one can argue that A could anyway achieve something similar by additionally encrypting the message with another encryption scheme. Nevertheless, for some use cases, actually precisely enforcing the policy can be required (consider, e.g., a logging system), and one might intuitively expect that ACE schemes achieve this.

New security definitions. We propose new, stronger security definitions for ACE that exclude all issues mentioned above. First, we give the adversary access to a decryption oracle. More precisely, the oracle first sanitizes the given ciphertext and then decrypts it, since this is what happens in the application if a dishonest party sends a ciphertext to the sanitizer. Second, we incorporate ciphertext-revealing attacks by giving the adversary access to an encryption oracle that returns unsanitized ciphertexts for arbitrary roles. Finally, we introduce a new security game in which an adversary can obtain encryption keys and decryption keys from an oracle and has to output a ciphertext such that one of the following events occur: either the set of roles that can successfully decrypt the ciphertext (to an arbitrary message) is inconsistent with the policy for all sender roles for which the adversary has an encryption key (in this case, we say the adversary is not role-respecting); or the ciphertext can be successfully decrypted with two keys such that two different messages are obtained (in this case, we say the uniform-decryption property is violated).

Construction of an ACE scheme for our stronger notions. Our construction proceeds in three steps and follows the general structure of the generic construction by Fuchsbauer et al. [9]. Since we require much stronger security notions in all three steps, our constructions and proofs are consequently more involved than existing ones. First, we construct a scheme for a primitive we call enhanced sanitizable public-key encryption (sPKE). Second, we use an sPKE scheme to construct an ACE scheme satisfying our strong security notion for the equality policy, i.e., for the policy that allows s to send to r if and only if $r = s$. Third, we show how to lift an ACE scheme for the equality policy to an ACE scheme for the disjunction of equalities policy. This policy encodes roles as vectors $\mathbf {x} = (x_1, \ldots , x_{\ell })$ and allows role $\mathbf {x}$ to send to role $\mathbf {y}$ if and only if $x_1 = y_1 \vee \ldots \vee x_\ell = y_\ell$. As shown by Fuchsbauer et al. [9], useful policies including the inequality predicate corresponding to the Bell-LaPadula model can efficiently be implemented using this policy by encoding the roles appropriately.

Enhanced sanitizable PKE. An sPKE scheme resembles publicy-key encryption with an additional setup algorithm that outputs sanitizer parameters and a master secret key. The master secret key is needed to generate a public/private key pair and the sanitizer parameters can be used to sanitize a ciphertext. A sanitized ciphertext cannot be linked to the original ciphertext without the decryption key. We require the scheme to be CCA secure (with respect to a sanitize-then-decrypt oracle) and anonymous. Sanitization resembles rerandomization [12, 15], also called universal re-encryption [10], but we allow sanitized ciphertexts to be syntactically different from unsanitized ciphertexts. This allows us to achieve full CCA security, which is needed for our ACE construction and unachievable for rerandomizable encryption.

Our scheme is based on ElGamal encryption [7], which can easily be rerandomized and is anonymous. We obtain CCA security using the technique of Naor and Yung [14], i.e., encrypting the message under two independent keys and proving in zero-knowledge that the ciphertexts are encryptions of the same message, which was shown by Sahai to achieve full CCA security if the zero-knowledge proof is simulation-sound [16]. A technical issue is that if the verification of the NIZK proof was done by the decrypt algorithm, the sanitization would also need to sanitize the proof. Instead, we let the sanitizer perform the verification. Since we want to preserve anonymity, this needs to be done without knowing under which public keys the message was encrypted. Therefore, the public keys are part of the witness in the NIZK proof. Now the adversary could encrypt the same message under two different public keys that were not produced together by the key-generation, which would break the reduction. To prevent this, the pair of public keys output by the key-generation is signed using a signature key that is contained in the master secret key and the corresponding verification key is contained in the sanitizer parameters.

ACE for equality. The basic idea of our ACE scheme for the equality policy is to use for each role, encryption and decryption keys of an sPKE scheme as the encryption and decryption keys of the ACE scheme, respectively. Since we need to prevent dishonest senders without an encryption key for some role from producing valid ciphertexts for that role even after seeing encryptions of other messages for this role and obtaining encryption keys for other roles, we add a signature key to the encryption key, sign this pair using a separate signing key, where the corresponding verification key is part of the sanitizer parameters, and let senders sign their ciphertexts. To preserve anonymity, this signature cannot be part of the ciphertext. Instead, senders prove in zero-knowledge that they know such a signature and that the encryption was performed properly.

ACE for disjunction of equalities. The first step of our lifting is identical to the lifting described by Fuchsbauer et al. [9]: for each component of the role-vector, the encryption and decryption keys contain corresponding keys of an ACE scheme for the equality policy. To encrypt a message, this message is encrypted under each of the key-components. In a second step, we enforce role-respecting security with the same trick we used in our ACE scheme for equality; that is, we sign encryption key-vectors together with a signing key for that role, and senders prove in zero-knowledge that they have used a valid key combination to encrypt and that they know a signature of the ciphertext vector.

1.3 Related Work

The concept of access control encryption has been introduced by Damgård et al. [6]. They provided the original security definitions and first schemes. Subsequent work by Fuchsbauer et al. [9], by Tan et al. [18], and by Kim and Wu [13] focused on new schemes that are more efficient, based on different assumptions, or support more fine grained access control policies. In contrast to our work, they did not attempt to strengthen the security guarantees provided by ACE.

2 Preliminaries

2.1 Notation

We write $x \leftarrow y$ for assigning the value y to the variable x. For a finite set X, $x \twoheadleftarrow X$ denotes assigning to x a uniformly random value in X. For $n \in \mathbb {N}$, we use the convention

$$\begin{aligned}{}[n] := \{ 1, \ldots , n\}. \end{aligned}$$

By $\mathbb {Z}_n$ we denote the ring of integers modulo n, and by $\mathbb {Z}^*_n$ its multiplicative group of units. The probability of an event A in an experiment E is denoted by ${\text {Pr}}^{E}[A]$, e.g., ${\text {Pr}}^{x \twoheadleftarrow \{0,1\}}[x=0] = \frac{1}{2}$. If the experiment is clear from the context, we omit the superscript. The conditional probability of A given B is denoted by $\Pr [A \mid B]$ and the complement of A is denoted by $\lnot A$. For a probabilistic algorithm $\mathcal {A}$ and $r \in \{0,1\}^*$, we denote by $\mathcal {A}(x; r)$ the execution of $\mathcal {A}$ on input x with randomness r. For algorithms $\mathcal {A}$ and $\mathcal {O}$, $\mathcal {A}^{\mathcal {O}(\cdot )}(x)$ denotes the execution of $\mathcal {A}$ on input x, where $\mathcal {A}$ has oracle access to $\mathcal {O}$.

2.2 Security Definitions, Advantages, Efficiency, and Negligibility

We define the security of a scheme via a random experiment (or game) involving an adversary algorithm $\mathcal {A}$. For a given scheme $\mathcal {E}$ and adversary $\mathcal {A}$, we define the advantage of $\mathcal {A}$, which is a function of the security parameter $\kappa$. To simplify the notation, we omit the security parameter when writing the advantage, e.g., we write $\mathsf {Adv}^{\mathsf {Sig\text {-}EUF\text {-}CMA}}_{\mathcal {E},\mathcal {A}}$ instead of $\mathsf {Adv}^{\mathsf {Sig\text {-}EUF\text {-}CMA}}_{\mathcal {E},\mathcal {A}}(\kappa )$ for the advantage of $\mathcal {A}$ in the existential unforgeability game for the signature scheme $\mathcal {E}$. Such a scheme is considered secure if $\mathsf {Adv}^{\mathsf {Sig\text {-}EUF\text {-}CMA}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$. An algorithm $\mathcal {A}$ is efficient if it runs in probabilistic polynomial time (PPT), i.e., $\mathcal {A}$ has access to random bits and there is a polynomial p such that $\mathcal {A}(x)$ terminates after at most $p({|}x{|})$ steps (on some computational model, e.g., Turing machines) for all inputs x, where ${|}x{|}$ denotes the bit-length of x. A function f is negligible if for every polynomial p, there exists $n_0 \in \mathbb {N}$ such that $f(n) < 1/p(n)$ for all $n \ge n_0$. While these asymptotic definitions yield concise statements, we will in all proofs derive precise bounds on the advantages, following a concrete security approach.

2.3 Access Control Encryption

We recall the definition of access control encryption by Damgård et al. [6]. Following Fuchsbauer et al. [9], we do not have sanitizer keys and require $\mathsf {Gen}$ to be deterministic. The set of roles is assumed to be $\mathcal {R}= [n]$.

Definition 1

An access control encryption (ACE) scheme $\mathcal {E}$ consists of the following five PPT algorithms:

• Setup: The algorithm $\mathsf {Setup}$ on input a security parameter $1^{\kappa }$ and a policy $P:[n] \times [n] \rightarrow \{0,1\}$, outputs a master secret key $msk$ and sanitizer parameters $sp$. We implicitly assume that all keys include the finite message space $\mathcal {M}$ and the ciphertext spaces $\mathcal {C}, \mathcal {C}'$.

• Key generation: The algorithm $\mathsf {Gen}$ is deterministic and on input a master secret key $msk$, a role $i \in [n]$, and the type $\mathtt {sen}$, outputs an encryption key $ek _i$; on input $msk$, $j \in [n]$, and the type $\mathtt {rec}$, outputs a decryption key $dk _j$.

• Encryption: The algorithm $\mathsf {Enc}$ on input an encryption key $ek _i$ and a message $m\in \mathcal {M}$, outputs a ciphertext $c\in \mathcal {C}$.

• Sanitization: The algorithm $\mathsf {San}$ on input sanitizer parameters $sp$ and a ciphertext $c\in \mathcal {C}$, outputs a sanitized ciphertext $c'\in \mathcal {C}'\cup \{\bot \}$.

• Decryption: The algorithm $\mathsf {Dec}$ on input a decryption key $dk _j$ and a sanitized ciphertext $c'\in \mathcal {C}'$, outputs a message $m\in \mathcal {M}\cup \{ \bot \}$; on input $dk _j$ and $\bot$, it outputs $\bot$.

For a probabilistic algorithm $\mathcal {A}$, consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}CORR}}_{\mathcal {E},\mathcal {A}}$ that given a security parameter $1^{\kappa }$ and a policy $P$, executes $( sp , msk ) \leftarrow \mathsf {Setup}(1^{\kappa }, P)$, $(m, i, j) \leftarrow \mathcal {A}^{\mathsf {Gen}( msk , \cdot , \cdot )}( sp )$, $ek _i \leftarrow \mathsf {Gen}( msk , i, \mathtt {sen})$, and $dk _j \leftarrow \mathsf {Gen}( msk , j, \mathtt {rec})$. We define the correctness advantage of $\mathcal {A}$ (for security parameter $\kappa$ and policy $P$) as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [P(i,j) = 1 \ \wedge \ \mathsf {Dec}\bigl ( dk _j, \mathsf {San}( sp , \mathsf {Enc}( ek _i, m)) \bigr ) \ne m\bigr ], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}CORR}}_{\mathcal {E},\mathcal {A}}$ and the random coins of $\mathsf {Enc}$, $\mathsf {San}$, and $\mathsf {Dec}$. The scheme $\mathcal {E}$ is called correct if $\mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$, and perfectly correct if $\mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathcal {E},\mathcal {A}} = 0$ for all $\mathcal {A}$.

Remark 1

Correctness of an encryption scheme is typically not defined via a game with an adversary, but by requiring that decryption of an encryption of $m$ yields $m$ with probability 1. This perfect correctness requirement is difficult to achieve for ACE schemes and not necessary for applications because it is sufficient if a decryption error only occurs with negligible probability in any execution of the scheme. Damgård et al. [6] define correctness by requiring that for all $m$, i, and j with $P(i,j) = 1$, the probability that a decryption fails is negligible, where the probability is over setup, key generation, encrypt, sanitize, and decrypt. While this definition is simpler than ours, it does not guarantee that decryption errors only occur with negligible probability in any execution of the scheme. For example, a scheme could on setup choose a random message m and embed it into all keys such that decryption always fails for encryptions of this particular message. This does not violate the definition by Damgård et al. since for any fixed message, the probability that this message is sampled during setup is negligible (if the message space is large). Nevertheless, an adversary can always provoke a decryption error by sending that particular message m, which is not desirable. The above example might at first sight seem somewhat artificial, and typically, schemes do not have such a structure. However, capturing correctness via an experiment is important when thinking of composition, since we expect that the correctness guarantee still holds when the ACE scheme is run as part of a larger system. In order to meet this expectation, and to exclude the above issue, we formalize correctness via an experiment.

Additionally, Fuchsbauer et al. have defined detectability, which guarantees that decrypting with a wrong key yields $\bot$ with high probability [9]. This allows receivers to detect whether a message was sent to them. As for correctness, we define it via an experiment. The notion is related to robustness for public-key encryption [1]. We additionally define strong detectability, in which the randomness for the encryption is adversarially chosen.

Definition 2

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an ACE scheme and let $\mathcal {A}$ be a probabilistic algorithm. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}DTCT}}_{\mathcal {E},\mathcal {A}}$ that given a security parameter $1^{\kappa }$ and a policy $P$, executes $( sp ) \leftarrow \mathsf {Setup}(1^{\kappa }, P)$, $(m, i, j) \leftarrow \mathcal {A}^{\mathsf {Gen}( msk , \cdot , \cdot )}( sp , msk )$, $ek _i \leftarrow \mathsf {Gen}( msk , i, \mathtt {sen})$, and $dk _j \leftarrow \mathsf {Gen}( msk , j, \mathtt {rec})$. We define the detectability advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}DTCT}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [P(i,j) = 0 \ \wedge \ \mathsf {Dec}\bigl ( dk _j, \mathsf {San}( sp , \mathsf {Enc}( ek _i, m)) \bigr ) \ne \bot \bigr ], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}DTCT}}_{\mathcal {E},\mathcal {A}}$ and the random coins of $\mathsf {Enc}$, $\mathsf {San}$, and $\mathsf {Dec}$. The scheme $\mathcal {E}$ is called detectable if $\mathsf {Adv}^{\mathsf {ACE\text {-}DTCT}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$. The experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}sDTCT}}_{\mathcal {E},\mathcal {A}}$ is identical to $\mathsf {Exp}^{\mathsf {ACE\text {-}DTCT}}_{\mathcal {E},\mathcal {A}}$ except that $\mathcal {A}$ returns $(m, r, i, j)$. The strong detectability advantage of $\mathcal {A}$ is defined as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}sDTCT}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [P(i,j) = 0 \ \wedge \ \mathsf {Dec}\bigl ( dk _j, \mathsf {San}( sp , \mathsf {Enc}( ek _i, m; r)) \bigr ) \ne \bot \bigr ], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}sDTCT}}_{\mathcal {E},\mathcal {A}}$ and the random coins of $\mathsf {San}$ and $\mathsf {Dec}$. The scheme $\mathcal {E}$ is called strongly detectable if $\mathsf {Adv}^{\mathsf {ACE\text {-}sDTCT}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

2.4 Existing Security Definitions

Existing notions for ACE specify two core properties: the so-called no-read rule and the no-write rule. The no-read rule formalizes privacy and anonymity: roughly, an honestly generated ciphertext should not leak anything about the message, except possibly its length, or about the role of the sender. The security game allows an adversary to interact with a key-generation oracle (to obtain encryption and decryption keys for selected roles), and an encryption oracle to obtain encryptions of chosen messages for roles for which the adversary does not possess the encryption key. This attack model reflects that an adversary cannot obtain useful information by observing the ciphertexts that are sent to the sanitizer. To exclude trivial attacks, it is not considered a privacy breach if the adversary knows a decryption key that allows to decrypt the challenge ciphertext according to the policy. Similarly, it is not considered an anonymity breach if the encrypted messages are different. We next state the definition of the no-read rule.¹

Definition 3

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an ACE scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}no\text {-}read}}_{\mathcal {E},\mathcal {A}}$ in Fig. 1 and let J be the set of all j such that $\mathcal {A}_1$ or $\mathcal {A}_2$ issued the query $(j, \mathtt {rec})$ to the oracle $\mathcal {O}_{G}$. The payload-privacy advantage and the sender-anonymity advantage of $\mathcal {A}$ are defined as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}read, priv}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ {|}m_0{|} = {|}m_1{|} \\& \wedge \ \forall j \in J \ P(i_0, j) = P(i_1, j) = 0 \bigr ] - 1, \\ \mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}read, anon}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ m_0 = m_1 \\& \wedge \ \forall j \in J \ P(i_0, j) = P(i_1, j) \bigr ] - 1, \end{aligned}$$

respectively, where the probabilities are over the randomness of all algorithms in $\mathsf {Exp}^{\mathsf {ACE\text {-}no\text {-}read}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ satisfies the payload-privacy no-read rule and the sender-anonymity no-read rule if $\mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}read, priv}}_{\mathcal {E},\mathcal {A}}$ and $\mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}read, anon}}_{\mathcal {E},\mathcal {A}}$ are negligible for all efficient $\mathcal {A}$, respectively. If it satisfies both, it is said to satisfy the no-read rule.

Fig. 1.

The no-read and no-write experiments for an ACE scheme $\mathcal {E}$ and an adversary $\mathcal {A}=(\mathcal {A}_1, \mathcal {A}_2)$. The oracles are defined as $\mathcal {O}_{G}(\cdot , \cdot ) := \mathsf {Gen}( msk , \cdot , \cdot )$, $\mathcal {O}_{E}(\cdot , \cdot ) := \mathsf {Enc}(\mathsf {Gen}( msk , \cdot , \mathtt {sen}), \cdot )$, and $\mathcal {O}_{ES}(\cdot , \cdot ) := \mathsf {San}( sp , \mathsf {Enc}(\mathsf {Gen}( msk , \cdot , \mathtt {sen}), \cdot ))$.

The no-write rule of ACE is the core property to capture access control. In a nutshell, if the adversary only possesses encryption keys for roles i and decryption keys for roles j with $P(i,j) = 0$, then he should not be able to create a ciphertext from which, after being sanitized, he can retrieve any information. Technically, in the corresponding security game, the adversary is given a key-generation oracle as above, and in addition an oracle to obtain sanitized ciphertexts for selected messages and roles. This attack model corresponds to a setting where an adversary only sees the outputs of a sanitizer, but not its inputs, and in particular no unsanitized ciphertexts generated for roles for which he does not possess the encryption key. The adversary wins if he manages to distinguish the sanitized version of a ciphertext of his choice from a sanitized version of a freshly generated encryption of a random message, and if he does not obtain the encryption key for any role i and the decryption key of any role j for which $P(i,j) = 1$, as this would trivially allow him to distinguish.

Definition 4

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an ACE scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}no\text {-}write}}_{\mathcal {E},\mathcal {A}}$ in Fig. 1, let $I_1$ be the set of all i such that $\mathcal {A}_1$ issued the query $(i, \mathtt {sen})$ to $\mathcal {O}_{G}$, and let J be the set of all j such that $\mathcal {A}_1$ or $\mathcal {A}_2$ issued the query $(j, \mathtt {rec})$ to $\mathcal {O}_{G}$. We define the no-write advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}write}}_{\mathcal {E},\mathcal {A}} := 2 \cdot \Pr \bigl [ b' = b \ \wedge \ i' \in I_1&\ \wedge \ \forall i \in I_1 \ \forall j \in J \ P(i, j) = 0 \\&\wedge \ \mathsf {San}( sp , c_0) \ne \bot \bigr ] - 1, \end{aligned}$$

where the probability is over the randomness of all algorithms in $\mathsf {Exp}^{\mathsf {ACE\text {-}no\text {-}write}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ satisfies the no-write rule if $\mathsf {Adv}^{\mathsf {ACE\text {-}no\text {-}write}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

Remark 2

Our definition follows the one by Fuchsbauer et al. [9] by requiring $\mathsf {San}( sp , c_0) \ne \bot$ in the winning condition for the no-write rule, which was not required in the original definition by Damgård et al. [6]. Schemes can be made secure with respect to the original definition by letting the algorithm $\mathsf {San}$ create a fresh ciphertext for a random message when given an invalid ciphertext.

The condition $i' \in I_1$ together with $\forall i \in I_1 \ \forall j \in J \ P(i, j) = 0$ ensures that $\mathcal {A}$ does not have a key to decrypt $c_1$, which would trivially allow to distinguish. Requiring that $\mathcal {A}$ obtains a key for $i'$ however excludes adversaries that obtain no key at all. The original definitions [6] therefore include a special role 0 with $P(0, j) = 0$ for all j. One can then assume without loss of generality that anyone obtains a key for this role. Since assuming the existence of such a role appears to be a technicality that is only needed for the no-write rule, we do not make this assumption and present new security definitions in Sect. 4.2 that do not rely on such a role.

3 Ciphertext-Revealing Attacks Against Existing Schemes

3.1 Generic Description of Attack

We describe a fundamental practical issue of schemes which meet the above no-read and no-write definitions and show why the guarantees expected from an ACE scheme need to be strengthened. We show that schemes fulfilling the definition can suffer from what we call a malleability attack, which effectively bypasses the given policy and allows communication that is forbidden by the policy. The attack does not abuse any peculiarities of existing models and in fact only requires that the semi-honest sanitizer shares its inputs and outputs with colluding parties, which is arguably possible when the sanitizer is outsourced. In particular, security against such a sanitizer is desirable from a practical point of view.

We first give a high-level explanation of the attack, formalize it as a second step, and finally show that the “linear” scheme by Damgård et al. [6] based on ElGamal is vulnerable. In the full version, we also show this for the ElGamal-based scheme by Fuchsbauer et al. [9].

Assume there are three parties, Alice, Bob, and Charlie, each having a different role assigned. We denote by $\mathsf {A}$, $\mathsf {B}$, and $\mathsf {C}$ the associated roles. In our example, Alice and Charlie are always honest. Alice is allowed to communicate with Bob and Charlie. Bob is dishonest and forbidden to send messages to Charlie (and to Alice). The attack now proceeds as follows: When Alice sends her first message, Bob requests the corresponding ciphertext and the sanitized ciphertext from the semi-honest sanitizer. He then decrypts the sanitized ciphertext and thus receives the message Alice has sent. With the knowledge of this message, as we show below, he is able to create a valid ciphertext for a chosen message $m'$, which will be correctly sanitized and later decrypted by Charlie, hence allowing unrestricted communication from Bob to Charlie. Details follow.

Consider the policy defined by

$$\begin{aligned} P(i,j) := {\left\{ \begin{array}{ll} 1, &{}i = \mathsf {A},\\ 0, &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

For the sake of presentation, we assume that the ACE scheme $\mathcal {E}$ under consideration enjoys perfect correctness. Also, we assume that the setup-phase has completed and the three parties thus possess the encryption and decryption keys, $ek _i$ and $dk _i$, respectively. Now, imagine that the ACE scheme admits an efficient function $\mathsf {maul}_{\mathcal {E}}$ with the following property (later we show how to implement such a function for some existing schemes): For all messages $m$ and $m'$, any role i, and sanitizer parameters $sp$ in the range of $\mathsf {Setup}$, and for any fixed randomness r,

$$\begin{aligned} \mathsf {maul}_{\mathcal {E}}\bigl (\mathsf {Enc}( ek _i, m; r), sp , m, m') \bigr ) = \mathsf {Enc}( ek _i, m' ; r). \end{aligned}$$

(1)

If such a malleability function exists, the communication policy can be bypassed as follows:

• 1. Alice encrypts a message $c\leftarrow \mathsf {Enc}( ek _\mathsf {A}, m)$ and the sanitizer computes $c'\leftarrow \mathsf {San}( sp , c)$ and gives $c$ and $c'$ to Bob.

• 2. Bob computes $m\leftarrow \mathsf {Dec}( dk _\mathsf {B}, c')$ and $\hat{c} \leftarrow \mathsf {maul}_{\mathcal {E}}(c, sp , m, m')$ and sends $\hat{c}$ to the sanitizer.

• 3. The ciphertext is sanitized $\hat{c}' \leftarrow \mathsf {San}( sp , \hat{c})$ and subsequently sent to Charlie. By the (perfect) correctness of the assumed ACE scheme and by our assumption on $\mathsf {maul}_{\mathcal {E}}$, $\hat{c}'$ is a valid ciphertext (under the encryption key of Alice) and Charlie is able to decrypt $m' \leftarrow \mathsf {Dec}( dk _\mathsf {C}, \hat{c}')$, effectively receiving Bob’s message $m'$.

3.2 DHO Scheme Based on ElGamal

We briefly recall the ElGamal based ACE scheme for a single identity. The sanitizer parameters of the scheme contain the description of a finite cyclic group $G=\langle g \rangle$ and its group order q, and additionally an element $h=g^x$ for a uniform random $x \in \mathbb {Z}_q$. The encryption key for $\mathsf {A}$ is a random value $ek \in \mathbb {Z}_q$, and the decryption key is $-x$. The algorithm $\mathsf {Enc}$ on input an encryption key $ek _i$ and a message $m\in \mathcal {M}$, samples $r_1, r_2 \in \mathbb {Z}_q$ uniformly at random and outputs the ciphertext

$$\begin{aligned} c= (c_0, c_1, c_2, c_3) := (g^{r_1}, h^{r_1} g^{ ek _i}, g^{r_2}, m\cdot h^{r_2}). \end{aligned}$$

We can define the function $\mathsf {maul}_{\mathsf {DHO}}$ as

$$\begin{aligned} \mathsf {maul}_{\mathsf {DHO}}\bigl ((c_0, c_1, c_2, c_3), sp , m, m'\bigr ) := \bigl (c_0, c_1, c_2, m' \cdot m^{-1} \cdot c_3 \bigr ). \end{aligned}$$

Since the group order q is part of $sp$, this function is efficiently computable. For $c_3 = m\cdot h^{r_2}$, we thus get a new fourth component $c'_3 = m' \cdot h^{r_2}$ and Eq. (1) is satisfied.

The malleability for more than one identity (and in particular in our scenario described above) follows since the scheme for several identities is composed of independent instances of the basic single-identity scheme.

4 A Stronger Notion of ACE

In this section, we introduce our new security definitions, which exclude the issues we have discovered. In the full version, we also show in which sense they imply the original notions.

4.1 ACE with Modification Detection

To be resilient against the ciphertext-revealing attacks described in Sect. 3, the sanitizer should ideally only sanitize fresh encryptions and block ciphertexts that are either replays or obtained by modifying previous ciphertexts. Therefore, we introduce an additional algorithm for detecting modified ciphertexts. If the sanitizer receives a ciphertext that is detected to be a modification of a previously received one, this ciphertext is blocked. Since such ciphertexts will not be stored in the repository and consequently not be decrypted, we define chosen-ciphertext security with respect to a decryption oracle that does not return a decryption if the received ciphertext is detected to be a modification of the challenge ciphertext. Our definitions can therefore be seen as a variant of publicly-detectable replayable-CCA security, which was introduced by Canetti et al. [5] for public key encryption. Before defining the security, we define the syntax of ACE schemes with this additional algorithm.

Definition 5

An access control encryption with modification detection scheme is an ACE scheme $\mathcal {E}$ together with a PPT algorithm $\mathsf {DMod}$ that on input sanitizer parameters $sp$ and two ciphertexts $c, \tilde{c} \in \mathcal {C}$, outputs a bit b (where $b=1$ means that $\tilde{c}$ was obtained via modifying $c$).

From now on, we will only consider ACE schemes with modification detection and thus often refer to them simply as ACE schemes.

The algorithm $\mathsf {DMod}$ should output 1 if $\tilde{c}$ is an adversarial modification of $c$, and 0 otherwise. We have the following intuitive requirements on $\mathsf {DMod}$:

• 1. All ciphertexts $\tilde{c}$ an adversary can produce given ciphertexts $c_1, \ldots , c_l$ and no encryption key, are either invalid (i.e., sanitize to $\bot$) or we have $\mathsf {DMod}( sp , c_i, \tilde{c}) = 1$ for some $i \in \{1, \ldots , n\}$.

• 2. Given encryption and decryption keys, an adversary is unable to produce a ciphertext $c$ such that a ciphertext produced by $\mathsf {Enc}$ for a message of the adversary’s choice is detected to be a modification of $c$. In particular, independent encryptions of messages collide only with negligible probability.

The first requirement is captured by role-respecting security as defined in Definition 9, the second one by non-detection of fresh encryptions defined in Definition 8.

Remark 3

Canetti et al. (translated to our setting) additionally require that if $\mathsf {DMod}( sp , c, \tilde{c}) = 1$, then $c$ and $\tilde{c}$ decrypt to the same message [5]. For our purpose, this is not needed. This means that we do not want to detect replays in the sense that the same message is replayed, but more generally, whether the given ciphertext was obtain via some modification of another ciphertext.

4.2 New Security Definitions

We formalize chosen-ciphertext attacks by giving the adversary access to an oracle $\mathcal {O}_{SD}$ that first sanitizes a given ciphertext and then decrypts the result. One could also consider chosen-sanitized-ciphertext attacks by providing the adversary access to an oracle $\mathcal {O}_{D}$ that only decrypts. This is potentially stronger since the adversary can emulate the oracle $\mathcal {O}_{SD}$ by first sanitizing the ciphertexts and then giving the result to $\mathcal {O}_{D}$, but given $\mathcal {O}_{SD}$, it is not necessarily possible to emulate $\mathcal {O}_{D}$. Since in the application, users can only send ciphertexts to the sanitizer but not directly write ciphertexts to the repository such that they are decrypted without being sanitized, the weaker notion is sufficient.

In principle, the adversary has in all definitions access to $\mathcal {O}_{SD}$, as well as to an encryption oracle and a key-generation oracle. To simplify the definitions, we omit the encryption or decryption oracles if the winning condition places no restriction on the encryption or decryption keys obtained from the key-generation oracle, respectively.

Privacy and anonymity. We first give definitions for (payload) privacy and sender-anonymity. The former guarantees that encryptions of different messages under the same encryption key cannot be distinguished as long as the adversary has no decryption key that allows to decrypt. We also require this for messages of different length, i.e., schemes satisfying our definition do not leak the length of the encrypted message, which means that the message space has to be bounded. Anonymity guarantees that encryptions of the same message under different keys cannot be distinguished. We distinguish a weak and a strong variant of anonymity, where the weak one provides no guarantees if the adversary can decrypt the ciphertext, and the strong one guarantees that even if the adversary has decryption keys, nothing is leaked about the sender role beyond which of the adversary’s decryption keys can be used to decrypt.

Definition 6

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec}, \mathsf {DMod})$, be an ACE with modification detection scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}PRV\text {-}ANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ in Fig. 2 and let J be the set of all j such that $\mathcal {A}_1$ or $\mathcal {A}_2$ issued the query $(j, \mathtt {rec})$ to the oracle $\mathcal {O}_G$. We define the privacy under chosen-ciphertext attacks advantage and the sender-anonymity under chosen-ciphertext attacks advantages of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}PRV\text {-}CCA}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ i_0 = i_1 \ \wedge \ \forall j \in J \ P(i_0, j) = 0 \bigr ] - 1, \\ \mathsf {Adv}^{\mathsf {ACE\text {-}wANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ m_0 = m_1 \\& \wedge \ \forall j \in J \ P(i_0, j) = P(i_1, j) = 0 \bigr ] - 1, \\ \mathsf {Adv}^{\mathsf {ACE\text {-}sANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ m_0 = m_1 \\& \wedge \ \forall j \in J \ P(i_0, j) = P(i_1, j) \bigr ] - 1, \end{aligned}$$

respectively, where all probabilities are in $\mathsf {Exp}^{\mathsf {ACE\text {-}PRV\text {-}ANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ is called private under chosen-ciphertext attacks (PRV-CCA secure), weakly sender-anonymous under chosen-ciphertext attacks (wANON-CCA secure), and strongly sender-anonymous under chosen-ciphertext attacks (sANON-CCA secure) if $\mathsf {Adv}^{\mathsf {ACE\text {-}PRV\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$, $\mathsf {Adv}^{\mathsf {ACE\text {-}wANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$, and $\mathsf {Adv}^{\mathsf {ACE\text {-}sANON\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ are negligible for all efficient $\mathcal {A}$, respectively.

Fig. 2.

Security experiments for an ACE with modification detection scheme $\mathcal {E}$ and an adversary $\mathcal {A}$, where $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ in the first two experiments.

Remark 4

Weak anonymity corresponds to the anonymity notion considered by Fuchsbauer et al. [9] and strong anonymity to the one considered by Damgård et al. [6]. We state both definitions because weak anonymity is easier to achieve but strong anonymity might be required by some applications. If anonymity is only required against the sanitizer or if all messages are anyway signed by the sender, weak anonymity is sufficient. Strong anonymity is required in settings where senders also want to retain as much anonymity as possible against legitimate receivers.

Sanitization security. We next define sanitization security, which excludes that dishonest parties can communicate via the ciphertexts. We formalize this by requiring that the output of the sanitizer for two different ciphertexts cannot be distinguished, as long as both sanitized ciphertexts are not $\bot$ and the adversary has no decryption key that decrypts one of the ciphertexts. This provides no security guarantees if the adversary can decrypt the ciphertexts, which does not seem to be an issue since in this case, the parties can anyway directly communicate via the messages. However, we additionally consider a stronger variant, where the adversary is allowed to possess a decryption key that decrypts the ciphertexts, as long as they both decrypt to the same message. This stronger variant excludes subliminal channels, i.e., even if the involved parties are allowed to communicated by the policy, they cannot exchange information via ciphertexts beyond the encrypted message.

Since the adversary provides the two ciphertexts that are sanitized, we do not know to which roles they correspond; they could even be particularly crafted without belonging to an existing role. Hence, we cannot state the requirement (in the weak variant) that the adversary should not be able to decrypt by only considering the policy and the obtained decryption keys, as in the no-write rule in Definition 4. Instead, we require that the decryption algorithm returns $\bot$ for all decryption keys the adversary possesses. For this to provide the intended security, we need that the decrypt algorithm returns $\bot$ whenever the receiver role corresponding to the used key is not supposed to read the message. This is guaranteed by role-respecting security which is defined later.

Definition 7

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec}, \mathsf {DMod})$ be an ACE with modification detection scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ in Fig. 2 and let J be the set of all j such that $\mathcal {A}_1$ or $\mathcal {A}_2$ issued the query $(j, \mathtt {rec})$ to the oracle $\mathcal {O}_G$. We define the sanitization under chosen-ciphertext attacks advantage and the strong sanitization under chosen-ciphertext attacks advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ c'_0 \ne \bot \ne c'_1 \\& \wedge \ \forall j \in J \ m_{0,j} = m_{1,j} = \bot \bigr ] - 1,\\ \mathsf {Adv}^{\mathsf {ACE\text {-}sSAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}&:= 2 \cdot \Pr \bigl [ b' = b \ \wedge \ c'_0 \ne \bot \ne c'_1 \ \wedge \ \forall j \in J \ m_{0,j} = m_{1,j} \bigr ] - 1, \end{aligned}$$

respectively, where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ is called sanitization under chosen-ciphertext attacks secure (SAN-CCA secure) and strongly sanitization under chosen-ciphertext attacks secure (sSAN-CCA secure) if $\mathsf {Adv}^{\mathsf {ACE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ and $\mathsf {Adv}^{\mathsf {ACE\text {-}sSAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ are negligible for all efficient $\mathcal {A}$, respectively.

Non-detection of fresh encryptions. In the intended way of using a scheme satisfying our notions, the sanitizer only adds sanitized ciphertexts to the repository if the given ciphertext is not detected to be a modification of a previously received ciphertext. This means that if an adversary can find a ciphertext $c$ such that another ciphertext $c^*$ that is later honestly generated is detected as a modification of $c$, the delivery of the message at that later point can be prevented by sending the ciphertext $c$ to the sanitizer earlier. We exclude this by the following definition, which can be seen as an extended correctness requirement.

Definition 8

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec}, \mathsf {DMod})$ be an ACE with modification detection scheme and let $\mathcal {A}$ be a probabilistic algorithm. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}NDTCT\text {-}FENC}}_{\mathcal {E},\mathcal {A}}$ in Fig. 2. We define the non-detection of fresh encryptions advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}NDTCT\text {-}FENC}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [ b = 1 \bigr ], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}NDTCT\text {-}FENC}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ has non-detecting fresh encryptions (NDTCT-FENC) if $\mathsf {Adv}^{\mathsf {ACE\text {-}NDTCT\text {-}FENC}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

Role-respecting and uniform-decryption security. We finally define role-respecting and uniform-decryption security. The former means that an adversary cannot produce a ciphertext for which the pattern of roles that can decrypt does not correspond to a role for which the adversary has an encryption key. For example, if the adversary has only an encryption key for the role i such that roles $j_0$ and $j_1$ are the only roles j with $P(i, j) = 1$, all ciphertexts produced by the adversary are either invalid (i.e., sanitized to $\bot$ or detected as a modification) or decrypt to a message different from $\bot$ precisely under the decryption keys for $j_0$ and $j_1$. On the one hand, this means that receivers who are not allowed to receive the message get $\bot$ and hence know that the message is not for them.² On the other hand, it also guarantees that the adversary cannot prevent receivers with role $j_1$ from receiving a message that is sent to receivers with role $j_0$. Furthermore, uniform decryption guarantees for all ciphertexts $c$ output by an adversary that if $c$ decrypts to a message different from $\bot$ for different decryption keys, it always decrypts to the same message. In the example above, this means that $j_0$ and $j_1$ not only both receive some message, but they both receive the same one.

Definition 9

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc},\mathsf {San},\mathsf {Dec},\mathsf {DMod})$ be an ACE with modification detection scheme and let $\mathcal {A}$ be a probabilistic algorithm. Consider the experiment $\mathsf {Exp}^{\mathsf {ACE\text {-}URR}}_{\mathcal {E},\mathcal {A}}$ in Fig. 2 and let I and J be the sets of all i and j such that $\mathcal {A}$ issued the query $(i, \mathtt {sen})$ and $(j, \mathtt {rec})$ to the oracle $\mathcal {O}_G$, respectively. We define the role-respecting advantage and the uniform-decryption advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}RR}}_{\mathcal {E},\mathcal {A}}&:= \Pr \bigl [ c'\ne \bot \ \wedge \ \mathtt {dct} = \mathtt {false} \\& \wedge \ \lnot \bigl (\exists i \in I \ \forall j \in J \ (m_j \ne \bot \leftrightarrow P(i, j) = 1) \bigr ) \bigr ], \\ \mathsf {Adv}^{\mathsf {ACE\text {-}UDEC}}_{\mathcal {E},\mathcal {A}}&:= \Pr \bigl [\exists j, j' \in J \ m_j \ne \bot \ne m_{j'} \ \wedge \ m_j \ne \ m_{j'} \bigr ], \end{aligned}$$

respectively, where the probabilities are over the randomness in $\mathsf {Exp}^{\mathsf {ACE\text {-}URR}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ is role-respecting (RR secure) and uniform-decryption (UDEC) secure if $\mathsf {Adv}^{\mathsf {ACE\text {-}RR}}_{\mathcal {E},\mathcal {A}}$ and $\mathsf {Adv}^{\mathsf {ACE\text {-}UDEC}}_{\mathcal {E},\mathcal {A}}$ are negligible for all efficient $\mathcal {A}$, respectively.

Remark 5

Note that in Definition 9, we only check the decryptions for receiver roles for which $\mathcal {A}$ has requested the corresponding decryption key. This means that an adversary in addition to producing a ciphertext that causes an inconsistency, also has to find a receiver role for which this inconsistency manifests. If the total number of roles n is small (say polynomial in the security parameter), $\mathcal {A}$ can simply query $\mathcal {O}_G$ on all receiver keys, but for large n this condition is nontrivial. For example, we consider a scheme secure if an adversary can efficiently produce a ciphertext such that there is a receiver role that can decrypt it even though the policy does not allow it, as long as this receiver role is hard to find. The rationale is that in this case, the inconsistency cannot be exploited and will only be observed with negligible probability in an execution of the protocol.

5 Enhanced Sanitizable Public-Key Encryption

5.1 Definitions

As a stepping stone toward ACE schemes satisfying our new security definitions, we introduce enhanced sanitizable public-key encryption. Sanitizable public-key encryption has been considered by Damgård et al. [6] and Fuchsbauer et al. [9] as a relaxation of universal re-encryption [10] and rerandomizable encryption [12, 15]. It allows to sanitize a ciphertext to obtain a sanitized ciphertext that cannot be linked to the original ciphertext except that it decrypts to the correct message. In contrast to rerandomizable encryption, sanitized ciphertexts can have a different syntax than ciphertexts, i.e., it is not required that a sanitized ciphertext is indistinguishable from a fresh encryption. We introduce an enhanced variant with a different syntax and stronger security guarantees.

Definition 10

An enhanced sanitizable public-key encryption (sPKE) scheme consists of the following five PPT algorithms:

• Setup: The algorithm $\mathsf {Setup}$ on input a security parameter $1^{\kappa }$, outputs sanitizer parameters $sp$, and a master secret key $msk$. We implicitly assume that all parameters and keys include the finite message space $\mathcal {M}$ and the ciphertext spaces $\mathcal {C}, \mathcal {C}'$.

• Key generation: The algorithm $\mathsf {Gen}$ on input a master secret key $msk$, outputs an encryption key $ek$ and a decryption key $dk$.

• Encryption: The algorithm $\mathsf {Enc}$ on input an encryption key $ek$ and a message $m\in \mathcal {M}$, outputs a ciphertext $c\in \mathcal {C}$.

• Sanitization: The algorithm $\mathsf {San}$ on input sanitizer parameters $sp$ and a ciphertext $c\in \mathcal {C}$, outputs a sanitized ciphertext $c'\in \mathcal {C}'\cup \{\bot \}$.

• Decryption: The algorithm $\mathsf {Dec}$ on input a decryption key $dk$ and a sanitized ciphertext $c'\in \mathcal {C}'$, outputs a message $m\in \mathcal {M}\cup \{ \bot \}$; on input $dk$ and $\bot$, it outputs $\bot$.

For correctness, we require for all $( sp , msk )$ in the range of $\mathsf {Setup}$, all $( ek , dk )$ in the range of $\mathsf {Gen}( msk )$, and all $m\in \mathcal {M}$ that

$$\begin{aligned} \mathsf {Dec}\bigl ( dk , \mathsf {San}\bigl ( sp , \mathsf {Enc}( ek , m)\bigr ) \bigr ) = m\end{aligned}$$

with probability 1.

We require robustness in the sense that no ciphertext decrypts to a message different from $\bot$ for two different decryption keys (except with negligible probability). This is similar to detectability for ACE schemes, but we allow the adversary to directly output a ciphertext, instead of a message, which is then honestly encrypted. Our notion therefore closely resembles unrestricted strong robustness (USROB), introduced by Farshim et al. [8] for public-key encryption, which also allows the adversary to choose a ciphertext and, in contrast to strong robustness by Abdalla et al. [1], gives the adversary access to decryption keys.

Definition 11

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme. For a probabilistic algorithm $\mathcal {A}$, we define the experiment $\mathsf {Exp}^{\mathsf {sPKE\text {-}USROB}}_{\mathcal {E},\mathcal {A}}$ that executes $( sp , msk ) \leftarrow \mathsf {Setup}(1^\kappa )$ and $(c, i_0, i_1) \leftarrow \mathcal {A}^{\mathcal {O}_{G}(\cdot )}( sp )$, where the oracle $\mathcal {O}_{G}$ on input $\mathtt {getNew}$, outputs a fresh key pair $( ek , dk ) \leftarrow \mathsf {Gen}( msk )$. Let q be the number of oracle queries and let for $i \in \{1, \ldots , q\}$, $( ek _i, dk _i)$ be the i-th answer from $\mathcal {O}_{G}$. We define the (unrestricted strong) robustness advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {sPKE\text {-}USROB}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [&1 \le i_0, i_1 \le q \ \wedge \ i_0 \ne i_1 \\&\wedge \ \mathsf {Dec}\bigl ( dk _{i_0}, \mathsf {San}( sp , c) \bigr ) \ne \bot \ne \mathsf {Dec}\bigl ( dk _{i_1}, \mathsf {San}( sp , c) \bigr ) \bigr ], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {sPKE\text {-}USROB}}_{\mathcal {E},\mathcal {A}}$ and the random coins of $\mathsf {San}$ and $\mathsf {Dec}$ (both executed independently twice). The scheme $\mathcal {E}$ is (unrestricted strongly) robust (USROB secure) if $\mathsf {Adv}^{\mathsf {sPKE\text {-}USROB}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

We next define IND-CCA security analogously to the definition for ordinary public-key encryption. In contrast to the usual definition, we do not require the adversary to output two messages of equal length, which implies that schemes satisfying our definition do not leak the length of the encrypted message.

Definition 12

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {sPKE\text {-}IND\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ in Fig. 3 and let $C_{\mathcal {A}_2}$ be the set of all ciphertexts that $\mathcal {A}_2$ queried to the oracle $\mathcal {O}_{SD}$. We define the ciphertext indistinguishability under chosen-ciphertext attacks advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {sPKE\text {-}IND\text {-}CCA}}_{\mathcal {E},\mathcal {A}} := 2 \cdot \Pr \bigl [ b' = b \ \wedge \ c^* \notin C_{\mathcal {A}_2} \bigr ] - 1, \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {sPKE\text {-}IND\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ has indistinguishable ciphertexts under chosen-ciphertext attacks (is IND-CCA secure) if $\mathsf {Adv}^{\mathsf {sPKE\text {-}IND\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

Fig. 3.

Security experiments for an sPKE scheme $\mathcal {E}$ and an adversary $\mathcal {A}$, where $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ in the experiments $\mathsf {Exp}^{\mathsf {sPKE\text {-}IND\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$, $\mathsf {Exp}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$, and $\mathsf {Exp}^{\mathsf {sPKE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. The oracle $\mathcal {O}_{SD}$ is defined as $\mathcal {O}_{SD}(c) = \mathsf {Dec}( dk , \mathsf {San}( sp , c))$ and the oracle $\mathcal {O}_{SD_j}$ as $\mathcal {O}_{SD_j}(c) = \mathsf {Dec}( dk _j, \mathsf {San}( sp , c))$. Moreover, the oracle $\mathcal {O}_{G}$ on input $\mathtt {getNew}$, outputs a fresh key pair $( ek , dk ) \leftarrow \mathsf {Gen}( msk )$.

We also need that it is hard to predict a ciphertext generated by $\mathsf {Enc}$ from a message of the adversary’s choice given encryption and decryption keys. Note that this is not implied by IND-CCA security since the adversary here obtains the decryption key.

Definition 13

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme and let $\mathcal {A}$ be a probabilistic algorithm. Consider the experiment $\mathsf {Exp}^{\mathsf {sPKE\text {-}UPD\text {-}CTXT}}_{\mathcal {E},\mathcal {A}}$ in Fig. 3. We define the ciphertext unpredictability advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {sPKE\text {-}UPD\text {-}CTXT}}_{\mathcal {E},\mathcal {A}} := \Pr \bigl [ c= c^*], \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {sPKE\text {-}UPD\text {-}CTXT}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ has unpredictable ciphertexts (is UPD-CTXT secure) if $\mathsf {Adv}^{\mathsf {sPKE\text {-}UPD\text {-}CTXT}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

We further define anonymity or indistinguishability of keys following Bellare et al. [3].

Definition 14

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ in Fig. 3 and let $C_{\mathcal {A}_2}$ be the set of all ciphertexts that $\mathcal {A}_2$ queried to the oracle $\mathcal {O}_{SD_0}$ or $\mathcal {O}_{SD_1}$. We define the indistinguishability of keys under chosen-ciphertext attacks advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}} := 2 \cdot \Pr \bigl [ b' = b \ \wedge \ c^* \notin C_{\mathcal {A}_2} \bigr ] - 1, \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. The scheme $\mathcal {E}$ has indistinguishable keys under chosen-ciphertext attacks (is IK-CCA secure) if $\mathsf {Adv}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

Sanitization security formalizes that given certain public keys and a sanitized ciphertext, it is hard to tell which of two adversarially chosen ciphertexts was actually sanitized. To exclude trivial attacks, we require that both ciphertexts are encryptions relative to the two challenge public keys $ek _0$ and $ek _1$. Otherwise, the adversary could use the oracle $\mathcal {O}_{G}$ to obtain a fresh key-pair $( ek , dk )$ and encrypt two different messages under $ek$. It could then decrypt the challenge ciphertext using $dk$ and win the game.

Definition 15

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme and let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be a pair of probabilistic algorithms. Consider the experiment $\mathsf {Exp}^{\mathsf {sPKE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ in Fig. 3. We define the sanitization under chosen-ciphertext attacks advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {sPKE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}} := 2 \cdot \Pr \bigl [ b' = b \ \wedge \ \exists j, j' \in \{0,1\} \ m_{0,j} \ne \bot \ne m_{1,j'} \bigr ] - 1, \end{aligned}$$

where the probability is over the randomness in $\mathsf {Exp}^{\mathsf {sPKE\text {-}IK\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$. We say the scheme $\mathcal {E}$ is sanitization under chosen-ciphertext attacks (SAN-CCA) secure if $\mathsf {Adv}^{\mathsf {sPKE\text {-}SAN\text {-}CCA}}_{\mathcal {E},\mathcal {A}}$ is negligible for all efficient $\mathcal {A}$.

We finally define the probability that two independent executions of the key-generation algorithm produce the same encryption key. This probability has to be small for all IND-CCA-secure schemes because an attacker can otherwise obtain a new key pair from $\mathcal {O}_{G}$ and if the obtained encryption key matches the one with which the challenge ciphertext is generated, the attacker can decrypt and win the IND-CCA game. We anyway explicitly define this probability to simplify our reductions later.

Definition 16

Let $\mathcal {E}= (\mathsf {Setup}, \mathsf {Gen}, \mathsf {Enc}, \mathsf {San}, \mathsf {Dec})$ be an sPKE scheme. We define the encryption-key collision probability $\mathsf {Col}^{\mathsf {ek}}_{\mathcal {E}}$ as

$$\begin{aligned} \mathsf {Col}^{\mathsf {ek}}_{\mathcal {E}} := {\text {Pr}}^{( sp , msk ) \leftarrow \mathsf {Setup}(1^{\kappa });\; ( ek _0, dk _0) \leftarrow \mathsf {Gen}( msk );\; ( ek _1, dk _1) \leftarrow \mathsf {Gen}( msk )} [ ek _0 = ek _1]. \end{aligned}$$

5.2 Constructing an sPKE Scheme

We next construct an sPKE scheme satisfying our security definitions. Our construction resembles the weakly sanitizable PKE scheme by Fuchsbauer et al. [9]. We use a variant of ElGamal encryption and obtain security against chosen-ciphertext attacks using the technique of Naor and Yung [14], i.e., encrypting the message under two independent keys and proving in zero-knowledge that the ciphertexts are encryptions of the same message, which was shown to achieve full IND-CCA security if the zero-knowledge proof is one-time simulation sound by Sahai [16].

Let $\mathsf {PKE}$ be a (IND-CPA secure) public-key encryption scheme, let $\mathsf {Sig}$ be a (EUF-CMA-secure) signature scheme, and let $\mathsf {NIZK}$ be a (one-time simulation sound) NIZK proof system for the language $L:= \{x\mid \exists w\ (x, w) \in R\}$, where the relation $R$ is defined as follows: for $x= \bigl (g, ek ^{\mathsf {PKE}}, vk ^{\mathsf {Sig}}, c_1, c_2, c_{\sigma } \bigr )$ and $w= (m, g^a, g^b, r_1,s_1,r_2,s_2, \sigma , r)$, we have $(x, w) \in R$ if and only if

$$\begin{aligned} c_1 =&(g^{r_1}, g^{a\cdot r_1}, g^{s_1}, g^{a\cdot s_1} \cdot m) \ \wedge \ c_2 = (g^{r_2}, g^{b \cdot r_2}, g^{s_2}, g^{b \cdot s_2} \cdot m) \\&\wedge \ \mathsf {Sig}\mathsf {.Ver}\bigl ( vk ^{\mathsf {Sig}}, (g^a, g^b), \sigma \bigr ) = 1 \ \wedge \ c_{\sigma } = \mathsf {PKE}\mathsf {.Enc}\bigl ( ek ^{\mathsf {PKE}}, (g^a, g^b, \sigma ); r \bigr ). \end{aligned}$$

We define an sPKE scheme as follows:

• Setup: The setup algorithm $\mathsf {sPKE}\mathsf {.Setup}$ first generates

  $$\begin{aligned} \bigl ( ek ^{\mathsf {PKE}}, dk ^{\mathsf {PKE}}\bigr )&\leftarrow \mathsf {PKE}\mathsf {.Gen}(1^{\kappa }), \\ \bigl ( vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}\bigr )&\leftarrow \mathsf {Sig}\mathsf {.Gen}(1^{\kappa }), \\ crs&\leftarrow \mathsf {NIZK}\mathsf {.Gen}(1^{\kappa }). \end{aligned}$$

  Let $G = \langle g \rangle$ be a cyclic group with prime order p generated by g, with $p \ge 2^{\kappa }$, and let $\mathcal {M}\subseteq G$ such that ${|}\mathcal {M}{|}/p \le 2^{-\kappa }$. The sanitizer parameters $sp ^{\mathsf {sPKE}}$ contain $ek ^{\mathsf {PKE}}$, $vk ^{\mathsf {Sig}}$, $crs$, and a description of G, including g and p. The master secret key $msk ^{\mathsf {sPKE}}$ consists of $ek ^{\mathsf {PKE}}$, $vk ^{\mathsf {Sig}}$, $sk ^{\mathsf {Sig}}$, $crs$, and a description of G, including g and p.

• Key generation: The algorithm $\mathsf {sPKE}\mathsf {.Gen}$ on input $msk ^{\mathsf {sPKE}}$, samples two elements $dk _1, dk _2 \twoheadleftarrow \mathbb {Z}_p^*$ and computes $ek _1 \leftarrow g^{ dk _1}$, $ek _2 \leftarrow g^{ dk _2}$, as well as $\sigma \leftarrow \mathsf {Sig}\mathsf {.Sign}\bigl ( sk ^{\mathsf {Sig}}, ( ek _1, ek _2)\bigr )$. Finally, it outputs $ek ^{\mathsf {sPKE}}:= \bigl (g, p, crs , ek ^{\mathsf {PKE}}, vk ^{\mathsf {Sig}}, ek _1, ek _2, \sigma \bigr )$ and $dk ^{\mathsf {sPKE}}:= ( dk _1, dk _2)$.

• Encryption: The algorithm $\mathsf {sPKE}\mathsf {.Enc}$ on input an encryption key $ek ^{\mathsf {sPKE}}= \bigl (g, p, crs , ek ^{\mathsf {PKE}}, vk ^{\mathsf {Sig}}, ek _1, ek _2, \sigma \bigr )$ and a message $m\in \mathcal {M}$, samples randomness r, chooses $r_1, s_1, r_2, s_2 \twoheadleftarrow \mathbb {Z}_p^*$ uniformly at random, and computes

  $$\begin{aligned} c_1&\leftarrow \bigl (g^{r_1}, ek _1^{r_1}, g^{s_1}, ek _1^{s_1} \cdot m\bigr ), \\ c_2&\leftarrow \bigl (g^{r_2}, ek _2^{r_2}, g^{s_2}, ek _2^{s_2} \cdot m\bigr ), \\ c_{\sigma }&\leftarrow \mathsf {PKE}\mathsf {.Enc}\bigl ( ek ^{\mathsf {PKE}}, ( ek _1, ek _2, \sigma ); r \bigr ). \end{aligned}$$

  It then generates $\pi \leftarrow \mathsf {NIZK}\mathsf {.Prove}\bigl ( crs ,x:= (g, ek ^{\mathsf {PKE}}, vk ^{\mathsf {Sig}}, c_1, c_2, c_{\sigma }), w:=(m, ek _1, ek _2,r_1,s_1,r_2 ,s_2, \sigma , r)\bigr )$, and outputs the ciphertext $c:= (c_1, c_2, c_{\sigma }, \pi )$.

• Sanitization: The algorithm $\mathsf {sPKE}\mathsf {.San}$ on input sanitizer parameters $sp ^{\mathsf {sPKE}}$ and a ciphertext $c= (c_1, c_2, c_{\sigma }, \pi )$, first verifies the NIZK proof by evaluating $\mathsf {NIZK}\mathsf {.Ver}\bigl ( crs , x:= (g, ek ^{\mathsf {PKE}}, vk ^{\mathsf {Sig}}, c_1, c_2, c_{\sigma }), \pi \bigr )$. It then parses the first ciphertext component as $(c_{1,1}, c_{1,2}, c_{1,3}, c_{1,4}) \leftarrow c_1$. If the verification succeeds and $c_{1,1} \ne 1 \ne c_{1,2}$, then it chooses a random $t \twoheadleftarrow \mathbb {Z}_p^*$ and outputs the sanitized ciphertext

  $$\begin{aligned} c':= \bigl ((c_{1,1})^t \cdot c_{1,3}, \, (c_{1,2})^t \cdot c_{1,4} \bigr ). \end{aligned}$$

  If the verification fails or if $c_{1,1} = 1$ or $c_{1,2} = 1$, it outputs $\bot$.

• Decryption: The algorithm $\mathsf {sPKE}\mathsf {.Dec}$ on input a decryption key $dk ^{\mathsf {sPKE}}= ( dk _1, dk _2)$ and a sanitized ciphertext $c'= (c'_1, c'_2)$, computes the message $m\leftarrow c'_2 \cdot \bigl ((c'_1)^{ dk _1}\bigr )^{-1}$. It outputs $m$ if $m\in \mathcal {M}$, and otherwise it outputs $\bot$. On input $dk ^{\mathsf {sPKE}}$ and $\bot$, it outputs $\bot$.

The following proposition and theorem summarize the correctness and security properties of our scheme and are proven in the full version of this paper.

Proposition 1

If $\mathsf {Sig}$ is correct and $\mathsf {NIZK}$ has perfect completeness, the scheme $\mathsf {sPKE}$ from above is correct, robust, has unpredictable ciphertexts, and negligible encryption-key collision probability.

Theorem 1

If the DDH assumption holds in the group G, $\mathsf {PKE}$ is IND-CPA secure, $\mathsf {Sig}$ is EUF-CMA secure, and if $\mathsf {NIZK}$ is zero-knowledge, computationally sound, and one-time simulation sound, then the scheme $\mathsf {sPKE}$ from above is IND-CCA secure, IK-CCA secure, and SAN-CCA secure.

On a high level, our proof proceeds as follows. It is rather straightforward to show that our variant of ElGamal encryption satisfies the CPA versions of the three properties. The proof of CCA security follows the proof by Sahai for public-key encryption [16]: Since the NIZK ensures that both ciphertext components are encryptions of the same message, it does not matter which component is decrypted. In a reduction, where we assume an adversary $\mathcal {A}$ against the CCA variants of the desired properties, and we want to break the corresponding CPA variants, we only get one public key and no decryption oracle from the challenger. In order to emulate the view toward $\mathcal {A}$, the reduction chooses an additional public key and a CRS for the NIZK scheme. Since the reduction thus knows one of the secret keys, it can emulate a decryption oracle. To generate a challenge ciphertext, the reduction obtains one challenge ciphertexts from its CPA challenger, and encrypts another, arbitrary message to get a second ciphertext. The reduction uses the NIZK simulator to obtain an accepting proof that is indistinguishable from a “real proof”, even if the underlying statement is not true. A crucial point here is that the NIZK scheme has to be one-time simulation sound. This ensures that even if the adversary sees one simulated (accepting) proof of a wrong statement, it is not capable of producing accepting proofs of wrong statements, except by reproducing the exact proof obtained within the challenge, but which $\mathcal {A}$ is not allowed to ask to the decryption oracle by the CCA definition. The fundamental result of Sahai [16] is that the above strategy successfully simulates a complete CCA attack toward $\mathcal {A}$.

An additional obstacle we have is that to preserve anonymity, the NIZK needs to be verified without knowing which encryption keys were used. On the other hand, the reduction only works if the two used keys “match”, since otherwise, the emulated decryption oracle would use an incorrect key to decrypt. To prevent an adversary from mixing different key pairs for encryptions, the key-generation process signs valid key pairs, and the NIZK ensures that a signed pair was used. Due to anonymity, this signature cannot be directly contained in the ciphertexts. Instead, it is part of the witness. To prove that if a ciphertext is accepted, the used key pair was indeed signed by the key-generation process, we show that if $\mathcal {A}$ manages to produce a ciphertext that is accepted but the keys were not signed, we can break EUF-CMA security of the signature scheme. In this reduction, we have to provide a forgery. Hence, the reduction needs to extract the signature and the used encryption keys from the ciphertext. This could be achieved by assuming that the NIZK is extractable. Extractability and simulation-soundness at the same time is, however, a quite strong assumption. Instead, we add an encryption of the signature and the key pair under a separate PKE scheme to the ciphertexts. The reduction can then generate the keys for this PKE scheme itself and perform extraction by decrypting that ciphertext.

6 Construction of an ACE Scheme

6.1 Construction for Equality

Following Fuchsbauer et al. [9], we first construct an ACE scheme for the equality policy, i.e., $P(i,j) = 1 \Leftrightarrow i = j$, and then use such a scheme in another construction for richer policies. We base our construction on an sPKE scheme, which already has many important properties needed for a secure ACE scheme. A syntactical difference between sPKE and ACE schemes is that the key generation of the former on every invocation produces a fresh key pair, while the latter schemes allow the generation of keys for a given role. To bind key pairs to some role $i \in [n]$, we use the output of a pseudorandom function on input i as the randomness for the sPKE key generation. For role-respecting security, we have to ensure that an adversary can only produce ciphertexts for keys obtained from the key generation oracle. This is achieved by signing all keys with a signing key generated at setup. To prevent malleability attacks as the ones described in Sect. 3, the encryption algorithm additionally signs all ciphertexts with a separate signing key that is tied to the encryption key. To maintain anonymity, the signatures are not part of the ciphertext but the encrypters prove in zero-knowledge that they know such signatures. Finally, the modification detection simply checks whether the ciphertexts (without the NIZK proofs) are equal. Intuitively, this is sufficient since we assume the underlying sPKE scheme to be CCA secure, which implies that it is not possible to meaningfully modify a given ciphertext. Hence, a ciphertext is either equal to an existing one (and thus detected by the algorithm) or a fresh encryption.

Our construction. Let $\mathsf {sPKE}$ be a sanitizable public-key encryption scheme, let $\mathsf {Sig}$ be a signature scheme, and let $F$ be a PRF. Further let $\mathsf {NIZK}$ be a NIZK proof of knowledge system for the language $L:= \{ x\mid \exists w\ (x, w) \in R\}$, where the relation $R$ is defined as follows: for $x= \bigl ( vk ^{\mathsf {Sig}}, \tilde{c} \bigr )$ and $w= \bigl ( ek ^{\mathsf {sPKE}}_i, m, r, vk ^{\mathsf {Sig}}_i, \sigma ^{\mathsf {Sig}}_i, \sigma ^{\mathsf {Sig}}_c \bigr )$, $(x, w) \in R$ if and only if

$$\begin{aligned} \tilde{c} = \mathsf {sPKE}\mathsf {.Enc}\bigl (&ek ^{\mathsf {sPKE}}_i, m; r \bigr ) \ \wedge \ \mathsf {Sig}\mathsf {.Ver}\bigl ( vk ^{\mathsf {Sig}}, \bigl [ ek ^{\mathsf {sPKE}}_i, vk ^{\mathsf {Sig}}_i \bigr ], \sigma ^{\mathsf {Sig}}_i \bigr ) = 1 \\&\qquad \wedge \ \mathsf {Sig}\mathsf {.Ver}\bigl ( vk ^{\mathsf {Sig}}_i, \tilde{c}, \sigma ^{\mathsf {Sig}}_c \bigr ) = 1. \end{aligned}$$

We define an ACE with modification detection scheme $\mathsf {ACE}$ as follows:

• Setup: On input a security parameter $1^{\kappa }$ and a policy $P:[n] \times [n] \rightarrow \{0,1\}$ with $P(i,j) = 1 \Leftrightarrow i = j$, the algorithm $\mathsf {ACE}\mathsf {.Setup}$ picks a random PRF key $K$ for a PRF $F$, and runs

  $$\begin{aligned} \bigl ( sp ^{\mathsf {sPKE}}, msk ^{\mathsf {sPKE}}\bigr )&\leftarrow \mathsf {sPKE}\mathsf {.Setup}(1^{\kappa }), \\ \bigl ( vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}\bigr )&\leftarrow \mathsf {Sig}\mathsf {.Gen}(1^{\kappa }), \\ crs ^{\mathsf {NIZK}}&\leftarrow \mathsf {NIZK}\mathsf {.Gen}(1^{\kappa }). \end{aligned}$$

  It outputs the master secret key $msk ^{\mathsf {ACE}}:= \bigl (K, msk ^{\mathsf {sPKE}}, vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$ and the sanitizer parameters $sp ^{\mathsf {ACE}}:= \bigl ( sp ^{\mathsf {sPKE}}, vk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$.

• Key generation: On input a master secret key $msk ^{\mathsf {ACE}}= \bigl (K, msk ^{\mathsf {sPKE}}, vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$, a role $i \in [n]$, and a type $t \in \{ \mathtt {sen}, \mathtt {rec}\}$, $\mathsf {ACE}\mathsf {.Gen}$ computes

  $$\begin{aligned} \bigl ( ek ^{\mathsf {sPKE}}_i, dk ^{\mathsf {sPKE}}_i \bigr ) \leftarrow \mathsf {sPKE}\mathsf {.Gen}\bigl ( msk ^{\mathsf {sPKE}}; F_{K}([i, 0]) \bigr ). \end{aligned}$$

  If $t = \mathtt {sen}$, it further computes

  $$\begin{aligned} \bigl ( vk ^{\mathsf {Sig}}_i, sk ^{\mathsf {Sig}}_i \bigr )&\leftarrow \mathsf {Sig}\mathsf {.Gen}\bigl ( 1^{\kappa }; F_{K}([i, 1]) \bigr ),\\ \sigma ^{\mathsf {Sig}}_i&\leftarrow \mathsf {Sig}\mathsf {.Sign}\bigl ( sk ^{\mathsf {Sig}}, \bigl [ ek ^{\mathsf {sPKE}}_i, vk ^{\mathsf {Sig}}_i \bigr ]; F_{K}([i, 2]) \bigr ). \end{aligned}$$

  If $t = \mathtt {sen}$, it outputs the encryption key $ek ^{\mathsf {ACE}}_i := \bigl ( vk ^{\mathsf {Sig}}, ek ^{\mathsf {sPKE}}_i, vk ^{\mathsf {Sig}}_i, sk ^{\mathsf {Sig}}_i,\sigma ^{\mathsf {Sig}}_i, crs ^{\mathsf {NIZK}}\bigr )$; if $t = \mathtt {rec}$, it outputs the decryption key $dk ^{\mathsf {ACE}}_i := dk ^{\mathsf {sPKE}}_i$.

• Encryption: On input an encryption key $ek ^{\mathsf {ACE}}_i = \bigl ( vk ^{\mathsf {Sig}}, ek ^{\mathsf {sPKE}}_i, vk ^{\mathsf {Sig}}_i, sk ^{\mathsf {Sig}}_i,\sigma ^{\mathsf {Sig}}_i, crs ^{\mathsf {NIZK}}\bigr )$ and a message $m\in \mathcal {M}^{\mathsf {ACE}}$, the algorithm $\mathsf {ACE}\mathsf {.Enc}$ samples randomness r and computes

  $$\begin{aligned} \tilde{c}&\leftarrow \mathsf {sPKE}\mathsf {.Enc}\bigl ( ek ^{\mathsf {sPKE}}_i, m; r \bigr ), \\ \sigma ^{\mathsf {Sig}}_c&\leftarrow \mathsf {Sig}\mathsf {.Sign}\bigl ( sk ^{\mathsf {Sig}}_i, \tilde{c} \bigr ), \\ \pi ^{\mathsf {NIZK}}&\leftarrow \mathsf {NIZK}\mathsf {.Prove}\bigl ( crs ^{\mathsf {NIZK}}, x:= \bigl ( vk ^{\mathsf {Sig}}, \tilde{c} \bigr ),\\& w:= \bigl ( ek ^{\mathsf {sPKE}}_i, m, r, vk ^{\mathsf {Sig}}_i, \sigma ^{\mathsf {Sig}}_i, \sigma ^{\mathsf {Sig}}_c \bigr ) \bigr ). \end{aligned}$$

  It outputs the ciphertext $c:= \bigl (\tilde{c}, \pi ^{\mathsf {NIZK}}\bigr )$.

• Sanitization: On input sanitizer parameters $sp ^{\mathsf {ACE}}= \bigl ( sp ^{\mathsf {sPKE}}, vk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$ and a ciphertext $c= \bigl (\tilde{c}, \pi ^{\mathsf {NIZK}}\bigr )$, $\mathsf {ACE}\mathsf {.San}$ outputs the sanitized ciphertext $c'\leftarrow \mathsf {sPKE}\mathsf {.San}\bigl ( sp ^{\mathsf {sPKE}}, \tilde{c} \bigr )$ if $\mathsf {NIZK}\mathsf {.Ver}\bigl ( crs ^{\mathsf {NIZK}}, x:= \bigl ( vk ^{\mathsf {Sig}}, \tilde{c}, \bigr ), \pi ^{\mathsf {NIZK}}\bigr ) = 1$; otherwise, it outputs $\bot$.

• Decryption: The algorithm $\mathsf {ACE}\mathsf {.Dec}$ on input a decryption key $dk ^{\mathsf {ACE}}_j$ and a sanitized ciphertext $c'$, outputs the message $m\leftarrow \mathsf {sPKE}\mathsf {.Dec}( dk ^{\mathsf {ACE}}_j, c')$.

• Modification detection: The algorithm $\mathsf {ACE}\mathsf {.DMod}$ on input $sp ^{\mathsf {ACE}}$, $c_1 = \bigl (\tilde{c}_1, \pi ^{\mathsf {NIZK}}_1 \bigr )$, and $c_2 = \bigl (\tilde{c}_2, \pi ^{\mathsf {NIZK}}_2 \bigr )$, outputs 1 if $\tilde{c}_1 = \tilde{c}_2$, and 0 otherwise.

The following proposition states that our scheme is correct and strongly detectable, and is proven in the full version of the paper.

Proposition 2

Let $\mathsf {ACE}$ be the scheme from above. Then, $\mathsf {ACE}$ is perfectly correct, i.e., $\mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathsf {ACE},\mathcal {A}} = 0$ for all $\mathcal {A}$. Moreover, if $F$ is pseudorandom and $\mathsf {sPKE}$ is unrestricted strongly robust, then $\mathsf {ACE}$ is strongly detectable.

The security of our scheme is summarized by the theorem below, which we prove in the full version.

Theorem 2

If $F$ is pseudorandom, $\mathsf {NIZK}$ is zero-knowledge and extractable, $\mathsf {Sig}$ is EUF-CMA secure, and $\mathsf {sPKE}$ is IND-CCA, IK-CCA, SAN-CCA, USROB, and UPD-CTXT secure and has negligible encryption-key collision probability, then the scheme $\mathsf {ACE}$ from above is PRV-CCA, sANON-CCA, SAN-CCA, UDEC, and RR secure, and has NDTCT-FENC.

6.2 Lifting Equality to Disjunction of Equalities

We finally show how an ACE scheme for equality, as the one from Sect. 6.1, can be used to construct a scheme for the policy $P_{\mathsf {DEq}}: \mathcal {D}^\ell \times \mathcal {D}^\ell \rightarrow \{0,1\}$ with

where $\mathcal {D}$ is some finite set and $\ell \in \mathbb {N}$.³ This policy can for example be used to implement the no read-up and now write-down principle ($P(i,j) = 1 \Leftrightarrow i \le j$) from the Bell-LaPadula model [2] via an appropriate encoding of the roles [9].

The intuition of our construction is as follows. A key for a role $\mathbf {x} = (x_1, \ldots , x_\ell )$ contains one key of the ACE scheme for equality for each component $x_i$ of the role vector. To encrypt a message, this message is encrypted with each of these keys. To decrypt, one tries to decrypt each ciphertext component with the corresponding key. If at least one component of the sender and receiver roles match (i.e., if the policy is satisfied), one of the decryptions is successful. So far, the construction is identical to the one by Fuchsbauer et al. [9]. That construction is, however, not role-respecting, since a dishonest sender with keys for more than one role can arbitrarily mix the components of the keys for the encryption. Moreover, the construction does not guarantee uniform decryption, because different messages can be encrypted in different components. We fix these issues using the same techniques we used in our construction of the scheme for equality, i.e., we add a signature of the key vector to the encryption keys, sign the ciphertexts, and require a zero-knowledge proof of knowledge that a valid key combination was used to encrypt the same message for each component and that all signatures are valid.

Our construction. Let $\mathsf {ACE}_{=}$ be an ACE with modification detection scheme for the equality predicate on $\mathcal {D}\times [\ell ]$, let $\mathsf {Sig}$ be a signature scheme, let $F$ be a PRF, and let $\mathsf {NIZK}$ be a NIZK proof of knowledge system for the language $L:= \{ x\mid \exists w\ (x, w) \in R\}$, where the relation $R$ is defined as follows: for $x= \bigl ( vk ^{\mathsf {Sig}}, c_1, \ldots , c_\ell \bigr )$ and $w= \bigl ( ek ^{\mathsf {ACE}_{=}}_{(x_1, 1)}, \ldots , ek ^{\mathsf {ACE}_{=}}_{(x_\ell , \ell )}, m, r_1, \ldots , r_\ell , vk ^{\mathsf {Sig}}_{\mathbf {x}}, \sigma ^{\mathsf {Sig}}_{\mathbf {x}}, \sigma ^{\mathsf {Sig}}_c \bigr )$, $(x, w) \in R$ if and only if

$$\begin{aligned} \bigwedge _{i = 1}^{\ell } c_i =&\mathsf {ACE}_{=}\mathsf {.Enc}\bigl ( ek ^{\mathsf {ACE}_{=}}_{(x_i, i)}, m; r_i \bigr ) \ \wedge \ \mathsf {Sig}\mathsf {.Ver}\bigl ( vk ^{\mathsf {Sig}}_{\mathbf {x}}, [c_1, \ldots , c_\ell ], \sigma ^{\mathsf {Sig}}_c \bigr ) = 1 \\&\wedge \ \mathsf {Sig}\mathsf {.Ver}\bigl ( vk ^{\mathsf {Sig}}, \bigl [ ek ^{\mathsf {ACE}_{=}}_{(x_1, 1)}, \ldots , ek ^{\mathsf {ACE}_{=}}_{(x_\ell , \ell )}, vk ^{\mathsf {Sig}}_{\mathbf {x}} \bigr ], \sigma ^{\mathsf {Sig}}_{\mathbf {x}} \bigr ) = 1. \end{aligned}$$

We define an ACE scheme $\mathsf {ACE}_{\mathsf {DEq}}$ as follows:

• Setup: On input a security parameter $1^{\kappa }$ and the policy $P_{\mathsf {DEq}}$, $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.Setup}$ picks a random key $K$ for $F$ and runs

  $$\begin{aligned} \bigl ( msk ^{\mathsf {ACE}_{=}}, sp ^{\mathsf {ACE}_{=}}\bigr )&\leftarrow \mathsf {ACE}_{=}\mathsf {.Setup}(1^{\kappa }), \\ \bigl ( vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}\bigr )&\leftarrow \mathsf {Sig}\mathsf {.Gen}(1^{\kappa }), \\ crs ^{\mathsf {NIZK}}&\leftarrow \mathsf {NIZK}\mathsf {.Gen}(1^{\kappa }). \end{aligned}$$

  It outputs the master secret key $msk ^{\mathsf {ACE}_{\mathsf {DEq}}}:= \bigl (K, msk ^{\mathsf {ACE}_{=}}, vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}},$ $crs ^{\mathsf {NIZK}}\bigr )$ and the sanitizer parameters $sp ^{\mathsf {ACE}_{\mathsf {DEq}}}:= \bigl ( sp ^{\mathsf {ACE}_{=}}, vk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$.

• Key generation: The algorithm $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.Gen}$ on input a master secret key $msk ^{\mathsf {ACE}_{\mathsf {DEq}}}= \bigl (K, msk ^{\mathsf {ACE}_{=}}, vk ^{\mathsf {Sig}}, sk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$, a role $\mathbf {x} \in \mathcal {D}^\ell$, and type $\mathtt {sen}$, generates

  

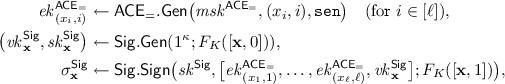
  and outputs the encryption key $ek ^{\mathsf {ACE}_{\mathsf {DEq}}}_{\mathbf {x}} := \bigl ( vk ^{\mathsf {Sig}}, ek ^{\mathsf {ACE}_{=}}_{(x_1, 1)}, \ldots , ek ^{\mathsf {ACE}_{=}}_{(x_\ell , \ell )}, vk ^{\mathsf {Sig}}_{\mathbf {x}}, sk ^{\mathsf {Sig}}_{\mathbf {x}},\sigma ^{\mathsf {Sig}}_{\mathbf {x}}, crs ^{\mathsf {NIZK}}\bigr )$; on input $msk ^{\mathsf {ACE}_{\mathsf {DEq}}}$, a role $\mathbf {y} \in \mathcal {D}^\ell$, and the type $\mathtt {rec}$, it generates for $i \in [\ell ]$,

  $$\begin{aligned} dk ^{\mathsf {ACE}_{=}}_{(y_i, i)} \leftarrow \mathsf {ACE}_{=}\mathsf {.Gen}\bigl ( msk ^{\mathsf {ACE}_{=}}, (y_i, i), \mathtt {rec} \bigr ), \end{aligned}$$

  and outputs the decryption key $dk ^{\mathsf {ACE}_{\mathsf {DEq}}}_{\mathbf {y}} := \bigl ( dk ^{\mathsf {ACE}_{=}}_{(y_1, 1)}, \ldots , dk ^{\mathsf {ACE}_{=}}_{(y_\ell , \ell )} \bigr )$.

• Encryption: On input an encryption key $ek ^{\mathsf {ACE}_{\mathsf {DEq}}}_{\mathbf {x}} = \bigl ( vk ^{\mathsf {Sig}}, ek ^{\mathsf {ACE}_{=}}_{(x_1, 1)}, \ldots , ek ^{\mathsf {ACE}_{=}}_{(x_\ell , \ell )}, vk ^{\mathsf {Sig}}_{\mathbf {x}}, sk ^{\mathsf {Sig}}_{\mathbf {x}},\sigma ^{\mathsf {Sig}}_{\mathbf {x}}, crs ^{\mathsf {NIZK}}\bigr )$ and a message $m\in \mathcal {M}^{\mathsf {ACE}_{\mathsf {DEq}}}$, $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.Enc}$ samples randomness $r_1, \ldots , r_\ell$ and computes

  $$\begin{aligned} c_i&\leftarrow \mathsf {ACE}_{=}\mathsf {.Enc}\bigl ( ek ^{\mathsf {ACE}_{=}}_{(x_i, i)}, m; r_i \bigr ) \quad (\text {for } i \in [\ell ]),\\ \sigma ^{\mathsf {Sig}}_c&\leftarrow \mathsf {Sig}\mathsf {.Sign}\bigl ( sk ^{\mathsf {Sig}}_{\mathbf {x}}, [c_1, \ldots , c_\ell ] \bigr ), \\ \pi ^{\mathsf {NIZK}}&\leftarrow \mathsf {NIZK}\mathsf {.Prove}\bigl ( crs ^{\mathsf {NIZK}}, x:= \bigl ( vk ^{\mathsf {Sig}}, c_1, \ldots , c_\ell \bigr ), \\& w:= \bigl ( ek ^{\mathsf {ACE}_{=}}_{(x_1, 1)}, \ldots , ek ^{\mathsf {ACE}_{=}}_{(x_\ell , \ell )}, m, r_1, \ldots , r_\ell , vk ^{\mathsf {Sig}}_{\mathbf {x}}, \sigma ^{\mathsf {Sig}}_{\mathbf {x}}, \sigma ^{\mathsf {Sig}}_c \bigr ) \bigr ). \end{aligned}$$

  It outputs the ciphertext $c:= \bigl (c_1, \ldots , c_\ell , \pi ^{\mathsf {NIZK}}\bigr )$.

• Sanitization: On input sanitizer parameters $sp ^{\mathsf {ACE}_{\mathsf {DEq}}}= \bigl ( sp ^{\mathsf {ACE}_{=}}, vk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$ and a ciphertext $c= \bigl (c_1, \ldots , c_\ell , \pi ^{\mathsf {NIZK}}\bigr )$, the algorithm $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.San}$ checks whether $\mathsf {NIZK}\mathsf {.Ver}\bigl ( crs ^{\mathsf {NIZK}},x:= \bigl ( vk ^{\mathsf {Sig}}, c_1, \ldots , c_\ell \bigr ), \pi ^{\mathsf {NIZK}}\bigr ) = 1$. If this is the case, it runs $c'_i \leftarrow \mathsf {ACE}_{=}\mathsf {.San}\bigl ( c_i \bigr )$ for $i \in [\ell ]$. If $c'_i \ne \bot$ for all $i \in [\ell ]$, it outputs the sanitized ciphertext $c':= \bigl ( c'_1, \ldots , c'_\ell \bigr )$. If the verification fails or any of the sanitized ciphertexts is $\bot$, it outputs $\bot$.

• Decryption: On input a decryption key $dk ^{\mathsf {ACE}_{\mathsf {DEq}}}_{\mathbf {y}} = \bigl ( dk ^{\mathsf {ACE}_{=}}_{(y_1, 1)}, \ldots , dk ^{\mathsf {ACE}_{=}}_{(y_\ell , \ell )} \bigr )$ and a sanitized ciphertext $c':= \bigl ( c'_1, \ldots , c'_\ell \bigr )$, the algorithm $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.Dec}$ computes for $i \in [\ell ]$ the message $m_i \leftarrow \mathsf {ACE}_{=}\mathsf {.Dec}\bigl ( dk ^{\mathsf {ACE}_{=}}_{(y_i, i)}, c'_i \bigr )$. If $m_i \ne \bot$ for some $i \in [\ell ]$, $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.Dec}$ outputs the first such $m_i$; otherwise it outputs $\bot$.

• Modification detection: On input sanitizer parameters $sp ^{\mathsf {ACE}_{\mathsf {DEq}}}:= \bigl ( sp ^{\mathsf {ACE}_{=}}, vk ^{\mathsf {Sig}}, crs ^{\mathsf {NIZK}}\bigr )$ and two ciphertexts $c= \bigl (c_1, \ldots , c_\ell ,\pi ^{\mathsf {NIZK}}\bigr )$ and $\tilde{c} := \bigl (\tilde{c}_1, \ldots , \tilde{c}_\ell ,\tilde{\pi }^{\mathsf {NIZK}} \bigr )$, $\mathsf {ACE}_{\mathsf {DEq}}\mathsf {.DMod}$ checks for $i \in [\ell ]$ if $\mathsf {ACE}_{=}\mathsf {.DMod}\bigl ( sp ^{\mathsf {ACE}_{=}}, c_i, \tilde{c}_i \bigr ) = 1$. If this is the case for some $i \in [\ell ]$, it outputs 1; otherwise, it outputs 0.

Weak and strong anonymity. As we show below, our scheme enjoys weak anonymity. It is easy to see that it does not have strong anonymity: Given a decryption key for the role (1, 2), one can decrypt ciphertexts encrypted under a key for the roles (1, 1) and (2, 2). One does, however, also learn which of the two components decrypted successfully. If it is the first one, the sender role must be (1, 1), if it is the second one, the sender role must be (2, 2). For similar reasons, we do not achieve strong sanitization security.

A similar construction can be used to achieve strong anonymity for less expressive policies: If a sender role still corresponds to a vector $(x_1, \ldots , x_\ell ) \in \mathcal {D}^\ell$ but a receiver role only to one component $(j, y) \in [\ell ] \times \mathcal {D}$, one can consider the policy that allows to receive if $x_j = y$. Now, we do not need several components for the decryption key and the problem sketched above disappears.

Proposition 3

If $\mathsf {ACE}_{=}$ is correct and detectable, then the scheme $\mathsf {ACE}_{\mathsf {DEq}}$ from above is correct and detectable. If $\mathsf {ACE}_{=}$ is strongly detectable, then $\mathsf {ACE}_{\mathsf {DEq}}$ is also strongly detectable. More precisely, for all probabilistic algorithms $\mathcal {A}$, there exist probabilistic algorithms $\mathcal {A}_{\mathsf {corr}}$, $\mathcal {A}_{\mathsf {dtct}}$, $\mathcal {A}'_{\mathsf {dtct}}$, and $\mathcal {A}_{\mathsf {sdtct}}$ such that

$$\begin{aligned} \mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathsf {ACE}_{\mathsf {DEq}},\mathcal {A}}&\le \mathsf {Adv}^{\mathsf {ACE\text {-}CORR}}_{\mathsf {ACE}_{=},\mathcal {A}_{\mathsf {corr}}} + (\ell - 1) \cdot \mathsf {Adv}^{\mathsf {ACE\text {-}DTCT}}_{\mathsf {ACE}_{=},\mathcal {A}_{\mathsf {dtct}}}, \\ \mathsf {Adv}^{\mathsf {ACE\text {-}DTCT}}_{\mathsf {ACE}_{\mathsf {DEq}},\mathcal {A}}&\le \ell \cdot \mathsf {Adv}^{\mathsf {ACE\text {-}DTCT}}_{\mathsf {ACE}_{=},\mathcal {A}'_{\mathsf {dtct}}}, \\ \mathsf {Adv}^{\mathsf {ACE\text {-}sDTCT}}_{\mathsf {ACE}_{\mathsf {DEq}},\mathcal {A}}&\le \ell \cdot \mathsf {Adv}^{\mathsf {ACE\text {-}sDTCT}}_{\mathsf {ACE}_{=},\mathcal {A}_{\mathsf {sdtct}}}. \end{aligned}$$

See the full version of this paper for proofs of this proposition and the following theorem, which summarizes the security properties of our scheme.

Theorem 3

If $F$ is pseudorandom, $\mathsf {NIZK}$ is zero-knowledge and extractable, $\mathsf {Sig}$ is EUF-CMA secure, and $\mathsf {ACE}_{=}$ is perfectly correct, strongly detectable, has NDTCT-FENC, and is PRV-CCA, wANON-CCA, SAN-CCA, RR, and UDEC secure, then the scheme $\mathsf {ACE}_{\mathsf {DEq}}$ from above has NDTCT-FENC and is PRV-CCA, wANON-CCA, SAN-CCA, RR, and UDEC secure.

7 Conclusion and Directions for Future Work

In this paper, we have critically revisited existing notions for access control encryption, proposed stronger security definitions, and presented a new scheme that provably achieves our strong requirements. The need for stronger notions is not only a theoretical one as we have shown: In particular, we have described a practical attack based on the observation that a semi-honest sanitizer might leak an unsanitized ciphertext to a dishonest party.

An important question is whether all realistic attacks are excluded by our definitions. Furthermore, we would like to understand the fundamental limits of ACE. This includes investigating in which scenarios it can or cannot be used. To settle these questions, the authors are currently working on a theoretical model to capture the use case of ACE in a simulation-based framework. Another interesting research direction is to find more efficient schemes for useful policies.