A Time Saver: Optimization Approach for the Fully Automatic 3D Planning of Forearm Osteotomies

Abstract

Three-dimensional (3D) computer-assisted preoperative planning has become the state-of-the-art for surgical treatment of complex forearm bone malunions. Despite benefits of these approaches, surgeon time and effort to generate a 3D-preoperative planning remains too high, and limits their clinical application. This motivates the development of computer algorithms able to expedite the process. We propose a staged multi-objective optimization method based on a genetic algorithm with tailored fitness functions, capable to generate a 3D-preoperative plan in a fully automatic fashion. A clinical validation was performed upon 14 cases of distal radius osteotomy. Solutions generated by our algorithm (OA) were compared to those created by surgeons using dedicated planning software (Gold Standard; GS), demonstrating that in 53% of the tested cases, OA solutions were better than or equal to GS solutions, successfully reducing surgeon’s interaction time. Additionally, a quantitative evaluation based on 4 different error measurement confirmed the validity of our method.

1 Introduction

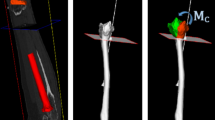
Non-anatomic post-traumatic healing (malunion) of the forearm bones can cause limitations in the range of motion (ROM), generate pain, and lead to arthrosis [1]. The mainstay surgical treatment for these pathologies is the restoration of the normal anatomy, by reduction of the bones through chirurgical intervention known as corrective osteotomy. In the procedure, the malunited bone is cut, the fragments are realigned to their correct anatomical position, and stabilized with an osteosynthesis plate [2]. Current state-of-the-art of corrective osteotomies contemplates the generation of a meticulous preoperative planning, using computer-assisted (CA) techniques based on CT-reconstructed 3D triangular surface models of the bones (hereinafter 3D models) [1,2,3,4,5,6]. ICP registration is used to align the cut fragments to a mirror-model of the contralateral bone serving as a reconstruction target [1,2,3,4] (registration-based reduction; Fig. 1A–B). Surgical navigation based on patient-specific instruments is applied to ensure implementation according to the preoperative planning [4,5,6].

Fig. 1.

(A) Reconstruction target (green) relative to the malunited bone (from palmar). (B) Post-operative situation from radial. Distal fragment has been reduced using transformation $A_{f}$. (C) Anatomical landmarks of the distal radius (i–vii).

A 3D preoperative plan of a distal radius corrective osteotomy entails the calculation of 4 different objectives (Fig. 1A–B): (1) position (3 degrees of freedom; DoF) and normal (3 DoF) of the osteotomy cut plane, (2) 6-DoF transformation representing the reduction of the generated fragments to the reconstruction target, (3) allocation of the fixation plate (6-DoF) and (4) screw purchase of the plate’s screws into the reduced fragments. These 4 objectives are nonlinear, discontinuous and non-differentiable, and encompass a set of parameters with 18 DoF (Table 1). The definition of an optimal planning for a distal radius osteotomy can take up to 3 h [7], often involving close collaboration between surgeons and engineers. Thus, an automatic method for determination of an optimal surgical planning is desired to speed up the process. However, the optimization problem is very complex, requiring a tailored optimization framework with dedicated fitness function for each of the 4 objectives.

Table 1. Challenges, fitness functions, parameters and constraints associated to each objective

Previous studies focusing on the automatization of corrective osteotomy planning did only solve a simplified sub-problem with reduced DoF, failing to include all necessary objectives. The approaches include the automatic calculation of osteotomy planes angles [8, 9], using also multi-objective optimization (MOO) techniques [10], and the automatic optimization-based calculation of the reduction to the reconstruction target [2]. The goal of the present work was the development of an automatic optimization approach able to generate a complete surgical plan for corrective osteotomies of malunited radius bones in a fully automated fashion. Key features of our work are (1) a multi-staged genetic MOO to gradually reduce the search space, (2) a weighted-landmark registration-based calculation of the optimal bone reduction, considering clinical constraints and (3) an automatic implant and screw placement method. The algorithm was evaluated qualitatively and quantitatively, showing our solutions to be clinically feasible and in some cases even better than those solutions created by a surgeon.

2 Methods

Patient-specific 3D bone models were generated from CT data (Philips, Brilliance 64, 1 mm slice thickness, 120 KVp) using commercial segmentation software, transformed to an anatomical reference frame described in [3], and used as input for our multi-stage MOO strategy (Sect. 2.1). The new fitness functions ($f_{1} - f_{4}$) tailored to each of the planning objectives are described in Sect. 2.2.

In the subsequent description, we refer to a cut of the 3D model of the pathological bone, as the triangular-mesh-based clipping algorithm process [11] to obtain distal and proximal fragments, using the osteotomy plane as clipping reference. An ${\text{A}}_{\text{f}}$-transformation refers to a 4 × 4 transformation matrix, constructed from rotation $R_{f} = R\left( {\varphi_{z} } \right)R\left( {\varphi_{y} } \right)R\left( {\varphi_{x} } \right)$ and translation $\vec{T}_{f} = \left( {T_{fx} , T_{fy} , T_{fz} } \right)$ (Table 1), which controls the registration of the distal fragment onto the reconstruction target. Similarly, ${\text{A}}_{\text{p}} {\text{A}}_{\text{p}}$-transformation ($R_{p} = R\left( {\theta_{z} } \right)R\left( {\theta_{y} } \right)R\left( {\theta_{x} } \right)$; $\vec{T}_{p} = (T_{px} , T_{py} , T_{pz}$)) describes the positioning of the fixation plate (pre-bending is not required) relative to the bone fragments.

2.1 Multi-stage Optimization

The proposed multi-stage strategy optimization approach permits (1) a reduction of the amount of simultaneous optimization objectives, (2) a gradual reduction of the algorithm search space, and (3) a faster convergence towards an optimized solution.

Optimization.

Due to its proven performance with more than 2 optimization objectives and ease for integration of nonlinear constraints ($g_{m} \left( {\vec{x}} \right)$), the optimization is based on a weighted genetic-based NSGA-II approach [12] in each stage of the optimization pipeline. Each optimization objective is described by means of a fitness function $f_{m} \left( {\vec{x}} \right)$, such that solving $\min_{{s.t.x \in {\text{X}}}} \left( { f_{1} \left( {\vec{x}} \right), f_{2} \left( {\vec{x}} \right), \ldots , f_{m} \left( {\vec{x}} \right) } \right)$, over $G_{N}$ generations, gives a Pareto set [12] of optimal solutions $X^{*}$, subject to $g_{m} \left( {\vec{x}} \right)$. The raw input of the optimization algorithm is a real-valued chromosome $\overrightarrow {\text{x }}$ (Table 1), which contains the set of parameters to be optimized and that mathematically describes each objective.

Weighting.

Standard NSGA-II is only able to find solutions where all objectives have the same importance on the solution space, i.e., they are symmetrically optimized. In our optimization problem, each objective has a different importance. Using retrospective data, we have defined the optimal weighting schema together with the surgeons, giving highest priority to the reduction alignment, followed by the plate and screw position, and osteotomy plane. We have set the weighting function accordingly, by developing a weighted version of the NSGA-II, through modification of the crowding distance as defined in [12]. The new crowding distance $d$ is expressed in Eq. 1. The weighting function $w$ increases the sparsity of solutions $X^{*}$ around the utopia point [13] (region where all solutions would be ideally optimized), for the $r$ (out of $m$) optimization objectives. The sparsity of $f_{m} \left( {\vec{x}} \right)$ along the Pareto set is controlled by the constant $k_{r}$, which represent the complementary percentage of the desired sparsity. We have chosen $k_{r} = 20$, i.e., 80% of solutions within the utopia point [14].

$$ d\left( {\vec{x}^{j} \in X^{ * } } \right) = w\left( {\vec{x}^{j} } \right)d\left( {\vec{x}^{j} } \right) + \frac{{f_{m} \left( {\vec{x}^{j + 1} } \right) - f_{m} \left( {\vec{x}^{j - 1} } \right)}}{{f_{m}^{max} - f_{m}^{min} }},w\left( {\vec{x}^{j} } \right) = \sum\nolimits_{r \in m} {e^{{ - {\text{k}}_{r} \vec{x}^{j} /e^{{{\text{k}}_{r} }} }} } . $$

(1)

Stages.

We designed the proposed weighted NSGA-II optimization in three stages:

• 1^st stage: Objectives $f_{1}$ and $f_{2}$ are used for finding the best alignment of the fragments, while minimizing the cut surface (Sec. 2.2). A $f_{1}$-weighted NSGA-II ($r = 1;m = 2; G_{N} = 200$) is applied to a reduced chromosome ${\vec{\text{x}}}_{1}$ (${\vec{\text{x}}}$ of the i-th stage) containing only the parameters associated to $f_{1}$ and $f_{2}$ (${\vec{\text{x}}}_{1} = \left[ {p_{y} ,N_{px} ,N_{py} , N_{pz} , \varphi_{z} , \varphi_{y} , \varphi_{z} , T_{fx} ,T_{fy} ,T_{fz} } \right]$; Table 1). Results are kept in matrix $X^{{1^{*} }}$.

• 2^nd stage: An optimization run using $f_{1}$, $f_{2}$ and $f_{3}$ (Sect. 2.2) is performed on a complete chromosome ${\vec{\text{x}}}_{2}$ (Table 1). The NSGA-II is weighted towards $f_{1}$ and $f_{2}$ (see Eq. 1), constraining the alignment of the distal fragment and the area of the cut surface, but allowing a larger freedom to the plate position ($r = 1,2 ;m = 3; G_{N} = 100$). Results are kept in matrix $X^{{2^{*}}}$.

• 3^rd stage: $X^{{1^{*} }}$ and $X^{{2^{*} }}$ are combined and used as initialization matrix ${\text{X}}^{\text{Init}} {\text{X}}^{\text{Init}}$ for a 3^rd and final stage. Solution space is further reduced by constraining the parameter range of ${\vec{\text{x}}}$ to the maximum and minimum values of ${\text{X}}^{\text{Init}} {\text{X}}^{\text{Init}}$, e.g., ${\vec{\text{x}}}_{3} \in \left[ {{ \hbox{min} }\left( {X^{Init} } \right), { \hbox{max} }\left( {X^{Init} } \right)} \right]$. The NSGA-II is weighted towards $f_{1}$, to guarantee solutions with good alignment, but this time an optimized allocation of the fixation plate ($f_{3} )$ and a feasible screw purchase ($f_{4} )$ are also desired ($r = 1 ;m = 3; G_{N} = 200$). The resulting Pareto set $X^{{3^{*} }}$ is used for classification and output of solutions.

Output.

The final output of the optimization, $\vec{x}_{best}$, corresponds to the solution with the best combined fitness, obtained through Eq. 2.

$$ \vec{x}_{best} = \hbox{min} \left( {\frac{1}{m}\sum\nolimits_{m} {\left( {f_{m} \left( {X^{3 * } } \right) - f_{m}^{\hbox{min} } \left( {X^{3 * } } \right)} \right)} /\left( {f_{m}^{\hbox{max} } \left( {X^{3 * } } \right) - f_{m}^{\hbox{min} } \left( {X^{3 * } } \right)} \right)} \right). $$

(2)

2.2 Fitness Functions

Landmark-Based Registration Error (f₁).

Bone reduction is the most critical goal to attain in a corrective osteotomy. Clinically, only certain bone regions must be precisely matched (e.g., joint regions) with the reconstruction template, while other parts can (or must) deviate. Consequently, previously described approaches [3, 7] relying on ICP-registration of the entire fragment surface always require manual fine-tuning by the surgeon. To determine clinically acceptable solutions in an automated fashion, we have introduced a weighted landmark registration-based approach to fine-control the reduction w.r.t. the reconstruction target. Annotated and clinically-relevant landmark regions $l$, of 5-mm radius, are defined on the distal part of both, pathological radius and reconstruction target. Subsequently, the average root mean square error ($RMSE_{Avg}$) is used to measure registration accuracy, based on a weighted point-to-point Euclidean distance between the $K$ ($K = 7)$, bony landmark areas $l$ (see Fig. 1C). A weight $w_{l}$ between 0 and 1, with $\sum\nolimits_{l = 1}^{K} {w_{l} = 1}$, is assigned to each $l$. Landmarks located on the joint surface (i–v; Fig. 1C) are assigned a bigger weight due to the importance of their reconstruction accuracy. The $RMSE_{Avg}$ is calculated between the $A_{f}$-transformed landmark areas of the pathological bone ($l_{p}^{l}$), e.g., $P_{tr}^{l} = A_{f} \cdot l_{p}^{l}$, and its reciprocal set $Q_{t}^{l}$ on the reconstruction target, as shown in Eq. 3.

$$ f_{1} = RMSE_{Avg } = \frac{1}{K}\sum\nolimits_{l = 1}^{K} {w_{l} \,RMSE\left( {P_{tr}^{l} ,Q_{t}^{l} } \right)} ;\;w_{l} = \left\{ {l_{1} - l_{5} :0.16 ; l_{6} ,l_{7} :0.10} \right\}. $$

(3)

Cut Surface (f₂).

In order to avoid individually controlling the 6-DoF of the osteotomy plane (proven to be challenging [9, 10]), we have decided to use a minimization of the bone cut surface $A_{cs}$ (an often-used clinical parameter), for guiding the position and orientation of the plane. We have approximated $A_{cs}$ to the area of an ellipse generated by the norm of the 1^st and 2^nd largest eigenvectors, $\overrightarrow {{W_{1} }}$ and $\overrightarrow {{W_{2} }}$, of the Principal Component Analysis (PCA) [15] of the projections {$\vec{t}_{i}$} of the pathological bone model points $\vec{v}_{i}$ where $\vec{t}_{i} = \left| {\vec{N}_{p} \left( {\vec{v}_{i} - \vec{P}} \right)} \right| < wd_{p}$. Threshold $wd_{p}$ is the width given by the thickness of the sawblade, and $\vec{N}_{p}$ and $\vec{P}$ are the normal and position vectors of the osteotomy plane. It results that $f_{2} = A_{cs} = \pi \left\| {\overrightarrow {{W_{1} }} } \right\|\left\| {\overrightarrow {{W_{2} }} } \right\|$.

Distance Fixation Plate – Bone Fragments (f₃).

The stability of the post-operative bone reduction and the successful healing of the surrounding soft tissue depend on a correct positioning of the fixation plate. Generally, a minimal distance between fixation plate ($\varvec{P}_{\varvec{f}}$) and bone surface is desirable. Therefore, the transformation of the fixation plate is controlled with a distance minimization strategy between the $A_{p}$-transformed fixation plate model ($\varvec{P}_{\varvec{f}}^{\varvec{p}} = \varvec{ A}_{\varvec{p}} \varvec{P}_{\varvec{f}} )$ and the two pathological bone fragments: proximal ($bp_{prox} )$, and $A_{f}$-transformed distal ($bp_{dist}^{f} = \varvec{A}_{\varvec{f}} bp_{dist}$) radius. The distance $\varvec{D}_{{\varvec{bp}}}$ between the two fragments and the fixation plate is assessed by the average of their Hausdorff distances ($\varvec{H})$ as described in Eq. 4.

$$ \varvec{f}_{{\mathbf{3}}} = \varvec{ D}_{{\varvec{bp}}} = \varvec{ }\frac{{\left( {\varvec{H}\left( {\varvec{ P}_{\varvec{f}}^{\varvec{p}} ,\varvec{ }bp_{prox} } \right) + \varvec{H}\left( {\varvec{P}_{\varvec{f}}^{\varvec{p}} ,\varvec{ }bp_{dist}^{f} } \right)} \right)}}{{\mathbf{2}}}. $$

(4)

Screw Purchase (f₄).

Proper placement of fixation screws can be surgically challenging but plays a crucial role in successful healing after forearm osteotomies. We have developed a method for automatic screw placement based on a novel fitness grid representation. A uniform 11 × 11 × 11 grid $Gd$ is constructed similarly to a 3D distance map [16]. $Gd$ is oriented according to three anatomical axes [3] and covering the most distal 15% of the radius (w.r.t pathological bone length) in the axial direction, and covering the entire radius in the other anatomical directions. Values $\left\{ { - 1,0,1,2,3} \right\}$ of the fitness grid correspond to the screw’s performance with respect to (a) bi-cortical purchase, (b) distance to distal joint, (c) penetration length, and (d) osteotomy plane. Assignment of values is demonstrated in Fig. 2. In each objective evaluation, penetration points ($y^{sIn} ,y^{sOut}$) are calculated for each distal screw $s$, using a ray-casting algorithm between the $A_{p}$-transformed model of $s$ (cylinder) and the $A_{f}$-transformed model of the pathological distal fragment. The grid is then queried using each penetration point (i.e., $Gd\left( {y^{s} } \right))$. A nearest-neighbor $\left( {nn = 2} \right)$ [17] interpolation of the queried values of $G_{d}$ is done to account for value border differences. The screw purchase $Sp$ is given by Eq. 5.

$$ f_{4} = {\text{Sp}} = \frac{1}{s.nn} \mathop \sum \limits_{s} \mathop \sum \limits_{nn} \frac{{\left( {Gd\left( {y^{sIn}_{nn} } \right) + Gd\left( {y^{sOut}_{nn} } \right) } \right)}}{2} . $$

(5)

Fig. 2.

(A) Sagittal cut of the proposed 3D fitness grid. The lower the value of the fitness, the better the positioning of the screw. (B) 3 examples of screw placements with the associated grid values (sagittal cut).

3 Results and Discussion

We have carried out a clinical study to compare the proposed algorithm with the state-of-the art. 14 consecutive cases of distal radius osteotomy were included in the study. All patients were treated in 2015 and underwent 3D preoperative planning and surgically navigated surgery through patient-specific instrumentation at our institution. The preoperative plans had been created manually using commercial preoperative planning software (CASPA, Balgrist CARD AG, Switzerland) by the responsible hand surgeon together with an engineer. These solutions were considered as the Gold Standard (GS). The baseline data was as follow: affected side: 7 left, 7 right; gender: 4 males, 10 females; 2 different fixation plates. We have implemented the MOO genetic algorithm in Matlab R2015b.

In order to test the validity of our algorithm on ready-to-use solutions, a clinical validation was performed by 5 readers (1 engineer specialized in CA osteotomy planning and 4 hand surgeons). The surveyees had to choose the better preoperative plan for each case, between the blinded solution obtained from the optimization algorithm (OA) and the blinded GS solutions (Table 2). To avoid bias, voting range and average were calculated excluding the answers of the surgeon who performed the planning for each case. Cases C13 and C14 were the only ones in which none of the surveyed surgeons was involved. The results of the clinical validation showed OA solutions to be judged 53% of the time as better than or equivalent to GS solutions.

Table 2. Validation results for each of the 14 cases. Readers had to blindly choose between OA and GS solutions as the optimal surgery planning. Each case was evaluated by 4 surgeons and 1 experienced planner. For C2, C3 and C14, GS solutions were more often preferred over those of the OA, due to a slightly better alignment of the fixation plate w.r.t the proximal fragment

Additionally, a quantitative comparison was performed between the OA and the GS solution, across all 14 cases, using 4 different error measures. The transformation error (Fig. 3A) and the distance to the fixation plate (Fig. 3B) for both OA and GS, were comparable within the millimeter scale. The average fitness of the screw purchase (Fig. 3C) and the inverse average distance from the distal screws to the osteotomy plane (Fig. 3D) for OA solutions were in average better than those of the GS. In general, OA solutions reported a better fitness than GS solutions among the 4 evaluated error measures. This indicates that the algorithm is capable of generating solutions of the same quality and feasibility as the ones generated by surgeons. Despite of an algorithm runtime of 1 h and 44 min for the calculation of an OA solution, the approach can render interaction times of the surgeon into the preoperative planning unnecessary, subsequently reducing the effective treatment costs.

Fig. 3.

Box plot (3/2 interquartile range whiskers) of OA solutions for each of the 14 cases compared to the GS. Red circle indicates the mean value of each fitness range. (A) $RMSE_{Avg}$ between distal fragment and reconstruction target. (B) Average Hausdorff distance between fixation plate and proximal and distal bone fragments (C) Average fitness of screw purchase of distal screws (D) Inverse average distance of distal screws to osteotomy plane.

Our approach does not attempt to be a magical solution for the planning of forearm osteotomies. The potential of our automatic optimization lies in (1) the capability of evaluating solutions with different trade-off among objectives, (2) reducing human workload and, consequently, associated costs, and (3) saving time of the surgeons, which is crucial in the clinical setting. Furthermore, we are confident that current calculations times of our method can be further decreased by implementing the algorithm in a compiled language.

4 Conclusion

The presented multi-stage optimization approach allows generating patient specific solutions for pre-operative planning of distal radius osteotomies, which are equivalent to, or even outperform gold standard (manual expert) solutions. Future works will target reduction of calculation times, inclusion of a larger data set and corresponding power analysis, and extension of the approach to a wider range of osteotomy types.