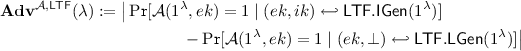All-But-Many Lossy Trapdoor Functions and Selective Opening Chosen-Ciphertext Security from LWE

Abstract

Selective opening (SO) security refers to adversaries that receive a number of ciphertexts and, after having corrupted a subset of the senders (thus obtaining the plaintexts and the senders’ random coins), aim at breaking the security of remaining ciphertexts. So far, very few public-key encryption schemes are known to provide simulation-based selective opening (SIM-SO-CCA2) security under chosen-ciphertext attacks and most of them encrypt messages bit-wise. The only exceptions to date rely on all-but-many lossy trapdoor functions (as introduced by Hofheinz; Eurocrypt’12) and the Composite Residuosity assumption. In this paper, we describe the first all-but-many lossy trapdoor function with security relying on the presumed hardness of the Learning-With-Errors problem ($\mathsf {LWE}$) with standard parameters. Our construction exploits homomorphic computations on lattice trapdoors for lossy $\mathsf {LWE}$ matrices. By carefully embedding a lattice trapdoor in lossy public keys, we are able to prove SIM-SO-CCA2 security under the $\mathsf {LWE}$ assumption. As a result of independent interest, we describe a variant of our scheme whose multi-challenge CCA2 security tightly relates to the hardness of $\mathsf {LWE}$ and the security of a pseudo-random function.

1 Introduction

Lossy Trapdoor Functions. As introduced by Peikert and Waters [66], lossy tradpoor functions (LTFs) are function families where injective functions – which can be inverted using a trapdoor – are indistinguishable from lossy functions, where the image is much smaller than the domain. The last decade, they received continuous attention (see, e.g., [3, 37, 46, 49, 71, 72]) and found many amazing applications in cryptography. These include black-box realizations of cryptosystems with chosen-ciphertext (IND-CCA2) security [66], deterministic public-key encryption in the standard model [19, 26, 68] and encryption schemes retaining some security in the absence of reliable randomness [8, 10]. As another prominent application, they enabled the design [11, 16] of encryption schemes secure against selective-opening (SO) adversaries, thereby providing an elegant solution to a 10 year-old problem raised by Dwork et al. [35].

When it comes to constructing CCA2-secure [67] encryption schemes, LTFs are often combined with all-but-one trapdoor functions (ABO-LTFs) [66], which enable a variant of the two-key simulation paradigm [63] in the security proof. In ABO-LTF families, each function takes as arguments an input x and a tag t in such a way that the function $f_{\mathsf {abo}}(t,\cdot )$ is injective for any t, except a special tag $t^*$ for which $f_{\mathsf {abo}}(t^*,\cdot )$ behaves as a lossy function. In the security proof of [66], the lossy tag $t^*$ is used to compute the challenge ciphertext, whereas decryption queries are handled by inverting $f_{\mathsf {abo}}(t, \cdot )$ for all injective tags $t \ne t^\star$. One limitation of ABO-LTFs is the uniqueness of the lossy tag $t^\star$ which must be determined at key generation time. As such, ABO-LTFs are in fact insufficient to prove security in attack models that inherently involve multiple challenge ciphertexts: examples include the key-dependent message [17] and selective opening [11] settings, where multi-challenge security does not reduce to single-challenge security via the usual hybrid argument [7].

To overcome the aforementioned shortcoming, Hofheinz [49] introduced all-but-many lossy trapdoor functions (ABM-LTFs) which extend ABO-LTFs by allowing the security proof to dynamically create arbitrarily many lossy tags using a trapdoor. Each tag $t=(t_\mathsf {c},t_\mathsf {a})$ is comprised of an auxiliary component $t_\mathsf {a}$ and a core component $t_\mathsf {c}$ so that, by generating $t_\mathsf {c}$ as a suitable function of $t_\mathsf {a}$, the reduction is able to assign a lossy (but random-looking) tag to each challenge ciphertext while making sure that the adversary will be unable to create lossy tags by itself in decryption queries. Using carefully designed ABM-LTFs and variants thereof [50], Hofheinz gave several constructions [49, 50] of public-key encryption schemes in scenarios involving multiple challenge ciphertexts.

Selective Opening Security. In the context of public-key encryption, selective opening (SO) attacks take place in a scenario involving a receiver and N senders. Those encrypt possibly correlated messages $(\mathsf {Msg}_1,\ldots ,\mathsf {Msg}_N)$ under the receiver’s public key PK and, upon receiving the ciphertexts $(\mathbf {C}_1,\ldots ,\mathbf {C}_N)$, the adversary decides to corrupt a subset of the senders. Namely, by choosing $I \subset [N]$, it obtains the messages $\{ \mathsf {Msg}_i\}_{i \in I}$ as well as the random coins $\{r_i\}_{i \in I}$ for which $\mathbf {C}_i=\mathsf {Encrypt}(PK,\mathsf {Msg}_i,r_i)$. Then, the adversary aims at breaking the security of unopened ciphertexts $\{\mathbf {C}_i\}_{i \in [N] \setminus I}$. It is tempting to believe that standard notions like semantic security carry over to such adversaries due to the independence of random coins $\{r_i\}_{i \in [N]}$. However, this is not true in general [29] as even the strong standard notion of IND-CCA security [67] was shown [9, 55] not to guarantee anything under selective openings. Proving SO security turns out to be a challenging task for two main reasons. The first one is that the adversary must also obtain the random coins $\{r_i\}_{i \in I}$ of opened ciphertexts (and not only the underlying plaintexts) as reliably erasing them can be very difficult in practice. Note that having the reduction guess the set I of corrupted senders beforehand is not an option since it is only possible with negligible probability $1/\left( {\begin{array}{c}N\\ N/2\end{array}}\right)$. The second difficulty arises from the potential correlation between $\{ \mathsf {Msg}_i\}_{i \in I}$ and $\{ \mathsf {Msg}_i\}_{i \in [N] \setminus I}$, which hinders the use of standard proof techniques and already makes selective opening security non-trivial to formalize.

Towards properly defining SO security, the indistinguishability-based (IND-SO) approach [11, 16] demands that unopened plaintexts $\{\mathsf {Msg}_i\}_{i \in [N] \setminus I}$ be indistinguishable from independently resampled ones $\{\mathsf {Msg}_i'\}_{i \in [N] \setminus I}$ conditionally on the adversary’s view. However, such definitions are not fully satisfactory. Indeed, since $\{\mathsf {Msg}_i\}_{i \in [N] }$ may be correlated, the resampling of $\{\mathsf {Msg}_i'\}_{i \in [N] \setminus I}$ must be conditioned on $\{\mathsf {Msg}_i \}_{i \in I}$ to make the adversary’s task non-trivial. This implies that, in the security game, the challenger can only be efficient for message distributions that admit efficient conditional resampling, which is a much stronger restriction than efficient samplability. Indeed, many natural message distributions (e.g., where some messages are hard-to-invert functions of other messages) do not support efficient conditional resampling.

Bellare et al. [11, 16] defined a stronger, simulation-based (SIM-SO) flavor of selective opening security. This notion mandates that, whatever the adversary outputs after having seen $\{\mathbf {C}_i\}_{i \in [N]}$ and $\{ (\mathsf {Msg}_i,r_i)\}_{i \in I}$ can be efficiently simulated from $\{\mathsf {Msg}_i\}_{i \in I }$, without seeing the ciphertexts nor the public key. Unlike its indistinguishability-based counterpart, SIM-SO security does not imply any restriction on the message distributions. While clearly preferable, it turns out to be significantly harder to achieve. Indeed, Böhl et al. [18] gave an example of IND-SO-secure scheme that fails to achieve SIM-SO security.

On the positive side, simulation-based chosen-plaintext (SIM-SO-CPA) security was proved attainable under standard number theoretic assumptions like Quadratic Residuosity [16], Composite Residuosity [45] or the Decision Diffie-Hellman assumption [16, 54]. In the chosen-ciphertext (SIM-SO-CCA) scenario, additionally handling decryption queries makes the problem considerably harder: indeed, very few constructions achieve this security property and most of them [36, 56, 57, 59] proceed by encrypting messages in a bit-by-bit manner. The only exceptions [38, 49] to date rely on all-but-many lossy trapdoor functions and Paillier’s Composite Residuosity assumption [64].

In this paper, we provide SIM-SO-CCA-secure realizations that encrypt many bits at once under lattice assumptions. Our constructions proceed by homomorphically evaluating a low-depth pseudorandom function (PRF) using the fully homomorphic encryption (FHE) scheme of Gentry, Sahai and Waters [41].

1.1 Our Results

Our contribution is three-fold. We first provide an all-but-many lossy trapdoor function based on the Learning-With-Errors ($\mathsf {LWE}$) assumption [69]. We tightly relate the security of our ABM-LTF to that of the underlying PRF and the hardness of the $\mathsf {LWE}$ problem.

As a second result, we use our ABM-LTF to pave the way towards public-key encryption schemes with tight (or, more precisely, almost tight in the terminology of [31]) chosen-ciphertext security in the multi-challenge setting [7]. By “tight CCA security”, as in [39, 51,52,53, 58], we mean that the multiplicative gap between the adversary’s advantage and the hardness assumption only depends on the security parameter and not on the number of challenge ciphertexts. The strength of the underlying $\mathsf {LWE}$ assumption depends on the specific PRF used to instantiate our scheme. So far, known tightly secure lattice-based PRFs rely on rather strong $\mathsf {LWE}$ assumptions with exponential modulus and inverse error rate [5], or only handle polynomially-bounded adversaries [34] (and hence do not fully exploit the conjectured exponential hardness of $\mathsf {LWE}$). However, any future realization of low-depth PRF with tight security under standard $\mathsf {LWE}$ assumptions (i.e., with polynomial approximation factor) could be plugged into our scheme so as to obtain tight CCA security under the same assumption. Especially, if we had such a tightly secure PRF with an evaluation circuit in $\mathsf {NC}^1$, our scheme would be instantiable with a polynomial-size modulus by translating the evaluation circuit into a branching program via Barrington’s theorem [6] and exploiting the asymmetric noise growth of the GSW FHE as in [27, 44].

As a third and main result, we modify our construction so as to prove it secure against selective opening chosen-ciphertext attacks in the indistinguishability-based (i.e., IND-SO-CCA2) sense. By instantiating our system with a carefully chosen universal hash function, we finally upgrade it from IND-SO-CCA2 to SIM-SO-CCA2 security. For this purpose, we prove that the upgraded scheme is a lossy encryption scheme with efficient opening. As defined by Bellare et al. [11, 16], a lossy encryption scheme is one where normal public keys are indistinguishable from lossy keys, for which ciphertexts statistically hide the plaintext. It was shown in [11, 16] that any lossy cryptosystem is in fact IND-SO-CPA-secure. Moreover, if a lossy ciphertext $\mathbf {C}$ can be efficiently opened to any desired plaintext $\mathsf {Msg}$ (i.e., by finding plausible random coins r that explain $\mathbf {C}$ as an encryption of $\mathsf {Msg}$) using the secret key, the scheme also provides SIM-SO-CPA security. We show that our IND-SO-CCA-secure construction satisfies this property when we embed a lattice trapdoor [40, 60] in lossy secret keys.

This provides us with the first multi-bit $\mathsf {LWE}$-based public-key cryptosystem with SIM-SO-CCA security. So far, the only known method [59] to attain the same security notion under quantum-resistant assumptions was to apply a generic construction where each bit of plaintext requires a full key encapsulation (KEM) using a CCA2-secure KEM. In terms of ciphertext size, our system avoids this overhead and can be instantiated with a polynomial-size modulus as long as the underlying PRF can be evaluated in $\mathsf {NC}^1$. For example, the Banerjee-Peikert PRF [4] – which relies on a much weaker $\mathsf {LWE}$ assumption than [5] as it only requires on a slightly superpolynomial modulus – satisfies this condition when the input of the PRF is hardwired into the circuit.

As a result of independent interest, we show in the full version of the paper that lattice trapdoors can also be used to reach SIM-SO-CPA security in lossy encryption schemes built upon lossy trapdoor functions based on $\mathsf {DDH}$-like assumptions. This shows that techniques from lattice-based cryptography can also come in handy to obtain simulation-based security from conventional number theoretic assumptions.

1.2 Our Techniques

Our ABM-LTF construction relies on the observation – previously used in [3, 12] – that the $\mathsf {LWE}$ function $f_{\mathsf {LWE}} : \mathbb {Z}_q^n \times \mathbb {Z}^m \rightarrow \mathbb {Z}_q^m : (\mathbf {x},\mathbf {e}) \rightarrow \mathbf {A} \cdot \mathbf {x} + \mathbf {e}$  is lossy. Indeed, under the $\mathsf {LWE}$ assumption, the random matrix $\mathbf {A} \in \mathbb {Z}_q^{m \times n}$ can be replaced by a matrix of the form $\mathbf {A} = \mathbf {B} \cdot \mathbf {C} + \mathbf {F}$, for a random $\mathbf {B} \in \mathbb {Z}_q^{m \times \ell }$ such that $\ell <n$ and a small-norm $\mathbf {F} \in \mathbb {Z}^{m \times n}$, without the adversary noticing. However, we depart from [3, 12] in several ways.

First, in lossy mode, we sample $\mathbf {C}$ uniformly in $\mathbb {Z}_q^{\ell \times n}$ (rather than as a small-norm matrix as in [12]) because, in order to achieve SIM-SO security, we need to generate $\mathbf {C}$ with a trapdoor. Our application to SIM-SO security also requires to sample $(\mathbf {x},\mathbf {e})$ from discrete Gaussian distributions, rather than uniformly over an interval as in [12]. Second, we assume that the noise $\mathbf {e} \in \mathbb {Z}^m$ is part of the input instead of using the Rounding technique¹ [5] as in the lossy function of Alwen et al. [3]. The reason is that, in our ABM-LTF, we apply the $\mathsf {LWE}$-based function $(\mathbf {x},\mathbf {e}) \rightarrow \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ for tag-dependent matrices $\mathbf {A}_t$ and, if we were to use the rounding technique, the lower parts of matrices $\mathbf {A}_t$ would have to be statistically independent for different tags. Since we cannot guarantee this independence, we consider the noise term $\mathbf {e}$ to be part of the input. In this case, we can prove that, for any lossy tag, the vector $\mathbf {x}$ retains at least $\varOmega (n \log n)$ bits of min-entropy conditionally on $\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ and this holds even if $\{\mathbf {A}_t\}_t$ are not statistically independent for distinct lossy tags t.

One difficulty is that our ABM-LTF only loses less than half of its input bits for lossy tags, which prevents it from being correlation-secure in the sense of [70]. For this reason, our encryption schemes cannot proceed exactly as in [49, 66] by simultaneously outputting an ABM-LTF evaluation $f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e})=\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ and a lossy function evaluation $f_{\mathsf {LTF}}(\mathbf {x},\mathbf {e})=\mathbf {A} \cdot \mathbf {x} + \mathbf {e}$ as this would leak $(\mathbf {x},\mathbf {e})$. Fortunately, we can still build CCA2-secure systems by evaluating $f_{\mathsf {LTF}}(\cdot )$ and $f_{\mathsf {ABM}}(\cdot )$ for the same $\mathbf {x}$ and distinct noise vectors $\mathbf {e}_0,\mathbf {e}$. In this case, we can prove that the two functions are jointly lossy: conditionally on $(f_{\mathsf {LTF}}(\mathbf {x},\mathbf {e}_0),f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e}))$, the input $\mathbf {x}$ retains $\varOmega (n \log n)$ bits of entropy, which allows us to blind the message as $\mathsf {Msg} + h(\mathbf {x})$ using a universal hash function h.

Our ABM-LTF extends the all-but-one trapdoor function of Alwen et al. [3] by homomorphically evaluating a pseudorandom function. Letting $\bar{\mathbf {A}} \in \mathbb {Z}_q^{m \times n}$ be a lossy matrix and $\mathbf {G} \in \mathbb {Z}_q^{m \times n}$ denote the gadget matrix of Micciancio and Peikert [60], the evaluation key of our ABM-LTF contains Gentry-Sahai-Waters (GSW) encryptions $\mathbf {B}_i = \mathbf {R}_i \cdot \bar{\mathbf {A}} + K[i] \cdot \mathbf {G} \in \mathbb {Z}_q^{m \times n}$ of the bits K[i] of a PRF seed $K \in \{0,1\}^\lambda$, where $\mathbf {R}_i \in \{-1,1\}^{m \times m}$. Given a tag $t=(t_\mathsf {c},t_\mathsf {a})$, the evaluation algorithm computes a GSW encryption $\mathbf {B}_t = \mathbf {R}_t \cdot \bar{\mathbf {A}} + h_t \cdot \mathbf {G} \in \mathbb {Z}_q^{m \times n}$ of the Hamming distance $h_t$ between $t_\mathsf {c}$ and $\mathsf {PRF}(K,t_\mathsf {a})$ before using $\mathbf {A}_t= [ \bar{\mathbf {A}}^\top \mid \mathbf {B}_t^\top ]^\top$ to evaluate $f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e})=\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$. In a lossy tag $t=(\mathsf {PRF}(K,t_\mathsf {a}),t_\mathsf {a})$, we have $h_t = 0$, so that the matrix $\mathbf {A}_t= [ \bar{\mathbf {A}}^\top \mid (\mathbf {R}_t \cdot \bar{\mathbf {A}})^\top ]^\top$ induces a lossy function $f_{\mathsf {ABM}}(t,\cdot )$. At the same time, any injective tag $t=(t_\mathsf {c},t_\mathsf {a})$ satisfies $t_\mathsf {c}\ne \mathsf {PRF}(K,t_\mathsf {a})$ and thus $h_t \ne 0$, which allows inverting $f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e})=\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ using the public trapdoor [60] of the matrix $\mathbf {G}$.

The pseudorandomness of the PRF ensures that: (i) Lossy tags are indistinguishable from random tags; (ii) They are computationally hard to find without the seed K. In order to prove both statements, we resort to the $\mathsf {LWE}$ assumption as the matrix $\bar{\mathbf {A}}$ is not statistically uniform over $\mathbb {Z}_q^{m \times n}$.

Our tightly CCA2-secure public-key cryptosystem uses ciphertexts of the form $(f_{\mathsf {LTF}}(\mathbf {x},\mathbf {e}_0),f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e}),\mathsf {Msg} + h(\mathbf {x}))$, where $t_\mathsf {a}$ is the verification key of the one-time signature. Instantiating this scheme with a polynomial-size modulus requires a tightly secure PRF which is computable in $\mathsf {NC}^1$ when the input of the circuit is the key (rather than the input of the PRF).² To overcome this problem and as a result of independent interest, we provide a tighter proof for the key-homomorphic PRF of Boneh et al. [21] (where the concrete security loss is made independent of the number of evaluation queries), which gives us tight CCA2-security under a strong $\mathsf {LWE}$ assumption.

In our IND-SO-CCA2 system, an additional difficulty arises since we cannot use one-time signatures to bind ciphertext components altogether. One alternative is to rely on the hybrid encryption paradigm as in [24] by setting $t_\mathsf {a}=f_{\mathsf {LTF}}(\mathbf {x},\mathbf {e}_0)$ and encrypting $\mathsf {Msg}$ using a CCA-secure secret-key encryption scheme keyed by $h(\mathbf {x})$. In a direct adaptation of this technique, the chosen-ciphertext adversary can modify $f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e})$ by re-randomizing the underlying $\mathbf {e}$. Our solution to this problem is to apply the encrypt-then-MAC approach and incorporate $f_{\mathsf {ABM}}(\mathbf {x},\mathbf {e})$ into the inputs of the MAC so as to prevent the adversary from randomizing $\mathbf {e}$. Using the lossiness of $f_{\mathsf {ABM}}(\cdot )$ and $f_{\mathsf {LTF}}(\cdot )$, we can indeed prove that the hybrid construction provides IND-SO-CCA2 security.

In order to obtain SIM-SO-CCA2 security, we have to show that lossy ciphertexts can be equivocated in the same way as a chameleon hash function. Indeed, the result of [11, 16] implies that any lossy encryption scheme with this property is simulation-secure and the result carries over to the chosen-ciphertext setting. We show that ciphertexts can be trapdoor-opened if we instantiate the scheme using a particular universal hash function $h : \mathbb {Z}^{n} \rightarrow \mathbb {Z}_q^{L}$ which maps $\mathbf {x} \in \mathbb {Z}^n$ to $h(\mathbf {x})=\mathbf {H}_{\mathcal {UH}} \cdot \mathbf {x} \in \mathbb {Z}_q^L$, for a random matrix $\mathbf {H}_{\mathcal {UH}} \in \mathbb {Z}_q^{L \times n}$. In order to generate the evaluation keys $ek'$ and ek of $f_{\mathsf {LTF}}$ and $f_{\mathsf {ABM}}$, we use random matrices $\mathbf {B}_{\mathsf {LTF}} \in \mathbb {Z}_q^{2m \times \ell }$, $\mathbf {C}_{\mathsf {LTF}} \in \mathbb {Z}_q^{\ell \times n}$, $\mathbf {B}_{\mathsf {ABM}} \in \mathbb {Z}_q^{m \times \ell }$, $\mathbf {C}_{\mathsf {ABM}} \in \mathbb {Z}_q^{\ell \times n}$ as well as small-norm $\mathbf {F}_{\mathsf {LTF}} \in \mathbb {Z}^{2m \times n}$, $\mathbf {F}_{\mathsf {ABM}} \in \mathbb {Z}^{m \times n}$ so as to set up lossy matrices $\mathbf {A}_\mathsf {LTF}= \mathbf {B}_\mathsf {LTF}\cdot \mathbf {C}_\mathsf {LTF}+ \mathbf {F}_\mathsf {LTF}$ and $\mathbf {A}_\mathsf {ABM}=\mathbf {B}_\mathsf {ABM}\cdot \mathcal {C}_\mathsf {ABM}+ \mathbf {F}_\mathsf {ABM}$. The key idea is to run the trapdoor generation algorithm of [60] to generate a statistically uniform $\mathbf {C}=[\mathbf {C}_\mathsf {LTF}^\top \mid \mathbf {C}_\mathsf {ABM}^\top \mid \mathbf {H}_{\mathcal {UH}}^\top ]^\top \in \mathbb {Z}_q^{(2 \ell + L) \times n}$ together with a trapdoor allowing to sample short integer vectors in any coset of the lattice $\varLambda ^\perp (\mathbf {C})$. By choosing the target vector $\mathbf {t} \in \mathbb {Z}_q^{ 2 \ell + L }$ as a function of the desired message $\mathsf {Msg}_1$, the initial message $\mathsf {Msg}_0$ and the initial random coins $(\mathbf {x} ,\mathbf {e}_0,\mathbf {e})$, we can find a short $\mathbf {x}' \in \mathbb {Z}^n$ such that $\mathbf {C} \cdot \mathbf {x}' = \mathbf {t} \mod q$ and subsequently define $(\mathbf {e}_0',\mathbf {e} ') \in \mathbb {Z}^{2m} \times \mathbb {Z}^m$ so that they explain the lossy ciphertext as an encryption of $\mathsf {Msg}_1$ using the coins $(\mathbf {x}',\mathbf {e}_0',\mathbf {e}')$. Moreover, we prove that these have the suitable distribution conditionally on the lossy ciphertext and the target message $\mathsf {Msg}_1$.

1.3 Related Work

While selective opening security was first considered by Dwork et al. [35], the feasibility of SOA-secure public-key encryption remained open until the work of Bellare, Hofheinz and Yilek [11, 16]. They showed that IND-SO security can be generically achieved from any lossy trapdoor function and, more efficiently, under the $\mathsf {DDH}$ assumption. They also achieved SIM-SO-CPA security under the Quadratic Residuosity and $\mathsf {DDH}$ assumptions, but at the expense of encrypting messages bitwise. In particular, they proved the SIM-SO security of the Goldwasser-Micali system [42] and their result was extended to Paillier [45]. Hofheinz, Jager and Rupp recently described space-efficient schemes under $\mathsf {DDH}$-like assumption. Meanwhile, the notion of SIM-SO-CPA security was realized in the identity-based setting by Bellare, Waters and Yilek [15]. Recently, Hoang et al. [48] investigated the feasibility of SO security using imperfect randomness.

Selective opening security was considered for chosen-ciphertext adversaries in several works [36, 49, 56, 57, 59]. Except constructions [38, 49] based on (variants of) the Composite Residuosity assumption, all of them process messages in a bit-wise fashion, incurring an expansion factor $\varOmega (\lambda )$. In the random oracle model [13], much more efficient solutions are possible. In particular, Heuer et al. [47] gave evidence that several practical schemes like RSA-OAEP [14] are actually secure in the SIM-SO-CCA sense.

The exact security of public-key encryption in the multi-challenge, multi-user setting was first taken into account by Bellare, Boldyreva and Micali [7] who proved that Cramer-Shoup [32] was tightly secure in the number of users, but not w.r.t. the number Q of challenge ciphertexts. Using ABM-LTFs, Hofheinz managed to obtain tight multi-challenge security [49] (i.e., without a security loss $\varOmega (Q)$ between the advantages of the adversary and the reduction) at the expense of non-standard, variable-size assumptions. Under simple $\mathsf {DDH}$-like assumptions, Hofheinz and Jager [53] gave the first feasibility results in groups with a bilinear map. More efficient tight multi-challenge realizations were given in [39, 51, 52, 58] but, for the time being, the only solutions that do not rely on bilinear maps are those of [39, 52]. In particular, constructions from lattice assumptions have remained lacking so far. By instantiating our scheme with a suitable PRF [5], we take the first step in this direction (albeit under a strong $\mathsf {LWE}$ assumption with an exponential approximation factor). Paradoxically, while we can tightly reduce the security of the underlying PRF to the multi-challenge security of our scheme, we do not know how to prove tight multi-user security.

A common feature between our security proofs and those of [39, 51, 52, 58] is that they (implicitly) rely on the technique of the Naor-Reingold PRF [62]. However, while they gradually introduce random values in semi-functional spaces (which do not appear in our setting), we exploit a different degree of freedom enabled by lattices, which is the homomorphic evaluation of low-depth PRFs.

The GSW FHE scheme [41] inspired homomorphic manipulations [20] of Micciancio-Peikert trapdoors [60], which proved useful in the design of attribute-based encryption (ABE) for circuits [20, 28] and fully homomorphic signatures [43]. In particular, the homomorphic evaluation of PRF circuits was considered by Brakerski and Vaikuntanathan [28] to construct an unbounded ABE system. Boyen and Li [22] used similar ideas to build tightly secure IBE and signatures from lattice assumptions. Our constructions depart from [22] in that PRFs are also used in the schemes, and not only in the security proofs. Another difference is that [22, 28] only need PRFs with binary outputs, whereas our ABM-LTFs require a PRF with an exponentially-large range in order to prevent the adversary from predicting its output with noticeable probability.

We finally remark that merely applying the Canetti-Halevi-Katz paradigm [30] to the Boyen-Li IBE [22] does not imply tight CCA2 security in the multi-challenge setting since the proof of [22] is only tight for one identity: in a game with Q challenge ciphertexts, the best known reduction would still lose a factor Q via the standard hybrid argument.

Concurrent Work. In a concurrent and independent paper, Boyen and Li [23] proposed an $\mathsf {LWE}$-based all-but-many lossy trapdoor function. While their construction relies on a similar idea of homomorphically evaluating a PRF over GSW ciphertexts, it differs from our ABM-LTF in several aspects. First, their evaluation keys contain GSW-encrypted matrices while our scheme encrypts scalars. As a result, their security proofs have to deal with invalid tags (which are neither lossy nor efficiently invertible with a trapdoor) that do not appear in our construction. Secondly, while their ABM-LTF loses more information on its input than ours, it does not seem to enable simulation-based security. The reason is that their use of small-norm $\mathsf {LWE}$ secrets (which allows for a greater lossiness) makes it hard to embed a lattice trapdoor in lossy keys. As a result, their IND-SO-CCA2 system does not readily extend to provide SIM-SO-CCA2 security. An advantage of their scheme is that it requires only a weak PRF rather than a strong PRF. This is a real benefit as weak PRFs are much easier to design with a low-depth evaluation circuit.

2 Background

For any $q\ge 2$, we let $\mathbb {Z}_q$ denote the ring of integers with addition and multiplication modulo q. We always set q as a prime integer. If $\mathbf {x}$ is a vector over $\mathbb {R}$, then $\Vert \mathbf {x}\Vert$ denotes its Euclidean norm. If $\mathbf {M}$ is a matrix over $\mathbb {R}$, then $\Vert \mathbf {M}\Vert$ denotes its induced norm. We let $\sigma _n(\mathbf {M})$ denote the least singular value of $\mathbf {M}$, where n is the rank of $\mathbf {M}$. For a finite set S, we let U(S) denote the uniform distribution over S. If X is a random variable over a countable domain, the min-entropy of X is defined as $H_{\infty }(X) = \min _x (-\log _2 \Pr [X = x])$. If X and Y are distributions over the same domain, then $\varDelta (X,Y)$ denotes their statistical distance.

2.1 Randomness Extraction

We first recall the Leftover Hash Lemma, as it was stated in [1].

Lemma 1

([1]). Let $\mathcal {H} = \{ h : X \rightarrow Y\}_{h \in \mathcal {H}}$ be a family of universal hash functions, for countable sets X, Y. For any random variable T taking values in X, we have $\varDelta \big ( (h,h(T)),(h,U(Y)) \big ) \le \frac{1}{2} \cdot \sqrt{2^{-H_{\infty }(T)} \cdot |Y| }.$ More generally, let $(T_i)_{i \le k}$ be independent random variables with values in X, for some $k>0$. We have $\varDelta \big ( (h,(h(T_i))_{i \le k}),(h,(U(Y))^{(i)})_{i \le k}) ) \big ) \le \frac{k}{2} \cdot \sqrt{2^{-H_{\infty }(T)} \cdot |Y|}.$

A consequence of Lemma 1 was used by Agrawal et al. [1] to re-randomize matrices over $\mathbb {Z}_q$ by multiplying them with small-norm matrices.

Lemma 2

([1]). Let us assume that $m > 2n \cdot \log q$, for some prime $q>2$. For any $k \in \mathsf {poly}(n)$, if $\mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{m \times n})$, $\mathbf {B} \hookleftarrow U(\mathbb {Z}_q^{k \times n})$, $\mathbf {R} \hookleftarrow U(\{-1,1\}^{k \times m})$, the distributions $(\mathbf {A} , \mathbf {R} \cdot \mathbf {A})$ and $(\mathbf {A}, \mathbf {B})$ are within $2^{-\varOmega (n)}$ statistical distance.

2.2 Reminders on Lattices

Let $\mathbf {\Sigma } \in \mathbb {R}^{n\times n}$ be a symmetric definite positive matrix, and $\mathbf {c} \in \mathbb {R}^n$. We define the Gaussian function on $\mathbb {R}^n$ by $\rho _{\mathbf {\Sigma },\mathbf {c}}(\mathbf {x})=\exp (-\pi (\mathbf {x}-\mathbf {c})^\top \mathbf {\Sigma }^{-1} (\mathbf {x}-\mathbf {c}))$ and if $\mathbf {\Sigma }=\sigma ^2 \cdot \mathbf {I}_n$ and $\mathbf {c}=\mathbf {0}$ we denote it by $\rho _{\sigma }$. For an n-dimensional lattice $\varLambda$, we define $\eta _{\varepsilon }(\varLambda )$ as the smallest $r>0$ such that $\rho _{1/r} (\widehat{\varLambda } \setminus \mathbf {0}) \le \varepsilon$ with $\widehat{\varLambda }$ denoting the dual of $\varLambda$, for any $\varepsilon \in (0,1)$. In particular, we have $\eta _{2^{-n}}(\mathbb {Z}^n) \le O(\sqrt{n})$. We denote by $\lambda ^{\infty }_1(\varLambda )$ the infinity norm of the shortest non-zero vector of $\varLambda$.

For a matrix $\mathbf {A} \in \mathbb {Z}_q^{m \times n}$, we define $\varLambda ^\perp (\mathbf {A}) = \{\mathbf {x}\in \mathbb {Z}^m: \mathbf {x}^\top \cdot \mathbf {A} = \mathbf {0} \bmod q\}$ and $\varLambda (\mathbf {A}) = \mathbf {A} \cdot \mathbb {Z}^n + q\mathbb {Z}^m$.

Lemma 3

(Adapted from [40, Lemma 5.3]). Let $m \ge 2n$ and $q\ge 2$ prime. With probability $\ge 1-2^{-\varOmega (n)}$, we have $\eta _{2^{-n}}(\varLambda ^\perp (\mathbf {A})) \le \eta _{2^{-m}}(\varLambda ^\perp (\mathbf {A})) \le O(\sqrt{m}) \cdot q^{n/m}$ and $\lambda ^{\infty }_1(\varLambda (\mathbf {A})) \ge q^{1-n/m}/4$.

Let $\varLambda$ be a full-rank n-dimensional lattice, $\mathbf {\Sigma } \in \mathbb {R}^{n\times n}$ be a symmetric definite positive matrix, and $\mathbf {x}', \mathbf {c} \in \mathbb {R}^n$. We define the discrete Gaussian distribution of support $\varLambda +\mathbf {x}'$ and parameters $\mathbf {\Sigma }$ and $\mathbf {c}$ by $D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}(\mathbf {x}) \sim \rho _{\mathbf {\Sigma },\mathbf {c}}(\mathbf {x})$, for every $\mathbf {x} \in \varLambda +\mathbf {x}'$. For a subset $S \subseteq \varLambda + \mathbf {x}'$, we denote by $D^{S}_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}$ the distribution obtained by restricting the distribution $D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}$ to the support S. For $\mathbf {x} \in S$, we have $D^{S}_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}(\mathbf {x}) = D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}(\mathbf {x}) / p_a$, where $p_a(S) =D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}(S)$. Assuming that $1/p_a(S) =n^{O(1)}$, membership in S is efficiently testable and $D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}$ is efficiently samplable, the distribution $D^{S}_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}$ can be efficiently sampled from using rejection sampling.

We will use the following standard results on lattice Gaussians.

Lemma 4

(Adapted from [25, Lemma 2.3]). There exists a $\mathsf {ppt}$ algorithm that, given a basis $(\mathbf {b}_i)_{i\le n}$ of a full-rank lattice $\varLambda$, $\mathbf {x}', \mathbf {c} \in \mathbb {R}^n$ and $\mathbf {\Sigma } \in \mathbb {R}^{n\times n}$ symmetric definite positive such that $\varOmega (\sqrt{\log n}) \cdot \max _i \Vert \mathbf {\Sigma }^{-1/2} \cdot \mathbf {b}_i \Vert \le 1$, returns a sample from $D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}$.

Lemma 5

(Adapted from [61, Lemma 4.4]). For any n-dimensional lattice $\varLambda$, $\mathbf {x}', \mathbf {c} \in \mathbb {R}^n$ and symmetric positive definite $\mathbf {\Sigma } \in \mathbb {R}^{n\times n}$ satisfying $\sigma _n(\sqrt{\mathbf {\Sigma }}) \ge \eta _{2^{-n}}(\varLambda )$, we have $\Pr _{\mathbf {x} \hookleftarrow D_{\varLambda + \mathbf {x}', \mathbf {\Sigma }, \mathbf {c}}} [ \Vert \mathbf {x} - \mathbf {c}\Vert \ge \sqrt{n} \cdot \Vert \sqrt{\mathbf {\Sigma }}\Vert ] \le 2^{-n+2}.$

Lemma 6

(Adapted from [61, Lemma 4.4]). For any n-dimensional lattice $\varLambda$, $\mathbf {x}', \mathbf {c} \in \mathbb {R}^n$ and symmetric positive definite $\mathbf {\Sigma } \in \mathbb {R}^{n\times n}$ satisfying $\sigma _n(\sqrt{\mathbf {\Sigma }}) \ge \eta _{2^{-n}}(\varLambda )$, we have $\rho _{\mathbf {\Sigma }, \mathbf {c}}(\varLambda + \mathbf {x}') \ \in \ [1-2^{-n},1+2^{-n}] \cdot {\det (\varLambda )}/{{\det (\mathbf {\Sigma })}^{1/2}}.$

We will also use the following result on the singular values of discrete Gaussian random matrices.

Lemma 7

([2, Lemma 8]). Assume that $m \ge 2n$. Let $\mathbf {F} \in \mathbb {Z}^{m\times n}$ with each entry sampled from $D_{\mathbb {Z}, \sigma }$, for some $\sigma \ge \varOmega (\sqrt{n})$. Then with probability $\ge 1 - 2^{-\varOmega (n)}$, we have $\Vert \mathbf {F}\Vert \le O(\sqrt{m} \sigma )$ and $\sigma _n(\mathbf {F}) \ge \varOmega (\sqrt{m} \sigma )$.

2.3 The Learning with Errors Problem

We recall the Learning With Errors problem [69]. Note that we make the number of samples m explicit in our definition.

Definition 1

Let $\lambda \in \mathbb {N}$ be a security parameter and let integers $n=n(\lambda )$, $m=m(\lambda )$, $q=q(\lambda )$. Let $\chi =\chi (\lambda )$ be an efficiently samplable distribution over $\mathbb {Z}_q$. The $\mathsf {LWE}_{n,m,q,\chi }$ assumption posits that the following distance is a negligible function for any $\mathsf {ppt}$ algorithm $\mathcal {A}$:

$$\begin{aligned}&\mathbf {Adv}^{\mathcal {A},\mathsf {LWE}}_{\ell , m, q, \chi }(\lambda ) := \big | \Pr [ \mathcal {A}(1^\lambda ,\mathbf {A}, \mathbf {u} )=1 \mid \mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{n \times m}) , \mathbf {u} \hookleftarrow U(\mathbb {Z}_q^m)] \\&\qquad -\,\Pr [ \mathcal {A}(1^\lambda , \mathbf {A}, \mathbf {A} \cdot \mathbf {s} + \mathbf {e})=1 \mid \mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{m \times n}) , \mathbf {s} \hookleftarrow U(\mathbb {Z}_q^n), \mathbf {e} \hookleftarrow \chi ^m ] \big |. \end{aligned}$$

A typical choice for $\chi$ is the integer Gaussian distribution $D_{\mathbb {Z},\alpha \cdot q}$ for some parameter $\alpha \in (\sqrt{n}/q,1)$. In particular, in this case, there exist reductions from standard lattice problems to $\mathsf {LWE}$ (see [25, 69]).

In [60], Micciancio and Peikert described a trapdoor mechanism for $\mathsf {LWE}$. Their technique uses a “gadget” matrix $\mathbf {G} \in \mathbb {Z}_q^{m \times n}$ for which anyone can publicly sample short vectors $\mathbf {x} \in \mathbb {Z}^m$ such that $\mathbf {x}^\top \mathbf {G} = \mathbf {0}$. As in [60], we call $\mathbf {R} \in \mathbb {Z}^{m \times m}$ a $\mathbf {G}$-trapdoor for a matrix $\mathbf {A} \in \mathbb {Z}_q^{2m \times n}$ if $[\mathbf {R} ~|~\mathbf {I}_m] \cdot \mathbf {A} = \mathbf {G} \cdot \mathbf {H}$ for some invertible matrix $\mathbf {H} \in \mathbb {Z}_q^{n \times n}$ which is referred to as the trapdoor tag. If $\mathbf {H}=\mathbf {0}$, then $\mathbf {R}$ is called a “punctured” trapdoor for $\mathbf {A}$.

Lemma 8

([60, Sect. 5]). Assume that $m \ge 2 n \log q$. There exists a $\mathsf {ppt}$ algorithm $\mathsf {GenTrap}$ that takes as inputs matrices $\bar{\mathbf {A}} \in \mathbb {Z}_q^{m \times n}$, $\mathbf {H} \in \mathbb {Z}_q^{n \times n}$ and outputs matrices $\mathbf {R} \in \{-1,1\}^{ m \times m}$ and

$$ \mathbf {A} = \begin{bmatrix} \bar{\mathbf {A}} \\ - \mathbf {R} \bar{\mathbf {A}} + \mathbf {G} \mathbf {H} \end{bmatrix} \in \mathbb {Z}_q^{ 2m \times n} $$

such that if $\mathbf {H} \in \mathbb {Z}_q^{n \times n}$ is invertible, then $\mathbf {R}$ is a $\mathbf {G}$-trapdoor for $\mathbf {A}$ with tag $\mathbf {H}$; and if $\mathbf {H}=\mathbf {0}$, then $\mathbf {R}$ is a punctured trapdoor.

Further, in case of a $\mathbf {G}$-trapdoor, one can efficiently compute from $\mathbf {A}, \mathbf {R}$ and $\mathbf {H}$ a basis $(\mathbf {b}_i)_{i\le 2m}$ of $\varLambda ^{\perp }(\mathbf {A})$ such that $\max _i \Vert \mathbf {b}_i\Vert \le O(m^{3/2})$.

Micciancio and Peikert also showed that a $\mathbf {G}$-trapdoor for $\mathbf {A} \in \mathbb {Z}_q^{ 2m \times n}$ can be used to invert the LWE function $(\varvec{s},\varvec{e}) \mapsto \mathbf {A} \cdot \varvec{s} + \varvec{e}$, for any $\varvec{s} \in \mathbb {Z}_q^n$ and any sufficiently short $\varvec{e} \in \mathbb {Z}^{2m}$.

Lemma 9

([60, Theorem 5.4]). There exists a deterministic polynomial time algorithm $\mathsf {Invert}$ that takes as inputs matrices $\mathbf {R}\in \mathbb {Z}^{m \times m}$, $\mathbf {A}\in \mathbb {Z}_q^{2m \times n}$, $\mathbf {H} \in \mathbb {Z}_q^{n \times n}$ such that $\mathbf {R}$ is a $\mathbf {G}$-trapdoor for $\mathbf {A}$ with invertible tag $\mathbf {H}$, and a vector $\mathbf {A}\cdot \mathbf {s} + \mathbf {e}$ with $\mathbf {s} \in \mathbb {Z}_q^n$ and $\Vert \mathbf {e}\Vert \le q/ (10 \cdot \Vert \mathbf {R}\Vert )$, and outputs $\mathbf {s}$ and $\mathbf {e}$.

As showed in [20, 41], homomorphic computations can be performed on $\mathbf {G}$-trapdoors with respect to trapdoor tags $\mathbf {H}_i$ corresponding to scalars. As observed in [27], when the circuit belongs to $\mathsf {NC}^1$, it is advantageous to convert the circuit into a branching program, using Barrington’s theorem. This is interesting to allow for a polynomial modulus q but imposes a circuit depth restriction (so that the evaluation algorithms are guaranteed to run in polynomial-time).

Lemma 10

(Adapted from [20, 41]). Let $C: \{0,1\}^{\kappa } \rightarrow \{0,1\}$ be a NAND Boolean circuit of depth d. Let $\mathbf {B}_i = \mathbf {R}_i \cdot \bar{\mathbf {A}} + x_i \cdot \mathbf {G} \in \mathbb {Z}_q^{m \times n}$ with $\bar{\mathbf {A}} \in \mathbb {Z}_q^{m \times n}$, $\mathbf {R}_i \in \{-1,1\}^{ m \times m}$ and $x_i \in \{0,1\}$, for $i\le \kappa$.

• There exist deterministic algorithms $\mathsf {Eval}^{\mathsf {pub}}_{\mathsf {CCT}}$ and $\mathsf {Eval}^{\mathsf {priv}}_{\mathsf {CCT}}$ with running times $\mathsf {poly}(|C|,\kappa , m,n,\log q)$, that satisfy:

  $$ \mathsf {Eval}^{\mathsf {pub}}_{\mathsf {CCT}}(C,(\mathbf {B}_i)_i) = \mathsf {Eval}^{\mathsf {priv}}_{\mathsf {CCT}}(C,(\mathbf {R}_i)_i) \cdot \bar{\mathbf {A}} + C(x_1,\ldots ,x_{\kappa }) \cdot \mathbf {G}, $$

  and $\Vert \mathsf {Eval}^{\mathsf {priv}}_{\mathsf {CCT}}(C,(\mathbf {R}_i)_i) \Vert \le m^{O(d)}.$

• There exist deterministic algorithms $\mathsf {Eval}^{\mathsf {pub}}_{\mathsf {BP}}$ and $\mathsf {Eval}^{\mathsf {priv}}_{\mathsf {BP}}$ with running times $\mathsf {poly}(4^d,\kappa , m,n,\log q)$, that satisfy:

  $$ \mathsf {Eval}^{\mathsf {pub}}_{\mathsf {BP}}(C,(\mathbf {B}_i)_i) = \mathsf {Eval}^{\mathsf {priv}}_{\mathsf {BP}}(C,(\mathbf {R}_i)_i) \cdot \bar{\mathbf {A}} + C(x_1,\ldots ,x_{\kappa }) \cdot \mathbf {G}, $$

  and $\Vert \mathsf {Eval}^{\mathsf {priv}}_{\mathsf {BP}}(C,(\mathbf {R}_i)_i) \Vert \le 4^d \cdot O(m^{3/2}).$

Note that we impose that the $\mathsf {Eval}^{\mathsf {pub}}$ and $\mathsf {Eval}^{\mathsf {priv}}$ algorithms are deterministic, although probabilistic variants are considered in the literature. This is important in our case, as it will be used in the function evaluation algorithm of our all-but-many lossy trapdoor function family LTF function evaluation.

2.4 Lossy Trapdoor Functions

We consider a variant of the notion of Lossy Trapdoor Functions (LTF) introduced by [66], for which the function input may be sampled from a distribution that differs from the uniform distribution. In our constructions, for lossiness security, we actually allow the function evaluation algorithm to sample from a larger domain $\mathsf {Dom}^E_\lambda$ than the domain $\mathsf {Dom}^D_\lambda$ on which the inversion algorithm guaranteed to succeed. A sample over $\mathsf {Dom}^E_\lambda$ has an overwhelming probability to land in $\mathsf {Dom}^D_\lambda$ with respect to the sampling distribution.

Definition 2

For an integer $l(\lambda ) >0$, a family of l-lossy trapdoor functions $\mathsf {LTF}$ with security parameter $\lambda$, evaluation sampling domain $\mathsf {Dom}^E_\lambda$, efficiently samplable distribution $D_{{\mathsf {Dom}^E_\lambda }}$ on $\mathsf {Dom}^E_\lambda$, inversion domain $\mathsf {Dom}^D_\lambda \subseteq \mathsf {Dom}^E_\lambda$ and range $\mathsf {Rng}_\lambda$ is a tuple $(\mathsf {IGen},\mathsf {LGen},\mathsf {Eval},\mathsf {Invert})$ of $\mathsf {ppt}$ algorithms with the following functionalities:

• $\mathbf {Injective~ key~ generation}$ . $\mathsf {LTF}.\mathsf {IGen}(1^\lambda )$ outputs an evaluation key ek for an injective function together with an inversion key ik.

• $\mathbf {Lossy~ key ~generation}$ . $\mathsf {LTF}.\mathsf {LGen}(1^\lambda )$ outputs an evaluation key ek for a lossy function. In this case, there is no inversion key and we define $ik=\bot$.

• $\mathbf {Evaluation}$ . $\mathsf {LTF}.\mathsf {Eval}(ek,X)$ takes as inputs the evaluation key ek and a function input $X \in \mathsf {Dom}^E_\lambda$. It outputs an image $Y=f_{ek}(X)$.

• $\mathbf {Inversion}$ . $\mathsf {LTF}.\mathsf {Invert}(ik,Y)$ inputs the inversion key $ik \ne \bot$ and a $Y \in \mathsf {Rng}_\lambda$. It outputs the unique $X=f_{ik}^{-1}(Y)$ such that $Y=f_{ek}(X)$ (if it exists).

In addition, $\mathsf {LTF}$ has to meet the following requirements:

• $\mathbf {Inversion~ Correctness}$ . For an injective key pair $(ek,ik) \leftarrow \mathsf {LTF}.\mathsf {IGen}(1^\lambda )$, we have, except with negligible probability over (ek, ik), that for all inputs $X \in \mathsf {Dom}^D_\lambda$, $X=f_{ik}^{-1}(f_{ek}(X))$.

• $\mathbf {Eval ~Sampling ~Correctness}$ . For X sampled from $D_{{\mathsf {Dom}^E_\lambda }}$, we have $X \in \mathsf {Dom}^D_{\lambda }$ except with negligible probability.

• $\varvec{l}\mathbf {\text {-}Lossiness}$ . For $(ek,\perp ) \hookleftarrow \mathsf {LTF}.\mathsf {LGen}(1^\lambda )$ and $X \hookleftarrow D_{{\mathsf {Dom}^E_\lambda }}$, we have that $H_{\infty }( X \mid ek=\overline{ek}, f_{ek}(X)=\overline{y} ) \ge l$, for all $(\overline{ek},\overline{y})$ except a set of negligible probability.

• $\mathbf {Indistinguishability}$ . The distribution of lossy functions is computationally indistinguishable from that of injective functions, namely:

  

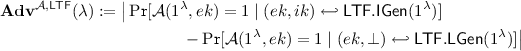
  is a negligible function for any $\mathsf {ppt}$ algorithm $\mathcal {A}$.

2.5 All-But-Many Lossy Trapdoor Functions

We consider a variant of the definition of All-But-Many Lossy Trapdoor Functions (ABM-LTF) from [49], in which the distribution over the function domain may not be the uniform one.

Definition 3

For an integer $l(\lambda ) >0$, a family of all-but-many l- lossy trapdoor functions $\mathsf {ABM}$ with security parameter $\lambda$, evaluation sampling domain $\mathsf {Dom}^E_\lambda$, efficiently samplable distribution $D_{{\mathsf {Dom}^E_\lambda }}$ on $\mathsf {Dom}^E_\lambda$, inversion domain $\mathsf {Dom}^D_\lambda \subseteq \mathsf {Dom}^E_\lambda$, and range $\mathsf {Rng}_\lambda$ consists of the following $\mathsf {ppt}$ algorithms:

• $\mathbf {Key generation}$ . $\mathsf {ABM}.\mathsf {Gen}(1^\lambda )$ outputs an evaluation key ek, an inversion key ik and a tag key tk. The evaluation key ek defines a set $\mathcal {T}=\mathcal {T}_\mathsf {c}\times \mathcal {T}_\mathsf {a}$ containing the disjoint sets of lossy tags $\mathcal {T}_\mathsf {loss}$ and injective tags $\mathcal {T}_{\mathsf {inj}}$. Each tag $t =(t_\mathsf {c},t_\mathsf {a})$ is described by a core part $t_\mathsf {c}\in \mathcal {T}_\mathsf {c}$ and an auxiliary part $t_\mathsf {a}\in \mathcal {T}_\mathsf {a}$.

• $\mathbf {Evaluation}$ . $\mathsf {ABM}.\mathsf {Eval}(ek,t,X)$ takes as inputs an evaluation key ek, a tag $t \in \mathcal {T}$ and a function input $X \in \mathsf {Dom}^E_\lambda$. It outputs an image $Y=f_{ek,t}(X)$.

• $\mathbf {Inversion}$ . $\mathsf {ABM}.\mathsf {Invert}(ik,t,Y)$ takes as inputs an inversion key ik, a tag $t \in \mathcal {T}$ and a $Y \in \mathsf {Rng}_\lambda$. It outputs the unique $X=f_{ik,t}^{-1}(Y)$ such that $Y=f_{ek,t}(X)$.

• $\mathbf {Lossy~ tag ~generation}$ . $\mathsf {ABM}.\mathsf {LTag}(tk,t_\mathsf {a})$ takes as input an auxiliary part $t_\mathsf {a}\in \mathcal {T}_\mathsf {a}$ and outputs a core part $t_\mathsf {c}$ such that $t=(t_\mathsf {c},t_\mathsf {a})$ forms a lossy tag.

In addition, $\mathsf {ABM}$ has to meet the following requirements:

• $\mathbf {Inversion ~Correctness}$ . For (ek, ik, tk) produced by $\mathsf {ABM}.\mathsf {Gen}(1^\lambda )$, we have, except with negligible probability over (ek, ik, tk), that for all injective tags $t \in \mathcal {T}_\mathsf {inj}$ and all inputs $X \in \mathsf {Dom}^D_\lambda$, that $X=f_{ik,t}^{-1}(f_{ek,t}(X))$.

• $\mathbf {Eval ~Sampling~ Correctness}$ . For X sampled from $D_{{\mathsf {Dom}^E_\lambda }}$, we have $X \in \mathsf {Dom}^D_{\lambda }$ except with negligible probability.

• $\mathbf {Lossiness}$ . For $(ek,ik,tk) \hookleftarrow \mathsf {ABM}.\mathsf {Gen}(1^\lambda )$, any $t_\mathsf {a}\in \mathcal {T}_{\mathsf {a}}$, $t_\mathsf {c}\hookleftarrow \mathsf {ABM}.\mathsf {LTag}(tk,t_\mathsf {a})$ and $X \hookleftarrow D_{{\mathsf {Dom}^E_\lambda }}$, we have that $H_{\infty }( X \mid ek=\overline{ek}, f_{ek,(t_\mathsf {c},t_\mathsf {a})}(X)=\overline{y} ) \ge l$, for all $(\overline{ek},\overline{y})$ except a set of negligible probability.

• $\mathbf {Indistinguishability}$ . Multiple lossy tags are computationally indistinguishable from random tags, namely:

  $$\begin{aligned} \mathbf {Adv}^{\mathcal {A},\mathsf {ind}}_{Q}(\lambda ) := \big | \Pr [\mathcal {A}(1^\lambda ,ek)^{\mathsf {ABM}.\mathsf {LTag}(tk,\cdot )} =1 ] - \Pr [\mathcal {A}(1^\lambda ,ek)^{\mathcal {O}_{\mathcal {T}_c}(\cdot )} =1 ] \big | \end{aligned}$$

  is negligible for any $\mathsf {ppt}$ algorithm $\mathcal {A}$, where $(ek,ik,tk) \hookleftarrow \mathsf {ABM}.\mathsf {Gen}(1^\lambda )$ and $\mathcal {O}_{\mathcal {T}_c}(\cdot )$ is an oracle that assigns a random core tag $t_\mathsf {c}\hookleftarrow U(\mathcal {T}_\mathsf {c})$ to each auxiliary tag $t_\mathsf {a}\in \mathcal {T}_{\mathsf {a}}$ (rather than a core tag that makes $t=(t_\mathsf {c},t_\mathsf {a})$ lossy). Here Q denotes the number of oracle queries made by $\mathcal {A}$.

• $\mathbf {Evasiveness}$ . Non-injective tags are computationally hard to find, even with access to an oracle outputting multiple lossy tags, namely:

  $$\begin{aligned} \mathbf {Adv}^{\mathcal {A},\mathsf {eva}}_{Q_1,Q_2} (\lambda ) := \Pr [\mathcal {A}(1^\lambda ,ek)^{\mathsf {ABM}.\mathsf {LTag}(tk,\cdot ),\mathsf {ABM}.\mathsf {IsLossy}(tk,\cdot )} \in \mathcal {T}\backslash \mathcal {T}_{\mathsf {inj}} ] \end{aligned}$$

  is negligible for legitimate adversary $\mathcal {A}$, where $(ek,ik,tk) \hookleftarrow \mathsf {ABM}.\mathsf {Gen}(1^\lambda )$ and $\mathcal {A}$ is given access to the following oracles:

  • – $\mathsf {ABM}.\mathsf {LTag}(tk,\cdot )$ which acts exactly as the lossy tag generation algorithm.

  • – $\mathsf {ABM}.\mathsf {IsLossy}(tk,\cdot )$ that takes as input a tag $t=(t_\mathsf {c},t_\mathsf {a})$ and outputs 1 if $t \in \mathcal {T}\backslash \mathcal {T}_{\mathsf {inj}}$ and otherwise outputs 0.

  We denote by $Q_1$ and $Q_2$ the number of queries to these two oracles. By “legitimate adversary”, we mean that $\mathcal {A}$ is $\mathsf {ppt}$ and never outputs a tag $t =(t_\mathsf {c},t_\mathsf {a})$ such that $t_\mathsf {c}$ was obtained by invoking the $\mathsf {ABM}.\mathsf {LTag}$ oracle on $t_\mathsf {a}$.

As pointed out in [49], the evasiveness property mirrors the notion of strong unforgeability for signature schemes. Indeed, the adversary is considered successful even if it outputs a $(t_\mathsf {c},t_\mathsf {a})$ such that $t_\mathsf {a}$ was submitted to $\mathsf {ABM}.\mathsf {LTag}(tk,\cdot )$ as long as the response $t_\mathsf {a}'$ of the latter was such that $t_\mathsf {a}' \ne t_\mathsf {a}$.

In order to simplify the tight proof of our public-key encryption scheme, we slightly modified the original definition of evasiveness in [49] by introducing a lossiness-testing oracle $\mathsf {ABM}.\mathsf {IsLossy}(tk,\cdot )$. When it comes to proving tight CCA security, it will save the reduction from having to guess which decryption query contradicts the evasiveness property of the underlying ABM-LTF.

2.6 Selective-Opening Chosen-Ciphertext Security

A public-key encryption scheme consists of a tuple of $\mathsf {ppt}$ algorithms $(\mathsf {Par}\text {-}\mathsf {Gen},$ $\mathsf {Keygen}, \mathsf {Encrypt}$,$\mathsf {Decrypt})$, where $\mathsf {Par}\text {-}\mathsf {Gen}$ takes as input a security parameter $1^\lambda$ and generates common public parameters $\varGamma$, $\mathsf {Keygen}$ takes in $\varGamma$ and outputs a key pair (SK, PK), while $\mathsf {Encrypt}$ and $\mathsf {Decrypt}$ proceed in the usual way.

As a first step, we will consider encryption schemes that provide SO security in the sense of an indistinguishability-based definition (or IND-SOA security). This notion is captured by a game where the adversary obtains $N(\lambda )$ ciphertexts, opens an arbitrary subset of these (meaning that it obtains both the plaintexts and the encryption coins) and asks that remaining ciphertexts be indistinguishable from messages that are independently re-sampled conditionally on opened ones. In the IND-SO-CCA2 scenario, this should remain true even if the adversary has a decryption oracle. A formal definition is recalled in the full paper.

A stronger notion is that of simulation-based security, which demands that an efficient simulator be able to perform about as well as the adversary without seeing neither the ciphertexts nor the public key. Formally, two experiments are required to have indistinguishable output distributions.

In the real experiment, the challenger samples $\varvec{\mathsf {Msg}}=(\mathsf {Msg}_1,\ldots ,\mathsf {Msg}_N) \leftarrow \mathcal {M}$ from the joint message distribution and picks random coins $r_1,\ldots ,r_N \leftarrow \mathcal {R}$ to compute ciphertexts $\{ \mathbf {C}_i \leftarrow \mathsf {Encrypt}(PK,\mathsf {Msg}_i,r_i) \}_{i \in [N]}$ which are given to the adversary $\mathcal {A}$. The latter responds by choosing a subset $I \subset [N]$ and gets back $\{(\mathsf {Msg}_i,r_i)\}_{i\in I}$. The adversary $\mathcal {A}$ outputs a string $out_\mathcal {A}$ and the output of the experiment is a predicate $\mathfrak {R}(\mathcal {M},\varvec{\mathsf {Msg}},out_\mathcal {A})$.

In the ideal experiment, the challenger samples $\varvec{\mathsf {Msg}}=(\mathsf {Msg}_1,\ldots ,\mathsf {Msg}_N) \leftarrow \mathcal {M}$ from the joint message distribution. Without seeing any encryptions, the simulator chooses a subset I and some state information st. After having seen the messages $\{\mathsf {Msg}_i\}_{i \in I}$ and the state information but without seeing any randomness, the simulator outputs a string $out_S$. The outcome of the ideal experiment is the predicate $\mathfrak {R}(\mathcal {M},\varvec{\mathsf {Msg}},out_S)$. As in [36, 54], we allow the adversary to choose the message distribution $\mathcal {M}$. While this distribution should be efficiently samplable, it is not required to support efficient conditional re-sampling.

Definition 4

([36, 54]). A PKE scheme $(\mathsf {Par}\text {-}\mathsf {Gen},\mathsf {Keygen},\mathsf {Encrypt}, \mathsf {Decrypt})$ provides simulation-based selective opening (SIM-SO-CPA) security if, for any $\mathsf {ppt}$ function $\mathfrak {R}$ and any $\mathsf {ppt}$ adversary $\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1,\mathcal {A}_2)$ in the real experiment $\mathbf {Exp}^{\mathsf {cpa}\text {-}\mathsf {so}\text {-}\mathsf {real}}(\lambda )$, there is an efficient simulator $S = (S_0,S_1,S_2)$ in the ideal experiment $\mathbf {Exp}^{\mathsf {so}\text {-}\mathsf {ideal}}(\lambda )$ s.t. $| \Pr [ \mathbf {Exp}^{\mathsf {cpa}\text {-}\mathsf {so}\text {-}\mathsf {real}}(\lambda ) = 1 ] - \Pr [ \mathbf {Exp}^{\mathsf {so}\text {-}\mathsf {ideal}} (\lambda ) = 1 ] |$ is negligible, where the two experiments are defined as follows:

As usual, the adversarially-chosen message distribution $\mathcal {M}$ is efficiently samplable and encoded as a polynomial-size circuit.

The notion of simulation-based chosen-ciphertext (SIM-SO-CCA) security is defined analogously. The only difference is in the real experiment $\mathbf {Exp}^{\mathsf {cca}\text {-}\mathsf {so}\text {-}\mathsf {real}}$, which is obtained from $\mathbf {Exp}^{\mathsf {cpa}\text {-}\mathsf {so}\text {-}\mathsf {real}}$ by granting the adversary access to a decryption oracle at all stages. Of course, the adversary is disallowed to query the decryption of any ciphertext in the set $\{\mathbf {C}_i\}_{i \in [N]}$ of challenge ciphertexts.

It is known [11] that SIM-SO-CPA security can be achieved from lossy encryption schemes [16] when there exists an efficient $\mathsf {Opener}$ algorithm which, using the lossy secret key, can explain a lossy ciphertext $\mathbf {C}$ as an encryption of any given plaintext. As observed in [16, 54], this $\mathsf {Opener}$ algorithm can use the initial coins used in the generation of $\mathbf {C}$ for this purpose. This property (for which a formal definition is recalled in the full version of the paper) is called efficient weak opening.

3 An All-But-Many Lossy Trapdoor Function from $\mathsf {LWE}$

As a warm-up, we first describe a variant of the lossy trapdoor function suggested by Bellare et al. [12, Sect. 5.2] that is better suited to our needs. We then extend this LWE-based LTF into an ABM-LTF in Sect. 3.2.

3.1 An $\mathsf {LWE}$-Based Lossy Trapdoor Function

All algorithms use a prime modulus $q > 2$, integers $n \in \mathsf {poly}(\lambda )$, $m \ge 2 n \log q$ and $\ell >0$, an $\mathsf {LWE}$ noise distribution $\chi$, and parameters $\sigma _x , \sigma _e, \gamma _x, \gamma _e >0$. The function evaluation sampling domain $\mathsf {Dom}^E_\lambda = \mathsf {Dom}^E_x \times \mathsf {Dom}^E_e$ where $\mathsf {Dom}^E_x$ (resp. $\mathsf {Dom}^E_e$) is the set of $\mathbf {x}$ (resp. $\mathbf {e}$) in $\mathbb {Z}^n$ (resp. $\mathbb {Z}^{2m}$) with $\Vert \varvec{x}\Vert \le \gamma _x \cdot \sqrt{n} \cdot \sigma _x$ (resp. $\Vert \varvec{e}\Vert \le \gamma _e \sqrt{2m} \cdot \sigma _e$). Its inversion domain is $\mathsf {Dom}^D_\lambda = \mathsf {Dom}^D_x \times \mathsf {Dom}^D_e$, where $\mathsf {Dom}^D_x$ (resp. $\mathsf {Dom}^D_e$) is the set of $\mathbf {x}$ (resp. $\mathbf {e}$) in $\mathbb {Z}^n$ (resp. $\mathbb {Z}^{2m}$) with $\Vert \varvec{x}\Vert \le \sqrt{n} \cdot \sigma _x$ (resp. $\Vert \varvec{e}\Vert \le \sqrt{2m} \cdot \sigma _e$) and its range is $\mathsf {Rng}_\lambda = \mathbb {Z}_q^{ 2m}$. The function inputs are sampled from the distribution $D_{{\mathsf {Dom}^E_\lambda }}= D^{\mathsf {Dom}^E_x}_{\mathbb {Z}^n,\sigma _x} \times D^{\mathsf {Dom}^E_e}_{\mathbb {Z}^{ 2m},\sigma _e}$.

• $\mathbf {Injective~ key~ generation}$ . $\mathsf {LTF}.\mathsf {IGen}(1^\lambda )$ samples $\bar{\mathbf {A}} \hookleftarrow U(\mathbb {Z}_q^{m \times n})$ and runs $(\mathbf {A},\mathbf {R}) \hookleftarrow \mathsf {GenTrap}(\bar{\mathbf {A}},\mathbf {I}_n)$ to obtain $\mathbf {A} \in \mathbb {Z}_q^{ 2m \times n}$ together with a $\mathbf {G}$-trapdoor $\mathbf {R} \in \{-1,1\}^{m \times m}$. It outputs $ek:=\mathbf {A}$ and $ik:=\mathbf {R}$.

• $\mathbf {Lossy~ key ~generation}$ . $\mathsf {LTF}.\mathsf {LGen}(1^\lambda )$ generates $\mathbf {A} \in \mathbb {Z}_q^{ 2m \times n}$ as a matrix of the form $\mathbf {A} = \mathbf {B} \cdot \mathbf {C} + \mathbf {F}$ with $\mathbf {B} \hookleftarrow U(\mathbb {Z}_q^{ 2m \times \ell })$, $\mathbf {C} \hookleftarrow U(\mathbb {Z}_q^{\ell \times n})$ and $\mathbf {F} \hookleftarrow \chi ^{ 2m \times n}$. It outputs $ek:= \mathbf {A}$ and $ik:=\perp$.

• $\mathbf {Evaluation}$ . $\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e}))$ takes as input a domain element $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}^E_\lambda$ and maps it to $\mathbf {y} = \mathbf {A} \cdot \mathbf {x} + \mathbf {e} \in \mathbb {Z}_q^{ 2m}$.

• $\mathbf {Inversion}$ . $\mathsf {LTF}.\mathsf {Invert}(ik,\mathbf {y})$ inputs a vector $\mathbf {y} \in \mathbb {Z}_q^{ 2m}$, uses the $\mathbf {G}$-trapdoor $ik= \mathbf {R}$ of $\mathbf {A}$ to find the unique $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}^D_\lambda$ such that $\mathbf {y} = \mathbf {A} \cdot \mathbf {x} + \mathbf {e}$. This is done by applying the $\mathsf {LWE}$ inversion algorithm from Lemma 9.

Note that the construction differs from the lossy function of [12] in two ways. First, in [12], the considered distribution over the function domain is uniform over a parallelepiped. We instead consider a discrete Gaussian distribution. Second, in [12], the matrix $\mathbf {C}$ is chosen as a small-norm integer matrix sampled from the $\mathsf {LWE}$ noise distribution. We instead sample it uniformly. Both modifications are motivated by our application to SO-CCA security. Indeed, in the security proof, we will generate $\mathbf {C}$ along with a lattice trapdoor (using $\mathsf {GenTrap}$), which we will use to simulate the function domain distribution conditioned on an image value.

We first study the conditional distribution of the pair $(\mathbf {x}, \mathbf {e})$ given its image under a lossy function. This will be used to quantify the lossiness of the LTF.

Lemma 11

Let $\mathbf {C} \in \mathbb {Z}_q^{\ell \times n}$ and $\mathbf {F} \in \mathbb {Z}^{2m \times n}$. Sample $(\mathbf {x}, \mathbf {e}) \hookleftarrow D^{\mathsf {Dom}_x}_{\mathbb {Z}^n,\sigma _x} \times D^{\mathsf {Dom}_e}_{\mathbb {Z}^{ 2m},\sigma _e}$ and define $(\mathbf {u},\mathbf {f}) = (\mathbf {C}\cdot \mathbf {x}, \mathbf {F} \cdot \mathbf {x} + \mathbf {e}) \in \mathbb {Z}_q^n \times \mathbb {Z}^{2m}$. Note that $\mathbf {e}$ is fully determined by $\mathbf {x}, \mathbf {u}$ and $\mathbf {f}$. Further, the conditional distribution of $\mathbf {x}$ given $(\mathbf {u},\mathbf {f})$ is $D^{S_{\mathbf {F},\mathbf {u},\mathbf {f}}}_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$, with support

$$ S_{\mathbf {F},\mathbf {u},\mathbf {f}} = \left\{ \bar{\mathbf {x}} \in \varLambda ^{\perp }(\mathbf {C}^\top )+\mathbf {x}': \bar{\mathbf {x}} \in \mathsf {Dom}_x,~ \mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}} \in \mathsf {Dom}_e \right\} , $$

where $\mathbf {x}'$ is any solution to $\mathbf {C} \cdot \mathbf {x}' = \mathbf {u}$ and:

$$ \mathbf {\Sigma } = \sigma _x^2 \cdot \sigma _e^2 \cdot (\sigma _x^2 \cdot \mathbf {F}^\top \cdot \mathbf {F} + \sigma _e^2 \cdot \mathbf {I}_n)^{-1}, \ \ \mathbf {c} = \sigma _x^2 \cdot (\sigma _x^2\mathbf {F}^\top \cdot \mathbf {F} + \sigma _e^2 \cdot \mathbf {I}_n)^{-1} \cdot \mathbf {F}^\top \cdot \mathbf {f}. $$

Proof

We first remark that the support of $\mathbf {x}| ( \mathbf {u},\mathbf {f})$ is $S_{\mathbf {F},\mathbf {u},\mathbf {f}}$, since the set of solutions ${\bar{\mathbf {x}}} \in \mathbb {Z}^n$ to $\mathbf {u} = \mathbf {C}\cdot \mathbf {x} \in \mathbb {Z}_q^{\ell }$ is $\varLambda ^{\perp }(\mathbf {C}^\top )+\mathbf {x}'$ and each such $\bar{\mathbf {x}}$ has a non-zero conditional probability if and only if the corresponding $\bar{\mathbf {e}}= \mathbf {f} - \mathbf {F} \cdot \mathbf {x}$ is in $\mathsf {Dom}_e$. Now, for $\bar{\mathbf {x}} \in \mathbb {Z}^n$ in the support $S_{\mathbf {F},\mathbf {u},\mathbf {f}}$, we have

$$\begin{aligned} \Pr [ \mathbf {x} = \bar{\mathbf {x}} | ( \mathbf {u},\mathbf {f})]\sim & {} D_{\mathbb {Z}^n,\sigma _x}(\bar{\mathbf {x}}) \cdot D_{\mathbb {Z}^{ 2m}, \sigma _e}( \mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}} ) \\\sim & {} \exp \left( -\pi \left( \frac{ \Vert \bar{\mathbf {x}}\Vert ^2}{\sigma _x^2} + \frac{\Vert \mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}}\Vert ^2}{\sigma _e^2}\right) \right) \\\sim & {} \exp \left( -\pi \left( (\bar{\mathbf {x}}-\mathbf {c})^\top \cdot \mathbf {\Sigma }^{-1} \cdot (\bar{\mathbf {x}}-\mathbf {c}) \right) \right) . \end{aligned}$$

The last equality follows from expanding the norms and collecting terms.    $\square$

We now formally state for which parameters we can prove that the scheme above is an LTF. The second part of the theorem will be useful for our SO-CCA encryption application.

Theorem 1

Let $\chi =D_{\mathbb {Z},\beta /(2\sqrt{\lambda })}$ for some $\beta >0$. Let us assume that $\ell \ge \lambda$, $n = \varOmega (\ell \log q)$ and $m\ge 2n\log q$, $\gamma _x \ge 3\sqrt{m/n}$ and $\gamma _e \ge 3$. Assume further that $\sigma _x \ge \varOmega (n)$, $\sigma _e \ge \varOmega (\sqrt{m n} \cdot \beta \cdot \sigma _x)$ and $\sigma _e \le O(q/m^{3/2})$. Then, under the $\mathsf {LWE}_{\ell , 2m,q,\chi }$ hardness assumption, the above construction is an l-lossy LTF with $l \ge n \log \sigma _x -2 - \ell \log q > \varOmega (n \log n)$. Further, any $\mathsf {ppt}$ indistinguishability adversary $\mathcal {A}$ implies an $\mathsf {LWE}$ distinguisher $\mathcal {D}$ with comparable running time such that

$$ \mathbf {Adv}^{\mathcal {A},\mathsf {LTF}}(\lambda ) \le n \cdot \mathbf {Adv}_{\ell , 2m,q,\chi }^{\mathcal {D}, \mathsf {LWE}}(\lambda ) . $$

Moreover, there exists a $\mathsf {ppt}$ sampling algorithm, that given $(\mathbf {B},\mathbf {C},\mathbf {F})$ generated by $\mathsf {LTF}.\mathsf {LGen}(1^\lambda )$, a trapdoor basis $(\varvec{b}_i)_{i\le n}$ for $\varLambda ^{\perp }(\mathbf {C}^\top )$ such that $\max _i \Vert \varvec{b}_i\Vert \le \sigma _x \sigma _e / (\varOmega (\log n) \cdot \sqrt{2mn \beta ^2 \sigma _x^2+ \sigma _e^2})$ and a function output $\varvec{y}=\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e}))$ for an input $(\mathbf {x}, \mathbf {e}) \hookleftarrow D^{\mathsf {Dom}^E_x}_{\mathbb {Z}^n,\sigma _x} \times D^{\mathsf {Dom}^E_e}_{\mathbb {Z}^{ 2m},\sigma _e}$, outputs, with probability $\ge 1-2^{-\varOmega (\lambda )}$ over ek and $(\mathbf {x}, \mathbf {e})$, an independent sample $(\bar{\mathbf {x}},\bar{\mathbf {e}})$ from the conditional distribution of $(\mathbf {x}, \mathbf {e})$ conditioned on $\varvec{y}=\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e}))$.

Proof

First, the construction is correct. Indeed, by Lemmas 4 and 5, if $\sigma _x \ge \varOmega (\sqrt{m})$ and $\sigma _e \ge \varOmega (\sqrt{m})$, the distribution $D_{\mathbb {Z}^n,\sigma _x} \times D_{\mathbb {Z}^{ 2m},\sigma _e}$ is efficiently samplable, and a sample from it belongs to $\mathsf {Dom}^{E}_\lambda$ with probability $\ge 1-2^{-\varOmega (\lambda )}$, so $D_{{\mathsf {Dom}^E_\lambda }}$ is efficiently samplable. For inversion correctness, we consider $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}^D_\lambda$, and set $\mathbf {y} = \mathbf {A}\cdot \mathbf {x} + \mathbf {e}$. By Lemma 9, we can recover $(\mathbf {x},\mathbf {e})$ from $\mathbf {y}$ using the $\mathbf {G}$-trapdoor $\mathbf {R}$ of $\mathbf {A}$ if $\Vert \mathbf {e}\Vert \le q/(10\cdot \Vert \mathbf {R}\Vert )$. The fact that $\Vert \mathbf {R}\Vert \le m$ and the parameter choices guarantee this.

The lossy and injective modes are computationally indistinguishable under the $\mathsf {LWE}_{\ell ,2m,q,\chi }$ assumption. A standard hybrid argument over the columns of $\mathbf {A} \in \mathbb {Z}_q^{2m \times n}$ provides the inequality between the respective success advantages.

We now focus on the lossiness property. Note that Lemma 11 describes the conditional distribution of $(\mathbf {x},\mathbf {e})$ conditioned on $(\mathbf {C}\cdot \mathbf {x}, \mathbf {F} \cdot \mathbf {x} + \mathbf {e})$. We claim that, except with probability $\le 2^{-\varOmega (\lambda )}$ over ek generated by $\mathsf {LTF}.\mathsf {LGen}(1^\lambda )$, this is also the distribution of  $(\mathbf {x},\mathbf {e})$ conditioned on $\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e}))$. Indeed, $\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e})) = \mathbf {B} \cdot \mathbf {C}\cdot \mathbf {x} + \mathbf {F} \cdot \mathbf {x} + \mathbf {e} \in \mathbb {Z}_q^{2m}$ uniquely determines $\mathbf {u} = \mathbf {C}\cdot \mathbf {x} \in \mathbb {Z}_q^{\ell }$ and $\mathbf {f} = \mathbf {F} \cdot \mathbf {x} + \mathbf {e} \in \mathsf {Dom}_e$ if $\Vert \mathbf {f}\Vert _{\infty } < \lambda ^{\infty }_1(\varLambda (\mathbf {B}))/2$ for all $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}^E$. The latter condition is satisfied except with probability $\le 2^{-\varOmega (\lambda )}$ over the choice of ek. This is because $\Vert \mathbf {f}\Vert _{\infty } \le \sqrt{2m} \cdot \beta \sqrt{n} \sigma _x + \sqrt{2m} \sigma _x \le 2\sqrt{2m} \cdot \sigma _e < q/8$ except with probability $2^{-\varOmega (\lambda )}$ over the choice of $\mathbf {F}$, and $\lambda ^{\infty }_1(\varLambda (\mathbf {B}))/2 \ge q/4$ with probability $\le 2^{-\varOmega (\lambda )}$ over the choice of $\mathbf {B}$, by Lemma 3.

We now show that the conditional distribution $D^{S_{\mathbf {F},\mathbf {u},\mathbf {f}}}_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$ given by Lemma 11 for $\mathbf {x}$ conditioned on $\mathsf {LTF}.\mathsf {Eval}(ek,(\mathbf {x},\mathbf {e}))$ has min-entropy at least l and is efficiently samplable. For every $\bar{\mathbf {x}} \in S_{\mathbf {F},\mathbf {u},\mathbf {f}}$, we have

$$ D^{S_{\mathbf {F},\mathbf {u},\mathbf {f}}}_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}(\bar{\mathbf {x}}) = \frac{1}{p_a} D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}(\bar{\mathbf {x}}), \ \ p_a = D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}(S_{\mathbf {F},\mathbf {u},\mathbf {f}}). $$

For min-entropy, we observe that, by Lemma 6, the point with highest probability in $D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$ has probability $\le 2\det (\varLambda ^\perp (\mathbf {C}^\top )/ \sqrt{\det (\mathbf {\Sigma })}$ . We can apply Lemma 6 because $\sigma _n(\sqrt{\mathbf {\Sigma }})\ge \eta _{2^{-n}}(\varLambda ^{\perp }(\mathbf {C}^\top ))$ with overwhelming probability. Indeed, thanks to assumption on $\chi$, we have $\Vert \mathbf {F}^\top \cdot \mathbf {F} \Vert \le 2mn \beta ^2$ with probability $\ge 1 - 2^{-\varOmega (\lambda )}$. When this inequality holds, we have

$$\sigma _n(\sqrt{\mathbf {\Sigma }}) \ge \sigma _x \sigma _e / \sqrt{2mn \beta ^2 \sigma _x^2+ \sigma _e^2} .$$

Further, by Lemma 3, we have $\eta _{2^{-n}}(\varLambda ^\perp (\mathbf {C}^\top )) \le O(\sqrt{n} q^{\ell /n})$ with probability $\ge 1- 2^{-\varOmega (\ell )}$. Hence the assumption of Lemma 6 holds, thanks to our parameter choices. Overall, we obtain that the scheme is l-lossy for

$$ l \ge \log \sqrt{\det (\mathbf {\Sigma })} - \log \det (\varLambda ^\perp (\mathbf {C}^\top )) -1 - \log (1/p_a). $$

By calculations similar to those above, we have that $\sqrt{\det \mathbf {\Sigma }} \le \sigma _x^n$. Further, matrix $\mathbf {C}$ has rank $\ell$ with probability $\ge 1 - 2^{-\varOmega (\ell )}$, and, when this is the case, we have $\det (\varLambda ^\perp (\mathbf {C}^\top )) = q^\ell$. We obtain $l \ge n \log \sigma _x - 1 - \ell \log q - \log (1/p_a)$.

To complete the lossiness proof, we show that $p_a \ge 1-2^{-\varOmega (\lambda )}$ so that $\log (1/p_a) \le 1$, except with probability $\le 2^{-\varOmega (\lambda )}$ over $(\mathbf {F},\mathbf {C}$,$\mathbf {x}$,$\mathbf {e}$). For this, we have by a union bound that $p_a \ge 1-(p_x+p_e)$, where $p_x$ is the probability that a sample $\bar{\mathbf {x}}$ from $D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$ lands outside $\mathsf {Dom}^E_x$ (i.e., $\Vert \bar{\mathbf {x}}\Vert > \gamma _x \cdot \sqrt{n} \cdot \sigma _x$), and $p_e$ is the probability that a sample $\bar{\mathbf {x}}$ from $D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$ is such that $\mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}}$ lands outside $\mathsf {Dom}^E_e$ (i.e., $\Vert \mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}}\Vert > \gamma _e \cdot \sqrt{2m} \cdot \sigma _e$).

In order to bound $p_x$, we observe that it is at most

$$p'_x = \mathop {\Pr }\limits _{ \bar{\mathbf {x}} \hookleftarrow D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}} [\Vert \bar{\mathbf {x}}-\mathbf {c}\Vert > \Vert \sqrt{\mathbf {\Sigma }}\Vert \cdot \sqrt{n} ]$$

if $\gamma _x \cdot \sqrt{n} \cdot \sigma _x \ge \Vert \mathbf {c}\Vert + \Vert \sqrt{\mathbf {\Sigma }}\Vert \cdot \sqrt{n}$. Now, using that $\Vert \mathbf {F}\Vert \le \sqrt{2mn} \cdot \beta , \Vert \mathbf {x}\Vert \le \sqrt{n} \cdot \sigma _x$ and $\Vert \mathbf {e}\Vert \le \sqrt{2m} \cdot \sigma _e$ except with probability $2^{-\varOmega (\lambda )}$, by Lemma 5, we get with the same probability that $\Vert \mathbf {c}\Vert \le (\sigma _x/\sigma _e)^2 \cdot \sqrt{2mn}\beta \cdot (\sqrt{2mn} \cdot \beta \cdot \sigma _x \cdot \sqrt{n} + \sigma _e \cdot \sqrt{2m})$. Furthermore, using $\Vert \sqrt{\mathbf {\Sigma }}\Vert \le \sigma _x/\sigma _e$, we have that the condition $\gamma _x \cdot \sqrt{n} \cdot \sigma _x \ge \Vert \mathbf {c}\Vert + \Vert \sqrt{\mathbf {\Sigma }}\Vert \cdot \sqrt{n}$ is satisfied by our choice of parameters. Also, as shown above, we have $\sigma _n(\sqrt{\mathbf {\Sigma }})\ge \eta _{2^{-n}}(\varLambda ^{\perp }(\mathbf {C}^\top ))$ with overwhelming probability, so that we can apply Lemma 5 to conclude that $p_x \le p'_x \le 2^{-n+2}$ with probability $\ge 1 - 2^{-\varOmega (\lambda )}$.

To bound $p_e$, we follow a similar computation as for $p_x$. Namely, we first observe that, if $\bar{\mathbf {x}}$ is sampled from $D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$, then $\bar{\mathbf {e}} = \mathbf {f} - \mathbf {F} \cdot \bar{\mathbf {x}}$ is distributed as $D_{\mathbf {F} \cdot \varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {f} - \mathbf {F} \cdot \mathbf {x}', \sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top },\mathbf {f}-\mathbf {F} \cdot \mathbf {c}}$. Therefore, the probability $p_e$ is at most the probability $p'_e$ that a sample $\bar{\mathbf {e}}$ from $D_{\mathbf {F} \cdot \varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {f} - \mathbf {F} \cdot \mathbf {x}', \sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top },\mathbf {f}-\mathbf {F} \cdot \mathbf {c}}$ satisfies $\Vert \bar{\mathbf {e}}-(\mathbf {f} - \mathbf {F} \cdot \mathbf {c})\Vert > \Vert \sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top }\Vert \cdot \sqrt{2m}$, assuming that the condition

$$\begin{aligned} \gamma _e \cdot \sqrt{2m} \cdot \sigma _e \ge \Vert \mathbf {f} - \mathbf {F} \cdot \mathbf {c}\Vert + \Vert \sqrt{\mathbf {F} \mathbf {\Sigma } \mathbf {F}^\top }\Vert \cdot \sqrt{2m}, \end{aligned}$$

(1)

is satisfied. Now, using $\Vert \mathbf {f}-\mathbf {F} \cdot \mathbf {c}\Vert \le \Vert \mathbf {f}\Vert + \Vert \mathbf {F}\Vert \cdot \Vert \mathbf {c}\Vert$ and the above bounds on $\Vert \mathbf {F}\Vert$, $\Vert \mathbf {f}\Vert$ and $\Vert \mathbf {c}\Vert$ and our choice of parameters, we have that condition (1) is satisfied with overwhelming probability. To apply Lemma 5 to bound $p'_e$, we also need to show that $\sigma _n(\sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top }) \ge \eta _{2^{-n}}(\mathbf {F} \cdot \varLambda ^{\perp }(\mathbf {C}^\top ))$. Now, note that

$$\sigma _n(\sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top }) = \sigma _x \cdot \sigma _e / \sqrt{\sigma _x^2+\sigma _e^2/\sigma _n(\mathbf {F})^2}.$$

By Lemma 7, we have $\sigma _n(\mathbf {F}) \ge \varOmega (\sqrt{m} \cdot \beta )$ with overwhelming probability. We conclude that $\sigma _n(\sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top }) \ge \varOmega (\sigma _x \cdot \sqrt{m} \cdot \beta )$. On the other hand, we have $\eta _{2^{-n}}(\mathbf {F} \cdot \varLambda ^{\perp }(\mathbf {C}^\top )) \le \Vert \mathbf {F}\Vert \cdot \eta _{2^{-n}}(\varLambda ^{\perp }(\mathbf {C}^\top ))=O(\Vert \mathbf {F}\Vert \cdot \sqrt{n}) \le O(\beta \cdot \sqrt{m} \cdot n )$ with overwhelming probability, also by Lemma 7. For this reason, the condition $\sigma _n(\sqrt{\mathbf {F}\mathbf {\Sigma }\mathbf {F}^\top }) \ge \eta _{2^{-n}}(\mathbf {F} \cdot \varLambda ^{\perp }(\mathbf {C}^\top ))$ holds with with the same probability thanks to our choice of parameters. We can thus apply Lemma 5 to conclude that $p_e \le p'_e \le 2^{-n+2}$ with overwhelming probability.

Overall, we have that $p_a \ge 1 - (p_x+p_e) \ge 1-2^{-\varOmega (\lambda )}$ which completes the proof of lossiness. This also immediately implies that the conditional distribution $D^{S_{\mathbf {F},\mathbf {u},\mathbf {f}}}_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$ is efficiently samplable by rejection sampling, given an efficient sampler for $D_{\varLambda ^{\perp }(\mathbf {C}^\top ) + \mathbf {x}' , \sqrt{\mathbf {\Sigma }}, \mathbf {c}}$. The latter sampler can be implemented with a $\mathsf {ppt}$ algorithm by Lemma 4 and the fact that $\max _i \Vert \varvec{b}_i\Vert < \sigma _n(\mathbf {\Sigma })$ with overwhelming probability by the bound on $\sigma _n(\sqrt{\mathbf {\Sigma }})$.    $\square$

3.2 An All-But-Many Lossy Trapdoor Function from $\mathsf {LWE}$

Parameters and domains are defined as in Sect. 3.1.

• $\mathbf {Key~ generation}$ . $\mathsf {ABM}.\mathsf {Gen}(1^\lambda )$ conducts the following steps.

  • 1. For parameters $n, \ell , {m}, \gamma , \chi$, generate $\bar{\mathbf {A}} \in \mathbb {Z}_q^{m \times n}$ as $\bar{\mathbf {A}} = \mathbf {B}\cdot \mathbf {C} + \mathbf {F}$ with $\mathbf {B}\hookleftarrow U(\mathbb {Z}_q^{m \times \ell })$, $\mathbf {C} \hookleftarrow U(\mathbb {Z}_q^{\ell \times n})$ and $\mathbf {F} \hookleftarrow \chi ^{m \times n}$.

  • 2. Choose a PRF family $\mathsf {PRF}: \{0,1\}^\lambda \times \{0,1\}^k \rightarrow \{0,1\}^\lambda$ with input length $k=k(\lambda )$ and key length $\lambda$. Choose a seed $K \hookleftarrow U( \{0,1\}^\lambda )$ for $\mathsf {PRF}$.

  • 3. Sample matrices $\mathbf {R}_1,\ldots , \mathbf {R}_{\lambda } \hookleftarrow U(\{-1,1\}^{ {m} \times {m}})$ and compute

    $$ \mathbf {B}_i = \mathbf {R}_i \cdot {\bar{\mathbf {A}}} + K[i] \cdot \mathbf {G} ~\in \mathbb {Z}_q^{ {m} \times n} \qquad \qquad \forall i \le \lambda . $$

  • 4. Output the evaluation key ek, the inversion key ik and the lossy tag generation key tk, which consist of

    $$\begin{aligned} ek := \Bigl ( {\bar{\mathbf {A}}}, (\mathbf {B}_i)_{i \le \lambda } \Bigr ) , \qquad ik := \bigl ( ( \mathbf {R}_i )_{i \le \lambda } , K \bigr ) , \qquad tk := K. \quad ~~~ \end{aligned}$$

    (2)

  A tag $t=(t_\mathsf {c},t_\mathsf {a}) \in \{0,1\}^\lambda \times \{0,1\}^k$ will be injective whenever $t_\mathsf {c}\ne \mathsf {PRF}(K,t_\mathsf {a})$.

• $\mathbf {Lossy ~tag~ generation}$ . $\mathsf {ABM}.\mathsf {LTag}(tk,t_\mathsf {a})$ takes as input an auxiliary tag component $t_\mathsf {a}\in \{0,1\}^k$ and uses $tk=K$ to compute and output$t_\mathsf {c}= \mathsf {PRF}(K,t_\mathsf {a})$.

• $\mathbf {Evaluation}$ . $\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$ takes in the function input $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}_\lambda ^E$, the tag $t =(t_\mathsf {c},t_\mathsf {a}) \in \{0,1\}^\lambda \times \{0,1\}^k$ and proceeds as follows.

  • 1. For each $j \le \lambda$, let $C_{\mathsf {PRF},j} (t_\mathsf {a}) : \{0,1\}^\lambda \rightarrow \{0,1\}$ be the NAND Boolean circuit, where $t_\mathsf {a}\in \{0,1\}^k$ is hard-wired, which evaluates the j-th bit of $\mathsf {PRF}(\widetilde{K},t_\mathsf {a}) \in \{0,1\}^\lambda$ for any $\widetilde{K} \in \{0,1\}^\lambda$. Run the public evaluation algorithm of Lemma 10 to obtain³ $\mathbf {B}_{\mathsf {PRF},j} \leftarrow \mathsf {Eval}^{\mathsf {pub}}(C_{\mathsf {PRF},j} (t_{\mathsf {a}}), (\mathbf {B}_i)_{i \le \lambda } ).$

  • 2. Define the matrix

    $$ \mathbf {A}_t = \begin{bmatrix} {\bar{\mathbf {A}}} \\ \hline \mathop {\sum }\nolimits _{j\le \lambda } \big ( (-1)^{t_\mathsf {c}[j]} \cdot \mathbf {B}_{\mathsf {PRF},j} + t_\mathsf {c}[j] \cdot \mathbf {G} \big ) \end{bmatrix} \in \mathbb {Z}_q^{ 2 {m} \times n}, $$

    and compute the output $\mathbf {y} = \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e} ~ \in \mathbb {Z}_q^{ 2{m}}.$

• $\mathbf {Inversion}$ . $\mathsf {ABM}.\mathsf {Invert}(ik,t,\mathbf {y})$ inputs the inversion key $ik := \big ( (\mathbf {R}_i )_{i\le \lambda } , K \big )$, the tag $t =(t_\mathsf {c},t_\mathsf {a}) \in \{0,1\}^\lambda \times \{0,1\}^k$ and $\mathbf {y} \in \mathsf {Rng}_\lambda$, and proceeds as follows.

  • 1. Return $\perp$ if $t_\mathsf {c}= \mathsf {PRF}(K,t_\mathsf {a})$.

  • 2. Otherwise, for each $j \le \lambda$, run the private evaluation algorithm from Lemma 10 to obtain $\mathbf {R}_{\mathsf {PRF},j} \leftarrow \mathsf {Eval}^{\mathsf {priv}}(C_{\mathsf {PRF},j} (t_{\mathsf {a}}),(\mathbf {R}_i)_{i \le \lambda } )$ and compute the (small-norm) matrix $\mathbf {R}_{t} = \sum _{j\le \lambda } (-1)^{t_\mathsf {c}[j]} \cdot \mathbf {R}_{\mathsf {PRF},j} ~ \in \mathbb {Z}^{m \times m}.$

  • 3. Let $h_t$ denote the Hamming distance between $t_\mathsf {c}$ and $\mathsf {PRF}(K,t_\mathsf {a})$. Use the $\mathbf {G}$-trapdoor $\mathbf {R}_{t}$ of $\mathbf {A}_t$ with tag $h_t$ to find the unique $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}_\lambda ^D$ such that $\mathbf {y} = \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$. This is done by applying the $\mathsf {LWE}$ inversion algorithm of Lemma 9.

All algorithms involved run in polynomial-time, if one uses $\mathsf {Eval}^{\mathsf {pub}}_\mathsf {CCT}$ and $\mathsf {Eval}^{\mathsf {priv}}_\mathsf {CCT}$ from Lemma 10. If the circuits $C_{\mathsf {PRF},j}(t_\mathsf {a})$ (having the PRF key as input, and the PRF input hardwired) have logarithmic depth $d \le O(\log \lambda )$, then it is preferable to use $\mathsf {Eval}^{\mathsf {pub}}_\mathsf {BP}$ and $\mathsf {Eval}^{\mathsf {priv}}_\mathsf {BP}$ instead. Indeed, under this small-depth assumption, these algorithms still run in polynomial-time, and have the advantage of leading to smaller $\mathbf {R}_t$’s. This eventually allows one to set q as a polynomial function of $\lambda$. In the rest of this section, we choose these variants of $\mathsf {Eval}^{\mathsf {pub}}$ and $\mathsf {Eval}^{\mathsf {priv}}$. The results can be readily adapted to the other option.

Theorem 2

Let $\chi =D_{\mathbb {Z},\beta /(2\sqrt{\lambda })}$ for some $\beta >0$. Assume that $\mathsf {PRF}$ has depth $d=O(\log \lambda )$ when the circuit input is the key and the PRF input is hard-coded in the circuit. Assume that $\ell \ge \lambda$, $n = \varOmega (\ell \log q)$ and $m\ge 2n\log q$, $\gamma _x \ge 3\sqrt{m/n}$ and $\gamma _e \ge 3$. Assume also that $\sigma _x \ge \varOmega (n)$, $\sigma _e \ge \varOmega (4^d \cdot m^{2} \cdot \beta \cdot \sqrt{n} \cdot \sigma _x)$ and $\sigma _e \le O(q/(\lambda \cdot 4^d \cdot m^{2}))$. Then, under the PRF security and $\mathsf {LWE}_{\ell ,2m,q,\chi }$ hardness assumptions, the above function is an l-lossy ABM LTF with $l=\varOmega (n \log n)$.

The theorem follows from the lemmas below.

Lemma 12

(Correctness). Let us assume that and $q/\sigma _e \ge \lambda \cdot 4^d \cdot O(m^2)$. Assume that  $\mathsf {PRF}$ has logarithmic depth $O(\log \lambda )$ when the circuit input is the key and the PRF input is hard-coded in the circuit. Then, for any triple (ek, ik, tk) produced by $\mathsf {ABM}.\mathsf {Gen}(1^\lambda )$, for any tag $t =(t_\mathsf {c},t_\mathsf {a}) \in \{0,1\}^\lambda \times \{0,1\}^k$ satisfying $t_\mathsf {c}\ne \mathsf {PRF}(K,t_\mathsf {a})$ and for any input $(\mathbf {x},\mathbf {e}) \in \mathsf {Dom}_\lambda ^D$, the inversion correctness condition $(\mathbf {x},\mathbf {e}) = \mathsf {ABM}.\mathsf {Invert}(ik,t,\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e})))$ is satisfied.

Proof

By Lemma 10, we have $\Vert \mathbf {R}_{t}\Vert \le \lambda \cdot 4^d \cdot O(m^{3/2})$ and

$$\begin{aligned} \mathbf {A}_t = \begin{bmatrix} {\bar{\mathbf {A}}} \\ \hline \mathbf {R}_{t} \cdot {\bar{\mathbf {A}}} + h_t \cdot \mathbf {G} \end{bmatrix} \bmod q , \end{aligned}$$

where $h_t$ is the Hamming distance between $t_\mathsf {c}$ and $\mathsf {PRF}(K,t_\mathsf {a}) \in \{0,1\}^{\lambda }$. As $q > \lambda$ is prime, integer $h_t$ is invertible modulo q, and $\mathbf {R}_{t}$ is a $\mathbf {G}$-trapdoor with tag $h_t$ for $\mathbf {A}_t$. Thanks to our parameters, we have $\Vert \mathbf {e}\Vert \le q/(10\cdot \Vert \mathbf {R}_{t}\Vert )$ and hence algorithm $\mathsf {Invert}$ from Lemma 9 recovers $(\mathbf {x},\mathbf {e})$.    $\square$

Our ABM-LTF provides evasiveness unless the PRF family is not unpredictable, which would contradict its pseudorandomness. In order to meaningfully rely on the pseudorandomness of $\mathsf {PRF}$, the proof of Lemma 13 also appeals to the $\mathsf {LWE}$ assumption so as to first move to a game where the lossy matrix $\bar{\mathbf {A}} \in \mathbb {Z}_q^{m \times n}$ is traded for a random matrix. Since the matrices $\mathbf {B}_i = \mathbf {R}_i \cdot \bar{\mathbf {A}} + K[i] \cdot \mathbf {G}$ depend the bits of the seed K, moving to a uniform matrix $\bar{\mathbf {A}}$ is necessary to make sure that the evaluation key ek is statistically independent of K.

Lemma 13

(Evasiveness). Assume that $m \ge 2n \log q$. Any $\mathsf {ppt}$ evasiveness adversary $\mathcal {A}$ making $Q_1$ and $Q_2$ queries to $\mathsf {ABM}.\mathsf {LTag}$ and $\mathsf {ABM}.\mathsf {IsLossy}$, respectively, implies an $\mathsf {LWE}$ distinguisher $\mathcal {D}_1$ and a PRF distinguisher $\mathcal {D}_2$ such that

$$ \mathbf {Adv}^{\mathcal {A},\mathsf {eva}}_{Q_1,Q_2} (\lambda ) \le n \cdot \mathbf {Adv}^{\mathcal {D}_1,\mathsf {LWE}}_{\ell ,m,q,\chi }(\lambda ) + \mathbf {Adv}_{Q_1+Q_2}^{\mathcal {D}_2, \mathsf {PRF}} (\lambda ) + \frac{Q_2+1}{2^{\lambda }} . $$

(The proof is deferred to the full version of the paper.)

The pseudo-randomness of core tag components also guarantees that lossy tags are computationally indistinguishable from uniformly random tags. The proof of Lemma 14 also relies on the $\mathsf {LWE}$ assumption since the evaluation key ek only hides the PRF seed K in the computational sense. It follows the same strategy as the proof of Lemma 13 and given in the full version of the paper.

Lemma 14

(Indistinguishability). Assume that $m > 2n \log q$. Then $\mathsf {ppt}$ indistinguishability adversary $\mathcal {A}$ implies either either an $\mathsf {LWE}$ distinguisher $\mathcal {D}_1$ or a PRF distinguisher $\mathcal {D}_2$ such that:

$$ \mathbf {Adv}^{\mathcal {A},\mathsf {ind}}_{Q}(\lambda ) \le 2 n \cdot \mathbf {Adv}^{\mathcal {D}_1,\mathsf {LWE}}_{\ell ,m,q,\chi }(\lambda ) + \mathbf {Adv}_{Q}^{\mathcal {D}_2, \mathsf {PRF}} (\lambda ) + \frac{1}{2^{\lambda -1}} , $$

where Q denotes the number of (genuine or uniform) lossy tag generation queries.

The proof of lossiness is essentially identical to that of the LTF (Theorem 1).

Lemma 15

(Lossiness). Let $\chi =D_{\mathbb {Z},\beta /(2\sqrt{\lambda })}$ for some $\beta >0$. Assume that the depth d of $\mathsf {PRF}$ is in $O(\log \lambda )$, when the circuit input is the key and the PRF input is hardwired in the circuit. Let us assume that $\ell \ge \lambda$ and $n = \varOmega (\ell \log q)$. Assume also that $\sigma _e \ge \varOmega (4^d \cdot m^2 \cdot \beta \cdot \sigma _x \cdot \sqrt{n})$. Then, for any lossy tag $t=(t_\mathsf {c},t_\mathsf {a})$, the above ABM-LTF is l-lossy with $l=\varOmega (n \log n)$.

Proof

We rely on the fact that, for any lossy tag $t=(t_\mathsf {c},t_\mathsf {a})$ (i.e., for which $t_\mathsf {c}= \mathsf {PRF}(K,t_\mathsf {a})$), we have

$$\begin{aligned} \mathbf {A}_t = \begin{bmatrix} {\bar{\mathbf {A}}} \\ \hline \mathbf {R}_{t} \cdot {\bar{\mathbf {A}}} \end{bmatrix} = \begin{bmatrix} \mathbf {B} \\ \hline \mathbf {R}_{t} \cdot \mathbf {B} \end{bmatrix} \cdot \mathbf {C} + \begin{bmatrix} \mathbf {F} \\ \hline \mathbf {R}_{t} \cdot \mathbf {F} \end{bmatrix}, \end{aligned}$$

(3)

where $\mathbf {B} \hookleftarrow U(\mathbb {Z}_q^{m \times \ell })$, $\mathbf {C} \hookleftarrow U(\mathbb {Z}_q^{\ell \times n})$, $\mathbf {F} \hookleftarrow \chi ^{m \times n}$ and $\mathbf {R}_t$ is as in the $\mathsf {ABM}.\mathsf {Invert}$ description.

As a consequence, by the same argument as in the proof of Theorem 1, the distribution of the input $(\mathbf {x},\mathbf {e})$ conditioned on $\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$ is the same as the distribution of $(\mathbf {x},\mathbf {e})$ conditioned on  $(\mathbf {C} \cdot \mathbf {x}, \mathbf {F} \cdot \mathbf {x} + \mathbf {e})$. From this point, the proof is identical to that of Theorem 1, with $\mathbf {F}_{new} = [\mathbf {F}^\top \mid (\mathbf {R}_t \cdot \mathbf {F})^\top ]^\top$ playing the role of $\mathbf {F}$ in the original proof. The two properties of $\mathbf {F}_{new}$ used in the proof are $\Vert \mathbf {F}_{new}\Vert \le (1+\Vert \mathbf {R}_t\Vert ) \cdot \Vert \mathbf {F}\Vert \le O(4^d \cdot m^{3/2}) \cdot \Vert \mathbf {F}\Vert$, using Lemma 10, which leads to a larger $\sigma _e$ by the factor $O(4^d \cdot m^{3/2})$. The other property is a lower bound on $\sigma _n(\mathbf {F}_{new})$ and since the latter is $\ge \sigma _n(\mathbf {F})$, no parameters are affected.    $\square$

In [3, Sect. 7], Alwen et al. used the a rounding technique [5] to build an all-but-one trapdoor function. While our construction bears resemblance with theirs, our proof of lossiness is very different. In [3, Theorem 7.3], they consider a matrix of the form (3) and crucially rely on the statistical independence of the rows of $[ \mathbf {B}^\top \mid ( \mathbf {R}_{0} \cdot \mathbf {B})^\top ]^\top$, for some $\mathbf {R}_0 \in \{-1,1\}^{m \times m}$, conditionally on $\mathbf {R}_0 \cdot \mathbf {F}$. Here, we cannot guarantee that matrices $\mathbf {R}_{t} \cdot \mathbf {B}$ be statistically independent for different tags t, and hence it does not seem possible to directly use the rounding technique from [3]. Fortunately, the proof of Lemma 15 does not require the rows of the matrix $[ \mathbf {B}^\top \mid ( \mathbf {R}_{t} \cdot \mathbf {B})^\top ]^\top$ to be statistically independent and neither does it rely on the independence of $\mathbf {R}_{t} \cdot \mathbf {B}$ for different tags t.

3.3 Joint Use of Lossy and All-But-Many Functions

We remark that our LTF and ABM-LTF are not lossy enough to be correlation-secure in the sense of Rosen and Segev [70]: indeed, the result of [70, Theorem 3.3] requires lossy functions that lose at least half of their input. In particular, we cannot reveal $\mathbf {y}_0= \mathbf {A} \cdot \mathbf {x} + \mathbf {e}$ and $\mathbf {y} = \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ for the same input $(\mathbf {x},\mathbf {e})$ as this would expose $\mathbf {y}-\mathbf {y}_0=(\mathbf {A}-\mathbf {A}_t) \cdot \mathbf {x}$, which would leak $(\mathbf {x},\mathbf {e})$. However, we can safely reveal $\mathbf {y}_0=\mathsf {LTF}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0 )) = \mathbf {A} \cdot \mathbf {x} + \mathbf {e}_0$ and $\mathbf {y}=\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e})) = \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ for distinct Gaussian terms $\mathbf {e}_0,\mathbf {e} \in \mathbb {Z}^{2m}$.

Indeed, conditionally on $\mathsf {LTF}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0))$ and $\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$, the distribution of $\mathbf {x}$ retains l bits of min-entropy, where $l= \varOmega (n \cdot \log n)$. As in the proof of Theorem 1, this follows by observing that the residual distribution on $\mathbf {x}$ is a discrete Gaussian (by Lemma 15) whose covariance matrix is above the smoothing parameter of the support.

Lemma 16

The LTF of Sect. 3.1 and the above ABM-LTF are jointly lossy when they share the first part $\mathbf {x}$ of their inputs.

Let $\chi =D_{\mathbb {Z},\beta /(2\sqrt{\lambda })}$ for some $\beta >0$. Assume that the depth d of $\mathsf {PRF}$ is in $O(\log \lambda )$, when the circuit input is the key and the PRF input is hardwired in the circuit. Let us assume that $\ell \ge \lambda$ and $n = \varOmega (\ell \log q)$. Assume also that $\sigma _e \ge \varOmega (4^d \cdot m^2 \cdot \beta \cdot \sqrt{n} \cdot \sigma _x)$. Then, except with probability $\le 2^{-\varOmega (\lambda )}$ over the choice of $ek' \hookleftarrow \mathsf {LTF}.\mathsf {LGen}(1^\lambda )$, $ek \hookleftarrow \mathsf {ABM}.\mathsf {Gen}(1^\lambda )$, $\mathbf {x} \hookleftarrow \mathsf {Dom}_x$, and $\mathbf {e}_0,\mathbf {e} \hookleftarrow \mathsf {Dom}_e$, we have, for any lossy tag t:

$$\begin{aligned}&H_{\infty } \big (\mathbf {x} \mid \mathsf {LTF}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0)), ~\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e})) \big ) \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad \,\, \ge n \cdot \log \sigma _x - 2 - \ell \log q > \varOmega ( {n} \cdot \log n). \end{aligned}$$

Proof

The result follows by generalizing the proofs of Theorem 1 and Lemma 15 in a straightforward manner. Indeed, if $\mathbf {A}_{\mathsf {LTF}}=\mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} + \mathbf {F}_{\mathsf {LTF}} \in \mathbb {Z}_q^{ 2m \times n}$ and $\bar{\mathbf {A}}=\mathbf {B}_{\mathsf {ABM}} \cdot \mathbf {C}_{\mathsf {ABM}} + \mathbf {F}_{\mathsf {ABM}} \in \mathbb {Z}_q^{m \times n}$ are the lossy matrices of both functions, the information revealed by $\mathsf {LTF}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0))$ and $\mathsf {ABM}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$ is

$$\begin{aligned} \left[ \begin{array}{c|c} \mathbf {B}_{\mathsf {LTF}} &{}~ \mathbf {0}^{2m \times \ell } \\ \hline ~\mathbf {0}^{m \times \ell } ~ &{} \mathbf {B}_{\mathsf {ABM}} \\ ~\mathbf {0}^{m \times \ell } ~ &{} ~ \mathbf {R}_{t} \cdot \mathbf {B}_{\mathsf {ABM}} ~ \end{array} \right] \cdot \begin{bmatrix} \mathbf {C}_{\mathsf {LTF}} \\ \hline \mathbf {C}_{\mathsf {ABM}} \end{bmatrix} \cdot \mathbf {x} + \begin{bmatrix} \mathbf {F}_{\mathsf {LTF}} \\ \hline \mathbf {F}_{\mathsf {ABM}} \\ \mathbf {R}_{t} \cdot \mathbf {F}_{\mathsf {ABM}} \end{bmatrix} \cdot \mathbf {x} + \begin{bmatrix} \mathbf {e}_0 \\ \hline \mathbf {e} \end{bmatrix} . \end{aligned}$$

It is thus entirely determined by the vectors $[ \mathbf {C}_{\mathsf {LTF}}^\top \mid \mathbf {C}_{\mathsf {ABM}}^\top ]^\top \cdot \mathbf {x} \in \mathbb {Z}_q^{2 \ell }$ and $[\mathbf {F}_{\mathsf {LTF}}^\top \mid \mathbf {F}_{\mathsf {ABM}}^\top \mid ( \mathbf {R}_{t} \cdot \mathbf {F}_{\mathsf {ABM}})^\top ]^\top \cdot \mathbf {x} + [\mathbf {e}_0^\top \mid \mathbf {e}_1^\top ]^\top \in \mathbb {Z}^{4m}$ and we obtain the result by repeating the arguments in the proof of Theorem 1 and Lemma 15.    $\square$

4 Selective Opening Chosen-Ciphertext Security

We now combine our ABM-LTF and the $\mathsf {LWE}$-based LTF of Sect. 3 to build an IND-SO-CCA2-secure public-key encryption scheme from the $\mathsf {LWE}$ assumption. The scheme can be seen as instantiating a variant of the Peikert-Waters methodology [66], as generalized by Hofheinz [49, Sect. 6.3] to the case of multiple lossy tags. In [49], ciphertexts consists of $(f_{\mathsf {lossy}}(x),f_{\mathsf {ABM}}(t,x),\mathsf {Msg} \oplus h(x))$, where $f_{\mathsf {lossy}}(x)$ (resp. $f_{\mathsf {ABM}}(t,x)$) is a lossy (resp. all-but-many) function of the input x; t is the tag of the ciphertext; and h(x) is a universal hash of x.

Nevertheless, our scheme is not a generic instantiation of this paradigm as we cannot use exactly the same input x in the two functions $f_{\mathsf {lossy}}(\cdot )$ and $f_{\mathsf {ABM}}(t,\cdot )$. As we mentioned earlier, we cannot give out function outputs $\mathbf {y}_0=\mathbf {A} \cdot \mathbf {x} + \mathbf {e}$ and $\mathbf {y} =\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$ for the same input $(\mathbf {x},\mathbf {e})$. For this reason, our lossy and ABM functions have to use distinct noise terms $(\mathbf {e}_0,\mathbf {e})$ in the two evaluations $\mathbf {y}_0=\mathbf {A} \cdot \mathbf {x} + \mathbf {e}_0$ and $\mathbf {y} =\mathbf {A}_t \cdot \mathbf {x} + \mathbf {e}$. The decryption algorithm can proceed by inverting $(\mathbf {x},\mathbf {e}_0) \leftarrow f_{\mathsf {lossy}}^{-1}(\mathbf {y}_0)$ as before. However, instead of simply testing if $\mathbf {y}=f_{\mathsf {ABM}}(t,(\mathbf {x},\mathbf {e}_0))$ by evaluating $f_{\mathsf {ABM}}(t,.)$ in the forward direction as in [49, 66], the receiver has to test whether $\mathbf {y} - \mathbf {A}_t \cdot \mathbf {x}$ is a small-norm vector, analogously to [65, Sect. 4.4]. For this reason, the message $\mathsf {Msg}$ is hidden by the universal hash of $\mathbf {x}$ only, which is sufficient in our security proof. Moreover, our extension to SIM-SO-CCA2 security requires $h(\cdot )$ to operate on $\mathbf {x}$ alone.

Unlike [66], we cannot use one-time signatures to bind ciphertext components in a non-malleable manner. Indeed, at each corruption query, the challenger would have to reveal the one-time secret keys of the challenge ciphertexts, which would allow the adversary to make decryption queries for lossy tags.

Instead, we can proceed analogously to Boyen et al. [24] and define the auxiliary tags to be the output $\mathbf {y}_0 = \varPi ^{\mathsf {LTF}}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0))$ of the lossy function while resorting to the hybrid encryption paradigm and authenticate the message-carrying part $\mathbf {c}_0 = \mathsf {Msg} + h(\mathbf {x})$ of the ciphertext via the encrypt-then-MAC approach. One difficulty is that, since $\mathbf {y}_0 = \varPi ^{\mathsf {LTF}}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0))$ and $\mathbf {y}=\varPi ^{\mathsf {ABM}}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$ involve distinct small-norm vectors $\mathbf {e}_0$, $\mathbf {e}$, we must find a different way to prevent the adversary from tampering with $\mathbf {e}$ in one of the challenge ciphertexts (indeed, $\mathbf {y}$ is no longer authenticated by a one-time signature). Our solution to this problem is to include $\mathbf {y}=\varPi ^{\mathsf {ABM}}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e}))$ in the input of the MAC, which simultaneously authenticates $\mathbf {y}$ and $\mathbf {c}_0$. For simplicity, we assume MACs with the uniqueness property but the proof can be adapted to rely on any strongly unforgeable MAC.

As mentioned in [49, Sect. 6], the application to IND-SO-CCA2 security requires the core tag space $\mathcal {T}_{\mathsf {c}}$ of ABM-LTFs to be efficiently samplable and explainable. As defined in [49, Definition 6.2], “explainability” (a.k.a. “invertible samplability” [33]) means that any core tag $t_\mathsf {c}$ can be explained by the challenger as having been uniformly chosen “without ulterior motive” when the adversary opens a given ciphertext. Our ABM-LTF clearly satisfies this property since core tags $t_\mathsf {c}$ are just random $\lambda$-bit strings.

4.1 Description

• ${\varvec{\mathsf {Par}\text {-}\mathsf {Gen}}(1^\lambda )}{} \mathbf{:}$ Selects public parameters consisting of:

  • – A modulus $q>2$, integers $\ell ,\ell _0, \ell _1 , n \in \mathsf {poly}(\lambda )$, ${m} = \lceil c n \cdot \log q \rceil$, for some constant $c>0$, and parameters $\beta ,\sigma _x,\sigma _e >0$.

  • – The specification $\mathsf {MAC}=(\mathsf {KG},\mathsf {Sig},\mathsf {Ver})$ of a unique MAC with message space $\mathsf {MsgSp}^{mac} := \mathbb {Z}_q^{2m} \times \mathbb {Z}_q^{\ell _0}$ and key space $\mathcal {K}^{mac}:=\mathbb {Z}_q^{\ell _1}$.

  • – A family $\mathcal {UH}$ of universal hash functions $h : [-\sigma _x \sqrt{n},\sigma _x \sqrt{n}]^{n} \rightarrow \mathbb {Z}_q^{\ell _0 + \ell _1}$ that range over $\mathsf {MsgSp}:= \mathbb {Z}_q^{\ell _0}$.

  The public parameters $\varGamma =\{ \ell , \ell _0,\ell _1,n,m,q ,\beta , \sigma _x,\sigma _e, \mathsf {MAC}\}$ define the plaintext space $\mathsf {MsgSp}:= \mathbb {Z}_q^{\ell _0}$ and will be shared by the $\mathsf {LWE}$-based LTF of Sect. 3.1 and our ABM-LTF of Sect. 3.2.

• ${\varvec{\mathsf {Keygen}}(\varGamma )}{} \mathbf{:}$ Let $\varPi ^{\mathsf {LTF}}=(\mathsf {IGen},\mathsf {LGen},\mathsf {Eval},\mathsf {Invert})$ be an instance of the LTF of Sect. 3.1 and let $\varPi ^{\mathsf {ABM}}=(\mathsf {Gen},\mathsf {Eval},\mathsf {Invert},\mathsf {LTag})$ be an instance of the ABM-LTF of Sect. 3.2. We assume $\varPi ^{\mathsf {LTF}}$ and $\varPi ^{\mathsf {ABM}}$ both operate over the domain $\mathsf {Dom}_{\lambda }^D := \{ (\mathbf {x},\mathbf {e}) \in \mathbb {Z}^n \times \mathbb {Z}^{2m} \mid \Vert \mathbf {x} \Vert \le \sigma _x \sqrt{n},~\Vert \mathbf {e} \Vert \le \sigma _e \sqrt{2m} \}$. The public key is generated via the following steps.

  • 1. Generate a pair $(ek',ik') \leftarrow \varPi ^{\mathsf {LTF}}.\mathsf {IGen}(1^\lambda )$ for an injective function of the lossy trapdoor function family $\varPi ^{\mathsf {LTF}}$.

  • 2. Generate $(ek,ik,tk) \leftarrow \varPi ^{\mathsf {ABM}}.\mathsf {Gen}(1^\lambda )$ as an ABM-LTF key pair. We assume that the space of auxiliary tags is $\mathcal {T}_\mathsf {a}=\mathbb {Z}_q^m$

  • 3. Choose a random member $h \leftarrow \mathcal {UH}$ of the universal hash family.

  Output (PK, SK) where $PK= \big (ek',ek,h \big )$ and $SK=ik'$.

• ${\varvec{\mathsf {Encrypt}}(PK,\mathsf {Msg})}{} \mathbf{:}$ To encrypt $\mathsf {Msg} \in \mathbb {Z}_q^{\ell _0}$, choose $\mathbf {x} \hookleftarrow D_{\mathbb {Z}^n,\sigma _x}$, $\mathbf {e}_0 \hookleftarrow D_{\mathbb {Z}^{2m},\sigma _e}$, $\mathbf {e} \hookleftarrow \mathcal {D}_{\mathbb {Z}^{2m},\sigma _e}$ and do the following.

  • 1. Compute $\mathbf {y}_0 = \varPi ^{\mathsf {LTF}}.\mathsf {Eval}(ek',(\mathbf {x},\mathbf {e}_0)) = \mathbf {A} \cdot \mathbf {x} + \mathbf {e}_0 ~\in \mathbb {Z}_q^{2m}$.

  • 2. Define $t_\mathsf {a}= \mathbf {y}_0$ and choose a random $t_\mathsf {c}\hookleftarrow U (\mathcal {T}_\mathsf {c})$. Then, let $t=(t_\mathsf {c},t_\mathsf {a})$ and compute $\mathbf {y}=\varPi ^{\mathsf {ABM}}.\mathsf {Eval}(ek,t,(\mathbf {x},\mathbf {e})) = \mathbf {A}_t \cdot \mathbf {x} + \mathbf {e} ~\in \mathbb {Z}_q^{2m}$.

  • 3. Compute $(\mathbf {k}^{sym},\mathbf {k}^{mac}) = h(\mathbf {x}) \in \mathbb {Z}_q^{\ell _0} ~\times \mathbb {Z}_q^{\ell _1}$.

  • 4. Set $\mathbf {c}_0= \mathsf {Msg} + \mathbf {k}^{sym} ~\in \mathbb {Z}_q^{\ell _0}$ and $\mathbf {c}_1 = \mathsf {MAC}.\mathsf {Sig}(\mathbf {k}^{mac},(\mathbf {y},\mathbf {c}_0))$.

  Output the ciphertext $\mathbf {C}=(t_\mathsf {c},\mathbf {c}_0,\mathbf {c}_1,\mathbf {y}_0,\mathbf {y})$.

• ${\varvec{\mathsf {Decrypt}}(SK,C)}{} \mathbf{:}$ To decrypt $\mathbf {C}=(t_\mathsf {c},\mathbf {c}_0,\mathbf {c}_1,\mathbf {y}_0,\mathbf {y})$ using $SK=ik'$,

  • 1. Compute $(\mathbf {x},\mathbf {e}_0) \leftarrow \varPi ^{\mathsf {LTF}}.\mathsf {Invert}(ik',\mathbf {y}_0)$. Return $\perp$ if $\mathbf {y}_0$ is not in the range⁴ of $\varPi ^{\mathsf {LTF}}.\mathsf {Eval}(ek',\cdot )$ or if $(\mathbf {x},\mathbf {e}_0) \not \in \mathsf {Dom}_\lambda ^D$.

  • 2. Define the tag $t =(t_\mathsf {c}, \mathbf {y}_0)$. If $\Vert \mathbf {y} - \mathbf {A}_t \cdot \mathbf {x} \Vert > \sigma _e \sqrt{2m}$, return $\perp$.

  • 3. Compute $(\mathbf {k}^{sym},\mathbf {k}^{mac}) = h(\mathbf {x}) ~\in \mathbb {Z}_q^{\ell _0} \times \mathbb {Z}_q^{\ell _1}$.

  • 4. If $\mathsf {MAC}.\mathsf {Ver}(\mathbf {k}^{mac}, (\mathbf {y},\mathbf {c}_0),\mathbf {c}_1)=0$, return $\perp$. Otherwise, return the plaintext $\mathsf {Msg}= \mathbf {c}_0 - \mathbf {k}^{sym} \in \mathbb {Z}_q^{\ell _0}$.

In order to instantiate the scheme with a polynomial-size modulus q, we need a PRF with an evaluation circuit in $\mathsf {NC}^1$, which translates into a polynomial-length branching program. By applying Lemma 10 and exploiting the asymmetric noise growth of the GSW FHE as in [27], we can indeed keep q small.

For this purpose, the Banerjee-Peikert PRF [4] is a suitable candidate. While its evaluation circuit is in $\mathsf {NC}^2$ in general, we can still homomorphically evaluate input-dependent circuits $C_{\mathsf {PRF},j}(\cdot )$ over the encrypted key K using an $\mathsf {NC}^1$ circuit. For public moduli p, q and matrices $\mathbf {A}_0,\mathbf {A}_1 \in \mathbb {Z}_q^{ n \times n \lceil \log q \rceil }$, their PRF maps an input ${x} \in \{0,1\}^k$ to $\lfloor (p/q) \cdot (\mathbf {k}^\top \cdot \mathbf {A}_{ {x}} \bmod q) \rfloor$, where $\mathbf {k} \in \mathbb {Z}_q^n$ is the secret key and the input-dependent matrix $\mathbf {A}_{ {x}}$ is publicly computable from $\mathbf {A}_0,\mathbf {A}_1$. This allows hard-coding $\mathbf {A}_{ {x}}$ into an $\mathsf {NC}^1$ circuit to be evaluated over the “encrypted” bits of $\mathbf {k}$ in order to obtain “encryptions” of the bits of $\lfloor (p/q) \cdot \mathbf {k}^\top \cdot \mathbf {A}_{ {x}} \rfloor$. Indeed, matrix-vector products and rounding can both be computed in $\mathsf {TC}^0 \subseteq \mathsf {NC}^1$, which allows using a polynomial-size q by applying Lemma 10. The resulting instantiation relies on the same $\mathsf {LWE}$ assumption as the Banerjee-Peikert PRF [4], where the modulus-to-noise ratio is only slightly super-polynomial.

4.2 Indistinguishability-Based (IND-SO-CCA2) Security

We first prove that the scheme provides IND-SO-CCA2 security. While we can tightly relate the IND-SO-CCA security of the scheme to the pseudorandomness of the underlying PRF, the reduction from the unforgeability of the MAC loses a factor proportional to the number of challenges.

Theorem 3

The scheme provides IND-SO-CCA2 security assuming that: (i) $\varPi ^{\mathsf {LTF}}$ is a LTF; (ii) $\varPi ^{\mathsf {ABM}}$ is an ABM-LTF; (iii) $\mathsf {PRF}$ is a pseudorandom function family; (iv) $\mathsf {MAC}$ provides sUF-OT-CMA security. In our instantiation, for any adversary $\mathcal {A}$, there exists an $\mathsf {LWE}_{\ell ,m,q,\chi }$ distinguisher $\mathcal {D}_1$, a PRF adversary $\mathcal {D}_2$ and a MAC forger $\mathcal {B}$ with comparable running time and such that

$$\begin{aligned}&\mathbf {Adv}_{\mathcal {A}}^{\mathrm {IND}\text {-}\mathrm {SO}\text {-}\mathrm {CCA2}}( \lambda ) \le 4 n \cdot \mathbf {Adv}^{\mathcal {D}_1,\mathsf {lwe}}_{\ell ,m,q,\chi }(\lambda ) + 2 \cdot \mathbf {Adv}_{N+Q_D}^{\mathcal {D}_2, \mathrm {prf}} (\lambda ) \\&\qquad \qquad \qquad \qquad \quad + \frac{Q_D+2+ N \cdot (Q_D+1)}{2^{\lambda -2}} + N \cdot \mathbf {Adv}^{\mathrm {mac},Q_D}_\mathcal {B}(\lambda ), \end{aligned}$$

where N is the number of challenge ciphertexts and $Q_{D}$ is the number of decryption queries made by the adversary. (The proof is given in the full paper.)

In the full version of this paper, we describe a variant of the scheme which, while not secure under selective openings, can be proved tightly CCA2-secure in the multi-challenge setting as long as the PRF is itself tightly secure. In order to enable instantiations with a polynomial-size modulus q, we give a tighter security proof for the PRF of [21] in the full version of the paper.

4.3 Achieving Simulation-Based (SIM-SO-CCA2) Security

We show that our scheme can be instantiated so as to achieve the stronger notion of SIM-SO-CCA2 security. To this end, we show that it is in fact a lossy encryption scheme with weak efficient opening. We first detail the lossy key generation algorithm (which can be used in the final game in the proof of IND-SO-CCA2 security) and the $\mathsf {Opener}$ algorithm.

In order for $\mathsf {Opener}$ to run efficiently, we instantiate our scheme with a universal hash family $\mathcal {UH}$, where each function $h: [-\sigma _x \sqrt{n},\sigma _x \sqrt{n}]^n \rightarrow \mathbb {Z}_q^{\ell _0+\ell _1}$ is keyed by a public matrix $\mathbf {H}_{\mathcal {UH}} \in \mathbb {Z}_q^{(\ell _0 + \ell _1) \times n}$, which is included in the public key $PK_{\mathsf {loss}}$ and allows evaluating

$$ h_{\mathbf {H}_{\mathcal {UH}}} (\mathbf {x} ) = \begin{bmatrix} \mathbf {k}^{sym} \\ \mathbf {k}^{mac} \end{bmatrix} = \mathbf {H}_{\mathcal {UH}} \cdot \mathbf {x} ~ \bmod q $$

before computing $\mathbf {c}_0 = \mathsf {Msg} + \mathbf {k}^{sym} \in \mathbb {Z}_q^{\ell _0}$ and $\mathbf {c}_1=\mathsf {MAC}.\mathsf {Sig}(\mathbf {k}^{sym},(\mathbf {y},\mathbf {c}_0))$.

We also require $\mathsf {Par}\text {-}\mathsf {Gen}$ to output public parameters $\ell ,\ell _0,n$ satisfying the constraint $n> 2 \cdot (2 \ell + \ell _0 + \ell _1) \cdot \log q$, where $\ell _0$ is the message length, $\ell _1$ is the key length of the MAC and $\ell$ is the dimension of the underlying $\mathsf {LWE}$ assumption.

• ${{\varvec{\mathsf {Keygen}}}(\varGamma ,\mathsf {loss})}{} \mathbf{:}$ Given public parameters $\varGamma =\{ \ell , \ell _0,\ell _1,n,m,q ,\beta , \sigma _x,\sigma _e \}$ containing integers $\ell ,\ell _0,n,m$ such that $n> 2 \cdot (2 \ell + \ell _0+\ell _1) \cdot \lceil \log q \rceil$ and $m > 2(n + \ell ) \cdot \log q$, conduct the following steps.

  • 1. Choose a random matrix $\mathbf {C}_0 \hookleftarrow U \big (\mathbb {Z}_q^{\bar{n} \times \bar{\ell } } \big )$, where $\bar{\ell } = (2 \ell + \ell _0 + \ell _1)$ and $\bar{n} = n - \bar{\ell } \cdot \lceil \log q \rceil$ which is used to run the $(\mathbf {C},\mathbf {R}_{sim}) \leftarrow \mathsf {GenTrap}(\mathbf {C}_0,\mathbf {I}_{\bar{\ell }},\sigma _x)$ algorithm of Lemma 8 to produce a statistically uniform $\mathbf {C} \in \mathbb {Z}_q^{ \bar{\ell } \times n }$ with a a small-norm $\mathbf {R}_{sim} \in \mathbb {Z}^{ \bar{\ell } \cdot \lceil \log q \rceil \times \bar{n}}$ forming a $\mathbf {G}_{sim}$-trapdoor, where $\mathbf {G}_{sim} \in \mathbb {Z}_q^{ \bar{\ell } \cdot \lceil \log q \rceil \times \bar{\ell } }$ is the gadget matrix of [60]. Parse $\mathbf {C} \in \mathbb {Z}_q^{\bar{\ell } \times n}$ as

    $$\begin{aligned} \mathbf {C} = \begin{bmatrix} \mathbf {C}_{\mathsf {LTF}} \\ \hline \mathbf {C}_{\mathsf {ABM}} \\ \hline \mathbf {H}_{\mathcal {UH}} \end{bmatrix} \in \mathbb {Z}_q^{ \bar{\ell } \times n }, \end{aligned}$$

    (4)

    where $\mathbf {C}_{\mathsf {LTF}}, \mathbf {C}_{\mathsf {ABM}} \in \mathbb {Z}_q^{\ell \times n}$ and $\mathbf {H}_{\mathcal {UH}} \in \mathbb {Z}_q^{(\ell _0 + \ell _1) \times n}$.

  • 2. Sample matrices $\mathbf {B}_{\mathsf {LTF}} \hookleftarrow U(\mathbb {Z}_q^{2m \times \ell })$, $\mathbf {B}_{\mathsf {ABM}} \hookleftarrow U(\mathbb {Z}_q^{m \times \ell })$, $\mathbf {F}_{\mathsf {LTF}} \hookleftarrow \chi ^{2m \times n}$, $\mathbf {F}_{\mathsf {ABM}} \hookleftarrow \chi ^{m \times n}$ in order to define $\mathbf {A}_{\mathsf {LTF}} = \mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} + \mathbf {F}_{\mathsf {LTF}} ~\in \mathbb {Z}_q^{2m \times n}$ and $\mathbf {A}_{\mathsf {ABM}} = \mathbf {B}_{\mathsf {ABM}} \cdot \mathbf {C}_{\mathsf {ABM}} + \mathbf {F}_{\mathsf {ABM}} ~\in \mathbb {Z}_q^{m \times n}$, which are statistically close to outputs of $\mathsf {Lossy}(1^n,1^{{m}},1^{\ell },q,\chi )$ as $\mathbf {C}_{\mathsf {LTF}}$ and $\mathbf {C}_{\mathsf {ABM}}$ are statistically uniform over $\mathbb {Z}_q^{ \ell \times n}$.

  • 3. Define $ek'= \mathbf {A}_{\mathsf {LTF}} \in \mathbb {Z}_q^{2m \times n}$ to be the evaluation key of $\varPi ^{\mathsf {LTF}}$. Then, run Steps 2-4 of the key generation algorithm of $\varPi ^{\mathsf {ABM}}$ while setting $\bar{\mathbf {A}} = \mathbf {A}_{\mathsf {ABM}} \in \mathbb {Z}_q^{m \times n}$ at Step 1. The resulting keys (ek, ik, tk) consist of

    $$\begin{aligned} ek := \Bigl ( {\mathbf {A}_{\mathsf {ABM}}}, \{\mathbf {B}_i \}_{i=1}^\lambda \Bigr ) , \qquad ik := \bigl ( \{ \mathbf {R}_i \}_{i=1}^\lambda , K \bigr ) , \qquad tk := K \end{aligned}$$

    and are statistically close to the output distribution (2) of $\varPi ^{\mathsf {ABM}}.\mathsf {Gen}$.

  Return $PK_{\mathsf {loss}}=(ek',ek, \mathbf {H}_{\mathcal {UH}})$ and

  $$\begin{aligned} SK_{\mathsf {loss}}= \big ( \mathbf {R}_{sim}, \mathbf {C}_0, \mathbf {B}_{\mathsf {LTF}} ,\mathbf {B}_{\mathsf {ABM}} , \mathbf {F}_{\mathsf {LTF}} ,\mathbf {F}_{\mathsf {ABM}} , ik \big ). \end{aligned}$$

  (5)

• ${\varvec{\mathsf {Opener}}}(\varGamma ,PK_{\mathsf {loss}},SK_{\mathsf {loss}},\mathsf {Msg}_0,(\mathbf {x} ,\mathbf {e}_0,\mathbf {e}_1),\mathsf {Msg}_1)$ : Parse $SK_{\mathsf {loss}}$ as in (5) and conduct the following steps.

  • 1. Compute $\mathbf {t}_{\mathsf {LTF},\mathbf {x} } = \mathbf {C}_{\mathsf {LTF}} \cdot \mathbf {x} \in \mathbb {Z}_q^{\ell }$, $\mathbf {t}_{\mathsf {ABM},\mathbf {x} } = \mathbf {C}_{\mathsf {ABM}} \cdot \mathbf {x} \in \mathbb {Z}_q^{\ell }$ and

    $$ \begin{bmatrix} \mathbf {k}^{sym,\mathbf {x} } \\ \mathbf {k}^{mac ,\mathbf {x} } \end{bmatrix} = \mathbf {H}_{\mathcal {UH}} \cdot \mathbf {x} ~\in \mathbb {Z}_q^{\ell _0 + \ell _1} . $$

    Then, set $\mathbf {t}_{ \mathsf {Msg}, \mathbf {x} } = (\mathsf {Msg}_0 - \mathsf {Msg}_1) + \mathbf {k}^{sym,\mathbf {x} } \in \mathbb {Z}_q^{\ell _0}$ and define

    $$\mathbf {t}_{\mathbf {x} } = \begin{bmatrix} ~ \mathbf {t}_{\mathsf {LTF},\mathbf {x} }^\top \mid \mathbf {t}_{\mathsf {ABM},\mathbf {x} }^\top \mid \mathbf {t}_{ \mathsf {Msg}, \mathbf {x} }^\top \mid {\mathbf {k}^{mac,\mathbf {x} }}^\top ~ \end{bmatrix}^\top \in \mathbb {Z}_q^{\bar{\ell }}.$$

  • 2. Using the trapdoor $\mathbf {R}_{sim} \in \mathbb {Z}^{ \bar{\ell } \cdot \lceil \log q \rceil \times \bar{n}}$, sample a small-norm vector $\mathbf {x}' \hookleftarrow D^{S_{\underline{\mathbf {F}},\mathbf {t}_{\mathbf {x}},\mathbf {f}}}_{\varLambda ^\perp (\mathbf {C})+\mathbf {z}, \sqrt{\mathbf {\Sigma }},\mathbf {c} }$ so as to have a short integer vector $\mathbf {x}' \in \mathbb {Z}^n$ satisfying $\mathbf {C} \cdot \mathbf {x}' = \mathbf {t}_{\mathbf {x} } \bmod q$, using an arbitrary solution $\mathbf {z} \in \mathbb {Z}^{n}$ of $\mathbf {C} \cdot \mathbf {z} = \mathbf {t}_{\mathbf {x} } \in \mathbb {Z}_q^{\bar{\ell }}$, where $\mathbf {\Sigma }$ and $\mathbf {c}$ are defined based on Lemma 11, for

    $$\begin{aligned} \underline{\mathbf {F}} := \begin{bmatrix} \mathbf {F}_{\mathsf {LTF}} \\ \hline \mathbf {F}_{\mathsf {ABM}} \\ \hline \mathbf {R}_{t}\cdot \mathbf {F}_{\mathsf {ABM}} \end{bmatrix} \in \mathbb {Z}^{4m \times n}, \underline{\mathbf {e}} := \begin{bmatrix} \mathbf {e}_{0} \\ \hline \mathbf {e} \end{bmatrix} \in \mathbb {Z}^{4m} ,~ \mathbf {f}:=\underline{\mathbf {F}} \cdot \mathbf {x} + \underline{\mathbf {e}}\in \mathbb {Z}^{4m}. \qquad \end{aligned}$$

    (6)

  • 3. Output $(\mathbf {x}',\mathbf {e}_0',\mathbf {e}')$ where

    $$\begin{aligned} \left\{ \begin{array}{ll} \mathbf {e}_0' &{}= \mathbf {F}_{\mathsf {LTF}} \cdot (\mathbf {x} - \mathbf {x}') + \mathbf {e}_0 ~\in \mathbb {Z}^{2m} \\ \mathbf {e}' &{}= \begin{bmatrix} \mathbf {F}_{\mathsf {ABM}} \\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_{\mathsf {ABM}} \end{bmatrix} \cdot (\mathbf {x} - \mathbf {x}') + \mathbf {e} ~\in \mathbb {Z}^{2m} \end{array} \right. \end{aligned}$$

    (7)

We observe that algorithm $\mathsf {Opener}$ is efficient. In particular, at Step 2, it can compute the matrix $\mathbf {\Sigma }$ and the vector $\mathbf {c}$ of Lemma 11 by first reconstructing the matrix $\underline{\mathbf {F}} \in \mathbb {Z}^{4m \times n}$ of (6) and the vector $\mathbf {f}=\underline{\mathbf {F}} \cdot \mathbf {x} + \underline{\mathbf {e}} \in \mathbb {Z}^{4m}$, which requires to deterministically re-compute the integer matrix $\mathbf {R}_{t}$ obtained at Step 2 of $\mathsf {ABM}.\mathsf {Invert}(ik,t,.)$ using $ik=((\mathbf {R}_i)_{i\le \lambda },K)$.

We easily check that, for any vector $\mathbf {x}'$ sampled at Step 2, the corresponding

$$ \begin{bmatrix} {\mathbf {k}^{sym,\mathbf {x}'}} \\ {\mathbf {k}^{mac,\mathbf {x}'}} \end{bmatrix} = \mathbf {H}_{\mathcal {UH}} \cdot \mathbf {x}' ~\in \mathbb {Z}_q^{\ell _0+\ell _1} $$

satisfy $\mathbf {k}^{mac,\mathbf {x}'}=\mathbf {k}^{mac,\mathbf {x}_0}$ and $\mathbf {k}^{sym,\mathbf {x}'} = (\mathsf {Msg}_0 - \mathsf {Msg}_1) + \mathbf {k}^{sym,\mathbf {x} } ~\bmod q .$

As a consequence, if $C=(t_\mathsf {c},\mathbf {c}_0,\mathbf {c}_1,\mathbf {y}_0,\mathbf {y})$ is the ciphertext obtained by running $\mathsf {Encrypt}(PK_{\mathsf {loss}},\mathsf {Msg}_0,(\mathbf {x},\mathbf {e}_0,\mathbf {e}))$, this ciphertext contains

$$ \mathbf {c}_0 = \mathsf {Msg}_0 + \mathbf {k}^{sym,\mathbf {x} } \bmod q , \qquad \quad \mathbf {c}_1 = \mathsf {MAC}.\mathsf {Sig}(\mathbf {k}^{mac,\mathbf {x} } , (\mathbf {y}, \mathbf {c}_0)),$$

which coincide with $\mathbf {c}_0 = \mathsf {Msg}_1 + \mathbf {k}^{sym,\mathbf {x}'}$ and $\mathbf {c}_1 = \mathsf {MAC}.\mathsf {Sig}(\mathbf {k}^{mac,\mathbf {x}'} , ( \mathbf {y}, \mathbf {c}_0))$. Moreover, we also have $\mathbf {C}_{\mathsf {LTF}} \cdot \mathbf {x} = \mathbf {C}_{\mathsf {LTF}} \cdot \mathbf {x}'$ and $\mathbf {C}_{\mathsf {ABM}} \cdot \mathbf {x} = \mathbf {C}_{\mathsf {ABM}} \cdot \mathbf {x}'$.

The following theorem formally states the correctness of the $\mathsf {Opener}$ algorithm.

Theorem 4

For any key pair $(PK_{\mathsf {loss}},SK_{\mathsf {loss}})$ in the support of $\mathsf {Keygen}(\varGamma ,\mathsf {loss})$, algorithm $\mathsf {Opener}$ outputs $(\mathbf {x}',\mathbf {e}_0',\mathbf {e}')$ with the correct distribution conditionally on $\mathsf {Encrypt}(PK_{\mathsf {loss},},\mathsf {Msg}_0,(\mathbf {x},\mathbf {e}_0,\mathbf {e}))=\mathsf {Encrypt}(PK_{\mathsf {loss},},\mathsf {Msg}_1,(\mathbf {x}',\mathbf {e}_0',\mathbf {e}'))$.

Proof

For any lossy tag $t=(t_\mathsf {c},t_\mathsf {a})$, the matrix $\mathbf {A}_t$ used by $\varPi ^{\mathsf {ABM}}.\mathsf {Eval}(ek,t,.)$ is of the form

$$\begin{aligned} \mathbf {A}_t = \begin{bmatrix} {\mathbf {A}_\mathsf {ABM}} \\ \hline \mathbf {R}_{t} \cdot {\mathbf {A}_\mathsf {ABM}} \end{bmatrix} = \begin{bmatrix} \mathbf {B}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {B}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {C}_\mathsf {ABM}+ \begin{bmatrix} \mathbf {F}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_\mathsf {ABM}\end{bmatrix}, \end{aligned}$$

(8)

where $\mathbf {R}_{t} \in \mathbb {Z}^{m \times m}$ is the integer matrix obtained in $\mathsf {ABM}.\mathsf {Invert}(ik,t,.)$. At the same time, $ek'$ consists of a matrix of the form $\mathbf {A}_{\mathsf {LTF}} = \mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} + \mathbf {F}_{\mathsf {LTF}} .$

We now claim that, due to the way to sample $\mathbf {x}'$ and $\mathbf {e}_0'$ and $\mathbf {e}'$ at Steps 2 and 3 of $\mathsf {Opener}$, the distribution of $\mathbf {y}_0'$ and $\mathbf {y}'$, with

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf {y}_0' &{}= \mathbf {A}_{\mathsf {LTF}} \cdot \mathbf {x}' + \mathbf {e}_0' ~\in \mathbb {Z}^{2m} \\ \mathbf {y}' &{}= \mathbf {A}_{t} \cdot \mathbf {x}' + \mathbf {e}' ~\in \mathbb {Z}^{2m} \\ \end{array} \right. \end{aligned}$$

(9)

is the same as that of the real encryptions explained in the beginning of this Section. By replacing $\mathbf {A}_{\mathsf {LTF}},\mathbf {A}_{t}$ and $\mathbf {e}_0'$ and $\mathbf {e}'$ we get:

$$\begin{aligned} \mathbf {y}_0'= & {} (\mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} + \mathbf {F}_{\mathsf {LTF}}) \cdot \mathbf {x}' + (\mathbf {F}_{\mathsf {LTF}} \cdot (\mathbf {x} - \mathbf {x}') + \mathbf {e}_0)\\= & {} \mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} \cdot \mathbf {x}' + \mathbf {F}_{\mathsf {LTF}} \cdot \mathbf {x}+ \mathbf {e}_0\\= & {} \mathbf {B}_{\mathsf {LTF}} \cdot \mathbf {C}_{\mathsf {LTF}} \cdot \mathbf {x} + \mathbf {F}_{\mathsf {LTF}} \cdot \mathbf {x}+ \mathbf {e}_0\\= & {} \mathbf {A}_{\mathsf {LTF}} \cdot \mathbf {x} + \mathbf {e}_0~\in \mathbb {Z}^m \end{aligned}$$

and

$$\begin{aligned} \nonumber \mathbf {y}'= & {} \left( \begin{bmatrix} \mathbf {B}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {B}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {C}_\mathsf {ABM}+ \begin{bmatrix} \mathbf {F}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_\mathsf {ABM}\end{bmatrix} \right) \cdot \mathbf {x}' \\&\quad + \left( \begin{bmatrix} \mathbf {F}_{\mathsf {ABM}} \\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_{\mathsf {ABM}} \end{bmatrix} \cdot (\mathbf {x} - \mathbf {x}') + \mathbf {e}\right) \\= & {} \begin{bmatrix} \mathbf {B}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {B}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {C}_\mathsf {ABM}\cdot \mathbf {x}' + \begin{bmatrix} \mathbf {F}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {x} + \mathbf {e} \nonumber \\= & {} \begin{bmatrix} \mathbf {B}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {B}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {C}_\mathsf {ABM}\cdot \mathbf {x} + \begin{bmatrix} \mathbf {F}_\mathsf {ABM}\\ \hline \mathbf {R}_{t} \cdot \mathbf {F}_\mathsf {ABM}\end{bmatrix} \cdot \mathbf {x} + \mathbf {e} \nonumber \\= & {} \mathbf {A}_{t} \cdot \mathbf {x} + \mathbf {e} ~\in \mathbb {Z}^{2m} \nonumber \end{aligned}$$

(10)

It remains to show that $(\mathbf {x}',\mathbf {e}_0',\mathbf {e}')$ have the correct distribution. By applying Lemma 11 to the matrix $\mathbf {C}$ of (4) with $\mathbf {u} = \mathbf {t}_{\mathbf {x}}$, the conditional distribution of $\mathbf {x}'$ given $(\mathbf {t}_{\mathbf {x}},\underline{\mathbf {F}} \cdot \mathbf {x}+\underline{\mathbf {e}})$ is statistically close to $D^{S_{\underline{\mathbf {F}},\mathbf {t}_{\mathbf {x}},\mathbf {f}}}_{\varLambda ^\perp (\mathbf {C})+\mathbf {z}, \sqrt{\mathbf {\Sigma }},\mathbf {c} }$, where $\mathbf {z}$ is an arbitrary solution of $\mathbf {C} \cdot \mathbf {z} = \mathbf {t}_{\mathbf {x}}$. It is also efficiently samplable, by Theorem 1. This provides the claimed result.    $\square$

In the full version of the paper, we show that lattice trapdoors can also be used to obtain SIM-SO-CPA security from LTFs based on $\mathsf {DDH}$-like assumptions.