Abstract
We present a multi-input functional encryption scheme (MIFE) for the inner product functionality based on the k-Lin assumption in prime-order bilinear groups. Our construction works for any polynomial number of encryption slots and achieves adaptive security against unbounded collusion, while relying on standard polynomial hardness assumptions. Prior to this work, we did not even have a candidate for 3-slot MIFE for inner products in the generic bilinear group model. Our work is also the first MIFE scheme for a non-trivial functionality based on standard cryptographic assumptions, as well as the first to achieve polynomial security loss for a super-constant number of slots under falsifiable assumptions. Prior works required stronger non-standard assumptions such as indistinguishability obfuscation or multi-linear maps.
M. Abdalla—CNRS. Supported in part by SAFEcrypto (H2020 ICT-644729).
M. Raykova—Supported by NSF grants CNS-1633282, 1562888, 1565208, and DARPA SafeWare W911NF-15-C-0236, W911NF-16-1-0389.
H. Wee—CNRS and Columbia University. Supported in part by the ERC Project aSCEND (H2020 639554) and NSF Award CNS-1445424.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In a functional encryption (FE) scheme [11, 25], an authority can generate restricted decryption keys that allow users to learn specific functions of the encrypted messages and nothing else. That is, each FE decryption key \(\mathsf {sk}_f\) is associated with a function f and decrypting a ciphertext \(\mathsf {Enc}(x)\) with \(\mathsf {sk}_f\) results in f(x). Multi-input functional encryption (MIFE) introduced by Goldwasser et al. [19] is a generalization of functional encryption to the setting of multi-input functions. A MIFE scheme has several encryption slots and each decryption key \(\mathsf {sk}_f\) for a multi-input function f decrypts jointly ciphertexts \(\mathsf {Enc}(x_1), \ldots , \mathsf {Enc}(x_n)\) for all slots to obtain \(f(x_1, \ldots , x_n)\) without revealing anything more about the encrypted messages. The MIFE functionality provides the capability to encrypt independently messages for different slots. This facilitates scenarios where information, which will be processed jointly during decryption, becomes available at different points of time or is provided by different parties. MIFE has many applications related to computation and data-mining over encrypted data coming from multiple sources, which include examples such as executing search queries over encrypted data, processing encrypted streaming data, non-interactive differentially private data releases, multi-client delegation of computation, order-revealing encryption [10, 19]. The security requirement for FE and MIFE is that the decryption keys are resilient to collusion attacks, namely any group of users holding different decryption keys learns nothing about the underlying messages beyond what each of them could individually learn.
We now have several constructions of MIFE schemes, which can be broadly classified as follows: (i) feasibility results for general circuits [5, 6, 12, 19], and (ii) constructions for specific functionalities, notably comparison, which corresponds to order-revealing encryption [10]. Unfortunately, all of these constructions rely on indistinguishability obfuscation, single-input FE for circuits, or multi-linear maps [15, 16], which we do not know how to instantiate under standard and well-understood cryptographic assumptions.Footnote 1
1.1 Our Contributions
In this work, we present a multi-input functional encryption scheme (MIFE) for the inner product functionality based on the k-Lin assumption in prime-order bilinear groups. This is the first MIFE scheme for a non-trivial functionality based on standard cryptographic assumptions with polynomial security loss, and for any polynomial number of slots and secure against unbounded collusions.
Concretely, the functionality we consider is that of “bounded-norm” multi-input inner product: each function is specified by a collection of n vectors \(\mathbf {y}_1,\ldots ,\mathbf {y}_n\), takes as input n vectors \(\mathbf {x}_1,\ldots ,\mathbf {x}_n\), and outputs
We require that the \(\mathbf {x}_1,\ldots ,\mathbf {x}_n,\mathbf {y}_1,\ldots ,\mathbf {y}_n\) have bounded norm, and inner product is computed over the integers. The functionality is a natural generalization of single-input inner product functionality introduced by Abdalla et. al [1], and studied in [1, 2, 4, 7, 13], and captures several useful computations arising in the context of data-mining. A summary of our results and prior works on single-input inner product is shown in Fig. 1.
Summary of constructions from cyclic or bilinear groups. We have 8 security notions xx-yy-zzz where xx \(\in \) {one, many} refers to the number of challenge ciphertexts; yy \(\in \) {SEL, AD} refers to encryption queries are selectively or adaptively chosen; zzz \(\in \) {IND, SIM} refers to indistinguishability vs simulation-based security.
Prior Approaches. Prior constructions of MIFE schemes in [10] requires (at least) nm-linear maps for n slots with m-bit inputs as they encode each input bit for each slot into a fresh level of a multi-linear map. In addition, there is typically a security loss that is exponential in n due to the combinatorial explosion arising from combining different ciphertexts across the slots. In the case of inner product, one can hope to reduce the multi-linearity to n by exploiting linearity as in the single-input FE; indeed, this was achieved in two independent works [22, 23]Footnote 2 showing how to realize a two-slot MIFE for inner product over bilinear groups. We stress that our result is substantially stronger: we show how to realize n-slot MIFE for inner product for any polynomial n over bilinear groups under standard assumptions, while in addition avoiding the exponential security loss. In particular, we deviate from the prior approaches of encoding each slot into a fresh level of a multi-linear map. We stress that prior to this work, we do not even have a candidate for 3-slot MIFE for inner product in the generic bilinear group model.
A Public-Key Scheme. Our first observation is that we can build a public-key MIFE for inner product by running n independent copies of a single-input FE for inner product. Combined with existing instantiations of the latter in [1], this immediately yields a public-key MIFE for inner product under the standard DDH in cyclic groups.
In a bit more detail, we recall the DDH-based public-key single-input FE scheme from [1]:Footnote 3
Decryption computes \([\langle \mathbf {x},\mathbf {y} \rangle ] = [\mathbf {x}+ \mathbf {w}s]^{\!\scriptscriptstyle {\top }}\mathbf {y}\cdot [s]^{-\langle \mathbf {w},\mathbf {y} \rangle }\) and then recovers \(\langle \mathbf {x},\mathbf {y} \rangle \) by computing the discrete log.
Our public-key MIFE scheme is as follows:
We note that the encryption of \(\mathbf {x}_i\) uses fresh randomness \(s_i\); to decrypt, we need to know each \(\langle \mathbf {w}_i,\mathbf {y}_i \rangle \), and not just \(\langle \mathbf {w}_1,\mathbf {y}_1 \rangle +\cdots +\langle \mathbf {w}_n,\mathbf {y}_n \rangle \). In particular, an adversary can easily recover each \([\langle \mathbf {x}_i,\mathbf {y}_i \rangle ]\), whereas the ideal functionality should only leak the sum \(\sum _{i=1}^n \langle \mathbf {x}_i,\mathbf {y}_i \rangle \). In the public-key setting, it is easy to see that \(\langle \mathbf {x}_i,\mathbf {y}_i \rangle \) is in fact inherent leakage from the ideal functionality. Concretely, an adversary can always pad an encryption of \(\mathbf {x}_i\) in the i’th slot with encryptions of \(\mathbf {0}\)’s in the remaining \(n-1\) slots and then decrypt.
Our Main Scheme. The bulk of this work lies in constructing a multi-input FE for inner product in the private-key setting, where we can no longer afford to leak \(\langle \mathbf {x}_i,\mathbf {y}_i \rangle \). We modify the previous scheme by introducing additional rerandomization into each slot with the use of bilinear groups as follows:
The ciphertext \(\mathsf {ct}_{\mathbf {x}_i}\) can be viewed as encrypting \(\mathbf {x}_i \Vert z_i\) using the single-input FE, where \(z_1,\ldots ,z_n\) are part of \({\mathsf {msk}}\). In addition, we provide a single-input FE key for \(\mathbf {y}_i \Vert r\) in the secret key, where a fresh r is sampled for each key. Decryption proceeds as follows: first compute
and then
The intuition underlying security is that by the DDH assumption \([z_ir]_T\) is pseudorandom and helps mask the leakage about \(\langle \mathbf {x}_i,\mathbf {y}_i \rangle \) in \([\langle \mathbf {x}_i,\mathbf {y}_i \rangle + z_i r]_T\); in particular,
constitutes a computational secret-sharing of \([\langle \mathbf {x}_1,\mathbf {y}_1 \rangle + \cdots + \langle \mathbf {x}_n,\mathbf {y}_n \rangle ]_T\), even upon reusing \(z_1,\ldots ,z_n\) as long as we pick a fresh r. In addition, sharing the same exponent r across n elements in the secret key helps prevent mix-and-match attacks across secret keys.
Our main technical result is that a variant of the private-key MIFE scheme we just described selective indistinguishability-based security under the k-Lin assumption in bilinear groups; a straight-forward extension of an impossibility in [3, 11] rules out simulation-based security. Our final scheme as described in Fig. 6 remains quite simple and achieves good concrete efficiency. We focus on selective security in this overview, and explain at the end the additional ideas needed to achieve adaptive security.
Overview of Security Proof. There are two main challenges in the security proof: (i) avoiding leakage beyond the ideal functionality, (ii) avoiding super-polynomial hardness assumptions. Our proof proceeds in two steps: first, we establish security with a single challenge ciphertext per slot, and from which we bootstrap to achieve security with multiple challenge ciphertexts per slot. We will address the first challenge in the first step and the second challenge in the second. For notation simplicity, we focus on the setting with \(n=2\) slots and a single key query \(\mathbf {y}_1 \Vert \mathbf {y}_2\).
Step 1. To prove indistinguishability-based security, we want to switch encryptions \(\mathbf {x}^0_1,\mathbf {x}^0_2\) to encryptions of \(\mathbf {x}^1_1,\mathbf {x}^1_2\). Here, the leakage from the ideal functionality imposes the restriction that
and this is the only restriction we can work with. The natural proof strategy is to introduce an intermediate hybrid that generates encryptions of \(\mathbf {x}^1_1,\mathbf {x}^0_2\). However, to move from encryptions \(\mathbf {x}^0_1,\mathbf {x}^0_2\) to this hybrid, we would require that \(\langle \mathbf {x}^0_1 \Vert \mathbf {x}^0_2,\mathbf {y}_1 \Vert \mathbf {y}_2 \rangle = \langle \mathbf {x}^1_1 \Vert \mathbf {x}^0_2,\mathbf {y}_1 \Vert \mathbf {y}_2 \rangle \), which implies the extraneous restriction \(\langle \mathbf {x}^0_1,\mathbf {y}_1 \rangle = \langle \mathbf {x}^1_1,\mathbf {y}_1 \rangle \). (Indeed, the single-input inner product scheme in [7] imposes extraneous restrictions to overcome similar difficulties in the function-hiding setting.)
To overcome this challenge, we rely on a single-input FE that achieves simulation-based security, which allows us to avoid the intermediate hybrid. See Theorem 1 and Remark 4 for further details.
Step 2. Next, we consider the more general setting with \(Q_1\) challenge ciphertexts in the first slot and \(Q_2\) in the second, but still a single key query. We achieve security loss \(O(Q_1 + Q_2)\) for two slots, and more generally, \(O(Q_1 + \cdots + Q_n)\) —as opposed to \(Q_1 Q_2 \cdots Q_n\) corresponding to all possible combinations of the challenge ciphertexts— for n slots.
Our first observation is that we can bound the leakage from the ideal functionality by \(O(Q_1 + Q_2)\) relations (the trivial bound being \(Q_1 \cdot Q_2\)). Denote the j’th ciphertext query in the i’th slot by \(\mathbf {x}^{j,b}_i\), where b is the challenge bit. By decrypting the encryptions of \(\mathbf {x}^{2,b}_1,\mathbf {x}^{1,b}_2\) and \(\mathbf {x}^{1,b}_1,\mathbf {x}^{1,b}_2\) and substracting the two, the adversary learns \(\langle \mathbf {x}^{2,b}_1 - \mathbf {x}^{1,b}_1,\mathbf {y}_1 \rangle \) and more generally, \(\langle \mathbf {x}^{j,b}_i - \mathbf {x}^{1,b}_i,\mathbf {y}_i \rangle \). Indeed, these are essentially the only constraints we need to work with, namely:
Next, we need to translate the bound on the constraints to a \(O(Q_1+Q_2)\) bound on the security loss in the security reduction. We will switch from encryptions of \(\mathbf {x}^{j,0}_i\) to those of \(\mathbf {x}^{j,1}_i\) as follows: we write \(\mathbf {x}^{j,0}_i = \mathbf {x}^{1,0}_i+(\mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i)\).
We can switch the first terms in the sums from \(\mathbf {x}^{1,0}_i\) to \(\mathbf {x}^{1,1}_i\) using security for a single challenge ciphertext, and then switch \(\mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i\) to \(\mathbf {x}^{j,1}_i-\mathbf {x}^{1,1}_i\) by relying on security of the underlying single-input FE and the fact that \(\langle \mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i,\mathbf {y}_i \rangle = \langle \mathbf {x}^{j,1}_i-\mathbf {x}^{1,1}_i,\mathbf {y}_i \rangle \). Here, we will require that the underlying single-input FE satisfies a malleability property, namely given \(\varDelta \), we can maul an encryption of \(\mathbf {x}\) into that of \(\mathbf {x}+\varDelta \). Note that this does not violate security because given \(\langle \mathbf {x},\mathbf {y} \rangle ,\mathbf {y},\varDelta \), we can efficiently compute \(\langle \mathbf {x}+\varDelta ,\mathbf {y} \rangle \). See Theorem 2 for further details.
Extension to Adaptive Security. The previous argument for selective security requires to embed the challenge into the setup parameters. To circumvent this issue, we use a two-step strategy for the adaptive security proof of MIFE. The first step uses an adaptive argument (this is essentially the argument used for the selective case, but applied to parameters that are picked at setup time), while the second step uses a selective argument, with perfect security. Thus, we can use complexity leveraging without incurring an exponential security loss, since the exponential term is multiplied by a zero term. The idea of using complexity leveraging to deduce adaptive security from selective security when the security is perfect, already appears in [27, Remark 1].
Theoretical Perspective. The focus of this work is on obtaining constructions for a specific class of functions with good concrete efficiency. Nonetheless, we believe that our results do shed some new insights into general feasibility results for MIFE:
-
First, our results are indicative of further qualitative differences between MIFE in the public-key and the private-key settings. Indeed, we already know that the security guarantees are quite different due to additional inherent leakages in the public-key setting. In the case of order-revealing encryption [10], the differences are sufficient to enable positive results in the private-key setting, while completely ruling out any construction in the public-key setting. Our results hint at a different distinction, where the private-key setting seems to require qualitative stronger assumptions than in the public-key setting, namely the use of pairings.
-
Next, our results provide the first evidence supporting the intuition that MIFE requires qualitatively stronger assumptions than FE, but not too much stronger. Concretely, for the inner product FE, we have existing positive results under the DDH assumption in pairing-free groups. Prior to this work, it was not clear if we could extend the positive results to MIFE for n-ary inner product under the same assumptions, or if n-ary inner product would already require the same complex assumptions as MIFE for circuits. Our results suggest a rather different picture, namely that going from single-input to multi-input should require no more than an extra level of multi-linearity, even for restricted functionalities. The situation is somewhat different for general circuits, where we now know that going from single-input to multi-input incurs no more than a quantitative loss in the underlying assumptions [5, 12].
-
Finally, we presented the first MIFE for a non-trivial functionality that polynomial security loss for a super-constant number of slots under falsifiable assumptions. Recall that indistinguishability obfuscation and generic multi-linear maps are not falsifiable, whereas the constructions based on single-input FE in [5, 8, 12] incur a security loss which is exponential in the number of slots. Indeed, there is a reason why prior works relied on non-falsifiable assumptions or super-polynomial security loss. Suppose an adversary makes \(Q_0\) key queries, and \(Q_1,\ldots ,Q_n\) ciphertext queries for the n slots. By combining the ciphertexts and keys in different ways, the adversary can learn \(Q_0 Q_1 \cdots Q_n\) different decryptions. When n is super-constant, the winning condition in the security game may not be efficiently checkable in polynomial-time, hence the need for either a non-falsifiable assumption or a super-polynomial security loss. To overcome this difficulty, we show that for inner product, we can exploit linearity to succinctly characterize the \(Q_0Q_1\cdots Q_n\) constraints by roughly \(Q_0 \cdot (Q_1 + \cdots Q_n)\) constraints.
1.2 Discussion
Beyond Inner Product? Our constructions and techniques may seem a-priori largely tailored to the inner product functionality and properties of bilinear groups. We clarify here that our high-level approach (which builds upon [9, 27]) may be applicable beyond inner product, namely:
-
i.
start with a multi-input FE that is only secure for a single ciphertext per slot and one secret key, building upon a single-input FE whose security is simulation-based for a single ciphertext (in our case, this corresponds to introducing the additional \(z_1,\ldots ,z_n\) to hide the intermediate computation \(\langle \mathbf {x}_i,\mathbf {y}_i \rangle \));
-
ii.
achieve security for a single ciphertext per slot and multiple secret keys, by injecting additional randomness to the secret keys to prevent mix-and-match attacks (for this, we replaced \(z_1,\ldots ,z_n\) with \(z_1 r, \ldots ,z_n r,r\) in the exponent);
-
iii.
“bootstrap” to multiple ciphertexts per slot, where we also showed how to avoid incurring an exponential security loss.
In particular, using simulation-based security for i. helped us avoid additional leakage beyond what is allowed by the ideal functionality.
Additional Related Work. Goldwasser et al. [19] showed that both two-input public-key MIFE as well as n-input private-key MIFE for circuits already implies indistinguishability obfuscation for circuits.
There have also been several works that proposed constructions for private-key multi-input functional encryption. The work of Boneh et al. [10] constructs a single-key MIFE in the private key setting, which is based on multilinear maps and is proven secure in the idealized generic multilinear map model. Two other papers explore the question how to construct multi-input functional encryption starting from the single input variant. In their work [5] Ananth and Jain demonstrate how to obtain selectively secure MIFE in the private key setting starting from any general-purpose public key functional encryption. In an independent work, Brakerski et al. [12] reduce the construction of private key MIFE to general-purpose private key (single input) functional encryption. The resulting scheme achieves selective security when the starting private key FE is selectively secure. Additionally in the case when the MIFE takes any constant number of inputs, adaptive security for the private key FE suffices to obtain adaptive security for the MIFE construction as well. The constructions in that work provide also function hiding properties for the MIFE encryption scheme.
While this line of work reduces MIFE to single-input FE for general-purpose constructions, the only known instantiations of construction for public and private key functional encryption with unbounded number of keys require either indistinguishability obfuscation [16] or multilinear maps with non-standard assumptions [17]. We stress that the transformations from single-input to MIFE in [5, 12] are not applicable in the case of inner product since these transformations require that the single-input FE for complex functionalities related to computing a PRF, which is not captured by the simple inner functionality.
Open Problems. One natural open problem is to eliminate the use of pairings in MIFE for inner product; we think such a result would be quite surprising though. Another open problem is to achieve function privacy, as considered in the setting of single-input inner product functional encryption in [7, 13]. Note that these latter results require pairings. Our first guess is that it would be possible to achieve private-key, function-hiding MIFE for inner product under the k-Lin assumption in bilinear groups.
2 Preliminaries
Notation. We denote by \(s \leftarrow _\mathrm{{R}}S\) the fact that s is picked uniformly at random from a finite set S. By PPT, we denote a probabilistic polynomial-time algorithm. Throughout, we use \(1^\lambda \) as the security parameter. We use lower case boldface to denote (column) vectors and upper case boldface to denote matrices.
Cryptographic Assumptions. We follow the notation and algebraic framework for Diffie-Hellman-like assumptions in [14]. We fix a pairing group \(\mathcal {PG}:= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\) with \(e: \mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) of prime order q, where q is a prime of \(\varTheta (\lambda )\) bits. We use the implicit representation notation for group elements: for fixed generators \(g_1\) and \(g_2\) of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively, and for a matrix \(\mathbf {M}\) over \(\mathbb {Z}_q\), we define \([\mathbf {M}]_1:= g_1^{\mathbf {M}}\) and \([\mathbf {M}]_2 := g_2^{\mathbf {M}}\), where exponentiation is carried out component-wise.
We recall the definitions of the Matrix Decision Diffie-Hellman (MDDH) Assumption [14].
Definition 1
(Matrix Distribution). Let \(k,\ell \in \mathbb {N}\), with \(\ell > k\). We call \(\mathcal {D}_{\ell ,k}\) a matrix distribution if it outputs matrices in \(\mathbb {Z}_q^{\ell \times k}\) of full rank k in polynomial time. We write \(\mathcal {D}_k := \mathcal {D}_{k+1,k}\).
Without loss of generality, we assume the first k rows of \(\mathbf {A}\leftarrow _\mathrm{{R}}\mathcal {D}_{\ell ,k}\) form an invertible matrix. The \(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman problem is to distinguish the two distributions \(([\mathbf {A}], [\mathbf {A}\mathbf {w}])\) and \(([\mathbf {A}],[\mathbf {u}])\) where \(\mathbf {A}\leftarrow _\mathrm{{R}}\mathcal {D}_{\ell ,k}\), \(\mathbf {w}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\) and \(\mathbf {u}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{\ell }\).
Definition 2
( \(\mathcal {D}_{k}\) -Matrix Diffie-Hellman Assumption \(\mathcal {D}_{k}\) -MDDH). Let \(\mathcal {D}_{k}\) be a matrix distribution. We say that the \(\mathcal {D}_{k}\)-Matrix Diffie-Hellman (\(\mathcal {D}_{k}\)-MDDH) Assumption holds relative to \(\mathcal {PG}\) in \({\mathbb {G}}_s\) for \(s \in \{1,2\}\), if for all PPT adversaries \(\mathcal {A}\), there exists a negligible function \({\mathsf {Adv}}\) such that:
where the probability is taken over \(\mathbf {A}\leftarrow _\mathrm{{R}}\mathcal {D}_{k}, \mathbf {w}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^k, \mathbf {u}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{k+1}\).
For each \(k \ge 1\), [14] specifies distributions \(\mathcal {L}_k\), \(\mathcal {SC}_k\), \(\mathcal {C}_k\) (and others) over \(\mathbb {Z}_q^{(k+1)\times k}\) such that the corresponding \(\mathcal {D}_k\)-MDDH assumptions are generically secure in bilinear groups and form a hierarchy of increasingly weaker assumptions. \(\mathcal {L}_k\)-MDDH is the well known k-Linear Assumption k-Lin with 1-Lin = DDH. In this work we are mostly interested in the uniform matrix distribution \(\mathcal {U}_{\ell ,k}\).
Definition 3
(Uniform Distribution). Let \(\ell ,k\in \mathbb {N}\), with \(\ell > k\). We denote by \(\mathcal {U}_{\ell ,k}\) the uniform distribution over all full-rank \(\ell \times k\) matrices over \(\mathbb {Z}_q\). Let \(\mathcal {U}_k := \mathcal {U}_{k+1,k}\).
Let \(Q \ge 1\). For \(\mathbf {W}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{k \times Q},\mathbf {U}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{(k+1) \times Q}\), we consider the Q-fold \(\mathcal {U}_{\ell ,k}\)-MDDH Assumption which consists in distinguishing the distributions \(([\mathbf {A}], [\mathbf {A}\mathbf {W}])\) from \(([\mathbf {A}], [\mathbf {U}])\). That is, a challenge for the Q-fold \(\mathcal {U}_{\ell ,k}\)-MDDH Assumption consists of Q independent challenges of the \(\mathcal {U}_{\ell ,k}\)-MDDH Assumption (with the same \(\mathbf {A}\) but different randomness \(\mathbf {w}\)). We recall in Lemma 1 the random self reducibility of the Q-fold \(\mathcal {U}_{\ell ,k}\)-MDDH assumption, namely, the fact that it reduces to the 1-fold \(\mathcal {U}_k\) assumption.
Lemma 1
( \(\mathcal {U}_{k}\) -MDDH \(\Rightarrow \) Q -fold \(\mathcal {U}_{\ell ,k}\) -MDDH [14, 18]). Let \(\ell ,k \in \mathbb {N}^*\), with \(\ell > k\), and \(s \in \{1,2\}\). For any PPT adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {B}\) such that
where \(\mathsf {Adv}^{Q\text {-}\mathcal {U}_{\ell ,k}\text {-}\textsc {mddh}}_{{\mathbb {G}}_s,\mathcal {A}}(\lambda ) := | \Pr [\mathcal {A}(\mathcal {PG},[\mathbf {A}]_s, [\mathbf {A}\mathbf {W}]_s)=1]-\Pr [\mathcal {A}(\mathcal {PG},[\mathbf {A}], [\mathbf {U}]) =1] |\) and the probability is taken over \(\mathbf {A}\leftarrow _\mathrm{{R}}\mathcal {U}_{\ell ,k}, \mathbf {W}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{k \times Q}, \mathbf {U}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{(k+1) \times Q}\).
Among all possible matrix distributions \(\mathcal {D}_k\), the uniform matrix distribution \(\mathcal {U}_k\) is the hardest possible instance, so in particular k-Lin \(\Rightarrow \mathcal {U}_k\)-MDDH, as stated in Lemma 2.
Lemma 2
( \(\mathcal {D}_k\) -MDDH \(\Rightarrow \mathcal {U}_k\) -MDDH, [14]). Let \(\mathcal {D}_k\) be a matrix distribution. For any PPT adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {B}\) such that \(\mathsf {Adv}^{\mathcal {U}_k\text {-}\textsc {mddh}}_{{\mathbb {G}}_s,\mathcal {B}}(\lambda ) \le \mathsf {Adv}^{\mathcal {D}_k\text {-}\textsc {mddh}}_{{\mathbb {G}}_s,\mathcal {A}}(\lambda )\).
3 Definitions for Multi-input Functional Encryption
We recall the definitions for multi-input functional encryption from [19]. We focus here on the private-key setting, which allows us to simplify the definitions.
Definition 4
(Multi-input Function Encryption). Let \(\{ \mathcal {F}_n \}_{n \in \mathbb {N}}\) be an ensemble where each \(\mathcal {F}_n\) is a family of n-ary functions. A function \(f \in \mathcal {F}_n\) is defined as follows \(f : \mathcal {X}_{1} \times \ldots \times \mathcal {X}_{n} \rightarrow \mathcal {Y}\). A multi-input functional encryption scheme \(\mathcal {MIFE}\) for \(\mathcal {F}\) consists of the following algorithms:
-
\(\mathsf {Setup}(1^\lambda , \mathcal {F}_n)\): on input the security parameter \(\lambda \) and a description of \(\mathcal {F}_n \in \mathcal {F}\), outputs a master public key \(\mathsf {mpk}\) Footnote 4 and a master secret key \({\mathsf {msk}}\). All of the remaining algorithms get \(\mathsf {mpk}\) as part of its input.
-
\(\mathsf {Enc}({\mathsf {msk}},i,x_i)\): on input the master secret key \({\mathsf {msk}}\), \(i \in [n]\), and a message \(x_i \in \mathcal {X}_i\), outputs a ciphertext \(\mathsf {ct}\). We assume that each ciphertext has an associated index i, which denotes what slot this ciphertext can be used for. If \(n=1\), we omit the input i.
-
\(\mathsf {KeyGen}({\mathsf {msk}}, f)\): on input the master secret key \({\mathsf {msk}}\) and a function \(f \in \mathcal {F}_n\), outputs a decryption key \(\mathsf {sk}_f\).
-
\(\mathsf {Dec}(\mathsf {sk}_f,f,\mathsf {ct}_{1}, \ldots , \mathsf {ct}_n)\): on input a decryption key \(\mathsf {sk}_f\) for function f and n ciphertexts, outputs a string \(y \in \mathcal {Y}\).
The scheme \(\mathcal {MIFE}\) is correct if for all \(f \in \mathcal {F}\) and all \(x_i \in \mathcal {X}_i\) for \(1 \le i \le n\), we have
where the probability is taken over the coins of \(\mathsf {Setup}\), \(\mathsf {KeyGen}\) and \(\mathsf {Enc}\).
3.1 Security Notions
Following [3], we may consider 8 security notions xx-yy-zzz where xx \(\in \) {one, many} refers to the number of challenge ciphertexts; yy \(\in \) {SEL, AD} refers to encryption queries are selectively or adaptively chosen; zzz \(\in \) {IND, SIM} refers to indistinguishability vs simulation-based security. We have the following trivial relations: many \(\Rightarrow \) one, AD \(\Rightarrow \) SEL, and the following standard relations: SIM \(\Rightarrow \) IND, and one-yy-IND \(\Rightarrow \) many-yy-IND, the latter in the public-key setting. Here, we focus on {one,many}-SEL-IND and one-SEL-SIM, which are the notions most relevant to our positive results.
Definition 5
(xx-SEL-IND-secure MIFE). For every multi-input functional encryption \(\mathcal {MIFE} := (\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) for \(\mathcal {F}\), every security parameter \(\lambda \), every stateful adversary \(\mathcal {A}\), and every xx \(\in \) {one,many}, the advantage of \(\mathcal {A}\) is defined as
where the experiments are defined as follows:

where \(\mathcal {A}\) only makes queries f to \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\) satisfying
for all \(j_1,\ldots ,j_1 \in [Q_1] \times \cdots \times [Q_n]\). For xx \(=\) one, we require additionally that the adversary \(\mathcal {A}\) only sends one challenge per slot, i.e. for all \(i \in [n]\), \(Q_i = 1\).
The private key multi-input functional encryption \(\mathcal {MIFE}\) is xx-SEL-IND-secure if for every PPT adversary \(\mathcal {A}\), there exists a negligible function \({\mathsf {negl}}\) such that for all \(\lambda \in \mathbb {N}\): \(\mathsf {Adv}^{\mathcal {MIFE}, xx\text {-}SEL\text {-}IND}_{\mathcal {A}}(\lambda ) = {\mathsf {negl}}(\lambda )\).
Remark 1
(winning condition). Note that the winning condition is in general not efficiently checkable because of the combinatorial explosion in the restriction on the queries.
Next, we present the simulation-based security definition for MIFE, in the setting with a single challenge ciphertext per slot.
Definition 6
(one-SEL-SIM-secure FE). A single-input functional encryption \(\mathcal {FE}\) for function \(\mathcal {F}\) is one-SEL-SIM-secure if there exists a PPT simulatorFootnote 5 \((\mathsf {{\widetilde{Setup}}},\mathsf {{\widetilde{Encrypt}}},\mathsf {{\widetilde{KeyGen}}})\) such that for every PPT adversary \(\mathcal {A}\) and every \(\lambda \in \mathbb {N}\), the following two distributions are computationally indistinguishable:

The oracle \(\mathcal {O}(\cdot )\) in the above ideal experiment has access to an oracle that provides the value \(\langle \mathbf {x}, \mathbf {y} \rangle \), for each \(\mathbf {y}\in \mathbb {Z}_p^{m}\) queried to \(\mathcal {O}(\cdot )\). Then, \(\mathcal {O}(\cdot )\) returns \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\mathbf {y},\langle \mathbf {x},\mathbf {y} \rangle )\).
Namely, for every stateful adversary \(\mathcal {A}\),we define
and we require that for every PPT \(\mathcal {A}\), there exists a negligible function \({\mathsf {negl}}\) such that for all \(\lambda \in \mathbb {N}\), \(\mathsf {Adv}^{\mathcal {FE}, one\text {-}SEL\text {-}SIM}(\lambda ,\mathcal {A}) = {\mathsf {negl}}(\lambda )\).
Zero vs Multiple Queries in Private-Key Setting. It is convenient in our proof of security to assume that \(Q_1,\ldots ,Q_n \ge 1\), that is, there is at least one ciphertext for each encryption slot, which is where the technical bulk of the work lies as we would need to reason about leakage from the ideal functionality. In the setting where some \(Q_i = 0\), the ideal functionality leaks nothing, and here, we can easily achieve semantic security for all of the messages being encrypted in the private key MIFE setting, via the following simple generic transformation.
Lemma 3
Let \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) be a private key MIFE construction for n-input functions in the class \(\mathcal {F}_n\), which satisfies any xx-yy-zzz MIFE security definition when the adversary receives at least one ciphertext for each encryption slot. Let \((\mathsf {Gen}_{\mathsf {SE}}, \mathsf {Enc}_{\mathsf {SE}}, \mathsf {Dec}_{\mathsf {SE}})\) be symmetric key encryption. The private key MIFE scheme \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) described in Fig. 2 satisfies xx-yy-zzz security without any restrictions on the ciphertext challenge sets.
Proof
(Sketch). We consider two cases:
-
Case 1: there exists some \(i \in [n]\) for which \(Q_i = 0\). Here, \(k_i\) and thus \(\mathsf {K}\) is perfectly hidden from the adversary. Then, security follows readily from semantic security of \((\mathsf {Gen}_{\mathsf {SE}}, \mathsf {Enc}_{\mathsf {SE}}, \mathsf {Dec}_{\mathsf {SE}})\).
-
Case 2: for all i, \(Q_i \ge 1\). Here, security follows immediately from that of \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\). \(\square \)
3.2 Inner Product Functionality
Multi-input Inner Product. We construct a multi-input functional encryption that supports the class of multi-input bounded-norm inner product functions, which is defined as \(\mathcal {F}_n^{m,B}= \{ f_{\mathbf {y}_1,\ldots ,\mathbf {y}_n}: (\mathbb {Z}^m)^n \rightarrow \mathbb {Z}\}\) where
We require that the norm of the inner product of any two vector components from function and input \(\langle \mathbf {x},\mathbf {y} \rangle \) is bounded by B. This bound will determine the parameters of the bilinear map groups that we will be using in our constructions; in particular, we will choose a target group that has order \(q \gg n\cdot B\). To simplify naming conventions, we will omit “bounded-norm” for the rest of the paper, but we will always refer to a multi-input inner-product functionality with this property.
Remark on Leakage. Let \((\mathbf {x}^{j,0}_i,\mathbf {x}^{j,1}_i)_{i \in [n], j \in [Q_i]}\) be the ciphertext queries, and \(\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n\) be a secret key query. For all slots \(i \in [n]\), all \(j \in [Q_i]\), and all bits \(b \in \{0,1\}\), the adversary can learn \(\langle \mathbf {x}^{j,b}_i-\mathbf {x}^{j,b}_i,\mathbf {y}_i \rangle \) via the ideal functionality. In the IND security game, this means the adversary is restricted to queries satisfying \(\langle \mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i,\mathbf {y}_i \rangle = \langle \mathbf {x}^{j,1}_i-\mathbf {x}^{1,1}_i,\mathbf {y}_i \rangle \). In the hybrid, we want to avoid additional constraints such as
4 Private-Key MIFE for Inner Product
In this section, we present a private-key MIFE for inner product that achieves many-SEL-IND security. We use a pairing group \(({\mathbb {G}}_1,{\mathbb {G}}_2,{\mathbb {G}}_T)\) with \(e: {\mathbb {G}}_1\times {\mathbb {G}}_2 \rightarrow {\mathbb {G}}_T\) of prime order q, where q is a prime of \(\varTheta (\lambda )\) bits. Our construction relies on the k-Lin Assumption in \({\mathbb {G}}_1\) and in \({\mathbb {G}}_2\) and is shown in Fig. 6.
We present our construction in two steps: first, in Sect. 4.1, we show how to construct a selectively-secure MIFE scheme starting from a single-input one-SEL-SIM scheme that satisfies some additional structural properties. Then, we show how to instantiate the underlying single-input scheme (cf. Fig. 7) and we present a self-contained description of the scheme in Fig. 6. We refer the reader to Sect. 1.1 for an overview of the construction.
4.1 Selectively-Secure, Multi-input Scheme from Single-Input Scheme
Main Construction. We build a private key multi-input FE \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) for the class \(\mathcal {F}_n^{m,B}\), starting from a private key one-SEL-SIM secure, single-input FE \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) for the class \(\mathcal {F}_1^{m+k,B}\). We present our construction in Fig. 3.
Correctness. Correctness follows readily from the correctness of the underlying scheme and the equation:
Finally, we use the fact that \(\langle \mathbf {x}_1 \Vert \cdots \Vert \mathbf {x}_n, \mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n \rangle \mod q = \langle \mathbf {x}_1 \Vert \cdots \Vert \mathbf {x}_n, \mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n \rangle \), since for all slots \(i \in [n]\), we have \(\langle \mathbf {x}_i,\mathbf {y}_i \rangle \le B\), and \(q> Bn\).
Multi-input functional encryption scheme \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) for the class \(\mathcal {F}_n^{m,B}\). \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) refers to the single-input functional encryption scheme for the class \(\mathcal {F}_1^{m+k,B}\).
Additional Requirements. The construction and the analysis requires that \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) satisfies the following structural properties:
-
The scheme can be instantiated over \({\mathbb {G}}_1\), where the ciphertext is a vector \([\mathbf {c}]_1\) over \({\mathbb {G}}_1\) and the secret key is a vector \(\mathbf {d}_i\) over \(\mathbb {Z}_q\).
-
\(\mathsf {Enc}\) is linearly homomorphic and public-key. More specifically, we only require that, given \(\mathsf {mpk},\mathsf {Enc}({\mathsf {msk}},\mathbf {x}),\mathbf {x}'\), we can generate a fresh random encryption of \(\mathbf {x}+\mathbf {x}'\), i.e. \(\mathsf {Enc}({\mathsf {msk}},\mathbf {x}+\mathbf {x}')\).
-
For correctness, \(\mathsf {Dec}\) should be linear in its inputs \((\mathbf {d},\mathbf {y})\) and \(\mathbf {c}\), so that \(\mathsf {Dec}([\mathbf {d}]_2,[\mathbf {y}]_2,[\mathbf {c}]_1) = [\mathsf {Dec}(\mathbf {d},\mathbf {y},\mathbf {c})]_T\in {\mathbb {G}}_T\) can be computed using a pairing.
-
For an efficient MIFE decryption, \(\mathsf {Dec}\) must work without any restriction on the norm of the output as long as the output is in the exponent.
-
Let \((\mathsf {{\widetilde{Setup}}},\mathsf {{\widetilde{Enc}}},\mathsf {{\widetilde{KeyGen}}})\) be the stateful simulator for the one-SEL-SIM security of the single-input inner-product FE scheme. We require that \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\cdot ,\cdot )\) is linear in its inputs \((\mathbf {y}, a)\), so that we can compute \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},[\mathbf {y}]_2,[a]_2) = [\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\mathbf {y},a)]_2\). This property is used in the proof of Lemma 5.
Remark 2
(notation). We use subscripts and superscripts for indexing over multiple copies, and never for indexing over positions or exponentiation. Concretely, the j’th ciphertext query in slot i is \(\mathbf {x}^j_i\).
Security. Theorem 1 and Theorem 2 below, together with the fact that one-SEL-SIM security implies one-SEL-IND security, which itself implies many-SEL-IND security for a public-key FE, such as \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen})\) used in the construction presented in Fig. 3, implies the many-SEL-IND security of the MIFE \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}')\).
Theorem 1
(one-SEL-IND Security of \(\mathcal {MIFE}\) ). Suppose the single-input FE \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) is one-SEL-SIM secure, and that the \(\mathcal {D}_k\)-MDDH assumption holds in \({\mathbb {G}}_2\). Then, the multi-input FE \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) is one-SEL-IND-secure.
That is, we show that our multi-input FE is selectively secure when there is only a single challenge ciphertext.
Game\(_i\) for \(i\in \{0,\ldots ,3\}\) for the proof of Theorem 1.
Proof
(of Theorem 1 ). We proceed via a series of Game\(_i\) for \(i \in \{0,\ldots ,3\}\), described in Fig. 4. Let \(\mathcal {A}\) be a PPT adversary, and \(\lambda \in \mathbb {N}\) be the security parameter.
Game \(_\mathbf{0}\) : is the experiment \(\mathbf {one\text {-}SEL\text {-}IND}^{\mathcal {MIFE}}\) (see Definition 5).
Game \(_\mathbf{1}\) : we replace \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc})\) by the efficient simulator \((\mathsf {{\widetilde{Setup}}},\mathsf {{\widetilde{KeyGen}}},\mathsf {{\widetilde{Enc}}})\), using the one-SEL-SIM security of \(\mathcal {FE}\), via a hybrid argument across all slots \(i \in [n]\) (cf Lemma 4).
Lemma 4
(Game \(_0\) to Game \(_1\) ). There exists a PPT adversary \(\mathcal {B}_1\) such that
Description of \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}')\) defining game \(0.\ell \) for the proof of Lemma 4.
Proof
In Game\(_1\), we replace \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen})\) by \((\mathsf {{\widetilde{Setup}}},\mathsf {{\widetilde{Enc}}},\mathsf {{\widetilde{KeyGen}}})\), which is a PPT simulator whose existence is ensured by the one-SEL-SIM security of \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc})\) (see Definition 6). A complete description of Games\(_0\) and Game\(_1\) is given in Fig. 4.
We use a hybrid argument, which involves hybrid Game\(_{0.\ell }\) for \(\ell \in \{0,\ldots ,n\}\), defined in Fig. 5, and we use \({\mathsf {Adv}}_{0,\ell }(\lambda ,\mathcal {A})\) to denote \(\Pr [\text {Game}_{0.\ell }(\lambda ,\mathcal {A})=1]\), where the probability is taken over the random coins of \(\mathcal {A}\) and Game\(_{0.\ell }\). Notice that Game\(_0\) and Game\(_1\) are identical to Game\(_{0.0}\) and Game\(_{0.n}\), respectively. For any \(\ell \in [n]\), we build a PPT adversary \(\mathcal {B}_{0.\ell }\) such that
-
Simulation of
 First, \(\mathcal {B}_{0.\ell }\) receives the challenge \(\{\mathbf {x}_i^b\}_{i \in [n], b \in \{0,1\}}\) from \(\mathcal {A}\). Then, it picks \(\beta \leftarrow _\mathrm{{R}}\{0,1\}\), \(\mathbf {z}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\) for all \(i \in [n]\), and sends \(\mathbf {x}_\ell ^\beta \Vert \mathbf {z}_\ell \) to the experiment it is interacting with, which is either \(\mathbf {REAL^{\mathcal {FE}}}\) or \(\mathbf {{\widetilde{IDEAL}}^{\mathcal {FE}}}\). Then, \(\mathcal {B}_{0.\ell }\) receives \(\mathsf {mpk}'_\ell \), and a ciphertext \(\mathsf {ct}\), which are either of the form \(\mathsf {mpk}'_\ell := \mathsf {mpk}_\ell \), where \(({\mathsf {msk}}_\ell ,\mathsf {mpk}_\ell ) \leftarrow \mathsf {Setup}(1^\lambda ,\mathcal {F}_1^{m+k,B})\), and \(\mathsf {ct}:= \mathsf {Enc}({\mathsf {msk}}_\ell ,\mathbf {x}_\ell ^\beta \Vert \mathbf {z}_\ell )\) if \(\mathcal {B}_{3.\ell }\) is interacting with the experiment \(\mathbf {REAL^{\mathcal {FE}}}\); or of the form \(\mathsf {mpk}'_\ell := \mathsf {{\widetilde{mpk}}}_\ell \), where \((\mathsf {{\widetilde{msk}}}_\ell ,\mathsf {{\widetilde{mpk}}}_\ell ) \leftarrow \mathsf {{\widetilde{Setup}}}(1^\lambda ,\mathcal {F}_1^{m+k,B})\), \(\mathsf {ct}:= \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_\ell )\) if \(\mathcal {B}_{3.\ell }\) is interacting with the experiment \(\mathbf {{\widetilde{IDEAL}}^{\mathcal {FE}}}\). It samples \((\mathsf {{\widetilde{mpk}}}_i,\mathsf {{\widetilde{msk}}}_i) \leftarrow \mathsf {{\widetilde{Setup}}}(1^\lambda ,\mathcal {F}_1^{m+k,B})\) for \(i=1,\ldots ,\ell -1\), \((\mathsf {mpk}_i,{\mathsf {msk}}_i) \leftarrow \mathsf {Setup}(1^\lambda ,\mathcal {F}_1^{m+k,B})\) for \(i = \ell +1,\ldots ,n\), and returns \(\mathsf {mpk} := (\mathsf {{\widetilde{mpk}}}_1,\ldots ,\mathsf {{\widetilde{mpk}}}_{\ell -1},\mathsf {mpk}'_\ell ,{\mathsf {mpk}}_{\ell +1},\ldots ,\mathsf {mpk}_n)\) to \(\mathcal {A}\).
First, \(\mathcal {B}_{0.\ell }\) receives the challenge \(\{\mathbf {x}_i^b\}_{i \in [n], b \in \{0,1\}}\) from \(\mathcal {A}\). Then, it picks \(\beta \leftarrow _\mathrm{{R}}\{0,1\}\), \(\mathbf {z}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\) for all \(i \in [n]\), and sends \(\mathbf {x}_\ell ^\beta \Vert \mathbf {z}_\ell \) to the experiment it is interacting with, which is either \(\mathbf {REAL^{\mathcal {FE}}}\) or \(\mathbf {{\widetilde{IDEAL}}^{\mathcal {FE}}}\). Then, \(\mathcal {B}_{0.\ell }\) receives \(\mathsf {mpk}'_\ell \), and a ciphertext \(\mathsf {ct}\), which are either of the form \(\mathsf {mpk}'_\ell := \mathsf {mpk}_\ell \), where \(({\mathsf {msk}}_\ell ,\mathsf {mpk}_\ell ) \leftarrow \mathsf {Setup}(1^\lambda ,\mathcal {F}_1^{m+k,B})\), and \(\mathsf {ct}:= \mathsf {Enc}({\mathsf {msk}}_\ell ,\mathbf {x}_\ell ^\beta \Vert \mathbf {z}_\ell )\) if \(\mathcal {B}_{3.\ell }\) is interacting with the experiment \(\mathbf {REAL^{\mathcal {FE}}}\); or of the form \(\mathsf {mpk}'_\ell := \mathsf {{\widetilde{mpk}}}_\ell \), where \((\mathsf {{\widetilde{msk}}}_\ell ,\mathsf {{\widetilde{mpk}}}_\ell ) \leftarrow \mathsf {{\widetilde{Setup}}}(1^\lambda ,\mathcal {F}_1^{m+k,B})\), \(\mathsf {ct}:= \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_\ell )\) if \(\mathcal {B}_{3.\ell }\) is interacting with the experiment \(\mathbf {{\widetilde{IDEAL}}^{\mathcal {FE}}}\). It samples \((\mathsf {{\widetilde{mpk}}}_i,\mathsf {{\widetilde{msk}}}_i) \leftarrow \mathsf {{\widetilde{Setup}}}(1^\lambda ,\mathcal {F}_1^{m+k,B})\) for \(i=1,\ldots ,\ell -1\), \((\mathsf {mpk}_i,{\mathsf {msk}}_i) \leftarrow \mathsf {Setup}(1^\lambda ,\mathcal {F}_1^{m+k,B})\) for \(i = \ell +1,\ldots ,n\), and returns \(\mathsf {mpk} := (\mathsf {{\widetilde{mpk}}}_1,\ldots ,\mathsf {{\widetilde{mpk}}}_{\ell -1},\mathsf {mpk}'_\ell ,{\mathsf {mpk}}_{\ell +1},\ldots ,\mathsf {mpk}_n)\) to \(\mathcal {A}\). -
Simulation of
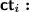 \(\mathcal {B}_{0.\ell }\) computes \(\mathsf {ct}_i := \mathsf {Enc}({\mathsf {msk}}_i,\mathbf {x}_i^{\beta } \Vert \mathbf {z}_i)\) for all \(i < \ell \) (note that \(\mathcal {B}_{0.\ell }\) can do so since it knows \({\mathsf {msk}}_i\), \(\mathbf {x}_i^\beta \), and \(\mathbf {z}_i\)), and computes \(\mathsf {ct}_i := \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_i)\) for all \(i > \ell \) (again, \(\mathcal {B}_{0.\ell }\) can do so since it knows \(\mathsf {{\widetilde{msk}}}_i\)). Finally, \(\mathcal {B}_{0.\ell }\) sets \(\mathsf {ct}_\ell := \mathsf {ct}\) and returns \(\{\mathsf {ct}_i\}_{i \in [n]}\) to \(\mathcal {A}\).
\(\mathcal {B}_{0.\ell }\) computes \(\mathsf {ct}_i := \mathsf {Enc}({\mathsf {msk}}_i,\mathbf {x}_i^{\beta } \Vert \mathbf {z}_i)\) for all \(i < \ell \) (note that \(\mathcal {B}_{0.\ell }\) can do so since it knows \({\mathsf {msk}}_i\), \(\mathbf {x}_i^\beta \), and \(\mathbf {z}_i\)), and computes \(\mathsf {ct}_i := \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_i)\) for all \(i > \ell \) (again, \(\mathcal {B}_{0.\ell }\) can do so since it knows \(\mathsf {{\widetilde{msk}}}_i\)). Finally, \(\mathcal {B}_{0.\ell }\) sets \(\mathsf {ct}_\ell := \mathsf {ct}\) and returns \(\{\mathsf {ct}_i\}_{i \in [n]}\) to \(\mathcal {A}\). -
Simulation of
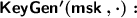 For each query \(\mathbf {y}_1 \Vert \ldots \Vert \mathbf {y}_n\) that \(\mathcal {A}\) makes to \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\), \(\mathcal {B}_{0.\ell }\) picks \(\mathbf {r}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\), and computes \(\mathbf {d}_i \leftarrow \mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i \Vert \mathbf {r},\langle \mathbf {x}_i^\beta \Vert \mathbf {z}_i, \mathbf {y}_i\Vert \mathbf {r} \rangle )\) for \(i = 1,\ldots ,\ell -1\), \(\mathbf {d}_i \leftarrow \mathsf {KeyGen}({\mathsf {msk}}_i,\mathbf {y}_i \Vert \mathbf {r})\) for \(i = \ell +1,\ldots ,n\). Then it computes \(\mathbf {d}_\ell \) by querying the oracle it has access to, which is \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\) in the experiment \(\mathbf {REAL^{\mathcal {FE}}}\), or \(\mathcal {O}(\cdot )\) in the experiment \(\mathbf {IDEAL^{\mathcal {FE}}}\), on input \(\mathbf {y}_\ell \Vert \mathbf {r}\). Then, it computes \(z := \langle \mathbf {z}_1 + \cdots + \mathbf {z}_n, \mathbf {r} \rangle \) and it returns \(\mathsf {sk}_{\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n} := \left( \{ [\mathbf {d}_i]_2\}_{i \in [n]}, [\mathbf {r}]_2,[z]_T\right) \).
For each query \(\mathbf {y}_1 \Vert \ldots \Vert \mathbf {y}_n\) that \(\mathcal {A}\) makes to \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\), \(\mathcal {B}_{0.\ell }\) picks \(\mathbf {r}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\), and computes \(\mathbf {d}_i \leftarrow \mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i \Vert \mathbf {r},\langle \mathbf {x}_i^\beta \Vert \mathbf {z}_i, \mathbf {y}_i\Vert \mathbf {r} \rangle )\) for \(i = 1,\ldots ,\ell -1\), \(\mathbf {d}_i \leftarrow \mathsf {KeyGen}({\mathsf {msk}}_i,\mathbf {y}_i \Vert \mathbf {r})\) for \(i = \ell +1,\ldots ,n\). Then it computes \(\mathbf {d}_\ell \) by querying the oracle it has access to, which is \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\) in the experiment \(\mathbf {REAL^{\mathcal {FE}}}\), or \(\mathcal {O}(\cdot )\) in the experiment \(\mathbf {IDEAL^{\mathcal {FE}}}\), on input \(\mathbf {y}_\ell \Vert \mathbf {r}\). Then, it computes \(z := \langle \mathbf {z}_1 + \cdots + \mathbf {z}_n, \mathbf {r} \rangle \) and it returns \(\mathsf {sk}_{\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n} := \left( \{ [\mathbf {d}_i]_2\}_{i \in [n]}, [\mathbf {r}]_2,[z]_T\right) \).
Finally, \(\mathcal {B}_{0.\ell }\) outputs 1 if \(\mathcal {A}\) outputs 1, 0 otherwise. It is clear that when \(\mathcal {B}_{0.\ell }\) interacts with the experiment \(\mathbf {REAL^{\mathcal {FE}}}\), it simulates the Game 0, whereas it simulates the Game 1 when it interacts with \(\mathbf {IDEAL^{\mathcal {FE}}}\). Therefore,
Summing up for all \(\ell \in [n]\), we obtain the lemma. \(\square \)
Game \(_\mathbf{2}\) : we replace the values \(\langle \mathbf {z}_i,\mathbf {r} \rangle \) used by \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\) to \({\tilde{z}}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q\), for all slots \(i \in [n]\), using the \(\mathcal {D}_k\)-MDDH assumption in \({\mathbb {G}}_2\) (cf Lemma 5).
Lemma 5
(Game \(_\mathbf{1}\) to Game \(_\mathbf{2}\) ). There exists a PPT adversary \(\mathcal {B}_2\) such that:
Proof
Here, we switch \(\{[\mathbf {r}]_2,[\langle \mathbf {z}_i, \mathbf {r} \rangle ]_2\}_{i \in [n]}\) used by \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\) to \(\{[\mathbf {r}]_2,[{\tilde{z}}_i]_2\}_{i \in [n]}\), where for all \(i \in [n]\), \(\mathbf {z}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\), \({\tilde{z}}_1,\ldots ,{\tilde{z}}_n \leftarrow _\mathrm{{R}}\mathbb {Z}_p\) and \(\mathbf {r}\leftarrow _\mathrm{{R}}\mathbb {Z}_q^{k}\). This is justified by the fact that \([\mathbf {r}^{\!\scriptscriptstyle {\top }}\Vert \langle \mathbf {z}_1,\mathbf {r} \rangle \Vert \cdots \Vert \langle \mathbf {z}_n,\mathbf {r} \rangle ]_2 \in {\mathbb {G}}_2^{1 \times (k+n)}\) is identically distributed to \([\mathbf {r}^{\!\scriptscriptstyle {\top }}\mathbf {U}^{\!\scriptscriptstyle {\top }}]_2\) where \(\mathbf {U}\leftarrow _\mathrm{{R}}\mathcal {U}_{k+n,k}\) (wlog. we assume that the upper k rows of \(\mathbf {U}\) are full rank), which is indistinguishable from a uniformly random vector over \({\mathbb {G}}_2^{1 \times (k+n)}\), that is, of the form: \([\mathbf {r}\Vert {\tilde{z}}_1 \Vert \cdots \Vert {\tilde{z}}_n]_2\), according to the \(\mathcal {U}_{k+n,k}\)-MDDH assumption. To do the switch simultaneously for all calls to \(\mathsf {KeyGen}\), that is, to switch \(\{[\mathbf {r}^j]_2,[\langle \mathbf {z}_i,\mathbf {r}^j \rangle ]_2\}_{i \in [n], j \in [Q_0]}\) to \(\{[\mathbf {r}^j]_2,[{\tilde{z}}^j_i]_2\}_{i \in [n], j \in [Q_0]}\), where \(Q_0\) denotes the number of calls to \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\), and for all \(i \in [n]\), \(\mathbf {z}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q^k\), \({\tilde{z}}^j_1,\ldots ,{\tilde{z}}^j_n \leftarrow _\mathrm{{R}}\mathbb {Z}_p\) and for all \(j \in [Q_0]\), \(\mathbf {r}^j \leftarrow _\mathrm{{R}}\mathbb {Z}_q^{k}\), we use the \(Q_0\)-fold \(\mathcal {U}_{k+n,k}\)-MDDH assumption. Namely, we build a PPT adversary \(\mathcal {B}'_2\) such that \({\mathsf {Adv}}_1(\mathcal {A}) - {\mathsf {Adv}}_2(\mathcal {A}) \le \mathsf {Adv}^{n\text {-fold }\mathcal {U}_{Q_0,k}\text {-}\textsc {mddh}}_{{\mathbb {G}}_2,\mathcal {B}'_2}(\lambda )\). This, together with Lemma 1 (\(\mathcal {U}_{k}\)-MDDH \(\Rightarrow \) n-fold \(\mathcal {U}_{Q_0,k}\)-MDDH), implies the lemma.
-
Simulation of
 Upon receiving an \(Q_0\)-fold \(\mathcal {U}_{k+n,k}\)-MDDH challenge $$\begin{aligned} \left( \mathcal {PG},[\mathbf {U}]_2 \in {\mathbb {G}}_2^{(k+n) \times k}, \left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2 \in {\mathbb {G}}_2^{(k+n) \times Q_0}\right) , \end{aligned}$$
Upon receiving an \(Q_0\)-fold \(\mathcal {U}_{k+n,k}\)-MDDH challenge $$\begin{aligned} \left( \mathcal {PG},[\mathbf {U}]_2 \in {\mathbb {G}}_2^{(k+n) \times k}, \left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2 \in {\mathbb {G}}_2^{(k+n) \times Q_0}\right) , \end{aligned}$$and the challenge \(\{\mathbf {x}_i^b\}_{i \in [n], b \in \{0,1\}}\) from \(\mathcal {A}\), \(\mathcal {B}_1'\) picks \(\beta \leftarrow _\mathrm{{R}}\{0,1\}\), samples \((\mathsf {{\widetilde{mpk}}}_i,\mathsf {{\widetilde{msk}}}_i) \leftarrow \mathsf {{\widetilde{Setup}}}(1^\lambda ,\mathcal {F}_1^{m+k,B})\) for \(i \in [n]\), and returns \(\mathsf {mpk} := (\mathsf {{\widetilde{mpk}}}_1,\ldots ,\mathsf {{\widetilde{mpk}}}_n)\) to \(\mathcal {A}\).
-
Simulation of
 \(\mathcal {B}'_2\) computes \(\mathsf {ct}_i := \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_i)\) for all \(i \in [n]\), which it can do since it knows \(\mathsf {{\widetilde{msk}}}_i\), and returns \(\{\mathsf {ct}_i\}_{i \in [n]}\) to \(\mathcal {A}\).
\(\mathcal {B}'_2\) computes \(\mathsf {ct}_i := \mathsf {{\widetilde{Enc}}}(\mathsf {{\widetilde{msk}}}_i)\) for all \(i \in [n]\), which it can do since it knows \(\mathsf {{\widetilde{msk}}}_i\), and returns \(\{\mathsf {ct}_i\}_{i \in [n]}\) to \(\mathcal {A}\). -
Simulation of
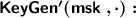 On the j’th query \(\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n\) of \(\mathcal {A}\) to \(\mathsf {KeyGen}'\), \(\mathcal {B}'_2\) sets \([\mathbf {r}^j]_2 := [\overline{\mathbf {h}^j}]_2\), where \(\overline{\mathbf {h}^j} \in \mathbb {Z}_q^k\) denotes the k-upper components of \(\mathbf {h}^j \in \mathbb {Z}_q^{k+n}\), and for each \(i \in [n]\), computes \([\mathbf {d}_i]_2 := [\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i\Vert \mathbf {r}^j,\langle \mathbf {x}_i^\beta ,\mathbf {y}_i \rangle + \mathbf {h}^j_{k+i})]_2\), where \(\mathbf {h}^j_{k+i}\) denotes the \(k+i\)’th coordinate of the vector \(\mathbf {h}^j \in \mathbb {Z}_p^{k+n}\). Here we rely on the fact that \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\cdot ,\cdot )\) is linear in its inputs \((\mathbf {y}, a)\), so that we can compute \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},[\mathbf {y}]_2,[a]_2) = [\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\mathbf {y},a)]_2\). Note that when \(\left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2\) is a real MDDH challenge, \(\mathcal {B}'_2\) simulate Game\(_1\), whereas it simulates Game\(_2\) when \(\left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2\) is uniformly random over \({\mathbb {G}}_1^{(k+n) \times Q_0}\). \(\square \)
On the j’th query \(\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n\) of \(\mathcal {A}\) to \(\mathsf {KeyGen}'\), \(\mathcal {B}'_2\) sets \([\mathbf {r}^j]_2 := [\overline{\mathbf {h}^j}]_2\), where \(\overline{\mathbf {h}^j} \in \mathbb {Z}_q^k\) denotes the k-upper components of \(\mathbf {h}^j \in \mathbb {Z}_q^{k+n}\), and for each \(i \in [n]\), computes \([\mathbf {d}_i]_2 := [\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i\Vert \mathbf {r}^j,\langle \mathbf {x}_i^\beta ,\mathbf {y}_i \rangle + \mathbf {h}^j_{k+i})]_2\), where \(\mathbf {h}^j_{k+i}\) denotes the \(k+i\)’th coordinate of the vector \(\mathbf {h}^j \in \mathbb {Z}_p^{k+n}\). Here we rely on the fact that \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\cdot ,\cdot )\) is linear in its inputs \((\mathbf {y}, a)\), so that we can compute \(\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},[\mathbf {y}]_2,[a]_2) = [\mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}},\mathbf {y},a)]_2\). Note that when \(\left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2\) is a real MDDH challenge, \(\mathcal {B}'_2\) simulate Game\(_1\), whereas it simulates Game\(_2\) when \(\left[ \mathbf {h}^1 \Vert \cdots \Vert \mathbf {h}^{Q_0}\right] _2\) is uniformly random over \({\mathbb {G}}_1^{(k+n) \times Q_0}\). \(\square \)
Game
\(_\mathbf{3}\)
: here the values \(\mathbf {d}_i\) for \(i \in [n]\), and z, computed by \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\), are of the form:  , and
, and  . In Lemma 6, we prove that Game\(_3\) and Game\(_2\) are perfectly indistinguishable, using a statistical argument that crucially relies on the fact that Game\(_3\) and Game\(_2\) are selective. In Lemma 7, we prove that no adversary can win Game\(_3\), using the restriction on the queries to \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\) and the challenge \(\{\mathbf {x}_i^b\}_{i \in [n]}\) imposed by the ideal functionality.
. In Lemma 6, we prove that Game\(_3\) and Game\(_2\) are perfectly indistinguishable, using a statistical argument that crucially relies on the fact that Game\(_3\) and Game\(_2\) are selective. In Lemma 7, we prove that no adversary can win Game\(_3\), using the restriction on the queries to \(\mathsf {KeyGen}'({\mathsf {msk}},\cdot )\) and the challenge \(\{\mathbf {x}_i^b\}_{i \in [n]}\) imposed by the ideal functionality.
Lemma 6
(Game \(_\mathbf{2}\) to Game \(_\mathbf{3}\) ). \({\mathsf {Adv}}_2(\mathcal {A}) = {\mathsf {Adv}}_3(\mathcal {A})\).
Proof
Here, we use the fact that for all \(\mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n \in (\mathbb {Z}_q^{m})^n\), for all \(\{\mathbf {x}_i^b \in \mathbb {Z}_q^m\}_{i \in [n], b \in \{0,1\}}\), all \(\beta \in \{0,1\}\), the following are identically distributed: \(\{{\tilde{z}}_i\}_{i \in [n]}\) and  , where \({\tilde{z}}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q\) for all \(i \in [n]\).
, where \({\tilde{z}}_i \leftarrow _\mathrm{{R}}\mathbb {Z}_q\) for all \(i \in [n]\).
For each query \(\mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n\), \(\mathsf {KeyGen}'({\mathsf {msk}}, \mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n)\) picks values \(\tilde{z_i} \leftarrow _\mathrm{{R}}\mathbb {Z}_q\) for \(i \in [n]\) that are independent of \(\mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n\) and the challenge \(\{\mathbf {x}_i^b \in \mathbb {Z}_q^m\}_{i \in [n], b \in \{0,1\}}\) (note that here we crucially rely on the fact the Game\(_{2}\) and Game\(_{3}\) are selective), therefore, using the previous fact, we can switch  to
to  without changing the distribution of the game. This way, \(\mathsf {KeyGen}'({\mathsf {msk}}, \mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n)\) computes \(\mathbf {d}_i \leftarrow \mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i \Vert \mathbf {r}, {\tilde{z}}_i)\) for all \(i \in [n]\), and \(z := {\tilde{z}}_1 + \ldots + {\tilde{z}}_n - \sum _{i=1}^n \langle \mathbf {x}_i^\beta , \mathbf {y}_i \rangle \), as in Game\(_3\). \(\square \)
without changing the distribution of the game. This way, \(\mathsf {KeyGen}'({\mathsf {msk}}, \mathbf {y}_1\Vert \cdots \Vert \mathbf {y}_n)\) computes \(\mathbf {d}_i \leftarrow \mathsf {{\widetilde{KeyGen}}}(\mathsf {{\widetilde{msk}}}_i,\mathbf {y}_i \Vert \mathbf {r}, {\tilde{z}}_i)\) for all \(i \in [n]\), and \(z := {\tilde{z}}_1 + \ldots + {\tilde{z}}_n - \sum _{i=1}^n \langle \mathbf {x}_i^\beta , \mathbf {y}_i \rangle \), as in Game\(_3\). \(\square \)
Lemma 7
(Game \(_\mathbf{3}\) ). \({\mathsf {Adv}}_3(\mathcal {A}) = 0\).
Proof
We use the fact that for all \(i\in [n]\), the query \((i,\mathbf {x}_i^0,\mathbf {x}_i^1)\) to \(\mathsf {Enc}'\) (recall that there can be at most one query per slot \(i \in [n]\)), and for all queries \(\mathbf {y}_1 \Vert \cdots \Vert \mathbf {y}_n\) to \(\mathsf {KeyGen}'\), by definition of the security game, we have:
Therefore, for each call to \(\mathsf {KeyGen}({\mathsf {msk}},\cdot )\), the value z, which is of the form \(z := \sum _i {\tilde{z}}_i - \sum _i\langle \mathbf {x}_i^\beta ,\mathbf {y}_i \rangle \), is independent of \(\beta \). Since the challenge ciphertext and the public key are also independent of \(\beta \), we have \({\mathsf {Adv}}_{3}(\mathcal {A})=0\). \(\square \)
Summing up, we proved that for all security parameter \(\lambda \in \mathbb {N}\) and all PPT adversaries \(\mathcal {A}\), the following holds.
-
In Lemma 4, we show that there exists a PPT adversary \(\mathcal {B}_1\) such that \({\mathsf {Adv}}_0(\mathcal {A}) - {\mathsf {Adv}}_1(\mathcal {A}) \le n \cdot \mathsf {Adv}^{\mathcal {FE}, one\text {-}SEL\text {-}SIM}(1^\lambda ,\mathcal {B}_1)\).
-
In Lemma 5, we show that there exists a PPT adversary \(\mathcal {B}_2\) such that \({\mathsf {Adv}}_1(\mathcal {A}) - {\mathsf {Adv}}_2(\mathcal {A}) \le \mathsf {Adv}^{\mathcal {U}_k\text {-}\textsc {mddh}}_{{\mathbb {G}}_2,\mathcal {B}_2}(\lambda ) +\frac{1}{q-1}\).
-
In Lemma 6, we show that \({\mathsf {Adv}}_2(\mathcal {A}) ={\mathsf {Adv}}_3(\mathcal {A})\).
-
In Lemma 7, we show that \({\mathsf {Adv}}_3(\mathcal {A})=0\).
Putting everything together, we obtain:
By Definition 6, \({\mathsf {Adv}}_0(\mathcal {A}) = \mathsf {Adv}^{\mathcal {MIFE}, one\text {-}SEL\text {-}IND}(1^\lambda ,\mathcal {A})\). Therefore, by the one-SEL-SIM security of \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen})\) and the \(\mathcal {D}_k\)-MDDH assumption in \({\mathbb {G}}_2\), \(\mathsf {Adv}^{\mathcal {MIFE}, one\text {-}SEL\text {-}IND}(1^\lambda ,\mathcal {A})\) is a negligible function of \(\lambda \). \(\square \)
Remark 3
(decryption capabilities). As a sanity check, we note that the simulated secret keys will correctly decrypt a simulated ciphertext. However, unlike schemes proven secure via the standard dual system encryption methodology [26], a simulated secret key will incorrectly decrypt a normal ciphertext. This is not a problem because we are in the private-key setting, so a distinguisher will not be able to generate normal ciphertexts by itself.
Remark 4
(why a naive argument is inadequate). We cannot afford to do a naive hybrid argument across the n slots for the challenge ciphertext as it would introduce extraneous restrictions on the adversary’s queries. Concretely, suppose we want to use a hybrid argument to switch from encryptions of \(\mathbf {x}^0_1,\mathbf {x}^0_2\) in game 0 to those of \(\mathbf {x}^1_1,\mathbf {x}^1_2\) in game 2 with an intermediate hybrid that uses encryptions of \(\mathbf {x}^1_1,\mathbf {x}^0_2\) in Game\(_1\). To move from game 0 to game 1, the adversary’s query \(\mathbf {y}_1 \Vert \mathbf {y}_2\) must satisfy \(\langle \mathbf {x}^0_1 \Vert \mathbf {x}^0_2,\mathbf {y}_1 \Vert \mathbf {y}_2 \rangle = \langle \mathbf {x}^1_1 \Vert \mathbf {x}^0_2,\mathbf {y}_1 \Vert \mathbf {y}_2 \rangle \), which implies the extraneous restriction \(\langle \mathbf {x}^0_1,\mathbf {y}_1 \rangle = \langle \mathbf {x}^1_2,\mathbf {y}_1 \rangle \).
As described in the proof above, we overcome the limitation by using simulation-based security. Note that what essentially happens in the first slot in our proof is as follows (for \(k=1\), that is, DDH): we switch from \(\mathsf {Enc}({\mathsf {msk}}_1,\mathbf {x}^0_1 \Vert z_1)\) to \(\mathsf {Enc}({\mathsf {msk}}_1,\mathbf {x}^1_1 \Vert z_1)\) while giving out a secret key which contains \(\mathsf {KeyGen}({\mathsf {msk}}_1,\mathbf {y}_1 \Vert r^1),[r^1]_2\). Observe that
may not be equal, since we want to avoid the extraneous restriction \(\langle \mathbf {x}^0_1,\mathbf {y}_1 \rangle = \langle \mathbf {x}^1_2,\mathbf {y}_1 \rangle \). This means that one-SEL-IND security does not provide any guarantee that the ciphertexts are indistinguishable. However, one-SEL-SIM security does provide such a guarantee, because
via the DDH assumption in \({\mathbb {G}}_2\). Since the outcomes of the decryption are computationally indistinguishable, the output of the simulated ciphertext would also be computationally indistinguishable.
Theorem 2
(many-SEL-IND Security of \(\mathcal {MIFE}\) ). Suppose the single-input FE \((\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec})\) is many-SEL-IND-secure and the multi-input FE \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) is one-SEL-IND-secure. Then, the multi-input FE \((\mathsf {Setup}',\mathsf {Enc}',\mathsf {KeyGen}',\mathsf {Dec}')\) is many-SEL-IND-secure.
That is, we show that our multi-input FE is selectively secure in the setting with multiple challenge ciphertexts (and since our multi-input FE is a private key scheme, one-SEL-IND security does not immediately imply many-SEL-IND security).
Proof Overview.
-
We first switch encryptions of \(\mathbf {x}^{1,0}_1,\ldots ,\mathbf {x}^{1,0}_n\) to those of \(\mathbf {x}^{1,1}_1,\ldots ,\mathbf {x}^{1,1}_n\) in a “single shot”, and for the remaining ciphertexts, we switch from an encryption of \(\mathbf {x}^{j,0}_i = (\mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i)+\mathbf {x}^{1,0}_i\) to that of \((\mathbf {x}^{j,0}_i-\mathbf {x}^{1,0}_i)+\mathbf {x}^{1,1}_i\). This basically follows from the setting where there is only a single ciphertext in each slot.
-
Then, we apply a hybrid argument across the slots to switch from encryptions of \((\mathbf {x}^{2,0}_i-\mathbf {x}^{1,0}_i)+\mathbf {x}^{1,1}_i, \ldots , (\mathbf {x}^{Q_i,0}_i-\mathbf {x}^{1,0}_i)+\mathbf {x}^{1,1}_i\) to those of \((\mathbf {x}^{2,1}_i-\mathbf {x}^{1,1}_i)+\mathbf {x}^{1,1}_i, \ldots , (\mathbf {x}^{Q_i,1}_i-\mathbf {x}^{1,1}_i)+\mathbf {x}^{1,1}_i\).
As described earlier, to carry out the latter hybrid argument, the queries must satisfy the constraint
where the latter is already imposed by the ideal functionality.
We defer to the full version of this paper for the complete proof.
5 Achieving Adaptive Security
In this section, we show that the multi-input FE in Fig. 7 is many-AD-IND secure. Roughly speaking, xx-AD-IND security, where \(\text {xx} \in \{\text {many, one}\}\), is defined as xx-SEL-IND security (see Definition 5), except that the adversary does not have to commit to its challenge beforehand, and queries secret keys adaptively. See the full version of this paper for the formal definition of xx-AD-IND security.
Our private-key MIFE scheme for the class \(\mathcal {F}_n^{m,B}\) (self-contained description). The scheme is many-AD-IND-secure under the \(\mathcal {D}_k\)-MDDH assumption in \({\mathbb {G}}_1\) and \({\mathbb {G}}_2\). We use \(e([\mathbf {X}]_1,[\mathbf {Y}]_2)\) to denote \([\mathbf {X}^{\!\scriptscriptstyle {\top }}\mathbf {Y}]_T\).
Theorem 3
Suppose the \(\mathcal {D}_k\)-MDDH assumption holds in \({\mathbb {G}}_1\) and \({\mathbb {G}}_2\). Then, the multi-input FE in Fig. 6 is many-AD-IND-secure.
Proof Overview. The security proof proceeds in three steps:
-
First, we show that the MIFE in Fig. 6 is one-AD-IND secure, that is, it is adaptively secure when there is only a single challenge ciphertext. To achieve adaptive security, we borrow the techniques used in the selective security proof, using complexity leveraging to obtain adaptive security. Note that in our case, we can afford the exponential security loss from complexity leveraging, since this is used in the proof in combination with perfect indistinguishability, therefore, the exponential term is multiplied by a zero term.
-
Then, we show that the generic construction of MIFE in Fig. 3 is many-AD-IND secure, if the underlying single-input FE is many-AD-IND secure, and the MIFE is one-AD-IND secure.
-
Finally, we show that the single-input scheme in Fig. 7 is many-AD-IND.
Putting everything together, we obtain many-AD-IND security of the MIFE in Fig. 6. We defer to the full version of this paper for a complete proof, and for the definition of one-AD-IND and many-AD-IND security.
Notes
- 1.
- 2.
This work is independent of both works.
- 3.
Here, we use the implicit representation notation for group elements, using [s] to denote \(g^s\) and \([\mathbf {w}]\) to denote \(g^\mathbf {w}\), etc.
- 4.
We note that in the private key setting of MIFE, we can make \(\mathsf {mpk}\) part of \({\mathsf {msk}}\), but we allow for a separate master public key for better clarity in our proofs. In constructions where we do not need \(\mathsf {mpk}\) we omit it.
- 5.
That is, \(\mathsf {{\widetilde{Setup}}},\mathsf {{\widetilde{Encrypt}}},\mathsf {{\widetilde{KeyGen}}}\) correspond respectively to the simulated \(\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen}\).
References
Abdalla, M., Bourse, F., Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_33
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Better security for functional encryption for inner product evaluations. Cryptology ePrint Archive, Report 2016/011 (2016). http://eprint.iacr.org/2016/011
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_28
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_12
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Badrinarayanan, S., Gupta, D., Jain, A., Sahai, A.: Multi-input functional encryption for unbounded arity functions. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 27–51. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_2
Bishop, A., Jain, A., Kowalczyk, L.: Function-hiding inner product encryption. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 470–491. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_20
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: 56th FOCS, pp. 171–190. IEEE Computer Society Press, October 2015
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_23
Boneh, D., Lewi, K., Raykova, M., Sahai, A., Zhandry, M., Zimmerman, J.: Semantically secure order-revealing encryption: multi-input functional encryption without obfuscation. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 563–594. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_19
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Brakerski, Z., Komargodski, I., Segev, G.: Multi-input functional encryption in the private-key setting: stronger security from weaker assumptions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 852–880. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_30
Datta, P., Dutta, R., Mukhopadhyay, S.: Functional encryption for inner product with full function privacy. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 164–195. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49384-7_7
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_8
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_1
Goldwasser, S., Gordon, S.D., Goyal, V., Jain, A., Katz, J., Liu, F.-H., Sahai, A., Shi, E., Zhou, H.-S.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Kim, S., Lewi, K., Mandal, A., Montgomery, H., Roy, A., Wu, D.J.: Function-hiding inner product encryption is practical. Cryptology ePrint Archive, Report 2016/440 (2016). http://eprint.iacr.org/2016/440
Lee, K., Lee, D.H.: Two-input functional encryption for inner products from bilinear maps. Cryptology ePrint Archive, Report 2016/432 (2016). http://eprint.iacr.org/2016/432
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: ACM CCS 2010, pp. 463–472. ACM Press, October 2010
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_36
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_26
Wee, H.: New techniques for attribute-hiding in prime-order bilinear groups (2016, in preparation)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A One-SEL-SIM, Many-AD-IND Secure Scheme for Single-Input Inner Products
A One-SEL-SIM, Many-AD-IND Secure Scheme for Single-Input Inner Products
In Fig. 7, we describe the scheme for Single-Input Inner Products from [28], which is essentially the same as those in [2, 4], extended explicitly to the \(\mathcal {D}_k\)-MDDH assumption. In the full version of this paper, we recall the proof of one-SEL-SIM-security from [28] and we prove its many-AD-IND security. Moreover, note that the scheme is public key, linearly homomorphic, and satisfies additional requirements for the construction in Fig. 3.
A one-SEL-SIM scheme for single-input inner product \(\mathcal {F}_1^{m,B}\) [28].
Theorem 4
(one-SEL-SIM, many-AD-IND Security of \(\mathcal {FE}\) ). If the \(\mathcal {D}_k\)-MDDH assumption holds in \({\mathbb {G}}\), then the single-input FE in Fig. 7 is one-SEL-SIM secure (see Definition 6), and many-AD-IND secure.
We defer to the full version of this paper for the complete proof. We provide the description of the simulator for the proof of one-SEL-SIM security from [28], in Fig. 8.
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Abdalla, M., Gay, R., Raykova, M., Wee, H. (2017). Multi-input Inner-Product Functional Encryption from Pairings. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10210. Springer, Cham. https://doi.org/10.1007/978-3-319-56620-7_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-56620-7_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56619-1
Online ISBN: 978-3-319-56620-7
eBook Packages: Computer ScienceComputer Science (R0)










 First,
First, 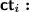
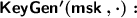 For each query
For each query  Upon receiving an
Upon receiving an 
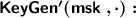 On the j’th query
On the j’th query 

