Approximate Inference in Related Multi-output Gaussian Process Regression

Abstract

In Gaussian Processes a multi-output kernel is a covariance function over correlated outputs. Using a prior known relation between outputs, joint auto- and cross-covariance functions can be constructed. Realizations from these joint-covariance functions give outputs that are consistent with the prior relation. One issue with gaussian process regression is efficient inference when scaling upto large datasets. In this paper we use approximate inference techniques upon multi-output kernels enforcing relationships between outputs. Results of the proposed methodology for theoretical data and real world applications are presented. The main contribution of this paper is the application and validation of our methodology on a dataset of real aircraft flight tests, while imposing knowledge of aircraft physics into the model.

A. Chiplunkar—Ph.D. Candidate, Flight Physics Airbus Operations, 316 Route de Bayonne, 31060 Toulouse, France.

E. Rachelson—Associate Professor, Université de Toulouse, ISAE-SUPAERO, Département d’Ingénierie des Systèmes Complexes (DISC), 10 Avenue Edouard Belin, 31055 Toulouse Cedex 4, France.

M. Colombo—Loads and Aeroelastics Engineer, Flight Physics, 316 Route de Bayonne, 31060 Toulouse, France.

J. Morlier—Professor, Université de Toulouse, CNRS, ISAE-SUPAERO, Institut Clément Ader (ICA), 10 Avenue Edouard Belin, 31077 Toulouse Cedex 4, France.

1 Introduction

The main difference between the physical sciences and machine learning can be explained by the difference between deduction and induction. Physical sciences is deduction: where a very general formula is applied to a particular case. The basics of newtonian physics when applied to a particular aircraft geometry give us inertial loads. The basics of aerodynamics when applied to particular set of aircraft geometry and aircraft states give out aerodynamic pressures. Physical sciences take global rules and apply them to local configurations, whereas machine learning is induction [9]. It looks at local features and data, tries to find similarity measures between them and gives a global formula for the environment. For this reason machine learning algorithms perform better in presence of more and more data.

Unfortunately, gathering highly accurate data for physical systems is a costly exercise. Highly accurate CFD simulations may run for weeks and flight test campaigns cost millions of dollars. In this regard there is a dichotomy between these two fields of science, where machine learning needs more data for good performance but procuring data from physical systems is a costly exercise. In this work we consider using prior information of relationships between several outputs thereby effectively increasing the number of data-points.

We use multiple-output Gaussian Process (GP) regression [12] to encode the physical laws of the system and effectively increase the amount of training data points. Inference on multiple output data is also known as co-kriging [14], multi-kriging [3] or Gradient Enhanced Kriging. Using a general framework [7] to calculate covariance functions between multiple-outputs, we extend the framework of gradient enhanced kriging to integral enhanced kriging, quadratic enhanced kriging or any functional relationship between inputs.

Let us start by defining a $P$ dimensional input space and a $D$ dimensional output space. Such that $\{(x_{i}^{j}, y_{i}^{j})\}$ for $j \in [1; n_{i}]$ are the training datasets for the $i^{th}$ output. Here $n_{i}$ is the number of measurement points for the $i^{th}$ output, while $x_{i}^{j} \in \mathbb {R}^{P}$ and $y_{i}^{j} \in \mathbb {R}$. We next define $x_{i} = \{x_{i}^{1}; x_{i}^{2}; \ldots ; x_{i}^{n_{i}}\}$ and $y_{i} = \{y_{i}^{1}; y_{i}^{2}; \ldots ; y_{i}^{n_{i}}\}$ as the full matrices containing all the training points for the $i^{th}$ output such that $x_{i} \in \mathbb {R}^{n_{i} \times P}$ and $y_{i} \in \mathbb {R}^{n_{i} }$. Henceforth we define the joint output vector $Y = [y_{1}; y_{2}; y_{3}; \ldots ; y_{D}]$ such that all the output values are stacked one after the other. Similarly, we define the joint input matrix as $X = [x_{1}, x_{2}, x_{3}, \ldots , x_{D}]$. If $\varSigma n_{i} = N$ for $i \in [1, D]$. Hence $N$ represents the total number of training points for all the outputs combined. Then $Y \in \mathbb {R}^{N}$ and $X \in \mathbb {R}^{N \times P}$.

For simplicity take the case of an explicit relationship between two outputs $y_{1}$ and $y_{2}$. Suppose we measure two outputs with some error, while the true physical process is defined by latent variables $f_{1}$ and $f_{2}$. Then the relation between the output function, measurement error and true physical process can be written as follows.

$$\begin{aligned} y_{1} = f_{1} + \epsilon _{n1} \end{aligned}$$

$$\begin{aligned} y_{2} = f_{2} + \epsilon _{n2} \end{aligned}$$

(1)

Where, $\epsilon _{n1}$ and $\epsilon _{n2}$ are measurement error sampled from a white noise gaussian $\mathcal {N}(0, \sigma _{n1})$ and $\mathcal {N}(0, \sigma _{n2})$ respectively. While the physics based relation can be expressed as follows.

$$\begin{aligned} f_{1} = g\left( f_{2}, x_{1} \right) \end{aligned}$$

(2)

Here $g$ is an operator defining the relation between $f_{1}$ and an independent latent output $f_{2}$.

While a joint model developed using correlated covariance functions gives better predictions, it incurs a huge cost on memory occupied and computational time. The main contribution of this paper is to apply approximate inference on these models of large datasets and reduce the heavy computational costs incurred. For a multi-output GP as defined earlier the covariance matrix is of size $N$, needing $\mathcal {O}\left( N^{3} \right)$ calculations for inference and $\mathcal {O}\left( N^{2} \right)$ for storage. In this work we compare performance of variational inference [15] and distributed GP [8] to approximate the inference in a joint-kernel.

The remaining paper proceeds as follows, Sect. 2 provides the theoretical framework for Gaussian Process regression. Section 3 extends the multi-output GP regression in presence of correlated covariances. In Sect. 4 various methods of approximating inference of a multi-output GP are derived. Finally, in Sect. 5 we demonstrate the approach on both theoretical and flight-test data.

2 Gaussian Process Regression

A gaussian process is an infinite dimensional multi-variate gaussian. Such that any subset of the process is a multi-variate gaussian distribution. A gaussian process can be fully parametrized by a mean and covariance function Eq. 3.

$$\begin{aligned} y(x) = GP(m(x, \theta ), k(x, x', \theta )) \end{aligned}$$

(3)

A random draw from a Gaussian Process gives us a random function around the mean function $m(x, \theta )$ and of the shape as defined by covariance function $k(x, x', \theta )$. Hence, Gaussian Process gives us a method to define a family of functions whose shape is defined by its covariance function. A popular choice of covariance function is a squared exponential function Eq. 4, because it defines a family of highly smooth (infinitely differentiable) non-linear functions as shown in Fig. 1(a).

$$\begin{aligned} k(x, x', \theta ) = \theta _{1}^2exp[-\frac{(x-x')^2}{2\theta _{2}^2}] \end{aligned}$$

(4)

A covariance function is fully parametrized by its hyperparameters $\theta _{i}$’s. For the case of Squared exponential kernel the hyperparameters are its amplitude $\theta _{1}$ and length scale $\theta _{2}$.

Given a dataset $(x, y)$ regression deals with finding latent function $f$ between the inputs $x$ and outputs $y$. While performing polynomial regression we assume that our function $f$ comes from a family of polynomial functions. Since Gaussian Processes are such handy tools to define a family of non-linear functions. In a Gaussian Process Regression (GPR) we start with an initial family of functions defined by a GP called prior Fig. 1(a).

$$\begin{aligned} \mathbb {P}(f\mid x, \theta ) = GP(y| 0, K_{xx} ) \end{aligned}$$

(5)

Due to the bayesian setting of GP we can calculate the posterior mean and variance as shown in Eqs. 6 and 7. This means that we are effectively eliminating all the functions in the prior that do not pass through our data points Fig. 1(c).

$$\begin{aligned} m(y_{*}) = k_{x_{*}x}( K_{xx} )^{-1}y \end{aligned}$$

(6)

$$\begin{aligned} Cov( y_{*}) = k_{x_{*}x_{*}} - k_{x_{*}x}\ ( K_{xx} )^{-1}k_{xx_{*}} \end{aligned}$$

(7)

We can also improve our predictions by choosing a better prior. This involves optimizing the Marginal Likelihood (ML) $\mathbb {P}(y\mid x, \theta )$ calculated as Eq. 8. The probability that our dataset $(x, y)$ comes from a family of functions defined by the prior is called the ML [12]. Hence, when we optimize the ML we are actually finding the optimal $\theta$ or family of functions that describe our data Fig. 1(b).

$$\begin{aligned} \mathbb {P}(y\mid x, \theta ) = GP(y| 0, K_{xx} + \sigma ^2I ) \end{aligned}$$

(8)

Fig. 1.

Gaussian process regression.

3 Multi-output Gaussian Process

Given a dataset for multiple outputs $\{(x_{i}, y_{i})\}$ for $i \in [1; D]$ we define the joint output vector $Y = [y_{1}; y_{2}; y_{3}; \ldots ; y_{D}]$ such that all the output values are stacked one after the other. Similarly, we define the joint input matrix as $X = [x_{1}; x_{2}; x_{3}; \ldots ; x_{D}]$. For the sake of simplicity, suppose we measure two outputs $y_{1}$ and $y_{2}$ with some error, while the true physical process is defined by latent variables $f_{1}$ and $f_{2}$ Eq. 2. The operator $g(.)$ can be a known physical equation or a computer code between the outputs, it basically represents a transformation from one output to another.

3.1 Related Work

Earlier work developing such joint-covariance functions [2] have focused on building different outputs as a combination of a set of latent functions. GP priors are placed independently over all the latent functions thereby inducing a correlated covariance function. More recently it has been shown that convolution processes [1, 3] can be used to develop joint-covariance functions for differential equations. In a convolution process framework output functions are generated by convolving several latent functions with a smoothing kernel function. In the current paper we assume one output function to be independent and evaluate the remaining auto- and cross-covariance functions exactly if the physical relation between them is linear [13] or use approximate joint-covariance for non-linear physics-based relationships between the outputs [7].

3.2 Multi-output Joint-Covariance Kernels

A GP prior in such a setting with 2 output variables is expressed in Eq. 9.

$$\begin{aligned} \begin{bmatrix} f_{1}\\ f_{2} \end{bmatrix} \sim GP \begin{bmatrix} \begin{pmatrix} 0\\ 0 \end{pmatrix} ,&\begin{pmatrix} K_{11} &{} K_{12}\\ K_{21} &{} K_{22} \end{pmatrix} \end{bmatrix} \end{aligned}$$

(9)

$K_{12}$ and $K_{21}$ are cross-covariances between the two inputs $x_{1}$ and $x_{2}$. $K_{22}$ is the auto-covariance function of independent output, while $K_{11}$ is the auto-covariance of the dependent output variable. The full covariance matrix $K_{XX}$ is also called the joint-covariance. While, the joint error matrix will be denoted by $\varSigma$;

$$\begin{aligned} \varSigma = \begin{bmatrix} \sigma _{n1}^{2}&0 \\ 0&\sigma _{n2}^{2} \end{bmatrix} \end{aligned}$$

(10)

Where, $\epsilon _{n1}$ and $\epsilon _{n2}$ are measurement error sampled from a white noise gaussian $\mathcal {N}(0, \sigma _{n1})$ and $\mathcal {N}(0, \sigma _{n2})$.

For a linear operator $g(.)$ the joint-covariance matrix can be derived analytically [14], due to the affine property of Gaussian’s Eq. 11.

$$\begin{aligned} \begin{bmatrix} f_{1}\\ f_{2} \end{bmatrix} \sim GP\begin{bmatrix} \begin{pmatrix} 0\\ 0 \end{pmatrix} ,&\begin{pmatrix} g(g(K_{22}, x_{2}), x_{1}) &{} g(K_{22}, x_{1})\\ g(K_{22}, x_{2}) &{} K_{22} \end{pmatrix} \end{bmatrix} \end{aligned}$$

(11)

Using the known relation between outputs we have successfully correlated two GP priors from Eq. 2. This effectively means that when we randomly draw a function $f_{2}$ it will result in a correlated draw of $f_{1}$ such that the two draws satisfy the Eq. 2. We have effectively represented the covariance function $K_{11}$ in terms of the hyperparameters of covariance function $K_{22}$ using the known relation between outputs.

Fig. 2.

Multi-output gaussian process random draws. (Color figure online)

Without loss of generality we can assume that the independent output $f_{2}$ belongs to a family of functions defined by a Squared Exponential kernel. The joint-covariance between $f_{1}$ and $f_{2}$, means that a random draw of independent function $f_{2}$ will result in a correlated draw of the function $f_{1}$. The Fig. 2(a) shows random draws coming from a differential relationship between $f_{1}$ (red) and $f_{2}$ (blue) such that $f_{1} = \frac{\partial f_{2}}{\partial x}$. We can see that the top figure is derivative of the bottom one since $f_{derivative}$ goes to zero where $f_{independent}$ goes to maxima or minima. Similarly, the Fig. 2(b) shows random draws coming from an integral relationship between $f_{1}$ (red) and $f_{2}$ (blue) such that $f_{1} = \int f_{2}$. We can see that the top figure is integral of the bottom one since $f_{independent}$ goes to zero where $f_{integral}$ goes to maxima or minima.

3.3 GP Regression Using Joint-Covariance

We start with defining a zero-mean prior for our observations and make predictions for $y_{1}\left( x_{*} \right) = y_{*1}$ and $y_{2}\left( x_{*} \right) = y_{*2}$. The corresponding prior according to Eqs. 9 and 10 will be:

$$\begin{aligned} \begin{bmatrix} Y(X))\\ Y(X_{*})) \end{bmatrix} = GP \begin{bmatrix} \begin{bmatrix} 0\\ 0 \end{bmatrix},&\begin{bmatrix} K_{XX} + \varSigma&K_{XX_{*}}\\ K_{X_{*}X}&K_{X_{*}X_{*}} + \varSigma \end{bmatrix} \end{bmatrix} \end{aligned}$$

(12)

The posterior distribution is then given as a normal distribution with expectation and covariance matrix given by [12]

$$\begin{aligned} m(y_{*}) = K_{X_{*}X}\left( K_{XX} \right) ^{-1}Y \end{aligned}$$

(13)

$$\begin{aligned} Cov(y_{*}) = K_{X_{*}X_{*}} - K_{X_{*}X}\left( K_{XX} \right) ^{-1}K_{XX_{*}} \end{aligned}$$

(14)

Here, the elements $K_{XX}$, $K_{X_{*}X}$ and $K_{X_{*}X_{*}}$ are block covariances derived from Eq. 11. Due to the bayesian setting we have basically eliminated all the functions that do not pass through the points defined by the observed data.

The joint-covariance matrix depends on several hyperparameters $\theta$. They define a basic shape of the GP prior. To end up with good predictions it is important to start with a good GP prior. We minimize the negative log-marginal likelihood to find a set of good hyperparameters. This leads to an optimization problem where the objective function is given by Eq. 15

$$\begin{aligned} \log (\mathbb {P}(y\mid X, \theta )) = \log [GP(Y| 0, K_{XX} + \varSigma )] \end{aligned}$$

(15)

With its gradient given by Eq. 16

$$\begin{aligned} \frac{\partial }{\partial \theta }\log (\mathbb {P}(y\mid X, \theta )) = \frac{1}{2}Y^{T}K_{XX}^{-1}\frac{\partial K_{XX}}{\partial \theta }K_{XX}^{-1}Y&\\&\quad \quad \quad - \frac{1}{2}tr(K_{XX}^{-1}\frac{\partial K_{XX}}{\partial \theta }) \end{aligned}$$

(16)

Fig. 3.

Multi-output Gaussian process regression predictions. (Color figure online)

Here the hyperparameters of the prior are $\theta = \left\{ l_{2}, \sigma _{2}^{2}, \sigma _{n1}^{2}, \sigma _{n2}^{2} \right\}$. These correspond to the hyperparameters of the independent covariance function $K_{22}$ and errors in the measurements $\sigma _{n1}^{2}$ and $\sigma _{n2}^{2}$. Calculating the negative log-marginal likelihood involves inverting the matrix $K_{XX} + \varSigma$. The size of the $K_{XX} + \varSigma$ matrix depends on total number of input points $N$, hence inverting the matrix becomes intractable for large number of input points.

The Fig. 3(a) shows mean and variance for a differential relationship between independent function $f_{2}$ (blue) and differential function $f_{1}$ (red) and such that $f_{1} = \frac{\partial f_{2}}{\partial x}$. We have conditioned the two functions such that $f_{1} = 5; x = 0$ and $f_{2} = 0; x = 0$. This means that the function $f_{2}$ passes through $0$ and has a derivative equal to $5$ at $x = 0$. We have not maximized the marginal likelihood for this case and the hyperparameters of $K_{22}$ are $\theta _{1} = 1; \theta _{2} = 0.2$. All the corresponding draws from the posterior GP also follow the conditioning.

The Fig. 3(b) shows mean and variance for a integral relationship between independent function $f_{2}$ (blue) and differential function $f_{1}$ (red) and such that $f_{1} = \int f_{2} . dx$. We have conditioned the two functions such that $f_{1} = 0; x = 1$ and $f_{1} = 0; x = 0$. This means that the function $f_{2}$ has an integral $0$ at the two points $[0, 1]$. We have not maximized the marginal likelihood for this case and the hyperparameters of $K_{22}$ are $\theta _{1} = 1; \theta _{2} = 0.2$. All the corresponding draws from the posterior GP also follow the conditioning. We can observe that the draws will also have an integral $0$ between the range $[0, 1]$.

In the next section we describe how to solve the problem of inverting huge $K_{XX} + \varSigma$ matrices using approximate inference techniques.

4 Approximating Inference

The above GP approach is intractable for large datasets. For a multi-output GP as defined in Sect. 3.2 the covariance matrix is of size $N$, where $\mathcal {O}\left( N^{3} \right)$ time is needed for inference and $\mathcal {O}\left( N^{2} \right)$ memory for storage. Thus, we need to consider approximate methods in order to deal with large datasets.

Inverting the covariance matrix takes considerable amount of time and memory during the process. Hence, almost all techniques to approximate inference try and approximate the inversion of covariance matrix $K_{XX}$. If a covariance matrix is diagonal or block-diagonal in nature then methods such as mixture of experts are used eg. distributed GP. Whereas if the covariance matrix is more spread out and has similar terms in its cross diagonals then low-rank approximations are used eg. variational approximation. The remaining section details the two methods for approximating covariance matrix which can be later used to resolve Eqs. 13, 14 and 16.

4.1 Variational Approximation on Multi-output GP

Sparse methods use a small set of $m$ function points as support or inducing variables. Suppose we use $m$ inducing variables to construct our sparse GP. The inducing variables are the latent function values evaluated at inputs $x_{M}$. Learning $x_{M}$ and the hyperparameters $\theta$ is the problem we need to solve in order to obtain a sparse GP method. An approximation to the true log marginal likelihood in Eq. 15 can allow us to infer these quantities (Fig. 4).

Fig. 4.

Variational approximation of covariance matrix for Gaussian process regression.

We try to approximate the joint-posterior distribution $p(X| Y)$ by introducing a variational distribution $q(X)$. In the case of varying number of inputs for different outputs, we place the inducing points over the input space and extend the derivation of [15] to multi-output case.

$$\begin{aligned} q(X) = \mathcal {N}(X| \mu , A) \end{aligned}$$

(17)

Here $\mu$ and $A$ are parameters of the variational distribution. We follow the derivation provided in [15] and obtain the lower bound of true marginal likelihood.

$$\begin{aligned} F_{V} = log(\mathcal {N}[Y| 0, \sigma ^{2}I + Q_{XX}]) - \frac{1}{2\sigma ^{2}}Tr(\tilde{K}) \end{aligned}$$

(18)

where $Q_{XX} = K_{XX_{M}}K_{X_{M}X_{M}}^{-1}K_{X_{M}X}$ and $\tilde{K} = K_{XX} - K_{XX_{M}}K_{X_{M}X_{M}}^{-1}K_{X_{M}X}$. $K_{XX}$ is the joint-covariance matrix derived using Eq. 11 using the input vector $X$ defined in Sect. 1. $K_{X_{M}X_{M}}$ is the joint-covariance function on the inducing points $X_{M}$, such that $X_{M} = [x_{M1}, x_{M2}, ..., x_{M2}]$. We assume that the inducing points $x_{Mi}$ will be same for all the outputs, hence $x_{M1} = x_{M2} = ... = x_{M2} = x_{M}$. While $K_{XX_{M}}$ is the cross-covariance matrix between $X$ and $X_{M}$.

Note that this bound consists of two parts. The first part is the log of a GP prior with the only difference that now the covariance matrix has a lower rank of $MD$. This form allows the inversion of the covariance matrix to take place in $\mathcal {O}\left( N(MD)^{2} \right)$ time. The second part as discussed above can be seen as a penalization term that regularizes the estimation of the parameters.

The bound can be maximized with respect to all parameters of the covariance function; both model hyperparameters and variational parameters. The optimization parameters are the inducing inputs $x_{M}$, the hyperparameters $\theta$ of the independent covariance matrix $K_{22}$ and the error while measuring the outputs $\sigma$. There is a trade-off between quality of the estimate and amount of time taken for the estimation process. On the one hand the number of inducing points determine the value of optimized negative log-marginal likelihood and hence the quality of the estimate. While, on the other hand there is a computational load of $\mathcal {O}\left( N(MD)^{2} \right)$ for inference. We increase the number of inducing points until the difference between two successive likelihoods is below a predefined quantity.

4.2 Distributed Inference on Multi-output GP

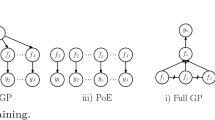
An alternative to sparse approximations is to learn local experts on subset of data. Traditionally, each subset of data learns a different model from another, this is done to increase the expressiveness in the model [11]. The final predictions are then made by combining the predictions of local experts [5].

An alternative way is to tie all the different experts using one single set of hyperparameters [8]. This is equivalent to assuming one single GP on the whole dataset such that there is no correlation across experts as seen in Fig. 5(b). This tying of experts acts as a regularization and inhibits overfitting. Although ignoring correlation among experts is a strong assumption, it can be justified if the experts are chosen randomly and with enough overlap.

Fig. 5.

Distributed approximation of covariance matrix for Gaussian process regression. (Color figure online)

If we partition the dataset into M subsets such as $\mathcal {D}^{(i)} = {X^{(i)}, y^{(i)}}, i = 1, \ldots M$.

$$\begin{aligned} \log p(y| X, \theta ) \approx \sum _{k=1}^{M} \log p_{k}(y^{(i)}| X^{(i)}, \theta ) \end{aligned}$$

(19)

The above Eq. 19 describes the formulation for marginal likelihood. Due to the independence assumption the marginal likelihood can be written as a sum of individual likelihoods and then can be optimized to find the best-fit hyperparameters. After learning the hyperparameters we can combine the predictions of local experts to give mean and variance predictions. The robust Bayesian Commitee Machine (rBCM) model combines the various experts using their confidence on the prediction point [8]. In such manner experts which have high confidence at the prediction points get more weight when compared to experts with low confidence.

$$\begin{aligned} m(Y_{*}) = (Cov(X_{*}))^{-2}\sum \beta _{k}\sigma _{k}^{-2}m_{k}(X_{*}) \end{aligned}$$

(20)

$$\begin{aligned} (Cov_((Y_{*}))^{^-2} = \sum _{k} \beta _{k}\sigma _{k}^{-2} + (1- \sum _{k} \beta _{k})\sigma ^{-2}_{**} \end{aligned}$$

(21)

In the above equations $m_{k}(X_{*})$ and $\sigma _{k}$ are the mean and covariance predictions from expert $k$ at point $X_{*}$. $\sigma _{**}$ is the auto-covariance of the prior at prediction points $X_{*}$. $\beta _{k}$ determines the influence of experts on the final predictions [4] and is given as $\beta _{k} = \frac{1}{2}(\log \sigma _{**}^{-2} - \log \sigma _{k}^{-2})$.

5 Experiments

We empirically assess the performance of distributed Gaussian Process and Variational Inference with respect to the training time and accuracy. We start with a synthetic dataset where we try to learn the model over derivative relationship and compare the two inference techniques. We then evaluate the improvement on real world flight-test dataset.

The basic toolbox used for this paper is GPML provided with [12], we generate covariance functions to handle relationships as described in Eq. 11 using the “Symbolic Math Toolbox” in MATLAB 2014b. Variational inference is wrapped from gpStuff toolbox [16] and distributed GP is inspired from [8]. All experiments were performed on an Intel quad-core processor with 4 Gb RAM.

5.1 Experiments on Theoretical Data

We consider a derivative relationship between two output functions as described in Eq. 2. Such that

$$\begin{aligned} g(f, x) = \frac{\partial f}{\partial x} \end{aligned}$$

Since the differential relationship $g(.)$ is linear in nature we use the Eq. 11 to calculate the auto- and cross-covariance functions as shown in Table 1.

Table 1. Auto- and cross-covariance functions for a differential relationship.

Data is generated from Eq. 22, a random function is drawn from GP to get $f_{2}$ whose derivative is then calculated to generate $f_{1}$. $y_{1}$ and $y_{2}$ are then calculated by adding noise according the Eq. 22. 10,000 points are generated for both the outputs $y_{1}$ and $y_{2}$. Values of $y_{2}$ are masked in the region $x \in [0, 0.3]$ the remaining points now constitute our training dataset.

$$\begin{aligned} f_{2} \sim GP[0, K_{SE}(0.1, 1)] \end{aligned}$$

$$\begin{aligned} \sigma _{n2} \sim \mathcal {N}[0, 0.2] \end{aligned}$$

$$\begin{aligned} \sigma _{n1} \sim \mathcal {N}[0, 2] \end{aligned}$$

(22)

$K_{SE}(0.1, 1)$ means squared exponential kernel with length scale 0.1 and variance as 1.

Fig. 6.

Experimental results for differential relationship while using variational approximation. (Color figure online)

Figure 6 shows comparison between an independent fit GP and a joint multi-output GP whose outputs are related through a derivative relationship described in Sect. 5.1. For Fig. 6(a) using variational inference algorithm we optimize the lower bound of log-marginal likelihood, for independent GP’s on $y_{1}$ and $y_{2}$. For Fig. 6(b) using variational inference we optimize the same lower bound but with a joint-covariance approach as described in Sect. 4.1 using $y_{1}$, $y_{2}$ and $g(.)$. We settled on using 100 equidistant inducing points for this exercise [6] and have only optimized the hyperparameters to learn the model.

Figure 6(a) shows the independent fit of two GP for the differential relationship, while Fig. 6(b) shows the joint GP fit. The GP model with joint-covariance gives better prediction even in absence of data of $y_{2}$ for $x \in [0, 0.3]$.

Fig. 7.

Comparison of run time and RMSE between distributed GP and variational inference.

For the second experiment we compare the Root Mean Squared Error (RMSE) and run-times of distributed GP and Variational Inference algorithms while performing approximate inference. We progressively generate from 10e3 to 10e5 data-points according to the Eq. 22 and Sect. 5.1. We separated 75% of the data as training set and 25% of the data as the test set, the training and test sets were chosen randomly. The variational inference relationship kernel as described in Sect. 4.1 with 100 equidistant inducing points was used. We learn the optimal values of hyper-parameters for all the sets of training data. The distributed GP algorithm as described in Sect. 4.2 was used with randomly chosen 512 points per expert. We learn the optimal values of hyper-parameters for all the sets of training data. The accuracy is plotted as RMSE values with respect to the test set. The runtime is defined as time taken to calculate negative log marginal likelihood Eqs. 18 and 19. The RMSE values are calculated for only the dependent output $y_{1}$ and then plotted in the Fig. 7(a).

In Fig. 7(a) the time to calculate negative log-marginal likelihood with increasing number of training points is calculated. As expected the full GP takes more time when compared to variational inference or distributed GP algorithms. The Variational inference algorithm has better run-time till 10e4 data-points after that distributed GP takes lesser time. In Fig. 7(b) the RMSE error with test set is compared between the variational inference and distributed GP algorithm. Here too the variational inference algorithm performs better lesser number of datapoints but distributed GP starts performing better when we reach more than 10e4 datapoints.

One thing to note is that we have fixed the number and position of inducing points while performing this experiment. While a more optimized set of inducing points will have better results, for datasets of the order 10e5 distributed GP algorithm starts outperforming variational inference. Moreover, upon observing Fig. 5(b) we can say that the covariance matrix in a joint GP setting is not diagonal in nature and hence an approximation technique which can compensate between low-rank approximation and diagonal approximation should be investigated [10].

5.2 Experiments on Flight Test Data

We perform experiments on flight loads data produced during flight test phase at Airbus. Loads are measured across the wing span using strain gauges. Shear load $T_{z}$ and bending moment $M_{x}$ as described in Fig. 8 are used as two outputs for this exercise. $\eta$ or point of action of forces and angle of attack $\alpha$ are the two inputs. The aircraft is in quasi-equillibrium in all conditions and there are no dynamic effects observed throughout this dataset. All data is normalized according to airbus policy.

Fig. 8.

Wing load diagram.

The relation between $T_{z}$ and $M_{x}$ can be written as:

$$\begin{aligned} M_{x}(\eta , \alpha ) = \int _{\eta }^{\eta _{edge}} T_{Z}(x, \alpha )(x-\eta )dx. \end{aligned}$$

(23)

The Eq. 23 is applicable for the $\eta$ axis. Here, $\eta _{edge}$ denotes the edge of the wing span. The forces are measured at 5 points on the wing span and at 8800 points on the $\alpha$ dimension. We compare plots of relationship-imposed multioutput GP and independent GP. Then we compare the measures of negative-log marginal likelihood and RMSE for varying number of inducing points.

Fig. 9.

Experimental results for aircraft flight loads. (Color figure online)

Figure 9(a) shows the independent (blue shade) and joint fit (red shade) of two GP. The top figure shows $T_{Z}$ with the variance of dependent GP plotted in red and variance of independent GP plotted in blue. Bottom figure shows plots for $M_{X}$. Since the number of input points is less than 10e5 we use variational inference. 100 inducing points in the input space are used to learn and plot the figure. The variance of red is smaller than that of blue showing the improvement in confidence when imposing relationships in the GP architecture. The relationship between $T_{Z}$ and $M_{X}$ gives rise to better confidence during the loads prediction. This added information is very useful when identifying faulty sensor data since Eq. 23 will push data points which do not satisfy the relationship out of the tight confidence interval.

Figure 9(b) shows improvement in the negative log-marginal likelihood and RMSE plots upon increasing number of inducing points. 10 sets of experiments were run on 75% of the data as training set and 25% of the data as the test set, the training and test sets were chosen randomly. We learn the optimal values of hyper-parameters and inducing points for all the 10 sets of experiments of training data. Finally, RMSE values are evaluated with respect to the test set and negative log-marginal likelihood are evaluated for each learned model. The RMSE and log-likelihood improve upon increasing the number of inducing points.

6 Conclusions and Future Work

This paper presents approximate inference methods for physics-based multiple output GP’s. We extend the variational inference and distributed GP inference techniques to be applied on physics-based multi-output GP’s and reduce the computational load for inference.

Section 5.1 demonstrates the advantage of using multi-output GP in presence of prior known relationships on a theoretical dataset. Significant improvement in prediction can be observed in presence of missing data due to transfer of information occuring due to the prior relationship. Then, we compare the difference in accuracy and run times upon using distributed GP or variational inference to approximate inference. Although variational inference performs better for datasets of size less than 10e4, distributed GP becomes significantly advantageous for datasets greater than 10e5.

Section 5.2 shows real world application of joint kernel on flight loads data. We demonstrate that adding prior physics-based relationships allows us to create a robust, physically consistent and interpretable surrogate model for these loads. Aircraft flight domain consists of various maneuvers, this is further complicated by several relationships between outputs. In the future we wish to develop better strategies to exploit the clustered nature of flight-domain and more than two relationships.