The Crossing Number of the Cone of a Graph

Abstract

Motivated by a problem asked by Richter and by the long standing Harary-Hill conjecture, we study the relation between the crossing number of a graph G and the crossing number of its cone CG, the graph obtained from G by adding a new vertex adjacent to all the vertices in G. Simple examples show that the difference $cr(CG)-cr(G)$ can be arbitrarily large for any fixed $k=cr(G)$. In this work, we are interested in finding the smallest possible difference, that is, for each non-negative integer k, find the smallest f(k) for which there exists a graph with crossing number at least k and cone with crossing number f(k). For small values of k, we give exact values of f(k) when the problem is restricted to simple graphs, and show that $f(k)=k+\varTheta (\sqrt{k})$ when multiple edges are allowed.

C.A. Alfaro—Supported by SNI and CONACYT grant 166059.

A. Arroyo—Suported by CONACYT.

B. Mohar—Supported in part by an NSERC Discovery Grant (Canada), by the Canada Research Chairs program, and by a Research Grant of ARRS (Slovenia). On leave from: IMFM, Department of Mathematics, Ljubljana, Slovenia.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Little is known on the relation between the crossing number and the chromatic number. In this sense Albertson’s conjecture (see [1]), that if $\chi (G)\ge r$, then $cr(G)\ge cr(K_r)$, has taken a great interest. Albertson’s conjecture has been proved [1, 3, 14] for $r\le 16$. It is related to Hajós’ Conjecture that every r-chromatic graph contains a subdivision of $K_r$. If G contains a subdivision of $K_r$, then $cr(G)\ge cr(K_r)$. Thus Albertson’s conjecture is weaker than Hajós’ conjecture, however Hajós’ conjecture is false for any $r\ge 7$ [6].

The cone of a graph G is the graph CG obtained from G by adding an apex, a new vertex that is adjacent to each vertex in G. Many properties of a graph are automatically transferred to its cone. For example, if G is r-coloring-critical, then CG is $(r+1)$-coloring-critical. During the Crossing Numbers Workshop in 2013, in an attempt to understand Alberston’s conjecture, Richter proposed the following problem: Given an integer $n\ge 5$ and a graph G with crossing number at least $cr(K_{n})$, does it follow that the crossing number of its cone CG is at least $cr(K_{n+1})$? There are examples where these two values can differ arbitrarily (for instance, if G is the disjoint union of $K_{4}$’s and $K_{5}$’s). What is less clear is how close these values can be.

The answer to Richter’s question is positive for the first interesting case when $n=5$: Kuratowski’s theorem implies that the cone of any graph with crossing number at least $cr(K_{5})=1$ contains a subdivision of $CK_{5}$ or $CK_{3,3}$, and each of these graphs has crossing number at least $cr(K_{6})=3$. Unfortunately, the answer is negative for the next case, as the graph in Fig. 1 shows. This graph has crossing number 3, and a cone with crossing number at most 6, and this is less than $cr(K_{7})=9$. This motivated us to investigate the following question.

Problem 1

For each $k\ge 0$, find the smallest integer f(k) for which there is a graph G with crossing number at least k and its cone has $cr(CG)=f(k)$.

Fig. 1.

A counterexample to Richter’s question when $n=6$.

Note that f(k) can also be defined as the largest integer such that every graph with $cr(G)\ge k$, has $cr(CG)\ge f(k)$. An upper bound to the function f(k) is obtained from the graph in Fig. 1, by changing the multiplicity of each edge to r. Any drawing of the new graph has at least $3r^{2}$ crossings, and its cone has crossing number $3r^{2}+3r$. This shows that $f(k)\le k+\sqrt{3k}$. Our main result shows that this is close to be best possible.

Theorem 2

Let G be a graph with $cr(G)\ge k$. Then $cr(CG)\ge k+\sqrt{k/2}$.

Thus we have the following:

Corollary 3

For multigraphs we have $f(k) = k + \varTheta (\sqrt{k}\,)$.

The paper is organized as follows. Page drawings, a concept intimately related to drawings of the cone of a graph, are defined in Sect. 2 and used throughout the subsequent sections. Although, there seems to be a connection between 1-page drawings and drawings of the cone, their exact relationship is much more subtle. Our proofs are instructive in this manner and provide further understanding of these concepts.

The proof of our main result, Theorem 2 is provided in Sect. 3. In Sect. 4, we restrict Problem 1 to the case of simple graphs. To distinguish between these two problems we use $f_{s}(k)$ instead of f(k). Along this paper, a graph is allowed to have multiple edges but no loops; when our graphs have no multiple edges, then we refer them as simple graphs. We find the smallest values of $f_s$ by showing that $f_s(1)=3$, $f_s(2)=5$, $f_s(3)=6$, $f_s(4)=8$ and $f_s(5)=10$. These initial values may suggest that $f_s(k)\ge 2k$. However, in Sect. 5 we show that

$$\begin{aligned} f_s(k)=k+o(k), \end{aligned}$$

and provide additional justification for a more specific conjecture that

$$\begin{aligned} f_s(k) = k + \sqrt{2}\,k^{3/4}(1+o(1)). \end{aligned}$$

2 Page Drawings

In this section we describe a perspective provided from considering page drawings of graphs, a concept that has been studied in its own and has interesting applications. The relation between 1- and 2-page drawings has shown to be handy as it is used in the proofs of Theorems 2 and 7. A more detailed discussion on the relevant aspects of this section can be found in [2, 5, 13].

For an integer $k\ge 1$, a k-page book consists of k half planes sharing their boundary line $\ell$ (spine). A k-page-drawing is a drawing of a graph in which vertices are placed in the spine of a k-page book, and each edge arc is contained in one page. A convenient way to visualize a k-page drawing is by means of the circular model. In this model each page is represented by a unit 2-dimensional disk, so that the vertices are arranged identically on each disk boundary and each edge is drawn entirely in exactly one disk. In this work we are only interested in 1 and 2-page drawings, and, to be more precise, in the following problem.

Problem 4

Given a 1-page drawing of a graph G with k crossings, find an upper bound on the number of crossings of an optimal 2-page drawing of G while having the order of vertices of G on the spine unchanged.

In other words, if the drawing of G in the plane is such that all the vertices are incident to the outer-face (which is equivalent to having a 1-page drawing), what is the most efficient way to redraw some edges in the outer-face to reduce the number of crossings? For this purpose, we define the circle graph $C_{D}$ of any 1-page drawing D of G as the graph whose vertices are the edges of G, and any two elements are adjacent if they cross in D. Note that $C_D$ depends only on the cyclic order of the vertices of G in the spine.

A related problem was previously formulated by Kainen in [11], where he studied the outerplanar crossing number of a graph as the minimum number of crossings in any drawing of G so that all its vertices are incident to the same face. Clearly, the crossing number of CG is at most the outer-planar crossing number of G. Although, Kainen was interested in finding an n-vertex graph that has the largest difference between its crossing number and its outer-planar crossing number, for us it will be useful to consider drawings in which the vertices are incident to the same face.

Turning a 1-page drawing into a 2-page drawing is equivalent to finding a bipartition $(X,V(C_{D})\setminus X)$ of the vertices of $C_{D}$, each part representing the set of edges of G drawn in one of the pages. Minimizing the number of crossings in the obtained 2-page drawing of G is equivalent to maximize the number edges in $C_{D}$ between X and $V(C_{D})\setminus X$. This last problem is known as the max-cut problem, and if the considered graph $C_D$ has m edges, then, a well-known result of Erdős [7] states that its maximum edge-cut has size more than m / 2. Improvements to this general bound are known (see [8, 9] and a more recent survey [4]). For our purpose the following bound of Edwards will be useful.

Lemma 5

(Edwards [8, 9]). Suppose that G is a graph of order n with $m\ge 1$ edges. Then G contains a bipartite subgraph with at least $\frac{1}{2}m + \sqrt{\frac{1}{8}m+\frac{1}{64}} - \frac{1}{8} > \frac{1}{2}m$ edges.

In our context, this result translates to the following observation that we will use.

Corollary 6

Let D be a 1-page drawing of a graph G with $k\ge 1$ crossings. Then some edges of G can be redrawn in a new page, obtaining a 2-page drawing with at most $\frac{1}{2}k - \sqrt{\frac{1}{8}k+\frac{1}{64}} + \frac{1}{8}$ crossings. Such a drawing can be found in time $O(|E(G)|+k)$.

The proof of Corollary 6 will be provided in the full version.

3 Lower Bound on the Crossing Number of the Cone

This section contains the proof of our main result.

Proof

(of Theorem 2 ). Let $\widehat{D}$ be an optimal drawing of the cone CG of G with apex a, and suppose $\widehat{D}$ has less than $k+\sqrt{ k/2}$ crossings. We consider $D=\widehat{D}|_{G}$, the drawing of G induced by $\widehat{D}$. If we let t to be the number of crossings in D, then we have

$$\begin{aligned} k\le t< k+\sqrt{k/2}\text {.} \end{aligned}$$

(1)

For each vertex $v\in V(G)\cup \{a\}$, let $s_{v}$ be the number of crossings in $\widehat{D}$ involving edges incident with v. Using that $cr(\widehat{D})<k+\sqrt{ k/2}$ and the left-hand side inequality in (1), we obtain that $s_{a}<\sqrt{ k/2}$.

Consider $x_{1},\ldots ,x_{s_{a}}$, the crossings involving edges incident with a. Since $\widehat{D}$ is optimal, each of these crossings is between an edge incident to a and an edge in G. Let $e_{1},\ldots ,e_{s_{a}}$ be the list of edges in G (we allow repetitions) so that $x_{i}$ is the crossing between $e_{i}$ and an edge incident with a. We subdivide each edge $e_{i}$ in D using two points close to the crossing $x_{i}$, and we remove the edge segment $\sigma _{i}$ joining these new two vertices, in order to obtain a drawing $D_{0}$ of a graph $G_{0}$ with t crossings (see Fig. 2).

Fig. 2.

A drawing where the crossed edges are cut.

The obtained drawing $D_0$ has all its vertices incident to the face of $D_{0}$ containing the point corresponding to the apex vertex a of CG in $\widehat{D}$. For simplicity, we may assume that this is the unbounded face of $D_{0}$. It follows that there exists a simple closed curve $\ell$ in the closure of this face, containing all the vertices of $G_{0}$. Thus, $D_{0}$ gives rise to a 1-page drawing of $G_{0}$ with spine $\ell$.

Now construct a new drawing of G as follows:

• 1. Start with the 1-page drawing $D_0$. Partition the edges of $G_{0}$ according to Corollary 6, and draw the edges of one part in page 2 outside $\ell$.

• 2. Reinsert edge segments $\sigma _{1},\ldots ,\sigma _{s_{a}}$ as they where drawn in D, to obtain a drawing $D_{1}$ (of a subdivision) of G. These segments do not cross each other, but they may cross some of the edges of $G_0$ that we placed in page 2 in step 1.

Now we estimate the number of crossings in $D_{1}$. According to Corollary 6, after step 1 we obtain a 2-page drawing $D_{0}$ with less than $t/2-\sqrt{t/8}+1/8$ crossings. After step 2 we gain some new crossings between the added segments $\sigma _{1},\ldots ,\sigma _{s_{a}}$ and the edges of $G_0$ drawn on page 2 in step 1.

Claim

The number of new crossings between $\sigma _{1},\dots ,\sigma _{s_{a}}$ and the edges drawn on page 2 in step 1 is at most $(k-1)/2$.

Proof

We may assume that, for each $v\in V(G)$, $s_{v}< \sqrt{ k/2}$. Otherwise, by removing v and all the edges incident to v, we obtain a drawing of $CG-v$ containing a subdrawing of G, in which v is represented as the apex, and this drawing has less than k crossings, a contradiction.

Let $e\in E(G)$ be an edge having ends u, $v\in V(G)$. Suppose that $ay_1$,$\ldots$,$ay_{r_e}$ are the edges incident to a that cross e in $\widehat{D}$. We may assume that, for every i, j with $1\le i<j\le r_e$, when we traverse e from u to v, the crossing $x_i=e\cap ay_i$ precedes the crossing $x_j=e\cap ay_j$. It is convenient to let $x_0=u$ and $x_{r_{e}+1}=v$.

The edges of $G_0$ included in D[e] are the segments of $D[e]-\{\sigma _1,\ldots ,\sigma _{s_a}\}$. We enumerate these edges as $\tau _0^e$,$\dots$,$\tau _{r_e}^e$, so that $\tau _i^e$ is included in the $x_ix_{i+1}$-arc of D[e]. Note that $\tau _1^e$ is incident to u, while $\tau _{r_e}$ is incident to v.

Let $T=\{\tau _i^e\;:\; e\in E(G)\; \text {and } 0\le i\le r_e\}$ be the set of edges of $G_0$. In Step 1, when we apply Corollary 2.2 to the edges in $D_0$, we obtain a partition $T_1\cup T_2$ of T. Instead of counting how many crossings are between the segments in $\sigma _1,\ldots ,\sigma _{s_a}$ and the edges in one of the $T_i$’s when we redraw $T_i$ in page 2, we estimate the number m of crossings between $\sigma _1,\ldots ,\sigma _{s_a}$ and the edges in T when we draw all the crossing edges in T in page 2. This will show that one of the two parts, either $T_1$ or $T_2$, can be drawn in page 2 creating at most m / 2 crossings with the segments $\sigma _1,\ldots ,\sigma _{s_a}$. To show our claim, it suffices to prove that $m\le k-1$, and this is what we do next.

For every point p distinct from a and contained in an edge f incident to a, the depth h(p) of p is the number of crossings in $\widehat{D}$, contained in the open subarc of f connecting a to p. When we redraw an edge $\tau _i^e$ in page 2, we can draw it so that it crosses at most $h(x_i)+h(x_{i+1})$ segments in $\sigma _1,\ldots ,\sigma _{s_a}$. Such new drawing of $\tau _i^e$ is obtained from letting the segment of $\tau _{i}^e$ near to $x_i$ follow the same dual path in D that $x_i$ follows to reach a via $ay_i$. Likewise the new end of $\tau _i^e$ near $x_{i+1}$ is defined. The new $\tau _{i}^e$ is obtained from connecting the two end segments of $\tau _i^e$ inside the face of D containing a.

Let X(a) be the set of crossings involving edges incident to a. For every $x\in X(a)$, there are precisely two elements in T, so that when they are redrawn in page 2, one of its end segments mimics the arc between x and a inside the edge including x and a. Each $v\in V(G)$ is incident to at most $s_v$ edges crossing in $D_0$. Then, for every $v\in V(G)$, there are are most $s_v$ edges in T, so that when we redraw them in page 2, one of their ends mimics the dual path followed by the edge $\widehat{D}[xa]$. These two observations together imply that

$$\begin{aligned} m\le & {} \sum _{x\in X(a)} 2h(x)+\sum _{v\in V} h(v)s_v\\< & {} 2\sum _{v\in V}\left( 1+2+\ldots +(h(v)-1)\right) +\sqrt{k/2}\sum _{v\in V}h(v) \\\le & {} \sum _{v\in V }{h(v)^2}+(\sqrt{k/2})s_a\le \left( \sum _{v\in V} h(v)\right) ^2+k/2\\= & {} s_a^2+k/2< k\text {.} \end{aligned}$$

Because m is an integer less than k, $m\le k-1$ as desired.    $\square$

At the end, we obtained a drawing $D_1$ of (a subdivision of) G with less than $t/2 - \sqrt{t/8} + 1/8 + (k-1)/2$ crossings. Using (1) it follows that

$$\begin{aligned} cr(D_{1})< \frac{1}{2}(k+\sqrt{k/2}) - \sqrt{t/8} + 1/8 + k/2 - 1/2 = k + \sqrt{k/8} -\sqrt{t/8} - 3/8 < k\text {,} \end{aligned}$$

contradicting the fact that $cr(D_1)\ge cr(G)\ge k$.    $\square$

4 Exact Values of the Crossing Number of the Cone for Simple Graphs

In this section, we investigate the minimum crossing number of a cone, with the restriction of only considering simple graphs. We are interested in finding the smallest integer $f_{s}(k)$ for which there is a simple graph with crossing number at least k, whose cone has crossing number $f_{s}(k)$. On one hand, we describe below a family of simple graphs that shows that $f_{s}(k)\le 2k$. Our best general lower bound is obtained from Theorem 2. The main result in this section, Theorem 7, help us to obtain exact values on $f_{s}(k)$ for cases when k is small.

Theorem 7

Let G be a simple graph with crossing number k. Then

• (1) if $k\ge 2$, then $cr(CG)\ge k+3$;

• (2) if $k\ge 4$, then $cr(CG)\ge k+4$; and

• (3) if $k\ge 5$, then $cr(CG)\ge k+5$.

Fig. 3.

The graph $F_k$.

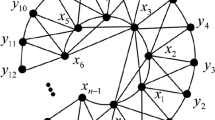
Before proving Theorem 7, we describe a family of examples that is used to find an upper bound for $f_s(k)$, that is exact for the values $k=3,4,5$. Given an integer $k\ge 3$, the graph $F_{k}$ (Fig. 3) is obtained from two disjoint cycles $C_{1}=x_{0}\dots x_{k-1}x_0$ and $C_{2} = y_{0}\dots y_{2k-1}y_0$ by adding, for each $i=0,\dots ,k-1$, the edges $x_{i}y_{2i-2}$, $x_{i}y_{2i-1}$, $x_{i}y_{2i}$, $x_{i}y_{2i+1}$ (where the indices of the vertices $y_j$ are taken modulo 2k). It is not hard to see that $F_{k}$ has crossing number k: a drawing with k crossings is shown in Fig. 3. To show that $cr(F_{k})\ge k$, for $i\in \{ 0,\ldots ,k-1\}$, consider $L^i$, the $K_4$ induced by the vertices in $\{x_{i},x_{i+1},y_{2i},y_{2i+1}\}$. Every $L^i$ is a subgraph of a $K_5$ subdivision of $F_k$, thus, in an optimal drawing of $F_k$, at least one of the edges in $L^i$ is crossed. This only guarantees that $\mathop {cr}(F_k)\ge k/2$, as two edges from distinct $L^i$’s might be crossed. However, if an edge from $L^i$ crosses an edge $e_j$ from some other $L^j$, then $F_k-e_j$ has a $K_5$ subdivision including $L^i$, exhibiting a new crossing in some edge in $L^i$. Therefore, every $L^i$ either has a crossing not involving an edge in another $L^j$, or there are least two crossings involving edges in $L^i$. This shows that $\mathop {cr}(F_k)\ge k$.

The graph shown in Fig. 4 has crossing number 2, and its cone has crossing number 5. This shows that $f_{s}(2)\le 5$. On the other hand, $F_{3}$, $F_{4}$, and $F_5$ serve as examples to show that $f_s(k)\le 2k$ for $k=3,4,5$. These bounds are tight for $2\le k\le 5$ by Theorem 7.

Fig. 4.

A graph with crossing number 2 whose cone has crossing number 5.

Proof

(Proof of Theorem 7 ). Suppose G is a graph with $cr(G)=k$. Let $\widehat{D}$ be an optimal drawing of the cone CG, D its restriction to G, and $F_{a}$ be the face of D containing the apex a. The vertices of G incident to $F_{a}$ are the planar neighbors of a.

Assume that $k\ge 2$, and suppose $\widehat{D}$ has exactly $k+t$ crossings. Theorem 2 guarantees that $t\ge 1$. Since each edge from a to a non-planar-neighbor introduce at least one crossing, the apex a has either 0, 1, 2, 3 or 4 non-planar neighbors (if a has more than 4 non-planar neighbours, then any of the items in Theorem 7 is satisfied).

We start by assuming that a has no non-planar neighbors. In this case, D is a 1-page drawing of G. Corollary 6 implies that we can obtain a new drawing of G with less than $(k+t)/2$ crossings. Thus $(k+t)/2> cr(G)=k$, which implies that $t\ge k+1$. In any case of the theorem, this implies the conclusion, thus we may now assume that a has at least one and at most t non-planar neighbors.

(1) Let us now assume that $k\ge 2$ and $t\le 2$.

Suppose a has exactly one non-planar neighbor u. Then cr(D) has at most $k+1$ crossings. At least one edge incident to u is crossed in D, otherwise, all the crossed edges have ends in $F_{a}$, and using Corollary 6, we obtain a drawing of G with less than $(k+1)/2$ crossings, contradicting that $cr(G)=k$. If at least two crossings in D involve edges incident to u, or if D has k crossings, then by redrawing u in $F_{a}$, and adding all the edges to its neighbors without creating any crossings, we obtain a drawing of G with less than k crossings. Therefore D has $k+1$ crossings, and exactly k of them involve edges not incident to u. Again, we apply Corollary 6 to obtain a drawing of G with at most $\frac{1}{2}(k-1)<k$ crossings (this time we are more careful by setting our two pages in such way that the edge not incident to u that crosses an edge incident to u is redrawn in the page contained in $F_{a}$).

Finally, suppose a has exactly two distinct non-planar neighbors u and v. Then, $\widehat{D}$ has $k+2$ crossings; D has k crossings, and the edges au, av are crossed exactly once. Notice that any crossed edge in D is incident to either u or v; otherwise, we can redraw such edge inside $F_{a}$, obtaining a drawing of G with less than k crossings. Redraw v in $\widehat{D}[a]$ (where $\widehat{D}[a]$ denotes the point representing a in $\widehat{D}$); draw the edge uv (if it exists in G) as the arc $\widehat{D}[au]$, and draw the edges from v to its neighbors distinct from u, inside $F_{a}$ without creating new crossings. Since every crossing in D involves an edge incident with v, we obtain a drawing of G with at most one crossing, a contradiction.

(2) Now, suppose that $k\ge 4$ and that $t=3$.

The case when the apex a has only one non-planar neighbor u is similar to the above. If at least three crossings in D involve edges incident with u, then by redrawing u and the edges incident to u in $F_{a}$, we obtain a drawing with less than k crossings, a contradiction. Thus, at most two crossings involve edges incident to u. We redraw the remaining crossed edges according to Corollary 6 (if there is an edge e that crosses an edge incident to u, in order to remove an extra crossing, we may choose this new drawing so that e is redrawn in the page contained in $F_{a}$). If 2 crossings involve edges incident to u, then the obtained drawing has at most $\frac{k}{2}+1$ crossings, where the $+1$ comes from the fact that e was drawn in the page contained in $F_{a}$. If at most one of the edges at u is crossed, then the new drawing has at most $(k+1)/2$ crossings. In any case, since $k\ge 4$, the new drawing has less than k crossings, a contradiction.

Let us now consider the case when the apex has two non-planar neighbors u and v. In this case, the drawing D has either k or $k+1$ crossings, and one of $\{au, av\}$, say au, is crossed only once. Let L be the set of crossed edges in D that are not incident to u or v. Suppose there are at least two crossings involving only edges in L. Then, either there are two edges in L that do not cross, or L has an edge e that crosses two other edges in L. In the former case, we redraw such pair of edges in $F_{a}$; in the latter case, we redraw e in $F_{a}$. Any of these modifications yield a drawing with less than k crossings. Thus, we may assume that at most one crossing in D involves two edges not incident to u or v. Redraw v in $\widehat{D}[a]$; draw the edge vu (if such edge exists in G) as $\widehat{D}[au]$; and the remaining edges from v to its neighbors distinct from u without creating new crossings. The new drawing of G has at most two crossings: possibly one in $\widehat{D}[av]$ and another between edges in L, a contradiction.

Finally suppose that the apex a has three non-planar neighbors u, v, w. In this case D has precisely k crossings, and the edges au, av, aw are crossed exactly once. Observe that any crossed edge in D is incident to one of $\{u,v,w\}$, otherwise we can redraw such edge in $F_{a}$, obtaining a drawing of G with less than k crossings.

Let H be the graph induced by $\{u,v,w\}$. If, for $x\in \{u,v,w\}$, $d_{H}(x)$ denotes the degree of x in H, then at most $d_{H}(x)$ crossings involve edges at x. Otherwise, by redrawing x in $\widehat{D}[a]$; drawing the edges from x to its neighbors in H by using the respective edges from a; and, by drawing the remaining edges at x in $F_{a}$ without creating new crossings, we obtain a drawing of G with less than k crossings. So for each vertex $x\in \{u,v,w\}$, there are at most two crossings involving edges at x. Hence D has at most three crossings, a contradiction.

(3) The proof will be included in the full version of the paper.    $\square$

5 Asymptotics for Simple Graphs

Lastly, we try to understand the behaviour of $f_s(k)$ when k is large. The important part is the increase of the crossing number after adding the apex, thus we define

$$\begin{aligned} \phi _s(k) = f_s(k)-k. \end{aligned}$$

We have proved that $\phi (k)=f(k)-k\ge \frac{1}{2}k^{1/2}$. The term $k^{1/2}$ is asymptotically tight in the case when we allow multiple edges. However, it is unclear how large $\phi _s(k)$ is. This question is treated next.

Theorem 8

$\phi _s(k)=O(k^{3/4})$.

Proof

Let us consider a positive integer k and let n be the smallest integer such that $\mathop {cr}(K_n)\ge k$. Then $G=K_n$ has a crossing number at least k and its cone is $K_{n+1}$.

To find an upper bound for $\mathop {cr}(K_{n+1})$ in terms of $\mathop {cr}(K_n)$, start with a drawing of $K_n$ with $\mathop {cr}(K_n)$ crossings. Then clone a vertex, that is, place a new vertex very close to an original vertex, and draw the new edges along the original edges. Each edge incident to the new vertex cross $O(n^2)$ edges, thus the obtained drawing has $\mathop {cr}(K_n)+O(n^3)$ crossings. Therefore

$$\begin{aligned} \phi _s(k)\le \mathop {cr}(K_{n+1})-\mathop {cr}(K_n)\le O(n^3)\text {.} \end{aligned}$$

It is known [12] that

$$\begin{aligned} \frac{3}{10}\left( {\begin{array}{c}n\\ 4\end{array}}\right) \le \mathop {cr}(K_n) \le \frac{3}{8}\left( {\begin{array}{c}n\\ 4\end{array}}\right) . \end{aligned}$$

(The constant 3 / 10 in the lower bound has been recently improved to 0.32025, see [12] for more information.) Then $\phi _s(k)=O(n^3)=O(k^{3/4})$.    $\square$

The Harary-Hill Conjecture [10] states that

$$\begin{aligned} \mathop {cr}(K_n) = \left\{ \begin{array}{ll} \tfrac{1}{64}n(n-2)^2(n-4), &{} n \text { is even;} \\ \tfrac{1}{64}(n-1)^2(n-3)^2, &{} n \text { is odd.} \end{array} \right. \end{aligned}$$

Proposition 9

If the Harary-Hill conjecture holds, then

$$\begin{aligned} \phi _s(k) \le \sqrt{2}\, k^{3/4}(1+o(1)). \end{aligned}$$

Proof

As in the proof of Theorem 8, but with a slight twist for added precision, we take n such that $\mathop {cr}(K_{n-1}) < k \le \mathop {cr}(K_n)$. We also take $n_1$ such that for $k_1 = k-\mathop {cr}(K_{n-1})$ we have $\mathop {cr}(K_{n_1-1}) < k_1 \le \mathop {cr}(K_{n_1})$. Let $G = K_{n-1} \cup K_{n_1}$. Then $\mathop {cr}(G) = \mathop {cr}(K_{n-1}) + \mathop {cr}(K_{n_1}) \ge k$ and $\mathop {cr}(CG) = \mathop {cr}(K_{n}) + \mathop {cr}(K_{n_1+1})$. Therefore,

$$\begin{aligned} \phi _s(k)\le & {} \mathop {cr}(K_n)+\mathop {cr}(K_{n_1+1})-\mathop {cr}(K_{n-1})-\mathop {cr}(K_{n_1})\\\le & {} \mathop {cr}(K_n)-\mathop {cr}(K_{n-1})+\mathop {cr}(K_{n_1+1})-\mathop {cr}(K_{n_1-1})\text {.} \end{aligned}$$

By inserting the values for the crossing number from the Harary-Hill Conjecture, we obtain (the calculation given is for odd n and odd $n_1$, it is similar when n or $n_1$ is even):

$$\begin{aligned} \mathop {cr}(K_n) - \mathop {cr}(K_{n-1}) =\tfrac{1}{64}((n-1)^2(n-3)^2-(n-1)(n-3)^2(n-5)) = \tfrac{1}{16}n^3(1+o(1)) \end{aligned}$$

and

$$\begin{aligned} \mathop {cr}(K_{n_1+1}) - \mathop {cr}(K_{n_1-1})= & {} \tfrac{1}{64}((n_1+1)(n_1-1)^2(n_1-3)\\&-(n_1-1)(n_1-3)^2(n_1-5))\\= & {} \tfrac{1}{8}n_1^3(1+o(1)). \end{aligned}$$

Noticing that $k=\tfrac{1}{64}n^4(1+o(1))$ and $k_1 = \tfrac{1}{64}n_1^4(1+o(1)) = O(n^3)$ because $k_1\le cr(K_n)-cr(K_{n-1})$, we conclude that $n_1^3 = O(n^{9/4}) = o(k^{3/4})$ and henceforth

$$\begin{aligned} \phi _s(k) \le \tfrac{1}{16}n^3(1+o(1)) + \tfrac{1}{8}n_1^3(1+o(1)) = \sqrt{2}\, k^{3/4}(1+o(1)). \end{aligned}$$

   $\square$

The above proof works even under a weaker hypothesis that $\mathop {cr}(K_n) = \alpha n^4 + \beta n^3(1+o(1))$, where $\alpha$ and $\beta$ are constants. This would imply that $\phi _s(k) = O(k^{3/4})$. Our conjecture is that (9) gives the precise asymptotics.

Conjecture 10

$\phi _s(k) = \sqrt{2}\, k^{3/4} (1+o(1))$.

A reviewer noted that this asymptotic is matched when the graph we are considering is dense.

Remark 11

Let G be a graph with n vertices, m edges, $\mathop {cr}(G)=k$ and such that $m\ge 4n$. If $m=\varOmega (n^2)$, then $\mathop {cr}(CG)\ge k+\varOmega (k^{3/4})$.

The details will be provided in the full version.

Summary

To put the results of this paper into context, let us overview some of the motivation and some of directions for future work. The starting point of this paper was an attempt to understand Albertson’s conjecture. The results of the paper (and their proofs) show that the crossing number behavior when adding an apex vertex is intimately related to 1-page drawings, but the exact relationship is quite subtle. There is some evidence that the minimal increase of the crossing number when an apex is added should be achieved with very dense graphs, close to the complete graphs. Our Conjecture 10 entails this problem. Although very dense graphs have fewer vertices than sparser graphs with the same crossing number and thus need fewer connections to be made from the apex to their vertices, their near optimal drawings are far from 1-page drawings and therefore more crossings are needed. The full understanding of this antinomy would shed new light on the Harary-Hill conjecture.

Finally, it is worth pointing out that neither exact nor approximation algorithm is known for computing the crossing number of graphs of bounded tree-width. Adding an apex to a graph increases the tree-width of the graph by 1, thus understanding the crossing number of the cone is an important special case that would need to be understood before devising an algorithm for general graphs of bounded tree-width.