Keywords

1 Introduction

In the molecular field, polymer chains [17] are observed and studied by microscopy imaging techniques [5, 10, 14]. The obtained shapes are often corrupted due to convolution effect and/or diffraction of microscopic acquisition [17]. Consequently, the observed polymer chain appears like a thick curve with noise and blur. The shape analysis become problematic and chemist and biologist researchers need dedicated image processing methods. In this paper, the term “Shape” denotes the thick curve representing the studied polymer chain acquired by microscopy. Polymers are widely studied and scientists still have many questions about their organization, structure and dynamics [17]. For example, several properties strongly depend on the polymer length [9]. To be able to effectively deal with this material, we quote its principal characteristics [5, 17]:

  1. (i)

    a polymer chain have a constant width and moves in a snake-like fashion (Reptation), it can self-intersect and forms complex geometries including loops,

  2. (ii)

    the studied images are two dimensional projections of three dimensional motions,

  3. (iii)

    a higher intensity occurs near to the centerline of the shape with noise and blur around, which is typically obtained by microscopic acquisition.

To study the polymer chains dynamics, scientists reduce the shape acquired by microscope to its minimal representation which is a curve [5]. The extracted curve allows shape measurements, dynamic analysis, motion tracking ... These analysis strongly depend on the extracted curve which must represent properly the shape to achieve accurate analysis. In this paper we propose a method for curve extraction to help polymer chains reptation studies. This curve has to be near to the centerline of the shape and keeps its motion direction.

In the current studies, the curve is typically performed using manual or semi-automated methods. Maximum intensity near to the centerline of the shape is often exploited: several points are selected and the curve is extracted by interpolation [5, 6]. The curve can be approximated by computing a skeleton [13, 14, 16] in order to get the axial shape representation but gives rough boundary [7]. In order to avoid this problem, pruning process can be considered or the skeleton can be combined with other processing methods such as active contour [14]. These methods, however, do not always explicitly model the curve orientation and do not deal with self-intersecting geometries. We propose to extract an oriented curve dealing with such geometries by computing geodesics.

Geodesic is a shortest path connecting two points. When the two points are located at the shape extremities, and the geodesic is near to the shape centerline, this geodesic can give a good shape representation. A geodesic can be extracted by propagation from a point to the other, which allows keeping the curve orientation. This characteristic is not present on classical curve extraction methods and it is important for polymer studying. Moreover, comparing to medial axis, the use of geodesic avoids the problem of spurious branches. As polymer chains can self-intersect, three-dimensional interpretation of the shape [7] is considered. Then, one geodesic cannot travel the entire polymer chain relying its ends because of wave propagation on bifurcation and wave collision (Fig. 1 (a)). We propose to extract a piecewise curve browsing the shape by computing several geodesics each one browsing a part of the shape. By fusion, we obtain the complete curve representing the polymer chain reptation. The fusion is performed in order to keep the natural curve orientation (Sect. 4).

In Sect. 2, we give geodesic definition, present the problematic and explain the proposed method. We present the first part of the algorithm (Separate geodesics extraction) in Sect. 3 and the second part (Separate geodesics fusion) in Sect. 4. Evaluations are done in Sect. 5, and finally conclusions and perspectives follow in Sect. 6.

2 Methodology

Considering a shape Z, and two points s and e within Z. A shortest path in Z linking s and e is called Geodesic. In [7] authors show that the length of an open thick curve is defined as the length of its longest geodesic. To be representative, the geodesic must have a maximal length within the shape. We call it in this paper Maximal Geodesic, then it connects the two most distant points in this shape. For an open thick curve, these two points are located at shape extremities.

Considering closed and/or self-intersected shapes, a maximal geodesic cannot travel the entire shape because of the front propagation: on the intersection the front will go in all directions (Fig. 1 (a)) and the geodesic extraction becomes ambiguous. Closed shapes cause front collision stopping the geodesic propagation (Fig. 1 (a)). Considering such geometries, a shape returns a set of maximal geodesics (Sect. 3), where each one travels a specific part of the shape.

To extract a curve traveling the entire shape, we propose to generate it by fusing all the extracted maximal geodesics (Sect. 4). The fusion is performed in order to keep the natural orientation of polymer motion. Two steps perform our algorithm: the separate geodesics extraction (Sect. 3) and the separate geodesics fusion (Sect. 4).

Fig. 1.
figure 1

Geodesics propagation and extraction. (a)...(c): equivalent maximal geodesics according to the same propagation. (g)...(i): maximal geodesics. (j)...(l): geodesic segments after considering bifurcations

Full size image

3 Separate Geodesics Extraction

Since a geodesic is a shortest path between two points in the shape, its extraction can be seen as a front propagation problem [11] from one point to the other. The distance transform maps each image pixel into its smallest distance to regions of interest [15]. Tracing the distance map from a specified point to a referred one will give a geodesic between these two points. To force the geodesic to be near the centerline of the shape, we compute a weighted distance map related to grey level of the shape (Sect. 1 (iii)). Let Z be the studied greyscale shape, Z(a) the normalized intensity at pixel \(a\in Z\). The weighted distance map WDT of Z is given by:

$$\begin{aligned} WDT(a)= DT(a).\exp (-coef.Z(a)^2), \end{aligned}$$
(1)

with \(DT(a)=\min \limits _{p\in Z}(d(p,a))\) where d() is the Euclidian distance and coef a weighting coefficient.

The set of maximal geodesics is extracted as follow: we propagate a front within the shape from an arbitrary point \(S_i\), and locate the maxima \(E_i=\max (WDT(S_i))\). A geodesic \((TemG_i)\) is built considering \(S_i\) and \(E_i\). The newly detected point \(E_i\) is immediately defined as a new source of front propagation and the procedure is iterated. The longest geodesic is kept between two successive iterations: \(G_i=\max (Length (TemG_i),Length (TemG_{i-1}))\). When \(Length (TemG_i) = Length (TemG_{i-1})\), the maximal length is reached and a maximal geodesic is obtained. Then it is subtracted from the shape \(Z_{i+1} = Z_i - Dil_B(G_i)\) where \(Dil_B(G_i)\) is the morphological dilation operation and B a disk of radius b corresponding to the observed shape width. If \(Z_{i+1}\) is empty, the process is stopped. This means that the set of the extracted maximal geodesics (here \(\lbrace G_i \rbrace \)) covers the entire shape. If \(Z_{i+1}\) is not empty, maximal geodesics are iteratively extracted from the remaining shape. \(G_{i+1}\) is then computed from the remaining shape \(Z_{i+1}\).

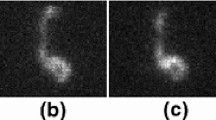
For complex geometries, several equivalent maximal geodesics can exist notably due to intersections (Fig. 1 (a), (b) and (c)). Avoiding intersections leads to a partial shape covering (Fig. 1 (g), (h) and (i)). To manage this point, we decided to split maximal geodesics at each intersection in order to obtain a set of distinct geodesic segments (Fig. 1 (j), (k) and (l)).

Once the geodesic segments set obtained, a complete curve is computed by fusing those elements (Sect. 4).

4 Separate Geodesics Fusion

The goal is to follow the reptation keeping its orientation; we trace the curve unicursally following the less curvature variation at junctions. The geodesic segments previously extracted have to be fused following the correct order to generate the desired curve. We solve the problem by graph theory, and identify the fusion order by finding the optimal path traversing the graph.

According to the studied shape, the modeling graph can be Eulerian (Sect. 4.1) or non Eulerian (Sect. 4.2). A non Eulerian graph is generated when overlapping problem occurs: a polymer chain moves in a snake-like fashion and can self-intersect, as the studied images are two dimensional projections of three dimensional motions (Sect. 1 (ii)), overlapping problem can occurs at intersections (Fig. 2 (c) and (d)).

Fig. 2.
figure 2

Algorithm steps. (e)...(h): geodesics segments before fusion. (i)...(l): graph representation. (i)-(j): Eulerian graphs. (k)-(l): non Eulerian graphs become Eulerian after edges duplication. (m)...(p): oriented curves after fusion

Full size image

4.1 Eulerian Graph

We define an undirected graph \(G=(V,E)\), where \(V=\lbrace v_1, v_2,..., v_i\rbrace \) is a set of vertices modeling junctions and \(E= \lbrace e_1, e_2,..., e_j \rbrace \) a set of edges modeling geodesic segments. The fusion order search can be seen as the Königsberg bridge problem [8] which can be solved by finding Eulerian path. We consider undirected graph G whose edges are visited only one time. An Eulerian path exists over these graphs if all nodes got even degree except for start and end nodes (Fig. 2 (j)). A cycle can be considered if the start and the end belong to the same node (Fig. 2 (i)). If a graph G has one or more odd degree edges (except start and end ones), it is needed to consider double pass edges. Regarding Eulerian path, it is more adequate to duplicate specific edges (Fig. 2 (k) and (l)).

4.2 Non Eulerian Graph Consideration

In the Chinese Postman Problem [3], double traced edges are identified by maximum matching. A matching in a graph is a set of edges without common nodes. A maximum matching [2] tries to find the maximum matching that has the highest or lowest total weight. Each edge belonging to the maximal matching is duplicated to allow double pass. For duplication, we build another weighted graph \(G_1=(V,E,C_1)\) from G with same nodes and edges (Algorithm 1. Step 2), \(C_1\) corresponds to edges costs. The edge weight is computed using angles between adjacent edges, at both extremities. The aim is to duplicate edges with less curvature variation. Each edge weight \(C(e_i)\) is calculated considering the attached nodes weight \(N_1\) and \(N_2\): \(C(e_i)=C(N_1)+C(N_2)\). At a node N, we compute angles \(w_{ij}\) between \(e_i\) and all incident edgesFootnote 1 \(e_j\). The nodes cost is calculated as follow:

$$\begin{aligned} C(N_i)=\sqrt{\sum _{j=1}^{K}(\pi -w_{ij})^2}. \end{aligned}$$
(2)

For angles, we compute the direction vectors \(d_i\) for each geodesic segment at an extremity and then the normalized angle \(w_{ij}\) between \(d_i\) and \(d_j\):

$$\begin{aligned} {w_{ij} =} \left\{ \begin{array}{r c l} \frac{1}{\pi } arccos(\frac{|d_i.d_j|}{\Vert d_i\Vert \,\Vert d_j\Vert }), ~ if ~ i \ne j \\ 1 \qquad \qquad \qquad , ~ if ~ i = j \end{array} \right. \end{aligned}$$
(3)

Once the weighted graph \(G_1\) computed, a third graph \(G_m\) for matching is constructed only with the odd degree nodes from \(G_1\), except start and end nodes. Each node pair in \(G_m\) is linked by an edge having the cost of the shortest path between them in \(G_1\). The maximum matching having the lowest total weight in \(G_m\) is identified. Each matching edge corresponds to a double-traced segment. Theses edges are duplicated in G where the Eulerian path can be extracted.

4.3 Eulerian Path

Two incident edges \(e_i\) and \(e_j\) connected to a node are referred as a fusion pair \((e_i, e_j)\). The fusion cost \(C(e_i, e_j)\) is given for each fusion pair in G. The path \(P = e_1,e_2,..,e_n\) cost is defined as the sum of the fusion costs of every two adjacent edges along P. The fusion cost of a pair \(c(e_i, e_j)\) is set as the deviation angle from the tangent:

$$\begin{aligned} C(e_i,e_j)=\pi -w_{ij}. \end{aligned}$$
(4)

The optimal Euler path is the one minimizing deviations at junctions (Algorithm 1. Step 3).

figure a

4.4 Geodesics Fusion

Geodesics fusion is performed according to the optimal path selected. Fusion consists in locally pairing geodesic segments extremities. To keep the curve chaining, attention is made on the pixels order of geodesic segments before fusion. To ensure the continuity along two geodesic segments, the fusion links the ending point of \(G_i\) to the starting one of \(G_j\). Inversing pixels order is considered if necessary.

5 Experimental Results

The polymer considered in our study is a polyisocyanopeptide [5]. Visual validation of our method by experts on real polymer images has been done. Ground truth isn’t available to validate quantitatively our method (MGF). To confirm the results we simulated polymer reptations by computing several kind of curves, convoluted with Gaussian distribution (the diffraction pattern is commonly modeled by Gaussian distribution [9]) and realistic amount of Poissonian noises was added to images. The simulated polymers were validated by experts (Fig. 3).

Fig. 3.
figure 3

Visual comparison between real and simulated polymer

Full size image

50 curves for each kind provide the simulated database: open (Fig. 3), closed (Fig. 2 (a)) and self-intersected (Fig. 2 (b), (c) and (d)). We compare our algorithm to classical skeletonization methods: Skeleton (Skel) [4] and a thinning method (Thin) [12]. For quantitative evaluations, distances between the computed curves and the extracted ones are calculated. The comparison criterions used are Hausdorff distance (HD), Dice coefficient (D), Mean Absolute Distance (MAD) and the Mean Sum of Squared Distance (MSSD), equations can be found in [1, 18]. Our proposed method aims to approach a continuous representation of the curve by designing it with few pixels. This way, a fine representation is more effective for measurement and tracking applications. To quantify the method ability to extract a fine curve, we introduce the following coefficient: \(TH= \frac{R\cap S}{S},\) Where R and S the reference curve and the calculated one. Dice and TH coefficient measure the correspondence between the two curves. They vary from 0 to 1: 1 corresponds to identical curves. The TH coefficient represents the percentage of S covered by R. While the MAD and MSSD measure a global correspondence between the two curves, the Hausdorff distance evaluates the local behavior of the algorithm.

We start by removing the blur accumulated around the shape, which is typical of microscopy acquisition (Sect. 1): a residual image R is built with the result of a mean filter and a median one: \(R=MeanFilter(Z)- MedianFilter(Z)\), where Z is the initial shape. The residual image R is after deconvoluted by two successive kernels having the same size but two different amplitudes and standard deviations, using Lucy-Richardson operation. The size of kernel corresponds to the observed width of the shape, the amplitude and standard deviations to the observed intensity distribution. Curves are extracted from the deconvoluted shapes. Comparison results between the extracted curves and the ground truths are summarized in Table 1.

Fig. 4.
figure 4

Visual comparison between our method and the thinning method

Full size image
Table 1. Results of curves extraction.
Full size table

Observing overall results according to HD, MAD, and MSSD we note a slight difference between our method and those of the literature. Regarding curves produced by literature methods, we noticed that they provide more pixels representation than our method (Fig. 4): These criterions compute the global distances selecting the maximal of minimal local distances: small variations adversely affect our results unlike the literature methods where their produced curve totally covers the reference one. This is quantitatively expressed regarding results according to TH, we note that best performances are obtained with our method (MGF) (TH= 0.84). These results prove that our extracted curve fits the reference better than the literature methods (Skel: 0.75, Thin: 0.77, Thin_prun1: 0.80). With pruning, the results according to the TH criterion are improved (Thin_prun1: 0.80), but curve behavior gets worse (HD: 3.84, MAD: 1.16, MSSD: 1.83): we noticed that the pruning distorts the curve losing information at extremities.

Generally observing, our method performs promising results compared to the classical methods of the literature, while providing better results with complex geometries (closed and self-intersected). Figure 2 presents all the steps of the algorithm. The ordering feature of our extracted curve is shown in the last row: the grayscale gradient shows the curves orientation.

6 Conclusion

We proposed in this paper a method for curve extraction to help polymer analysis. This curve is performed by geodesics extraction and fusion. An important feature is its ability to keep the curve orientation following the natural polymer motion. We simulated polymer reptation to estimate the extracted curve by comparison with ground truth. Obtained results show that the extracted curve represents correctly the shape, and is comparable to the classical skeletonization methods. The method can therefore be used for polymers chemical and physical analysis. In future works, more comparisons will be performed considering real polymers.