Quantifying Conformance Using the Skorokhod Metric

Abstract

The conformance testing problem for dynamical systems asks, given two dynamical models (e.g., as Simulink diagrams), whether their behaviors are “close” to each other. In the semi-formal approach to conformance testing, the two systems are simulated on a large set of tests, and a metric, defined on pairs of real-valued, real-timed trajectories, is used to determine a lower bound on the distance. We show how the Skorokhod metric on continuous dynamical systems can be used as the foundation for conformance testing of complex dynamical models. The Skorokhod metric allows for both state value mismatches and timing distortions, and is thus well suited for checking conformance between idealized models of dynamical systems and their implementations. We demonstrate the robustness of the metric by proving a transference theorem: trajectories close under the Skorokhod metric satisfy “close” logical properties in the timed linear time logic TLTL augmented with a rich class of temporal and spatial constraint predicates. We provide an efficient window-based streaming algorithm to compute the Skorokhod metric, and use it as a basis for a conformance testing tool for Simulink. We experimentally demonstrate the effectiveness of our tool in finding discrepant behaviors on a set of control system benchmarks, including an industrial challenge problem.

This research was funded in part by a Humboldt foundation grant, FCT grant SFRHBPD902672012, and by a contract from Toyota Motors.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A fundamental question in model-based design is conformance testing: whether two models of a system display similar behavior. For discrete systems, this question is well-studied [19, 20, 28, 29], and there is a rich theory of process equivalences based, e.g., on bisimilarity. For continuous and hybrid systems, however, the state of the art is somewhat unsatisfactory. While there is a straightforward generalization of process equivalences to the continuous case, in practice, equivalence notions such as bisimilarity are always too strong and most systems are not bisimilar. Since equivalence is a Boolean notion, one gets no additional information about the systems other than they are “not bisimilar.” Further, even if two dynamical systems are bisimilar, they may still differ in many control-theoretic properties. Thus, classical notions for equivalence and conformance have been of limited use in industrial practice.

In recent years, the notion of bisimulation has therefore been generalized to metrics on systems, which quantify the distance between them. For example, one approach is that of $\epsilon$-bisimulation, which requires that the states of the two systems remain “close” forever (within an $\epsilon$-ball), rather than coincide exactly. Under suitable stability assumptions on the dynamics, one can construct $\epsilon$-bisimulations [17, 18]. Unfortunately, proving the pre-requisites for the existence of $\epsilon$-bisimulations for complex dynamical models, or coming up with suitable and practically tractable bisimulation functions is extremely difficult in practice. In addition, establishing $\epsilon$-bisimulation requires full knowledge of the system dynamics making the scheme inapplicable where one system is an actual physical component with unknown dynamics. So, these notions have also been of limited industrial use so far.

Instead, a more pragmatic semi-formal approach has gained prominence in industrial practice. In this approach, the two systems are executed on the same input sequences and a metric on finite trajectories is used to evaluate the closeness of these trajectories. The key to this methodology is the selection of a good metric, with the following properties:

• Transference. Closeness in the metric must translate to preserving interesting classes of logical and functional specifications between systems, and

• Tractability. The metric should be efficiently computable.

In addition, there is the more informal requirement of usability: the metric should classify systems which the engineers consider close as being close, and conversely.

The simplest candidate metric is a pointwise metric that computes the maximum pointwise difference between two trajectories, sometimes generalized to apply a constant time-shift to one trajectory [15]. Unfortunately, for many practical models, two trajectories may be close only under variable time-shifts. This is the case, for example, for two dynamical models that may use different numerical integration techniques (e.g., fixed step versus adaptive step) or when some component in the implementation has some jitter. Thus, the pointwise metric spuriously reports large distances for “close” models. More nuanched hybrid distances have been proposed [1], but the transference properties of these metrics w.r.t. common temporal logics are not yet clear.

In this work we present a methodology for quantifying conformance between real-valued dynamical systems based on the Skorokhod metric [12]. The Skorokhod metric allows for mismatches in both the trace values and in the timeline, and quantifies temporal and spatial variation of the system dynamics under a unifying framework. The distortion of the timeline is specified by a retiming function $\mathsf {r}$ which is a continuous bijective strictly increasing function from ${\mathbb {R}}_+$ to ${\mathbb {R}}_+$. Using the retiming function, we obtain the retimed trace $x\left( \mathsf {r}(t)\right)$ from the original trace x(t). Intuitively, in the retimed trace $x\left( \mathsf {r}(t)\right)$, we see exactly the same values as before, in exactly the same order, but the time duration between two values might now be different than the corresponding duration in the original trace. The amount of distortion for the retiming $\mathsf {r}$ is given by $\sup _{t\ge 0} |{\mathsf {r}(t)-t}|$. Using retiming functions, the Skorokhod distance between two traces x and y is defined to be the least value over all possible retimings $\mathsf {r}$ of:

$$\begin{aligned} \max \left( \sup _{t\in [0,T]} |{\mathsf {r}(t)-t}|,\, \sup _{t\in [0,T]}{\mathscr {D}}\big (x\left( \mathsf {r}(t)\right) , y(t)\big ) \right) , \end{aligned}$$

where ${\mathscr {D}}$ is a pointwise metric on values. In this formula, the first component quantifies the timing discrepancy of the timing distortion required to “match” two traces, and the second quantifies the value mismatch (in the metric space ${\mathscr {O}}$) of the values under the timing distortion. The Skorokhod metric was introduced as a theoretical basis for defining the semantics of hybrid systems by providing an appropriate hybrid topology [8, 9]. We now demonstrate its usefulness in the context of conformance testing.

Transference. We show that the Skorokhod metric gives a robust quantification of system conformance by relating the metric to TLTL (timed LTL) enriched with (i) predicates of the form $f(x_1,\dots , x_n) \ge 0$, as in Signal Temporal Logic [15], for specifying constraints on trace values; and (ii) freeze quantifiers, as in TPTL  [4], for specifying temporal constraints (freeze quantifiers can express more complex timing constraints than bounded timing constraints, e.g., of MTL). TLTL subsumes MTL and STL  [15]. We prove a transference theorem: flows (and propositional traces) which are close under the Skorokhod metric satisfy “close” TLTL formulae for a rich class of temporal and spatial predicates, where the untimed structure of the formulae remains unchanged, only the predicates are enlarged.

Tractability. We improve on recent polynomial-time algorithms for the Skorokhod metric [25] by taking advantage of the fact that, in practice, only retimings that map the times in one trace to “close” times in the other are of interest. This enables us to obtain a streaming sliding-window based monitoring procedure which takes only O(W) time per sample, where W is the window size (assuming the dimension n of the system to be a constant).

Usability. Using the Skorokhod distance checking procedure as a subroutine, we have implemented a Simulink toolbox for conformance testing. Our tool integrates with Simulink’s model-based design flow for control systems, and provides a stochastic search-based approach to find inputs which maximize the Skorokhod distance between systems under these inputs.

We present three case studies from the control domain, including industrial challenge problems; our empirical evaluation shows that our tool computes sharp estimates of the conformance distance reasonably fast on each of them. Our input models were complex enough that techniques such as $\epsilon$-bisimulation functions are inapplicable. We conclude that the Skorokhod metric can be an effective foundation for semi-formal conformance testing for complex dynamical models. Proofs of the theorems are given in the accompanying technical report [13].

Related Work. The work of [1, 2] is closely related to ours. In it, robustness properties of hybrid state sequences are derived with respect to a trace metric which also quantifies temporal and spatial variations. Our work differs in the following ways. First, we guarantee robustness properties over flows rather than only over (discrete) sequences. Second, the Skorokhod metric is a stronger form of the $(T,J,(\tau , \epsilon ))$-closeness degree^{1 , 2} (for systems which do not have hybrid time); and allows us to give stronger robustness transference guarantees. The Skorokhod metric requires order preservation of the timeline, which the $(T,J,(\tau , \epsilon ))$-closeness function does not. Preservation of the timeline order allows us to (i) keep the untimed structure of the formulae the same (unlike in the transference theorem of [1]); (ii) show transference of a rich class of global timing constraints using freeze quantifiers (rather than only for the standard bounded time quantifiers of MTL/MITL). However, for implementations where the timeline order is not preserved, we have to settle for the less stronger guarantees provided by [1]. The work of [15] deals with spatial robustness of STL; the only temporal disturbances considered are constant time-shifts for the entire signal where the entire signal is moved to the past, or to the future by the same amount. In contrast, the Skorokhod metric incorporates variable time-shifts.

2 Conformance Testing with the Skorokhod Metric

2.1 Systems and Conformance Testing

Traces and Systems. A (finite) trace or a signal $\pi : [T_i,T_e] \mapsto {\mathscr {O}}$ is a mapping from a finite closed interval $[T_i,T_e]$ of ${\mathbb {R}}_+$, with $0 \le T_i < T_e$, to some topological space ${\mathscr {O}}$. If $\mathscr {O}$ is a metric space, we refer to the associated metric on $\mathscr {O}$ as ${\mathscr {D}}_{\mathscr {O}}$. The time-domain of $\pi$, denoted ${\mathsf {tdom}}(\pi )$, is the time interval $[T_i,T_e]$ over which it is defined. The time-duration of $\pi$, denoted ${\mathsf {tlen}}(\pi )$, is $\sup \left( {\mathsf {tdom}}(\pi ) \right)$. The t-suffix of $\pi$ for $t\in {\mathsf {tdom}}(\pi )$, denoted $\pi ^t$, is the trace $\pi$ restricted to the interval $( {\mathsf {tdom}}(\pi ) \cap [t, {\mathsf {tlen}}(\pi )]$. We denote by $\pi _{\downarrow T'_e}$ the prefix trace obtained from $\pi$ by restricting the domain to $[T_i,T'_e]\subseteq {\mathsf {tdom}}(\pi )$.

A (continuous-time) system , where is the set of finite closed intervals of ${\mathbb {R}}_+$, transforms input traces $\pi _{{\mathsf {ip}}}: [T_i,T_e] \mapsto {\mathscr {O}}_{{\mathsf {ip}}}$ into output traces $\pi _{{\mathsf {op}}}: [T_i,T_e] \mapsto {\mathscr {O}}_{{\mathsf {op}}}$ (over the same time domain). We require that the system is causal: if $\mathfrak {A}(\pi _{{\mathsf {ip}}}) \mapsto \pi _{{\mathsf {op}}}$, then for every $\min {\mathsf {tdom}}(\pi ) \le T_e' < \max {\mathsf {tdom}}(\pi )$, the system $\mathfrak {A}$ maps ${\pi _{{\mathsf {ip}}}}_{\downarrow T'_e}$ to ${\pi _{{\mathsf {op}}}}_{\downarrow T'_e}$. Common examples of such systems are (causal) dynamical and hybrid dynamical systems [7, 30].

Conformance Testing. Let $\mathfrak {A}_1$ and $\mathfrak {A}_2$ be systems and let ${\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}$ be a metric over output traces. For a set $\varPi _{{\mathsf {ip}}}$ of input traces, we define the (quantitative) conformance between $\mathfrak {A}_1$ and $\mathfrak {A}_2$ w.r.t. $\varPi _{{\mathsf {ip}}}$ as $\sup _{\pi _{{\mathsf {ip}}}\in \varPi _{{\mathsf {ip}}}} {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}\left( \mathfrak {A}_1\left( \pi _{{\mathsf {ip}}}\right) , \mathfrak {A}_2\left( \pi _{{\mathsf {ip}}}\right) \right)$ The conformance between $\mathfrak {A}_1$ and $\mathfrak {A}_2$ is their conformance w.r.t. the set of all input traces.

The conformance testing problem asks, given systems $\mathfrak {A}_1, \mathfrak {A}_2$, a trace metric ${\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}$, a tolerance $\delta$, and a set of test input traces $\varPi _{ test }$, if the quantitative conformance between $\mathfrak {A}_1$ and $\mathfrak {A}_2$ w.r.t. $\varPi _{ test }$ is more than $\delta$. Clearly, conformance w.r.t. $\varPi _{ test }$ is a lower bound on the conformance between $\mathfrak {A}_1$ and $\mathfrak {A}_2$.

Algorithm 1 is a standard optimization-guided adaptive testing algorithm. To define the set $\varPi _{ test }$ of test inputs, we use a fixed finite parameterization of the input space using a finite set F of basis functions and fix a time horizon T. We only generate inputs obtained as a linear combination $\sum _{f \in F} p_f \cdot f$ of basis functions over the interval [0, T], where the coefficients $\{ p_f \mid f\in F \}$ come from a closed convex subset of ${\mathbb {R}}^{|F|}$.

In each step, Algorithm 1 picks an input signal u and computes the distance between the corresponding outputs $y_1 = \mathfrak {A}_1(u)$ and $y_2 = \mathfrak {A}_2(u)$. Based on heuristics that rely on the current distance, and a possibly bounded history of costs, the procedure then picks a new value for u by choosing new values for the coefficients $\{ p_f\mid f\in F \}$. For instance, in a gradient-ascent based procedure, the new value of u is chosen by estimating the local gradient in each direction in the input-parameter space, and then picking the direction that has the largest (positive) gradient. In our implementation, we use the Nelder-Mead (or nonlinear simplex) algorithm to pick new inputs.

On termination (e.g., when some maximum number of iterations is reached), the algorithm returns the conformance distance between $\mathfrak {A}_1$ and $\mathfrak {A}_2$ w.r.t. the set of tests generated. One can compare the distance to some tolerance $\delta$ chosen based on engineering requirements.

Sampling and Polygonal Traces. In practice, the output behaviors of the systems are observed with a sampling process, thus $y_1$ and $y_2$ on line 4 are discrete time-sampled sequences. We go from these sequences to output traces by linearly interpolating between the sampled time points.

Formally, a polygonal trace $\pi : I_{\pi } \mapsto \mathscr {O}$ where $\mathscr {O}$ is a vector space with the scalar field ${\mathbb {R}}$ is a continuous trace such that there exists a finite sequence $\min I_{\pi }= t_0 < t_1 < \dots < t_m = \max I_{\pi }$ of time-points such that the trace segment between $t_k$ and $t_{k+1}$ is affine for all $0\le k < m$, i.e., for $t_k \le t \le t_{k+1}$ we have $\pi (t) = \pi (t_k) + \frac{t- t_k}{t_{k+1}-t_k}\!\cdot \!\left( \pi ( t_{k+1}) - \pi (t_k)\right)$.

Given a timed trace sequence ${\mathsf {tseq}}$, let $[\![ {\mathsf {tseq}} ]\!]_{{\mathsf {LI}}}$ denote the polygonal trace obtained from ${\mathsf {tseq}}$ by linear interpolation. Let ${\mathsf {tseq}}_{\pi }, {\mathsf {tseq}}_{\pi '}$ be two corresponding samplings of the traces $\pi , \pi '$, respectively. For a trace metric ${\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}$, we have:

$$\begin{aligned} \ {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}(\pi , \pi ') \le {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}\left( [\![ {\mathsf {tseq}}_{\pi } ]\!]_{{\mathsf {LI}}}, [\![ {\mathsf {tseq}}_{\pi '} ]\!]_{{\mathsf {LI}}}\right) \, +\, {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}\left( [\![ {\mathsf {tseq}}_{\pi } ]\!]_{{\mathsf {LI}}}, \pi \right) + {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}\left( [\![ {\mathsf {tseq}}_{\pi '} ]\!]_{{\mathsf {LI}}}, \pi '\right) . \end{aligned}$$

If $\varDelta _{{\mathsf {samerr}}}$ is a bound on the distance between a trace and an interpolated completion of its sampling, we have that ${\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}(\pi , \pi ') \le {\mathscr {D}}_{\mathcal {T}\!\mathcal {R}}([\![ {\mathsf {tseq}}_{\pi } ]\!]_{{\mathsf {LI}}}, [\![ {\mathsf {tseq}}_{\pi '} ]\!]_{{\mathsf {LI}}})\, +\, 2\!\cdot \!\varDelta _{{\mathsf {samerr}}}$. Thus, a value of $2\!\cdot \!\varDelta _{{\mathsf {samerr}}}$ needs to be added in the testing algorithm to account for the error due to polygonal approximations.

2.2 The Skorokhod Metric

We now define the Skorokhod metric, which we use as the metric in Algorithm 1. A retiming $\mathsf {r}: I \mapsto I'$, for closed intervals $I, I'$ of ${\mathbb {R}}_+$ is an order-preserving (i.e., monotone) continuous bijective function from I to $I'$; thus if $t<t'$ then $\mathsf {r}(t) < \mathsf {r}(t')$. Let ${\mathsf {R}}_{I \mapsto I' }$ be the class of retiming functions from I to $I'$ and let $\mathcal {I}$ be the identity retiming. Intuitively, retiming can be thought of as follows: imagine a stretchable and compressible timeline; a retiming of the original timeline gives a new timeline where some parts have been stretched, and some compressed, without the timeline having been broken. Given a trace $\pi : I_{\pi } \rightarrow {\mathscr {O}}$, and a retiming $\mathsf {r}: I \mapsto I_{\pi }$; the function $\pi \circ \mathsf {r}$ is another trace from I to ${\mathscr {O}}$.

Definition 1

(Skorokhod Metric). Given a retiming $\mathsf {r}: I \mapsto I'$, let $||\mathsf {r}-\mathcal {I}||_{\sup }$ be defined as $||\mathsf {r}-\mathcal {I}||_{\sup } =\sup _{t\in I }|\mathsf {r}(t)-t|$. Given two traces $\pi : I_{\pi }\mapsto {\mathscr {O}}$ and $\pi ': I_{\pi '} \mapsto {\mathscr {O}}$, where ${\mathscr {O}}$ is a metric space with the associated metric ${\mathscr {D}}_{{\mathscr {O}}}$, and a retiming $\mathsf {r}: I_{\pi } \mapsto I_{\pi '}$, let $\Vert {\pi \,-\, \pi '\circ \mathsf {r}}\Vert _{\sup }$ be defined as:

$$ \Vert {\pi \,-\, \pi '\circ \mathsf {r}}\Vert _{\sup } = \sup \nolimits _{t\in I_{\pi }} {\mathscr {D}}_{{\mathscr {O}}}\big (\, \pi (t),\ \pi '\left( \mathsf {r}(t)\right) \, \big ). $$

The Skorokhod distance ³ between the traces $\pi ()$ and $\pi '()$ is defined to be:

$$\begin{aligned} {\mathscr {D}}_{{\mathscr {S}}}(\pi ,\pi ') = \inf _{r\in {\mathsf {R}}_{ I_{\pi } \mapsto I_{\pi '}}} \max (\Vert {\mathsf {r}-\mathcal {I}}\Vert _{\sup } \, ,\, \Vert {\pi \,-\, \pi '\circ \mathsf {r}}\Vert _{\sup }).\qquad \square \end{aligned}$$

(1)

Intuitively, the Skorokhod distance incorporates two components: the first component quantifies the timing discrepancy of the timing distortion required to “match” two traces, and the second quantifies the value mismatch (in the metric space ${\mathscr {O}}$) of the values under the timing distortion. In the retimed trace $\pi \circ \mathsf {r}$, we see exactly the same values as in $\pi$, in exactly the same order, but the times at which the values are seen can be different.

The following theorem shows that the Skorokhod distance between polygonal traces can be computed efficiently. We remark that after retiming, the retimed version $\pi \circ \mathsf {r}$ of a polygonal trace $\pi$ need not be polygonal (see e.g., [24]).

Theorem 1

(Computing the Distance Between Polygonal Traces [25]). Let $\pi : I_{\pi } \mapsto {\mathbb {R}}^n$ and $\pi ': I_{\pi '}\mapsto {\mathbb {R}}^n$ be two polygonal traces with $m_{\pi }$ and $m_{\pi '}$ affine segments respectively. Let the Skorokhod distance between them (for the $L_2$ norm on ${\mathbb {R}}^n$) be denoted as ${\mathscr {D}}_{{\mathscr {S}}} (\pi , \pi ')$.

• 1. Given $\delta \ge 0$, it can be checked whether ${\mathscr {D}}_{{\mathscr {S}}} (\pi , \pi ') \le \delta$ in time $O\left( m_{\pi }\!\cdot \!m_{\pi '}\!\cdot \!n\right)$.

• 2. Suppose we restrict retimings to be such that the i-th affine segment of $\pi$ can only be matched to $\pi '$ affine segments $i-W$ through $i+W$ for all i, where $W\ge 1$. Under this retiming restriction, we can determine, with a streaming algorithm, whether ${\mathscr {D}}_{{\mathscr {S}}} (\pi , \pi ') \le \delta$ in time $O\left( \left( m_{\pi }+ m_{\pi '}\right) \!\cdot \!n\!\cdot \!W\right)$.$\quad \square$

Let us denote by ${\mathscr {D}}_{{\mathscr {S}}}^W (\pi , \pi ')$ the Skorokhod difference between $\pi , \pi '$ under the retiming restriction of the second part of Theorem 1, i.e., the value obtained by restricting the retimings in Eq. 1 ⁴. The value ${\mathscr {D}}_{{\mathscr {S}}}^W (\pi , \pi ')$ is an upper bound on ${\mathscr {D}}_{{\mathscr {S}}} (\pi , \pi ')$. In addition, for $W' < W$, we have ${\mathscr {D}}_{{\mathscr {S}}}^W (\pi , \pi ') \le {\mathscr {D}}_{{\mathscr {S}}}^{W'} (\pi , \pi ')$.

3 Transference of Logical Properties

In this section, we demonstrate a transference result for the Skorokhod metric for a version of the timed linear time logic TLTL  [4]. The logic we consider generalizes MTL and STL. We show that if the Skorokhod distance between two traces is small, they satisfy close TLTL formulae. Given a formula $\phi$ of TLTL satisfied by trace $\pi _1$, we can compute a “relaxation” of $\phi$ that will be satisfied by the “close” trace $\pi _2$. We first present the results in a propositional framework, and then extend to ${\mathbb {R}}^n$-valued spaces for a logic generalizing STL.

3.1 The Logic TLTL

Let $\mathcal {P}$ be a set of propositions. A propositional trace $\pi$ over $\mathcal {P}$ is a trace where the topological space is $2^{\mathcal {P}}$, with the associated metric ${\mathscr {D}}_{\mathcal {P}}(\sigma , \sigma ') = 0$ if $\sigma = \sigma '$, and $\infty$ otherwise, for $\sigma ,\sigma '\in 2^{\mathcal {P}}$. We restrict our attention to propositional traces with finite variability: we require that there exists a finite partition of ${\mathsf {tdom}}(\pi )$ into disjoint subintervals $I_0, I_1, \dots , I_m$ such that $\pi$ is constant on each subinterval. The set of all timed propositional traces over $\mathcal {P}$ is denoted by $\varPi (\mathcal {P})$.

Definition 2

( TLTL $(\mathcal {F}_{{\mathsf {T}}})$ Syntax). Given a set of propositions $\mathcal {P}$, a set of (time) variables $V_{\mathsf {T}}$, and a set $\mathcal {F}_{{\mathsf {T}}}$ of functions from ${\mathbb {R}}_+^l$ to ${\mathbb {R}}$, the formulae of TLTL($\mathcal {F}_{{\mathsf {T}}}$) are defined by the following grammar.

$$\begin{aligned} \phi := p \mid {true}\mid f_{\mathsf {T}}(\overline{x}) \sim 0 \mid \lnot \phi \mid \phi _1 \wedge \phi _2 \mid \phi _1 \vee \phi _2 \mid \phi _1 {\,\mathcal{U}\,}\phi _2 \mid x.\phi \quad \text { where} \end{aligned}$$

• $p\in \mathcal {P}$ and $x\in V_{\mathsf {T}}$, and $\overline{x} = (x_1, \dots , x_l)$ with $x_i\in V_{\mathsf {T}}$ for all $1\le i \le l$;

• $f_{\mathsf {T}} \in \mathcal {F}_{{\mathsf {T}}}$ is a real-valued function, and $\sim$ is one of $\{ \le , <, \ge , > \}$. $\quad \square$

The quantifier “x.” is known as the freeze quantifier, and binds variable x to the current time. A variable x is defined to be free in $\phi$ as follows. The variable x is not free in $x.\varPsi$, or in p (a proposition), or in ${true}$, or in $f_{\mathsf {T}}(x_1, \dots , x_l) \sim 0$ where $x_i\ne x$ for all i. It is also not free in $\phi$ if $\phi$ does not contain an occurrence of x. It is free in $\lnot \psi$ iff x is free in $\psi$; and it is free in $\phi _1 \mathrel {\begin{array}{c} \wedge \\ \vee \end{array}}\phi _2$, or in $\phi _1 {\,\mathcal{U}\,}\phi _2$, iff x is free in either $\phi _1$ or in $\phi _2$. Finally, variable x is free in $f_{\mathsf {T}}(x_1, \dots , x_l) \sim 0$ if some $x_i$ is x. A formula is closed if it has no free variables.

Definition 3

( TLTL $(\mathcal {F}_{{\mathsf {T}}})$ Semantics). Let $\pi : I \mapsto 2^{\mathcal {P}}$ be a timed propositional trace, and let $\mathcal {E}: V_{\mathsf {T}} \mapsto I$ be the time environment mapping the variables in $V_{\mathsf {T}}$ to time values in I. The satisfaction of the trace $\pi$ with respect to the TLTL($\mathcal {F}_{{\mathsf {T}}})$ formula $\phi$ in the time environment $\mathcal {E}$ is written as $\pi \models _{\mathcal {E}} \phi$, and is defined inductively as follows (denoting $t_0 = \min {\mathsf {tdom}}(\pi )$).

$$\begin{aligned} \pi&\models _{\mathcal {E}} p \text { for } p\in \mathcal {P}\text { iff } p\in \pi (t_0); \qquad \pi \models _{\mathcal {E}} {true}; \qquad \pi \models _{\mathcal {E}} \lnot \varPsi \text { iff } \pi \not \models _{\mathcal {E}} \varPsi ;\\ \pi&\models _{\mathcal {E}} \phi _1 \wedge \phi _2 \text { iff } \pi \models _{\mathcal {E}} \phi _1 \text { and } \pi \models _{\mathcal {E}} \phi _2; \quad \pi \models _{\mathcal {E}} \phi _1 \vee \phi _2 \text { iff } \pi \models _{\mathcal {E}} \phi _1 \text { or } \pi \models _{\mathcal {E}} \phi _2;\\ \pi&\models _{\mathcal {E}} f_{\mathsf {T}}(x_1, \dots , x_l) \sim 0 \text { iff } f_{\mathsf {T}}(\mathcal {E}(x_1), \dots , \mathcal {E}(x_l)) \sim 0 \text { for } \sim \,\in \{ \le , <, \ge , > \};\\ \pi&\! \models _{\mathcal {E}}\! x.\psi \text { iff } \pi \! \models _{\mathcal {E}[x\!:=\!t_0]}\! \psi \text { where } \mathcal {E}[x\!:=\!t_0] \text { agrees}\, \text {with } \mathcal {E}\! \text { for}\, \text {all } x_i\!\!\ne \! x, \!\text { and}\,\text {maps}\, x\, \text {to } t_0; \\ \pi&\models _{\mathcal {E}} \phi _1 {\,\mathcal{U}\,}\phi _2 \text { iff } \pi ^t \models _{\mathcal {E}} \phi _2 \text { for some } t\in I \text { and } \pi ^{t'} \models _{\mathcal {E}} \phi _1\vee \phi _2 \text { for all } t_0\le t' < t. \end{aligned}$$

A timed trace $\pi$ is said to satisfy the closed formula $\phi$ (written as $\pi \models \phi$) if there is some environment $\mathcal {E}$ such that $\pi \models _{\mathcal {E}} \phi$. $\quad \square$

We define additional temporal operators in the standard way: the “eventually” operator $\Diamond \phi$ stands for ${true}{\,\mathcal{U}\,}\phi$; and the “always” operator $\Box \phi$ stands for $\lnot \Diamond \lnot \phi$. TLTL $(\mathcal {F}_{{\mathsf {T}}})$ provides a richer framework than MTL  [23] for expressing timing constraints as: (i) freeze quantifiers allow specification of constraints between distant contexts, which the bounded temporal operators in MTL cannot do; and (ii) the predicates $f_{\mathsf {T}}() \sim 0$ for $f_{\mathsf {T}}\in \mathcal {F}_{{\mathsf {T}}}$ allow the specification of complex timing requirements not expressible in MTL. Note that even if the predicates $f_{\mathsf {T}}() \sim 0$ are restricted to be of the form $x_1-x_2 +c \sim 0$, where $x_1, x_2$ are freeze variables, and c is a constant, TLTL $(\mathcal {F}_{{\mathsf {T}}})$ is more expressive than MTL  [6] (and hence more expressive than MITL on which STL is based).

Example 1

( TLTL $(\mathcal {F}_{{\mathsf {T}}})$ Subsumes MTL ). Let $\mathcal {F}_{{\mathsf {T}}}$ be the set of two variable functions of the form $f(x,y) = x-y+c$ where c is a rational constant. Then TLTL $(\mathcal {F}_{{\mathsf {T}}})$ subsumes MTL. The MTL formula $p {\,\mathcal{U}\,}_{[a,b]} q$ can be written as

$$\begin{aligned} x. \Big (p {\,\mathcal{U}\,}y. \big ( \,(y\le x+b) \wedge (y\ge x+a) \wedge q\big )\Big ). \end{aligned}$$

We explain the formula as follows. We assign the “current” time $t_x$ to the variable x, and some future time $t_y$ to the variable y. The values $t_x$ and $t_y$ are such that at time $t_y$, we have q to be true, and moreover, at all times between $t_x$ and $t_y$, we have $p\vee q$ to be true. Furthermore, $t_y$ must be such that $t_y\in [t_x+a, t_x+b]$, which is specified by the term $(y\le x+b) \wedge (y\ge x+a)$. $\quad \square$

Example 2

(Temporal Constraints). Suppose we want to express that whenever the event p occurs, it must be followed by a response q, and then by r. In addition, we have the following timing requirement: if $\varepsilon _{pq}, \varepsilon _{qr}, \varepsilon _{pr}$ are the time delays between p and q, between q and r, and between p and r, respectively, then: we must have $\varepsilon ^2_{pq}+ \varepsilon ^2_{qr}+\varepsilon ^2_{pr} \le d$ for a given positive constant d. This can be written using freeze quantifiers as the TLTL formula $\phi$:

$$\begin{aligned} x. \left( p \rightarrow \Diamond \big (y. \left( q \wedge \Diamond \left[ z. \left( r \wedge \left( (y-x)^2 + (z-y)^2 + (z-x)^2 \le d \right) \right) \right] \right) \big )\right) .\qquad \quad \ \square \end{aligned}$$

3.2 Transference of TLTL Properties for Propositional Traces

We now show that if a timed propositional trace $\pi$ satisfies a TLTL $(\mathcal {F}_{{\mathsf {T}}})$ formula $\phi$, then any timed trace $\pi '$ that is at most $\delta$ distance away from $\pi$ satisfies a slightly relaxed version of the formula $\phi$, the degree of relaxation being governed by $\delta$; and the variance of the functions in $\mathcal {F}_{{\mathsf {T}}}$ over the time interval containing the time domains of $\pi$ and $\pi '$.

We define the distance ${\mathscr {D}}_{{\mathscr {S}}}$ between two propositional traces as the Skorokhod distance, where we use ${\mathscr {D}}_{\mathcal {P}}$ as the distance between two sets of propositions.

Next, we define relaxations of TLTL $(\mathcal {F}_{{\mathsf {T}}})$ formulae. The relaxations are defined as a syntactic transformation on formulae in negation-normal form, i.e., in which negations only appear at the propositions. It can be showed that every TLTL $(\mathcal {F}_{{\mathsf {T}}})$ formula can be rewritten in negation-normal form, when we additionally use the waiting for operator, $\,\mathcal{W}\,$, defined as: $\pi \models _{\mathcal {E}} \phi _1 \,\mathcal{W}\,\phi _2$ iff either (1) $\pi ^t \models _{\mathcal {E}}\phi _1$ for all $t\in I_{\pi }$; or (2) $\pi ^t \models _{\mathcal {E}} \phi _2$ for some $t\in I_{\pi }$; and $\pi ^{t'} \models _{\mathcal {E}} \phi _1\vee \phi _2$ for all $\min I_{\pi } \le t' < t$.

Definition 4

( $\delta$ -relaxation of TLTL $(\mathcal {F}_{{\mathsf {T}}})$ Formulae). Let $\phi$ be a TLTL $(\mathcal {F}_{{\mathsf {T}}})$ formula in which negations appear only on the propositional symbols. The $\delta$ relaxation of $\phi$ (for $\delta \! \ge \! 0$) over a closed interval J, denoted ${\mathsf {rx}}_{J}^{\delta }(\phi )$, is defined as:

$$\begin{aligned} \begin{array}{l|l} \begin{array}{lll} {\mathsf {rx}}_{ J}^{ \delta }(p) &{} = &{} p \\ {\mathsf {rx}}_{ J}^{\delta }(\lnot p) &{} = &{} \lnot p \\ {\mathsf {rx}}_{ J}^{\delta }( \phi _1 \wedge \phi _2 ) &{} = &{} {\mathsf {rx}}_{ J}^{\delta }( \phi _1) \wedge {\mathsf {rx}}_{J}^{\delta }(\phi _2 ) \\ {\mathsf {rx}}_{ J}^{\delta }( x.\psi ) &{} = &{} x.{\mathsf {rx}}_{ J}^{\delta }(\psi )\\ {\mathsf {rx}}_{ J}^{\delta }( \phi _1 {\,\mathcal{U}\,}\phi _2 ) &{} = &{} {\mathsf {rx}}_{ J}^{\delta }(\phi _1) {\,\mathcal{U}\,}{\mathsf {rx}}_{J}^{\delta }(\phi _2) \\ \end{array} &{} \begin{array}{lll} {\mathsf {rx}}_{ J}^{\delta }({true}) &{} = &{} {true}\\ {\mathsf {rx}}_{ J}^{\delta }({false}) &{} = &{} {false}\\ {\mathsf {rx}}_{ J}^{\delta }( \phi _1 \vee \phi _2 ) &{} = &{} {\mathsf {rx}}_{ J}^{\delta }( \phi _1) \vee {\mathsf {rx}}_{ J}^{\delta }(\phi _2 )\\ &{} &{} \\ {\mathsf {rx}}_{ J}^{\delta }( \phi _1 \,\mathcal{W}\,\phi _2 ) &{} = &{} {\mathsf {rx}}_{ J}^{\delta }(\phi _1) \,\mathcal{W}\,{\mathsf {rx}}_{ J}^{\delta }(\phi _2) \\ \end{array} \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{l} {\mathsf {rx}}_{ J}^{\delta }\left( f_{\mathsf {T}}(x_1, \dots , x_l) \right) \sim 0) = \left\{ \begin{array}{ll} f_{\mathsf {T}}(x_1, \dots , x_l) \, +\, K^{f_{\mathsf {T}}}_J(\delta ) \ \sim \, 0 &{} \text { if } \sim \, \in \{ >, \ge \}\\ f_{\mathsf {T}}(x_1, \dots , x_l) \, -\, K^{f_{\mathsf {T}}}_J(\delta ) \ \sim \, 0 &{} \text { if } \sim \,\in \{ <, \le \},\\ \end{array} \right. \\ \text {where } K^{f_{\mathsf {T}}}_J:[0, \max {\mathsf {tdom}}( J)\, - \, \min {\mathsf {tdom}}( J)]\mapsto {\mathbb {R}}_+ \text {, and} \\ K^{f_{\mathsf {T}}}_J(\delta ) {\mathop {=}\limits ^{\mathrm{def}}} \displaystyle \sup _{ \begin{array}{l} {t_1,\dots ,t_l\in J}\\ {t_1',\dots ,t_l'\in J} \end{array} } \left\{ \left| \begin{array}{c} f_{\mathsf {T}}(t_1,\dots , t_l) \\ -\\ f_{\mathsf {T}}(t_1',\dots ,t_l') \end{array}\right| \ \text { s.t. } |t_i-t_i'| \le \delta \text { for all } i \right\} \end{array} \end{aligned}$$

(2)

Thus, instead of comparing the $f_{\mathsf {T}}()$ values to 0, we relax by comparing instead to $\pm K^{f_{\mathsf {T}}}_J(\delta )$. The other cases recursively relax the subformulae. The functions $K^{f_{\mathsf {T}}}_J(\delta )$ define the maximal change in the value of $f_{\mathsf {T}}$ that can occur when the input variables can vary by $\delta$. The role of J is to restrict the domain of the freeze quantifier variables to the time interval J (from ${\mathbb {R}}_+$) in order to obtain the least possible relaxation on a given trace $\pi$ (e.g., we do not care about the values of a function in ${\mathcal {F}_{{\mathsf {T}}}}$ outside of the domain ${\mathsf {tdom}}(\pi )$ of the trace).

Example 3

( $\delta$ -relaxation for Bounded Temporal Operators – MTL ). We demonstrate how $\delta$-relaxation operates on bounded time constraints. Consider again the MTL formula $\phi = p {\,\mathcal{U}\,}_{[a,b]} q$. When written as a TLTL formula and relaxed using the ${\mathsf {rx}}_{{\mathbb {R}}_+}^{\delta }$ function, the relaxed TLTL formula is equivalent to the MTL formula $p {\,\mathcal{U}\,}_{[a-2\cdot \delta \,,\, b+2\cdot \delta ]} q$. $\quad \square$

Theorem 2

(Transference for Propositional Traces). Let $\pi , \pi '$ be two timed propositional traces such that ${\mathscr {D}}_{{\mathscr {S}}}(\pi , \pi ') < \delta$ for some finite $\delta$. Let $\phi$ be a closed TLTL $(\mathcal {F}_{{\mathsf {T}}})$ formula in negation-normal form. If $\pi \models \phi$, then $\pi '\models {\mathsf {rx}}_{I_{\pi ,\pi '}}^{\delta }(\phi )$ where ${I_{\pi ,\pi '}}$ is the convex hull of ${\mathsf {tdom}}(\pi ) \cup {\mathsf {tdom}}(\pi ')$. $\quad \square$

Theorem 2 relaxes the freeze variables over the entire signal time-range ${I_{\pi ,\pi '}}$; it can be strengthened by relaxing over a smaller range: if $\pi \models \phi$, and $t_1, \dots , t_k$ are time-stamp assignments to the freeze variables $x_1, \dots , x_k$ which witness $\pi$ satisfying $\phi$, then $x_i$ only needs to be relaxed over $[t_i-\delta , t_i+\delta ]$ rather than the larger interval ${I_{\pi ,\pi '}}$. These smaller relaxation intervals for the freeze variables can be incorporated in Eq. 2. We omit the details for ease of presentation.

Example 4

Recall Example 2, and the formula $\phi$ presented in it. Suppose a trace $\pi$ satisfies $\phi$; and let ${\mathscr {D}}_{{\mathscr {S}}}\left( \pi , \pi '\right) < \delta$ (using the Skorokhod metric for propositional traces). Our transference theorem ensures that (i) $\pi '$ will satisfy the same untimed formula $p\rightarrow \, \Diamond \left( q \wedge \Diamond r\right)$; and (ii) it gives a bound on how much the timing constraints need to be relaxed in $\phi$ in order to ensure satisfaction by $\pi '$; it states that $\pi '$ satisfies the following relaxed formula $\phi '$.

$$\begin{aligned} \pi '\models x. \left( p \rightarrow \Diamond \big (y. \left( q \wedge \Diamond \left[ z. \left( r \wedge \left( (y-x)^2 + (z-y)^2 + (z-x)^2 \le d^{\dagger } \right) \right) \right] \right) \big )\right) \end{aligned}$$

where $d^{\dagger } = d + 12 \cdot \delta ^2 + 4\sqrt{3}\cdot \delta \cdot \sqrt{d}\$ (see [13]). $\quad \square$

3.3 Transference of TLTL Properties for ${\mathbb {R}}^n$-valued Signals

A timed ${\mathbb {R}}^n$ -valued trace $\pi$ is a function from a closed interval I of ${\mathbb {R}}_+$ to ${\mathbb {R}}^n$. For $\overline{\alpha } = (\alpha ^0, \dots , \alpha ^n)\in {\mathbb {R}}^n$, we denote the k-th dimensional value $\alpha ^k$ as $\overline{\alpha }[k]$. The $\pi$ projected function onto the k-th ${\mathbb {R}}$ dimension is denoted by $\pi _{k}: I \mapsto {\mathbb {R}}$.

To define the semantics of TLTL formulae over timed ${\mathbb {R}}^n$-valued sequences, we use booleanizing predicates $\mu : {\mathbb {R}}^n \mapsto {\mathbb {B}}$, as in STL  [15], to transform ${\mathbb {R}}^n$-valued sequences into timed propositional sequences. These predicates are part of the logical specification. In this work, we restrict our attention to traces and predicates such that each predicate varies only finitely often on the finite time traces under consideration. Since we also have freeze variables, TLTL with predicates is strictly more expressive than STL ⁵ (as in the propositional case [6]).

Definition 5

( TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$ Syntax). Given a set of variables $V_{\mathsf {T}}$ (the freeze variables), a set of ordered variables $V_{\mathsf {S}}$ (the signal variables), and two sets $\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}}$ of functions, the formulae of TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$ are defined by the grammar:

$$\begin{aligned} \phi := {true}\mid f_{\mathsf {T}}(\overline{x}) \sim 0 \mid f_{\mathsf {S}}(\overline{y}) \sim 0 \mid \lnot \phi \mid \phi _1 \wedge \phi _2 \mid \phi _1\vee \phi _2\mid \phi _1 {\,\mathcal{U}\,}\phi _2 \mid x.\phi \quad \text { where} \end{aligned}$$

• $x\in V_{\mathsf {T}}$, and $\overline{x} = (x_1, \dots , x_l)$ with $x_i\in V_{\mathsf {T}}$ for all $1\le i\le l$;

• $\overline{z} = (z_1, \dots , z_d)$ with $z_j\in V_{\mathsf {S}}$ for all $1\le j \le d$ (with $d\le n$);

• $V_{\mathsf {T}}$ and $V_{\mathsf {S}}$ are disjoint;

• $f_{\mathsf {T}} \in \mathcal {F}_{{\mathsf {T}}}$ and $f_{\mathsf {S}} \in \mathcal {F}_{{\mathsf {S}}}$ are real-valued functions, and $\sim$ is $\le , <, \ge ,$ or $>$. $\quad \square$

The semantics of TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$ is straightforward and similar to the propositional case (Definition 3). The only new ingredients are the booleanizing predicates $f_{\mathsf {S}}(\overline{z}) \sim 0$: we define $\pi \models _{\mathcal {E}} f_{\mathsf {S}}(z_1, \dots , z_d) \sim 0$ iff $f_{\mathsf {S}}( \pi _{j_1}[t_0], \dots , \pi _{j_d}[t_0]) \sim 0$ for any freeze variable environment $\mathcal {E}$, where $t_0 = \min {\mathsf {tdom}}(\pi )$, and $z_i$ is the $j_i$-th variable in $V_{\mathsf {S}}$ (i.e., $z_i$ refers to the $j_i$-th dimension in the signal trace). We require that for a timed ${\mathbb {R}}^n$-valued trace $\pi$ to satisfy $\phi$, the arity of the functions in $\mathcal {F}_{{\mathsf {S}}}$ occurring in $\phi$ should not be more than n, that is, functions should not refer to dimensions greater than n for an ${\mathbb {R}}^n$ trace.

$\delta$ relaxation of TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$. Let $\mathbf {J}_{V_{\mathsf {S}}}$ be a mapping from $V_{\mathsf {S}}$ to closed intervals of ${\mathbb {R}}$, thus $\mathbf {J}_{V_{\mathsf {S}}}(z)$ denotes a sub-domain of $z\in V_{\mathsf {S}}$. The relaxation function ${\mathsf {rx}}_{{J}, \mathbf {J}_{V_{\mathsf {S}}}}^{\delta }$ which operates on TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$ formulae is defined analogous to the relaxation function ${\mathsf {rx}}_{J}^{\delta }$ in Definition 4. We omit the similar cases, and only present the new case for the predicates formed from $\mathcal {F}_{{\mathsf {S}}}$.

$$\begin{aligned} {\mathsf {rx}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}^{\delta }\left( f_{\mathsf {S}}(z_1, \dots , z_l) \right) \sim 0) \ = {\left\{ \begin{array}{ll} f_{\mathsf {S}}(z_1, \dots , z_l) \, +\, K^{f_{\mathsf {S}}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}(\delta ) \ \sim \, 0 &{} \text { if } \sim \, \in \{ >, \ge \};\\ f_{\mathsf {S}}(z_1, \dots , z_l) \, -\, K^{f_{\mathsf {S}}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}(\delta ) \ \sim \, 0 &{} \text { if } \sim \,\in \{ <, \le \} \end{array}\right. } \end{aligned}$$

where $K^{f_{\mathsf {S}}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}: \big [0,\ \max _{z\in V_{\mathsf {S}}} |\max \mathbf {J}_{V_{\mathsf {S}}}(z) \, - \, \min \mathbf {J}_{V_{\mathsf {S}}}(z)| \big ] \mapsto {\mathbb {R}}_+$ is a function s.t.

$$\begin{aligned} K^{f_{\mathsf {S}}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}(\delta ) = \! \sup _{\begin{array}{c} u_i\in \mathbf {J}_{V_{\mathsf {S}}}(z_i); \, u'_i\in \mathbf {J}_{V_{\mathsf {S}}}(z'_i)\\ \text { for all } i \end{array}} \!\! \left\{ \! \left| \begin{array}{c} f_{\mathsf {S}}(u_1,\dots , u_l) \\ -\\ f_{\mathsf {S}}(u_1',\dots ,u_l') \end{array}\right| \text { s.t. } |u_i \!-\!u_i'| \le \delta \text { for all } i \right\} \!. \end{aligned}$$

The functions $K^{f_{\mathsf {S}}}_{J, \mathbf {J}_{V_{\mathsf {S}}}}(\delta )$ define the maximal change in the value of $f_{\mathsf {S}}$ that can occur when the input variables can vary by $\delta$ over the intervals in $\mathbf {J}_{V_{\mathsf {S}}}(z)$ and J. The role of $\mathbf {J}_{V_{\mathsf {S}}}$ in the above definition is to restrict the domain of the signal variables in order to obtain the least possible relaxation bounds on the signal constraints; as was done in Definition 4 for the freeze variables.

Theorem 3

(Transference for ${\mathbb {R}}^n$ -valued Traces). Let $\pi , \pi '$ be two ${\mathbb {R}}^n$-valued traces such the Skorokhod distance between them is less than $\delta$ for some finite $\delta$. Let $\phi$ be a closed TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$ formula in negation-normal form. If $\pi \models \phi$, then $\pi '\models {\mathsf {rx}}_{I_{\pi , \pi '}, \mathbf {I}_{V_{\mathsf {S}}}}^{\delta }(\phi )$, where

• ${I_{\pi ,\pi '}}$ is the convex hull of ${\mathsf {tdom}}(\pi ) \cup {\mathsf {tdom}}(\pi ')$; and

• $\mathbf {I}_{V_{\mathsf {S}}}(z)$ is the convex hull of $\{ \pi (t)[k] \mid t\in {\mathsf {tdom}}(\pi ) \} \cup \{ \pi '(t)[k] \mid t\in {\mathsf {tdom}}(\pi ') \}$; where z is the k-th variable in the ordered set $V_{\mathsf {S}}$. $\quad \square$

Theorem 3 can be strengthened similar to the strengthening mentioned for Theorem 2 by relaxing the variables over smaller intervals obtained from assignments to variables which witness $\pi \models \phi$.

Example 5

(Spatial Constraints and Transference). Recall Example 2, suppose that the events p, q, and r are defined by the following predicates over real variables $\alpha _1$ and $\alpha _2$. Let $p \equiv \alpha _1 + 10\!\cdot \!\alpha _2 \ge 3$; the predicate $q \equiv |\alpha _1| + |\alpha _2| \le 20$; and $r \equiv |\alpha _1| + |\alpha _2| \le 15$. Let $\pi$ satisfy this formula with these predicates, and let $\pi '$ be $\delta$ close to $\pi$, for a finite $\delta$ under the Skorokhod metric for ${\mathbb {R}}^2$. Our robustness theorem ensures that $\pi '$ will satisfy the relaxed formula

$$ x. \left( p^{\delta } \rightarrow \Diamond \big (y. \left( q^{\delta } \wedge \Diamond \left[ z. \left( r^{\delta } \wedge \left( (y-x)^2 + (z-y)^2 + (z-x)^2 \le d+12\!\cdot \!\delta ^2 \right) \right) \right] \right) \big )\right) \!. $$

where the relaxed predicates $p^{\delta },q^{\delta },r^{\delta }$ are defined as follows: $p^{\delta } \equiv \alpha _1 + 10\!\cdot \!\alpha _2 \ge 3- 22\!\cdot \!\delta$; $q^{\delta } \equiv |\alpha _1| + |\alpha _2| \le 20+4\!\cdot \!\delta$; and $r^{\delta } \equiv |\alpha _1| + |\alpha _2| \le 15+4\!\cdot \!\delta$. $\quad \square$

Fig. 1.

System $\mathfrak {A}_1$ used for benchmarking Skorokhod Distance computation. Inflow rate i, Drain rate $d_1$ for tank 1 and $d_2$ for tank 2 are all inputs to the system.

4 Experimental Evaluation

We have implemented a streaming, sliding window-based monitoring routine which checks, given a fixed $\delta$, whether the linear interpolations of two time-sampled traces are at Skorokhod distance at most $\delta$ away from each other. The least such $\delta$ value is then computed by binary search over the monitoring routine. The upper limit of the search range is set to the pointwise metric (i.e., assuming the identity retiming) between the two traces. The traces to the monitoring routine are pre-scaled, each dimension (and the time-stamp) is scaled by a different constant. The constants are chosen so that after scaling, one unit of deviation in one dimension is as undesirable as one unit of jitter in other dimensions.

We have integrated the monitoring routine in an adaptive testing procedure for Simulink blocks based on Algorithm 1. The output of Algorithm 1 is compared against tolerance levels (e.g., maximum allowed jitter) given by the engineering requirements. In the following, we evaluate the effectiveness of the Skorokhod metric in conformance testing of Simulink applications.

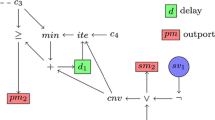
Skorokhod Distance Computation Benchmark. We first show that the window-based implementation is efficient using the following benchmark. Figure 1 shows a hybrid dynamical system $\mathfrak {A}_1$ consisting of two water tanks, each with an outlet from which water drains at a constant rate $d_j$. Both tanks share a single inlet pipe that is switched between the tanks, filling only one tank at any given time at a constant inflow rate of i. When the water-level in tank j falls below level $\ell _j$, the pipe switches to fill it. The drain and inflow rates $d_1$, $d_2$ and i are assumed to be inputs to the system. Now consider a version $\mathfrak {A}_2$ that incorporates an actuation delay that is a function of the inflow rate. This means that after the level drops to $\ell _j$ for tank j, the inlet pipe starts filling it only after a finite time. $\mathfrak {A}_1$ and $\mathfrak {A}_2$ have the same initial water level. We perform a fixed number of simulations by systematically choosing drain and inflow rates $d_1$, $d_2$, i to generate traces (water-level vs. time) of both systems and compute their Skorokhod distance. We summarize the results in Table 1.

Table 1. Computation of ${\mathscr {D}}_{{\mathscr {S}}}(\pi _1,\pi _2)$, where $\pi _1$ is a trace of system $\mathfrak {A}_1$ described in Fig. 1, and $\pi _2$ is a trace of system $\mathfrak {A}_2$, which is $\mathfrak {A}_1$ with an actuation delay. ${\mathscr {D}}_2$ is the pointwise $L_2$ distance. Both $\pi _1$ and $\pi _2$ contain equally spaced 2001 time points over a simulation horizon of 100 s.

Recall that the Skorokhod distance computation involves a sequence of monitoring calls with different $\delta$ values picked by a binary-search procedure. Thus, the total time to compute ${\mathscr {D}}_{\mathscr {S}}$ is the sum over the computation times for individual monitoring calls plus some bookkeeping. In Table 1, we make a distinction between the average time to monitor traces (given a $\delta$ value), and the average time to compute ${\mathscr {D}}_{\mathscr {S}}$. There are an average of 6 monitoring calls per ${\mathscr {D}}_{\mathscr {S}}$ computation. We ran 64 simulations by choosing different input values, and then computing ${\mathscr {D}}_{\mathscr {S}}$ for increasing window sizes. As the window size increases, the average ${\mathscr {D}}_{\mathscr {S}}$ decreases and the computation time increases linearly, as expected from Theorem 1. Finally, the Skorokhod distance can be significantly smaller than the simpler metric ${\mathscr {D}}_2$ (defined as the maximum of the pointwise $L_2$ norm). This discrepancy becomes more prominent with increased window size. With a window size of 100, the variation between ${\mathscr {D}}_{\mathscr {S}}$ and ${\mathscr {D}}_2$ was up to $38\,\%$ (mean difference of $10\,\%$ with std. deviation of $11\,\%$).

Case Study I: LQR-Based Controller. The first case study for conformance testing is an aircraft pitch control application taken from the openly accessible control tutorials for Matlab and Simulink [27]. The authors describe a linear dynamical system of the form: $\dot{\mathbf {x}} = (A-BK)\mathbf {x} + B\theta _{des}$. Here, $\mathbf {x}$ describes the vector of continuous state variables and $\theta _{des}$ is the desired reference provided as an external input. One of the states in the $\mathbf {x}$ vector is the pitch angle $\theta$, which is also the system output. The controller gain matrix K is computed using the linear quadratic regulator method [5], a standard technique from optimal control. We are interested in studying a digital implementation of the continuous-time controller obtained using the LQR method. To do so, we consider sampled-data control where the controller samples the plant output, computes, and provides the control input to the plant every $\varDelta$ s. To model sensor delay, we add a fixed delay element to the system; thus, the overall system now represents a delay-differential equation.

Control engineers are typically interested in the step response of a system. In particular, quantities such as the overshoot/undershoot of the output signal (maximum positive/negative deviation from a reference value) and the settling time (time it takes for transient behaviors to converge to some small region around the reference value) are of interest. Given a settling time and overshoot for the first system, we would like the second system to display similar characteristics. We remark that both of these properties can be expressed in STL (and hence in TLTL $(\mathcal {F}_{{\mathsf {T}}}, \mathcal {F}_{{\mathsf {S}}})$), see [21] for details. We quantify system conformance (and thereby adherence to requirements) in terms of the Skorokhod distance, or, in other words, maximum permitted time/space-jitter value $\delta$. For this system, we know that at nominal conditions, the settling time is approximately 2.5 s, and that we can tolerate an increase in settling time of about 0.5 s. Thus, we chose a time-scaling factor of $2 = \frac{1}{0.5}$. We observe that the range of $\theta$ is about 0.4 radians, and specify an overshoot of $20\,\%$ of this range as being permissible. Thus, we pick a scaling factor of $\frac{1}{0.08}$ for the signal domain. In other words, Skorokhod distance $\delta = 1$ corresponds to either a time-jitter of 0.5 s, or a space-discrepancy of 0.08 radians.

We summarize the results of conformance testing for different values of sampling time $\varDelta$ in Table 2. As expected, the conformance increases with increasing $\varDelta$. The time taken to compute the Skorokhod distance decreases with increasing $\varDelta$, as the number of time-points in the two traces decreases.

Table 2. Variation in Skorokhod Distance with changing sampling time for an aircraft pitch control system with an LQR-based controller. Time taken indicates the total time spent in computing the upper bound on the Skorokhod distance across all simulations. We choose a window size chosen of 150 samples and simulate the system for 5 s with a variable-step solver.

Case Study II: Air-Fuel Ratio Controller. In [21], the authors present three systems representing an air-fuel ratio ($\lambda$) controller for a gasoline engine, that regulate $\lambda$ to a given reference value of $\lambda _{\text {ref}} = 14.7$. Of interest to us are the second and the third systems. The former has a continuous-time plant model with highly nonlinear dynamics, and a discrete-time controller model. In [22], the authors present a version of this system where the controller is also continuous. We take this to be $\mathfrak {A}_1$. The third system in [21] is a continuous-time closed-loop system where all the system differential equations have right-hand-sides that are polynomial approximations of the nonlinear dynamics in $\mathfrak {A}_1$. We call this polynomial dynamical system $\mathfrak {A}_2$. The rationale for these system versions is as follows: existing formal methods tools cannot reason about highly nonlinear dynamical systems, but tools such as Flow* [10], C2E2 [16], and CORA [3] demonstrate good capabilities for polynomial dynamical systems. Thus, the hope is to analyze the simpler systems instead. In [21], the authors comment that the system transformations are not accompanied by formal guarantees. By quantifying the difference in the system behaviors, we hope to show that if the system $\mathfrak {A}_2$ satisfies the temporal requirements $\varphi$ presented in [21], then $\mathfrak {A}_1$ satisfies a relaxation of $\varphi$. We pick a scaling factor of 2 for the time domain, as a time-jitter of 0.5 s is the maximum deviation we wish to tolerate in the settling time, and pick $0.68 = \frac{1}{0.1*\lambda _{\text {ref}}}$ as the scaling factor for $\lambda$ (which corresponds to the worst case tolerated discrepancy in the overshoot).

Table 3 summarizes the results of conformance testing for these systems. In [14], the authors posed a challenge problem for conformance testing. They reported that the original nonlinear system and the approximate polynomial system both satisfy the STL requirements specifying overshoot/undershoot and settling time. We, however, found an input that causes the outputs of the two systems to have a high Skorokhod distance. Thus, comparing the two systems by considering equi-satisfaction of a given set of STL requirements such as overshoot/undershoot and settling time may not always be sufficient. Our experiment indicates that the Skorokhod metric may be a better measure of conformance.

Table 3. Conformance testing for closed-loop A/F ratio controller at different engine speeds. We scale the signals such that 0.5 s of time-jitter is treated equivalent to 10 % of the steady-state value (14.7) of the A/F ratio signal. The simulation traces correspond to a time horizon of 10 s and the window size is 300.

Fig. 2.

Outputs showing a Skorokhod distance of 1.04.

Case Study III: Engine Timing Model. The Simulink demo palette from Mathworks [26] contains a system representing a four-cylinder spark ignition internal combustion engine based on a model by Crossley and Cook [11]. This system is then enhanced by adding a proportional plus integral (P+I) control law. The integrator is used to adjust the steady-state throttle as the desired engine speed set-point changes, and the proportional term compensates for phase lag introduced by the integrator. In an actual implementation of such a system, such a P+I controller is implemented using a discrete-time integrator. Such integrator blocks are typically associated with a particular numerical integration technique, e.g., forward-Euler, backward-Euler, trapezoidal, etc. It is expected that different numerical techniques will produce slight variation in the results. We wish to quantify the effect of using different numerical integrators in a closed-loop setting. We checked if the user-provided tolerance of $\delta = 1.0$ is satisfied by systems $\mathfrak {A}_1$ and $\mathfrak {A}_2$, where $\mathfrak {A}_1$ is the original system provided in [26] and $\mathfrak {A}_2$ is a modified system that uses the backward Euler method to compute the discrete-time integral in the controller. We scale the outputs in such a way that a value discrepancy of $1\,\%$ of the the output range ($\sim 1000$) is equivalent to a time discrepancy of 0.1 s. These values are chosen to bias the search towards finding signals that have a small time jitter. This is an interesting scenario for this case study where the two systems are equivalent except for the underlying numerical integration solver. We find the signal shown in Fig. 2, for which we find output traces with Skorokhod distance 1.04. The experiment uses 296 simulations and the total time taken to find the counterexample is 677 s.

5 Conclusion

We argue that the Skorokhod metric provides a robust basis for checking conformance between dynamical systems. We showed that it provides transference of a rich class of temporal logic properties and that it can be computed efficiently, both in theory and in practice. Our experiments indicate that conformance checking using the Skorokhod metric can be integrated into a testing flow for Simulink models and can find non-conformant behaviors effectively, allowing for independent weighing of time and value distortions.