Abstract
The polarization lemma for statistical distance (\({\text {SD}}\)), due to Sahai and Vadhan (JACM, 2003), is an efficient transformation taking as input a pair of circuits \((C_0,C_1)\) and an integer k and outputting a new pair of circuits \((D_0,D_1)\) such that if \({\text {SD}}(C_0,C_1) \ge \alpha \) then \({\text {SD}}(D_0,D_1) \ge 1-2^{-k}\) and if \({\text {SD}}(C_0,C_1) \le \beta \) then \({\text {SD}}(D_0,D_1) \le 2^{-k}\). The polarization lemma is known to hold for any constant values \(\beta < \alpha ^2\), but extending the lemma to the regime in which \(\alpha ^2 \le \beta < \alpha \) has remained elusive. The focus of this work is in studying the latter regime of parameters. Our main results are:
-
1.
Polarization lemmas for different notions of distance, such as Triangular Discrimination (\({{\,\mathrm{TD}\,}}\)) and Jensen-Shannon Divergence (\({{\,\mathrm{JS}\,}}\)), which enable polarization for some problems where the statistical distance satisfies \( \alpha ^2< \beta < \alpha \). We also derive a polarization lemma for statistical distance with any inverse-polynomially small gap between \( \alpha ^2 \) and \( \beta \) (rather than a constant).
-
2.
The average-case hardness of the statistical difference problem (i.e., determining whether the statistical distance between two given circuits is at least \(\alpha \) or at most \(\beta \)), for any values of \(\beta < \alpha \), implies the existence of one-way functions. Such a result was previously only known for \(\beta < \alpha ^2\).
-
3.
A (direct) constant-round interactive proof for estimating the statistical distance between any two distributions (up to any inverse polynomial error) given circuits that generate them. Proofs of closely related statements have appeared in the literature but we give a new proof which we find to be cleaner and more direct.
This is an extended abstract. The full version of this paper, with formal statements of the theorems and proofs, may be found at: https://eccc.weizmann.ac.il/report/2019/038/.
I. Berman and A. Degwekar—Research supported in part by NSF Grants CNS-1413920 and CNS-1350619, MIT-IBM Award, and by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under Vinod Vaikuntanathan’s DARPA Young Faculty Award and contracts W911NF-15-C-0226 and W911NF-15-C-0236.
R. D. Rothblum—This research was supported in part by the Israeli Science Foundation (Grant No. 1262/18).
P. N. Vasudevan—Research supported in part from DARPA/ARL SAFEWARE Award W911NF15C0210, AFOSR Award FA9550-15-1-0274, AFOSR YIP Award, a Hellman Award and research grants by the Okawa Foundation, Visa Inc., and Center for LongTerm Cybersecurity (CLTC, UC Berkeley).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The Statistical Difference Problem, introduced by Sahai and Vadhan [SV03], is a central computational (promise) problem in complexity theory and cryptography, which is also intimately related to the study of statistical zero-knowledge (\({\mathsf {SZK}}\)). The input to this problem is a pair of circuits \(C_0\) and \(C_1\), specifying probability distributions (i.e., that are induced by feeding the circuits with a uniformly random string). YES instances are those in which the statistical distanceFootnote 1 between the two distributions is at least 2/3 and NO instances are those in which the distance is at most 1/3. Input circuits that do not fall in one of these two cases are considered to be outside the promise (and so their value is left unspecified).
The choice of the constants 1/3 and 2/3 in the above definition is somewhat arbitrary (although not entirely arbitrary as will soon be discussed in detail). A more general family of problems can be obtained by considering a suitable parameterization. More specifically, let \(0 \le \beta < \alpha \le 1\). The \((\alpha ,\beta )\) parameterized version of the Statistical Difference Problem, denoted \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), has as its YES inputs pairs of circuits that induce distributions that have distance at least \(\alpha \) whereas the NO inputs correspond to circuits that induce distributions that have distance at most \(\beta \).
Definition 1.1
 Let
Let  with \(\alpha (n)>\beta (n)\) for every n. The Statistical Difference Problem with promise \((\alpha ,\beta )\), denoted \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), is given by the sets
with \(\alpha (n)>\beta (n)\) for every n. The Statistical Difference Problem with promise \((\alpha ,\beta )\), denoted \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), is given by the sets
where n is the output length of the circuits \(C_0\) and \(C_1\).Footnote 2
(Here and below we abuse notation and use \(C_0\) and \(C_1\) to denote both the circuits and the respective distributions that they generate.)
The elegant polarization lemma of [SV03] shows how to polarize the statistical distance between two distributions. In more detail, for any constants \(\alpha \) and \(\beta \) such that \(\beta < \alpha ^2\), the lemma gives a transformation that makes distributions that are at least \(\alpha \)-far be extremely far and distributions that are \(\beta \)-close be extremely close. Beyond being of intrinsic interest, the polarization lemma is used to establish the \({\mathsf {SZK}}\) completeness of \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), when \(\alpha ^2 > \beta \), and has other important applications in cryptography such as the amplification of weak public key encryption schemes to full fledged ones [DNR04, HR05].
Sahai and Vadhan left the question of polarization for parameters \(\alpha \) and \(\beta \) that do not meet the requirements of their polarization lemma as an open question. We refer to this setting of \(\alpha \) and \(\beta \) as the non-polarizing regime. We emphasize that by non-polarizing we merely mean that in this regime polarization is not currently known and not that it is impossible to achieve (although some barriers are known and will be discussed further below). The focus of this work is studying the \( \textsc {Statistical\,Difference\,Problem} \) in the non-polarizing regime.
1.1 Our Results
We proceed to describe our results.
1.1.1 Polarization and \({\mathsf {SZK}}\) Completeness for Other Notions of Distance
The statistical distance metric is one of the central information theoretic tools used in cryptography as it is very useful for capturing similarity between distributions. However, in information theory there are other central notions that measure similarity such as mutual information and KL divergence as well as others.
Loosely speaking, our first main result shows that polarization is possible even in some cases in which \(\beta \ge \alpha ^2\). However, this result actually stems from a more general study showing that polarization is possible for other notions of distance between distributions from information theory, which we find to be of independent interest.
When distributions are extremely similar or extremely dissimilar, these different notions of distance are often (but not always) closely related and hence interchangeable. This equivalence is particularly beneficial when considering applications of \({\mathsf {SZK}}\)—for some applications one distance measure may be easier to use than others. For example, showing that the average-case hardness of \({\mathsf {SZK}}\) implies one-way functions can be analyzed using statistical distance (e.g., [Vad99, Section 4.8]), but showing that every language in \({\mathsf {SZK}}\) has instance-dependent commitments is naturally analyzed using entropy (e.g., [OV08]).
However, as the gaps in the relevant distances get smaller (i.e., the distributions are only somewhat similar or dissimilar), the relation between different statistical properties becomes less clear (for example, the reduction from \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) to the Entropy Difference Problem of [GV99] only works when roughly \(\alpha ^2>\beta \)). This motivates studying the computational complexity of problems defined using different notions of distance in this small gap regime. Studying this question can be (and, as we shall soon see, indeed is) beneficial in two aspects. First, providing a wider bag of statistical properties related to \({\mathsf {SZK}}\), which can make certain applications easier to analyze. Second, the computational complexity of these distance notions might shed light on the computational complexity of problems involving existing distance notions (e.g., \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) when \(\alpha ^2<\beta \)).
We focus here on two specific distance notions—the triangular discrimination and the Jensen-Shannon divergence, defined next.
Definition 1.2
(Triangular Discrimination). The Triangular Discrimination (a.k.a. Le Cam divergence) between two distributions P and Q is defined as
where \(\mathcal {Y}\) is the union of the supports of P and Q.
The Triangular Discrimination Problem with promise \((\alpha ,\beta )\), denoted \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\), is defined analogously to \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), but with respect to \({{\,\mathrm{TD}\,}}\) rather than \({\text {SD}}\).
The triangular discrimination is commonly used, among many other applications, in statistical learning theory for parameter estimation with quadratic loss, see [Cam86, P. 48] (in a similar manner to how statistical distance characterizes the 0–1 loss function in hypothesis testing). Jumping ahead, while the definition of triangular discrimination seems somewhat arbitrary at first glance, in Sect. 2 we will show that this distance notion characterizes some basic phenomena in the study of statistical zero-knowledge. Triangular discrimination has recently found usage in theoretical computer science, and even specifically in problems related to \({\mathsf {SZK}}\). Yehudayoff [Yeh16] showed that using TD yields a tighter analysis of the pointer chasing problem in communication complexity. The work of Komargodski and Yogev [KY18] uses triangular discrimination to show that the average-case hardness of \({\mathsf {SZK}}\) implies the existence of distributional collision resistant hash functions.
Next, we define the Jensen-Shannon Divergence. To start with, recall that the KL-divergence between two distributions P and Q is definedFootnote 3 as \({{\,\mathrm{KL}\,}}(P||Q) = \sum _{y \in \mathcal {Y}} P_y \log (P_y/Q_y)\). Also, given distributions \(P_0\) and \(P_1\) we define the distribution \(\frac{1}{2} P_0+ \frac{1}{2} P_1\) as the distribution obtained by sampling a random coin \(b \in \{0,1\}\) and outputting a sample y from \(P_b\) (indeed, this notation corresponds to arithmetic operations on the probability mass functions). The Jensen-Shannon divergence measures the mutual information between b and y.
Definition 1.3
(Jensen-Shannon Divergence). The Jensen-Shannon divergence between two distributions P and Q is defined as

The Jensen-Shannon Divergence Problem with promise \((\alpha ,\beta )\), denoted \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\), is defined analogously to \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\), but with respect to \({{\,\mathrm{JS}\,}}\) rather than \({\text {SD}}\).
The Jensen-Shannon divergence enjoys a couple of important properties (in our context) that the KL-divergence lacks: it is symmetric and bounded. Both triangular discrimination and Jensen-Shannon divergence (as well as statistical distance and KL-divergence) are types of f-divergences, a central concept in information theory (see [PW17, Section 6] and references therein). They are both non-negative and bounded by one.Footnote 4 Finally, the Jensen-Shannon divergence is a metric, while the triangular discrimination is a square of a metric.
With these notions of distance and corresponding computational problems in hand, we are almost ready to state our first set of results. Before doing so, we introduce an additional useful technical definition.
Definition 1.4
(Separated functions). Let  . A pair of \({\mathsf {poly}}(n)\)-time computable functions \((\alpha ,\beta )\), where \(\alpha =\alpha (n) \in [0,1]\) and \(\beta = \beta (n) \in [0,1]\), is g -separated if \(\alpha (n)\ge \beta (n)+g(n)\) for every
. A pair of \({\mathsf {poly}}(n)\)-time computable functions \((\alpha ,\beta )\), where \(\alpha =\alpha (n) \in [0,1]\) and \(\beta = \beta (n) \in [0,1]\), is g -separated if \(\alpha (n)\ge \beta (n)+g(n)\) for every  .
.
We denote by (1/poly)-separated the set of all pairs of functions that are (1/p)-separated for some polynomial p. Similarly, we denote by (1/log)-separated the set of all pairs of functions that are \((1/(c\log ))\)-separated for some constant \(c>0\).
We can now state our first set of results: that both \({{\,\mathrm{TDP}\,}}\) and \({{\,\mathrm{JSP}\,}}\), with a noticeable gap, are \({\mathsf {SZK}}\) complete.
Theorem 1.5
Let \((\alpha ,\beta )\) be \((1/{\mathsf {poly}})\)-separated functions such that there exists a constant \(\varepsilon \in (0,1/2)\) such that \(2^{-n^{1/2-\varepsilon }} \le \beta (n)\) and \(\alpha (n) \le 1-2^{-n^{1/2-\varepsilon }}\), for every  . Then, \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\) complete.
. Then, \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\) complete.
Theorem 1.6
For \((\alpha ,\beta )\) as in Theorem 1.5, the problem \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\) complete.
The restriction on \(2^{-n^{1/2-\varepsilon }} \le \beta (n)\) and \(\alpha (n) \le 1-2^{-n^{1/2-\varepsilon }}\) should be interpreted as a non-degeneracy requirement (which we did not attempt to optimize), where we note that some restriction seems inherent. Moreover, we can actually decouple the assumptions in Theorems 1.5 and 1.6 as follows. To show that \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) and \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) are \({\mathsf {SZK}}\)-hard, only the non-degeneracy assumption (i.e., \(2^{-n^{1/2-\varepsilon }} \le \beta (n)\) and \(\alpha (n) \le 1-2^{-n^{1/2-\varepsilon }}\)) is needed. On the other hand, to show that these problems are in \({\mathsf {SZK}}\) we only require that \((\alpha ,\beta )\) are \((1/{\mathsf {poly}})\)-separated.
Note that in particular, Theorems 1.5 and 1.6 imply polarization lemmas for both \({{\,\mathrm{TD}\,}}\) and \({{\,\mathrm{JS}\,}}\). For example, for triangular discrimination, since \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta } \in {\mathsf {SZK}}\) and \({{\,\mathrm{TDP}\,}}^{1-2^{-k},2^{-k}}\) is \({\mathsf {SZK}}\)-hard, one can reduce the former to the latter.
Beyond showing polarization for triangular discrimination, Theorem 1.5 has implications regarding the question of polarizing statistical distance, which was our original motivation. It is known that the triangular discrimination is sandwiched between the statistical distance and its square; namely, for every two distributions P and Q it holds that (see [Top00, Eq. (11)]):
Thus, the problem \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) is immediately reducible to \({{\,\mathrm{TDP}\,}}^{\alpha ^2,\beta }\), which Theorem 1.5 shows to be \({\mathsf {SZK}}\)-complete, as long as the gap between \(\alpha ^2\) and \(\beta \) is noticeable. Specifically, we have the following corollary.
Corollary 1.7
Let \((\alpha ,\beta )\) be as in Theorem 1.5, with the exception that \((\alpha ^2,\beta )\) are \((1/{\mathsf {poly}})\)-separated (note that here \(\alpha \) is squared). Then, the promise problem \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\) complete.
We highlight two implications of Theorem 1.5 and Corollary 1.7 (which were also briefly mentioned above).
Polarization with Inverse Polynomial Gap. Observe that Corollary 1.7 implies polarization of statistical distance in a regime in which \(\alpha \) and \(\beta \) are functions of n, the output length of the two circuits, and \(\alpha ^2\) and \(\beta \) are only separated by an inverse polynomial. This is in contrast to most prior works which focus on \(\alpha \) and \(\beta \) that are constants. In particular, Sahai and Vadhan’s [SV03] proof of the polarization lemma focuses on constant \(\alpha \) and \(\beta \) and can be extended to handle an inverse logarithmic gap, but does not seem to extend to an inverse polynomial gap.Footnote 5 Corollary 1.7 does yield such a result, by relying on a somewhat different approach.
Polarization Beyond \(\alpha ^2 > \beta \). Theorem 1.5 can sometimes go beyond the requirement that \(\alpha ^2>\beta \) for polarizing statistical distance. Specifically, it shows that any problem with noticeable gap in the triangular discrimination can be polarized. Indeed, there are distributions (P, Q) and \((P',Q')\) with \({\text {SD}}(P,Q)> {\text {SD}}(P',Q') > {\text {SD}}(P,Q)^2\) but still \({{\,\mathrm{TD}\,}}(P,Q) > {{\,\mathrm{TD}\,}}(P',Q')\).Footnote 6 Circuits generating such distributions were until now not known to be in the polarizing regime, but can now be polarized by combining Theorem 1.5 and Eq. (1.1).
1.1.2 From Statistical Difference to One-Way Functions
We continue our study of the Statistical Difference Problem, focusing on the regime where \(\beta < \alpha \) (and in particular even when \(\beta \ge \alpha ^2\)). We show that in this regime the \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) problem shares many important properties of \({\mathsf {SZK}}\) (although we fall short of actually showing that it lies in \({\mathsf {SZK}}\)—which is equivalent to polarization for any \(\beta <\alpha \)).
First, we show that similarly to \({\mathsf {SZK}}\), the average-case hardness of \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) implies the existence of one-way functions. The fact that average-case hardness of \({\mathsf {SZK}}\) (or equivalently \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) for \(\beta < \alpha ^2\)) implies the existence of one-way functions was shown by Ostrovsky [Ost91]. Indeed, our contribution is in showing that the weaker condition of \(\beta <\alpha \) (rather than \(\beta < \alpha ^2\)) suffices for this result.
Theorem 1.8
Let \((\alpha ,\beta )\) be \((1/{\mathsf {poly}})\)-separated functions. Suppose that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) is average-case hard. Then, there exists a one-way function.
The question of constructing one-way functions from the (average-case) hardness of \({{\,\mathrm{SDP}\,}}\) is closely related to a result of Goldreich’s [Gol90] showing that the existence of efficiently sampleable distributions that are statistically far but computationally indistinguishable implies the existence of one-way functions. Our proof of Theorem 1.8 allows us to re-derive the following strengthening of [Gol90], due to Naor and Rothblum [NR06, Theorem 4.1]: for any \((1/{\mathsf {poly}})\)-separated \((\alpha ,\beta )\), the existence of efficiently sampleable distributions whose statistical distance is \(\alpha \) but no efficient algorithm can distinguish between them with advantage more than \(\beta \), implies the existence of one-way functions. See further discussion in Theorem 2.1.
1.1.3 Interactive Proof for Statistical Distance Approximation
As our last main result, we construct a new interactive protocol that lets a verifier estimate the statistical distance between two given circuits up to any noticeable precision.
Theorem 1.9
There exists a constant-round public-coin interactive protocol between a prover and a verifier that, given as input a pair of circuits \((C_0,C_1)\), a claim \(\varDelta \in [0,1]\) for their statistical distance, and a tolerance parameter \(\delta \in [0,1]\), satisfies the following properties:
-
Completeness: If \({\text {SD}}(C_0,C_1) = \varDelta \), then the verifier accepts with probability at least 2/3 when interacting with the honest prover.
-
Soundness: If \(\left| {\text {SD}}(C_0,C_1) - \varDelta \right| \ge \delta \), then when interacting with any (possibly cheating) prover, the verifier accepts with probability at most 1/3.
-
Efficiency: The verifier runs in time \({\mathsf {poly}}(|C_0|,|C_1|,1/\delta )\).
(As usual the completeness and soundness errors can be reduced by applying parallel repetition. We can also achieve perfect completeness using a result from [FGM+89].)
Theorem 1.9 is actually equivalent to the following statement.
Theorem 1.10
([BL13, Theorem 6], [BBF16, Theorem 2]). For any \((\alpha ,\beta )\) that are \((1/{\mathsf {poly}})\)-separated, it holds that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta } \in {\mathsf {AM}}\cap {\mathsf {coAM}}\).Footnote 7
It is believed that \({\mathsf {AM}}\cap {\mathsf {coAM}}\) lies just above \({\mathsf {SZK}}\), and if we could show that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\), that would imply \({\text {SD}}\) polarization for such \(\alpha \) and \(\beta \).
Since Theorem 1.9 can be derived from existing results in the literature, we view our main contribution to be the proof which is via a single protocol that we find to be cleaner and more direct than alternate approaches.
Going into a bit more detail, [BL13, BBF16]’s proofs are in fact a combination of two separate constant-round protocols. The first protocol is meant to show that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta } \in {\mathsf {AM}}\) and follows directly by taking the interactive proof for \({{\,\mathrm{SDP}\,}}\) presented by Sahai and Vadhan (which has completeness error \((1-\alpha )/2\) and soundness error \((1+\beta )/2\)), and applying parallel repetition (and the private-coin to public-coin transformation of [GS89]).
The second protocol is meant to show that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta } \in {\mathsf {coAM}}\), and is based on a protocol by Bhatnagar, Bogdanov, and Mossel [BBM11]. Another approach for proving that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta } \in {\mathsf {coAM}}\) is by combining results of [GVW02] and [SV03]. Goldreich, Vadhan and Wigderson [GVW02] showed that problems with laconic interactive proofs, that is proofs where the communication from the prover to the verifier is small, have \( {\mathsf {co}}{\mathsf {AM}}\) proofs. Sahai and Vadhan [SV03], as described earlier, showed that \( {{\,\mathrm{SDP}\,}}^{\alpha , \beta } \), and \({\mathsf {SZK}}\) in general, has an interactive proof where the prover communicates a single bit. Combining these results immediately gives a \( {\mathsf {co}}{\mathsf {AM}}\) protocol for \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) when \((\alpha ,\beta )\) are \(\varOmega (1)\)-separated. As for \((\alpha ,\beta )\) that are only \((1/{\mathsf {poly}})\)-separated, while the [GVW02] result as-stated does not suffice, it seems that their protocol can be adapted to handle this case as well.Footnote 8
As mentioned above, we give a different, and direct, proof of Theorem 1.9 that we find to be simpler and more natural than the above approach. In particular, our proof utilizes the techniques developed for our other results, which enable us to give a single and more general protocol—one that approximates the statistical difference (as in Theorem 1.9), rather than just deciding if that distance is large or small.
At a very high level, our protocol may be viewed as an application of the set-lower-bound-based techniques of Akavia et al. [AGGM06] or Bogdanov and Brzuska [BB15] to our construction of a one-way function from the average-case hardness of \({{\,\mathrm{SDP}\,}}\) (i.e., Theorem 1.8), though there are technical differences in our setting. Both these papers show how to construct a \({\mathsf {coAM}}\) protocol for any language that can be reduced, to inverting a size-verifiable one-way function.Footnote 9 While we do not know how to reduce solving \({{\,\mathrm{SDP}\,}}\) in the worst-case to inverting any specific function, we make use of the fact that associated with each instance of \({{\,\mathrm{SDP}\,}}\), there is an instance-dependent function [OW93], that is size-verifiable on the average.
1.2 Additional Related Works
Barriers to Improved Polarization. Holenstein and Renner [HR05] show that in a limited model dubbed “oblivious polarization”, the condition \( \alpha ^2 > \beta \) on the statistical distance is necessary for polarizing statistical distance.Footnote 10 All the past polarization reductions fit in this framework and so do ours. Specifically, Holenstein and Renner show distributions where \( \alpha ^2 < \beta \) and cannot be polarized in this model. We show a condition that suffices for polarization, even for distributions where \( \alpha ^2 \le \beta \). This does not contradict the [HR05] result because their distributions do not satisfy this condition.
In a more general model, [LZ17, CGVZ18] showed lower bounds for \({\mathsf {SZK}}\)-related distribution manipulation tasks. The model they consider allows the reduction arbitrary oracle access to the circuits that sample the distributions, as opposed to the more restricted model of oblivious polarization. In this model, Lovett and Zhang [LZ17] show that efficient entropy reversal is impossibleFootnote 11, and Chen, Göös, Vadhan and Zhang [CGVZ18] showed that entropy flattening requires \( \varOmega (n^2) \) invocations to the underlying circuit. Showing lower bounds for polarization in this more general model remains an interesting open question.
Polarization for Other Notions of Distance. In the process of characterizing zero-knowledge in the help model, Ben-Or and Gutfreund [BG03] and Chailloux et al. [CCKV08] gave a polarization procedure that considers two different distances for every \((1/{\mathsf {log}})\)-separated \(\alpha >\beta \): if the statistical distance is at most \(\beta \), then it decreases to \(2^{-k}\); and if the mutual disjointnessFootnote 12 is at least \(\alpha \), then it increases to \(1-2^{-k}\). Fehr and Vaudenay [FV17] raise the question of polarization for the fidelity measureFootnote 13 but leave resolving it as an open problem (see Sect. 2.3.3 for details).
\({{\,\mathrm{SDP}\,}}\) and Cryptography. We show that average-case hardness of \( {{\,\mathrm{SDP}\,}}^{\alpha , \beta } \) implies one-way functions. In the reverse direction, Bitansky et al. [BDV17] show that one-way functions do not imply even worst-case hardness of \( {{\,\mathrm{SDP}\,}}^{\alpha , \beta } \) in a black-box manner for any \( (1/{\mathsf {poly}})\)-separated \( \alpha , \beta \).Footnote 14
2 Techniques
We begin in Sect. 2.1 by describing how to construct a one-way function from the average-case hardness of \({\text {SD}}\) with any noticeable gap (Theorem 1.8). The techniques used there are also central in our interactive protocol for \({\text {SD}}\) estimation (Theorem 1.9), which is described in Sect. 2.2, as well as in our proof that triangular discrimination and Jensen-Shannon divergence are \({\mathsf {SZK}}\) complete (Theorems 1.5 and 1.6), which are outlined in Sect. 2.3 below.
2.1 One-Way Function from Statistical Difference with Any Noticeable Gap
We first show the existence of distributionally one-way functions. Namely, an efficiently computable function f for which it is hard to sample a uniformly random pre-image for a random output y (rather than an arbitrary pre-image as in a standard one-way function). This suffices since Impagliazzo and Luby [IL89] showed how to convert a distributionally one-way function into a standard one.
Assume that we are given a distribution over a pair of circuits \((C_0,C_1)\) such that it is hard to distinguish between the cases \({\text {SD}}(C_0,C_1)\ge \alpha \) or \({\text {SD}}(C_0,C_1)\le \beta \), for some \(\alpha >\beta +1/{\mathsf {poly}}\). A natural candidate for a one-way function is the (efficiently computable) function
Namely, f is parameterized by the circuits \((C_0,C_1)\) (which are to be sampled according to the hard distribution), and the bit b chooses which of the two circuits would be evaluated on the string x. This function appears throughout the \({\mathsf {SZK}}\) literature (e.g., it corresponds to the verifier’s message in the \({{\,\mathrm{SDP}\,}}\) protocol of [SV03]).
Assume that f is not distributionally one-way, and let \(\mathsf {A}\) be an algorithm that given \((C_0,C_1)\) and a random input y—sampled by first drawing a uniformly random bit b and a string x and then computing \(y=C_b(x)\)—outputs a uniformly random element \((b',x')\) from the set  . For simplicity, we assume that \(\mathsf {A}\) is a perfect distributional inverter, that is for every fixed \((C_0, C_1, y)\) it outputs uniformly random elements of \( f^{-1}_{C_0, C_1}(y) \).
. For simplicity, we assume that \(\mathsf {A}\) is a perfect distributional inverter, that is for every fixed \((C_0, C_1, y)\) it outputs uniformly random elements of \( f^{-1}_{C_0, C_1}(y) \).
Arguably, the most natural approach for distinguishing between the cases of high or low statistical distance given the two circuits and the inverter, is to choose x and b at random, invoke the inverter to obtain \((b',x')\), and check whether \(b=b'\). Indeed, if \({\text {SD}}(C_0,C_1)=1\), then  , and if \({\text {SD}}(C_0,C_1)=0\), then
, and if \({\text {SD}}(C_0,C_1)=0\), then  . Thus, we can distinguish between the cases with constant advantage.
. Thus, we can distinguish between the cases with constant advantage.
But what happens when the gap in the statistical distance is smaller? To analyze this case we want to better understand the quantity  . It turns out that this quantity is characterized by the triangular discrimination between the circuits. Let \(P_b\) denote the output distribution of \(C_b\). Using elementary manipulations (and the fact that \(\frac{1}{2}(P_0+P_1)\) is a distribution), it holds thatFootnote 15
. It turns out that this quantity is characterized by the triangular discrimination between the circuits. Let \(P_b\) denote the output distribution of \(C_b\). Using elementary manipulations (and the fact that \(\frac{1}{2}(P_0+P_1)\) is a distribution), it holds thatFootnote 15

Based on the general bounds between triangular discrimination and statistical distance (Eq. (1.1)), which are known to be tight, all we are guaranteed is

So, this approach is limited to settings in which \(\alpha ^2>\beta \).
To overcome this limitation we want to find a quantity that is more tightly characterized by the statistical distance of the circuits. This quantity, which we call imbalance, will be central in all of the proofs in this work. The imbalance measures how likely it is that an output string y was generated from \(C_1\) versus \(C_0\). Formally,

Elementary manipulations yields that

(Recall that y is sampled by first drawing a uniform random bit b and a string x, and setting \(y=C_b(x)\). Hence, using the notation that \(P_b\) denotes the output distributions of the circuit \(C_b\), the marginal distribution of y is \(\frac{1}{2}P_0+\frac{1}{2}P_1\).)
Equation (2.4) naturally gives rise to the following algorithm for approximating \({\text {SD}}(C_0,C_1)\):

The quantities \(p_1\) and \(p_0\) are in fact the empirical distribution of b conditioned on y, computed using k samples. By choosing large enough k, we get that  and so \(\widehat{\theta }_i\approx \theta _{y_i}\). By then choosing large enough t, we get that \(\frac{1}{t}\sum _{i=1}^t|{\widehat{\theta }_i}|\approx {\text {SD}}(C_0,C_1)\). Hence, we can distinguish between the cases \({\text {SD}}(C_0,C_1)\ge \alpha \) or \({\text {SD}}(C_0,C_1)\le \beta \), for any \(\alpha >\beta +1/{\mathsf {poly}}\).
and so \(\widehat{\theta }_i\approx \theta _{y_i}\). By then choosing large enough t, we get that \(\frac{1}{t}\sum _{i=1}^t|{\widehat{\theta }_i}|\approx {\text {SD}}(C_0,C_1)\). Hence, we can distinguish between the cases \({\text {SD}}(C_0,C_1)\ge \alpha \) or \({\text {SD}}(C_0,C_1)\le \beta \), for any \(\alpha >\beta +1/{\mathsf {poly}}\).
Essentially the same proof continues to work if \(\mathsf {A}\) is not a perfect distributional inverter, but is close enough to being so—that is, on input y its output distribution is close to being uniform over \(f^{-1}(y)\) for most (but not all) tuples \(C_0,C_1,y\).
The above proof strategy also yields a new proof for the strengthening of [Gol90] by Naor and Rothblum [NR06].Footnote 16 See Theorem 2.1 below for a discussion about the differences between our techniques and those of [NR06].
Distributional Collision Resistant Hash Function. As a matter of fact, the above proof also shows that the average-case hardness of \( {{\,\mathrm{SDP}\,}}^{\alpha , \beta } \) also implies that the function \( f_{C_0, C_1}(b,x) = C_b(x) \) is a distributional k-multi-collisionFootnote 17 resistant hash function, for \( k = O \left( \frac{\log n}{(\alpha - \beta )^2} \right) \). That is, for a random output y of f, it is difficult to find k random preimages of y. This is because access to such a set of k random pre-images of random \(y_i\)’s is all we use the inverter \(\mathsf {A}\) for in the above reduction, and it could handily be replaced with a k-distributional multi-collision finder.
Remark 2.1
(Comparison to [NR06]). Naor and Rothblum’s proof implicitly attempts to approximate the maximal likelihood bit of y; that is, the bit \(b_{ml}\) such that  (breaking ties arbitrarily). Indeed, the maximal likelihood bit, as shown by [SV03], is closely related to the statistical distance:
(breaking ties arbitrarily). Indeed, the maximal likelihood bit, as shown by [SV03], is closely related to the statistical distance:

To approximate \(b_{ml}\), [NR06] make, like us, many calls to \(\mathsf {A}(y)\), and take the majority of the answered bits. The idea is that when the statistical distance is large, the majority is likely to be \(b_{ml}\), and when the statistical distance is small, the majority is equally likely to be \(b_{ml}\) or \(1-b_{ml}\).
To formally prove this intuition, it must hold that if \({\text {SD}}(C_0,C_1)\) is large, then  is sufficiently large; putting in our terminology and using Eq. (2.4), if
is sufficiently large; putting in our terminology and using Eq. (2.4), if  is sufficiently large, then \(\left| \theta _y\right| \) should be large for a random y (and the opposite should hold if \({\text {SD}}(C_0,C_1)\) is small). While these statements are true, in order to prove them, [NR06]’s analysis involves some work which results in a more complicated analysis.
is sufficiently large, then \(\left| \theta _y\right| \) should be large for a random y (and the opposite should hold if \({\text {SD}}(C_0,C_1)\) is small). While these statements are true, in order to prove them, [NR06]’s analysis involves some work which results in a more complicated analysis.
We manage to avoid such complications by using the imbalance \(\theta _y\) and its characterization of statistical distance (Eq. 2.4). Furthermore, [NR06]’s approach only attempts to distinguish between the cases when \({\text {SD}}(C_0,C_1)\) is high or low, while our approach generalizes to approximate \({\text {SD}}(C_0,C_1)\). Lastly, Naor and Rothblum do not construct one-way functions based on the average-case hardness of \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) with any noticeable gap as we do. Using their technique to do so seems to require additional work—work that our analysis significantly simplifies.
2.2 Interactive Proof for Statistical Distance Approximation
We proceed to describe a constant-round public-coin protocol in which a computationally unbounded prover convinces a computationally bounded verifier that the statistical difference of a given pair of circuits is what the prover claims it to be, up to any inverse polynomial (additive) error. Such a protocol simultaneously establishes the inclusion of \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) in both \({\mathsf {AM}}\) and \({\mathsf {coAM}}\) for any \(\alpha >\beta +1/{\mathsf {poly}}\).
Our starting point is the algorithm we described above that used a one-way function inverter to estimate the statistical distance. Specifically, that algorithm used the inverter to estimate \(\theta _y\) for random y’s, and then applied Eq. (2.4). We would like to use the prover, instead of the inverter, to achieve the same task.
In our protocol, the verifier draws polynomially many y’s and sends them to the prover. The prover responds with values \(\widehat{\theta }_i\)’s, which it claims are the genuine \(\theta _{y_i}\)’s. But how can the verifier trust that the prover sent the correct values? In the reduction in Sect. 2.1, we used k many samples of b conditioned on y to estimate b’s true distribution. A standard concentration bound shows that as k grows, the number of ones out of \(b_1,\dots ,b_k\), all sampled from (b|y), is very close to  . Similarly, the number of zeros is very close to
. Similarly, the number of zeros is very close to  . Consider the following typical set for any fixed y and arbitrary value \(\theta \):
. Consider the following typical set for any fixed y and arbitrary value \(\theta \):
Namely, \(\mathcal {T}^{k,\theta }_y\) contains every k-tuple of \((b_i,x_i)\) such that all map to y, and each tuple can be used to estimate \(\theta \) well—the difference between the number of ones and the number of zeros, normalized by k, is close to \(\theta \). Also consider the pre-image set of y:  . Since as k grows the estimation of \(\theta _y\) improves, we expect that \(\mathcal {T}^{k,\theta _y}_y\)—the typical set of y with the value \(\theta _y\)—to contain almost all tuples. Indeed, standard concentration bounds show that
. Since as k grows the estimation of \(\theta _y\) improves, we expect that \(\mathcal {T}^{k,\theta _y}_y\)—the typical set of y with the value \(\theta _y\)—to contain almost all tuples. Indeed, standard concentration bounds show that
On the other hand, the sets \(\mathcal {T}^{k,\theta '}_y\), corresponding to values \(\theta '\) that are far from \(\theta _y\), should be almost empty. Indeed, if \(\left| \theta '-\theta _y\right| \ge \varOmega (1)\), then,
So, for the verifier to be convinced that the value \(\widehat{\theta }\) sent by the prover is close to \(\theta _y\), the prover can prove that the typical set \(\mathcal {T}^{k,\widehat{\theta }}_y\) is large. To do so, the parties will use the public-coin constant round protocol for set lower-bound of [GS89], which enables the prover to assert statements of the form “the size of the set \(\mathcal {S}\) is at least s”.
However, there is still one hurdle to overcome. The typical set \(\mathcal {T}^{k,\theta _y}_y\) is only large relative to \(\left| \mathcal {I}_y\right| ^k\). Since we do not known how to compute \(|\mathcal {I}_y|\) it is unclear what should be the size s that we run the set lower-bound protocol with. Our approach for bypassing this issue is as follows. First observe that the expected value, over a random y, of the logarithm of the size of \(\mathcal {I}_y\) is the entropyFootnote 18 of (b, x) given y. Namely,

where the jointly distributed random variables (B, X, Y) take the values of randomly drawn (x, b, y). Thus, if we draw t independent elements \(y_1,\dots ,y_t\), the average of \(\log \left| \mathcal {I}_y\right| \) gets closer to \(t\cdot {{\,\mathrm{H}\,}}(B,X|Y)\), as t grows. Specifically,

where n denotes the output length of the given circuits. For large enough t, we can thus assume that the size of this product set is approximately \(2^{t\cdot H(B,X|Y)}\), and run the set lower bound protocol for all the \(y_i\)’s together. That is, we ask the prover to send t estimates \((\widehat{\theta }_1, \dots , \widehat{\theta }_t)\) for the values \((\theta _{y_1},\dots ,\theta _{y_t})\), and prove that the size of the product set \(\mathcal {T}^{k,\widehat{\theta }_1}_{y_1} \times \cdots \times \mathcal {T}^{k,\widehat{\theta }_1}_{y_1}\) is almost \(2^{t\cdot {{\,\mathrm{H}\,}}(B,X|Y)}\).
So far we have reduced knowing the size of \(\mathcal {I}_y\) to knowing \({{\,\mathrm{H}\,}}(B,X|Y)\), but again it seems difficult for the verifier to compute this quantity on its own. Actually, standard entropy manipulations show that
where m denotes the input length of the given circuits. It thus suffices to approximate \({{\,\mathrm{H}\,}}(Y)\). Recall that y is the output of the circuit that maps (x, b) to \(C_b(x)\), so Y is drawn according to an output distribution of a known circuit. Luckily, Goldreich, Sahai and Vadhan [GSV99] showed that approximating the output entropy of a given circuit is in \({\mathsf {NISZK}}\), and thus has a constant-round public-coin protocol (since \({\mathsf {NISZK}}\subseteq {\mathsf {AM}}\cap {\mathsf {coAM}}\)).
To conclude, we describe the entirety of our protocol, which proves Theorem 1.9.

2.3 \({{\,\mathrm{TDP}\,}}\) and \({{\,\mathrm{JSP}\,}}\) Are \({\mathsf {SZK}}\)-Complete
We show that both \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) and \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) with \(\alpha >\beta +1/{\mathsf {poly}}\) are \({\mathsf {SZK}}\)-complete. Since the proof of the former uses that of the latter we start by giving an outline that \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\)-complete.
2.3.1 \( \textsc {Jensen}\text {-}\textsc {Shannon}\,\textsc {Divergence}\,\textsc {Problem} \) Is \({\mathsf {SZK}}\)-Complete
We need to show that \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) with \(\alpha >\beta +1/{\mathsf {poly}}\) is both in \({\mathsf {SZK}}\) and \({\mathsf {SZK}}\)-hard. In both parts we use the following characterization of the Jensen-Shannon divergence, which follows from its definition. Given a pair of circuits \(C_0\) and \(C_1\), consider the jointly distributed random variables (B, X, Y), where B is a uniformly random bit, X is a uniformly random string and \(Y=C_B(X)\). Then, it follows from some elementary manipulations that:
We use this characterization to tie Jensen-Shannon Divergence Problem to another \({\mathsf {SZK}}\)-complete problem—the Entropy Difference Problem (\({{\,\mathrm{EDP}\,}}\)) with a gap function g. The input to \({{\,\mathrm{EDP}\,}}^g\) is also a pair of circuits \(C_0\) and \(C_1\). YES instances are those in which the entropy gap \({{\,\mathrm{H}\,}}(C_0)-{{\,\mathrm{H}\,}}(C_1)\) is at least g(n) (where n is the output length of the circuits) and NO instances are those in which the gap is at most \(-g(n)\). Goldreich and Vadhan [GV99] showed that \({{\,\mathrm{EDP}\,}}^{g}\) is \({\mathsf {SZK}}\)-complete for any noticeable function g. Our proof that \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\)-complete closely follows the reduction from the reverse problem of \({{\,\mathrm{SDP}\,}}{}\) (i.e., in which YES instances are distributions that are statistically close) to \({{\,\mathrm{EDP}\,}}{}\) [Vad99, Section 4.4].
-
\({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\): We reduce \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) to \({{\,\mathrm{ED}\,}}^{(\alpha -\beta )/2}\). Given \(C_0\) and \(C_1\), the reduction outputs a pair of circuits \(D_0\) and \(D_1\) such that \(D_1\) outputs a sample from (B, Y) and \(D_0\) outputs a sample from \((B',Y)\), where \(B'\) is an independent random bit with \({{\,\mathrm{H}\,}}(B')=1-\frac{\alpha +\beta }{2}\). The chain rule for entropyFootnote 19 implies that
$$\begin{aligned} {{\,\mathrm{H}\,}}(D_0)-{{\,\mathrm{H}\,}}(D_1) = 1-\frac{\alpha +\beta }{2}-{{\,\mathrm{H}\,}}(B|Y) = {{\,\mathrm{JS}\,}}(C_0,C_1)-\frac{\alpha +\beta }{2}, \end{aligned}$$where the second equality follows from Eq. (2.10). Thus, if \({{\,\mathrm{JS}\,}}(C_0,C_1)\ge \alpha \), then \({{\,\mathrm{H}\,}}(D_0)-{{\,\mathrm{H}\,}}(D_1)\ge \frac{\alpha -\beta }{2}\); and if \({{\,\mathrm{JS}\,}}(C_0,C_1)\le \beta \), then \({{\,\mathrm{H}\,}}(D_0)-{{\,\mathrm{H}\,}}(D_1)\le -\frac{\alpha -\beta }{2}\). And since \({{\,\mathrm{ED}\,}}^{(\alpha -\beta )/2} \in {\mathsf {SZK}}\), we get that \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta } \in {\mathsf {SZK}}\).
-
\({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\)-hard: We reduce \({{\,\mathrm{SDP}\,}}^{1-2^{-k},2^{-k}}\) to the problem \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\), for some large enough k. This is sufficient since \({{\,\mathrm{SDP}\,}}^{1-2^{-k},2^{-k}}\) is known to be \({\mathsf {SZK}}\)-hard [SV03].Footnote 20 In the presentation of related results in his thesis, Vadhan relates the statistical distance of the circuits to the entropy of B given Y [Vad99, Claim 4.4.2]. For example, if \({\text {SD}}(C_0,C_1)=0\) (i.e., the distributions are identical), then B|Y is a uniformly random bit, and so \({{\,\mathrm{H}\,}}(B|Y)=1\); and if \({\text {SD}}(C_0,C_1)=1\) (i.e., the distributions are disjoint), then B is completely determined by Y, and so \({{\,\mathrm{H}\,}}(B|Y)=0\). More generally, Vadhan showed that if \({\text {SD}}(C_0,C_1)=\delta \), thenFootnote 21
$$\begin{aligned} 1-\delta \le {{\,\mathrm{H}\,}}(B|Y) \le h\left( \frac{1+\delta }{2}\right) . \end{aligned}$$(2.11)By taking k to be large enough (as a function of \(\alpha \) and \(\beta \)), and applying Eqs. (2.10) and (2.11), we have that if \({\text {SD}}(C_0,C_1)\ge 1-2^{-k}\), then \({{\,\mathrm{JS}\,}}(C_0,C_1)\ge \alpha \); and if \({\text {SD}}(C_0,C_1)\le 2^{-k}\), then \({{\,\mathrm{JS}\,}}(C_0,C_1)\le \beta \). Thus, the desired reduction is simply the identity function that outputs the input circuits.
2.3.2 Triangular Discrimination Problem is \({\mathsf {SZK}}\)-Complete
We need to show that \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) with \(\alpha >\beta +1/{\mathsf {poly}}\) is both in \({\mathsf {SZK}}\) and \({\mathsf {SZK}}\)-hard. Showing the latter is very similar to showing that \({{\,\mathrm{JSP}\,}}^{\alpha ,\beta }\) is \({\mathsf {SZK}}\)-hard, but using Eq. (1.1) to relate the triangular discrimination to statistical distance (instead of Eq. (2.11) that relates the Jensen-Shannon divergence to statistical distance). We leave the formal details to the body of this paper and focus here on showing that \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\).
A natural approach to show that \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\) is to follow Sahai and Vadhan’s proof that \({{\,\mathrm{SDP}\,}}^{2/3,1/3}\) is in \({\mathsf {SZK}}\). Specifically, a main ingredient in that proof is to polarize the statistical distance of the circuits (to reduce the simulation error). Indeed, if we can reduce \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) to, say, \({{\,\mathrm{TDP}\,}}^{0.9,0.1}\) by polarizing the triangular discrimination, then Eq. (1.1) would imply that we also reduce \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) to \({{\,\mathrm{SDP}\,}}^{2/3,1/3}\), which we know is in \({\mathsf {SZK}}\).
We are indeed able to show such a polarization lemma for triangular discrimination (using similar techniques to [SV03]’s polarization lemma). However, this lemma only works when the gap between \(\alpha \) and \(\beta \) is roughly \(1/\log \). Actually, the polarization lemma of [SV03] also suffers the same limitation with respect to the gap between \(\alpha ^2\) and \(\beta \).
Still, we would like to handle also the case that the gap between \(\alpha \) and \(\beta \) is only \(1/{\mathsf {poly}}\). To do so we take a slightly different approach. Specifically, we reduce \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) to \({{\,\mathrm{JSP}\,}}^{\alpha ', \beta '}\), where \( \alpha '\) and \(\beta '\) are also noticeably separated.
An important step toward showing this reduction is to characterize the triangular discrimination and the Jensen-Shannon divergence via the imbalance \(\theta _y\) (see Eq. (2.3)), as we already did for statistical distance. Recall that given \(Y=y\), the random variable B takes the value 1 with probability \(\frac{1+\theta _y}{2}\), and 0 otherwise. Hence, Eq. (2.10) can also be written as

As for the triangular discrimination, it follows from the definition that

Furthermore, by Taylor approximation, for small values of \(\theta \), it holds that
As we can see, the above equations imply that if all the \(\theta _y\)’s were small, a gap in the triangular discrimination would also imply a gap in the Jensen-Shannon divergence. Thus, we would like an operation that reduces all the \(\theta _y\).
The main technical tool we use to reduce \(\theta _y\) is to consider the convex combination of the two input circuits. Given a pair of circuits \(C_0\) and \(C_1\), consider the pair of circuits \(D_0\) and \(D_1\) such that \(D_b=\lambda \cdot C_b+(1-\lambda ) \cdot \frac{C_0+C_1}{2}\).Footnote 22 Let \(Q_b\) denote the output distribution of \(D_b\), and recall that \(P_b\) denotes the output distribution of \(C_b\). We also let \(\theta '_y\) be defined similarly to \(\theta _y\), but with respect to \(D_0\) and \(D_1\) (rather than \(C_0\) and \(C_1\)). Using this notation, we have that \(\theta _y=\frac{P_1(y)-P_0(y)}{P_1(y)+P_0(y)}\), and it may be seen that
So, our reduction chooses a sufficiently small \(\lambda \), and outputs the circuits \(D_0\) and \(D_1\). Some care is needed when choosing \(\lambda \). Equations (2.13) and (2.15) yield that \({{\,\mathrm{TD}\,}}(D_0,D_1)=\lambda ^2 \cdot {{\,\mathrm{TD}\,}}(C_0,C_1)\). Hence, the convex combination also shrinks the gap in triangular discrimination. We show that by choosing \(\lambda \approx \sqrt{\alpha -\beta }\), the approximation error in Eq. (2.14) is smaller than the aforementioned shrinkage, and the reduction goes through. The resulting gap in the Jensen-Shannon divergence is roughly \((\alpha -\beta )^2\), which is noticeable by the assumption that \(\alpha >\beta +1/{\mathsf {poly}}\).
This shows that \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\) if \(\alpha > \beta + 1/{\mathsf {poly}}\). By the relationship between \({{\,\mathrm{TD}\,}}\) and \({\text {SD}}\) (Eq. (1.1)), this implies that \({{\,\mathrm{SDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\) if \(\alpha ^2 > \beta + 1/{\mathsf {poly}}\). This, in turn, by the \({\mathsf {SZK}}\)-hardness of \({{\,\mathrm{SDP}\,}}^{2/3,1/3}\) and the known polarization lemma that applies for the same, implies polarization for statistical distance for any \((\alpha ,\beta )\) such that \(\alpha ^2 > \beta + 1/{\mathsf {poly}}\).
2.3.3 Reflections and an Open Problem
Many f-divergences of interest can be expressed as an expectation, over \(y \sim Y\), of a simple function of \(\theta _y\). That is, an expression of the form  , for some function \(g : [-1,1] \rightarrow [0,1]\). For example:
, for some function \(g : [-1,1] \rightarrow [0,1]\). For example:
-
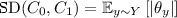 (i.e., \(g(z)=|z|\), see Eq. (2.4));
(i.e., \(g(z)=|z|\), see Eq. (2.4)); -
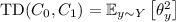 (i.e., \(g(z)=z^2\), see Eq. (2.13)); and
(i.e., \(g(z)=z^2\), see Eq. (2.13)); and -
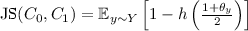 (i.e., \(g(z) = 1-h\left( \frac{1+z}{2}\right) \), see Eq. (2.12)).
(i.e., \(g(z) = 1-h\left( \frac{1+z}{2}\right) \), see Eq. (2.12)).
To reduce \({{\,\mathrm{TDP}\,}}\) to \({{\,\mathrm{JSP}\,}}\), we took a convex combination of the two circuits and used the fact that \(1-h\left( \frac{1+\theta _y}{2}\right) \approx O(\theta _y^2)\) for small values of \(\theta _y\). While this worked for polarization of \({{\,\mathrm{TD}\,}}\) (which corresponds to \(g(z)=z^2)\), it seems unlikely to yield a polarization lemma for \({\text {SD}}\) for an arbitrarily small (but noticeable) gap. The reason is that the function \(g(z) = \left| z\right| \)—the g-function corresponding to \({\text {SD}}\)—is not differentiable at 0 and in particular does not act like \(z^2\) for small values of z. As we find this similarity between the different notions of distance striking, and indeed our proofs leverage the relations between them, we provide in Fig. 1 a plot comparing the different choices for the function g.
Comparison between the difference choices of the function g that were discussed. Since all functions are symmetric around 0, we restrict to the domain [0, 1]. Recall that \(g_1(\theta )=|\theta |\) corresponds to \({\text {SD}}\), \(g_2(\theta )=\theta ^2\) to \({{\,\mathrm{TD}\,}}\), \(g_3(\theta )=1-h\left( \frac{1+\theta }{2}\right) \) to \({{\,\mathrm{JS}\,}}\) and \(g_4(\theta )=1-\sqrt{1-\theta ^2}\) to \({{\,\mathrm{H}\,}}^2\).
Another popular f-divergence that we have not discussed thus farFootnote 23 is the squared Hellinger distance, defined as \({{\,\mathrm{H}\,}}^2(P,Q) = \frac{1}{2}\sum _{y}\left( \sqrt{P_y}-\sqrt{Q_y}\right) ^2\). It can be shown that  , and so also this distance falls within the above framework (i.e., by considering \(g(z) = 1-\sqrt{1-z^2}\)).
, and so also this distance falls within the above framework (i.e., by considering \(g(z) = 1-\sqrt{1-z^2}\)).
Notably, the squared Hellinger distance also acts like \({{\,\mathrm{JS}\,}}\) (and \({{\,\mathrm{TD}\,}}\)) around 0; namely, \(1-\sqrt{1-\theta _y^2}\approx O(\theta _y^2)\) for small values of \(\theta _y\). However, unlike \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\), we do not know how to show that the Hellinger Difference Problem, denoted \({{\,\mathrm{HDP}\,}}^{\alpha ,\beta }\) and defined analogously to \({{\,\mathrm{TDP}\,}}^{\alpha ,\beta }\) (while replacing the distance \({{\,\mathrm{TD}\,}}\) with \({{\,\mathrm{H}\,}}^2\)), is in \({\mathsf {SZK}}\) for all \((1/{\mathsf {poly}})\)-separated \((\alpha ,\beta )\). We do mention that \({{\,\mathrm{H}\,}}^2(P,Q)\le {{\,\mathrm{TD}\,}}(P,Q)\le 2{{\,\mathrm{H}\,}}^2(P,Q)\), and thus \({{\,\mathrm{HDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\) if \(\alpha \) and \(\beta /2\) are \((1/{\mathsf {poly}})\)-separated. However, the proof described above does not go through if we try to apply it to the Hellinger distance—we cannot guarantee that the gap in the Hellinger distance after taking the convex combination is larger than the error in the Taylor approximation. Indeed, the question whether \({{\,\mathrm{HDP}\,}}^{\alpha ,\beta }\) is in \({\mathsf {SZK}}\) for any \((1/{\mathsf {poly}})\)-separated \((\alpha ,\beta )\), first raised by Fehr and Vaudenay [FV17], remains open.
Notes
- 1.
Recall that the statistical distance between two distributions P and Q over a set \(\mathcal {Y}\) is defined as \({\text {SD}}(P,Q) = \frac{1}{2} \sum _{y \in \mathcal {Y}} \left| P_y - Q_y\right| \), where \(P_y\) (resp., \(Q_y\)) is the probability mass that P (resp., Q) puts on \(y\in \mathcal {Y}\).
- 2.
In prior works \(\alpha \) and \(\beta \) were typically thought of as constants (and so their dependence on the input was not specified). In contrast, since we will want to think of them as parameters, we choose to let them depend on the output length of the circuit since this size seems most relevant to the distributions induced by the circuits. Other natural choices could have been the input length or the description size of the circuits. We remark that these different choices do not affect our results in a fundamental way.
- 3.
To be more precise, in this definition we view \(0\cdot \log \frac{0}{0}\) as 0 and define the KL-divergence to be \(\infty \) if the support of P is not contained in that of Q.
- 4.
In the literature these distances are sometimes defined to be twice as much as our definitions. In our context, it is natural to have the distances bounded by one.
- 5.
Actually, it was claimed in [GV11] that the [SV03] proof does extend to the setting of an inverse polynomial gap between \(\alpha ^2\) and \(\beta \) but this claim was later retracted, see http://www.wisdom.weizmann.ac.il/~/oded/entropy.html.
- 6.
For example, for a parameter \(\gamma \in [0,1]\) consider the distributions \(R^\gamma _0\) and \(R^\gamma _1\) over
 : \(R^\gamma _b\) puts \(\gamma \) mass on b and \(1-\gamma \) mass on 2. It holds that \({\text {SD}}(R^\gamma _0,R^\gamma _1)={{\,\mathrm{TD}\,}}(R^\gamma _0,R^\gamma _1)=\gamma \). If, say, \((P,Q)=(R^{1/2}_0,R^{1/2}_1)\) and \((P',Q')=(R^{1/3}_0,R^{1/3}_1)\), then \({\text {SD}}(P,Q)> {\text {SD}}(P',Q') > {\text {SD}}(P,Q)^2\) but \({{\,\mathrm{TD}\,}}(P,Q)>{{\,\mathrm{TD}\,}}(P',Q')\).
: \(R^\gamma _b\) puts \(\gamma \) mass on b and \(1-\gamma \) mass on 2. It holds that \({\text {SD}}(R^\gamma _0,R^\gamma _1)={{\,\mathrm{TD}\,}}(R^\gamma _0,R^\gamma _1)=\gamma \). If, say, \((P,Q)=(R^{1/2}_0,R^{1/2}_1)\) and \((P',Q')=(R^{1/3}_0,R^{1/3}_1)\), then \({\text {SD}}(P,Q)> {\text {SD}}(P',Q') > {\text {SD}}(P,Q)^2\) but \({{\,\mathrm{TD}\,}}(P,Q)>{{\,\mathrm{TD}\,}}(P',Q')\). - 7.
Recall that \({\mathsf {AM}}\) is the class of problems that have constant-round public-coin interactive proofs. \({\mathsf {coAM}}\) is simply the complement of \({\mathsf {AM}}\).
- 8.
In more detail, the [GVW02] result is stated for protocols in which the gap between completeness and soundness is constant (specifically 1/3). In case \(\alpha \) and \(\beta \) are only \(1/{\mathsf {poly}}\)-separated, the [SV03] protocol only has a \(1/{\mathsf {poly}}\) gap (and we cannot afford repetition since it will increase the communication). Nevertheless, by inspecting the [GVW02] proof, it seems as though it can be adapted to cover any noticeable gap.
- 9.
Informally, a function f is size-verifiable if given an output \( y = f(x) \), there exists an \( {\mathsf {AM}}\) protocol to estimate \( |f^{-1}(y)| \).
- 10.
Roughly speaking, an oblivious polarization is a randomized procedure to polarize without invoking the circuits; it takes as input a bit \(\sigma \) and an integer k, and outputs a sequence of bits \((b^\sigma _1,\dots ,b^\sigma _\ell )\) and a string \(r^{\sigma }\). Given a pair of circuits \((C_0,C_1)\), such a procedure defines a pair of circuits \((D_0,D_1)\) as follows: \(D_\sigma \) samples \((b^\sigma _1,\dots ,b^\sigma _\ell )\) and \(r^{\sigma }\) and outputs \((C_{b^\sigma _1},\dots ,C_{b^\sigma _\ell },r^{\sigma })\). We are guaranteed that if \({\text {SD}}(C_0,C_1)\ge \alpha \), then \({\text {SD}}(D_0,D_1)\ge 1-2^{-k}\), and if \({\text {SD}}(C_0,C_1)\le \beta \), then \({\text {SD}}(D_0,D_1)\le 2^{-k}\).
- 11.
Entropy reversal refers to the task of given circuit C and parameter t output \((C', t')\) such that when \( {{\,\mathrm{H}\,}}(C) > t \), then \( {{\,\mathrm{H}\,}}(C') < t'-1 \) and if \( {{\,\mathrm{H}\,}}(C) < t-1 \), then \( {{\,\mathrm{H}\,}}(C') > t' \).
- 12.
For an ordered pair of distributions P and Q, their disjointness is
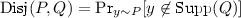 , and their mutual disjointness is \(\text {MutDisj}(P,Q)=\min (\text {Disj}(P,Q),\text {Disj}(Q,P))\).
, and their mutual disjointness is \(\text {MutDisj}(P,Q)=\min (\text {Disj}(P,Q),\text {Disj}(Q,P))\). - 13.
For two distributions P and Q, their fidelity is defined as \( \mathrm {Fidelity}(P,Q) = \sum _y \sqrt{P_y\cdot Q_y}\).
- 14.
While [BDV17] state the result for constant \( \alpha , \beta \), the construction and analysis extend to our setting.
- 15.
In Sect. 1 we used \(P_y\) to denoted the probability mass a distribution P puts on an element y, while here we use P(y). In the rest of this work we choose which notation to use based on readability and context.
- 16.
Namely, that for any \((1/{\mathsf {poly}})\)-separated \((\alpha ,\beta )\), the existence of efficiently sampleable distributions whose statistical distance is \(\alpha \) but no efficient algorithm can distinguish between them with advantage more than \(\beta \), implies the existence of one-way functions.
- 17.
- 18.
Recall that the entropy of a random variable X over \(\mathcal {X}\) is defined as
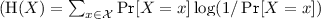 . The conditional entropy of X given Y is
. The conditional entropy of X given Y is 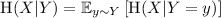 .
. - 19.
For a jointly distributed random variables X and Y, it holds that \({{\,\mathrm{H}\,}}(X,Y) = {{\,\mathrm{H}\,}}(X)+{{\,\mathrm{H}\,}}(Y|X)\).
- 20.
For the simplicity of presentation, we are ignoring subtle details about the relation of k to the output length of the circuits. See the full version for the formal proof.
- 21.
The function h is the binary entropy function. That is, \(h(p)=-p\log (p)-(1-p)\log (1-p)\) is the entropy of a Bernoulli random variable with parameter p.
- 22.
This definition of convex combination is more convenient to analyze than perhaps the more natural definition of \(D_b=\lambda \cdot C_b+(1-\lambda ) \cdot C_{1-b}\).
- 23.
Actually we will use the squared Hellinger distance to analyze triangular discrimination of direct product distributions (see the full version for details). Also, the squared Hellinger distance is closely related to the Fidelity distance: \(\mathrm {Fidelity}(P,Q)=1-{{\,\mathrm{H}\,}}^2(P,Q)\).
References
Applebaum, B., Arkis, B., Raykov, P., Vasudevan, P.N.: Conditional disclosure of secrets: amplification, closure, amortization, lower-bounds, and separations. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 727–757. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_24
Akavia, A., Goldreich, O., Goldwasser, S., Moshkovitz, D.: On basing one-way functions on NP-hardness. In: Kleinberg, J.M. (ed.) Symposium on Theory of Computing, pp. 701–710. ACM (2006)
Aiello, W., Hastad, J.: Statistical zero-knowledge languages can be recognized in two rounds. J. Comput. Syst. Sci. 42(3), 327–345 (1991)
Bogdanov, A., Brzuska, C.: On basing size-verifiable one-way functions on NP-hardness. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 1–6. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_1
Brakerski, Z., Brzuska, C., Fleischhacker, N.: On statistically secure obfuscation with approximate correctness. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 551–578. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_19
Bhatnagar, N., Bogdanov, A., Mossel, E.: The computational complexity of estimating MCMC convergence time. In: Goldberg, L.A., Jansen, K., Ravi, R., Rolim, J.D.P. (eds.) APPROX/RANDOM -2011. LNCS, vol. 6845, pp. 424–435. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22935-0_36
Bouland, A., Chen, L., Holden, D., Thaler, J., Vasudevan, P.N.: On the power of statistical zero knowledge. In: FOCS (2017)
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: Multi-collision resistant hash functions and their applications. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 133–161. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_5
Bitansky, N., Degwekar, A., Vaikuntanathan, V.: Structure vs. hardness through the obfuscation lens. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 696–723. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_23
Ben-Or, M., Gutfreund, D.: Trading help for interaction in statistical zero-knowledge proofs. J. Cryptol. 16(2), 95–116 (2003)
Boppana, R.B., Håstad, J., Zachos, S.: Does co-NP have short interactive proofs? Inf. Process. Lett. 25(2), 127–132 (1987)
Bitansky, N., Kalai, Y.T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. In: STOC (2018)
Bogdanov, A., Lee, C.H.: Limits of provable security for homomorphic encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 111–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_7
Le Cam, L.: Part I. Springer, New York (1986). https://doi.org/10.1007/978-1-4612-4946-7
Chailloux, A., Ciocan, D.F., Kerenidis, I., Vadhan, S.: Interactive and noninteractive zero knowledge are equivalent in the help model. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 501–534. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_28
Chen, Y.-H., Göös, M., Vadhan, S.P., Zhang, J.: A tight lower bound for entropy flattening. In: CCC (2018)
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_21
Fürer, M., Goldreich, O., Mansour, Y., Sipser, M., Zachos, S.: On completeness and soundness in interactive proof systems. Adv. Comput. Res. 5, 429–442 (1989)
Fortnow, L.: The complexity of perfect zero-knowledge. Adv. Comput. Res. 5, 327–343 (1989)
Fehr, S., Vaudenay, S.: Personal Communication (2017)
Goldreich, O.: A note on computational indistinguishability. Inf. Process. Lett. 34(6), 277–281 (1990)
Goldreich, O.: Introduction to Property Testing. Cambridge University Press, Cambridge (2017)
Goldwasser, S., Sipser, M.: Private coins versus public coins in interactive proof systems. Adv. Comput. Res. 5, 73–90 (1989)
Goldreich, O., Sahai, A., Vadhan, S.: Honest-verifier statistical zero-knowledge equals general statistical zero-knowledge. In: STOC (1998)
Goldreich, O., Sahai, A., Vadhan, S.: Can statistical zero knowledge be made non-interactive? Or on the relationship of SZK and NISZK. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 467–484. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_30
Goldreich, O., Vadhan, S.P.: Comparing entropies in statistical zero knowledge with applications to the structure of SZK. In: CCC (1999)
Goldreich, O., Vadhan, S.: On the complexity of computational problems regarding distributions. In: Goldreich, O. (ed.) Studies in Complexity and Cryptography. Miscellanea on the Interplay Between Randomness and Computation. LNCS, vol. 6650, pp. 390–405. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22670-0_27
Goldreich, O., Vadhan, S., Wigderson, A.: On interactive proofs with a laconic prover. Comput. Complex. 11(1–2), 1–53 (2002)
Holenstein, T., Renner, R.: One-way secret-key agreement and applications to circuit polarization and immunization of public-key encryption. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 478–493. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_29
Impagliazzo, R., Luby, M.: One-way functions are essential for complexity based cryptography. In: STOC, pp. 230–235 (1989)
Komargodski, I., Naor, M., Yogev, E.: White-box vs. black-box complexity of search problems: Ramsey and graph property testing. In: FOCS (2017)
Komargodski, I., Naor, M., Yogev, E.: Collision resistant hashing for paranoids: dealing with multiple collisions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 162–194. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_6
Komargodski, I., Yogev, E.: On distributional collision resistant hashing. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 303–327. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_11
Lovett, S., Zhang, J.: On the impossibility of entropy reversal, and its application to zero-knowledge proofs. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 31–55. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_2
Naor, M., Rothblum, G.N.: Learning to impersonate. In: ICML, pp. 649–656 (2006)
Ostrovsky, R.: One-way functions, hard on average problems, and statistical zero-knowledge proofs. In: Structure in Complexity Theory Conference, pp. 133–138 (1991)
Ong, S.J., Vadhan, S.: An equivalence between zero knowledge and commitments. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 482–500. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_27
Ostrovsky, R., Wigderson, A.: One-way functions are essential for non-trivial zero-knowledge. In: ISTCS, pp. 3–17 (1993)
Polyanskiy, Y., Wu, Y.: Lecture notes on information theory (2017). http://people.lids.mit.edu/yp/homepage/data/itlectures_v5.pdf
Sahai, A., Vadhan, S.: A complete problem for statistical zero knowledge. J. ACM (JACM) 50(2), 196–249 (2003)
Topsøe, F.: Some inequalities for information divergence and related measures of discrimination. IEEE Trans. Inf. Theory 46(4), 1602–1609 (2000)
Vadhan, S.P.: A study of statistical zero-knowledge proofs. Ph.D. thesis, Massachusetts Institute of Technology (1999)
Yehudayoff, A.: Pointer chasing via triangular discrimination. Electron. Colloq. Comput. Complex. (ECCC) 23, 151 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N. (2019). Statistical Difference Beyond the Polarizing Regime. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11892. Springer, Cham. https://doi.org/10.1007/978-3-030-36033-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-36033-7_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36032-0
Online ISBN: 978-3-030-36033-7
eBook Packages: Computer ScienceComputer Science (R0)





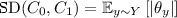 (i.e.,
(i.e., 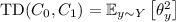 (i.e.,
(i.e., 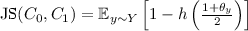 (i.e.,
(i.e., 
 :
: 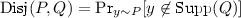 , and their mutual disjointness is
, and their mutual disjointness is 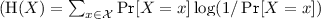 . The conditional entropy of X given Y is
. The conditional entropy of X given Y is 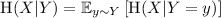 .
.