Abstract
Approximation via sampling is a widespread technique whenever exact solutions are too expensive. In this paper, we present techniques for an efficient parallelization of adaptive (a.k.a. progressive) sampling algorithms on multi-threaded shared-memory machines. Our basic algorithmic technique requires no synchronization except for atomic load-acquire and store-release operations. It does, however, require \(\mathcal {O}(n)\) memory per thread, where n is the size of the sampling state. We present variants of the algorithm that either reduce this memory consumption to \(\mathcal {O}(1)\) or ensure that deterministic results are obtained.
Using the
 algorithm for betweenness centrality (a popular measure in network analysis) approximation as a case study, we demonstrate the empirical performance of our techniques. In particular, on a 32-core machine, our best algorithm is \(2.9{\times }\) faster than what we could achieve using a straightforward OpenMP-based parallelization and \(65.3{\times }\) faster than the existing implementation of
algorithm for betweenness centrality (a popular measure in network analysis) approximation as a case study, we demonstrate the empirical performance of our techniques. In particular, on a 32-core machine, our best algorithm is \(2.9{\times }\) faster than what we could achieve using a straightforward OpenMP-based parallelization and \(65.3{\times }\) faster than the existing implementation of
 .
.
Partially supported by grant ME 3619/3-2 within German Research Foundation (DFG) Priority Programme 1736 Algorithms for Big Data.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
When a computational problem cannot be solved exactly within the desired time budget, a frequent solution is to employ approximation algorithms [12]. With large data sets being the rule and not the exception today, approximation is frequently applied, even to polynomial-time problems [6]. We focus on a particular subclass of approximation algorithms: sampling algorithms. They sample data according to some (usually algorithm-specific) probability distribution, perform some computation on the sample and induce a result for the full data set.
More specifically, we consider adaptive sampling (ADS) algorithms (also called progressive sampling algorithms). Here, the number of samples that are required is not statically computed (e.g., from the input instance) but also depends on the data that has been sampled so far. While non-adaptive sampling algorithms can often be parallelized trivially by drawing multiple samples in parallel, adaptive sampling constitutes a challenge for parallelization: checking the stopping condition of an ADS algorithm requires access to all the data generated so far and thus mandates some form of synchronization.
Motivation and Contribution. Our initial motivation was a parallel implementation of the sequential state-of-the-art approximation algorithm
 [6] for betweenness centrality (BC) approximation. BC is a very popular centrality measure in network analysis, see Sect. 2.2 for more details. To the best of our knowledge, parallel adaptive sampling has not received a generic treatment yet. Hence, we propose techniques to parallelize ADS algorithms in a generic way, while scaling to large numbers of threads. While we turn to
[6] for betweenness centrality (BC) approximation. BC is a very popular centrality measure in network analysis, see Sect. 2.2 for more details. To the best of our knowledge, parallel adaptive sampling has not received a generic treatment yet. Hence, we propose techniques to parallelize ADS algorithms in a generic way, while scaling to large numbers of threads. While we turn to
 to demonstrate the effectiveness of the proposed algorithms, our techniques can be adjusted easily to other ADS algorithms.
to demonstrate the effectiveness of the proposed algorithms, our techniques can be adjusted easily to other ADS algorithms.
We introduce two new parallel ADS algorithms, which we call local-frame and shared-frame. Both algorithms try to avoid extensive synchronization when checking the stopping condition. This is done by maintaining multiple copies of the sampling state and ensuring that the stopping condition is never checked on a copy of the state that is currently being written to. Local-frame is designed to use the least amount of synchronization possible – at the cost of an additional memory footprint of \(\varTheta (n)\) per thread, where n denotes the size of the sampling state. This algorithm performs only atomic load-acquire and store-release operations for synchronization, but no expensive read-modify-write operations (like CAS or fetch-add). Shared-frame, in turn, aims instead at meeting a desired trade-off between memory footprint and synchronization overhead. In contrast to local-frame, it requires only \(\varTheta (1)\) additional memory per thread, but uses atomic read-modify-write operations (e.g., fetch-add) to accumulate samples. We also propose the deterministic indexed-frame algorithm; it guarantees that the results of two different executions is the same for a fixed random seed, regardless of the number of threads.
Our experimental results show that local-frame, shared-frame and indexed-frame achieve parallel speedups of \(15.9 {\times }\), \(18.1 {\times }\), and \( 10.8 {\times }\) on 32 cores, respectively. Using the same number of cores, our OpenMP-based parallelization (functioning as a baseline) only yields a speedup of \(6.3 {\times }\); thus our algorithms are up to \(2.9 {\times }\) faster. Moreover, also due to implementation improvements and parameter tuning, our best algorithm performs adaptive sampling \(65.3 {\times }\) faster than the existing implementation of
 (when all implementations use 32 cores).
(when all implementations use 32 cores).
A full-length version of this paper (including an Appendix) is available from https://arxiv.org/abs/1903.09422 [13].

2 Preliminaries and Baseline for Parallelization
2.1 Basic Definitions
Memory Model. Throughout this paper, we target a multi-threaded shared-memory machine with T threads. We work in the C11 memory model [15] (more details in Appendix A of our full-length paper [13]); in particular, we assume the existence of the usual atomic operations, as well as load-acquire and store-release barriers.
Adaptive Sampling. For our techniques to be applicable, we expect that an ADS algorithm behaves as depicted in Algorithm 1: it iteratively samples data (in
 ) and aggregates it (using some operator \(\circ \)), until a stopping condition (
) and aggregates it (using some operator \(\circ \)), until a stopping condition (
 ) determines that the data sampled so far is sufficient to return an approximate solution within the required accuracy. This condition does not only consider the number of samples (\(d\mathtt {{.}num}\)), but also the sampled data (\(d\mathtt {{.}data}\)). Throughout this paper, we denote the size of that data (i.e., the number of elements of \(d.\mathtt {data}\)) by n. We assume that the stopping condition needs to be checked on a consistent state, i.e., a state of d that can occur in a sequential execution.Footnote 1 Furthermore, to make parallelization feasible at all, we need to assume that \(\circ \) is associative. For concrete examples of stopping conditions, we refer to Sect. 2.3 and Appendix A.
) determines that the data sampled so far is sufficient to return an approximate solution within the required accuracy. This condition does not only consider the number of samples (\(d\mathtt {{.}num}\)), but also the sampled data (\(d\mathtt {{.}data}\)). Throughout this paper, we denote the size of that data (i.e., the number of elements of \(d.\mathtt {data}\)) by n. We assume that the stopping condition needs to be checked on a consistent state, i.e., a state of d that can occur in a sequential execution.Footnote 1 Furthermore, to make parallelization feasible at all, we need to assume that \(\circ \) is associative. For concrete examples of stopping conditions, we refer to Sect. 2.3 and Appendix A.
2.2 Betweenness Centrality and Its Approximation
Betweenness Centrality (BC) is one of the most popular vertex centrality measures in the field of network analysis. Such measures indicate the importance of a vertex based on its position in the network [4] (we use the terms graph and network interchangeably). Being a centrality measure, BC constitutes a function \(\mathbf {b}: V \rightarrow \mathbb {R}\) that maps each vertex of a graph \(G = (V, E)\) to a real number – higher numbers represent higher importance. To be precise, the BC of \(u \in V\) is defined as \( \mathbf {b}(u) = \sum _{s \ne t \in V \setminus \{u\}} \frac{\sigma _{st}(u)}{\sigma _{st}}, \) where \(\sigma _{st}\) is the number of shortest s-t-paths and \(\sigma _{st}(u)\) is the number of shortest s-t-paths that contain u. Betweenness is extensively used to identify the key vertices in large networks, e.g., cities in a transportation network [14], or lethality in protein networks [16].
Unfortunately, BC is rather expensive to compute: the standard exact algorithm [8] has time complexity \(\varTheta (|V||E|)\) for unweighted graphs. Moreover, unless the Strong Exponential Time Hypothesis fails, this asymptotic running time cannot be improved [5]. Numerous approximation algorithms for BC have thus been developed (we refer to Sect. 5 for an overview). The state of the art of these approximation algorithms is the
 algorithm [6] of Borassi and Natale, which happens to be an ADS algorithm. With probability \((1 - \delta )\),
algorithm [6] of Borassi and Natale, which happens to be an ADS algorithm. With probability \((1 - \delta )\),
 approximates the BC values of the vertices within an additive error of \(\epsilon \) in nearly-linear time complexity, where \(\epsilon \) and \(\delta \) are user-specified constants.
approximates the BC values of the vertices within an additive error of \(\epsilon \) in nearly-linear time complexity, where \(\epsilon \) and \(\delta \) are user-specified constants.
While our techniques apply to any ADS algorithm, we recall that, as a case study, we focus on scaling the
 algorithm to a large number of threads.
algorithm to a large number of threads.
2.3 The
 algorithm
algorithm
KADABRA samples vertex pairs (s, t) of \(G = (V, E)\) uniformly at random and then selects a shortest s-t-path uniformly at random (in
 in Algorithm 1). After \(\tau \) iterations, this results in a sequence of randomly selected shortest paths \(\pi _1, \pi _2, \dots , \pi _\tau \); from those paths, BC is estimated as:
in Algorithm 1). After \(\tau \) iterations, this results in a sequence of randomly selected shortest paths \(\pi _1, \pi _2, \dots , \pi _\tau \); from those paths, BC is estimated as:
\(\sum _{i = 1}^\tau x_i\) is exactly the sampled data (\(d\mathtt {{.}data}\)) that the algorithm has to store (i.e., the accumulation \(\circ \) in Algorithm 1 sums \(x_i\) over i). To compute the stopping condition (
 in Algorithm 1),
in Algorithm 1),
 maintains the invariants
maintains the invariants
for two functions \(f = f(\widetilde{\mathbf {b}}(v), \delta _{L}(v), \omega , \tau )\) and \(g = g(\widetilde{\mathbf {b}}(v), \delta _{U}(v), \omega , \tau )\) depending on a maximal number \(\omega \) of samples and per-vertex probability constants \(\delta _L\) and \(\delta _U\) (more details in the original paper [6]). The values of those constants are computed in a preprocessing phase (mostly consisting of computing an upper bound on the diameter of the graph). \(\delta _L\) and \(\delta _U\) satisfy \(\sum _{v \in V} \delta _L(v) + \delta _U(v) \le \delta \) for a user-specified parameter \(\delta \in (0, 1)\). Thus, the algorithm terminates once \(f, g < \epsilon \); the result is correct with an absolute error of \(\pm \epsilon \) and probability \((1 - \delta )\). We note that checking the stopping condition of
 on an inconsistent state leads to incorrect results. For example, this can be seen from the fact that g is increasing with \(\widetilde{\mathbf {b}}\) and decreasing with \(\tau \), see Appendix B of our full-length paper [13].
on an inconsistent state leads to incorrect results. For example, this can be seen from the fact that g is increasing with \(\widetilde{\mathbf {b}}\) and decreasing with \(\tau \), see Appendix B of our full-length paper [13].
2.4 First Attempts at
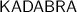 Parallelization
Parallelization
In the original
 implementationFootnote 2, a lock is used to synchronize concurrent access to the sampling state. As a first attempt to improve the scalability, we consider an algorithm that iteratively computes a fixed number of samples in parallel (e.g., using an OpenMP parallel for loop), then issues a synchronization barrier (as implied by the parallel for loop) and checks the stopping condition afterwards. While sampling, atomic increments are used to update the global sampling data. This algorithm is arguably the “natural” OpenMP-based parallelization of an ADS algorithm and can be implemented in a few extra lines of code. Moreover, it already improves upon the original parallelization. However, as shown by the experiments in Sect. 4, further significant improvements in performance are possible by switching to more lightweight synchronization.
implementationFootnote 2, a lock is used to synchronize concurrent access to the sampling state. As a first attempt to improve the scalability, we consider an algorithm that iteratively computes a fixed number of samples in parallel (e.g., using an OpenMP parallel for loop), then issues a synchronization barrier (as implied by the parallel for loop) and checks the stopping condition afterwards. While sampling, atomic increments are used to update the global sampling data. This algorithm is arguably the “natural” OpenMP-based parallelization of an ADS algorithm and can be implemented in a few extra lines of code. Moreover, it already improves upon the original parallelization. However, as shown by the experiments in Sect. 4, further significant improvements in performance are possible by switching to more lightweight synchronization.
3 Scalable Parallelization Techniques
To improve upon the OpenMP parallelization from Sect. 2.4, we have to avoid the synchronization barrier before the stopping condition can be checked. This is the objective of our epoch-based algorithms that constitute the main contribution of this paper. In Sect. 3.1, we formulate the main idea of our algorithms as a general framework and prove its correctness. The subsequent subsections present specific algorithms based on this framework and discuss trade-offs between them.
3.1 Epoch-Based Framework
In our epoch-based algorithms, the execution of each thread is subdivided into a sequence of discrete epochs. During an epoch, each thread iteratively collects samples; the stopping condition is only checked at the end of an epoch. The crucial advantage of this approach is that the end of an epoch does not require global synchronization. Instead, our framework guarantees the consistency of the sampled data by maintaining multiple copies of the sampling state.
As an invariant, it is guaranteed that no thread writes to a copy of the state that is currently being read by another thread. This is achieved as follows: each copy of the sampling state is labeled by an epoch number e, i.e., a monotonically increasing integer that identifies the epoch in which the data was generated. When the stopping condition has to be checked, all threads advance to a new epoch \(e + 1\) and start writing to a new copy of the sampling state. The stopping condition is only verified after all threads have finished this transition and it only takes the sampling state of epoch e into account.
More precisely, the main data structure that we use to store the sampling state is called a state frame (SF). Each SF f (depicted in Fig. 1(a) consists of (i) an epoch number (\(f{.}\mathtt {epoch}\)), (ii) a number of samples (\(f{.}\mathtt {num}\)) and (iii) the sampled data (\(f{.}\mathtt {data}\)). The latter two symbols directly correspond to \(d{.}{} \texttt {num}\) and \(d{.}\mathtt {data}\) in our generic formulation of an adaptive sampling algorithm (Algorithm 1). Aside from the SF structures, our framework maintains three global variables that are shared among all threads (depicted in Fig. 1(b): (i) a simple Boolean flag stop to determine if the algorithm should terminate, (ii) a variable epochToRead that stores the number of the epoch that we want to check the stopping condition on and (iii) a pointer sfFin[t] for each thread t that points to a SF finished by thread t. Incrementing \(\mathtt {epochToRead}\) is our synchronization mechanism to notify all threads that they should advance to a new epoch. Figure 2 visualizes such an epoch transition. In particular, it depicts the update of the \(\mathtt {sfFin}\) pointers after an epoch transition is initiated by incrementing \(\mathtt {epochToRead}\).
Transition after \(\mathtt {epochToRead}\) is set to 5. Thread 2 already writes to the SF of epoch 6 (using the \(f_\mathrm {sam}\) pointer). Thread 9 still writes to the SF of epoch 5 but advances to epoch 6 once it checks \(\mathtt {epochToRead}\) (dashed orange line). Afterwards, thread 9 publishes its SF of epoch 5 to \(\mathtt {sfFin}\) (dashed blue line). Finally, the stopping condition is checked using both SFs of epoch 5 (i.e., the SFs now pointed to by \(\mathtt {sfFin}\)). (Color figure online)

Algorithm 2 states the pseudocode of our framework. By \({{\,\mathrm{\leftarrow _\mathsf {relaxed}}\,}}\), \({{\,\mathrm{\leftarrow _\mathsf {acquire}}\,}}\) and \({{\,\mathrm{\leftarrow _\mathsf {release}}\,}}\), we denote relaxed memory access, load-acquire and store-release, respectively (see Sects. 2.1 and Appendix A of our full-length paper [13]). In the algorithm, each thread maintains an epoch number \(e_\mathrm {sam}\). To be able to check the stopping condition, thread 0 maintains another epoch number \(e_\mathrm {chk}\). Indeed, thread 0 is the only thread that evaluates the stopping condition (in checkFrames) after accumulating the SFs from all threads. checkFrames determines whether there is an ongoing check for the stopping condition (inCheck is true; line 16). If that is not the case, a check is initiated (by incrementing \(e_\mathrm {chk}\)) and all threads are signaled to advance to the next epoch (by updating \(\texttt {epochToRead}\)). Note that inCheck is needed to prevent thread 0 from repeatedly incrementing \(e_\mathrm {chk}\) without processing data from the other threads. Afterwards, checkFrames only continues if all threads t have published their SFs for checking (i.e., \(\mathtt {sfFin}[t]\) points to a SF of epoch \(e_\mathrm {chk}\); line 20). Once that happens, those SFs are accumulated (line 27) and the stopping condition is checked on the accumulated data (line 31). Eventually, the termination flag (stop; line 32) signals to all threads that they should stop sampling. The main algorithm, on the other hand, performs a loops until this flag is set (line 2). Each iteration collects one sample and writes the results to the current SF (\(f_\mathrm {sam}\)). If a thread needs to advance to a new epoch (because an incremented epochToRead is read in line 7), it publishes its current SF to sfFin and starts writing to a new SF (\(f_\mathrm {sam}\); line 12). Note that the memory used by old SFs can be reclaimed (line 9; however, note that there is no SF for epoch 0). How exactly that is done is left to the algorithms described in later subsections. In the remainder of this subsection, we prove the correctness of our approach.
Proposition 1
Algorithm 2 always checks the stopping condition on a consistent state; in particular, the epoch-based approach is correct.
Proof
The order of lines 10 and 12 implies that no thread t issues a store to a SF f which it already published to \(\mathtt {sfFin}[t]\). Nevertheless, we need to prove that all stores by thread t are visible to
 before the frames are accumulated.
before the frames are accumulated.
 only accumulates \(f{.}\mathtt {data}\) after f has been published to \(\mathtt {sfFin}[t]\) via the store-relase in line 10. Furthermore, in line 21,
only accumulates \(f{.}\mathtt {data}\) after f has been published to \(\mathtt {sfFin}[t]\) via the store-relase in line 10. Furthermore, in line 21,
 performs at least one load-acquire on \(\mathtt {sfFin}[t]\) to read the pointer to f. Thus, all stores to f are visible to
performs at least one load-acquire on \(\mathtt {sfFin}[t]\) to read the pointer to f. Thus, all stores to f are visible to
 before the accumulation in line 27. The proposition now follows from the fact that \(\circ \) is associative, so that line 27 indeed produces a SF that occurs in some sequential execution. \(\square \)
before the accumulation in line 27. The proposition now follows from the fact that \(\circ \) is associative, so that line 27 indeed produces a SF that occurs in some sequential execution. \(\square \)
3.2 Local-Frame and Shared-Frame Algorithm
We present two epoch-based algorithms relying on the general framework from the previous section: namely, the local-frame and the shared-frame algorithm. Furthermore, in Appendix D.2 of our full-length paper [13], we present the deterministic indexed-frame algorithm (as both local-frame and shared-frame are non-deterministic). Local-frame and shared-frame are both based on the pseudocode in Algorithm 2. They differ, however, in their allocation and reuse (in line 9 of the code) of SFs. The local frame algorithm allocates one pair of SFs per thread and cycles through both SFs of that pair (i.e., epochs with even numbers are assigned the first SF while odd epochs use the second SF). This yields a per-thread memory requirement of \(\mathcal {O}(n)\); as before, n denotes the size of the sampling state. The shared-frame algorithm reduces this memory requirement to \(\mathcal {O}(1)\) by only allocating F pairs of SFs in total, for a constant number F. Thus, \(T{/}F\) threads share a SF in each epoch and atomic fetch-add operations need to be used to write to the SF. The parameter F can be used to balance the memory bandwidth and synchronization costs – a smaller value of F lowers the memory bandwidth required during aggregation but leads to more cache contention due to atomic operations.
3.3 Synchronization Costs
In Algorithm 2, all synchronization of threads \(t > 0\) is done wait-free in the sense that the threads only have to stop sampling for \(\varTheta (1)\) instructions to communicate with other threads (i.e., to check \(\mathtt {epochToRead}\), update per-thread state and write to \(\mathtt {sfFin}[t]\)). At the same time, thread \(t = 0\) generally needs to check all \(\mathtt {sfFin}\) pointers. Taken together, this yields the following statement:
Proposition 2
In each iteration of the main loop, threads \(t > 0\) of local-frame and shared-frame algorithms spend \(\varTheta (1)\) time to wait for other threads. Thread \(t = 0\) spends up to \(\mathcal {O}(T)\) time to wait for other threads.
In particular, the synchronization cost does not depend on the problem instance – this is in contrast to the OpenMP parallelization in which threads can idle for \(\mathcal {O}(\mathcal {S})\) time, where \(\mathcal {S}\) denotes the time complexity of a sampling operation (e.g., \(\mathcal {S} = \mathcal {O}(|V| + |E|)\) in the case of
 ).
).
Nevertheless, this advantage in synchronization costs comes at a price: the accumulation of the sampling data requires additional evaluations of \(\circ \). \(\mathcal {O}(Tn)\) evaluations are required in the local-frame algorithm, whereas shared-frame requires \(\mathcal {O}(Fn)\). No accumulation is necessary in the OpenMP baseline. As can be seen in Algorithm 2, we perform the accumulation in a single thread (i.e., thread 0). Compared to a parallel implementation (e.g., using parallel reductions), this strategy requires no additional synchronization and has a favorable memory access pattern (as the SFs are read linearly). A disadvantage, however, is that there is a higher latency (depending on T) until the algorithm detects that it is able to stop. Appendix C.3 discusses how a constant latency can be achieved heuristically.
4 Experiments
The platform we use for our experiments is a Linux server equipped with 1.5 TB RAM and two Intel Xeon Gold 6154 CPUs with 18 cores (for a total of 36 cores) at 3.00 GHz. Each thread of the algorithm is pinned to a unique core; hyperthreading is disabled. Our implementation is written in C++ building upon the NetworKit toolkit [29].Footnote 3 We use 27 undirected real-world graphs in the experiments (see Appendix E of our full-length paper [13] for more details). The largest instances take tens of minutes for our OpenMP baseline and multiple hours for the original implementation of
 . The error probability for
. The error probability for
 is set to \(\delta = 0.1\) for all experiments. Absolute running times of our experiments are reported in Appendix F. The deviation in running time among different runs of the same algorithm turned out to be small (e.g., around 3% for our local-frame algorithm using 36-cores, in geom. mean running time over all instances). As it is specifically small compared to our speedups, we report data on a single run per instance.
is set to \(\delta = 0.1\) for all experiments. Absolute running times of our experiments are reported in Appendix F. The deviation in running time among different runs of the same algorithm turned out to be small (e.g., around 3% for our local-frame algorithm using 36-cores, in geom. mean running time over all instances). As it is specifically small compared to our speedups, we report data on a single run per instance.
In a first experiment, we compare our OpenMP baseline against the original implementation of
 (see Sect. 2.4 for these two approaches). We set the absolute approximation error to \(\epsilon = 0.01\). The overall speedup (i.e., both preprocessing and ADS) is reported in Fig. 3a. The results show that our OpenMP baseline outperforms the original implementation considerably (i.e., by a factor of \(6.9 {\times }\)), even in a single-core setting. This is mainly due to implementation tricks (see Appendix C.1) and parameter tuning (as discussed in Appendix C.2). Furthermore, for 32 cores, our OpenMP baseline performs \(13.5 {\times }\) better than the original implementation of
(see Sect. 2.4 for these two approaches). We set the absolute approximation error to \(\epsilon = 0.01\). The overall speedup (i.e., both preprocessing and ADS) is reported in Fig. 3a. The results show that our OpenMP baseline outperforms the original implementation considerably (i.e., by a factor of \(6.9 {\times }\)), even in a single-core setting. This is mainly due to implementation tricks (see Appendix C.1) and parameter tuning (as discussed in Appendix C.2). Furthermore, for 32 cores, our OpenMP baseline performs \(13.5 {\times }\) better than the original implementation of
 – or \(22.7 {\times }\) if only the ADS phase is considered. Hence, for the remaining experiments, we discard the original implementation as a competitor and focus on the parallel speedup of our algorithms.
– or \(22.7 {\times }\) if only the ADS phase is considered. Hence, for the remaining experiments, we discard the original implementation as a competitor and focus on the parallel speedup of our algorithms.
To understand the relation between the preprocessing and ADS phases of
 , we break down the running times of the OpenMP baseline in Fig. 3b. In this figure, we present the fraction of time that is spent in ADS on three exemplary instances and for different values of \(\epsilon \). Especially if \(\epsilon \) is small, the ADS running time dominates the overall performance of the algorithm. Thus, improving the scalability of the ADS phase is of critical importance. For this reason, we neglect the preprocessing phase and only consider ADS when comparing to our local-frame and shared-frame algorithms.
, we break down the running times of the OpenMP baseline in Fig. 3b. In this figure, we present the fraction of time that is spent in ADS on three exemplary instances and for different values of \(\epsilon \). Especially if \(\epsilon \) is small, the ADS running time dominates the overall performance of the algorithm. Thus, improving the scalability of the ADS phase is of critical importance. For this reason, we neglect the preprocessing phase and only consider ADS when comparing to our local-frame and shared-frame algorithms.
In Fig. 4a, we report the parallel speedup of the ADS phase of our epoch-based algorithms relative to the OpenMP baseline. All algorithms are configured to check the stopping condition after a fixed number of samples (see Appendix C.3 for details). The number F of SF pairs of shared-frame has been configured to 2, which we found to be a good setting for \(T = 32\). On 32 cores, local-frame and shared-frame achieve parallel speedups of \(15.9 {\times }\) and 18.1; they both significantly improve upon the OpenMP baseline, which can only achieve a parallel speedup of \(6.3 {\times }\) (i.e., local-frame and shared-frame are \(2.5 {\times }\) and \(2.9 {\times }\) faster, respectively; they also outperform the original implementation by factors of 57.3 and 65.3, respectively). The difference between local-frame and shared-frame is insignificant for lower numbers of cores; this is explained by the fact that the reduced memory footprint of shared-frame only improves performance once memory bandwidth becomes a bottleneck. For the same reason, both algorithms scale very well until 16 cores; due to memory bandwidth limitations, this nearly ideal scalability does not extend to 32 cores. This bandwidth issue is known to affect graph traversal algorithms in general [2, 18].
The indexed-frame algorithm is not as fast as local-frame and shared-frame on the instances depicted in Fig. 4a: it achieves a parallel speedup of \(10.8 {\times }\) on 32 cores. However, it is still considerably faster than the OpenMP baseline (by a factor of \(1.7 {\times }\)). There are two reasons why the determinism of indexed-frame is costly: index-frame has similar bandwidth requirements as local-frame; however, it has to allocate more memory as SFs are buffered for longer periods of time. On the other hand, even when enough samples are collected, the stopping condition has to be checked on older samples first, while local-frame and shared-frame can just check the stopping condition on the most recent sampling state.
In a final experiment, we evaluate the impact of the parameter F of shared-frame on its performance. Note that this experiment also demonstrates the difference in memory consumption of shared-frame (\(F \in \{1, \ldots , T\}\)) and local-frame (equivalent to \(F = T\)). Figure 4b depicts the results. The experiment is done with 36 cores; hence memory pressure is even higher than in the previous experiments. The figure demonstrates that in this situation, minimizing the memory bandwidth requirements at the expense of synchronization overhead is a good strategy. Hence for larger numbers of cores, we can minimize memory footprint and maximize performance at the same time.
5 Related Work
Our parallelization strategy can be applied to arbitrary ADS algorithms. ADS was first introduced by Lipton and Naughton to estimate the size of the transitive closure of a digraph [17]. It is used in a variety of fields, e.g., in statistical learning [26]. In the context of BC, ADS has been used to approximate distances between pairs of vertices of a graph [25], to approximate the BC values of a graph [3, 6, 28] and to approximate the BC value of a single vertex [9]. An analogous strategy is exploited by Mumtaz and Wang [24] to find approximate solutions to the group betweenness maximization problem.
Regarding more general (i.e., not necessarily ADS) algorithms for BC, a survey from Matta et al. [20] provides a detailed overview of the state of the art. The RK [27] algorithm represents the leading non-adaptive sampling algorithm for BC approximation;
 was shown to be 100 times faster than RK in undirected real-world graphs, and 70 times faster than RK in directed graphs [6]. McLaughlin and Bader [22] introduced a work-efficient parallel algorithm for BC approximation, implemented for single- and multi-GPU machines. Madduri et al. [19] presented a lock-free parallel algorithm optimized for specific massively parallel non-x86_64 architectures to approximate or compute BC exactly in massive networks. Unlike our approach, this lock-free algorithm parallelizes the collection of individual samples and is thus only applicable to betweenness centrality and not to general ADS algorithms. Additionally, according to the authors of [19], this approach hits performance bottlenecks on x86_64 even for 4 cores.
was shown to be 100 times faster than RK in undirected real-world graphs, and 70 times faster than RK in directed graphs [6]. McLaughlin and Bader [22] introduced a work-efficient parallel algorithm for BC approximation, implemented for single- and multi-GPU machines. Madduri et al. [19] presented a lock-free parallel algorithm optimized for specific massively parallel non-x86_64 architectures to approximate or compute BC exactly in massive networks. Unlike our approach, this lock-free algorithm parallelizes the collection of individual samples and is thus only applicable to betweenness centrality and not to general ADS algorithms. Additionally, according to the authors of [19], this approach hits performance bottlenecks on x86_64 even for 4 cores.
The SFs used by our algorithms are concurrent data structures that enable us to minimize the synchronization latencies in multithread environments. Devising concurrent (lock-free) data structures that scale over multiple cores is not trivial and much effort has been devoted to this goal [7, 23]. A well-known solution is the Read-Copy-Update mechanism (RCU); it was introduced to achieve high multicore scalability on read-mostly data structures [21], and was leveraged by several applications [1, 10]. Concurrent hash tables [11] are another popular example.
6 Conclusions and Future Work
In this paper, we found that previous techniques to parallelize ADS algorithms are insufficient to scale to large numbers of threads. However, significant speedups can be achieved by employing adequate concurrent data structures. Using such data structures and our epoch mechanism, we were able to devise parallel ADS algorithms that consistently outperform the state of the art but also achieve different trade-offs between synchronization costs, memory footprint and determinism of the results.
Regarding future work, a promising direction for our algorithms is parallel computing with distributed memory; here, the stopping condition could be checked via (asynchronous) reduction of the SFs. In the case of BC this, might yield a way to avoid bottlenecks for memory bandwidth on shared-memory systems.
Notes
- 1.
That is, \(d\mathtt {{.}num}\) and all entries of \(d\mathtt {{.}data}\) must result from an integral sequence of samples; otherwise, parallelization would be trivial.
- 2.
Available at: https://github.com/natema/kadabra.
- 3.
The algorithms of this paper have been integrated into NetworKit, in the KadabraBetweenness class. NetworKit is publicly available at https://github.com/kit-parco/networkit.
References
Arbel, M., Attiya, H.: Concurrent updates with RCU: search tree as an example. In: Proceedings of the 2014 ACM Symposium on Principles of Distributed Computing, pp. 196–205. ACM (2014)
Bader, D.A., Cong, G., Feo, J.: On the architectural requirements for efficient execution of graph algorithms. In: 2005 International Conference on Parallel Processing, ICPP 2005, pp. 547–556. IEEE (2005)
Bader, D.A., Kintali, S., Madduri, K., Mihail, M.: Approximating betweenness centrality. In: Bonato, A., Chung, F.R.K. (eds.) WAW 2007. LNCS, vol. 4863, pp. 124–137. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-77004-6_10
Boldi, P., Vigna, S.: Axioms for centrality. Internet Math. 10(3–4), 222–262 (2014). https://doi.org/10.1080/15427951.2013.865686
Borassi, M., Crescenzi, P., Habib, M.: Into the square: on the complexity of some quadratic-time solvable problems. Electr. Notes Theor. Comput. Sci. 322, 51–67 (2016). https://doi.org/10.1016/j.entcs.2016.03.005
Borassi, M., Natale, E.: KADABRA is an adaptive algorithm for betweenness via random approximation. In: 24th Annual European Symposium on Algorithms, ESA 2016, Aarhus, Denmark, 22–24 August 2016, pp. 20:1–20:18 (2016). https://doi.org/10.4230/LIPIcs.ESA.2016.20
Boyd-Wickizer, S., et al.: An analysis of Linux scalability to many cores. In: OSDI, vol. 10, pp. 86–93 (2010)
Brandes, U.: A faster algorithm for betweenness centrality. J. Math. Sociol. 25(2), 163–177 (2001)
Chehreghani, M.H., Bifet, A., Abdessalem, T.: Novel adaptive algorithms for estimating betweenness, coverage and k-path centralities. CoRR abs/1810.10094 (2018). http://arxiv.org/abs/1810.10094
Clements, A.T., Kaashoek, M.F., Zeldovich, N.: Scalable address spaces using RCU balanced trees. ACM SIGPLAN Not. 47(4), 199–210 (2012)
David, T., Guerraoui, R., Trigonakis, V.: Everything you always wanted to know about synchronization but were afraid to ask. In: ACM SIGOPS 24th Symposium on Operating Systems Principles, SOSP 2013, Farmington, PA, USA, 3–6 November 2013, pp. 33–48 (2013). https://doi.org/10.1145/2517349.2522714
Gonzalez, T.F.: Handbook of Approximation Algorithms and Metaheuristics (Chapman & Hall/Crc Computer & Information Science Series). Chapman & Hall/CRC, Boca Raton (2007)
van der Grinten, A., Angriman, E., Meyerhenke, H.: Parallel adaptive sampling with almost no synchronization. CoRR abs/1903.09422 (2019). https://arxiv.org/abs/1903.09422
Guimera, R., Mossa, S., Turtschi, A., Amaral, L.N.: The worldwide air transportation network: anomalous centrality, community structure, and cities’ global roles. Proc. Natl. Acad. Sci. 102(22), 7794–7799 (2005)
ISO: ISO/IEC 14882:2011 Information technology – Programming languages – C++. International Organization for Standardization, Geneva, Switzerland, February 2012. http://www.iso.org/iso/iso_catalogue/catalogue_tc/catalogue_detail.htm?csnumber=50372
Jeong, H., Mason, S.P., Barabási, A.L., Oltvai, Z.N.: Lethality and centrality in protein networks. Nature 411(6833), 41 (2001)
Lipton, R.J., Naughton, J.F.: Estimating the size of generalized transitive closures. In: Proceedings of the 15th International Conference on Very Large Data Bases (1989)
Lumsdaine, A., Gregor, D., Hendrickson, B., Berry, J.: Challenges in parallel graph processing. Parallel Process. Lett. 17(01), 5–20 (2007)
Madduri, K., Ediger, D., Jiang, K., Bader, D.A., Chavarria-Miranda, D.: A faster parallel algorithm and efficient multithreaded implementations for evaluating betweenness centrality on massive datasets. In: IEEE International Symposium on Parallel & Distributed Processing, IPDPS 2009, pp. 1–8. IEEE (2009)
Matta, J., Ercal, G., Sinha, K.: Comparing the speed and accuracy of approaches to betweenness centrality approximation. Comput. Soc. Netw. 6(1), 2 (2019)
McKenney, P.E., Slingwine, J.D.: Read-copy update: using execution history to solve concurrency problems. In: Parallel and Distributed Computing and Systems, pp. 509–518 (1998)
McLaughlin, A., Bader, D.A.: Scalable and high performance betweenness centrality on the GPU. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, pp. 572–583. IEEE Press (2014)
Michael, M.M.: Hazard pointers: safe memory reclamation for lock-free objects. IEEE Trans. Parallel Distrib. Syst. 6, 491–504 (2004)
Mumtaz, S., Wang, X.: Identifying top-k influential nodes in networks. In: Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, pp. 2219–2222. ACM (2017)
Oktay, H., Balkir, A.S., Foster, I., Jensen, D.D.: Distance estimation for very large networks using mapreduce and network structure indices. In: Workshop on Information Networks (2011)
Provost, F., Jensen, D., Oates, T.: Efficient progressive sampling. In: Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 23–32. ACM (1999)
Riondato, M., Kornaropoulos, E.M.: Fast approximation of betweenness centrality through sampling. Data Min. Knowl. Discov. 30(2), 438–475 (2016)
Riondato, M., Upfal, E.: ABRA: approximating betweenness centrality in static and dynamic graphs with rademacher averages. ACM Trans. Knowl. Discov. Data (TKDD) 12(5), 61 (2018)
Staudt, C.L., Sazonovs, A., Meyerhenke, H.: NetworKit: a tool suite for large-scale complex network analysis. Netw. Sci. 4(4), 508–530 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Grinten, A.v.d., Angriman, E., Meyerhenke, H. (2019). Parallel Adaptive Sampling with Almost No Synchronization. In: Yahyapour, R. (eds) Euro-Par 2019: Parallel Processing. Euro-Par 2019. Lecture Notes in Computer Science(), vol 11725. Springer, Cham. https://doi.org/10.1007/978-3-030-29400-7_31
Download citation
DOI: https://doi.org/10.1007/978-3-030-29400-7_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29399-4
Online ISBN: 978-3-030-29400-7
eBook Packages: Computer ScienceComputer Science (R0)





 algorithm
algorithm
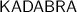 Parallelization
Parallelization

