Institutions for SQL Database Schemas and Datasets

Abstract

Databases and the query language SQL play a major role in modern applications. In this paper we present an institution-based formalisation of relational databases that uses structures close to those used in SQL. This is the essential difference to other category-theoretical formalisations of databases, which often depart quite far from the SQL standard. We also study SQL queries, using institutional monads, and prove cocompleteness and amalgamation results for the institution.

1 Introduction

Database techniques have a long tradition in computer science and build the foundation for numerous modern applications. The Structured Query Language (SQL) [11] forms the fundamental specification for most state-of-the-art query languages for many database systems.¹ Near to all applications that rely on databases use some query language that conforms to the SQL specification, e.g. MySQL or PostgreSQL. This central role made SQL an essential building block of modern database technology that can not be replaced by other languages easily. Thus, formal approaches towards databases should focus this existing standard rather than develop a rivalling query language.

The diversity and heterogeneity of data needed for one specific application raises the need for frictionless interaction and migration between different database schemas. The growing role of Linked Open Data underlines this need. As a result there this a vast landscape of formal approaches towards databases and data migration, including many category-theoretical approaches. The relational make-up of many database schemas makes it natural to model them as categories and yields the intuitive notion of a schema merge as pushouts of functors. In [21,22,23] tables are represented as categories and values and relations between tables are functors. The Functorial Query Language yields functionalities to query those structures. A similar approach towards schema integration was defined for the first time in an institutional setting in [1]. Institutions were defined in [10] as a framework to cover the vast, heterogeneous landscape of logical formalisms used in computer science. The benefits of a categorical or institutional formalisation are (1) better tools for database structuring, (2) database integration can be achieved via colimits and (3) the possibility of heterogeneous integration of databases with logical languages.

However, previous approaches to category-theoretic formalisation of databases do not well integrate with actual practice of SQL databases. The reasons are that the defined structures are not close to actual relational database structures, the logic is not three-valued as in SQL², data tables cannot contain duplicates, the operators are not exactly those of SQL, and more (see also [22] for differences between algebraic and relational databases). Therefore, in this work, we aim at formalising an SQL institution that comes as close as possible to the SQL standard. This means there should be a simple and obvious correspondence between SQL database schemas and theories in the institution. This is particularly important for tool support via the Heterogeneous tool set (Hets) [14], which provides a software interface for institutions. Only with an institution supporting SQL directly, Hets can read in standard SQL database schemas. If needed, these can then be translated to other institutions. The formalisation presented in this paper can be seen a first step towards institution based logical reasoning on relational databases and their heterogeneous integration with logical theories. For example, in [20], using institutions, (a simplified form of) a database schema is heterogeneously integrated with an ontology formulated in the description logic OWL, via a first-order theory playing the role of a bridge theory. Our work will enable the use of real-world SQL database schemas in such heterogeneous integration scenarios.

2 An Institution for Databases

There is a vast landscape of different logics with varying expressiveness, complexity and purpose. Yet, most logics define syntactical entities like signatures (vocabularies) and sentences, as well as concepts of model and satisfaction (of a sentence in a model). Goguen et al defined institutions in [10] as an overarching, abstract framework that covers all those concepts and thus integrates them into a common structure.

Definition 1

An institution $\mathcal {I} = (\mathbf{Sign }^{\mathcal {I}}, \mathbf{Sen }^{\mathcal {I}}, \mathbf{Mod }^{\mathcal {I}}, {\mathrel {\models ^{\mathcal {I}}_{}}})$ consists of

• (i) a category of signatures $\mathbf{Sign }^{\mathcal {I}}$ and signature morphisms;

• (ii) a sentence functor $\mathbf{Sen }^{\mathcal {I}} : \mathbf{Sign }^{\mathcal {I}} \rightarrow \mathbf {Set}$ (where $\mathbf {Set}$ is the category of sets), providing for each signature $\varSigma$ a set of sentences $\mathbf{Sen }^{\mathcal {I}}(\varSigma )$ and for each signature morphism $\sigma :\varSigma _1\rightarrow \varSigma _2$ a sentence translation map $\mathbf{Sen }^{\mathcal {I}}(\sigma ):\mathbf{Sen }^{\mathcal {I}}(\varSigma _1)\rightarrow \mathbf{Sen }^{\mathcal {I}}(\varSigma _2)$ (also written $\sigma ({-})$);

• (iii) a contra-variant model functor $\mathbf{Mod }^{\mathcal {I}} : (\mathbf{Sign }^{\mathcal {I}})^{\mathrm {op}}\rightarrow \mathbf {Cat}$ (where $\mathbf {Cat}$ is the category of categories³), providing for each signature $\varSigma$ a category of models $\mathbf{Mod }^{\mathcal {I}}(\varSigma )$ and for each signature morphism $\sigma :\varSigma _1\rightarrow \varSigma _2$ a model reduct functor $\mathbf{Mod }^{\mathcal {I}}(\sigma ):\mathbf{Sen }^{\mathcal {I}}(\varSigma _2)\rightarrow \mathbf{Sen }^{\mathcal {I}}(\varSigma _1)$ (also written ${-} | _\sigma$); and

• (iv) a family of satisfaction relations ${\mathrel {\models ^{\mathcal {I}}_{\varSigma }}} \subseteq |\mathbf{Mod }^{\mathcal {I}}(\varSigma )| \times \mathbf{Sen }^{\mathcal {I}}(\varSigma )$ indexed over $\varSigma \in |\mathbf{Sign }^{\mathcal {I}}|$,

such that the following satisfaction condition holds for every signature morphism $\sigma : \varSigma \rightarrow \varSigma '$ in $\mathbf{Sign }^{\mathcal {I}}$, every sentence $\varphi \in \mathbf{Sen }^{\mathcal {I}}(\varSigma )$ and for every $\varSigma '$-model $M' \in |\mathbf{Mod }^{\mathcal {I}}(\varSigma ')|$:

$$\begin{aligned} {M'} | _\sigma \mathrel {\models ^{\mathcal {I}}_{\varSigma }} \varphi \ \mathrel {\Leftrightarrow }\ M' \mathrel {\models ^{\mathcal {I}}_{\varSigma '}} \sigma (\varphi ) \ \text {.} \end{aligned}$$

Definition 2

A semi-institution $(\mathop {\mathbf{Sign }},\mathbf{Mod })$ (called specification frame in [7]) consists of a signature category $\mathop {\mathbf{Sign }}$ and a model functor $\mathbf{Mod }^{\mathcal {I}}:(\mathbf{Sign }^{\mathcal {I}})^{\mathrm {op}}\rightarrow \mathbf {Cat}$ (that is, it is an institution without sentences and satisfaction relation).

In this section we will define our institution for relational SQL databases. The general structure is as follows: Each object of the signature category defines the schema of a relational database (e.g. tables, their columns and sorts) as well as the building blocks for expressions (i.e. function and predicate symbols). Sentences represent constraints on these tables (e.g. foreign key constraints) that the data in the database must conform to. The data stored in the database are objects of the model category and morphisms amongst these models represent multiset inclusion. Finally, the satisfaction relation checks whether the data the database (i.e. a model) conforms to a specified constraint (i.e. a sentence). As a guidance all parts of the institution will be explained using the following example tables for persons and employees. Both tables feature a primary key that is an integer. The employee table contains a foreign key reference to the person table, with an according constraint (i.e. the pid of an employee always must be the id of a person). Moreover, the employee table contains a check constraint ensuring that the salary of an employee cannot negative.

Example 1

The database schema describes the general structure of a database. It includes information about all tables in the database, which columns belong to a specific table and their respective datatype. Information about the structure of a database is expressed in the Data Definition Language (DDL). Many basic components (e.g. datatypes, operators) of a database are fixed by the underlying database system. Similarly, the SQL Institution is parameterised over $(D\varSigma , DM)$ consisting of a datatype signature $D\varSigma$, which is a many-sorted first-order signature $D\varSigma =(\mathbb {S}^{D\varSigma }, \mathcal {F}_{D\varSigma })$ such that

• 1. there is a sort $bool \in \mathbb {S}^{D\varSigma }$

• 2. for each sort $s \in \mathbb {S}^{D\varSigma }$ there is a constant null : s, unary predicates $\textit{is}\_\textit{null}: s$ and $\textit{is}\_\textit{not}\_\textit{null}: s$, and a binary predicate $=_s : s\times s$.

and of a datatype model DM, which is a $D\varSigma$-model such that

• 1. $DM_{ bool }=\{\mathsf {T},\mathsf {F},\mathsf {U}\}$. (Note that SQL builds upon a 3-valued logic in order do cope with the existence of null-values.)

• 2. All operations are strict, i.e. they return $null _{DM}$ (or $\mathsf {U}$, in case of operations with result sort $bool$) if any of the operands is $null _{DM}$. The only exceptions to this rule are is_null and is_not_null.

• 3. $is\_null _{DM}$ is $\mathsf {T}$ for $null _{DM}$, and $\mathsf {F}$ otherwise.

• 4. $is\_not\_null _{DM}$ is $\mathsf {F}$ for $null _{DM}$, and $\mathsf {T}$ otherwise.

• 5. $a(=_s)_{DM}b={\left\{ \begin{array}{ll}\mathsf {T}&{} a=b\not = null _{DM}\\ \mathsf {F}&{} null _{DM}\not =a\not =b\not = null _{DM}\\ \mathsf {U}&{} otherwise \end{array}\right. }$

Example 2

A many-sorted first order signature for MySQL-datatypes may consist of the following components:

An extension for the database PostgreSQL (which also features geometrical datatypes, for geo databases) might look as follows:

Both signatures can be interpreted with a model in a standard way, following the SQL conventions for datatypes and their built-in operations.

For a given pair $(D\varSigma ,DM)$ of a data type signature and a data type model, we now define an institution $\mathcal {SQL}(D\varSigma ,DM)$ as follows.

A signature in $\mathcal {SQL}(D\varSigma ,DM)$ defines the tables the database contains as well as the corresponding columns and their datatypes.

Definition 3

(Signatures). An object $\varSigma$ of the category of signatures $\mathop {\mathbf{Sign }}$ consists of:

• a set of table names (or short: tables) $\mathbb {T}^{\varSigma }$,

• for each table $t\in \mathbb {T}^{\varSigma }$, a set $\text {col}^{\varSigma }(t)$ of columns,

• a function $\tau ^{}(\cdot ,\cdot ): \{(t,c)| t \in \mathbb {T}^{\varSigma }, c \in \text {col}^{\varSigma }(t) \} \rightarrow \mathbb {S}^{D\varSigma }$ assigning sorts (of the datatype signature) to columns in tables, and

• for each table $t\in \mathbb {T}^{\varSigma }$, a primary key $pk ^{\varSigma }(t)\subseteq \text {col}^{\varSigma }(t)$. Note $pk ^{\varSigma }(t)=\emptyset$ is possible, which expresses, in SQL terms, the absence of a primary key.

We include primary keys into signatures (instead of considering them to be sentences) because for each table there may be at most one primary key.

Definition 4

(Signature Morphisms). A signature morphism $\sigma : \varSigma \rightarrow \varSigma '$ in the category of signatures $\mathop {\mathbf{Sign }}$ consists of

• a table translation $\sigma _{\mathbb {T}^{}}:\mathbb {T}^{\varSigma } \rightarrow \mathbb {T}^{\varSigma '}$, and

• a family of column translations ,

such that types of columns are preserved

$$ \tau ^{\varSigma '}(\sigma _{\mathbb {T}^{}}(t),\sigma _{\text {col},t}(c)) = \tau ^{\varSigma }(t,c) $$

and for each table $t \in \mathbb {T}^{\varSigma }$, the primary key (if existing) is preserved

$$ pk ^{\varSigma '}(\sigma _{\mathbb {T}^{}}(t))=\sigma _{\text {col},t}( pk ^{\varSigma }(t)) \text { if } pk ^{\varSigma }(t)\ne \emptyset $$

Example 3

A signature $\varSigma$ for the tables shown in Example 1 is as follows:

• $\mathbb {T}^{\varSigma } = \{ \texttt {Employee}, \texttt {Person}\}$

• $\text {col}^{\varSigma }(\texttt {Employee}) = \{\texttt {id}, \texttt {salary}, \texttt {pid}\}$

• $\text {col}^{\varSigma }(\texttt {Person}) = \{\texttt {id}, \texttt {fname}, \texttt {lname}\}$

• $\tau ^{\varSigma }(\texttt {Employee},.) = \{\texttt {id} \mapsto \texttt {Int}, \texttt {salary} \mapsto \texttt {Int}, \texttt {pid} \mapsto \texttt {Int}\}$

• $\tau ^{\varSigma }(\texttt {Person},.) = \{\texttt {id} \mapsto \texttt {Int}, \texttt {fname} \mapsto \texttt {Text}, \texttt {lname} \mapsto \texttt {Text}\}$

• $pk ^{\varSigma }(\texttt {Person})=\{\texttt {id}\}$

• $pk ^{\varSigma }(\texttt {Employee})=\{\texttt {id}\}$

The database schema described above yields means to structure data in tables with little limitations regarding the actual content of the data. In order to ensure data integrity, the SQL defines several types of constraints that may be placed on a table. The sentences of the presented institution formulate the most common types of constraints (NOT NULL, UNIQUE, FOREIGN KEY and CHECK) specified in the SQL standard.

Definition 5

(Sentences). Given a signature $\varSigma$, a sentence $\varphi ^t$ is a constraint on a table $t \in \mathbb {T}^{\varSigma }$ of one of the following forms:

• A non-null constraint $notnull (t.c)$ ($c\in \text {col}^{}(t)$)

• A unique constraint $un (t.c_1,\ldots ,t.c_n)$ ($c_1,\ldots ,c_n\in \text {col}^{}(t)$)

• A foreign-key constraint $fk ((t.c_1,u.d_1),\ldots ,(t.c_n,u.d_n))$ for some a table $u \in \mathbb {T}^{\varSigma }$ and $c_i\in \text {col}^{}(t)$, $d_i\in \text {col}^{}(u)$ for $i=1,\ldots ,n$

• A check constraint $ck _t(\varphi )$, where $\varphi$ is a term of sort $Bool$ over the signature $D\varSigma$ (extended with logical connectives $\lnot$, $\vee$, $\wedge$ as operations on $Bool$) and variables from the set $Var(t)=\{t.c\mid t\in col(t)\}$.

Definition 6

(Sentence Translation). Given a signature morphism $\sigma : \varSigma \rightarrow \varSigma '$, a constraint $\varphi ^t$ on a table $t \in \mathbb {T}^{\varSigma }$ is translated along $\sigma$ to $\sigma (\varphi ^t)$ depending on its structure

• $\sigma ( un (t.c_1,\ldots ,t.c_n)) = un (\sigma _{\mathbb {T}^{}}(t).\sigma _{\text {col},t}(c_1),\ldots ,\sigma _{\mathbb {T}^{}}(t).\sigma _{\text {col},t}(c_n))$

• $\begin{array}[t]{lclll} \sigma ( fk ((t.c_1,u.d_1),\ldots ,(t.c_n,u.d_n))) &{}=&{} fk ( &{} (\sigma _{\mathbb {T}^{}}(t).\sigma _{\text {col},t}(c_1),\sigma _{\mathbb {T}^{}}(u).\sigma _{\text {col},t}(d_1)), &{} \\ &{} &{} &{} \cdots &{} \\ &{} &{} &{} (\sigma _{\mathbb {T}^{}}(t).\sigma _{\text {col},t}(c_n),\sigma _{\mathbb {T}^{}}(u).\sigma _{\text {col},t}(d_n))) &{} \end{array}$

• $\sigma ( ck _t(\varphi ))$ is obtained by mapping all variable names along $\sigma$, i.e. the variable c.t is replaced with $\sigma _{\text {col},t}(c).\sigma _{\mathbb {T}^{}}(t)$.

Example 4

Primary keys are already part of the signature. Thus, there are only two constraints remaining in Example 1 that can be formulated as sentences:

• The foreign key linking Employees to Persons

  $$\begin{aligned} fk (\texttt {(Employee.pid,Person.id)}) \end{aligned}$$

• The constraint that the salary of an employee must not be negative

  $$\begin{aligned} ck _t(\texttt {Employee.salary >= 0}) \end{aligned}$$

The signature fixes the structural make-up of the database and its tables. A model represents the data that may be stored in a database w.r.t. to the existing tables, columns and their datatypes. Note that in the interpretation of a table in a model, the same row may appear several times. Thus, tables are interpreted as multisets (also called bags) of rows. The use of multisets may seem overly complicated, because normalised databases cannot have duplicate rows. However, note that not all databases are normalised, and moreover duplicate rows can easily occur within views generated by queries.

For a set X, let $\wp _{multi}(X)$ be the set of finite multisets over X. A finite multiset $B\in \wp _{multi}(X)$ can be understood as a map $B:X\rightarrow \mathbb {N}$ such that $B(x)>0$ only for finitely many $x\in X$. For $x\in X$ and $B\in \wp _{multi}(X)$, let $B\#x$ be the multiplicity of x in B. We write $x\in B$ for the fact that $B\#x>0$. Moreover, we use the abbreviation $\exists ! x\in B.\,\varphi (x)$ for

$$\Big (\sum _{\varphi (x)}B\#x\Big )=1$$

i.e. there exists a unique x in B satisfying $\varphi (x)$, and this x has multiplicity 1. Furthermore, addition on finite multiset is defined element-wise:

$$(B_1+B_2)\#x=B_1\#x+B_2\#x.$$

Finally, inclusion of multisets is defined as $A\subseteq B$ iff for all $x\in X$, $A\#x\le B\#x$.

Definition 7

(Models). Given a signature $\varSigma$, an object of the model category $\mathbf{Mod }{(\varSigma )}$ is a function mapping tables to multisets of functions that map columns to elements of the datatype model, formally $M: t \in \mathbb {T}^{\varSigma } \rightarrow \wp _{multi}(c \in \text {col}^{}(t) \rightarrow DM_{\tau ^{}(t,c)})$, such that for each $t \in \mathbb {T}^{\varSigma }$ with $pk ^{\varSigma }(t)=\{c_1,\ldots ,c_n\}\ne \emptyset$

• $r(c_i)\ne null _{DM}$ for each row $r \in M(t)$ and $i=1,\ldots ,n$, and

• for all rows $r_1 \in M(t)$,

  $$\exists !r_2\in M(t).\, r_1(c_1)=r_2(c_1)\wedge \cdots \wedge r_1(c_n)=r_2(c_n)$$

Note that in presence of the satisfaction relation introduced below, these conditions could be rephrased as

• $M \models \{ notnull (t.c_1), \ldots , notnull (t.c_n) \}$

• $M \models un (t.c_1,\ldots ,t.c_n)$

Morphisms in the category of models represent inclusion of data multisets.

Definition 8

(Model Morphisms). Given a signature $\varSigma$, the model category $\mathbf{Mod }{(\varSigma )}$ is a partially ordered set, where $M_1\le M_2$ iff for each $t \in \mathbb {T}^{\varSigma }$, $M_1(t)\subseteq M_2(t)$.

Definition 9

(Model Reducts). Given a signature morphism $\sigma : \varSigma \rightarrow \varSigma '$ and a $\varSigma '$-model $M'$ and a table $t\in \mathbb {T}^{\varSigma }$, a row $r':(c' \in \text {col}^{}(\sigma _{\mathbb {T}^{}}(t)))\rightarrow DM_{\tau ^{}(\sigma _{\mathbb {T}^{}}(t),c')})$ can be reduced to a row $r' | _\sigma :(c \in \text {col}^{}(t))\rightarrow DM_{\tau ^{}(t,c)})$ by defining

$$r' | _\sigma (c)=r'(\sigma _{\textit{col},t}(c)) \textit{ for }c \in \text {col}^{\varSigma }(t).$$

Then $M' | _\sigma$, the reduction of $M'$ against $\sigma$, is defined by

$$\begin{aligned} \forall t \in \mathbb {T}^{\varSigma }, M' | _\sigma (t)\#r = \sum _{r' | _\sigma =r} M'(\sigma _{\mathbb {T}^{}}(t))\#r' \end{aligned}$$

(1)

for all $r:(c \in \text {col}^{}(t))\rightarrow DM_{\tau ^{}(t,c)})$. Note that $M' | _\sigma (t)\#r=0$ in case there is no $r'\in M'(\sigma _{\mathbb {T}^{}}(t))$ with $r' | _\sigma =r$. From M satisfying the primary key and not-null constraints of $\varSigma '$, it is straightforward to see that $M' | _\sigma$ satisfies those of $\varSigma$.

It is easily seen that reducts preserve the partial order on models; hence they are functorial.

Fig. 1.

Boolean operations in SQL’s 3-valued logic

Definition 10

(Satisfaction Relation). For every $M \in \mathbf{Mod }(\varSigma )$ the satisfaction relation is defined depending on the structure the sentence:

• $M \mathrel {\models ^{\mathcal {}}_{\varSigma }} notnull (t.c)$ iff $r(c)\ne null _{DM}$ for each row $r \in M(t)$

• $M \mathrel {\models ^{\mathcal {}}_{\varSigma }} un (t.c_1,\ldots ,t.c_n)$ iff for all rows $r_1 \in M(t)$,

  $$\exists !r_2\in M(t).\, r_1(c_1)=r_2(c_1)\wedge \cdots \wedge r_1(c_n)=r_2(c_n)$$

• $M \mathrel {\models ^{\mathcal {}}_{\varSigma }} fk ((t.c_1,u.d_1),\ldots ,(t.c_n,u.d_n))$ iff for all $r_1 \in M(t)$ there is exactly one $r_2 \in M(u)$ such that $r_1(c_i) = r_2(d_i)$ for $i=1,...,n$

• $M \mathrel {\models ^{\mathcal {}}_{\varSigma }} ck _t(\varphi )$ iff for all $r \in M(t)$, $\mathopen \llbracket \varphi \mathclose \rrbracket ^M_{\nu (r)}\in \{\mathsf {T}, \mathsf {U}\}$, where for $r \in M(t)$, $\nu (r)$ is the valuation defined by $\nu (t.c)=r(c)$ for all $c\in col(t)$.

Here, $\mathopen \llbracket \varphi \mathclose \rrbracket ^{DM}_\nu$ is the evaluation of the term $\varphi$ in the model DM using a valuation $\nu$ of the free variables, defined inductively in a standard way, where Boolean connectives are interpreted as shown in Fig. 1. Note that since $\mathopen \llbracket \varphi \mathclose \rrbracket ^{DM}_\nu$ is of sort $Bool$, $\mathopen \llbracket \varphi \mathclose \rrbracket ^{DM}_\nu \in \{\mathsf {T},\mathsf {F},\mathsf {U}\}$.

While internally, our institution $\mathcal {SQL}{(D\varSigma ,DM)}$ uses a three-valued logic for the semantics of integrity constraints, ultimately, it is a two valued logic. This is achieved by considering sentences evaluating to $\mathsf {T}$ or $\mathsf {U}$ (the designated truth values, in standard many-valued logic terminology [17]) to hold, and considering those evaluating to $\mathsf {F}$ as not to hold. (When eliminating $\mathsf {U}$ in the first place, one would obtain a different logic.) Further note that for conditions in queries, SQL takes $\mathsf {T}$ as the only designated truth value, see Sect. 3 below. This means that queries impose a stricter regime than integrity constraints, which is pragmatically motivated: missing data should not lead to violation of an integrity constraint, while in queries, all mentioned data should be present.

Proposition 1

(Satisfaction condition). Let $\sigma :\varSigma \rightarrow \varSigma '$ be a signature morphism between two database signatures. For all $\varSigma '$-models $M'$ and $\varSigma$-constraints $\varphi$ the following holds:

$$ M' | _\sigma \models \varphi \quad \Leftrightarrow \quad M' \models \sigma (\varphi ) $$

Proof

Let $M'$ be a $\varSigma '$-model and $\varphi$ a $\varSigma$-sentence. The satisfaction follows directly from the fact that model reducts do not alter the data contained in the tables, apart from altering table and column names:

• case $\varphi = notnull (t.c)$ :

  

• case $\varphi = un (t.c_1,\ldots ,t.c_n)$ :

  

• case $\varphi = fk ((t.c_1,u.d_1),\ldots ,(t.c_n,u.d_n))$ :

  

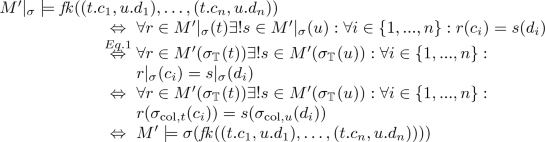
Concerning check constraints, one can prove by induction over $\varphi$ that

$$\mathopen \llbracket \varphi \mathclose \rrbracket ^{DM}_{\nu (r | _\sigma )}=\mathopen \llbracket \sigma (\varphi )\mathclose \rrbracket ^{DM}_{\nu (r)} $$

From this, the satisfaction condition for check constraints follows using Eq. 1.    $\square$

This completes the definition of the institution $\mathcal {SQL}{(D\varSigma ,DM)}$.

3 Queries and Views

Our institution $\mathcal {SQL}(D\varSigma ,DM)$ provides a formalisation of SQL database schemas as logical theories in that institution. Now an important feature of SQL is of course the Data Query Language (DQL). Queries cannot be directly represented as logical formulas in the institution, because as an answer, they deliver data and not just logical truth values. Therefore, formalisations for dealing with Prolog-style queries in an institutional setting usually use generalised substitutions [3, 5] or derived signature morphisms. The latter are a generalised version of signature morphisms that may map signature symbols not only to other such symbols, but also to complex terms and expressions [13, 19]. Then Prolog-style queries can be formalised as open sentences and their answer substitutions as derived signature morphisms⁴.

However, it turns out that queries in SQL are different from Prolog-style queries. Indeed, SQL queries do not provide answer substitutions that map variables to terms, and so they cannot naturally be extended to a translation of sentences either. This is because SQL queries have a rich syntax, which in general cannot be reflected in SQL sentences (constraints). Instead, SQL queries provide a mapping of databases, i.e. models (see also Table 1). Compared of abstract substitutions [3, 5], the syntactic half of the structure is missing. This means we would need to use abstract semi-substitutions. However, we follow a slightly different path. Namely we use Kleisli morphisms in an institutional monad as an institution-independent formalisation of derived signature morphisms. Queries can then be formalised as such Kleisli morphisms, and materialised views (answer to queries) are reducts against these. Moreover, Kleisli composition gives a means to compose queries, which is also called query unfolding in database terminology [6].

Table 1. Different types of queries

The notion of institutional monad [13] has been introduced for formalising the notion of derived signature morphism in an arbitrary institution; we weaken it here to the notion of semi-institutional monad, based on the notion of institution semi-morphism. We first recall the latter. Institution semi-morphisms relate two institutions by relating their signatures and models, while sentences are not related. This is useful if the institutions are semantically related, but differ too much in their sentences to have a full institution morphism between them.

Definition 11

([10]). Given institutions $\mathcal {I}$ and $\mathcal {J}$, an institution semi-morphism $\mu =(\varPhi ,\beta ):\mathcal {I}\!\longrightarrow \!\mathcal {J}$ consists of

• a functor $\varPhi :\mathbf{Sign }^{\mathcal {I}}\!\longrightarrow \!\mathbf{Sign }^{\mathcal {J}}$ and

• a natural transformation $\beta :\mathbf{Mod }^{\mathcal {I}}\!\longrightarrow \!\varPhi ^{op};\mathbf{Mod }^{\mathcal {J}}$.

Definition 12

([5]). Given two institution semi-morphisms $\mu _1,\mu _2:\mathcal {I}\!\longrightarrow \!\mathcal {J}$ with $\mu _i=(\varPhi _i,\beta _i)$, a (discrete) institution semi-morphism modification $\tau :\mu _1\!\longrightarrow \!\mu _2$ is a natural transformation $\tau :\varPhi _1\!\longrightarrow \!\varPhi _2$ such that

commutes.

Definition 13

(Semi-institutional monad). Let $\mathcal {I}$ be an institution. A semi-institutional monad $(T,\eta ,\mu )$ consists of

• An institution semi-morphism $T: \mathcal {I} \rightarrow \mathcal {I}$

• A institution semi-morphism modification $\eta : id \rightarrow T$ (the unit of the monad)

• A institution semi-morphism modification $\mu : TT\rightarrow T$ (the multiplication of the monad)

such that the usual laws of a monad are satisfied:

The semi-institutional monad for the SQL data query language can now be sketched as follows. The institution semi-morphism $(\varPhi ,\beta ): \mathcal {SQL}(D\varSigma ,DM)\rightarrow \mathcal {SQL}(D\varSigma ,DM)$ of the semi-institutional monad maps a signature $\varSigma$ to $\varPhi (\varSigma )$, which extends $\varSigma$ with tables q, where q is an SQL query over $\varSigma$. The tables q are also called views, because the table resulting from a query represents a new view on the database. Resulting in such a view, an SQL query naturally has an associated set of (result) columns (=materialised view), this will act as q’s set of columns in $\varPhi (\varSigma )$. q will not have a primary key. $\beta$ maps an SQL-model (aka database) M into the model $\beta _\varSigma (M)$ which interprets each query q as the multiset of solutions of q over M. The monad unit $\eta _\varSigma$ is simply the inclusion of $\varSigma$ into $\varPhi (\varSigma )$. The monad multiplication $\mu _\varSigma$ maps queries over queries to normal SQL queries. This is straightforward, because SQL allows to insert queries in positions where tables can occur (after all, views are special forms of tables), which is a form of query composition.

Since SQL is a rich language, the detailed formalisation of the complete SQL query language along the lines sketched above is beyond the scope of this paper. Instead, we concentrate on one particular form of SQL query, involving select, where and join. In a system, information is often distributed amongst multiple tables in order to prevent redundancies. In order to retrieve distributed data multiple tables can be joined into a view, using a query. When employing this restriction on queries, the above sketched semi-institutional monad can be detailed as follows, where the monad action given by the institution semi-morphism is denoted as $T= (\varPhi , \beta )$:

• The signature functor $\varPhi :\mathbf{Sign }^{\mathcal {SQL}} \rightarrow \mathbf{Sign }^{\mathcal {SQL}}$ extends a signature $\varSigma$ by tables of form

  $$\begin{aligned} t_1 \times \cdots \times t_n|_{\varphi _1,\ldots ,\varphi _k} \rightarrow c_1 \blacktriangleright e_1,\ldots , c_m \blacktriangleright e_m\end{aligned}$$

  written in SQL notation as

  

  where $t_1,\ldots ,t_n \in \mathbb {T}^{\varSigma }$, $\varphi _1,\ldots ,\varphi _k$ are check constraints with the columns of $t_1,\ldots ,t_n$ as variables, $c_1,\ldots ,c_m$ are new column names, and each $c_i$ is attached with a $\lambda$-expression $e_i$

  $$ \lambda ( t_1.c_1,\ldots ,t_1.c_{n_1},\ldots ,t_n.c_1,\ldots ,t_n.c_{n_m}).t $$

  that specifies the computation rules for this column depending on all columns of the joined tables. The type of t is called result type of $e_i$. The columns of these tables are given as

  $$ \text {col}^{}(t_1 \times \cdots \times t_n|_{\varphi _1,\ldots ,\varphi _k} \rightarrow c_1 \blacktriangleright e_1,\ldots , c_m \blacktriangleright e_m) = \{c_1,\ldots , c_m\}. $$

  Sorts of columns are set w.r.t to the column expressions:

  $$ \tau ^{}(t_1 \times \cdots \times t_n|_{\varphi _1,\ldots ,\varphi _k} \rightarrow c_1 \blacktriangleright e_1,\ldots , c_m \blacktriangleright e_m,c_i) = s_i $$

  where $s_i$ is the result type of $e_i$.

• $\beta _\varSigma (M)$ preserves the models behaviour on tables from $\varSigma$, i.e. $\beta _\varSigma (M)(t) = M(t)$ for $t \in \mathbb {T}^{\varSigma }$. In order to construct the interpretation of the new tables in $\varPhi (\varSigma )$, we define $e_i(r_1, \ldots ,r_n)$ as the evaluation of an expression $e_i$ ($i=1,\ldots ,m$) w.r.t. to rows $r_1,\ldots , r_n$, i.e.

  $$\begin{aligned}&e_i(r_1, \ldots ,r_n) := \\&\qquad \quad \quad \, (\lambda ( c_1^1,\ldots ,c_{m_1}^1,\ldots ,c_1^n,\ldots ,c_{m_n}^n).t)(r_1(col(t_1)),\ldots ,r_n(col(t_n))) \end{aligned}$$

  Each of the constructed rows has to conform to the constraints specified in $\varphi _1,\ldots ,\varphi _k$. This can be easily guaranteed by checking whether the model $M^{r_1,\ldots ,r_m}$ satisfies the set of constraints $(\varphi _1,\ldots ,\varphi _k)$ where $M^{r_1,\ldots ,r_n}$ contains just the row $r_i$ for each table $t_i$ ($i=1,\ldots ,n$) and no data for other tables. For a table $t=t_1 \times \cdots \times t_n|_{\varphi _1,\ldots ,\varphi _k} \rightarrow c_1 \blacktriangleright e_1,\ldots , c_m \blacktriangleright e_m$ we construct the dataset as the evaluations of the corresponding column expressions:

  

  Here $\nu _{r(\varphi _j)}$ is the valuation determined by the unique row $r_i$ in table $t_i$, where $t_i$ is the table over which $\varphi _j$ has been formulated. As stated above (after Definition 10), for constraints in queries, $\mathsf {T}$ is the only designated truth value.

• $\eta _\varSigma$ is the inclusion

• $\mu _\varSigma$ maps tables by collapsing an (outer) query over (inner) queries into a simple query. The result is the outer query, modified by substituting $\lambda$-terms for the inner queries into the column variables in $\lambda$-terms and check constraints of the outer query, and adding check constraints of the inner queries.

Example 5

The tables from Example 1. A query

would correspond to the table in the monad

$$ \begin{array}{l} \texttt {Person} \times \texttt {Employee}|_{\texttt {Employee.pid = Person.id}, \texttt {Employee.salary>= 10000}}\rightarrow \\ \texttt {salary} \blacktriangleright e_1, \texttt {fname} \blacktriangleright e_2, \texttt {lname} \blacktriangleright e_3 \end{array} $$

where

$$ \begin{array}{lcl} e_1 &{}=&{} \lambda \texttt {p\_id}, \texttt {p\_fname}, \texttt {p\_lname}, \texttt {e\_id}, \texttt {e\_salary}, \texttt {e\_pid.e\_salary} \\ e_2 &{}=&{} \lambda \texttt {p\_id}, \texttt {p\_fname}, \texttt {p\_lname}, \texttt {e\_id}, \texttt {e\_salary}, \texttt {e\_pid.e\_fname} \\ e_3 &{}=&{} \lambda \texttt {p\_id}, \texttt {p\_fname}, \texttt {p\_lname}, \texttt {e\_id}, \texttt {e\_salary}, \texttt {e\_pid.e\_lname} \\ \end{array} $$

In the sequel, we work with an arbitrary but fixed semi-institutional monad $(T,\eta ,\mu )$ over an institution $\mathcal {I}$ (with $T=(\varPhi ,\beta )$). We can define several derived notions:

Definition 14

(Kleisli semi-institution, adapted from [13]). The Kleisli signature category has a objects $\mathcal {I}$-signatures, and its morphisms $\varSigma _1\rightarrow \varSigma _2$ are $\mathcal {I}$-signature morphisms $\varSigma _1\rightarrow \varPhi (\varSigma _2)$. Kleisli composition is defined by

Model categories are inherited from $\mathcal {I}$. Model reduct against $\sigma :\varSigma _1\rightarrow \varPhi (\varSigma _2)$ is given by $\beta _{\varSigma _2};\mathbf{Mod }^{\mathcal {I}}(\sigma )$. This gives a semi-institution in the sense of Definition 2.

Due to the “semi”-nature of the monad, we do not have sentence translations along Kleisli signature morphisms. This reflects the fact that queries use a much more powerful language than constraints, and constraints are not closed under queries.

Queries are just Kleisli signature morphisms:

Definition 15

(Query). A query is a signature morphism $q:\varSigma ^Q\rightarrow \varPhi (\varSigma )$.

Here, $\varSigma ^Q$ typically is a “small” or “singleton” signature. In the case of $\mathcal {SQL}(D\varSigma ,DM)$, $\varSigma ^Q$ will typically consist of a single table only, providing a name and column types for the result of the query. The query itself is then given by $q(\varSigma ^Q)$, which singles out one particular query in the space $\varPhi (\varSigma )$ of all $\varSigma$-queries. The semantics of a query q as above is given by the Kleisli reduct $\beta _{\varSigma };\mathbf{Mod }^{\mathcal {I}}(q)$, mapping $\varSigma$-models (aka $\varSigma$-databases) to $\varSigma ^Q$-models (aka materialised views of signature $\varSigma ^Q$).

Two queries $q_1,q_2:\varSigma ^Q\rightarrow \varPhi (\varSigma )$ are equivalent [6] if their semantics agree, i.e. $\beta _{\varSigma };\mathbf{Mod }(q_1)=\beta _{\varSigma };\mathbf{Mod }(q_2)$. $q_1$ is contained in $q_2$ if for each $M\in \mathbf{Mod }(\varSigma )$, there is a model monomorphism $\beta _{\varSigma }(M) | _{q_1}\rightarrow \beta _{\varSigma }(M) | _{q_2}$.⁵

Next, we consider composition of queries, also known as query unfolding, which is an important tool for data base integration [6]. Given two queries $q_1:\varSigma ^Q_1\rightarrow \varPhi (\varSigma _1)$ and $q_2:\varSigma ^Q_2\rightarrow \varPhi (\varSigma _2)$, we cannot compose them directly. Rather, we have (assuming the existence of signature coproducts) to assume that the first query is built over the second database enriched with the result of the second query, i.e. that $\varSigma _1=\varSigma ^Q_2+\varSigma _2$. Then we can pair the second query with $\eta$ and take the Kleisli composition

We can also obtain a semi-substitution from a query. Substitutions have been introduced in [3, 5]. They run between variable sets that are represented as signature morphisms (extending a base signature with some constants playing the role of variables). We weaken the notion as follows:

Definition 16

Given two signature morphisms (“variable sets”) $\chi _1:\varSigma \rightarrow \varSigma _1$ and $\chi _2:\varSigma \rightarrow \varSigma _2$, a $\varSigma$-semi-substitution $\psi :\chi _1\rightarrow \chi _2$ is a functor

$$\mathbf{Mod }(\psi ):\mathbf{Mod }(\varSigma _2)\rightarrow \mathbf{Mod }(\varSigma _1)$$

such that the following diagram commutes:

For a query $q:\varSigma ^Q\rightarrow \varPhi (\varSigma )$, we consider the coproduct injection $\iota _1:\varSigma \rightarrow \varSigma +\varSigma ^Q$ as “variable set”, and define the semi-substitution $\psi :\iota _1\rightarrow 1_\varSigma$ via

Commutativity of the above diagram for semi-substitutions is ensured by the modification property of $\eta$ (see Definition 12).

Another view on (general) Kleisli morphisms is that they correspond to (complex) schema mappings [22], because they map table names to queries. This means that we can compose schema mappings, and also (via the Kleisli model functor) compute their semantics.

4 Database Integration via Colimits

The formalisation of SQL databases as an institution allows the use of colimits for database integration.

Proposition 2

Consider finite diagram $D:I\rightarrow \mathbf{Sign }^{\mathcal {SQL}}$, where for any span in I with $j\ne k$ and any $t\in \mathbb {T}^{D(i)}$, the following holds: if $D(m)_{\mathbb {T}^{}}(t)$ and $D(n)_{\mathbb {T}^{}}(t)$ both have a primary key, then so does t. Then D has a colimit.

Proof

Let a finite diagram $D:I\rightarrow \mathbf{Sign }^{\mathcal {SQL}}$ with the above property be given. We construct its colimit signature $\varSigma$ together with colimit injections $(\mu _i:D(i)\rightarrow \varSigma )_{i\in |I|}$ as follows. Let $D_{\mathbb {T}^{}}$ be the projection of D to tables and table translations. Then let $\mathbb {T}^{\varSigma }$ be the colimit of $D_{\mathbb {T}^{}}$ (in $\mathbf {Set}$), and let $(\mu _i)_{\mathbb {T}^{}}:\mathbb {T}^{D(i)}\rightarrow \mathbb {T}^{\varSigma }$ (for $i\in |I|$) be the colimit injections. This gives us the table part of the colimit. Concerning the column part, let $\mathbb {S}^{D\varSigma }\text {-}\mathbf {Set}$ be the category of $\mathbb {S}^{D\varSigma }$-sorted sets, which is given by the comma category $\mathbf {Set}\downarrow \mathbb {S}^{D\varSigma }$. For a table $t\in \mathbb {T}^{\varSigma }$, we construct a diagram of $\mathbb {S}^{D\varSigma }$-sorted column sets as follows. The index category $I_t$ has objects

$$|I_t|=\{(i,u)\mid u\in \mathbb {T}^{D(i)},(\mu _i)_{\mathbb {T}^{}}(u)=t\},$$

i.e. the set of tables that are mapped (by some colimit injection) to t. $I_t$ has a morphism $m:(i,u_1)\rightarrow (j,u_2)$ whenever $m:i\rightarrow j\in I$ and $D(m)_{\mathbb {T}^{}}(u_1)=u_2$. The diagram functor $D_t:I_t\rightarrow \mathbb {S}^{D\varSigma }\text {-}\mathbf {Set}$ acts on objects as

$$D_t(i,u)=\text {col}^{D(i)}(u),$$

which is $\mathbb {S}^{D\varSigma }$-sorted using $\tau ^{D(i)}(u,\cdot )$, and on morphisms as

$$D_t(m:(i,u_1)\rightarrow (j,u_2))=D(m)_{\text {col},u_1}:\text {col}^{D(i)}(u_1)\rightarrow \text {col}^{D(j)}(u_2)$$

Let $(C_t,(\theta ^t_{(i,u)})_{(i,u)\in |I_t|})$ be the colimit of $D_t$ in $\mathbb {S}^{D\varSigma }\text {-}\mathbf {Set}$ (recall that colimits in comma categories are constructed component-wise). Then $C_t$ is the sorted set of columns of table t in $\varSigma$. The column translation of $\mu _i:D(i)\rightarrow \varSigma$ is given by

$$(\mu _i)_{\text {col},u}=\theta ^{(\mu _i)_{\mathbb {T}^{}}(u)}_{(i,u)} \qquad (u\in \mathbb {T}^{D(i)}).$$

Finally, the primary key of C(t) is determined as $(\mu _i)_{\text {col},u}( pk ^{D(i)}(u))$ for any $(i,u)\in |I_t|$ with $pk ^{D(i)}(u)\ne \emptyset$. Since any two such (i, u) are connected via a zigzag path in $I_t$, the assumption about spans in I together with preservation of primary keys along signature morphisms ensures that this is independent of the choice of (i, u). This completes the construction of the colimit $(\varSigma ,(\mu _i:D(i)\rightarrow \varSigma )_{i\in |I|})$. Its universal property follows from the universal properties of the colimits involved in its construction.    $\square$

Example 6

Coproducts put database tables side by side:

Here, signature morphisms are inclusions.

An integration of tables can be achieved using pushouts:

Example 7

Here, signature morphisms map tables in the unique way and leave columns as they are. If table Person has primary key name, then this is also the primary key in the colimit. However, if Person does not have a primary key, but Birthdate and Address have one consisting of both of their respective columns, then the diagram does not have a colimit, because its primary key cannot be determined.

Since tables in one signature do not interact, the same effect can also be achieved with a coequaliser

Example 8

Here, signature morphisms leave columns as they are. For table Person, at the table level, we have the coequaliser (in $\mathbf {Set}$)

At the column level, we obtain a pushout

So the coequaliser involves a coequaliser at the level of tables plus a pushout at the level of columns.

The amalgamation property is a major technical assumption in the study of specification semantics [18] and is important in many respects. For example, it allows the computation of normal forms for specifications [2], and it is a prerequisite for good behaviour w.r.t. parameterization [8] and conservative extensions [4] and for soundness of proof systems for structured specification [15]. Intuitively, amalgamation of databases is just a rearrangement of the (partially shared) tables.

Definition 17

A cocone for a diagram in $\mathbf{Sign }^{\mathcal {I}}$ is called (weakly) amalgamable if it is mapped to a (Weak) limit under $\mathbf{Mod }^{\mathcal {I}}$. This can be characterised in more elementary terms as follows: Given a diagram $D:I\!\longrightarrow \!\mathbf{Sign }^{\mathcal {I}}$, a family of models $(M_i)_{i\in |I|}$ is called D-consistent if $M_j | _{D(m)}=M_i$ for each $m:i\!\longrightarrow \!j\in I$. Then a cocone $(\varSigma ,(\mu _i)_{i\in |I|})$ over the diagram in $D:I\!\longrightarrow \!\mathop {\mathbf{Sign }}^I$ is weakly amalgamable if for each D-consistent family of models $(M_i)_{i\in |I|}$, there is a $\varSigma$-model M with $M | _{\mu _i}=M_i$ ($i\in |I|$) (and moreover, an analogous condition holds for model morphisms). In case M is unique with these properties, the cocone is amalgamable.

An institution $\mathcal {I}$ admits (weak) finite amalgamation if all finite colimit cocones are (weakly) amalgamable.

Proposition 3

For colimit cocones as in Proposition 2, $\mathcal {SQL}(D\varSigma ,DM)$ admits weak finite amalgamation, and if all diagram signatures have a primary key, then also finite amalgamation.

Proof

Let $(\varSigma ,(\mu _i)_{i\in |I|})$ be a colimit cocone as in Proposition 2. Moreover, let $(M_i)_{i\in |I|}$ a D-consistent family of models. We need to define its amalgamation $M\in \mathbf{Mod }^{\mathcal {SQL}}(\varSigma )$. Given $t\in \mathbb {T}^{\varSigma }$, consider the diagram $D_t:I_t\rightarrow \mathbb {S}^{D\varSigma }\text {-}\mathbf {Set}$ defined in the proof of Proposition 2. Recall that $\text {col}^{\varSigma }(t)$ is the colimit of this diagram. The carrier sets of the model DM form an $\mathbb {S}^{D\varSigma }$-sorted set |DM|, and any row is an $\mathbb {S}^{D\varSigma }$-sorted map into |DM|. Hence, any compatible family of rows $(r_{(i,u)}\in M_i(u))_{(i,u)\in |I_t|}$ is a cocone for $D_t$, and by the colimit property of $\text {col}^{\varSigma }(t)$, it can be amalgamated to a row $r:(c \in \text {col}^{}(t))\rightarrow DM_{\tau ^{}(t,c)}$. If all diagram signatures have a primary key, then let $M(t)\#r=1$ for any such r, and M is the unique amalgamation. If not, then proceed with the following algorithm (working on a copy of $(M_i)_{i\in |I|}$ that is modified):

• 1. initially, set all multiplicities $M(t)\#r$ to 0.

• 2. Choose a compatible family of rows $(r_{(i,u)}\in M_i(u))_{(i,u)\in |I_t|}$, and for its amalgamation r, increase $M(t)\#r$ by one.

• 3. Decrease the multiplicities $M_i(u)\#r_{(i,u)}$ by one.

• 4. Repeat steps 2 and 3 until all multiplicities $M_i(u)\#r_{(i,u)}$ are zero. By Eq. 1, all $M_i(u)\#r_{(i,u)}$ will reach zero simultaneously.    $\square$

By very general results [10, 19], Propositions 2 and 3 carry over from signatures to presentations, i.e. signatures equipped with axioms, e.g. foreign key constraints.

5 Conclusion

We presented an institutional approach towards a formalisation of relational databases and their integration via colimits and amalgamation. Building on a foundation of a many-sorted first-order structure, the signatures and sentences reflect SQL’s Data Description Language, including tables, their columns and various constraints. The models of this institution capture the data that can be stored in those tables. Queries on a database can be formalised as a semi-institutional monad. Syntactic and semantic components of this institution were designed to closely follow those used in SQL, which allows an easy application of this new formalisation to existing database-related tools.

Many other categorical approaches define a new query language (e.g. FQL [24]). This limits the frictionless application of those approaches in real-world scenarios, as SQL is used in most software solutions that involve database communication. Therefore, we designed the presented institutional formalisation of databases to closely reflect the existing structures from the SQL specification.

Many open questions remain, e.g. whether model reducts have left and right adjoints as in [22], or whether colimits can be expressed as queries. Also, the existence of colimits in the Kleisli category should be studied, because these correspond to database integrations using queries. Note that by the results of [13], these colimits do not always exist.

Future work should also investigate the manipulation of data by insert and delete statements. Model morphisms could be used to capture a structure similar to those used in a categorical theory of patches [12], which may yield a logical framework for version tracking of databases.

Operations that involve multiple tables are present in most database-related application. The introduction of a suitable institutional semi-monad (and its Kleisli morphisms) enhances the presented institution for databases with functionalities such as inner joins that combine multiple tables. Yet, the current formalisation allows only inner joins. Full formalisations of all different types of joins (e.g. left join, outer join) and other principles (e.g. aggregations, unions) are yet to be done. The introduction of other join types can be achieved by introducing multiple join operators with appropriate model interpretations. A similar approach could be chosen for unions. Aggregations will pose a tougher problem. They require an adaption of the notion of reduct of a Kleisli morphism, because a single row in a query result would stem from multiple rows of a single base table.

Institutions were defined as a framework that allows integration of different logics. Similarly, one may define institution comorphisms [9] to different logics (including logics for algebraic databases) and thus open the doors for the vast and powerful landscape of logic reasoning tools. The Heterogeneous tool set (Hets) [14] offers functionalities for reasoning and proving not only across logics, but also integrates languages like UML. The integration of the SQL-institution into this tool set can be a step towards a logics-founded approach for model-driven development for databases with automated checks for coherence. Integration of queries could be done by representing Kleisli morphisms⁶, implementing their composition as well as checks for query containment and equivalence.