Abstract
To divide the definite integral
into several others of the same type, it suffices to decompose into several parts, either the function under the \(\int \) sign or the difference \( X-x_0. \ \) First, let us suppose
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
If Cauchy is supposing a finite series, this step is fine. Otherwise, he needs to be more careful with this claim. Cauchy’s “passing to the limits” is assuming the limit of a sum is equivalent to the sum of the individual limits. This step actually requires an exchange of limits operation which is only allowed under certain restrictions—the details of which were not worked out until later in the 19th century.
- 2.
The 1899 edition has \(X_0\) instead of X for the lower limit in its final integral to the right. This error does not occur in the original 1823 version.
- 3.
Cauchy is going to geometrically connect his definite integral to the area under a curve, something he has kept away from doing until now.
- 4.
Cauchy is using one of the average theorem results found in his Cours d’analyse text. In this case, he employs Theorem I from his Preliminaries, restated with an accompanying proof as Theorem XII in Note II at the end of his 1821 text. Cauchy also uses this result in Lecture Seven to help prove his Mean Value Theorem for Derivatives. Because of its important role in these Calcul infinitésimal lectures, a full translation of his Cours d’analyse Note II, Theorem XII—along with its proof—is included as Appendix B at the end of this book for reference.
- 5.
This “remarkable” property of the definite integral is known today as the General Mean Value Theorem for Definite Integrals. It is indeed remarkable.
- 6.
There are two significant mistakes here. In the 1899 text, the last equation reads,
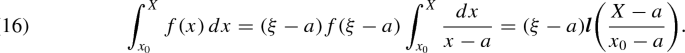
Interestingly, the original 1823 text is different, but is also incorrect. In this earlier edition, the equation reads,
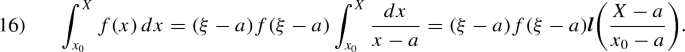
A corrected version of (16) is given here.
- 7.
Cauchy is referring to the Mean Value Theorem for Definite Integrals, a special case of the remarkable version derived earlier.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Cates, D.M. (2019). DECOMPOSITION OF A DEFINITE INTEGRAL INTO SEVERAL OTHERS. IMAGINARY DEFINITE INTEGRALS. GEOMETRIC REPRESENTATION OF REAL DEFINITE INTEGRALS. DECOMPOSITION OF THE FUNCTION UNDER THE \(\int \) SIGN INTO TWO FACTORS IN WHICH ONE ALWAYS MAINTAINS THE SAME SIGN.. In: Cauchy's Calcul Infinitésimal. Springer, Cham. https://doi.org/10.1007/978-3-030-11036-9_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-11036-9_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11035-2
Online ISBN: 978-3-030-11036-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)