Abstract
We introduce a new cryptographic primitive called signatures with flexible public key \((\mathsf{SFPK})\). We divide the key space into equivalence classes induced by a relation \(\mathcal {R}\). A signer can efficiently change his or her key pair to a different representatives of the same class, but without a trapdoor it is hard to distinguish if two public keys are related. Our primitive is motivated by structure-preserving signatures on equivalence classes (\(\mathsf{SPS\text {-}EQ}\)), where the partitioning is done on the message space. Therefore, both definitions are complementary and their combination has various applications.
We first show how to efficiently construct static group signatures and self-blindable certificates by combining the two primitives. When properly instantiated, the result is a group signature scheme that has a shorter signature size than the current state-of-the-art scheme by Libert, Peters, and Yung from Crypto’15, but is secure in the same setting.
In its own right, our primitive has stand-alone applications in the cryptocurrency domain, where it can be seen as a straightforward formalization of so-called stealth addresses. Finally, it can be used to build the first efficient ring signature scheme in the plain model without trusted setup, where signature size depends only sub-linearly on the number of ring members. Thus, we solve an open problem stated by Malavolta and Schröder at ASIACRYPT’2017.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Digital signatures aim to achieve two security goals: integrity of the signed message and authenticity of the signature. A great number of proposals relax these goals or introduce new ones to accommodate the requirements of specific applications. As one example, consider sanitizable signatures [1] where the goal of preserving the integrity of the message is relaxed to allow for authorized modification and redactions of the signed message.
The primitive we introduce in this work allows for a relaxed characterization of authenticity instead. The goal is not complete relaxation, such that an impostor could sign messages on behalf of a legitimate signer, but rather that authenticity holds with respect to some established legitimate signer, but who it is exactly remains hidden.
The new primitive, called signatures with flexible public key (\(\mathsf{SFPK}\)) formalizes a signature scheme, where verification and signing keys live in a system of equivalence classes induced by a relation \(\mathcal {R}\). Given a signing or verification key it is possible to transform the key into a different representative of the same equivalence class, i.e., the pair of old key and new key are related via \(\mathcal {R}\). Thus, we extend the requirement of unforgeability of signatures to the whole equivalence class of the given key under attack.
Additionally, it should be infeasible, without a trapdoor, to check whether two keys are in the same class. This property, which we call computational class-hiding, ensures that given an old verification key, a signature under a fresh representative is indistinguishable from a signature under a different newly generated key, which lives in a different class altogether with overwhelming probability. Intuitively this means that signers can produce signatures for their whole class of keys, but they cannot sign for a different class (because of unforgeability) and they are able to hide class to which the signature belongs to, i.e., to hide their own identity in the signature (because of class-hiding). This primitive is motivated by (structure-preserving) signatures on equivalence classes [29] (\(\mathsf{SPS\text {-}EQ}\)), where relations are defined for the message space, instead of the key space. Both notions are complementary, in the sense that we can use \(\mathsf{SPS\text {-}EQ}\) to certify the public key of an \(\mathsf{SFPK}\) scheme if the respective equivalence relations are compatible, which immediately gives so called signatures with self-blindable certificates [40].
Signatures with flexible public key are especially useful in applications where there is a (possibly pre-defined) set of known verification keys and a verifier only needs to know that the originator of a given signature was part of that set. Indeed, upon reading the first description of the scheme’s properties, what should come to mind immediately is the setting of group signatures [18] and to some extent ring signatures [36] where the group is chosen at signing time and considered a part of the signature. Our primitive yields highly efficient, cleanly constructed group and ring signature schemes, but it should be noted, that \(\mathsf{SFPK}\) on its own is neither of the two.
The basic idea to build a group signature scheme from signatures with flexible public key is to combine them with an equally re-randomizable certificate on the signing key. Such a certificate is easily created through structure-preserving signatures on equivalence classes by the group manager on the members’ verification key. A group signature is then produced by signing the message under a fresh representative of the flexible public key and tying that signature to the group by also providing a blinded certificate corresponding to the fresh flexible key. This fresh certificate can be generated from the one provided by the group manager. Opening of group signatures is done using the trapdoor that can be used to distinguish if public keys belong to the same equivalence class. In the case of ring signatures with n signers, the certification of keys becomes slightly more complex, since we cannot make any assumption on the presence of a trusted group manager. Therefore, the membership certificate is realized through a perfectly sound proof of membership, which has a size of \(\mathcal {O}(\sqrt{n})\) if we use general proofs and the square matrix idea for membership proofs due to Chandran et al. [15].
Our Contributions. This paper develops a new cryptographic building block from the ground up, presenting security definitions, concrete instantiations and applications. The main contributions are as follows:
- Signatures with flexible public key and their applications. :
-
Our new primitive is a natural counterpart of structure-preserving signatures on equivalence classes, but for the public key space. We demonstrate how \(\mathsf{SFPK}\) can be used to build group and ring signatures in a modularized fashion. For each construction, we give an efficient standard model \(\mathsf{SFPK}\) instantiation which takes into account the differences in setting between group and ring signatures. The resulting group and ring signature schemes have smaller (asymptotic and concrete) signature sizes than the previous state of the art schemes also secure in the strongest attacker model, including schemes with non-standard assumptions.
For instance, the static group signature scheme due to Libert, Peters, and Yung achieves fully anonymous signatures secure under standard non-interactive assumptions at a size of 8448 bits per signature. Our scheme, based on comparable assumptions, achieves the same security using 7680 bits per signature. Another variant of our scheme under an interactive assumption achieves signature sizes of only 3072 bits per signature, thus more than halving the size achieved in [32] and not exceeding by more than factor 3 the size of signatures in the scheme due to Bichsel et al. [7] which produces signatures of size 1280 bits but only offers a weaker form of anonymity under an interactive assumption in the random oracle model. A comprehensive comparison between our scheme and known group signature constructions can be found in Sect. 5.3. Our ring signature construction is the first to achieve signature sizes in \(\mathcal {O}(\sqrt{N})\) without trusted setup and with security under standard assumptions in the strongest security model by Bender et al. [6]. We also show how to efficiently instantiate the scheme using Groth-Sahai proofs and thereby we solve an open problem stated in the ASIACRYPT’2017 presentation of [34], namely: Are there efficient ring signature schemes without trusted setup provably secure under falsifiable assumptions?
- Applications of independent interest. :
-
We also show that signatures with flexible public key which also implement a key recovery property contribute to the field of cryptocurrencies. In particular, our definitions can be seen as a formalization of the informal requirements for a technique called stealth addresses [35, 37, 39], which allows a party to transfer currency to an anonymous address that the sender has generated from the receivers long-term public key. No interaction with the receiver is necessary for this transaction and the receiver can recover and subsequently spend the funds without linking them to their long-term identity. Moreover, existing schemes implementing stealth addresses are based on a variant of the Diffie-Hellman protocol and inherently bound to cryptography based on the discrete logarithm problem. On the other hand, our definition is generic and \(\mathsf{SFPK}\) can potentially be instantiated from e.g. lattice assumptions.
1.1 Related Work
At first glance, signatures with flexible public keys are syntactically reminiscent of structure-preserving signatures on equivalence classes [29]. While both primitives are similar in spirit, the former considers equivalence classes of key pairs while the latter only considers equivalence classes on messages.
There exist many primitives that allow for a limited malleability of the signed message. Homomorphic signatures [10] allow to sign any subspace of a vector space. In particular, given a number of signatures \(\sigma _i\) for vectors \({\varvec{v}}_i\), everyone can compute a signature of \(\sum _{i} \beta _i \cdot {\varvec{v}}_i\) for scalars \(\beta _i\).
Chase et al. [16] discussed malleable signatures, which allow any party knowing a signature of message m to construct a signature of message \(m' = T(m)\) for some defined transformation T. One can consider malleable signatures as a generalization of quotable [2] and redactable signatures [31].
Signatures on randomized ciphertexts by Blazy et al. [8] allow any party that is given a signature on a ciphertext to randomize the ciphertext and adapt the signature to maintain public verifiability.
Verheul [40] introduces so-called self-blindable certificates. The idea is to use the same scalar to randomize the signature and corresponding message. Verheul proposed that one can view the message as a public key, which allows to preserve the validity of this “certificate” under randomization/blinding. However, the construction does not yield a secure signature scheme. We will show that combining our primitive with signatures on equivalence classes [29] can be used to instantiate self-blindable certificates.
As noted above, all the mentioned works consider malleability of the message space. In our case we consider malleability of the key space. A related primitive are signatures with re-randomizable keys introduced by Fleischhacker et al. [22]. It allows a re-randomization of signing and verification keys such that re-randomized keys share the same distribution as freshly generated keys and a signature created under a randomized key can be verified using an analogously randomized verification key.
They also define a notion of unforgeability under re-randomized keys, which allows an adversary to learn signatures under the adversaries’ choice of randomization of the signing key under attack. The goal of the adversary is to output a forgery under the original key or under one of its randomizations. Regular existential unforgeability for signature schemes is a special case of this notion, where the attacker does not make use of the re-randomization oracle.
The difference to signatures with flexible public keys is that re-randomization in [22] is akin to sampling a fresh key from the space of all public keys, while changing the representative in our case is restricted to the particular key’s equivalence class. Note that one might intuitively think that signatures under re-randomizable keys are just signatures with flexible keys where there is only one class of keys since re-randomizing is indistinguishable from fresh sampling. In this case class-hiding would be perfect. However, such a scheme cannot achieve unforgeability under flexible keys, since it would be enough for an attacker to sample a fresh key pair and use a signature under that key as the forgery.
2 Preliminaries
We denote by \(y \leftarrow \mathcal {A}(x,\omega )\) the execution of algorithm \(\mathcal {A}\) outputting y, on input x with randomness \(\omega \), writing just  if the specific randomness used is not important. We will sometimes omit the use of random coins in the description of algorithms if it is obvious from the context (e.g. sampling group elements). The superscript \(\mathcal {O}\) in \(\mathcal {A}^{\mathcal {O}}\) means that algorithm \(\mathcal {A}\) has access to oracle \(\mathcal {O}\). Moreover, we say that \(\mathcal {A}\) is probabilistic polynomial-time (PPT) if \(\mathcal {A}\) uses internal random coins and the computation for any input \(x \in {\{0,1\}}^{*}\) terminates in polynomial time. By
if the specific randomness used is not important. We will sometimes omit the use of random coins in the description of algorithms if it is obvious from the context (e.g. sampling group elements). The superscript \(\mathcal {O}\) in \(\mathcal {A}^{\mathcal {O}}\) means that algorithm \(\mathcal {A}\) has access to oracle \(\mathcal {O}\). Moreover, we say that \(\mathcal {A}\) is probabilistic polynomial-time (PPT) if \(\mathcal {A}\) uses internal random coins and the computation for any input \(x \in {\{0,1\}}^{*}\) terminates in polynomial time. By  we mean that r is chosen uniformly at random from the set S. We will use \(1_{\mathbb {G}}\) to denote the identity element in group \(\mathbb {G}\), [n] to denote the set \(\{1,\ldots ,n\}\), \({\varvec{u}}\) to denote a vector and \(\left( x_0\ldots x_{|x|}\right) _{\mathsf {bin}}\) to denote the binary representation of x.
we mean that r is chosen uniformly at random from the set S. We will use \(1_{\mathbb {G}}\) to denote the identity element in group \(\mathbb {G}\), [n] to denote the set \(\{1,\ldots ,n\}\), \({\varvec{u}}\) to denote a vector and \(\left( x_0\ldots x_{|x|}\right) _{\mathsf {bin}}\) to denote the binary representation of x.
Remark 1
Due to space limitations, we omit full formal definitions of the syntax and security properties of ring and group signatures as well as some proofs. These omitted materials may be found in the full version of this work [3].
Definition 1
(Bilinear map). Let us consider cyclic groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) of prime order p. Let \(g_1, g_2\) be generators of respectively \(\mathbb {G}_1\) and \(\mathbb {G}_2\). We call \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) a bilinear map (pairing) if it is efficiently computable and the following conditions hold:
- Bilinearity: :
-
\(\forall (S,T) \in \mathbb {G}_1 \times \mathbb {G}_2\), \(\forall a, b \in \mathbb {Z}_p\), we have \(e(S^a,T^b) = {e(S,T)}^{a\cdot b}\),
- Non-degeneracy: :
-
\(e(g_1,g_2)\not =1\) is a generator of group \(\mathbb {G}_T\),
Definition 2
(Bilinear-group generator). A bilinear-group generator is a deterministic polynomial-time algorithm \(\mathsf{BGGen}\) that on input a security parameter \(\lambda \) returns a bilinear group \(\mathsf {BG}= (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,g_1,g_2)\) such that \(\mathbb {G}_1 = \langle g_1 \rangle \), \(\mathbb {G}_2 = \langle g_2 \rangle \) and \(\mathbb {G}_T\) are groups of order p and \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is a bilinear map.
Bilinear map groups with an efficient bilinear-group generator are known to be instantiable with ordinary elliptic curves introduced by Barreto and Naehrig [4] (in short BN-curves).
Invertible Sampling. We use a technique due to Damgård and Nielsen [21]:
-
A standard sampler returns a group element X on input coins \(\omega \).
-
A “trapdoor” sampler returns coins \(\omega '\) on input a group element X.
Invertible sampling requires that \((X,\omega )\) and \((X,\omega ')\) are indistinguishably distributed.
This technique was also used by Bender et al. [6] to prove full anonymity (where the adversary receives the random coins used by honest users to generate their keys) of their ring signature scheme.
2.1 Number Theoretical Assumptions
In this section we recall assumptions relevant to our schemes. They are stated relative to bilinear group parameters  .
.
Definition 3
(Decisional Diffie-Hellman Assumption in \(\mathbb {G}_i\)). Given \(\mathsf {BG}\) and elements \(g_i^a,g_i^b,g_i^z \in \mathbb {G}_i\) it is hard for all PPT adversaries \(\mathcal {A}\) to decide whether \(z = a \cdot b \mod p\) or  . We will use
. We will use  to denote the advantage of the adversary in solving this problem.
to denote the advantage of the adversary in solving this problem.
We now state the bilateral variant of the well known decisional linear assumption, where the problem instance is given in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\). This definition was also used by Ghadafi et al. [26].
Definition 4
(Symmetric Decisional Linear Assumption). Given \(\mathsf {BG}\), elements \(f_1 = g_1^f, h_1 = g_1^h, f_1^a, h_1^b, g_1^z \in \mathbb {G}_1\) and elements \(f_2 = g_2^f, h_2 = g_2^h, f_2^a, h_2^b,g_2^z \in \mathbb {G}_2\) for uniformly random \(f,h,a,b \in \mathbb {Z}_p^*\) it is hard for all PPT adversaries \(\mathcal {A}\) to decide whether \(z = a + b \mod p\) or  . We will use
. We will use  to denote the advantage of the adversary in solving this problem.
to denote the advantage of the adversary in solving this problem.
In this paper we use a variant of the 1-Flexible Diffie-Hellman assumption [33]. We show that this new assumption, which we call the co-Flexible Diffie-Hellman (co-Flex) assumption, holds if the decisional linear assumption holds.
Definition 5
(co-Flexible Diffie-Hellman Assumption). Given \(\mathsf {BG}\), elements \(g_1^a,g_1^b, g_1^c, g_1^d \in \mathbb {G}_1\) and \(g_2^a, g_2^b, g_2^c, g_2^d \in \mathbb {G}_2\) for uniformly random \(a,b ,c, d\in \mathbb {Z}_p^*\), it is hard for all PPT adversaries \(\mathcal {A}\) to output \({(g_1^c)}^r, {(g_1^d)}^r, g_1^{r \cdot a \cdot b} \). We will use  to denote the advantage of the adversary in solving this problem.
to denote the advantage of the adversary in solving this problem.
Lemma 1
The co-Flexible Diffie-Hellman assumption holds for \(\mathsf {BG}\) if the decisional linear assumption holds for \(\mathsf {BG}\).
Proof
Suppose we have an efficient algorithm \(\mathcal {A}\) that solves the co-Flexible Diffie-Hellman problem with non-negligible probability. We will show how to build algorithm \(\mathcal {R}\) that solves the decision linear problem. Let \((\mathsf {BG},f_1,f_2,h_1,h_2,f_1^a,f_2^a,h_1^b,h_2^b,g_1^{z},g_2^{z})\) be an instance of the decision linear problem. The algorithm \(\mathcal {R}\) first runs algorithm \(\mathcal {A}\) on input \((\mathsf {BG},f_1,f_2,g_1^z,g_2^z, f_1^a, f_2^a,h_1^b,h_2^b)\). With non-negligible probability \(\mathcal {A}\) outputs a solution to the co-Flexible Diffie-Hellman problem, i.e. it outputs the tuple \(( {(f_1^a)}^r, {(h_1^b)}^r, {(f_1^z)}^r )\). Then \(\mathcal {R}\) computes
and outputs 1 if \(T_1 = T_2 \cdot T_3\) and 0 otherwise.
2.2 Programmable Hash Functions
Programmable hash functions presented at Crypto’08 by Hofheinz and Kiltz [30] introduce a way to create hash functions with limited programmability. In particular, they show that the function introduced by Waters [41] is a programmable hash function. To formally define such function we first define so called group hash functions for a group \(\mathbb {G}\), which consists of two polynomial time algorithms \(\mathsf{PHF}.\mathsf{Gen}\), \(\mathsf{PHF}.\mathsf{Eval}\) and has an output length of \(\ell = \ell (\lambda )\). For a security parameter \(\lambda \) the generation algorithm \(\mathsf{PHF}.\mathsf{Gen}(\lambda )\) outputs a key \(K_\mathsf{PHF}\), which can be used in the deterministic algorithm \(\mathsf{PHF}.\mathsf{Eval}\) to evaluate the hash function via  . We will use \(\mathcal {H}_{K_\mathsf{PHF}}(X)\) to denote the evaluation of the function \(\mathsf{PHF}.\mathsf{Eval}(K_\mathsf{PHF},X)\) on \(X \in {\{0,1\}}^{\ell }\). We can now recall the definition of programmable has functions.
. We will use \(\mathcal {H}_{K_\mathsf{PHF}}(X)\) to denote the evaluation of the function \(\mathsf{PHF}.\mathsf{Eval}(K_\mathsf{PHF},X)\) on \(X \in {\{0,1\}}^{\ell }\). We can now recall the definition of programmable has functions.
Definition 6
A group hash function is an \((m,n,\gamma ,\delta )\)-programmable hash function if there are polynomial time algorithms \(\mathsf{PHF}.\mathsf{TrapGen}\) and \(\mathsf{PHF}.\mathsf{TrapEval}\) such that:
-
For any \(g, h \in \mathbb {G}\) the trapdoor algorithm
 outputs a key \(K'\) and trapdoor t. Moreover, for every \(X \in {\{0,1\}}^\ell \) we have
outputs a key \(K'\) and trapdoor t. Moreover, for every \(X \in {\{0,1\}}^\ell \) we have 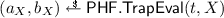 , where \(\mathsf{PHF}.\mathsf{Eval}(K_\mathsf{PHF}',X) = g^{a_X} h^{b_X}\).
, where \(\mathsf{PHF}.\mathsf{Eval}(K_\mathsf{PHF}',X) = g^{a_X} h^{b_X}\). -
For all \(g, h \in \mathbb {G}\) and for
 and
and  , the keys \(K_\mathsf{PHF}\) and \(K_\mathsf{PHF}'\) are statistically \(\gamma \)-close.
, the keys \(K_\mathsf{PHF}\) and \(K_\mathsf{PHF}'\) are statistically \(\gamma \)-close. -
For all \(g, h \in \mathbb {G}\) and all possible keys \(K_\mathsf{PHF}'\) from the range of \(\mathsf{PHF}.\mathsf{TrapGen}(\lambda , g,h)\), for all \(X_1,\ldots ,X_m, Z_1, \ldots , Z_n \in {\{0,1\}}^\ell \) such that \(X_i \not = Z_j\) for any i, j and for the corresponding
 and
and 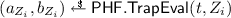 we have $$ \Pr [a_{X_1} = \cdots = a_{X_m} = 0 \;\; \wedge \;\; a_{Z_1} = \cdots = a_{Z_n} \not = 0] \ge \delta , $$
we have $$ \Pr [a_{X_1} = \cdots = a_{X_m} = 0 \;\; \wedge \;\; a_{Z_1} = \cdots = a_{Z_n} \not = 0] \ge \delta , $$where the probability is over trapdoor t that was generated with key \(K_\mathsf{PHF}'\).
Note that using this definition we can define the Waters hash function, with key \(K_\mathsf{PHF}= (h_0,\ldots ,h_\ell ) \in \mathbb {G}^{\ell +1}\) and message \(X = (x_1, \ldots , x_\ell ) \in {\{0,1\}}^\ell \) as \(h_0 \cdot \prod _{i=1}^{\ell } h_i^{x_i}\). Hofheinz and Kiltz prove that for any fixed \(q = q(\lambda )\) this is a \((1,q,0,1/8 \cdot (\ell +1) \cdot q)\)-programmable hash function. Unless mentioned otherwise, we will always instantiate the programmable hash function using the Waters function and use \(\ell = \lambda \).
2.3 Non-Interactive Proof Systems
In this paper we make use of non-interactive proof systems. Although we define the proof system for arbitrarily languages, in our schemes we use the efficient Groth-Sahai (GS) proof system for pairing product equations [28]. Let \(\mathcal {R}\) be an efficiently computable binary relation, where for \((x,w) \in \mathcal {R}\) we call x a statement and w a witness. Moreover, we denote by \(L_\mathcal {R}\) the language consisting of statements in \(\mathcal {R}\), i.e. \(L_\mathcal {R}= \{x | \exists w : (x,w) \in \mathcal {R}\}\).
Definition 7
(Non-Interactive Proof System). A non-interactive proof system \(\varPi \) consists of the following three algorithms \((\mathsf{Setup},\mathsf{Prove},\mathsf {Verify})\):
- \(\mathsf{Setup}(\lambda )\)::
-
on input security parameter \(\lambda \), this algorithm outputs a common reference string \(\rho \).
- \(\mathsf{Prove}(\rho ,x,w)\)::
-
on input common reference string \(\rho \), statement x and witness w, this algorithm outputs a proof \(\pi \).
- \(\mathsf {Verify}(\rho ,x,\pi )\)::
-
on input common reference string \(\rho \), statement x and proof \(\pi \), this algorithm outputs either \(\mathtt {accept}(1)\) or \(\mathtt {reject}(0)\).
Some proof systems do not need a common reference string. In such case, we omit the first argument to \(\mathsf{Prove}\) and \(\mathsf {Verify}\).
Definition 8
(Soundness). A proof system \(\varPi \) is called sound, if for all PPT algorithms \(\mathcal {A}\) the following probability, denoted by  , is negligible in the security parameter \(\lambda \):
, is negligible in the security parameter \(\lambda \):
We say that the proof system is perfectly sound if  .
.
Definition 9
(Witness Indistinguishability (WI)). A proof system \(\varPi \) is witness indistinguishable, if for all PPT algorithms \(\mathcal {A}\) we have that the advantage  computed as:
computed as:
where \((x, w_0),(x, w_1) \in \mathcal {R}\), is at most negligible in \(\lambda \). We say that the proof system if perfectly witness indistinguishable if  .
.
Perfectly Sound Proof System for Pairing Product Equations. We briefly recall the framework of pairing product equations that is used for the languages of the Groth-Sahai proof system [28]. For constants \(A_i \in \mathbb {G}_1\), \(B_i \in \mathbb {G}_2\), \(t_T \in \mathbb {G}_T\), \(\gamma _{ij} \in \mathbb {Z}_p\) which are either publicly known or part of the statement, and witnesses \(X_i \in \mathbb {G}_1\), \(Y_i \in \mathbb {G}_2\) given as commitments, we can prove that:
The system \((\mathsf{Setup}_\mathsf{PPE}, \mathsf{Prove}_\mathsf{PPE}, \mathsf {Verify}_\mathsf{PPE})\) has several instantiations based on different assumptions. In this paper we only consider the instantiation based on the symmetric linear assumption given by Ghadafi et al. [26].
For soundness it must be ensured, that \(\mathsf{Setup}_\mathsf{PPE}\) outputs a valid DLIN tuple. This can be enforced by requiring a trusted party perform the setup. However, our schemes require a proof system which is perfectly sound, even if a malicious prover executes the \(\mathsf{Setup}_\mathsf{PPE}\) algorithm.
To achieve this we use the ideas by Groth et al. [27]. They propose a perfectly sound and perfectly witness indistinguishable proof system \((\mathsf{Prove}_\mathrm {Linear}, \mathsf {Verify}_\mathrm {Linear})\) which does not require a trusted setup. Using it one can show that given tuples \(T_1\), \(T_2\) as a statement, at least one of \(T_1\) and \(T_2\) is a DLIN tuple. The results were shown for type 1 pairing but the proof itself is only given as elements in \(\mathbb {G}_2\). Moreover, our variant of the DLIN assumption gives the elements in both groups. Thus, we can apply the same steps as in [27]. The size of such a proof is 6 elements in \(\mathbb {G}_2\).
Next is the observation that the tuples \(T_1\) and \(T_2\) can each be used as common reference strings for the pairing product equation proof system. Since at least one of the tuples is a valid DLIN tuple, at least one of the resulting proofs will be perfectly sound. Witness-indistinguishability will be only computational, since we have to provide \(T_1\) and \(T_2\) to the verifier but that is sufficient in our case. The full scheme is presented in Scheme 1.
Theorem 1
Scheme 1 is a perfectly sound proof system for pairing product equations if the system \((\mathsf{Setup}_\mathsf{PPE}, \mathsf{Prove}_\mathsf{PPE}, \mathsf {Verify}_\mathsf{PPE})\) is perfectly sound in the common reference string model.
Theorem 2
Scheme 1 is a computational witness-indistinguishable proof system if the system \((\mathsf{Setup}_\mathsf{PPE}, \mathsf{Prove}_\mathsf{PPE}, \mathsf {Verify}_\mathsf{PPE})\) is perfectly witness-indistinguishable in the common reference string model.
2.4 Structure-Preserving Signatures on Equivalence Classes
Hanser and Slamanig introduced a cryptographic primitive called structure-preserving signatures on equivalence classes [29]. Their work was further extended by Fuchsbauer et al. in [24, 25]. The idea is simple but provides a powerful functionality. The signing \(\mathsf{Sign}_\mathsf {SPS}(M,\mathsf{sk}_\mathsf {SPS})\) algorithm defines an equivalence relation \(\mathcal {R}\) that induces a partition on the message space. By signing one representative of a partition, the signer in fact provides a signature for all elements in it. Moreover, there exists a procedure \(\mathsf{ChgRep}_\mathsf {SPS}(M,\sigma _\mathsf {SPS},r,\mathsf{pk}_\mathsf {SPS})\) that can be used to change the signature to a different representative without knowledge of the secret key. Existing instantiations allow to sign messages from the space \({(\mathbb {G}_i^*)}^\ell \), for \(\ell > 1\), and for the following relation \(\mathcal {R}_{exp}\): given two messages \(M = (M_1,\ldots ,M_\ell )\) and \(M' = (M_1',\ldots ,M_\ell ')\), we say that M and \(M'\) are from the same equivalence class (denoted by \({[M]}_\mathcal {R}\)) if there exists a scalar \(r \in \mathbb {Z}_p^*\), such that \(\forall _{i \in [\ell ]} {(M_i)}^r = M'_i\).
The original paper defines two properties of \(\mathsf{SPS\text {-}EQ}\) namely unforgeability under chosen-message attacks and class-hiding. Fuchsbauer and Gay [23] recently introduced a weaker version of unforgeability called unforgeability under chosen-open-message attacks, which restricts the adversary’s signing queries to messages where it knows all exponents.
Definition 10
(Signing Oracles). A signing oracle is an oracle \(\mathcal {O}_{\mathsf {SPS}}(\mathsf{sk}_\mathsf {SPS}, \cdot )\) (resp. \(\mathcal {O}_{\mathsf {op}}(\mathsf{sk}_\mathsf {SPS}, \cdot )\)), which accepts messages \((M_1,\ldots ,M_\ell ) \in {(\mathbb {G}_i^*)}^\ell \) (resp. vectors \(\left( e_1, \ldots , e_\ell \right) \in {(\mathbb {Z}_p^*)}^\ell \)) and returns a signature under \(\mathsf{sk}_\mathsf {SPS}\) on those messages (resp. on messages \(\left( g_1^{e_1}, \ldots , g_1^{e_\ell }\right) \in {({\mathbb {G}_i^*})}^\ell \)).
Definition 11
(EUF-CMA (resp. EUF-CoMA)). A \(\mathsf{SPS\text {-}EQ}\) scheme \((\mathsf{BGGen}_\mathsf {SPS},\mathsf{KGen}_\mathsf {SPS}, \mathsf{Sign}_\mathsf {SPS}, \mathsf{ChgRep}_\mathsf {SPS},\mathsf{Verify}_\mathsf {SPS},\mathsf{VKey}_\mathsf {SPS})\) on \({(\mathbb {G}_i^*)}^\ell \) is called existentially unforgeable under chosen message attacks (resp. adaptive chosen-open-message attacks), if for all PPT algorithms \(\mathcal {A}\) with access to an open signing oracle \(\mathcal {O}_\mathsf {SPS}(\mathsf{sk}_\mathsf {SPS}, \cdot )\) (resp. \(\mathcal {O}_\mathsf {op}(\mathsf{sk}_\mathsf {SPS}, \cdot )\)) the following advantage (with templates \(T_1, T_2\) defined below) is negligible in the security parameter \(\lambda \):

where Q is the set of messages signed by the signing oracle \(\mathcal {O}_{T_2}\) and for \(T_1 = \mathsf{euf\text {-}cma}\) we have \(T_2 = \mathsf {SPS}\), and for \(T_1 = \mathsf{euf\text {-}coma}\) we have \(T_2 = \mathsf {op}\).
A stronger notion of class hiding, called perfect adaptation of signatures, was proposed by Fuchsbauer et al. in [25]. Informally, this definition states that signatures received by changing the representative of the class and new signatures for the representative are identically distributed. In our schemes we will only use this stronger notion.
Definition 12
(Perfect Adaptation of Signatures). A \(\mathsf{SPS\text {-}EQ}\) scheme on \({(\mathbb {G}_i^*)}^\ell \) perfectly adapts signatures if for all \((\mathsf{sk}_\mathsf {SPS},\mathsf{pk}_\mathsf {SPS},M,\sigma ,r)\), where \(\mathsf{VKey}_\mathsf {SPS}(\mathsf{sk}_\mathsf {SPS},\mathsf{pk}_\mathsf {SPS})=1\), \(M \in {(\mathbb {G}_1^*)}^\ell \), \(r \in \mathbb {Z}_p^*\) and \(\mathsf{Verify}_\mathsf {SPS}(M,\sigma ,\mathsf{pk}_\mathsf {SPS})=1\), the distribution of
are identical.
3 Signatures with Flexible Public Key
We begin by motivating the idea behind our primitive. In the notion of existential unforgeability of digital signatures, the adversary must return a signature valid under the public key given to him by the challenger. Imagine now that we allow a more flexible forgery. The adversary can return a signature that is valid under a public key that is in some relation \(\mathcal {R}\) to the public key chosen by the challenger. Similar to the message space of \(\mathsf{SPS\text {-}EQ}\) signatures, this relation induces a system of equivalence classes on the set of possible public keys. A given public key, along with the corresponding secret key can be transformed to a different representative in the same class using an efficient, randomized algorithm. Since there may be other ways of obtaining a new representative, the forgery on the challenge equivalence class is valid as long as the relation holds, even without knowledge of the explicit randomness that leads to the given transformation.
Note, that because of this the challenger needs a way to efficiently ascertain whether the forgery is valid, even if no transformation randomness is given. Indeed, for the full definition of our schemes’ security we will require that it should not be feasible, in absence of the concrete transformation randomness, to determine whether a given public key belongs to one class or another. This property —called class-hiding in the style of a similar property for \(\mathsf{SPS\text {-}EQ}\) signatures— should hold even for an adversary who has access to the randomness used to create the key pairs in question.
The apparent conflict is resolved by introducing a trapdoor key generation algorithm \(\mathsf {TKeyGen}\) which outputs a key pair \((\mathsf {sk},\mathsf {pk})\) and a class trapdoor \(\tau \) for the class the key pair is in. The trapdoor allows the challenger to reveal whether a given key is in the same class as \(\mathsf {pk}\), even if doing so efficiently is otherwise assumed difficult. Since we require that the keys generated using the trapdoor key generation and the regular key generation are distributed identically, unforgeability results with respect to the former also hold with respect to the latter.
Definition 13
(Signature with Flexible Public Key). A signature scheme with flexible public key \((\mathsf{SFPK})\) is a tuple of \(\mathsf {PPT}\) algorithms \((\mathsf {KeyGen}, \mathsf {TKeyGen},\mathsf {Sign}, \mathsf {ChkRep}, \mathsf{ChgPK},\mathsf{ChgSK}, \mathsf {Verify})\) such that:
- \(\mathsf {KeyGen}(\lambda ,\omega )\)::
-
takes as input a security parameter \(\lambda \), random coins \(\omega \in \mathsf{coin}\) and outputs a pair \((\mathsf {sk},\mathsf {pk})\) of secret and public keys,
- \(\mathsf {TKeyGen}(\lambda ,\omega )\)::
-
a trapdoor key generation that takes as input a security parameter \(\lambda \), random coins \(\omega \in \mathsf{coin}\) and outputs a pair \((\mathsf {sk},\mathsf {pk})\) of secret and public keys, and a trapdoor \(\tau \).
- \(\mathsf {Sign}(\mathsf {sk}, m)\)::
-
takes as input a message \(m \in \{0,1\}^\lambda \) and a signing key \(\mathsf {sk}\), and outputs a signature \(\sigma \),
- \(\mathsf {ChkRep}(\tau ,\mathsf {pk})\)::
-
takes as input a trapdoor \(\tau \) for some equivalence class \({[\mathsf {pk}']}_\mathcal {R}\) and public key \(\mathsf {pk}\), the algorithm outputs 1 if \(\mathsf {pk}\in {[\mathsf {pk}']}_\mathcal {R}\) and 0 otherwise,
- \(\mathsf{ChgPK}(\mathsf {pk},r)\)::
-
on input a representative public key \(\mathsf {pk}\) of an equivalence class \({[\mathsf {pk}]}_\mathcal {R}\) and random coins r, this algorithm returns a different representative \(\mathsf {pk}'\), where \(\mathsf {pk}' \in {[\mathsf {pk}]}_\mathcal {R}\).
- \(\mathsf{ChgSK}(\mathsf {sk},r)\)::
-
on input a secret key \(\mathsf {sk}\) and random coins r, this algorithm returns an updated secret key \(\mathsf {sk}'\).
- \(\mathsf {Verify}( \mathsf {pk}, m, \sigma )\)::
-
takes as input a message m, signature \(\sigma \), public verification key \(\mathsf {pk}\) and outputs 1 if the signature is valid and 0 otherwise.
A signature scheme with flexible public key is correct if for all \(\lambda \in \mathbb {N}\), all random coins \(\omega ,r \in \mathsf{coin}\) the following conditions hold:
-
1.
The distribution of key pairs produced by \(\mathsf {KeyGen}\) and \(\mathsf {TKeyGen}\) is identical.
-
2.
For all key pairs
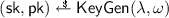 and all messages m we have \(\mathsf {Verify}( \mathsf {pk}, m, \mathsf {Sign}(\mathsf {sk}, m)) = 1\) and \(\mathsf {Verify}(\mathsf {pk}', m, \mathsf {Sign}( \mathsf {sk}',m)) = 1\), where \(\mathsf{ChgPK}(\mathsf {pk},r) = \mathsf {pk}'\) and \(\mathsf{ChgSK}(\mathsf {sk},r) = \mathsf {sk}'\).
and all messages m we have \(\mathsf {Verify}( \mathsf {pk}, m, \mathsf {Sign}(\mathsf {sk}, m)) = 1\) and \(\mathsf {Verify}(\mathsf {pk}', m, \mathsf {Sign}( \mathsf {sk}',m)) = 1\), where \(\mathsf{ChgPK}(\mathsf {pk},r) = \mathsf {pk}'\) and \(\mathsf{ChgSK}(\mathsf {sk},r) = \mathsf {sk}'\). -
3.
For all
 and all \(\mathsf {pk}'\) we have \(\mathsf {ChkRep}(\tau ,\mathsf {pk}') = 1\) if and only if \(\mathsf {pk}' \in {[\mathsf {pk}]}_\mathcal {R}\).
and all \(\mathsf {pk}'\) we have \(\mathsf {ChkRep}(\tau ,\mathsf {pk}') = 1\) if and only if \(\mathsf {pk}' \in {[\mathsf {pk}]}_\mathcal {R}\).
Definition 14
(Class-hiding). For scheme \(\mathsf{SFPK}\) with relation \(\mathcal {R}\) and adversary \(\mathcal {A}\) we define the following experiment:

A \(\mathsf{SFPK}\) is class-hiding if for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\), its advantage in the above experiment is negligible:

Definition 15
(Existential Unforgeability under Flexible Public Key). For scheme \(\mathsf{SFPK}\) with relation \(\mathcal {R}\) and adversary \(\mathcal {A}\) we define the following experiment:

A \(\mathsf{SFPK}\) is existentially unforgeable with flexible public key under chosen message attack if for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) the advantage in the above experiment is negligible:

Definition 16
(Strong Existential Unforgeability under Flexible Public Key). A \(\mathsf{SFPK}\) is strongly existentially unforgeable with flexible public key under chosen message attack if for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) the advantage  in the above experiment, where we replace the line \((m^*,\cdot ) \not \in Q\) with \((m^*,\sigma ^*) \not \in Q\), is negligible.
in the above experiment, where we replace the line \((m^*,\cdot ) \not \in Q\) with \((m^*,\sigma ^*) \not \in Q\), is negligible.
In a standard application, the public key and secret key are jointly randomized by the signer using the same randomness in \(\mathsf{ChgPK}\) and \(\mathsf{ChgSK}\). However, the \(\mathsf{ChgPK}\) algorithm alone can be executed by a third party given only the public key and random coins r. Revealing r to the signer allows them to compute the corresponding secret key. For some applications we want to avoid interaction during this recovery of the secret key. Allowing the user to extract the new secret key only using their old secret key would break class-hiding, since the attacker in this case has access to the pre-transformed secret keys. Fortunately, we can instead use the additional trapdoor returned by the \(\mathsf {TKeyGen}\) algorithm. More formally, we define this optional property as follows.
Definition 17
(Key Recovery). A \(\mathsf{SFPK}\) has recoverable signing keys if there exists an efficient algorithm \(\mathsf {Recover}\) such that for all security parameters \(\lambda \in \mathbb {N}\), random coins \(\omega , r\) and all  and
and  we have \(\mathsf{ChgSK}(\mathsf {sk},r) = \mathsf {Recover}(\mathsf {sk}, \tau , \mathsf {pk}')\).
we have \(\mathsf{ChgSK}(\mathsf {sk},r) = \mathsf {Recover}(\mathsf {sk}, \tau , \mathsf {pk}')\).
3.1 Flexible Public Key in the Multi-user Setting
In this subsection, we address applications where part of each user’s public key is shared with all the other public keys and is precomputed by a trusted third party in a setup phase, e.g. the key used in a programmable hash function. We therefore define an additional algorithm \(\mathsf {CRSGen}\) that, given a security parameter, outputs a common reference string \(\rho \). We assume that this string is an implicit input to all algorithms. If the \(\mathsf {KeyGen}\) is independent from \(\rho \), we say that such a scheme supports key generation without setup.
We will now discuss the implication of this new algorithm on the security definitions. Usually, we require that the common reference string is generated by an honest and trusted party (i.e. by the challenger in Definitions 14 and 15). We additionally define those notions under maliciously generated \(\rho \). We call a scheme class-hiding under malicious reference string if the class-hiding definition holds even if in Definition 14 the adversary is allowed to generate the string \(\rho \). Similarly, we call a \(\mathsf{SFPK}\) scheme unforgeable under malicious reference string if the unforgeability Definition 15 holds if \(\rho \) is generated by the adversary.
4 Applications
In this section we present natural applications of signatures with flexible public key. First we show how to implement cryptocurrency stealth addresses from schemes which have the additional key recovery property.
Then follow generic constructions of group and ring signature schemes. As we will see in Sect. 5, each of the schemes presented in this section can be instantiated with an \(\mathsf{SFPK}\) scheme such that it improves on the respective state-of-the-art in terms of concrete efficiency, necessary assumptions or both.
4.1 Cryptocurrency Stealth Addresses
In cryptocurrency systems transactions are confirmed through digital signatures from the spending party on, among other things, the public key of the receiving party. Using a technique called stealth addresses [37, 39], it is possible for the sender to create a fresh public key (address) for the receiving party from their known public key such that these two keys cannot be linked. The receiving party can recognize the fresh key as its own and generate a corresponding private key, subsequently enabling it to spend any funds send to the fresh unlinkable key. Crucially, there is no interaction necessary between sender and receiver to establish the fresh key and only the receiver can recover the right secret key.
Informally, a sender can take a recipient’s public address and transform it to a one-time address such that:
-
The new one is unlinkable to the original one and other one-time addresses,
-
only the recipient (or a party given the view key) can link all payments,
-
only the recipient can derive the spending key for the one-time address.
In existing schemes, stealth addresses are implemented using a variant of the Diffie-Hellman protocol [20, 37]. Let \(g^a\) be the public key of the sender and \(g^b\) the recipient’s public address. The sender computes the secret \(s = \mathsf {H}(g^{a\cdot b})\) and to finish the transaction sends the funds to the address \(g^s\). Note that this requires the recipient to immediately spend the coins, because the sender also knows s. To protect against this type of misuse, an asymmetric Diffie-Hellman was introduced, i.e. the funds are sent to the address \(g^{s + b} = {(g)}^s \cdot g^b\). Note that since only the recipient knows both s and b, only he can spend the money.
In practice, the sender’s public key \(g^a\) is ephemeral and unique for each transaction. Moreover, to increase efficiency a 2-key stealth address scheme was introduced. The recipient still holds the key for spending the coin, but gives a view key \(g^v\) to a third party for checking incoming transactions. Therefore, the recipient is not required to download all transactions and check if they correspond to their identity. However, the party holding the view key can break the anonymity of the recipient. To enable this feature, the sender also publishes \({(g^v)}^a\), as part of this transaction.
It is worth noting that the technique was introduced without a formal model and as an add-on for existing cryptocurrencies. In particular, as shown in [20] there exist many security pitfalls, which are exhibited by some of the schemes. Moreover, all existing schemes inherently rely on the Diffie-Hellman protocol, which is defined for groups in which the discrete logarithm is hard.
We will now show that signatures with flexible public keys that additionally implement the \(\mathsf {Recover}\) algorithm can be seen as a formalization of 2-key stealth addresses. Let us consider the following scenario. A sender wants to send funds to a recipient identified by an address \(\mathsf {pk}\), where  . In order to send the coins, the sender first chooses randomness r and computes the one-time address
. In order to send the coins, the sender first chooses randomness r and computes the one-time address  . The trapdoor \(\tau \) can be used as the view key to identify an incoming transaction using \(\mathsf {ChkRep}(\tau ,\mathsf {pk}')\). Finally, the recipient can use \(\mathsf {Recover}(\mathsf {sk}, \tau , \mathsf {pk}')\) to compute the secret key \(\mathsf {sk}'\) that can be used to spend funds sent to address \(\mathsf {pk}'\).
. The trapdoor \(\tau \) can be used as the view key to identify an incoming transaction using \(\mathsf {ChkRep}(\tau ,\mathsf {pk}')\). Finally, the recipient can use \(\mathsf {Recover}(\mathsf {sk}, \tau , \mathsf {pk}')\) to compute the secret key \(\mathsf {sk}'\) that can be used to spend funds sent to address \(\mathsf {pk}'\).
The main advantage of instantiating 2-key stealth addresses using \(\mathsf{SFPK}\) is that we can use the security arguments of the latter. In particular, unforgeability of \(\mathsf{SFPK}\) means that there cannot exist an efficient adversary that can spend the recipient’s coins. Note that this holds even if the adversary knows the view key \(\tau \). Privacy of the recipient is protected by class-hiding. Since the distributions of \(\mathsf {TKeyGen}\) and \(\mathsf {KeyGen}\) are identical, it follows that any adversary breaking privacy would break class-hiding. The party holding the view key \(\tau \) can distinguish transactions by definition, hence class-hiding does not hold for this party.
It is worth noting, that all previous descriptions of stealth addresses did not consider any formal model and rigorous proofs. As we have argued above, our definition of \(\mathsf{SFPK}\) with key recovery seems to directly address the requirements set before stealth addresses. Thus, our schemes are provable secure realizations of a stealth address scheme. Moreover, since we do not use a particular group structure, our construction could be instantiated using e.g. lattice-based cryptography. We leave an instantiation of \(\mathsf{SFPK}\) from lattices as an open problem.
Finally, note that Scheme 4 is an instance of signatures with flexible public key which has the required recovery algorithm. We also show how to extend Schemes 5 and 6 to support it.
4.2 Group Signatures/Self-Blindable Certificates
We now present an efficient generic construction of static group signatures that uses \(\mathsf{SFPK}\) as a building block and which is secure in the model by Bellare et al. [5]. The idea is to generate a \(\mathsf{SFPK}\) secret/public key pair and “certify” the public part with a \(\mathsf{SPS\text {-}EQ}\) signature. To sign a message, the signer changes the representation of their \(\mathsf{SFPK}\) key, and changes the representation of the \(\mathsf{SPS\text {-}EQ}\) certificate. The resulting signature is the \(\mathsf{SFPK}\) signature, the randomized public key and the \(\mathsf{SPS\text {-}EQ}\) certificate.
To enable subsequent opening, the group manager generates the \(\mathsf{SFPK}\) keys using \(\mathsf {TKeyGen}\) and stores their trapdoors. Opening is then performed using the stored trapdoors with the \(\mathsf {ChkRep}\) algorithm. The group manager can also generate  for the \(\mathsf{SFPK}\) signatures and use it as part of the group public key. This allows us to use schemes which are secure in the multi-user setting, e.g. Scheme 5. If the \(\mathsf {KeyGen}\) algorithm is used instead of \(\mathsf {TKeyGen}\) to compute the \(\mathsf{SFPK}\) key pairs, there is no efficient opening procedure and the combination of \(\mathsf{SFPK}\) and \(\mathsf{SPS\text {-}EQ}\) signature scheme yields a self-blindable certificate scheme [40].
for the \(\mathsf{SFPK}\) signatures and use it as part of the group public key. This allows us to use schemes which are secure in the multi-user setting, e.g. Scheme 5. If the \(\mathsf {KeyGen}\) algorithm is used instead of \(\mathsf {TKeyGen}\) to compute the \(\mathsf{SFPK}\) key pairs, there is no efficient opening procedure and the combination of \(\mathsf{SFPK}\) and \(\mathsf{SPS\text {-}EQ}\) signature scheme yields a self-blindable certificate scheme [40].
Due to space limitations, we only present the setup and signing algorithm for Scheme 2. Verification and opening procedures should be clear from the context.
Theorem 3
Scheme 2 is fully traceable if the \(\mathsf{SPS\text {-}EQ}\) and the \(\mathsf{SFPK}\) signature schemes are existentially unforgeable under chosen-message attack.
Proof
(Sketch). The proof relies on the fact that the only way for an adversary to win the full traceability game is by either creating a new group member (thus directly breaking the unforgeability of the \(\mathsf{SPS\text {-}EQ}\) scheme) or by creating a forged signature for an existing group member (thus breaking the unforgeability of the \(\mathsf{SFPK}\) scheme).
Theorem 4
Scheme 2 is fully anonymous if the \(\mathsf{SPS\text {-}EQ}\) signature scheme perfectly adapts signatures and is existentially unforgeable under chosen-message attacks, the \(\mathsf{SFPK}\) scheme is class-hiding and strongly existentially unforgeable.
Proof
(Sketch). We first use the perfect adaptation of \(\mathsf{SPS\text {-}EQ}\) signatures to re-sign the public key \(\mathsf {pk}'\) used in the challenge signature. Then we exclude the case that the adversary issues an open query that cannot be opened. This means that the adversary created a new group member and can be used to break the unforgeability of the \(\mathsf{SPS\text {-}EQ}\) scheme. In the next step we choose one of the users (and abort if he is not part of the query issued by the adversary to the challenge oracle) for which we change the way we generate the secret key. Instead of using \(\mathsf {TKeyGen}\), we use the standard key generation algorithm \(\mathsf {KeyGen}\). Note that in such a case, the open oracle cannot identify signatures created by this user. However, since signatures cannot be opened by the oracle for this user we can identify such a case and return his identifier. Finally, we replace the \(\mathsf{SFPK}\) public key and signature in the challenged group signature by a random one (which is indistinguishable by class-hiding). In the end the challenged signature is independent from the bit \(\hat{b}\). However, the adversary still has non-zero advantage. This follows from the fact that it can randomize the challenged signature and our oracle will output \(i_{\hat{b}}\) (because the \(\mathsf{SFPK}\) public key is random in the signature, the oracle will fail to open and return the user’s identifier). However, if the adversary is able to submit such a query we can break the strong existential unforgeability of the \(\mathsf{SFPK}\) scheme.
4.3 Ring Signatures
In ring signatures there is no trusted entity such as a group manager and groups are chosen ad hoc by the signers themselves. Thus, to certify ring members we use a membership proof instead of a \(\mathsf{SPS\text {-}EQ}\) signature. This proof is perfectly sound even if the common reference string is generated by the signer. In other words, the actual ring signature is a \(\mathsf{SFPK}\) signature \((\mathsf {pk}',\sigma )\) and a proof \(\varPi \) that there exists a public key \(\mathsf {pk}\in \mathtt {Ring}\) that is in relation to the public key \(\mathsf {pk}'\), i.e. the signer proves knowledge of the random coins used to get \(\mathsf {pk}'\). The signature’s anonymity relies on the class-hiding property of \(\mathsf{SFPK}\). Unfortunately, in the proof, the reduction does not know a valid witness for proof \(\varPi \), since it does not choose the random coins for the challenged signature. Thus, we extend the signer’s public keys by a tuple of three group elements (A, B, C) and prove an OR statement which allows the reduction to compute a valid proof \(\varPi \) if (A, B, C) is a non-DDH tuple (cf. Scheme 3). We can instantiate this scheme with a membership proof based on the \(\mathcal {O}(\sqrt{n})\) size ring signatures by Chandran et al. [15] and the perfectly sound proof system for NP languages by Groth et al. [27]. The resulting membership proof is perfectly sound and of sub-linear size in the size of the set. It follows, that our ring signature construction yields the first sub-linear ring signature from standard assumptions without a trusted setup.
Theorem 5
The generic construction of ring signatures presented in Scheme 3 is unforgeable w.r.t. insider corruption assuming the \(\mathsf{SFPK}\) scheme is existentially unforgeable, the proof system used is perfectly sound and the decisional Diffie-Hellman assumption holds.
Proof
(Sketch). We first fix all public keys of honest users to contain only DDH tuples. This ensures that the forgery \(\varSigma ^* = (\mathsf {pk}^*,\sigma ^*, \varPi ^*, \rho _\varPi ^*)\) includes a perfectly sound proof for the first clause of the statement, i.e. there exists a public key \(\mathsf {pk}\in \mathtt {Ring}\), which is in relation to \(\mathsf {pk}^*\) (all users in \(\mathtt {Ring}\) must be honest). This enables us to break existential unforgeability of the \(\mathsf{SFPK}\) scheme. Note that we have to guess the correct user to execute a successful reduction.
Theorem 6
The generic construction of ring signatures presented in Scheme 3 is anonymous against full key exposure assuming the \(\mathsf{SFPK}\) scheme is class-hiding and the used proof system is computationally witness-indistinguishable.
Proof
(Sketch). We first fix all public keys of honest users to contain only non-DDH tuples I. In the next step we randomly choose a fresh bit  and use the witness for the tuple \(I_{i_{\hat{b}}}\) in the challenged signature. Note that the proof is valid for both values of \(\hat{b}\) but now the proof part is independent from the bit b. Next we change the \(\mathsf{SFPK}\) scheme public key \(\mathsf {pk}'\) and signature \(\sigma \) returned as part of the challenged signature \(\varSigma = (\mathsf {pk}',\sigma ', \varPi )\). Again we choose a fresh bit
and use the witness for the tuple \(I_{i_{\hat{b}}}\) in the challenged signature. Note that the proof is valid for both values of \(\hat{b}\) but now the proof part is independent from the bit b. Next we change the \(\mathsf{SFPK}\) scheme public key \(\mathsf {pk}'\) and signature \(\sigma \) returned as part of the challenged signature \(\varSigma = (\mathsf {pk}',\sigma ', \varPi )\). Again we choose a fresh bit  and compute them using
and compute them using  ,
,  and
and  . Any adversary distinguishing this change can be used to break the class-hiding property of the \(\mathsf{SFPK}\) scheme. Finally, all elements of \(\varSigma \) are independent from b and the adversary’s advantage is zero.
. Any adversary distinguishing this change can be used to break the class-hiding property of the \(\mathsf{SFPK}\) scheme. Finally, all elements of \(\varSigma \) are independent from b and the adversary’s advantage is zero.
5 Efficient Instantiation from Standard Assumptions
In this section we present two efficient instantiations of signatures with flexible public key. All schemes support the same exponentiation relation \(\mathcal {R}_{exp}\). We say that public keys \(\mathsf {pk}_1 = (\mathsf {pk}_{1,1},\ldots ,\mathsf {pk}_{1,k})\) and \(\mathsf {pk}_2 = (\mathsf {pk}_{2,1},\ldots ,\mathsf {pk}_{2,k})\) are in this relation, denoted \((\mathsf {pk}_1,\mathsf {pk}_2) \in \mathcal {R}_{exp}\), if and only if there exists a value \(r \in \mathbb {Z}_p^*\) such that \(\forall _{i \in [k]} (\mathsf {pk}_{1,i})^r = \mathsf {pk}_{2,i}\). We assume that in the plain model scheme (i.e. without a common reference string) the public key contains the implicit security parameter \(\lambda \) and parameters \(\mathsf {BG}\). Since the bilinear-group generation algorithm \(\mathsf{BGGen}(\lambda )\) is deterministic, it follows that this does not influence the class-hiding property or the unforgeability property. Therefore, for readability we omit those parameters.
The first instantiation is based on a modified version of Waters signatures [41] for type-2 and type-3 pairings due to Chatterjee and Menezes [17]. The scheme has the key recovery property and can hence be used to implement stealth addresses and instantiate our ring signature construction.
The second scheme works in the multi-user setting and features small public key size, independent of the security parameter \(\lambda \). It is also based on the modified version of Waters signatures. A strongly unforgeable variant of this scheme is ideal for instantiating the group signature scheme presented in Sect. 4. In combination with the \(\mathsf{SPS\text {-}EQ}\) from [23] it results in the shortest static group signature scheme under standard assumptions. Further, using type-2 pairing and the random oracle model allows to use this scheme without a trusted party.
5.1 Warm-Up Scheme
Theorem 7
Scheme 4 is existentially unforgeable under flexible public key, assuming the decisional linear assumption holds and that \(\mathsf{PHF}\) is \((1, \mathsf {poly}\!\!\left( \lambda \right) )\)
Proof
In this particular proof we assume that we can re-run \(\mathsf{PHF}.\mathsf{TrapGen}\) using the same random coins on a different group, i.e. that we can generate key \(K_\mathsf{PHF}= (g_1^{\mu _0},\ldots ,g_1^{\mu _\lambda }) \in \mathbb {G}_1^{\lambda +1}\) and a corresponding key \(K_\mathsf{PHF}' = (g_2^{\mu _0},\ldots ,g_2^{\mu _\lambda }) \in \mathbb {G}_2^{\lambda +1}\). Note that this means that we make non-blackbox use of the underlying programmable hash function, but this re-running is possible for the hash function we use, i.e. the Waters hash function.
Let \((f_1,f_2,h_1,h_2,f_1^\alpha ,f_2^\alpha ,h_1^\beta ,h_2^\beta ,g_1^\gamma ,g_2^\gamma )\) be an instance of the decisional linear problem and let \(\mathcal {A}\) be an PPT adversary that has non-negligible advantage  . We will show an algorithm \(\mathcal {R}\) that uses \(\mathcal {A}\) to break the above problem instance.
. We will show an algorithm \(\mathcal {R}\) that uses \(\mathcal {A}\) to break the above problem instance.
In the first step, the reduction \(\mathcal {R}\) prepares the public key \(\mathsf{pk_{FW}}= (A,B,C,D,t,K_\mathsf{PHF})\) as follows. It sets:
and  . The reduction also prepares the trapdoor \(\tau = (d,f_2,f_2^{\alpha },h_2^{\beta },h_2,K_\mathsf{PHF}')\), where to generate \(K_\mathsf{PHF}'\) we re-run the algorithm \(\mathsf{PHF}.\mathsf{TrapGen}(\lambda ,g_2^\gamma ,g_2)\).
. The reduction also prepares the trapdoor \(\tau = (d,f_2,f_2^{\alpha },h_2^{\beta },h_2,K_\mathsf{PHF}')\), where to generate \(K_\mathsf{PHF}'\) we re-run the algorithm \(\mathsf{PHF}.\mathsf{TrapGen}(\lambda ,g_2^\gamma ,g_2)\).
Let (m, l) be one of \(\mathcal {A}'s\) signing queries. To answer it, \(\mathcal {R}\)
-
chooses random values
 ,
, -
it computes
 ,
, -
it computes
 ,
, -
it computes:
$$\begin{aligned} \sigma _\mathsf{FW}^1&= (g_1^\gamma )^{t \cdot l \cdot a_m} \cdot ( (f_1)^{(-a_m^{-1})} \cdot g_1^{t}) )^{l \cdot b_m}, \\ \sigma _\mathsf{FW}^2&= (f_1)^{-a_m^{-1}} \cdot g_1^{t}, \qquad \sigma _\mathsf{FW}^3 = (f_1)^{-a_m^{-1}} \cdot g_2^{t}, \end{aligned}$$ -
it returns the signature \( \sigma _\mathsf{FW}= (\sigma _\mathsf{FW}^1,\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3)\).
Let \(f_1 = g_1^\phi \). We will now show that this is a valid signature. Note that the a valid signature is of the form \((f_1^{\gamma \cdot l} \cdot ( (g_1^\gamma )^{a_m} \cdot g_1^{b_m})^{l \cdot r}, g_1^r, g_2^r)\). In this case, the reduction has set \(r = -a_m^{-1} \cdot \phi + t\) and this means that the \(f_1^{\gamma \cdot l}\) cancels out and the reduction does not need to compute \(f_1^{\gamma }\).
Finally, \(\mathcal {A}\) will output a valid signature under message \(m^*\): \( \hat{\sigma _\mathsf{FW}} = (\hat{\sigma _\mathsf{FW}}^1,\hat{\sigma _\mathsf{FW}}^2,\hat{\sigma _\mathsf{FW}}^3) = ((g_1^{\gamma \cdot \phi } \mathcal {H}_{K_\mathsf{PHF}}(m^*)^{r^*})^{l^*}, g_1^{r^*}, g_2^{r^*}), \) for which we hope that \(a_{m^*}=0\), where  . Moreover, since this should be a valid forgery then we have that this signature is under a public key \(\hat{\mathsf{pk_{FW}}}\) for which \((\mathsf{pk_{FW}},\hat{\mathsf{pk_{FW}}}) \in \mathcal {R}\). Thus, we have \( \hat{\sigma _\mathsf{FW}} = ( (f_1^{\gamma } (g_1^{r^*})^{b_{m^*}})^{l^*}, g_1^{r^*}, g_2^{r^*}), \) for some unknown \(r^*\) but known \(b_{m^*}\). Since \((\mathsf{pk_{FW}},\hat{\mathsf{pk_{FW}}}) \in \mathcal {R}\). This means that \(\hat{\mathsf{pk_{FW}}} = (A^{l^*},B^{l^*},C^{l^*},D^{l^*},t^{l^*},K_\mathsf{PHF}^{l^*}) = ((f_1^\alpha )^{l^*},(h_1^\beta )^{l^*}, (h_1)^{l^*}, (g_1^{\gamma \cdot d})^{l^*}, t^{l^*},K_\mathsf{PHF}^{l^*})\). We now compute
. Moreover, since this should be a valid forgery then we have that this signature is under a public key \(\hat{\mathsf{pk_{FW}}}\) for which \((\mathsf{pk_{FW}},\hat{\mathsf{pk_{FW}}}) \in \mathcal {R}\). Thus, we have \( \hat{\sigma _\mathsf{FW}} = ( (f_1^{\gamma } (g_1^{r^*})^{b_{m^*}})^{l^*}, g_1^{r^*}, g_2^{r^*}), \) for some unknown \(r^*\) but known \(b_{m^*}\). Since \((\mathsf{pk_{FW}},\hat{\mathsf{pk_{FW}}}) \in \mathcal {R}\). This means that \(\hat{\mathsf{pk_{FW}}} = (A^{l^*},B^{l^*},C^{l^*},D^{l^*},t^{l^*},K_\mathsf{PHF}^{l^*}) = ((f_1^\alpha )^{l^*},(h_1^\beta )^{l^*}, (h_1)^{l^*}, (g_1^{\gamma \cdot d})^{l^*}, t^{l^*},K_\mathsf{PHF}^{l^*})\). We now compute
Finally, the reduction \(\mathcal {R}\) returns 1 if \(T_1 \cdot T_2^{-1} = T_3 \cdot T_4\) and 0, otherwise. Note that \(T_1 \cdot T_2^{-1} = e(f_1^{\gamma },h_2^{l^*})\) and the above equation is correct only if \(\gamma = \alpha + \beta \).
The success probability of the reduction \(\mathcal {R}\) depends on whether it can answer all signing queries of \(\mathcal {A}\) and on the returned forgery (i.e. for which we must have \(a_{m^*}=0\)). However, since we assume that the used hash function is a \((1, \mathsf {poly}\!\!\left( \lambda \right) )\)-programmable hash function, it follows that \(\mathcal {R}\) has a non-negligible advantage in solving the decisional linear problem.
Theorem 8
Scheme 4 is class-hiding, assuming the decisional Diffie-Hellman assumption in \(\mathbb {G}_1\) holds.
Proof
In this proof we will use the game based approach. We start with \(\mathbf{GAME}_0\) which is the original class-hiding experiment and let \(S_0\) be an event that the experiment evaluates to 1, i.e. the adversary wins. We then make small changes and show in the end that the adversary’s advantage is zero. We will use \(S_i\) to denote the event that the adversary wins the class-hiding experiment in \(\mathbf{GAME}_i\). We will also use the vector \({\varvec{u}}\) to denote the key for the programmable hash function \(K_\mathsf{PHF}\). Let \(\mathsf{pk_{FW}}' = (A',B',C',D',t',{\varvec{u'}})\) be the public key given to the adversary as part of the challenge. Moreover, let \(\mathsf{pk_{FW}}_0 = (A_0,B_0,C_0,D_0,t_0,{\varvec{u}}_0)\) and \(\mathsf{pk_{FW}}_1 = (A_1,B_1,C_1,D_1,t_1,{\varvec{u}}_1)\) be the public keys that are returned by the \(\mathsf {KeyGen}\) algorithm on input of random coins \(\omega _0\) and \(\omega _1\) given to the adversary and \(\hat{b}\) be the bit chosen by the challenger.
- \(\mathbf{GAME}_1\)::
-
In this game we change the way we sample \(\mathsf{pk_{FW}}_0\) and \(\mathsf{pk_{FW}}_1\). Instead of sampling directly from \(\mathbb {G}_1\), we sample
 , \(B = g_1^b\), \(C = g_1^c\), \(D = g_1^d\), \(X = g_1^x\) and \({\varvec{u}} = (g_1^{\nu _0},\ldots , g_1^{\nu _\lambda })\). Moreover, we change the way \(\mathsf{sk_{FW}}'\) and \(\mathsf{pk_{FW}}'\) are computed from \(\mathsf{sk_{FW}}_{\hat{b}}\) \(\mathsf{pk_{FW}}_{\hat{b}}\), i.e. \(\mathsf{pk_{FW}}' = (Q^a,Q^b,Q^c, Q^d, e(Q^x,g_2^y) , (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }}))\), and \(\mathsf{sk_{FW}}' = (y, Q^{x}, \mathsf{pk_{FW}}')\). In other words, instead of using the value r to randomize the public key and secret key, we use a group element Q to do it.
, \(B = g_1^b\), \(C = g_1^c\), \(D = g_1^d\), \(X = g_1^x\) and \({\varvec{u}} = (g_1^{\nu _0},\ldots , g_1^{\nu _\lambda })\). Moreover, we change the way \(\mathsf{sk_{FW}}'\) and \(\mathsf{pk_{FW}}'\) are computed from \(\mathsf{sk_{FW}}_{\hat{b}}\) \(\mathsf{pk_{FW}}_{\hat{b}}\), i.e. \(\mathsf{pk_{FW}}' = (Q^a,Q^b,Q^c, Q^d, e(Q^x,g_2^y) , (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }}))\), and \(\mathsf{sk_{FW}}' = (y, Q^{x}, \mathsf{pk_{FW}}')\). In other words, instead of using the value r to randomize the public key and secret key, we use a group element Q to do it.Because we can use the invertible sampling algorithm to retrieve the random coins \(\omega _0\) and \(\omega _1\) and since the distribution of the keys does not change, it follows that \(\Pr [S_1] = \Pr [S_0]\). Note that since the secret key \(\mathsf{sk_{FW}}'\) is known, the signing oracle \(\mathsf {Sign}(\mathsf{sk_{FW}}', \cdot )\) can be properly simulated for any adversary.
- \(\mathbf{GAME}_2\)::
-
In this game instead of computing \(\mathsf{pk_{FW}}' = (Q^a,Q^b,Q^c,Q^d,e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}), (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }})) \) as in \(\mathbf{GAME}_1\), we sample
 set \(\mathsf{pk_{FW}}' = (A', Q^b, Q^c, Q^d, e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}) , (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }})).\)
set \(\mathsf{pk_{FW}}' = (A', Q^b, Q^c, Q^d, e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}) , (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }})).\)We will show that this transition only lowers the adversary’s advantage by a negligible fraction. In particular, we will show a reduction \(\mathcal {R}\) that uses an adversary \(\mathcal {A}\) that can distinguish between those two games to break the decisional Diffie-Hellman assumption in \(\mathbb {G}_1\). Let \((g_1^{\alpha },g_1^{\beta },g_1^{\gamma })\) be a instance of this problem in \(\mathbb {G}_1\). \(\mathcal {R}\) samples
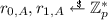 and sets \(A_0 = (g_1^{\alpha })^{r_{0,A}}\), \(A_1 = (g_1^{\alpha })^{r_{1,A}}\).
and sets \(A_0 = (g_1^{\alpha })^{r_{0,A}}\), \(A_1 = (g_1^{\alpha })^{r_{1,A}}\).Additionally, the reduction uses \(Q = g_1^{\beta }\) and the public key
$$\mathsf{pk_{FW}}' = ((g_1^\gamma )^{r_{\hat{b},A}},Q^b,Q^c,Q^d,e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}} ) , (Q^{\nu _0}, \ldots , Q^{\nu _{\lambda }})).$$Note that since \(\mathcal {R}\) knows the secret key \(\mathsf{sk_{FW}}'\) it can answer signing queries. Finally notice, that if \(\gamma = \alpha \cdot \beta \) then \((\mathsf{pk_{FW}}',\sigma _\mathsf{FW})\) have the same distribution as in \(\mathbf{GAME}_1\) and otherwise as in \(\mathbf{GAME}_2\). Thus, we have
 .
. - \(\mathbf{GAME}_3\) (series of sub-games)::
-
In this game instead of computing \(\mathsf{pk_{FW}}' = (A', Q^b,Q^c,Q^d,e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}) , (Q^{\nu _1}, \ldots , Q^{\nu _{\lambda }})) \) as in \(\mathbf{GAME}_2\), we sample
 and set \(\mathsf{pk_{FW}}' = (A', B', C',D', e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}) , (u_0', \ldots , u_{\lambda }')).\)
and set \(\mathsf{pk_{FW}}' = (A', B', C',D', e(Q^{x_{\hat{b}}},g_2^{y_{\hat{b}}}) , (u_0', \ldots , u_{\lambda }')).\)
This transition is composed of a number of sub-games, in which we change each element of the public key \(\mathsf{pk_{FW}}'\) separately. Obviously, we can use the same reduction as above and show that each change lowers the adversary’s advantage by at most  . It is worth noting, that the reduction can always create a valid signature, since the secret key \(\mathsf{sk_{FW}}' = (y_{\hat{b}}, Q^{x_{\hat{b}}},\mathsf{pk_{FW}}')\) can be computed by \(\mathcal {R}\). Thus, we have
. It is worth noting, that the reduction can always create a valid signature, since the secret key \(\mathsf{sk_{FW}}' = (y_{\hat{b}}, Q^{x_{\hat{b}}},\mathsf{pk_{FW}}')\) can be computed by \(\mathcal {R}\). Thus, we have  .
.
Let us now take a look at the randomized public key and signature given to the adversary. Because of all the changes, we have: \(\mathsf{pk_{FW}}' = (A', B', C' e(Q^{x_{\hat{b}} \cdot y_{\hat{b}}},g_2), {\varvec{u'}} )\) and signatures from the oracle are of the form \(( Q^{x_{\hat{b}} \cdot y_{\hat{b}}} (\mathcal {H}_{K_\mathsf{PHF}}(m))^r, g_1^r, g_2^r)\) for some \(r \in \mathbb {Z}_p^*\) and \(A', B', C',{\varvec{u'}} (=K_\mathsf{PHF}), Q\), which are independent from the bit \(\hat{b}\) and the original public keys. Since the value Q is random and only appears as part of the term \(Q^{x_{\hat{b}} \cdot y_{\hat{b}}}\), we can always restate this term to \(Q'^{x_{1-\hat{b}} \cdot y_{1-\hat{b}}}\) where \(Q' = Q^{(x_{1-\hat{b}} \cdot y_{1-\hat{b}}) \cdot (x_{\hat{b}} \cdot y_{\hat{b}})^{-1}}\) and \(Q'\) is a random value. It follows that the adversaries advantage is zero, i.e. \(\Pr [S_3] = 0\).
Finally, we have  .
.
5.2 Flexible Public Key Scheme in the Multi-user Setting
Theorem 9
Scheme 5 is existentially unforgeable under flexible public key in the common reference string model, assuming the co-Flexible Diffie-Hellman assumption holds and that \(\mathsf{PHF}\) is a \((1, \mathsf {poly}\!\!\left( \lambda \right) )\)-programmable hash function.
Proof
(Sketch). The proof follows the same idea as the proof of Theorem 7. The only difference is that in this case we will use a reduction directly to the co-Flexible Diffie-Hellman assumption. Let \((g_1^\alpha ,g_2^\alpha ,g_1^\beta ,g_2^\beta ,g_1^\gamma ,g_2^\gamma ,g_1^\theta ,g_2^\theta )\) be an instance of this problem. The reduction \(\mathcal {R}\) prepares the common reference string \(\rho = (\mathsf {BG},Y_1,Y_2,K_\mathsf{PHF})\) and the public key \(\mathsf{pk_{FW}}= (A,B,X)\) as follows. It sets \(X = g_1^\beta \), \(Y_1 = g_1^\alpha \), \(Y_2 = g_2^\alpha \),  . Moreover, \(\mathcal {R}\) sets \(\tau = (g_2^\gamma ,g_2^\theta ,g_2^\beta )\). Finally, the adversary \(\mathcal {A}\) will output a public key \(\hat{\mathsf{pk_{FW}}} = (A^{l^*},B^{l^*},X^{l^*})\) and a valid signature under message \(m^*\): \( \hat{\sigma _\mathsf{FW}} = ( (g_1^{\alpha \cdot \beta })^{l^*} (g_1^{r^*})^{b_{m^*}}, g_1^{r^*}, g_2^{r^*}), \) for some unknown \(r^*\) but known \(b_{m^*}\). The reduction can compute \(S = (g_1^{\alpha \cdot \beta })^{l^*}\) and return \((A^{l^*},B^{l^*},S)\) as a solution to the co-Flexible Diffie-Hellman problem.
. Moreover, \(\mathcal {R}\) sets \(\tau = (g_2^\gamma ,g_2^\theta ,g_2^\beta )\). Finally, the adversary \(\mathcal {A}\) will output a public key \(\hat{\mathsf{pk_{FW}}} = (A^{l^*},B^{l^*},X^{l^*})\) and a valid signature under message \(m^*\): \( \hat{\sigma _\mathsf{FW}} = ( (g_1^{\alpha \cdot \beta })^{l^*} (g_1^{r^*})^{b_{m^*}}, g_1^{r^*}, g_2^{r^*}), \) for some unknown \(r^*\) but known \(b_{m^*}\). The reduction can compute \(S = (g_1^{\alpha \cdot \beta })^{l^*}\) and return \((A^{l^*},B^{l^*},S)\) as a solution to the co-Flexible Diffie-Hellman problem.
Theorem 10
Scheme 5 is class-hiding under the DDH assumption in \(\mathbb {G}_1\).
Proof
(Sketch). The proof is analogous to the proof of Theorem 8.
Remark 2
(Key Recovery). To support key recovery, the public key must be extended to the form (A, B, C, X) for \(C = Y_1^c\). The value c is then part of \(\tau \) and can be used to restore the value \(Y_1^r\), where r is the randomness used to change the public key. Given \(Y_1^r\) we need to compute \(Z^r = Y_1^{xr}\), therefore we also have to include x as part of the original secret key \(\mathsf{sk_{FW}}= (x,Y_1^x) = (x,Z)\).
Transformation to Strong Existential Unforgeability. Scheme 5 is only existentially unforgeable under flexible public key and this directly follows from the fact that given a signature \((g_1^{x \cdot y \cdot l} \mathcal {H}_{K_\mathsf{PHF}}(m)^r, g_1^r, g_2^r)\) on message m, we can compute a randomized signature \((\sigma _\mathsf{FW}^1,\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3) = ( g_1^{x \cdot y \cdot l}\mathcal {H}_{K_\mathsf{PHF}}(m)^r \cdot \mathcal {H}_{K_\mathsf{PHF}}(m)^{r'}, g_1^{r}g_1^{r'}, g_2^{r}g_2^{r'})\) for a fresh value  .
.
A generic transformation from existentially unforgeable to strongly unforgeable signatures was proposed by Boneh et al. [11]. In particular, they use Waters signatures as a case study. It works for all schemes for which there exist two algorithms \(F_1\) and \(F_2\) with the following properties: (1) the output signature is \((\sigma _1,\sigma _2)\), where  and
and  , (2) given m and \(\sigma _2\) there exists at most one \(\sigma _1\) so that \((\sigma _1,\sigma _2)\) is a valid signature under \(\mathsf {pk}\). It is easy to see that these properties hold for standard Waters signatures and for Scheme 5, since we can compute \(\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3\) in algorithm \(F_2\) and \(\sigma _\mathsf{FW}^1\) in \(F_1\). What is more, once the random value r is set, there exists exactly one value \(\sigma _\mathsf{FW}^1\), for which \((\sigma _\mathsf{FW}^1,\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3)\) is valid under a given public key.
, (2) given m and \(\sigma _2\) there exists at most one \(\sigma _1\) so that \((\sigma _1,\sigma _2)\) is a valid signature under \(\mathsf {pk}\). It is easy to see that these properties hold for standard Waters signatures and for Scheme 5, since we can compute \(\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3\) in algorithm \(F_2\) and \(\sigma _\mathsf{FW}^1\) in \(F_1\). What is more, once the random value r is set, there exists exactly one value \(\sigma _\mathsf{FW}^1\), for which \((\sigma _\mathsf{FW}^1,\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3)\) is valid under a given public key.
The high level idea of the solution is to bind the part computed by \(F_2\) using a hash function, i.e. the output of \(F_2\) is hashed together with the actual message m and the output is signed. In a scenario where we consider a given public key, this means that the signature cannot be randomized. Any manipulation of the values \((\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3)\) would result in a different signed message, which would lead to an attack against existential unforgeability of the underlying scheme. Fixing \((\sigma _\mathsf{FW}^2,\sigma _\mathsf{FW}^3)\) fixes \(\sigma _\mathsf{FW}^1\), as required by the properties above. Unfortunately, the second argument does not hold for strong unforgeability under flexible public key. Note that the adversary can still change \(\sigma _\mathsf{FW}^1\) by randomizing the public key. We can overcome this by simply including the public key in the hash computation.
This idea prevents the randomization of the signature but breaks the security proof of the underlying scheme. To allow the security reduction to bypass this protection Boneh, Shen and Waters propose to sign a Pedersen commitment to this hash value, instead of the value itself. The reduction can use a trapdoor to bypass this protection using equivocation of the commitment. At the same time the binding property still makes it impossible for the adversary to randomize the signature. To apply this idea in our case, we first extend the common reference string  . This element is part of the commitment key for the Pedersen scheme. More details are given in Scheme 6.
. This element is part of the commitment key for the Pedersen scheme. More details are given in Scheme 6.
Strong Existential Unforgeable Variant of Scheme 5
Theorem 11
Scheme 6 is strongly existentially unforgeable under flexible public key in the CRS model, assuming the co-Flexible Diffie-Hellman assumption holds and the hash function \(\mathsf {H}\) is collision-resistant.
Proof
(Sketch). The proof follows directly from the proof given in [11].
Theorem 12
Scheme 6 is class-hiding under the DDH assumption in \(\mathbb {G}_1\).
Proof
(Sketch). We can apply the same reasoning as in the proof of Theorem 10.
5.3 Discussion
In this we instantiate the generic group signature Scheme 2 and the generic ring signature Scheme 3 with our \(\mathsf{SFPK}\) instantiations.
Note that in the case of group signatures we can use a \(\mathsf{SFPK}\) scheme that is strongly existentially unforgeable in the multi-user setting, since the group manager can be trusted to perform a proper setup of public parameters. Thus, a natural candidate is Scheme 6. We also require a \(\mathsf{SPS\text {-}EQ}\) signature scheme, which we instantiate using the scheme presented in [23]. A caveat to this scheme is that it only supports a one-time adaptation of signatures to a different representative. This does not impact our use of the scheme since in our application the group member performs the adaptation only once per signing. Further, the scheme is only unforgeable under adaptive chosen-open-message attacks, hence we require the following lemma.
Lemma 2
Let the public key of the \(\mathsf{SFPK}\) scheme consist only of elements sampled directly from \(\mathbb {G}_1\) or computed as \(g_1^x\), where  . Theorems 3 and 4 still hold if the \(\mathsf{SPS\text {-}EQ}\) scheme is only existential unforgeable under adaptive chosen-open-message attacks.
. Theorems 3 and 4 still hold if the \(\mathsf{SPS\text {-}EQ}\) scheme is only existential unforgeable under adaptive chosen-open-message attacks.
Proof
(Sketch). In the proof of Theorem 3, instead of excluding the case where the adversary creates a new user, we can toss a coin and chose the adversary’s strategy (forging the \(\mathsf{SPS\text {-}EQ}\) or \(\mathsf{SFPK}\) signature). In case we end up choosing the \(\mathsf{SPS\text {-}EQ}\), we can freely choose the \(\mathsf{SFPK}\) public keys and issue signing oracles to get all \(\sigma _\mathsf {SPS}^i\). In the proof of Theorem 4 we use the unforgeability of \(\mathsf{SPS\text {-}EQ}\) to exclude the case that the adversary issues an open query for a new user. Because this is the first change, we can again freely choose the \(\mathsf{SFPK}\) public keys and issue signing oracles to get all \(\sigma _\mathsf {SPS}^i\). Finally, we note that in such proofs we make a non-blackbox use of the \(\mathsf{SFPK}\) scheme.
For message space \((\mathbb {G}_1^*)^\ell \) the size of the \(\mathsf{SPS\text {-}EQ}\) signature is \((4 \cdot \ell + 2)\) elements in \(\mathbb {G}_1\) and 4 elements in \(\mathbb {G}_2\). The security of the \(\mathsf{SPS\text {-}EQ}\) scheme relies on the decisional linear assumption and the decisional Diffie-Hellman assumption in \(\mathbb {G}_2\), while the security of our \(\mathsf{SFPK}\) relies on the co-Flexible Diffie-Hellman assumption. All in all, the proposed instantiation yields a static group signature scheme that is secure under standard assumptions and has a signature size of 20 elements in \(\mathbb {G}_1\) (counting elements in \(\mathbb {Z}_q^*\) as \(\mathbb {G}_1\)) and 5 elements in \(\mathbb {G}_2\). It therefore has shorter signatures than the current state-of-the-art scheme in [32].
Even shorter signatures can be achieved at the expense of introducing stronger assumptions without relying on Lemma 2, by using the scheme found in [24], which is unforgeable in the generic group model and has signatures of size 2 elements in \(\mathbb {G}_1\) and 1 element in \(\mathbb {G}_2\). More details are given in Fig. 2.
We now focus on instantiating our ring signatures construction. Combining any scheme from Sect. 5 with a generic perfectly sound proof system would result in a ring signature scheme that is unlikely to be of interest, as there are already more efficient schemes with/without a trusted setup (see Fig. 3 for a comprehensive comparison). However, using the results presented by Chandran et al. [15] we can make the membership proof efficient. They propose a perfectly sound proof of size \(\mathcal {O}(\sqrt{n})\) that a public key \(\mathsf {pk}\in \mathbb {G}_1\) (or \(\mathsf {pk}\in \mathbb {G}_2\)), is in a \(\mathtt {Ring}\) of size n. This idea can be applied to arbitrary public keys (i.e. consisting of group elements in different groups) in combination with a perfectly sound proof system for NP languages. Thus, we must use a compatible \(\mathsf{SFPK}\) instantiation, leaving as the only scheme without a trusted party assumption Scheme 4. A public key of Scheme 4 contains an element in \(\mathbb {G}_T\) and therefore cannot be used with the proof system from Subsect. 2.3, which is based on the efficient Groth-Sahai proofs for pairing product equations. We solve this problem in the following way:
Lemma 3
Scheme 4 is unforgeable and class-hiding even if \(X = g_1^x\), \(Y=g_2^y\) are publicly known, where \(t = e(X^y,g_2) = e(X,Y)\) is part of the signer’s public key. Moreover, knowing the secret key one can compute such values.
Comparison of ring signature schemes without random oracles and secure in the strongest model from [6]
Proof
Class-hiding still holds, because the adversary is given the secret keys \(\mathsf {sk}_i\) for \(i \in \{0,1\}\), which contain \(X_i\) and \(y_i\) so it can compute \(X_i\) and \(Y_i\) by itself already. To show that unforgeability still holds, we first have to note that Y is part of the trapdoor \(\tau \) and does not provide new information for the adversary. Finally, in the proof of unforgeability of Scheme 4 X is set to be \(g_1^\gamma \), where \(g_1^\gamma \) is part of the decisional linear problem instance. This element is not given to the adversary directly but the same proof works if this value would be given to the adversary.
The idea is that instead of putting the public key \(\mathsf{pk_{FW}}= (A,B,C,D,t, K_\mathsf{PHF})\) into the ring, we put \((A,B,C,D,X,Y, K_\mathsf{PHF})\). Finally, we modify the first part of the statement proven during signing, i.e. we use
instead of \( \exists _{\mathsf {pk},r} \left( (i,\mathsf {pk}, \cdot ) \in \mathtt {Ring}\; \wedge \; \mathsf{ChgPK}(\mathsf {pk},r)=\mathsf {pk}' \right) , \) where \(\mathsf{pk_{FW}}' = (A',B',C',D',t', K_\mathsf{PHF}')\) is the randomized \(\mathsf{SFPK}\) public key used as part of the ring signature. Since all elements in the ring are now elements in \(\mathbb {G}_1\) or \(\mathbb {G}_2\), we can use the proof system from Subsect. 2.3 to efficiently instantiate the proof used in our ring signature construction. What is more, we can also apply the trick from [15] and create a membership proof of length only \(\mathcal {O}(\sqrt{n})\). The resulting ring signature scheme is the first efficient scheme that is secure under falsifiable assumptions, without a trusted party and with signature size that does not depend linearly on the number of ring members. This solves the open problem stated by Malavolta and Schröder [34].
References
Ateniese, G., Chou, D.H., de Medeiros, B., Tsudik, G.: Sanitizable signatures. In: di Vimercati, S.C., Syverson, P., Gollmann, D. (eds.) ESORICS 2005. LNCS, vol. 3679, pp. 159–177. Springer, Heidelberg (2005). https://doi.org/10.1007/11555827_10
Attrapadung, N., Libert, B., Peters, T.: Efficient completely context-hiding quotable and linearly homomorphic signatures. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 386–404. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_24
Backes, M., Hanzlik, L., Kluczniak, K., Schneider, J.: Signatures with Flexible Public Key: Introducing Equivalence Classes for Public Keys. Cryptology ePrint Archive, Report 2018/191 (2018)
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 319–331. Springer, Heidelberg (2006). https://doi.org/10.1007/11693383_22
Bellare, M., Micciancio, D., Warinschi, B.: Foundations of group signatures: formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_38
Bender, A., Katz, J., Morselli, R.: Ring signatures: stronger definitions, and constructions without random oracles. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 60–79. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_4
Bichsel, P., Camenisch, J., Neven, G., Smart, N.P., Warinschi, B.: Get shorty via group signatures without encryption. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 381–398. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_24
Blazy, O., Fuchsbauer, G., Pointcheval, D., Vergnaud, D.: Signatures on randomizable ciphertexts. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 403–422. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_25
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Boneh, D., Freeman, D., Katz, J., Waters, B.: Signing a linear subspace: signature schemes for network coding. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 68–87. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_5
Boneh, D., Shen, E., Waters, B.: Strongly unforgeable signatures based on computational Diffie-Hellman. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 229–240. Springer, Heidelberg (2006). https://doi.org/10.1007/11745853_15
Boyen, X.: Mesh signatures. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 210–227. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_12
Boyen, X., Waters, B.: Full-domain subgroup hiding and constant-size group signatures. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 1–15. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_1
Camenisch, J., Groth, J.: Group signatures: better efficiency and new theoretical aspects. In: Blundo, C., Cimato, S. (eds.) SCN 2004. LNCS, vol. 3352, pp. 120–133. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30598-9_9
Chandran, N., Groth, J., Sahai, A.: Ring signatures of sub-linear size without random oracles. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 423–434. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73420-8_38
Chase, M., Kohlweiss, M., Lysyanskaya, A., Meiklejohn, S.: Malleable signatures: new Definitions and delegatable anonymous credentials. In: CSF 2014. IEEE Computer Society (2014)
Chatterjee, S., Menezes, A.: On cryptographic protocols employing asymmetric pairings - the role of revisited. Discret. Appl. Math. 159(13), 1311–1322 (2011)
Chaum, D., van Heyst, E.: Group signatures. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 257–265. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_22
Chow, S.S.M., Wei, V.K.-W., Liu, J.K., Yuen, T.H.: Ring signatures without random oracles. In: Lin, F.-C., Lee, D.-T., Paul, B.-S.P., Lin, Shieh, S., Jajodia, S. (eds.) ASIACCS 2006. ACM (2006)
Courtois, N.T., Mercer, R.: Stealth address and key management techniques in blockchain systems. In: Mori, P., Furnell, S., Camp, O. (eds.) ICISSP 2017. SciTePress (2017)
Damgård, I., Nielsen, J.B.: Improved non-committing encryption schemes based on a general complexity assumption. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 432–450. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_27
Fleischhacker, N., Krupp, J., Malavolta, G., Schneider, J., Schröder, D., Simkin, M.: Efficient unlinkable sanitizable signatures from signatures with re-randomizable keys. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 301–330. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_12
Fuchsbauer, G., Gay, R.: Weakly Secure Equivalence-Class Signatures from Standard Assumptions. Cryptology ePrint Archive, Report 2018/037 (2018)
Fuchsbauer, G., Hanser, C., Slamanig, D.: EUF-CMA- Secure Structure-Preserving Signatures on Equivalence Classes. Cryptology ePrint Archive, Report 2014/944 (2014)
Fuchsbauer, G., Hanser, C., Slamanig, D.: Practical round-optimal blind signatures in the standard model. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 233–253. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_12
Ghadafi, E., Smart, N.P., Warinschi, B.: Groth–Sahai proofs revisited. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 177–192. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_11
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Hanser, C., Slamanig, D.: Structure-preserving signatures on equivalence classes and their application to anonymous credentials. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 491–511. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_26
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 21–38. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_2
Johnson, R., Molnar, D., Song, D., Wagner, D.: Homomorphic signature schemes. In: Preneel, B. (ed.) CT-RSA 2002. LNCS, vol. 2271, pp. 244–262. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45760-7_17
Libert, B., Peters, T., Yung, M.: Short group signatures via structure-preserving signatures: standard model security from simple assumptions. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 296–316. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_15
Libert, B., Vergnaud, D.: Multi-use unidirectional proxy resignatures. In: Ning, P., Syverson, P.F., Jha, S.: CCS 2008. ACM (2008)
Malavolta, G., Schröder, D.: Efficient ring signatures in the standard model. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 128–157. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_5
Nakamoto, S.: Bitcoin: a peer-to-peer electronic cash system. http://bitcoin.org/bitcoin.pdf
Rivest, R.L., Shamir, A., Tauman, Y.: How to leak a secret. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_32
van Saberhagen, N.: CryptoNote v 2.0., October 2013. https://cryptonote.org/whitepaper.pdf
Shacham, H., Waters, B.: Efficient ring signatures without random oracles. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 166–180. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_12
Todd, P.: Stealth Addresses. https://lists.linuxfoundation.org/pipermail/bitcoin-dev/2014-January/004020.html
Verheul, E.R.: Self-blindable credential certificates from the weil pairing. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 533–551. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_31
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_7
Acknowledgments
This work was supported by the German Federal Ministry of Education and Research (BMBF) through funding for CISPA and the CISPA-Stanford Center for Cybersecurity (FKZ: 16KIS0762).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Backes, M., Hanzlik, L., Kluczniak, K., Schneider, J. (2018). Signatures with Flexible Public Key: Introducing Equivalence Classes for Public Keys. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)


 outputs a key
outputs a key 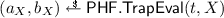 , where
, where  and
and  , the keys
, the keys  and
and 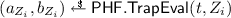 we have
we have 
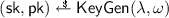 and all messages m we have
and all messages m we have  and all
and all 


 ,
, ,
, ,
, ,
,  set
set 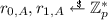 and sets
and sets  .
. and set
and set 




