Abstract
This chapter collects a number of important properties of Sobolev spaces. Almost every claim is provided together with a proof. The main result is the density of \(\mathcal D(\overline \varOmega )\) in W s, p(Ω) and proved in Theorem 3.4.5. The necessary tools to establish these proofs are introduced and intermediate results are presented in the following subsections. This entire chapter can be viewed as a preparation for subsequent ones on traces, Chap. 4, and to meaningfully define the weak forms of some partial differential equations in Chap. 5.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In this definition Ω may be \(\mathbb {R}^d\), then Ω ε = Ω for all ε.
- 2.
For simplicity here the norm on \(\mathbb {R}^d\) is the 1-norm, i.e.,
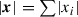 .
. - 3.
In contrast to the definition of the weak derivative, the test function φ is not in \(\mathcal D(\mathbb {R}^d_{+})\) but in \(\mathcal D(\mathbb {R}^d)\).
- 4.
- 5.
Of course this is only true for K ≥ 2, for K = 1 there is no integration over a second component y 2. Similarly in the following steps.
- 6.
The set (0, ∞)K + {y} has to be understood element-wise, i.e., it is defined as
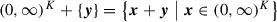 , see also Footnote 3 on page 15.
, see also Footnote 3 on page 15.
References
Robert A. Adams and John J. F. Fournier. Sobolev spaces, volume 140 of Pure and Applied Mathematics (Amsterdam). Elsevier/Academic Press, Amsterdam, second edition, 2003.
N. Kikuchi and J. T. Oden. Contact problems in elasticity: a study of variational inequalities and finite element methods, volume 8 of SIAM Studies in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1988.
Irina Mitrea and Marius Mitrea. The Poisson problem with mixed boundary conditions in Sobolev and Besov spaces in non-smooth domains. Trans. Amer. Math. Soc., 359(9):4143–4182 (electronic), 2007.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Wilbrandt, U. (2019). Properties of Sobolev Spaces. In: Stokes–Darcy Equations. Advances in Mathematical Fluid Mechanics(). Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-02904-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-02904-3_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-02903-6
Online ISBN: 978-3-030-02904-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


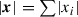 .
.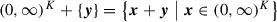 , see also Footnote
, see also Footnote