Abstract
With the popularity of RDF as an independent data model came the need for specifying constraints on RDF graphs, and for mechanisms to detect violations of such constraints. One of the most promising schema languages for RDF is SHACL, a recent W3C recommendation. Unfortunately, the specification of SHACL leaves open the problem of validation against recursive constraints. This omission is important because SHACL by design favors constraints that reference other ones, which in practice may easily yield reference cycles.
In this paper, we propose a concise formal semantics for the so-called “core constraint components” of SHACL. This semantics handles arbitrary recursion, while being compliant with the current standard. Graph validation is based on the existence of an assignment of SHACL “shapes” to nodes in the graph under validation, stating which shapes are verified or violated, while verifying the targets of the validation process. We show in particular that the design of SHACL forces us to consider cases in which these assignments are partial, or, in other words, where the truth value of a constraint at some nodes of a graph may be left unknown.
Dealing with recursion also comes at a price, as validating an RDF graph against SHACL constraints is NP-hard in the size of the graph, and this lower bound still holds for constraints with stratified negation. Therefore we also propose a tractable approximation to the validation problem.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The success of RDF was largely due the fact that it can be easily published and queried without bounding to a specific schema [4]. But RDF over time has turned into more than a simple data exchange format [2], and a key challenge for current RDF-based applications is checking quality (correctness and completeness) of a dataset. Several systems already provide facilities for RDF validation (see e.g. [12]), including commercial products.Footnote 1\(^,\)Footnote 2 This created a need for standardizing a declarative language for RDF constraints, and for formal mechanisms to detect and describe violations of such constraints.
One of the most promising efforts in this direction is SHACL, or Shapes Constraint Language,Footnote 3 which has become a W3C recommendation in 2017. SHACL groups constraints in so-called “shapes” to be verified by certain nodes of the graph under validation, and such that shapes may reference each other.
Figure 1 presents two SHACL shapes. The leftmost, named :NIAddressShape, is meant to define valid addresses in Northern Italy, whereas the right one, named :PolentoneShape, defines northern Italians, stereotypically referred to as Polentoni.Footnote 4 A node v satisfying the first shape must verify two constraints: the first one states that there can be at most one successor of v via property :telephone. The second one states that there must be exactly one successor (sh:minCount 1 and sh:maxCount 1) of v via property :locatedIn, with value :NorthernItaly.
Validating an RDF graph against a set of shapes is based on the notion of “target nodes”, which mandates for each shape which nodes have to conform to it. For instance, PolentoneShape contains the triple :PolentoneShape sh:targetClass :Polentone, stating that its targets are all instances of :Polentone in the graph under validation. But nodes may also have to conform to additional shapes, due to shape references. For instance, in Fig. 1, the shape to the right contains one (non-recursive) shape reference, to :NIAddressShape, stating that every node v conforming to :PolentoneShape must have exactly one :address, which must conform to :NIAddressShape, and one recursive reference, stating that each successor of v via :knows must conform to :PolentoneShape.
By recursion, we will always refer to such reference cycles, possibly n-ary (where shape \(s_1\) references \(s_2\), \(s_2\) references \(s_3\),.., \(s_n\) references \(s_1\)). Unfortunately, the semantics of graph validation with recursive shapes is left explicitly undefined in the SHACL specification: “... the validation with recursive shapes is not defined in SHACL and is left to SHACL processor implementations. For example, SHACL processors may support recursion scenarios or produce a failure when they detect recursion.” The specification nonetheless expresses the expectation that validation of recursive shapes end up being defined in future work. Indeed, shapes references are a core feature of SHACL. Furthermore, in a Semantic Web context, where shapes are expected to be exchanged or reused, reference cycles may naturally appear, intentional or not. Finally, recursion may be viewed as one of the distinctive features of SHACL: without recursion, one ends up with a constraint language whose expressive power is essentially the same as SPARQL.
Another current limitation of the SHACL specification is the lack of a unified and concise formal semantics for the so-called “core constraint components” of the language. Instead, the specification provides a combination of SPARQL queries and textual definitions to characterize these operators. This may be sufficient for reading or writing SHACL constraints, but a more abstract underlying formalization is still missing, in order for instance to devise efficient constraint validation algorithms, identify computational bottlenecks, or to compare SHACL’s expressivity with other languages.
Contributions. In this article, we propose a formal semantics for the core constraint components of SHACL, which is robust enough to handle arbitrary recursion, while being compliant with the current standard in the non-recursive case. It turns out that defining such a semantics is far from trivial, due essentially to the combination of three features of the language: recursion, arbitrary negation, and the target-based validation mechanism introduced above. One of the main difficulties is to define in a satisfactory way validation of shapes with so-called non-stratified constraints, where negation is used arbitrarily in reference cycles.
To do this, we base our semantic on the existence of a partial assignment of shapes to nodes that verifies both constraints and targets, i.e. intuitively a validation of nodes against shapes which may leave undetermined whether a given node verifies a shape or violates it. We show that this semantics has desirable formal properties, such as equivalence with classical validation in the presence of stratified constraints.
Recursion, however, comes at a cost, as we show that the problem of validating a graph is worst-case intractable in the size of the graph. Perhaps more surprisingly, we show that this property already holds for stratified constraints, and for a limited fragment of the language, without counting or path expressions. This observation leads us to propose a sound approximation, polynomial in the size of the graph, and whose worst-case execution time can be parameterized.
Organization. Section 2 discusses the problem of recursive SHACL constraints validation, with concrete examples. Then Sect. 3 defines a robust semantics for SHACL, together with a concise abstract syntax, and investigates its formal properties. Section 4 studies computational complexity of the graph validation problem under this semantics, and Sect. 5 proposes a sound approximation algorithm, in order to regain tractability (in the size of the graph under validation). Finally, Sect. 6 reviews alternative languages and formal semantics for graph constraints validation, with an emphasis on RDF.
An extended abstract of this paper has been accepted at the AMW workshop [9]. In addition, an appendix with detailed proofs and a translation from SHACL into our abstract syntax and conversely can be found at [8].
2 Validating a Graph Against SHACL Shapes
This section provides a brief overview of the constraint validation mechanism described in the SHACL specification, and discusses its extension to the case of recursive constraints. We focus here on the problem of deciding whether a graph is valid against a set of shapes. Therefore we purposely ignore the notion of “validation report” defined in the specification, and encourage the interested reader to consult the specification directly.
Checking whether a graph G is valid against a set S of shapes may be viewed as a two-step process. The first step consists in iterating over all shapes \(s \in S\), and retrieve their respective target nodes in G. SHACL provides a dedicated language to describe the intended targets of a shape (e.g. the sh:targetClass property in Fig. 1), which is orthogonal to the language used to define constraints. Furthermore, this language has a limited expressivity, allowing all targets of shape s in G to be retrieved in \(O(|G| \cdot \log |G|)\), before constraint validation.
A SHACL shapes for semi-Polentone, and a graph G to be validated against this shape, together with the shapes of Fig. 1
The second step consists in iterating over each target node v of each shape s, and check whether the node v satisfies s. This check can be represented as a call to a recursive function \(\textit{validates}(s, G, v)\). Some of the constraints for s may be validated by looking locally at the graph, i.e. at the IRI of v and its outgoing paths. But \(\textit{validates}(s, G, v)\) may also trigger a recursive call \(\textit{validates}(s', G, v')\), where \(s'\) is a shape referenced by s, and \(v'\) is a successor of v in G. It should be noted that \(v'\) does not need to be a target node of \(s'\). In turn, \(\textit{validates}(s', G, v')\) may trigger another recursive call, etc.
Another important feature of SHACL is the possibility to declare negated constraints. For instance, shape SemiPolentoneShape in Fig. 2 uses sh:not to describe someone who knows at least one person who is not a Polentone (but still lives in Northern Italy). In this case, \(\textit{validates}(\texttt {{\small SemiPolentoneShape}}, G, v)\) will succeed only if some successor of v via property :knows violates the constraints for :PolentoneShape.Footnote 5
2.1 Recursive Constraints with Stratified Negation
Figures 1 and 2, considered together, illustrate a simple case of recursive constraint validation (i.e. constraints with reference cycles). The RDF triple :SemiPolentoneShape sh:targetNode :Enrico indicates that :Enrico is the unique target of shape :SemiPolentoneShape. This is also the only target to be validated in the graph.
To check if :Enrico validates :SemiPolentoneShape, the validation process described in the specification would call \(\textit{validates}(\texttt {{\small SemiPolentoneShape}},G,\) \(\texttt {{\small :Enrico}})\), triggering an infinite sequence of recursive calls to \(\textit{validates}(\texttt {{\small PolentoneShape}}, G, \texttt {{\small :Davide}})\). Intuitively, the problems is that \(\textit{validates}\) does not keep track of what has been validated (or violated) so far.
A classical solution to ground constraint evaluation in such cases is to define it w.r.t. an assignment of (positive and negated) shape labels to nodes. In this example, Enrico can be assigned :SemiPolentoneShape, and :Davide can be assigned the negation of :PolentoneShape. This assignment complies with the constraints and the target, allowing us to validate the graph. Alternatively, it is possible to comply with all constraints by assigning :PolentoneShape to :Davide, and the negation of :SemiPolentoneShape to :Enrico. But this latter assignment does not comply with the target, therefore it would not allow us to validate the graph.
Several formal frameworks dealing with recursion (such as recursive Datalog [10]) have semantics based on a similar intuition. This notion of assignment is also used in [7] for ShEx, a constraint language for RDF very similar to SHACL. However, the semantics proposed in [7] would consider the graph of Fig. 2 as invalid, taking only one assignment into consideration, where :Davide is assigned :PolentoneShape, and therefore :Enrico cannot verify :SemiPolentoneShape. The semantics defined in [7] is also restricted to stratified constraints, i.e. constraints such that reference cycles have no reference in the scope of a negation (see Definition 8 further below).
2.2 Non-stratified Constraints
Extending assignment-based validation to the non-stratified case raises an interesting question, namely whether such an assignment should be \(total \), i.e. assign each shape or its negation to each node of the graph. We illustrate this with validating the graph G of Fig. 2 against the two shapes of Fig. 3.
:Davide is the only target node, for shape :HappyPersonShape. This shape is validated iff :Davide has an address, or knows a naive polentone. Because :Davide has an address, a simple call to \(\textit{validates}(\texttt {{\small HappyPersonShape}}, G, \texttt {{\small :Davide}})\) would validate the graph. But a total assignment must also assign either :NaivePolentoneShape or its negation to :Davide. And this cannot be done in a consistent manner. If :NaivePolentoneShape is assigned, then :Davide does not verify the corresponding constraint; if the negation of :NaivePolentoneShape is assigned, then :Davide does not violate the constraint. Therefore a semantics based on total assignments would consider the graph invalid.
It should be emphasized that this example is not a limit case: the same problem appears for any (satisfiable) set of shapes containing a reference cycle (of any size), and such that an odd number of references in this cycle are in the scope of a negation. Therefore, if one wants to defines a robust semantics based on assignments for recursive SHACL, it should be based on partial assignments, leaving the possibility to assign neither a shape nor its negation to some nodes.
3 Formal Semantics for SHACL
This section provides a formal semantics for recursive SHACL. As explained above, constraint validation is based on partial assignment. This semantics (i) complies with the current semantics of SHACL for non-recursive constraints, (ii) supports arbitrary recursion and negation, and (iii) can handle simultaneous validation of multiple targets.
A set of shapes is validated iff there exists an assignment (called here faithful) complying with it. This is a key difference from query answering, or cautious reasoning in Datalog, interested in certain answers, i.e. holding for all valid assignments. For instance, in Fig. 2, some faithful assignments assign :PolentoneShape to :Davide, and some do not.
3.1 Notation
Like the SHACL specification, we borrow from SPARQL the notion of property path, which describes regular constraints holding over a path in a graph (for the syntax and semantics, we defer to the SPARQL standard [15]). Following [16], if r is a property path and G a graph, we denote with r(G) the evaluation of r, which consists of all pairs \((v,v')\) of nodes in G such that there is a path from v to \(v'\) satisfying r.
Similarly, if \(\psi \) is a SPARQL query, we denote with \(\psi (G)\) the evaluation of \(\psi \) in G. Finally, we use |X| to denote the size of structure X.
3.2 Abstract Syntax and Semantics for SHACL Constraints
Syntax. As usual, we find more convenient to work with a logical abstraction of the concrete SHACL language. Our abstraction uses a fragment of first order logic to simulate node shapes, and then unravels so-called SHACL “property shapes” as modal formulas over nodes. Like the SHACL specification, we make the unique name assumption, i.e. we assume that two blank nodes in an RDF graph cannot denote the same individual. We also abstract away from constraints on IRIs and literals (regular expression, datatype, value comparison, etc.), and use a simple constant I instead. Constraints are defined by the following grammar:
where s is a shape name, I is an IRI, r is a property path, and \(n \in \mathbb {N}^+\). As syntactic sugar, we use \(\le _n r.\phi \) for \(\lnot (\ge _{n+1} r.\phi )\), and \(=_nr.\phi \) for \((\ge _n r.\phi ) \wedge (\le _n r.\phi )\).
Let \(\mathcal {L}\) be the language defined by this grammar. A full operator-by-operator translation from SHACL core constraint components to \(\mathcal {L}\) and conversely is provided in the online appendix [8] of this article. For non-recursive shape constraints, this is a correct translation, in the sense that a set of constraints in one language and its translation in the other language validate exactly the same graphs, given the same targets. Unfortunately, in the absence of formal semantics for SHACL, this claim cannot be formally proven, but is based on our understanding of the specification. We cannot claim that this also holds for recursive shapes though, because SHACL validation in this case is not defined.
Example 1
We illustrate the syntax with the example from Fig. 1. To express SHACL cardinality constraints (e.g. sh:maxCount), we use \(\le _1 r.\phi \), which means that a node can have at most 1 r-successor satisfying \(\phi \), or \(=_1 r.\phi \) for exactly one. Then the constraints for :NIAddressShape (abbreviated here as \(s_{\texttt {{\small niaddr}}}\)) can be translated as:
where \(\top \) is true at every node. In the same way, we can translate the constraints for :PolentoneShape (abbreviated here as \(s_\texttt {{\small pol}}\)). Both \(s_\texttt {{\small niaddr}}\) and \(s_\texttt {{\small pol}}\) appear in the constraint for \(s_\texttt {{\small pol}}\). This mimics the SHACL syntax, where both shapes were mentioned:
Semantics. Because shape names may appear in constraint formulas, we define the inductive evaluation of a formula in terms of a node, a graph, and an assignment that mandates which shapes are true or false at each node.
Definition 1
(Assignment). Let N be a set of shape names, and G a graph.
An assignment \(\sigma \) for G and N is a total function mapping nodes in G to subsets of \(N \cup \{\lnot s \mid s \in N\}\), such that s and \(\lnot s\) cannot be both in \(\sigma (v)\).
Definition 2
(Total assignment). A assignment \(\sigma \) for G and N is total if either \(s \in \sigma (v)\) or \(\lnot s \in \sigma (v)\), for each node in G and \(s \in N\).
The evaluation  of formula \(\phi \) at node v in graph G given \(\sigma \) is defined in Table 1. In order to evaluate a formula given a partial assignment, we use a 3-valued logic, which, in addition to the usual 1 and 0 for true and false, uses 0.5 to represent an unknown truth value. But if assignments are required to be total, then this third value is not needed:
of formula \(\phi \) at node v in graph G given \(\sigma \) is defined in Table 1. In order to evaluate a formula given a partial assignment, we use a 3-valued logic, which, in addition to the usual 1 and 0 for true and false, uses 0.5 to represent an unknown truth value. But if assignments are required to be total, then this third value is not needed:
Observation 1
Let \(\sigma \) be a total assignment for G and N, and \(\phi \) a constraint formula using shape names in N. Then for each node v of G, either  or
or  .
.
The inductive definition of  is standard, aside maybe for the operator \(\ge _n r\). Intuitively, \(\ge _n r.\phi \) evaluates to true iff at least n r-successors of v validate \(\phi \), whereas \(\ge _n r.\phi \) evaluates to false iff the number of r-successors of v which do or could validate \(\phi \) is strictly inferior to n. This allows the semantics to comply with SHACL cardinality constraints in the non-recursive case.
is standard, aside maybe for the operator \(\ge _n r\). Intuitively, \(\ge _n r.\phi \) evaluates to true iff at least n r-successors of v validate \(\phi \), whereas \(\ge _n r.\phi \) evaluates to false iff the number of r-successors of v which do or could validate \(\phi \) is strictly inferior to n. This allows the semantics to comply with SHACL cardinality constraints in the non-recursive case.
From SHACL Shapes to \(\mathcal {L}\) Constraints. We model a shape as a triple \((s,\phi _s,\text {target}_s)\), where s is a shape name, \(\phi _s\) is a constraint in \(\mathcal {L}\), and \(\text {target}_s\) is a (possibly empty) monadic query retrieving the target nodes of s. If S is a set of shapes, we assume that for each \((s,\phi _s,\text {target}_s) \in S\), if \(s'\) appears in \(\phi _s\), then \((s',\phi _s',\text {target}_s') \in S\). An assignment for G and S is an assignment for G and \(\{s \mid (s,\phi _s,\text {target}_s) \in S\}\). Abusing notation, we write “\(s \in S\)” instead of “\((s,\phi _s,\text {target}_s) \in S\)”.
3.3 Validation
We finally have all components in place to define graph validation. Intuitively, a graph is valid against a set S of shapes if one can find an assignment \(\sigma \) for G and S complying with targets and constraints. We call such an assignment faithful, defined as follows:
Definition 3
(Faithful Assignment). A assignment \(\sigma \) for G and S is faithful iff \(\text {target}_s(G) \subseteq \sigma (v)\) for each \((s,\phi _s,\text {target}_s) \in S\), and, for each node v in G:
-
if \(s \in \sigma (v)\), then

-
if \(\lnot s \in \sigma (v)\), then

Definition 4
(Validation). A graph G is valid against a set S of shapes iff there is a faithful assignment \(\sigma \) for G and S.
The (online) appendix provides a full translation from SHACL to sets of shapes and conversely, which preserves validation, provided the shapes are non-recursive (i.e. contain no reference cycle). Our notion of validation is more robust though, as it is also well-defined for recursive shapes. In Sect. 4, we study the complexity of the validation problem. But for now, we provide some insight on properties of this semantics.
3.4 Properties of Validation
We introduce some additional notation. First, \(\varSigma ^{G,S}\) will designate the set of all assignments for G and S. Then we define the “immediate evaluation” operator \(\mathbf T ^{G,S}\) for G and S (or simply \(\mathbf {T}\) when obvious from the context). It takes an assignment \(\sigma \), and returns the assignment \(\mathbf T (\sigma )\) obtained by evaluating each \(\phi _s\) at each node of G.
Definition 5
(Immediate evaluation operator T).
\( \mathbf{T }: \varSigma ^{G,S} \rightarrow \varSigma ^{G,S}\) is the function defined by
\(s \in ( \mathbf{T }(\sigma ))(v)\) iff  , and \(\lnot s \in ( \mathbf{T }(\sigma ))(v)\) iff
, and \(\lnot s \in ( \mathbf{T }(\sigma ))(v)\) iff 
Finally, we define the preorder \(\preceq \) over \(\varSigma ^{G,S}\) by:
Definition 6
(Preorder \(\preceq \) ).
\(\sigma _1 \preceq \sigma _2\) iff \(\sigma _1(v) \subseteq \sigma _2(v)\) for each node v in G.
Validation Without Target. The SHACL specification states that a graph G is valid against a set S of shapes if no shape in s has target in G. From Definitions 3 and 4, this also (trivially) holds in the recursive case for our semantics. Somehow surprisingly, validation without target may fail for total assignments. For instance, there is no total faithful assignment for the graph of Fig. 2 and the set of shapes containing only shape :NaivePolentoneShape from Fig. 3.
A Stricter Notion of Faithfulness. From Definition 3, a faithful assignment \(\sigma \) is only required to assign s to a node v if \(\phi _s\) is verified by v (given \(\sigma \)), and to assign \(\lnot s\) to v if \(\phi _s\) is violated by v (given \(\sigma \)). But it is also possible to assign none of these two, even though v verifies of violates \(\phi _s\) (given \(\sigma \)). This may seem counterintuitive, which leads to the following stricter notion of faithfulness:
Definition 7
(Strictly-faithful assignment). A assignment \(\sigma \) for G and S is strictly faithful iff \(\text {target}_s(G) \subseteq \sigma (v)\) for each \((s,\phi _s,\text {target}_s) \in S\), and, for each node v in G:
-
if \(s \in \sigma (v)\), then
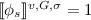
-
if \(\lnot s \in \sigma (v)\), then

-
otherwise,
 .
.
We also say that a graph G is strictly valid against a set of shapes S if there is a strictly faithful assignment for G and S.
For instance, there is only one strictly faithful assignment for the graph of in Fig. 2 and the two shapes of Fig. 3. It assigns \(\lnot \) :HappyPersonShape to :addr1, because :addr1 violates the constraint for this shape. There are also several (non-strictly) faithful assignments, some of which assign neither :HappyPersonShape nor its negation to :addr1. So intuitively, non-strict validation allows some form of “lazy” constraint evaluation.
The operator \(\mathbf {T}\) provides a more concise definition. Both faithful and strictly faithful assignments must comply with targets for G and S. But in addition, a faithful assignment \(\sigma \) must verify \(\sigma \preceq \mathbf {T}(\sigma )\), whereas a strictly faithful assignment \(\sigma '\) must verify \(\sigma ' = \mathbf {T}(\sigma ')\).
Interestingly, these two notions of validation coincide. To prove this, we first need a useful property, the monotonicity of \(\mathbf {T}\) w.r.t \(\preceq \):
Lemma 1
(monotonicity of T). For any G, S and \(\sigma _1, \sigma _2 \in \varSigma ^{G,S}\):
if \(\sigma _1 \preceq \sigma _2\), then \(\mathbf {T}(\sigma _1) \preceq \mathbf {T}(\sigma _2)\).
We can now state the equivalence:
Proposition 1
For any G and S, G is valid against S iff G is strictly valid against S.
Proof
(Sketch). The right direction is trivial, because a strictly faithful assignment is faithful. In the other direction, let \(\sigma _0\) be a faithful assignment for G and S. Define \(\varSigma ' \subseteq \varSigma ^{G,S}\) as all extensions of \(\sigma _0\), i.e. \(\sigma ' \in \varSigma '\) iff \(\sigma _0 \preceq \sigma '\). From Lemma 1, \(\mathbf {T}(\sigma _0) \preceq \mathbf {T}(\sigma ')\). And because \(\sigma _0\) is faithful, \(\sigma _0 \preceq \mathbf {T}(\sigma )\). Therefore \(\sigma _0 \preceq \mathbf {T}(\sigma ')\), i.e. \(\mathbf {T}(\sigma ') \in \varSigma '\).
Now consider the (meet) semi-lattice \(\langle \varSigma ', \preceq \rangle \) rooted in \(\sigma _0\). We just showed that for each \(\sigma ' \in \varSigma '\), \(\mathbf {T}(\sigma ') \in \varSigma '\). In addition, from Lemma 1, \(\mathbf {T}\) is monotone over \(\langle \varSigma ', \preceq \rangle \). So from a (weaker version of) the Knaster-Tarski Theorem, \(\mathbf {T}\) admits a fixed-point \(\sigma _2\) over \(\varSigma '\). And because \(\sigma _0 \preceq \sigma _2\), \(\sigma _2\) complies with all targets for G and S. Therefore \(\sigma _2\) is strictly faithful for G and S. \(\square \)
All We Need Is One Target. The following explains why the complexity results provided in Sect. 4 only consider graph validation with a single target node.
Proposition 2
Given a graph G, set S of shapes and target nodes in G for each \(s \in S\), one can construct in linear time a graph \(G'\) and set \(S'\) of shapes, such that G is valid against S iff \(G'\) is valid against \(S'\), and \(S'\) has a single target in \(G'\).
Proof
(Sketch). Let \(s_1, .., s_n\) be the shapes in S, with respective targets \(v_1^1, .., v_1^{m1}, .., v_n^1, .., v_n^{mn}\). Extend G with a fresh node \(v_0\), and an edge \((v_o, e_i^j, v_i^j)\) for each \(v_i^j\), with \(e_i^j\) a fresh edge label. Then delete all target expressions in S, and extend S with a fresh shape \(s_0\), with target node \(v_0\), and constraint \(\phi _{s_0} \doteq \ (\ge _1 e_1^{m1}.\top ) \wedge .. .. \wedge (\ge _1 e_1^{mn}.\top )\). \(\square \)
3.5 Validation and Stratified Negation
Section 2.2 suggested that the need for partial assignments comes from constraints combining circular references with negation, called non-stratified. We now make this intuition more precise, showing that we can indeed focus solely on total assignments if the constraints are stratified.
To formalize this idea, we borrow the notion of stratification from Datalog [10] (assuming w.l.o.g that constraints do not contain two consecutive negation symbols).
Definition 8
(stratification). A set S of shape definitions is stratified if there is a total function str: \(S \rightarrow \mathbb {N}\) such that:
-
If \(s_1\) appears in \(\phi _{s_2}\), then \(str (s_1) \le str (s_2)\)
-
If \(s_1\) appears in \(\phi _{s_2}\) in the scope of a negation then \(str (s_1) < str (s_2)\).
It must be emphasized that the language \(\mathcal {L}\) does not include \(\le _n r\) or \(=_n r\). If these operators were included, then one would need to redefine the second condition accordingly, as \(\le _n r\) is a form of negation.
The following result confirms that a semantics based on total assignment is sufficient for stratified sets of shapes.
Proposition 3
Let S be a stratified set of shapes and G a graph. Then there exists a faithful assignment for G and S iff there exists a total faithful assignment for G and S.
Proof
(Sketch). For the right direction, the proof is trivial. For the left direction, to simplify notation, we represent assignments as sets of positive and negative atoms. Let \(\sigma \) be a faithful assignment for G and S, and let \(S_1, .., S_n\) be the strata of S, from lowest to highest. The proof constructs an extension \(\sigma '\) of \(\sigma \), stratum by stratum, initialized with the empty set. For each stratum \(S_i\) (starting from \(S_0\)), \(\sigma '\) is extended in three steps. First, \(\sigma '\) is extended with \(\sigma \) reduced to atoms with shape names in \(S_i\). Then \(\mathbf {T}\) is applied to \(\sigma '\) recursively, until a fixed-point is reached. Finally, \(\sigma '\) is extended with each s(v) such that v is a node in G, \(s \in S_i\) and \(\lnot s(v) \not \in \sigma '\). It can be shown by induction on i that this extension of \(\sigma '\) always exists, and complies with all constraints for shapes in \(S_0, .., S_i\). So when i reaches n, the last extension of \(\sigma '\) is a total faithful assignment for G and S. \(\square \)
This result is important for computational reasons. It also implies that 3-valued validation is not easier than 2-valued validation, which may come as a surprise.
4 Complexity
We now study the computational complexity of the validation problem, defined as follows (full proofs are provided in the online appendix):

Based on Proposition 2, we focused on instances with one target node (for one shape in S). We also assume that this target node is already known. Table 2 summarizes our results. As is customary, since the size of G is likely to be orders of magnitude larger than the size of S, we also study the problems Validation(S) and Validation(G), for a fixed set S of shapes and fixed graph G, called data complexity and constraint complexity below.
We consider two fragments of the constraint language \(\mathcal {L}\): (i) \(\mathcal {L}_{\ge _1, \lnot , \wedge }\) is the fragment defined by the grammar \( \phi {:}{:}= \ \top \mid I \mid s \mid \phi _1 \wedge \phi _2 \mid \lnot \phi \mid \ \ge _1 p.\phi \), where p is an IRI, and (ii) \(\mathcal {L}_{\ge _n, \wedge , \vee , r, \text {EQ}}\) is the fragment defined with \( \phi {:}{:}= \ \top \mid I \mid s \mid \phi _1 \wedge \phi _2 \mid \phi _1 \vee \phi _2 \mid \) \(\ge _n r.\phi \mid \text {EQ}(r_1, r_2)\), where \(r, r_1, r_2\) are property paths and \(\phi _1 \vee \phi _2\) is interpreted (as expected) as \(\lnot (\lnot \phi _1 \wedge \lnot \phi _2)\).
We start by showing an \(\textsc {NP} \) upper bound for combined complexity, based on guessing a witnessing faithful assignment. Then we show that this upper bound is tight, even for a fixed set of shapes (data complexity) using stratified negation and basic operators (\(\ge _1, \lnot \) and \(\wedge \)). We also show that this bound is tight for a fixed graph. Lastly, we show that allowing disjunction but disallowing negation otherwise is sufficient to regain tractability.
Let us start with \(\textsc {NP} \) membership. First, all property paths present in S can be materialized in time polynomial in \(|G| \cdot |S|\) before validation. In addition, by introducing fresh shape names, S can be transformed in polynomial time into an equivalent set \(S'\) of shapes, whose constraints contain at most one operator. Then assuming that we can guess a faithful assignment \(\sigma \) for G and \(S'\), we only to check \(\sigma \) is indeed faithful. To do so, it is sufficient to compute the value of  for each node v in G and \(s \in S'\), which is again polynomial in \(|G|+|S|\), even with a binary encoding of cardinality constraints. Summing up, we have:
for each node v in G and \(s \in S'\), which is again polynomial in \(|G|+|S|\), even with a binary encoding of cardinality constraints. Summing up, we have:
Proposition 4
(Combined – Upper Bound). Validation is in \(\textsc {NP} \).
Now for the lower bound, validation is already intractable in data complexity for stratified \(\mathcal {L}_{\ge _1, \lnot , \wedge }\). This may come as a surprise, considering that data complexity of ground fact entailment in stratified Datalog is in PTime [10]. We show \(\textsc {NP} \)-hardness by a reduction from the satisfiability problem of a propositional circuit: there is a fixed set S of shapes such that every propositional circuit can be transformed (in linear time) into a graph, and this graph is valid against S iff the circuit is satisfiable.
Proposition 5
(Data – Lower Bound). There is a stratified fixed set S of shapes in \(\mathcal {L}_{\ge _1, \lnot , \wedge }\) such that Validation(S) is \(\textsc {NP} \)-hard.
We also show that the problem is \(\textsc {NP} \)-hard in constraint complexity for the same fragment (with a reduction from SAT):
Proposition 6
(Constraint – Lower Bound). There is a fixed graph G such that Validation(G) is \(\textsc {NP} \)-hard, even if S is restricted to stratified sets of shapes in \(\mathcal {L}_{\ge _1, \lnot , \wedge }\).
As a more optimistic result, validation is in PTime if one allows disjunction as a native operator, but disallows negation otherwise. The proof relies on the (unique) minimal fixed-point \(\sigma \) of \( \mathbf{T }\) w.r.t. \(\preceq \), which can be computed in time polynomial in \(|G|+|S|\). Let \(v_0\) be the (unique) target node to validate, against shape \(s_0\). If \(\lnot s_0 \in \sigma (v_0)\), then G is invalid. Otherwise, it can be shown that there must be an extension of \(\sigma \) (w.r.t. \(\preceq \)) which is faithful for G and S.
Proposition 7
(Combined – Upper Bound). Validation is in P for \(\mathcal {L}_{\ge _n, \wedge , \vee , r, \text {EQ}}\).
Finally, we show PTime hardness for a sub-fragment of \(\mathcal {L}_{\ge _n, \wedge , \vee , r, \text {EQ}}\) (without property paths and path equality), with a log-space reduction from the problem of evaluating a monotone boolean circuit.
Proposition 8
(Combined – Lower Bound). Validation is P-hard for \(\mathcal {L}_{\ge _n, \wedge , \vee , r, \text {EQ}}\).
5 Approximation
The above intractability result for data complexity (Proposition 6), and even for a stratified set of shapes, is an important limitation. In order to alleviate this problem, we present in this section an approximation algorithm to decide whether a graph G is valid against a set S of shapes, with an integer parameter k. If k is bounded, then the algorithm is sound, and runs in time polynomial in |G|. If k is unbound, then the algorithm is sound and complete, but may run in time exponential in |G|. The approximation is sound in that the algorithm returns Valid (resp. Invalid) only if G is valid (resp. not valid) against S.
For readability, from Proposition 2, we focus on validation with a single target node \(v_0\), for shape \(s_0\). Algorithm 1 describes the procedure, composed of two steps. The first step intuitively computes an assignment \(\sigma _{\text {minFix}}\) matching all constraints enforced by the graph, regardless of the target. If the validity of G cannot be decided after this (polynomial) step, then \(\sigma _{\text {minFix}}\) is extended by assigning \(s_0\) to \(v_0\), and an attempt is made to propagate constraints from \(v_0\) to its successors, in order for \(v_0\) to satisfy \(\phi _{s_0}\).
Step 1: Minimal Fixed-Point. As a reminder from Sect. 3.3, we use \(\varSigma ^{G,S}\) to denote the set of all (possibly partial) assignments for G and S. The first step of the algorithm computes the minimal fixed-point \(\sigma _{\text {minFix}}\) of the operator \(\mathbf {T}\) (see Definition 5) w.r.t. \(\preceq \). Because \(\langle \varSigma ^{G,S}, \preceq \rangle \) is a semi-lattice and \(\mathbf {T}\) is monotone w.r.t. \(\preceq \) (Lemma 1), \(\sigma _{\text {minFix}}\) must exist and be unique. It can also be computed in time polynomial in |G|, initializing \(\sigma _{\text {minFix}}\) with the empty set, and then applying \(\mathbf {T}\) to \(\sigma _{\text {minFix}}\) recursively, until a fixed-point is reached. This is performed by procedure ComputeMinFix. If \(s_0 \in \sigma _{\text {minFix}}(v_0)\), then the graph is valid, Line 2. Furthermore, any strictly faithful assignment of for G and S must be a fixed-point of \(\mathbf {T}\) (see Sect. 3.3), and therefore must extend \(\sigma _{\text {minFix}}\). So from Proposition 1, If \(\lnot s_0 \in \sigma _{\text {minFix}}(v_0)\), then the graph is invalid, Line 3.
Step 2: Breadth-First Search. The next step consists in searching for a faithful assignment, in a breadth-first fashion, starting from the target node \(v_0\). We abuse notation and use set operators (\(\cup , \in \), etc.) to describe the stack. Similarly, for brevity, we represent assignments interchangeably as functions or as sets of (positive and negative) atoms.
Each element of the stack (i.e. each “branch” of this exploration) is a tuple
\(\langle \sigma , \sigma ^P, A, n\rangle \), where:
-
\(\sigma \) is the current assignment being constructed, initialized with \(\sigma _{\text {minFix}} \cup \{s_0(v_0)\}\).
-
\(\sigma ^P \preceq \sigma \) keeps track of shapes freshly assigned to a node during the previous expansion of \(\sigma \). For any element of the stack, if \(\sigma ^P\) is empty, then no constraint needs to be propagated in this branch, i.e. \(\sigma \) is a faithful assignment, and so the graph is validated, line 7.
-
A is a set of atoms of the form s(v), such that \(s(v) \not \in \sigma \) and \(\lnot s(v) \not \in \sigma \),
-
n is the current depth of the exploration, incremented each time \(\sigma \) is extended. When n reaches k, the size of the stack cannot be extended anymore, which triggers a call to \(\textsc {Reduce}\), line 11, to merge some of the current branches.
Line 8, function extend computes each minimal extensions \(\sigma '\) of \(\sigma \) such that:
-
If \(s \in \sigma ^P(v)\), then
 ,
, -
If \(\lnot s \sigma ^P(v)\), then
 , and
, and -
if \(s(v) \in A\), then \(\{s, \lnot s\} \cap \sigma (v) = \emptyset \).
It can be shown that each call to extend can be executed in time \(O(|G|^{|S|})\).
Finally, if the depth n of the exploration reaches k, line 11, then procedure reduce prevents the number of elements in the stack to increase. Line 18, function getClosestPair retrieves the two closest assignments \(\sigma _1\) and \(\sigma _2\) (in terms of edit distance) in the Stack. Then function getConflicts 20 retrieves the (possibly empty) set A of atoms which \(\sigma _1(v)\) and \(\sigma _2(v)\) disagree on, i.e. \(s(v) \in A\) if both s and \(\lnot s\) are in \(\sigma _1(v) \cup \sigma _2(v)\), and the procedure replace sets each \(\sigma _i\) to \(\sigma _i \setminus \{s(v),\lnot s(v)\}\). After this step, either \(\sigma _1 \preceq \sigma _2\) or \(\sigma _2 \preceq \sigma _1\) must hold, and only the greater of the two (w.r.t \(\preceq \)) is retained (Line 23) and pushed in the stack.

The number of possible assignments is of \(O(2^{|G|})\), but the number of assignments created by extend is \(O(|G|^{|S|})\). So if the parameter k is fixed, the reduced stack makes sure that the execution time is \(O(|G|^{|S|.k})\).
6 Related Work
Several schema languages have been proposed or implemented for RDF before SHACL, and some of them are closely associated to the design of SHACL. But first, it should be mentioned that RDF Schema (RDFS), contrary to what its name may suggest, is not a schema language in the classical sense, but is primarily used to infer implicit facts.
Among the proposals which do not relate (to our knowledge) to the genesis of SHACL, are proposals for RDF integrity constraints [1, 13]. We have not explored a formal comparison between these formalisms and SHACL, but conjecture that they are incomparable with SHACL.
SPINFootnote 6 allows the user to express constraints as SPARQL queries (natively, or using templates) and to declare targets for these constraints, similar to SHACL targets. SPIN became a W3C member submission in 2011, before being explicitly superseded by SHACL in 2017. Being based on SPARQL, it supports negation, but not full recursion.
ShEx has been actively developed since 2012 [6], as a dedicated constraint language for RDF, strongly inspired by XML schema languages. The first version of ShEx did support recursion, but no negation. A formal semantics was provided in [21], based on regular bag expressions. Recently, ShEx 2.0Footnote 7 incorporated negation, and a formal semantics was provided in [7], together with a abstract language called Shape Schemas. As highlighted in [5], ShEx and SHACL have lot in common, and the semantics provided in [7] can be directly adapted to SHACL. This proposal is also similar to the one made in this article, in that validation is based on a typing verifying target and constraints, similar to our notion of shape assignment. A difference though is that the semantics proposed in [7] is restricted to stratified constraints. Moreover, the (unique) typing used in [7] to define validation favors the validation of shapes in the lowest stratum, so that the graph of Fig. 2 for instance would be considered invalid.
Another line of work is inspired by the Web Ontology Language (OWL), which is based on Description Logics (DLs) [3]. Like RDFS, OWL was not designed as a schema language, but adopts instead the open-world assumption, not well-suited to express constraints. Still, proposals have been made to reason with DLs understood as constraints: by introducing auto-epistemic operators [11], partitioning DL formulas into regular and constraint axioms [17, 22], or reasoning with closed predicates [19]. This last approach was actually proposed as a semantic grounding for SHACL [18], reducing constraint validation to first-order satisfiability with closed binary predicates. But as illustrated with Example Fig. 3, this semantics does not behave well in the presence of targets and non-stratified constraints.
Recursion over negation has been traditionally studied in logical programming (see e.g. [10]), and answer-set programming (see [20] in the context of SPARQL), where stable model semantics (SMS) is one of the most prominent paradigms [14]. But SMS is based on so-called minimal models, whereas shape assignments may not be minimal. This makes encoding SHACL into logical programming non trivial, as suggested by complexity results: ground-fact entailment is data-tractable for stratified Datalog, in contrast to our semantics (see Proposition 5). A possible way to relate the two semantics, at least for the stratified case, is to reason about shape “complements” under SMS. Still, our preliminary investigations tend to show that this is not straightforward.
7 Conclusion
The article proposes an abstract syntax and formal semantics for SHACL core constraint components. This semantics is robust enough to handle constraints with arbitrary recursion, which can be expressed in SHACL, but whose validation is left explicitly open in the specification. One of our contributions is to highlight semantic issues related to non-stratified SHACL targets. To address such cases, we adopt a notion of partial assignment of (positive and negated) shapes to nodes, and define a semantics with desirable properties, such as monotonicity of forward-chaining, or equivalence with total assignments in the stratified case. We then show that the validation problem is NP-complete for any fragment with at least conjunction, negation and existential quantification, in the size of either graph or constraints, regardless of stratification. Therefore we propose a sound approximation algorithm, parameterized by an integer k, which guarantees termination in time polynomial in the size of the graph.
As a continuation, we plan to investigate other problems, such as (finite) satisfiability of a set of shapes, or SPARQL query containment in the presence of SHACL constraints. We also expect this formalization to be abstract enough to be extended to other constraint languages for graphs, such as ShEx, in order to handle arbitrary recursion.
Notes
- 1.
- 2.
- 3.
- 4.
This example is borrowed from Peter Patel-Schneider: https://research.nuance.com/wp-content/uploads/2017/03/shacl.pdf.
- 5.
Constraints on node sucessors in SHACL are by default universally quantified. This is why sh:not here requires one successor violating :PolentoneShape to exist.
- 6.
- 7.
References
Akhtar, W., Cortés-Calabuig, Á., Paredaens, J.: Constraints in RDF. In: Schewe, K.-D., Thalheim, B. (eds.) SDKB 2010. LNCS, vol. 6834, pp. 23–39. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23441-5_2
Arenas, M., Gutierrez, C., Pérez, J.: Foundations of RDF databases. In: Tessaris, S., et al. (eds.) Reasoning Web 2009. LNCS, vol. 5689, pp. 158–204. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03754-2_4
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., Patel-Schneider, P.: The Description Logic Handbook: Theory, Implementation and Applications. Cambridge University Press, Cambridge (2003)
Berners-Lee, T., Hendler, J., Lassila, O.: The semantic web. Sci. Am. 284(5), 34–43 (2001)
Boneva, I.: Comparative expressiveness of ShEx and SHACL (early working draft) (2016)
Boneva, I., Labra-Gayo, J.E., Hym, S., Prud’hommeau, E.G., Solbrig, H.R., Staworko, S.: Validating RDF with shape expressions. CoRR, abs/1404.1270 (2014)
Boneva, I., Labra Gayo, J.E., Prud’hommeaux, E.G.: Semantics and validation of shapes schemas for RDF. In: d’Amato, C., et al. (eds.) ISWC 2017. LNCS, vol. 10587, pp. 104–120. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68288-4_7
Corman, J., Reutter, J.L., Savkovic, O.: Semantics and validation of recursive SHACL (extended version). Technical report KRDB18-1. KRDB Research Center, Free Univ. Bozen-Bolzano (2018)
Corman, J., Reutter, J.L., Savkovic, O.: Validating graph data against recursive constraints: a semantics for SHACL. AMW (2018, to appear)
Dantsin, E., Eiter, T., Gottlob, G., Voronkov, A.: Complexity and expressive power of logic programming. ACM Comput. Surv. 33(3), 374–425 (2001)
Donini, F.M., Nardi, D., Rosati, R.: Description logics of minimal knowledge and negation as failure. ACM Trans. Comput. Log. (TOCL) 3(2), 177–225 (2002)
Ekaputra, F.J., Lin, X.: SHACL4P: SHACL constraints validation within Protégé ontology editor. In: ICoDSE (2016)
Fischer, P.M., Lausen, G., Schätzle, A., Schmidt, M.: RDF constraint checking. In: Proceedings of the Workshops of the EDBT/ICDT 2015 Joint Conference, EDBT/ICDT, Brussels, Belgium, 27 March 2015, pp. 205–212 (2015)
Gelfond, M., Lifschitz, V.: The stable model semantics for logic programming, pp. 1070–1080. MIT Press (1988)
Harris, S., Seaborne, A., Prud’hommeaux, E.: SPARQL 1.1 query language. W3C Recomm. 21(10) (2013)
Kostylev, E.V., Reutter, J.L., Romero, M., Vrgoč, D.: SPARQL with property paths. In: Arenas, M., et al. (eds.) ISWC 2015. LNCS, vol. 9366, pp. 3–18. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25007-6_1
Motik, B., Horrocks, I., Sattler, U.: Bridging the gap between OWL and relational databases. Web Semant.: Sci. Serv. Agents World Wide Web 7(2), 74–89 (2009)
Patel-Schneider, P.F.: Using description logics for RDF constraint checking and closed-world recognition. In: AAAI (2015)
Patel-Schneider, P.F., Franconi, E.: Ontology constraints in incomplete and complete data. In: Cudré-Mauroux, P., et al. (eds.) ISWC 2012. LNCS, vol. 7649, pp. 444–459. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35176-1_28
Polleres, A., Wallner, J.P.: On the relation between SPARQL1.1 and answer set programming. J. Appl. Non-Class. Log. 23(1–2), 159–212 (2013)
Staworko, S., Boneva, I., Labra-Gayo, J.E., Hym, S., Prud’hommeaux, E.G., Solbrig, H.: Complexity and expressiveness of ShEx for RDF. In: ICDT (2015)
Tao, J., Sirin, E., Bao, J., McGuinness, D.L.: Integrity constraints in OWL. In: AAAI (2010)
Acknowledgements
This work was supported by the QUEST, ROBAST and OBATS projects at the Free University of Bozen-Bolzano, and the Millennium Institute for Foundational Research on Data (IMFD), Chile.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Corman, J., Reutter, J.L., Savković, O. (2018). Semantics and Validation of Recursive SHACL. In: Vrandečić, D., et al. The Semantic Web – ISWC 2018. ISWC 2018. Lecture Notes in Computer Science(), vol 11136. Springer, Cham. https://doi.org/10.1007/978-3-030-00671-6_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-00671-6_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00670-9
Online ISBN: 978-3-030-00671-6
eBook Packages: Computer ScienceComputer Science (R0)










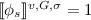

 .
. ,
, , and
, and