Skip to main content
SpringerLink
Log in

Multiscale analysis on two-dimensional nanoscale adhesive contacts

  • Published:
Chinese Journal of Mechanical Engineering Submit manuscript

Abstract

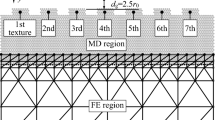
Nanoscale adhesive contacts play a key role in micro/nano-electro-mechanical systems as the dimension of the components come to nanometer. Experimental studies on nanoscale adhesive contacts are limited by some uncertain factors and the cost of experiments is too high. Besides, nanoscale textured surfaces are difficult to process and nanoscale adhesive contacts of textured surfaces are still lack of investigation. By using multiscale method, which couples molecular dynamics simulation and finite element method, two-dimensional nanoscale adhesive contacts between a rigid cylindrical tip and an elastic substrate are investigated. For the contacts between the rigid cylindrical tip and smooth surface, Von Mises stress distributions, the maximum Von Mises stresses, and contact forces are compared for different radii to show the size effects and adhesive effects. The phenomena of hysteresis are observed and more obvious as the radii of the tip increase. The influences of indentation depth and indentation speed are also discussed. Then two series of textured surfaces are employed, and the influences of the texture asperity shape, asperity height, and asperity spacing on contact forces are studied. The contact forces comparisons show that textured surfaces can reduce contact forces effectively in the range of the two series. Contact forces of textured surfaces increase as the asperity heights increase, and textured surfaces with smaller asperity spacing will get higher contact forces. Contact forces may be controlled through textured surfaces in the future. The obtained results will help to improve contact condition and provide theory basis for texture design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. DERJAGUIN B V, MULLER V M, TOPROV Y P. Effect of contact deformations on the adhesion of particles[J]. Journal of Colloid and Interface Science, 1975, 53(2): 314–326.

    Article  Google Scholar 

  2. JOHNSON K L, KENDALL K, ROBERTS A D. Surface energy and the contact of elastic solids[J]. Proceedings of the Royal Society of London Series A, 1971, 324(1558): 301–313.

    Article  Google Scholar 

  3. MAUGIS D. Adhesion of spheres: the JKR-DMT transition using a Dugdale model[J]. Journal of Colloid and Interface Science, 1992, 150(1): 243–269.

    Article  Google Scholar 

  4. LUAN B, ROBBINS M O. The breakdown of continuum models for mechanical contacts[J]. Nature, 2005, 435(7044): 929–932.

    Article  Google Scholar 

  5. LUO Jianbin, HE Yu, WEN Shizhu, et al. Challenges to tribology arisen form the development of micro- and nano-manufacturing technology[J]. Tribology, 2005, 25(3): 283–288. (in Chinese)

    Google Scholar 

  6. QUON R A, KNARR R F, VANDERLICK T K. Measurement of the deformation and adhesion of rough solids in contact[J]. The Journal of Physical Chemistry B, 1999, 103(25): 5 320–5 327.

    Article  Google Scholar 

  7. KNARR R F, QUON R A, VANDERLICK T K. Direct force measurements at the smooth gold/mica interface[J]. Langmuir, 1998, 14(22): 6 414–6 418.

    Article  Google Scholar 

  8. ALCANTAR N A, PARK C, PAN J M, et al. Adhesion and coalescence of ductile metal surfaces and nanoparticles[J]. Acta Materialia, 2003, 51(1): 31–47.

    Article  Google Scholar 

  9. VARENBERG M, PERESSADKO A, GORB S, et al. Effect of real contact geometry on adhesion[J]. Applied Physics Letters, 2006, 89(12): 121905 (1–3).

    Article  Google Scholar 

  10. BENZ M, ROSENBERG K J, KRAMER E J, et al. The deformation and adhesion of randomly rough and patterned surfaces[J]. The Journal of Physical Chemistry B, 2006, 110(24):11 884–11 893.

    Article  Google Scholar 

  11. ZOU M, WANG H, LARSON P R, et al. Ni nanodot-patterned surfaces for adhesion and friction reduction[J]. Tribology Letters, 2006, 24(2): 137–142.

    Article  Google Scholar 

  12. YONG C W, SMITH W, KENDALL K. Surface contact studies of NaCl and TiO2: molecular dynamics simulation studies[J]. Journal of Materials Chemistry, 2002, 12(9): 2 807–2 815.

    Article  Google Scholar 

  13. LANDMAN U, LUEDTKE W D, BURNHAM N A, et al. Atomistic mechanisms and dynamics of adhesion, nanoindentation, and fracture[J]. Science, 1990, 248(4954): 454–461.

    Article  Google Scholar 

  14. LANDMAN U, LUEDTKE W D, RINGER E M. Atomistic mechanisms of adhesive contact formation and interfacial processes[J]. Wear, 1992, 153(1): 3–30.

    Article  Google Scholar 

  15. LUAN B, ROBBINS M O. Contact of single asperities with varying adhesion: comparing continuum mechanics to atomistic simulations[J]. Physical Review E, 2006, 74(2): 026111 (1–17).

    Article  Google Scholar 

  16. LIU Tianxiang, LIU Geng, PETER Wiggers, et al. Study on contact characteristic of nanoscale asperities by using molecular dynamics simulations[J]. ASME Journal of Tribology, 2009, 131(2): 022001 (1–10).

    Article  Google Scholar 

  17. CURTIN W A, MILLER R E. Atomistic/continuum coupling in computational materials science[J]. Modeling and Simulation in Materials Science and Engineering, 2003, 11(3): R33–R68.

    Article  Google Scholar 

  18. LIU W K, KARPOV E G, ZHANG S, et al. An introduction to computational nanomechanics and materials[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(17–20): 1 529–1 578.

    MathSciNet  Google Scholar 

  19. GRAVEMEIER V, LENZ S, WALL W A. Towards a taxonomy for multiscale methods in computational mechanics: building blocks of existing methods[J]. Computational Mechanics, 2008, 41(2): 279–291.

    Article  MathSciNet  MATH  Google Scholar 

  20. LIU W K, PARK H S, QIAN D, et al. Bridging scale methods for nanomechanics and materials[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(13–16): 1 407–1 421.

    MathSciNet  Google Scholar 

  21. PARK H S, KARPOV E G, LIU W K, et al. The bridging scale for two-dimensional atomistic/continuum coupling[J]. Philosophical Magazine, 2005, 85(1): 79–113.

    Article  Google Scholar 

  22. BELYTSCHKO T, XIAO S P. Coupling methods for continuum model with molecular model[J]. International Journal for Multiscale Computational Engineering, 2003, 1(1): 115–126.

    Article  Google Scholar 

  23. XIAO S P, BELYTSCHKO T. A bridging domain method for coupling continua with molecular dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(17–20): 1 645–1 669.

    MathSciNet  Google Scholar 

  24. KARPOV E G, YU H, PARK H S, et al. Multiscale boundary conditions in crystalline solids: theory and application to nanoindentation[J]. International Journal of Solids and Structures, 2006, 43(21): 6 359–6 379.

    Article  Google Scholar 

  25. TADMOR E B, ORTIZ M, PHILLIPS R. Quasicontinuum analysis of defects in solids[J]. Philosophical Magazine A, 1996, 73(6):1 529–1 563.

    Article  Google Scholar 

  26. MEI J F, LI J W, NI Y S, et al. Multiscale simulation of indentation, retraction and fracture processes of nanocontact[J]. Nanoscale Research Letters, 2010, 5(4): 692–700.

    Article  Google Scholar 

  27. ANCIAUX G, MOLINARI J F. Contact mechanics at the nanoscale, a 3D multiscale approach[J]. International Journal for Numerical Methods in Engineering, 2009, 79(9): 1 041–1 067.

    Article  Google Scholar 

  28. SHILKROT L E, MILLER R E, CURTIN W A. Coupled atomistic and discrete dislocation plasticity[J]. Physical Review Letters, 2002, 89(2): 025501.

    Article  Google Scholar 

  29. SHILKROT L E, CURTIN W A, MILLER R E. A coupled atomistic/continuum model of defects in solids[J]. Journal of the Mechanics and Physics of Solids, 2002, 50(10): 2 085–2 106.

    Article  Google Scholar 

  30. LUAN B Q, HYUN S, MOLINARI J F, et al. Multiscale modeling of two-dimensional contacts[J]. Physical Review E, 2006, 74(4): 046710 (1–11).

    Article  Google Scholar 

  31. AGRAWAL P M, RICE B M, THOMPSON D L. Predicting trends in rate parameters for self-diffusion on FCC metal surfaces[J]. Surface Science, 2002, 515(1): 21–35.

    Article  Google Scholar 

  32. DOLL J D, MCDOWELL H K. Theoretical studies of surface diffusion: self-diffusion in the FCC (111) system[J]. Journal of Chemical Physics, 1982, 77(1): 479–483.

    Article  Google Scholar 

  33. SWOPE W C, ANDERSEN H C, BERENS P H, et al. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters[J]. Journal of Chemical Physics, 1982, 76(1): 637–649.

    Article  Google Scholar 

  34. RAY J R, RAHMAN A. Statistical ensembles and molecular dynamics studies of anisotropic solids[J]. Journal of Chemical Physics, 1984, 80(9): 4 423–4 428.

    Article  Google Scholar 

  35. RAY J R, RAHMAN A. Statistical ensembles and molecular dynamics studies of anisotropic solids II[J]. Journal of Chemical Physics, 1985, 82(9): 4 243–4 247.

    Article  Google Scholar 

  36. LENG Y S, YANG G P, HU Y Z, et al. Computer experiments on nano-indentation: a molecular dynamics approach to the elasto-plastic contact of metal copper[J]. Journal of Materials Science, 2000, 35(8): 2 061–2 067.

    Article  Google Scholar 

  37. YANG J, KOMVOPOULOS K. A molecular dynamics analysis of surface interference and tip shape and size effects on atomic-scale friction[J]. ASME, Journal of Tribology, 2005, 127(3): 513–521.

    Article  Google Scholar 

  38. ISRAELACHVILI J N. Skimming the surface[J]. Nature, 2005, 435(7044): 893–895.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Key Laboratory of Contemporary Design and Integrated Manufacturing Technology of Ministry of Education, Northwestern Polytechnical University, Xi’an, 710072, China

    Ruiting Tong, Geng Liu & Lan Liu

Authors
  1. Ruiting Tong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Geng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ruiting Tong.

Additional information

This project is supported by National Natural Science Foundation of China (Grant No. 50975232), and Fundamental Research Foundation of Northwestern Polytechnical University, China (Grant No. JC20110249)

TONG Ruiting, born in 1981, is currently a lecturer at Key Laboratory of Contemporary Design and Integrated Manufacturing Technology of Ministry of Education, Northwestern Polytechnical University, China. He received his doctor degree from Northwestern Polytechnical University, China, in 2010. His research interests include multiscale method, contact mechanics, nanoscale friction.

LIU Geng, born in 1961, is currently a professor at Northwestern Polytechnical University, China. His research interests include dynamics of mechanical system, tribology, contact mechanics, biomechanics, multiscale method, etc.

LIU Lan, born in 1974, is currently an associate professor at Northwestern Polytechnical University, China. His research interests include meshfree method, contact mechanics, biomechanics.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tong, R., Liu, G. & Liu, L. Multiscale analysis on two-dimensional nanoscale adhesive contacts. Chin. J. Mech. Eng. 25, 446–455 (2012). https://doi.org/10.3901/CJME.2012.03.446

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3901/CJME.2012.03.446

Key words

Search

Navigation