Dynamic fit index cutoffs for one-factor models

Abstract

Assessing whether a multiple-item scale can be represented with a one-factor model is a frequent interest in behavioral research. Often, this is done in a factor analysis framework with approximate fit indices like RMSEA, CFI, or SRMR. These fit indices are continuous measures, so values indicating acceptable fit are up to interpretation. Cutoffs suggested by Hu and Bentler (1999) are a common guideline used in empirical research. However, these cutoffs were derived with intent to detect omitted cross-loadings or omitted factor covariances in multifactor models. These types of misspecifications cannot exist in one-factor models, so the appropriateness of using these guidelines in one-factor models is uncertain. This paper uses a simulation study to address whether traditional fit index cutoffs are sensitive to the types of misspecifications common in one-factor models. The results showed that traditional cutoffs have very poor sensitivity to misspecification in one-factor models and that the traditional cutoffs generalize poorly to one-factor contexts. As an alternative, we investigate the accuracy and stability of the recently introduced dynamic fit cutoff approach for creating fit index cutoffs for one-factor models. Simulation results indicated excellent performance of dynamic fit index cutoffs to classify correct or misspecified one-factor models and that dynamic fit index cutoffs are a promising approach for more accurate assessment of model fit in one-factor contexts.

Many research interests in psychology and adjacent fields revolve around latent constructs that cannot be observed directly (Bollen, 2002). Multiple-item scales are commonly used to measure these latent constructs and confirmatory factor analysis is typically used to provide evidence that constructs are measured appropriately (Brown, 2015). The quality of this evidence is often summarized with approximate fit indices such as SRMR, RMSEA, and CFI (e.g., Jackson et al., 2009). These fit indices are effect size-type measures, not inferential tests of exact fit. That is, rather than testing for the presence of misspecification as in the context of exact fit, approximate fit indices seek to quantify the degree of misspecification present in a fitted model (Joreskog & Sorbom, 1982; Tucker & Lewis, 1973). Historically, a challenge in model evaluation with fit indices has been discerning which values of these indices suggest an acceptably close fit and which values suggest a poor fit (Marsh et al., 2004). That is, because fit indices are designed to quantify misfit, the answer to “how good is good enough” inherently contains some degree of subjectivity. The methodological literature began to rigorously study this question in the mid-1990s (MacCallum et al., 1996), culminating in the seminal simulation study by Hu & Bentler (1999).

Hu & Bentler (1999) designed a large simulation study to evaluate which fit index values were sensitive to misspecifications to provide more systematicity around the use of fit indices. They generated data from a three-factor model with five items per factor and fit models that (a) contained no misspecifications and (b) models that contained either omitted cross-loadings or omitted factor covariances. Conclusions from this simulation led to the now well-known fit index cutoffs of SRMR ≤ 0.08, RMSEA ≤ 0.06, and CFI ≥ 0.96, which were able to satisfactorily distinguish misspecified models correct models for their particular three-factor model. Despite Hu and Bentler’s own warnings against generalizing cutoffs beyond the model subspace they studied (Hu & Bentler, 1998, p. 446), researchers have adopted these cutoffs widely across different model types and model characteristics (McNeish et al., 2018).

One pertinent area where these cutoffs are tenuously overgeneralized is one-factor models. One-factor models are common in scale development and the psychometric literature has recently seen an uptick in in one-factor models for assessing psychometric properties of scales or as alternatives to sum or item-average scoring (e.g., Edwards & Wirth, 2009; Fried et al., 2016; Fried & Nesse, 2015; Kuhfeld & Soland, 2020; McNeish & Wolf, 2020; Shi et al., 2019; Shi & Maydeu-Olivares, 2020; Slof-Op’t Landt et al., 2009). The disconnect lies in that the cutoffs from the Hu & Bentler (1999) simulation were based on sensitivity to omitted cross-loadings and omitted factor covariances in three-factor models. However, one-factor models do not have other factors on which items can cross-load or with which the single factor can covary. There is therefore an incongruency whereby fit of one-factor models are often judged against criteria designed to be sensitive to misspecifications that cannot exist in one-factor models.

In this paper, we demonstrate by simulation that the traditional cutoffs derived by Hu & Bentler (1999) are not necessarily effective for evaluating fit of one-factor models because fit indices have different sensitivity to the model characteristics and the types of misspecifications of interest in one-factor models. As an alternative, we consider the recently proposed dynamic fit index (DFI) cutoff approach developed by McNeish & Wolf (2021). This method is a generalization of the proposal by Millsap (2007) for custom simulation of cutoffs for each model being evaluated to ensure that cutoffs are not overgeneralized from studies whose conditions deviate from the those of the model being evaluated. That is, if the traditional cutoffs from Hu & Bentler (1999) were derived from a simulation, then cutoffs can be re-derived from a simulation with different conditions that are tailored to the model being evaluated. A DFI cutoff procedure has been proposed for one-factor models, but its sensitivity to misspecifications has not yet been systematically studied. The two primary goals of the paper are therefore (a) to demonstrate potential issues when traditional cutoffs from Hu & Bentler (1999) are applied to one-factor models and (b) to evaluate whether the recently proposed DFI cutoffs are sufficiently sensitive to misspecifications relevant to one-factor models.

To outline the structure of the paper, we first provide background on the simulation study by Hu & Bentler (1999) that led to the traditional cutoffs and the associated methodological literature noting issues with overgeneralizing these traditional cutoffs. This literature tends to focus on different conditions for models with multiple factors but much less attention has been paid to potential issues with one-factor models. We then overview the history of simulation-based alternatives with a focus on the recently developed DFI cutoff method. Next, we calculate DFI cutoffs with an empirical example to give context about how DFI attempts to provide more appropriate cutoffs. We follow with a simulation study to explore how traditional cutoffs and DFI cutoffs perform in the context of one-factor models with respect to correctly classifying whether models are misspecified. We discuss the potential promise of simulation-based techniques like DFI as an accessible option for researchers looking to obtain more accurate evaluations of fit in one-factor models – especially in the modern computational environment where such custom simulations can be completed quickly – as well as limitations and future directions for this line of research.

Origin of traditional cutoffs

Though most researchers who use latent variable models are familiar with the cutoffs derived by Hu & Bentler (1999), appreciation for their origin and the degree to which they generalize is less widespread. This section covers (a) details of the approach taken by Hu & Bentler (1999) to derive cutoffs, (b) what the traditional cutoffs embody, and (c) criticisms of the traditional cutoffs that have appeared in the literature.

Two different models were tested in the simulation in Hu & Bentler (1999). The first was called the “Simple” model, which was a traditional confirmatory factor model with three correlated factors and five items per factor. The second model was called the “Complex” model, which was identical to the Simple model except that three cross-loadings were added (one per factor).

Manipulated conditions included six conditions for sample size (150, 250, 500, 1000, 2500, 5000), seven conditions for non-normality (specific details on p. 8 of Hu & Bentler, 1999), and three conditions for degree of fitted model misspecification (True, Minor, Major). In the True condition, the fitted model exactly matched the data generation model such that there are no misspecifications. For the Simple Model, the Minor condition omits one factor covariance and the Major condition omits two factor covariances. For the Complex Model, the Minor condition omits one cross-loading and the Major condition omits two cross-loadings. The number of factors (3), the number of items per factor (5), and the pattern of standardized factor loadings for the five items on each factor (0.70, 0.70, 0.75, 0.80, 0.80) were constant across all conditions.

Two hundred datasets were generated in each condition such that there was an empirical sampling distribution of cutoffs for each index, in each of the three misspecification conditions. Cutoffs were then derived by comparing the fit index distributions in the True condition to fit index distributions in the Minor condition to locate a value that was able to correctly classify a high percentage of models in the Minor misspecification condition (i.e., having a high true-positive rate; similar to power except that there are no null hypotheses for fit indices) while incorrectly classifying very few of models in the True condition as misspecified (i.e., a low false-positive rate; similar to type I error rate). Hu and Bentler selected the Minor condition for this determination because it seemed to represent a reasonably-sized misspecification that – if present – would be a concern to researchers.

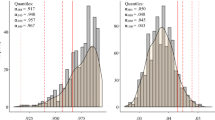
The reference points corresponding to this guideline were that 95% or more of models from the Minor misspecification condition be correctly classified as misspecified while no more than 5% of models from the True condition be misclassified. However, this was a guideline and not a strict rule and the false positive and false negative were sometimes allowed to approach as high 10%. To demonstrate, we have replicated Hu and Bentler’s approach for multivariate normality and N = 500. The empirical distributions are shown in Fig. 1 with True model distribution in dark grey and the Minor misspecification distribution in light grey. The value that correctly classifies at least 95% of misspecification models (the light grey distribution) while misclassifying no more than 5% of correct models (in dark grey) is 0.06, just as derived in Hu & Bentler (1999).

Fig. 1

Comparison of empirical sampling distributions of RMSEA for true model (in dark grey) and the Minor misspecification model (in light grey) using the conditions studied in Hu and Bentler (1999). The cutoff is derived from the value that correctly classifies at least 95% of misspecified models while misclassifying no more than 5% of true models, which in this case (and in Hu & Bentler, 1999) is 0.06

Although these traditional cutoffs are now used to assess the presence of misspecifications throughout a variety of models, there has been widespread criticism of doing so in the methodological literature (e.g., Chen et al., 2008; Fan & Sivo, 2007; Hancock & Mueller, 2011; Heene et al., 2011; Kenny & McCoach, 2003; McNeish et al., 2018; Shi et al., 2019; Savalei, 2012; Shi et al., 2020). The issue is that the simulation approach of Hu & Bentler (1999) is essentially a power analysis. In a traditional power analysis, the goal is to determine the sample size at which statistical tests are sensitive to the presence of an effect. Similarly, the goal of the Hu & Bentler (1999) simulation was to uncover fit index values that are sensitive to the presence of model misspecification. However, just as sufficient sample sizes in power analyses are affected by model characteristics, so too are fit index values that are sensitive to model misspecification.

For instance, interpreting whether N = 100 is a sufficient sample size is difficult without more context such as the research design, the expected effect size, the operating type I error rate, and the desired level of power. Depending on each of these characteristics, the sample size that is considered sufficient can vary (e.g., N = 100 might be reasonable for a repeated measures design or a large effect but may be inadequate for a cross-sectional design or a small effect). Likewise, an RMSEA value higher than 0.06 is not universally indicative of an acceptably small misspecification with all model characteristics. RMSEA values that are sensitive to model misspecifications can vary depending on aspects like the type of model, the number of latent variables, the number of indicators, or the strength of the loadings. Whereas 0.06 might be a great RMSEA cutoff for detecting misspecified models for the three-factor model with 15 items (as studied by Hu & Bentler, 1999), it could be completely inadequate for detecting misspecification in a one-factor model with eight items. Connecting back to the relation to power analysis, using a fixed set of cutoffs is analogous to assuming that there is one fixed sample size that is sufficient across all study designs and expected effect sizes.

Generally speaking, results of simulation studies have limited external validity and are only generalizable to the conditions that were studied (Paxton et al., 2001; Psychometric Society, 1979). There is no inherent statistical theory behind Hu and Bentler’s traditional cutoffs that makes them indicative of good fit, they are simply values derived from one empirical statistical simulation experiment. Just like power analyses for sample size planning, the fit index values that are sensitive to misspecifications are highly dependent on model characteristics. For instance, Hancock & Mueller (2011) showed that models with larger magnitude standardized loadings are more sensitive to misspecification, Kenny et al. (2015) showed that RMSEA is very sensitive to misspecification when models have few degrees, and McNeish & Wolf (2021) noted that the misspecifications used in Hu & Bentler (1999) do not make sense in other modeling context such as growth models or one-factor models because these models typically cannot have omitted cross-loadings.

The several methodological articles criticizing the overgeneralization of traditional cutoffs has led researchers to put forward alternative approaches, although they are seldom applied in empirical studies. These alternatives do not provide fixed values like the traditional cutoffs but rather propose general procedures and frameworks that provide customized cutoffs for assessing fit in each individual model. Though an appealing idea, these methods have tended to be computationally intensive and less accessible to empirical researchers, as there are no standardized approaches or point-and-click software that have adopted them. However, advances in computing and software capabilities have recently permitted broader accessibility of alternative methods. We overview these alternatives methods in the next section and discuss how the latest iteration – DFI cutoffs – may be able to provide improved cutoff values for one-factor models.

Simulation-based approaches to deriving custom cutoffs

Background and development

The DFI cutoff approach is the latest development in a line of research proposing that cutoffs be custom-simulated for each model to avoid overgeneralizing cutoffs (Kim & Millsap, 2014; Millsap, 2007, 2013; Pornprasertmanit et al., 2013, 2021). The prevailing thought of this line of research is that the simulation study by Hu & Bentler (1999) is a clever way to assess sensitivity of fit indices to misspecification, but it is inadequate to derive general cutoffs from a single set of model characteristics. Therefore, just as customized power analysis are performed to determine the sufficient sample size for a model of interest, studies proposing simulation-based techniques suggest that derivation of cutoffs should be customized to determine fit index values that are sufficiently sensitive to misspecification for the characteristics of the model being evaluated.

Earlier research on custom derivation of cutoffs via simulation was based on strong theoretical foundations and the lack of uptake of this approach is likely due to the complexity of coding a simulation for each empirical study. The simsem R package (Pornprasertmanit et al., 2021) provided some support, but some experience with simulation studies and knowledge of the coding in R was still required to successfully implement the method. Given that many empirical researchers are not well versed in simulation techniques or coding, custom derivation of cutoffs via simulation has struggled to gain traction in empirical studies. To address this, the DFI approach sought to provide standardization to simulation-based approaches so that the programmatic and computational aspects of the simulation are automated. The goal was that empirical researchers could take advantage of simulation techniques without necessarily needing to know how to program a simulation study from scratch.

Overview of dynamic fit index cutoff approach¹

The DFI approach features an algorithm that designs and executes a simulation study based on a user’s fitted model. For one-factor models, users only need to input the model’s standardized loadings for each item and the sample size. From this information, DFI internally conducts four simulations to assess sensitivity of SRMR, RMSEA, and CFI to different levels of hypothetical misspecification. Rather than omitted cross-loadings and factor covariances as used in Hu & Bentler (1999), misspecifications that tend to afflict one-factor models are (a) multidimensionality or (b) unmodeled local dependence between items. Though these two issues are not identical, both types of misspecifications can manifest through residual correlations (Ip, 2010, p. 396–399). In the case of local dependence, residual correlations may be needed to account for aspects like testlet effects (DeMars, 2012), method effects (Cole et al., 2007) or when a response to an item depends on a previous item response (e.g., Verhelst & Glas, 1993). For multidimensionality, items that should load on a second factor may have residual correlations when the factor structure is misspecified and their observed covariance is not adequately captured by a single factor (e.g., Ip, 2002).

To reflect the types of misspecifications of interest in one-factor models, the hypothetical levels of misspecification consider by the DFI algorithm are,

• Level 0: The fitted model is correct

• Level 1: The fitted model plus a 0.30 residual correlation between one-third of the items.

• Level 2: The fitted model plus a 0.30 residual correlation between two-thirds of the items.

• Level 3: The fitted model plus a 0.30 residual correlation between all of the items.

Basing the data generation models on the user’s fitted model allows idiosyncratic features like number of items and patterns of factor loadings to be accommodated so that derived cutoffs reflect the characteristics of the model being evaluated.

Residual correlations are used to create hypothetical misspecifications for a few reasons. First, residual correlations are versatile in that they can represent either misspecifications due to local dependence or misspecifications due to an incorrect factor structure. Second, from the perspective of automating the DFI method (and therefore to eliminate any coding necessary for empirical researchers), residual correlations are more straightforward when creating a hypothetical data generation model. Regarding the selection of 0.30 as the magnitude of the residual correlations, (a) a correlation of this magnitude is sufficiently large to be practically meaningful and (b) 0.30 residual correlations provided similar results to the traditional cutoffs during preliminary tests with three-factor models and a level 1 misspecification, so the level 1 misspecification with 0.30 residual correlations appeared to be roughly comparable to the misspecification magnitude upon which the traditional cutoffs are based. We thought this desirable in order to maintain a continuity between the traditional cutoffs and DFI cutoffs.

Three levels of misspecification were selected to reinforce the idea that approximate fit indices are effect sizes intended to quantify misfit rather than a binary tests of model fit (McNeish & Wolf, 2021). We selected three levels of misspecification to mimic the magnitude of the effect sizes typically reported with Cohen’s d (e.g., small, medium, and large; Cohen, 1988). In this case, the three levels of misspecification can be thought of as minor, moderate, and major misspecifications, similar to traditional “Close”, “Fair”, “Mediocre”,” benchmark bins for RMSEA and CFI provided by MacCallum et al., (1996).

The DFI algorithm generates 500 datasets from each of these four hypothetical models and then applies the original fitted model to all 2000 datasets. This results in one empirical distribution of fit index values assuming the fitted model is correct and three empirical distribution of fit index values with the fitted model hypothetically misspecified to varying degrees. This is similar to the approach of Hu & Bentler (1999) except that (a) multiple levels of misspecification severity are tested and (b) the proportion of added misspecifications is held constant across model subspaces. Importantly, the goal of the process is not to identify potential misspecifications in the fitted model. Instead, the goal is to use hypothetically misspecified models to understand the sensitivity of fit index values to different levels of misspecification given the characteristics of the model being evaluated.

The empirical distribution of fit index values for the level 0 model is then compared to each of empirical distributions of fit index values of the level 1, level 2, and level 3 misspecified models, one at a time. Following guidelines used by Hu and Bentler (1999), the cutoff should be chosen such that at least 95% of misspecified models are correctly classified while no more than 5% of correct models are misclassified. This is performed for level 0 vs. level 1, level 0 vs. level 2, and level 0 vs. level 3 to determine three separate cutoffs corresponding to different levels of misspecification severity. Multiple levels of misspecification are provided so that researchers are not consigned to choose between only “good” and “bad” fit as with traditional cutoffs. Instead, users can consider a range of options and build more holistic validity arguments for or against adequate fit of the model.

In the event that no cutoff value can be selected that satisfies the guideline that at least 95% of misspecified models are correctly classified while no more than 5% of correct models be misclassified, these rates can be relaxed slightly to 90% and 10%, respectively. Hu and Bentler (1999) took a similar approach in some conditions where overlap in the empirical distributions or large variance of empirical distributions preclude finding a cutoff that satisfies the original criteria. If no cutoff can be determined such that at least 90% of misspecified models are correctly classified while no more than 10% of correct models be misclassified, then the method reports that the model characteristics are not amenable to determining a cutoff for that specific misspecification severity.

An example of excessive overlap precluding a cutoff that correctly classifies 95% of misspecified models while misclassifying no more than 5% of correct models for SRMR is shown in Fig. 2. In Fig. 2, the two empirical distributions overlap to an extent that there are no possible cutoffs that would correctly classify 95% of the light grey distribution while misclassifying 5% or less of the dark grey distribution. In other words, the sampling variability under these conditions would be too large to reliably distinguish between a correct model and a model with a prescribed hypothetical misspecification because a large portion of potential fit indices could have conceivably come from either distribution.

Fig. 2

Example of empirical distributions with excessive overlap such that there is no cutoff that can correctly classify 95% of misspecified models while misclassifying no more than 5% of true models

To reiterate, the entire DFI approach is automated in a free, user-friendly, point-and-click Shiny web application (www.dynamicfit.app; Wolf & McNeish, 2020). Researchers need only provide their standardized loadings and are not required to write a single line of code. Additionally, DFI cutoffs can be computed in R using the package dynamic, which can be downloaded from CRAN and only requires a lavaan object (Rosseel, 2012) as the input to further streamline the process for R users. The next section walks through an empirical example to clarify how DFI cutoffs are derived.

Empirical example deriving DFI cutoffs

As an example, consider the recent article in the Journal of Personality Assessment by Catalino & Boulton (2021), which explored the psychometric properties of the Prioritizing Positivity Scale. This study featured three separate samples of moderate size to explore whether a one-factor structure held across diverse samples. Evaluation of model fit was assessed with traditional cutoffs derived from Hu & Bentler (1999), as is conventional in the field. We walk through one of the models fit in the paper and demonstrate how fit could be evaluated with DFI cutoffs for this model. To be as clear as possible, the use of this study as an example is not an indictment on how fit was evaluated in this study, nor does it imply that any aspects of this study were poorly done. We chose this real-life example to illustrate the DFI approach because it was extremely thorough in the presentation of its methods and results such that all relevant information was available to readers.

We focus on the six-item version of the scale presented in Catalino & Boulton (2021) where N = 240. Figure 3 shows a path diagram with the standardized loading estimates for this model. It was reported that the model did not fit exactly ${\chi }^{2}\left(9\right)=24.75,p<.01$ but fit indices might suggest acceptable fit with CFI = 0.97, RMSEA = 0.08, and SRMR = 0.04. Catalino & Boulton (2021) note that the CFI and SRMR are within the acceptable range based on traditional cutoffs, but that RMSEA is not (although note that RMSEA is expected to be inflated given that the model only has 9 degrees of freedom, as is common in many one-factor models; Kenny et al., 2015). This model has six items whose mean standardized loading is 0.66. As noted above, the traditional cutoffs are based on misspecifications involving omitted cross-loadings or factor covariances whereas the primary concern in a one-factor model tends to be misspecifications related to the factor structure or unmodeled local dependence.

Fig. 3

Path diagram and standardized loadings for the six-item Prioritizing Positivity (PP) Scale as reported in Catalino and Boulton (2021). N = 240

Instead of (improperly) generalizing the traditional cutoffs to this one-factor context, the DFI cutoff approach follows suggestions from Millsap (2007) to perform a simulation whose conditions match this exact model to derive customized fit indices that directly reflect sensitivity of fit indices to potential misspecification in this model. The DFI method automates this simulation so that researchers need not write any code, which attempts to make the approach accessible to researchers without knowledge of simulation techniques while also reducing the burden on researchers who may have knowledge of simulation techniques but may not want to exert the effort or time to conduct a simulation for each model they fit.

The first step of the DFI method relies on the user to write out the standardized model estimates in lavaan-style syntax (lavaan style is used because the algorithm is written in R and uses lavaan to calculate model fit). For users unfamiliar with lavaan, a one-factor model is specified by giving an arbitrary name for a factor (e.g., F1) followed by “ =  ~ ” to indicate the variables that follow are indicator variables for this factor. All the indicator variables then appear after “ =  ~ ” with a plus sign between each.² For use with the DFI algorithm, researchers need to provide the standardized estimate followed by “*” before each indicator. The lavaan style syntax for the Catalino & Boulton (2021) model in Fig. 3 would therefore be,

$$F1=\sim .67*x1+.72*x2+.63*x3+.77*x4+.66*x5+.51*x6$$

where “F1” represents Factor 1 and the “x” variables represent the indicators (the letters used for the indicator variable labels are arbitrary). If using the Shiny application by Wolf and McNeish (2020), users would save this syntax to a .txt file, upload it to the application, and specify the sample size in the box. If using the dynamic R package, users can apply the cfaOne function to a lavaan object containing the model estimates (the R package also accommodates manually model entry if, for example, a user is calculating cutoffs for a model from another researcher’s work). This is the extent of the user’s involvement and the remainder of the procedure is automated.

After the user submits the model, the DFI algorithm reads the lavaan style syntax and begins to setup the four different data generation models based on the submitted model and corresponding estimates. The level 0 data generation model treats the fitted model as if it were correct, meaning that the DFI algorithm generates 500 datasets from the same model the user submitted. The level 1 data generation model assumes that the fitted model is misspecified such that the correct model hypothetically had residual correlations between one-third of the items (where each item can have no more than one residual correlation). Fitted models that have existing correlations are permitted, but items with existing residual correlations in the fitted model are not eligible to receive a second residual correlation in the DFI data generation model.

For a six-item scale with no existing residual correlations, one-third of the possible items corresponds to a single 0.30 correlation between two items. The items to receive this residual correlation are determined by the items with the lowest standardized loadings. There is nothing necessarily important about the items with the lowest standardized loadings; they are chosen simply to make the process reproducible such that the same pair of items is selected each time if the procedure is run again on the same model.³ In this example, the items with the lowest loadings are item 3 and item 6. The algorithm then generates 500 datasets from the level 1 data generation model, which is shown in the top panel of Fig. 4.

Fig. 4

Path diagram of the DFI data generation models that treat the fitted model as it were misspecified. The top panel shows the level 1 misspecification data generation model, the middle panel shows the level 2 misspecification data generation model, and the bottom panel shows the level 3 misspecification data generation model. Each residual correlation has a magnitude of .30

The level 2 data generation model assumes that the fitted model is misspecified such that the correct model hypothetically had residual correlations between two-thirds of the items. For a six-item scale with no existing residual correlations, this corresponds to four items or two residual correlations. The first residual correlation is the same as the correlation included in the level 1 data generation model (item 3 and item 6 in this example). The second residual correlation is placed between items with the next two lowest standardized loadings (item 5 and item 1 in this example). Another 500 datasets are generated from the level 2 model, which is shown in the middle panel of Fig. 4.

The level 3 data generation model assumes that the fitted model is misspecified such that the correct model hypothetically had exactly one residual correlation for all items (if the number of items is odd, one item will be left out). For a six-item scale with no existing residual correlations, this corresponds to three residual correlations. The first two residual correlations are identical to the those included in the level 2 data generation model and the last residual correlation that is unique to the level 3 data generation models is between the only two items yet to have a residual correlation (item 2 and item 4). Lastly, 500 datasets are generated from the level 3 data generation model, which is shown in the bottom panel of Fig. 4.

The original fitted model is then applied to all 2000 generated datasets and the empirical distributions are compared to derive a cutoff at each level. Figure 5 shows the empirical distributions SRMR, RMSEA, and CFI for the level 0 model (dark grey) and the level 2 model (light grey). The thick vertical line is the DFI cutoff that correctly classifies at least 95% of misspecified model replication while misclassifying no more than 5% of correct models. Table 1 shows the level 1, level 2, and level 3 DFI cutoffs for this particular model, rounded to two decimal places to match the precision of the fit indices reported in Catalino & Boulton (2021).

Fig. 5

Empirical sampling distributions from the DFI simulation that treat the fitted model in Catalino and Boulton (2021) as if it were the correct model (in dark grey) and if it were misspecified in a manner consistent with the level 2 misspecification shown in the middle panel of Fig. 4 (in light grey). The dashed vertical line represents the DFI cutoff derived from this simulation and the dotted vertical line represented the traditional cutoff as a point of reference

Table 1 DFI cutoffs for different levels of misspecification severity for the model in Catalino and Boulton (2021)

The DFI cutoffs are designed to reflect values that are sensitive to misspecification for the same model characteristics of the fitted model. The fit indices from the fitted model can therefore be directly compared to these DFI cutoffs to evaluate whether there is evidence that the fitted model fits well to these data. Though the empirical values of SRMR (0.04) and CFI (0.97) appear to indicate good fit when compared to the traditional cutoffs (as reported in the original article), SRMR and CFI appear to be a little less sensitive to misspecification with these model characteristics and the tailored DFI cutoffs are consequently stricter than the traditional cutoffs. None of the fit indices indicate fit better than the level 1 cutoff, meaning that cumulative misspecification in the model is greater than one omitted 0.30 residual correlation. However, all three indices are at or below level 2 cutoffs (when rounded to two decimal points), suggesting that the cumulative misspecification in the model is no greater than two omitted 0.30 residual correlations.

Again, the DFI approach is not testing whether the population model for user’s data truly has these residual correlations, it is merely using this representative misspecification to inform the scaling and sensitivity of fit indices given the particular model characteristics so that researchers can make informed decisions about the potential fit of their particular model. It would then be up to the researcher to either investigate local areas of strain to see where the misspecifications may exist or to defend the that a model with evidence of a level 2 misspecification may be reasonable.⁴ Though this process is lengthy to explain and to conduct if writing code from scratch, it is fully automated in software and produces cutoffs that are tailored specifically to characteristics of the model being evaluated within minutes. Further, the type and magnitude of misspecification is standardized across all models that use the DFI approach to evaluate model fit.

Custom derivation of cutoffs via simulation has mostly been discussed conceptually, but it has not been evaluated systematically to demonstrate whether cutoffs derived by simulation are actually better at identifying poor models compared to the traditional cutoffs that empirical researchers commonly employ. This similarly applies to the DFI approach whereby the method has been described but its performance has not been systematically investigated. The next section reports results of a simulation study designed to assess the performance the DFI approach and compare its performance to the traditional cutoffs in the context of one-factor models to determine whether the improvement is large enough to justify recommending the approach to empirical researchers.

Simulation

Simulation design

The goal of this simulation is to assess the sensitivity of traditional and DFI cutoffs to misspecifications that are relevant in the context of one-factor models. Because the suitability of unidimensionality is a frequent interest of fit evaluation with one-factor models, in the first condition from which we generate data is a two-factor model but we fit a one-factor model to the generated data. The generated data are known to truly be multidimensional, so the outcome of interest is whether fit indices can identify that a one-factor model without any residual covariances is not appropriate for the generated data. Relatedly, generating data in this manner is distinct from the hypothetical misspecifications used in the DFI simulations (i.e., missing error correlations are not necessarily isomorphic with an incorrect factor structure), so it can help assess the ability of DFI to detect general forms of misspecification.

In a second condition, we generate data consistent with unidimensionality and fit a one-factor model to the generated data to assess whether traditional and DFI cutoffs are susceptible to misclassifying models that actually are correct. These two conditions will provide a holistic view as analogs of power and type I error rate, although fit indices have no null hypothesis so these terms do not technically apply in our context.

For the case where the generated data are truly multidimensional, we generate data such that 75% of the items load on factor 1 and 25% of the items load on factor 2 with no items loading on both factors. The number of total items is a manipulated condition in the simulation and will be either 8 or 12 items. This means that factor 1 will be indicated by either six or nine items and factor 2 will be indicated by either two or three items, depending on the condition. Number of items is manipulated because previous simulations have found that sensitivity of fit indices to misspecification (RMSEA in particular) can depend on the model size (Moshagen, 2012; Shi et al., 2019), degrees of freedom (Kenny et al., 2015; Shi et al., 2020), and the number of items per factor (Beivik & Olsson, 2001; Kenny & McCoach, 2003).

Sample size was also a manipulated condition and had two levels: 250 or 400. A review by Jackson et al. (2009) found that the average sample size from 1409 review studies was 389, which motivated our selection of the N = 400 condition. We choose N = 250 because for samples below 250 inferential tests of exact fit like the Chi-square test can outperform fit indices (Chen et al., 2008; McNeish, 2020; Sharma et al., 2005). Additionally, Jackson et al. (2009) also found that 80% of studies have at least N = 200, and this sample size reflects the empirical example shown earlier. We focus on the smaller end of the sample size range because one-factor models are more likely to be involved in scale validation studies and often have more modest sample sizes than the broader population of confirmatory factor analyses.

The last condition we manipulated was the magnitude of the standardized factor loadings for items loading on factor 1, which had three conditions: 0.60, 0.75, and 0.90. The standardized loadings of the items loading on factor 2 were held constant at 0.60. The factor 2 standardized loadings were not manipulated in order to preserve a constant magnitude of misspecification across all conditions. That is, if the factor 2 loadings were also manipulated, the severity of misspecification could fluctuate across conditions. This would confound assessment of whether fit indices can correctly classify misspecified models because changes in correct classifications could be attributable either to a poor sensitivity of indices in particular conditions or simply to the misspecification magnitude being smaller.

The factor 2 loadings were chosen to be 0.60 because such loadings (along with a 0.50 population factor correlation) results in standardized loadings near 0.30 for the items truly loading on factor 2 when all the items were fit with a one-factor model. A scale with a few items with standardized loadings near 0.30 seemed like it could plausibly be considered to have one underlying factor by empirical researchers. For instance, a model with six items loading at 0.75 and two items loading at 0.15 would not appear well modeled by one factor on its face; however, a model with six items loading at 0.75 and two items loading at 0.30 might be more plausibly interpreted as having one factor. Using loadings much larger than 0.60 made the misspecification highly conspicuous and too easy to identify, making comparisons of different approaches less informative. Therefore, 0.60 loadings provide balance between producing a misspecified one-factor models with believable estimates and not making the model so egregiously misspecified that the conclusion is never in question.

The magnitude of the factor loadings for items generated for factor 1 were manipulated because previous studies have noted that sensitivity to misspecification is greatly affected by differences in factor reliability, which is based on the standardized loadings (Browne et al., 2002; Heene et al., 2011; McNeish et al., 2018). Specifically, identical misspecifications are weighed more in models with stronger loadings than in models with weaker loadings, which has sometimes been referred to as the reliability paradox (Hancock & Mueller, 2011) because models with more reliable latent variables appears to fit worse relative to traditional fixed cutoffs. Hu & Bentler (1999) did not manipulate the magnitude of the standardized loadings, which has been noted as a major source of poor generalizability across different model conditions (Greiff & Heene, 2017).

The above conditions are used to assess whether the cutoffs will correctly identify a misspecified model (similar to power). However, it is also prudent to ensure that the cutoffs also properly identify when a model is correct (similar to type I error rate). Cutoffs that function properly should be able to accurately classify both types of situations, otherwise, it would be difficult to distinguish if one type of cutoff were actually more sensitive to misspecification or whether it simply classifies all models as poorly fitting (i.e., it is difficult to compare power if the type I error rate is not controlled).

To ensure that cutoffs do not classify correct models as misspecified, we also generate data from a one-factor model with 75% of the items having standardized loadings equal to the factor magnitude condition level (i.e., 0.60, 0.75, or 0.90) and 25% of the items having standardized loadings equal to 0.30. In this way, the pattern of the standardized loadings is similar to those that emerge in the condition where a one-factor model is (incorrectly) fit to two-factor data. A one-factor model is then fit to these data and the expectation is that few replications should be identified as containing non-trivial misspecifications because the model should fit exactly. Note that fit indices are not inferential tests and do not have null hypothesis, so there is no nominal type I error rate for fit indices. Therefore, 0% misclassification rates with the correct model do not signify an issue as they would in a null hypothesis testing framework where 0% may be problematic if the nominal type I error rate is 5%.

Data were generated in SAS 9.4 using Proc IML and models were fit using the lavaan package in R. We performed 500 replications for each combination of manipulated conditions. The SRMR, RMSEA, and CFI values from each replication were saved and compared to either the traditional cutoff or the DFI cutoff. DFI cutoffs were recalculated for each replication using the dynamic R package for deriving DFI cutoffs, which permits us to report on the stability of the cutoffs across replications. As noted earlier, the DFI method provides three different cutoffs for one-factor models. We focus on the level 1 cutoff because it is intended to roughly coincide with the magnitude of misspecification in Hu & Bentler (1999) and with the “Close” fit cutoff suggested by MacCallum et al. (1996). In other words, Hu and Bentler’s simulation study essentially generated what DFI refers to as a ‘level 1 misspecification’ to distinguish between correct and misspecified models. So although DFI cutoffs do not apply labels like “good” or “bad” fit and are designed to encourage researchers to think about fit more holistically, we impart this terminology onto DFI cutoffs to make them more directly comparable to traditional cutoffs. We want to stress that this choice was made to maximize comparability of DFI and traditional cutoffs and that researchers should treat DFI cutoffs as a spectrum of misfit (similar to effect size; McNeish & Wolf, 2021).

There are three primary outcomes in the simulation. The first is the percentage of replications for the misspecified models that are correctly classified as having worse than a level 1 misspecification with DFI cutoffs (i.e., the analog of power). The second is the percentage of replications from a correctly specified model that incorrectly classified as having worse than a level 1 misspecification with DFI cutoffs (i.e., the analog of the type I error rate). The classification rates for the first and second outcome are compared to the classification rates of the traditional fixed cutoffs to evaluate which performs better. As a third outcome, we are also interested in the stability of the DFI cutoffs under conditions typical of those encountered when validating scales. To assess this, we first record the number of replications in each condition where the DFI approach must resort to the more lenient criteria where 90% of hypothetically misspecified models are correctly classified while no more than 10% of hypothetically correct models be misclassified (rather than the default 95% and 5%, respectively). Second, we record the number of replications in each condition where the overlap in the empirical distributions of fit indices is too excessive to derive a suitable DFI cutoff.

Results for DFI stability

As noted earlier when describing the derivation of DFI cutoffs, one criterion for determining the cutoff is that no more than 5% of replications are misclassified while at least 95% of misspecified models are correctly classified (we refer to this as the 95/5 criteria). If the empirical distributions of fit indices overlap too much, we follow Hu and Bentler’s general approach of using more lenient criteria such that no more than 10% of correct models are misclassified and at least 90% of misspecified models are correctly classified (we refer to this as the 90/10 criteria). If the empirical distributions overlap to the extent that no cutoffs can reliably distinguish between correct and misspecified models at the 90/10 rate, then no cutoffs will be returned. Table 2 shows the percentage of replications in each condition that could be derived with the 95/5 criteria, the percentage of replications that required the 90/10 criteria, and the percentage of replications for which no cutoffs could reliably be derived.

Table 2 Percentage of DFI replications in each condition that required the 95/5 criteria, the 90/10 criteria, and the percentage of replications that returned no DFI cutoffs

As anticipated, there were no issues in the N = 400 conditions because the sampling variability decreases as sample size increases. As a result, these conditions universally were able to derive DFI cutoffs in all replications using the 95/5 criteria. The N = 250 conditions experience more difficulty, which is expected because sampling variability will be larger with a smaller sample size. Larger sampling variability increases the probability of requiring the 90/10 criteria because the empirical distributions are more likely to overlap when the sampling variability is larger. The N = 250 conditions often had to resort to the 90/10 criteria for RMSEA and CFI in a majority of replications, but SRMR appeared to be much less affected and was typically able to derive DFI cutoffs using the 95/5 criteria despite the smaller sample size. Note that conditions for which the 90/10 criteria are employed have a higher chance of incorrect classifications for the correctly specified models (this is conceptually similar to using an alpha level of 0.10 instead of an alpha level of 0.05 in a standard hypothesis test, though not exactly the same as we discuss in the next section).

Larger issues appeared when the small samples and weak loadings occurred simultaneously. When both characteristics were present together, DFI cutoffs could not be derived for some replications. This only occurred in one condition (N = 250, loadings = 0.60, items = 8) for both the misspecified and correctly specified models. CFI was again the most affected (36% and 47% returned no cutoffs for misspecified and correct models, respectively) whereas SRMR was more robust to these issues (4% and 3% returned no cutoffs for misspecified and correct models, respectively).

Results for correct models

Table 3 show the percentage of replications in each condition whose fit index values were worse than the traditional cutoff or worse than the level 1 DFI cutoff when the data generation model and the fitted model were congruent (i.e., the model is correct). Fit indices are not inferential tests, so there is no expected value for this table, although values closer to zero are better because it is desirable to not classify correct models as fitting poorly. Across all conditions, the traditional cutoffs consistently had low misclassification rates, often 0% but never more than 3%.

Table 3 Percentage of replications in which a correct one-factor model is improperly identified as misspecified (DFI percentages are conditional on cutoffs being returned)

The rates at which correct models were improperly classified as fitting poorly is low for DFI cutoffs when the 95/5 criteria can be implemented (i.e., always 4% or less). However, the misclassification rate was sometimes higher with DFI cutoffs in simulation conditions that required calculating cutoffs using the less stringent 90/10 criteria (although never more than 9%). This is expected for those conditions because higher probability of misclassification for correct models is embedded into how the cutoffs are derived (in other words, the upper bound for the misclassification rate of correct models with the 90/10 criteria is twice that of the 95/5 criteria). This occurs because the 90/10 criteria expand the tolerable misclassification rate of correct models in order to identify a suitable DFI cutoff when there is overlap in the empirical fit index distributions. Correspondingly, more correct models may be misclassified as poorly fitting when the characteristics of the model generate larger sampling variance, which increases the chance that the empirical distributions overlap (i.e., smaller samples, weaker loadings, or few items).

To be clear, the higher misclassification rates for the 90/10 criteria are not a property of DFI itself so much as it reflects the data being evaluated. With suboptimal data characteristics, there is more uncertainty in deriving the location of a suitable cutoff empirically. This is the burden one must bear with simulating custom cutoffs – if the model and data being evaluated contain a high degree of uncertainty, then the corresponding DFI cutoffs encode that uncertainty. In other words, there are conditions in which researchers must reconcile between not being able to optimally evaluate model fit using approximate fit indices or evaluating model fit with a higher risk of a misclassifying a model that may have reasonable fit.

As another clarification, the probability of misclassification is higher with the 90/10 criteria but misclassification will not necessarily be higher. DFI cutoffs are derived by first locating the fit index that correctly classifies misspecified models and second by checking that the misclassification rate of correct models is controlled. This makes the correct model misclassification rate (i.e., the “10” in the 90/10 criteria) an upper bound of misclassification rather than a nominal level of misclassification as with a type I error rate. Therefore, correct model misclassifications are more probable with the 90/10 criteria because the upper bound is higher, but correct model misclassifications will not necessarily be higher. This can be seen in Table 3 with DFI cutoffs for 12 items and N = 250 – even though nearly 100% of replications used 90/10 criteria, misclassification rates for correct models were 0% for all loading conditions.

Results for misspecified models

Table 4 shows the percentage of replications from each condition that correctly classified the one-factor model as misspecified when data were generated from a two-factor model. DFI percentages in Table 4 are conditional on cutoffs being returned (replications where DFI cutoffs could not be determined due to excessive overlap in empirical distributions are not counted in the numerator or the denominator). As anticipated, the performance of the traditional cutoffs was inconsistent, both across indices and conditions:

• SRMR with traditional cutoffs performed very poorly (i.e., models were correctly classified as misspecified in 0–1% of replications).

• RMSEA tended to be the best index when compared against traditional cutoffs, correctly classifying 64–77% of replications.

• Performance of CFI with traditional cutoffs was highly dependent on the magnitude of the standardized loadings and – to a lesser degree – the number of items, ranging from 0 to 98% correctly classified across conditions.

Table 4 Percentage of replications in which an incorrect one-factor model is correctly identified as misspecified (DFI percentages are conditional on cutoffs being returned)

Performance of DFI cutoffs has not been studied systematically given that the method was recently developed, so their performance was more difficult to anticipate. Nonetheless, the DFI cutoffs performed well across indices and conditions and were consistently able to correctly classify misspecified models. In conditions for which the 95/5 criteria was always employed, the correct classification rate was 94% or greater. In the conditions for which the 90/10 criteria was sometimes needed, the correct classification rate was 90% or greater. However, as mentioned earlier, the replications from the 8-item, 0.60 loading condition with N = 250 failed to derive cutoff values due to distributional overlap as often as 36% of the time. The correct classification rate was high when calculated as proportion of the total number of replications that returned cutoff values (91% or greater) but it should be noted that with small loadings and a small sample size, DFI cutoffs may be unavailable.

The poor performance of the traditional SRMR cutoff corroborates points from Fan & Sivo (2005) that the traditional SRMR cutoff is often too lenient because it was based on omitted factor covariances in the original Hu & Bentler (1999) simulation. An omitted factor covariance represents a serious misspecification because it eliminates the possibility of model-implied covariances between items on the factors that are not allowed to covary (unless there are residual covariances). This misspecification is likely to be too extreme to be meaningful for one-factor models because researchers cannot induce such a large misspecification in one-factor models through omission of only a single path, as can be accomplished in models with multiple factors with omitted factor covariances.

Similarly, the erratic performance of CFI is predictable from the mechanics of its calculation. That is, CFI calculates the improvement in non-centrality of the fitted model over the non-centrality of a null model, relative to the non-centrality of a null model. The null model typically estimates only the mean and variance of each indicator variable but no covariances among indicator variables. As anticipated from the reliability paradox from Hancock & Mueller (2011), misspecifications appear more severe when standardized loadings are stronger. This applies to both the fitted model and the null model.

Because the null model is intentionally poor, it is far more misspecified than the fitted model. However, the effect of the reliability paradox is non-linear, so the rate of increase in the null model’s non-centrality with strong loadings is much greater than the non-centrality of the fitted model. Therefore, the denominator of the CFI increases much faster than the numerator as the loadings increase. As a result, an identical misspecification will have a CFI value closer to 1.00 with stronger loadings and a CFI value further from 1.00 with weaker loadings. This leads to the traditional CFI cutoff identifying 0% of misspecified models in the 0.90 loading condition and 75% to 98% in the 0.60 loading condition because the CFI scales differently depending on the standardized loading magnitude. The DFI cutoffs take this differential scaling of the null model’s non-centrality into account through custom simulations and the CFI cutoff derived by DFI is therefore highly consistent across conditions.

This highlights points raised by Marsh et al. (2004) and Millsap (2007) that the desired misspecification to which fit indices should be sensitive is hard to generalize across all models and interpretation of fit indices would likely be improved if they were tailored more closely to the model being evaluated. Doing so with simulation-based techniques like DFI permits nuances of one-factor models and different model characteristics to be accommodated. The result is that the DFI cutoffs are far more capable of detecting misspecification across different conditions, especially for SRMR and CFI.

Results summary

• 1. DFI cutoffs could be stably derived in nearly all conditions that we studied. The only exception was when small samples, weak loadings, and few items were present simultaneously. This combination of characteristics increases sampling variability to the point where it can be difficult to differentiate correct from misspecified models, which can result in no DFI cutoffs being returned. SRMR was least affected by this whereas CFI was most affected.

• 2. DFI cutoffs are an overwhelming improvement over traditional cutoffs at detecting misspecified one-factor models for the conditions and type of misspecification that we studied.

• 3. The traditional SRMR cutoff appears too high to be useful for one-factor models and the appropriateness of the traditional CFI cutoff is highly dependent on the magnitude of the factor loadings. The standardized factor loadings are not always reported in empirical studies (only 31% did so in the studies reviewed by Jackson et al., 2009), so we encourage researchers to make this information accessible to inform interpretation of fit indices if traditional cutoffs are considered.

• 4. Both traditional and DFI cutoffs rarely misclassify correct models, although DFI misclassification will be more likely when data characteristics require resorting to the 90/10 criteria. To clarify, use of the 90/10 criteria will not necessarily result in more correct models being misclassified (e.g., nearly all replications in the 12-item, N = 250 conditions used the 90/10 criteria but the misclassification rates were near 0%). However, it will increase the probability that a correct model will be misclassified (as in the 8-item, N = 250 conditions) because the upper bound of the correct model misclassification rate is higher.

Discussion

The work of Hu & Bentler (1999) was undoubtedly helpful for imposing structure and systematicity into model fit evaluation and they were clear about risks of overgeneralizing their conclusions. The criticisms levied in this paper are towards the practice of overgeneralizing rather than towards the traditional cutoffs themselves, which are reasonable when used in proper context. Nonetheless, we are sympathetic to the struggles that empirical researchers face when trying to evaluate fit because the process is idiosyncratic and there can be comfort in the familiarity of fixed cutoffs serving as an encompassing benchmark for fit evaluation. Custom simulation to derive cutoffs tailored to the model being evaluated has been a commonly suggested approach to working around these issues, just as custom power analyses have routinely been performed to plan appropriate sample sizes more accurately for individual models. Just as open-source software like G*Power has made power analyses more accessible to empirical researchers, the DFI approach and the associated Shiny application will hopefully serve a similar purpose for model fit evaluation to make customized fit cutoffs more accessible, especially for one-factor models where simulation-based techniques for deriving cutoffs appear to better distinguish between correct and misspecified models.

The biggest potential drawback with simulation-based methods like DFI appeared in contexts where sampling variability will be high. Namely, contexts where the sample size is small, loadings are weak, or there are few items (especially when these conditions occur simultaneously). Small samples, in particular, may be common in pilot and scale validation studies where one-factor models are common. DFI will attempt to assuage moderate issues attributable to overlap in the distributions by reverting to the 90/10 criteria. In the simulation, this alternative was necessary in a majority of replications with smaller samples and led to small decreases in performance, although overall performance was still vastly improved relative to traditional cutoffs. If the distributions overlap too much to meet the 90/10 criteria, then no DFI cutoffs will not be returned because there are no DFI cutoffs that can reliably distinguish between a misspecified and correctly specified model. This occurred in one condition (N = 250, eight items, 0.60 loadings).

If DFI cutoffs cannot be returned, the solution would not be to revert to the traditional fixed cutoffs, as they similarly are not sufficiently sensitive to detect misspecification in one-factor models. Rather, researchers may choose to instead investigate local areas of strain (e.g., by examining the standardized residual matrix; e.g., McDonald, 2010) or rely on the Chi-square test (whose concerns about being overpowered are reduced with smaller samples). In the N = 250, 8-item, 0.60 loading condition of the simulation where DFI cutoffs could not always be returned; the Chi-square test correctly rejected 85% of misspecified models and incorrectly rejected 6% of correct models across all 500 replications (using a nominal 5% type I error rate). If only considering replications where DFI cutoffs could not be returned for at least one fit index, Chi-square correctly rejected 78% of misspecified models and incorrectly rejected 7% of correct models. Do note that the Chi-square test for exact fit is susceptible to inflated type I error rates for sample sizes below about 200 (Chou et al., 1991) and that corrections are often necessary to restore type I error rates to their nominal level (Wu & Lin, 2016; McNeish, 2020; Yuan & Bentler, 1999).

It is also worth mentioning that the Chi-square test and approximate fit indices contribute different information about the fit of a model. Unlike the Chi-square test, approximate fit indices are not a binary test for the presence of misspecification but function more like an effect size to quantify the extent of misspecification present in the model. The DFI approach reconceptualizes misspecification by introducing escalating levels of severity which are standardized across models. We encourage researchers to use the comparison between their indices and the cutoffs as one piece of evidence of validity for their scales and follow up by investigating local areas of strain if warranted. For example, if a researcher is concerned about the degree of misspecification implied by the DFI cutoffs, they could look at the standardized residual matrix and if they do not find any large values, they may be able to still make a reasonable argument in defense of the model fitting well (especially with only a level 1 misspecification). We hope that the DFI framework will motivate researchers to rethink the use of traditional fit index cutoffs.

Given that the proportion of replications in which no DFI cutoffs could be returned differed for SRMR, RMSEA, and CFI; a researcher may be unsure how to proceed if DFI cutoffs are output for some but not all fit indices. To address this empirically, we looked at the performance of SRMR and RMSEA for replications where DFI cutoffs were or were not returned for CFI in the N = 250, 8-item, 0.60 loading condition (i.e., replications where only one or two indices were able to return cutoffs). As a reminder, the percentage of replications in this condition that did not return DFI cutoffs for CFI was 47% for correct models (235 replications) and 36% for misspecification models (179 replications). For replications where DFI cutoffs for all indices were returned, SRMR correctly classified 95% of misspecified models and incorrectly classified 5% of correct models. For replications where DFI cutoffs were returned for SRMR but not for CFI, SRMR correctly classified 94% of misspecified models and incorrectly classified 7% of correct models. For replications where DFI cutoffs for all indices were returned, RMSEA correctly classified 91% of misspecified models and incorrectly classified 9% of correct models. For replications where DFI cutoffs were returned for RMSEA but not for CFI, RMSEA correctly classified 90% of misspecified models and incorrectly classified 11% of correct models. Given that the performance of SRMR and RMSEA is essentially unchanged regardless of whether DFI cutoffs for CFI were returned, our conclusion is that researchers can use DFI cutoffs with confidence if DFI cutoffs are returned for some but not all indices.

Though we were interested in one-factor model fit more broadly and not more specifically on issues of dimensionality, a potential future direction could be to assess the ability of DFI cutoffs for determining how many factors to retain in the related modeling area of exploratory factor analysis (rather than confirmatory factor models we consider). Several methods have been proposed to improve selecting the number of factors including Horn’s parallel analysis (Horn, 1965), the subsequent model Chi-square test, Velicer minimum absolute partial test (Velicer, 1976), the Kaiser rule (Kaiser, 1960), the hull method (Lorenzo-Seva et al., 2011), the empirical Kaiser Criterion (Braeken & van Assen, 2017), exploratory graph analysis (Golino & Epskamp, 2017; Golino et al., 2020), and machine learning methods (Goretzko & Bühner, 2020). Recent simulations have shown inconclusive results regarding the best measure for determining the number of factors and measures often disagree for the same data (Auerswald & Moshagen, 2019). Several recent studies have assessed whether fit indices may help determine the number of factors (Clark & Bowles, 2018; Finch, 2020; Garrido et al., 2016; Montoya & Edwards, 2021), but results have either been poor to mixed. However, these studies have only considered traditional benchmarks for fit indices, which our simulation found to be quite poor in the context of distinguishing one-factor from two-factor confirmatory factor models. An interesting extension would be determining (a) whether DFI cutoffs improve the utility of fit indices when then are employed for determining how many factors to retain and (b) whether DFI cutoffs compare favorably to other recently proposed approaches.

As limitations, simulation results are only generalizable to the conditions studied and our results may not necessarily be duplicated in other conditions (e.g., short scales or scales with consistently weak loadings). Additionally, missing data are a common incurrence in empirical data, but the problem of missing data has yet to be studied in the DFI approach given its nascency. As future directions, additional studies on the adequacy of DFI cutoffs would help to accumulate evidence for whether the approach continues to outperform traditional approaches or whether this outperformance is limited to particular contexts. If the latter, additional studies would be fruitful for identifying the circumstances where DFI does and does not perform well in order to better develop more complete recommendations for empirical researchers. The DFI approach is also currently only available for one-factor or multifactor confirmatory factor models and it is uncertain whether its current implementation generalizes to hierarchical factor models or to bifactor models, both of which are quite popular in scale development and validation studies. A future extension could entail comparing the feasibility of the current DFI approach to these other popular types of models or whether further methodological development is required for these extensions. Creating a more general method for creating misspecification in the DFI simulations could also reduce this reliance on extending the method model-by-model so that hypothetical misspecifications do not need to be directly tied to specific paths. Matrix perturbation methods such as those developed by Cudeck & Browne (1992) or Wu & Browne (2015) may be one approach to consider for generalizing hypothetical misspecifications to an arbitrary model.

As currently implemented, the DFI method is only applicable to continuous indicators and assumes multivariate normality in the DFI simulations. Generating data with categorical indicators is more involved and requires users to provide information about the number of possible response categories and the proportion of responses in each category. At the time of this writing, the authors have begun preliminary work on extending the DFI method to support categorical outcomes, but this work is not yet available and remains in progress. Multivariate normality is currently assumed in the DFI simulations because doing so does not require users to provide their original data. If users are willing to provide the original data, this assumption may not be necessary if adopting a bootstrapping rather than a simulation approach. That is, similar to the method of Bollen & Stine (1992) used to create an empirical distribution for the Chi-square statistic, the original data could be transformed such that a particular model-implied covariance structure necessarily holds. Rather than simulating new data, an empirical distribution would be formed by bootstrapping this transformed data and no distributional assumptions would be necessary.

Lastly, there is some methodological work on the proclivity for RMSEA and CFI to disagree relative to traditional cutoffs (e.g., Lai & Green, 2016). A potentially interesting future study could assess whether this disagreement is due to true differences in the sensitivity of indices to different specifications or whether the indices are just differentially sensitive to model characteristics. For example, the traditional cutoffs disagreed in the 0.90 loadings conditions in Table 4 because the RMSEA and CFI were differentially affected by changes in the standardized loadings, but this disagreement disappeared with the DFI cutoffs after rescaling the indices to account for characteristics of the model being evaluated.

Overall, the results in this study demonstrated that custom simulation of cutoffs with the DFI approach appear to be a viable alternative to assess fit with one-factor models in the conditions we studied. Correct models rarely were categorized as being misspecified and misspecified models were identified with high consistently across different model characteristic conditions. Though custom simulation of cutoffs has been suggested for the past 15 years, the modern computational environment greatly facilitates implementation of such an approach. There is still much to study with the new DFI approach, but – at least in the context of one-factor models – there appears to be much promise, especially when compared to the traditional cutoffs that have always been questionably appropriate in the one-factor context.