Covariance pattern mixture models: Eliminating random effects to improve convergence and performance

Abstract

Growth mixture models (GMMs) are prevalent for modeling unknown population heterogeneity via distinct latent classes. However, GMMs are riddled with convergence issues, often requiring researchers to atheoretically alter the model with cross-class constraints simply to obtain convergence. We discuss how within-class random effects in GMMs exacerbate convergence issues, even though these random effects rarely help answer typical research questions. That is, latent classes provide a discretization of continuous random effects, so including additional random effects within latent classes can unnecessarily complicate the model. These random effects are commonly included in order to properly specify the marginal covariance; however, random effects are inefficient for patterning a covariance matrix, resulting in estimation issues. Such a goal can be achieved more simply through covariance pattern models, which we extend to the mixture model context in this article (covariance pattern mixture models, or CPMMs). We provide evidence from theory, simulation, and an empirical example showing that employing CPMMs (even if they are misspecified) instead of GMMs can circumvent the computational difficulties that can plague GMMs, without sacrificing the ability to answer the types of questions commonly asked in empirical studies. Our results show the advantages of CPMMs with respect to improved class enumeration and less biased class-specific growth trajectories, in addition to their vastly improved convergence rates. The results also show that constraining the covariance parameters across classes in order to bypass convergence issues with GMMs leads to poor results. An extensive software appendix is included to assist researchers in running CPMMs in Mplus.

In longitudinal data analysis, mixture models are commonplace in the empirical literature in which the primary goal is to identify unobserved, latent classes of growth trajectories (Jung and Wickrama, 2007). As a hypothetical example, researchers may follow students’ test scores over time and wish to identify which students in the sample are “on-pace” learners, “accelerated” learners or “slow” learners (e.g., Musu-Gillette, Wigfield, Harring, & Eccles, 2015). These subgroups are latent and are not identified a priori as observed variables like other independent variables that may be of interest (e.g., gender, socioeconomic status [SES], treatment condition). Instead, their existence must be inferred from characteristics of the growth patterns themselves.

Common goals of a mixture analysis in this longitudinal context are to identify how many classes exist, to which of these latent classes an individual belongs, and to estimate the growth trajectory of each of the latent classes. These interests parallel how a researcher may want to estimate different growth trajectories for different levels of an observed variable. For instance, a researcher may wish to separately model growth trajectories for students identified as coming from households with high and low SES (i.e., whether SES moderates growth curves). The major difference in the mixture model context is that the classification variable of interest happens to be latent. When adding latent classes to growth models, two methods are common: latent class growth models and growth mixture models.

Latent class growth models (LCGMs; Nagin, 1999, 2005; Nagin & Tremblay, 2001) use trajectory groups to approximate a complex, non-normal underlying distribution (Nagin, 2005). To explain, a typical growth model incorporates continuous random effects for each individual, which are typically assumed to be normally distributed in order to create a unique subject-specific growth curve for each individual in the data. For continuous outcomes, LCGMs discretize this continuous distribution by estimating a handful of classes, each with a unique mean trajectory. Individuals are assigned to the class trajectory that most closely represents what their subject-specific growth curve would have been in a standard growth model with continuous random effects. This discretization of the random effects facilitates interpretation because the dimensionality is reduced from the number of individuals (where each individual has a unique growth curve) to a small number of easily interpretable representative trajectories. LCGMs do not allow for subject-specific growth trajectories within classes, meaning that any deviation from the class trajectory is assigned to an error term that is assumed to be independently and identically distributed across time with common variance. Though conceptually appealing, a noted downside of LCGMs is that the number of classes tends to be overextracted, especially at larger sample sizes (i.e., extracted classes are not necessarily substantively different from one another). The specification of the model is not always flexible enough to properly model the marginal covariances among the repeated measures, so covariance misspecification manifests as additional latent classes (e.g., Kreuter & Muthén, 2008).

Growth mixture models (GMMs) represent another method by which to model latent classes with longitudinal data (Muthén, 2001; Muthén & Shedden, 1999). Similar to LCGMs, GMMs estimate latent classes, each with a unique mean growth trajectory. Unlike LCGMs, GMMs also specify random effects of the growth factors within each class to allow between-individual and within-individual variability within classes. The benefit of such an approach is that the model more easily accommodates proper specification of the covariance of the repeated measures. As a result, the model is less likely to extract the spurious classes as a consequence of a misspecified covariance structure.

Though effective for accurately capturing the marginal covariance of the repeated measures, GMMs’ reliance on continuous within-class random effects can be inefficient. As we discuss in more detail in subsequent sections, GMMs are computationally demanding and as a result, routinely encounter estimation issues. In psychology-adjacent fields that are interested in modeling change over time, such as epidemiology and public health, population-averaged models (i.e. marginal models; Liang & Zeger, 1986) are popular alternatives to random-effect models for longitudinal data, because they can appropriately model the marginal covariance while requiring fewer assumptions and are much less demanding to estimate (Burton, Gurrin, & Sly, 1998; Harring & Blozis, 2016). To date, there has been no coverage in the literature extolling the advantages of and applying population-average models within a mixture model framework. This is precisely the goal of this article.

Specifically, we will use the existing literature, statistical theory, Monte Carlo simulation, and an empirical example to argue that most research questions being addressed with GMMs do not require the within-class random effects. That is, researchers are primarily interested in the discretization of individual growth-curves provided by the latent classes—individual deviation within each latent class is rarely a research focus and the use of random effects primarily serves the secondary function of properly specifying the marginal covariance between repeated measures. A primary aim of this article is to show that this objective can be satisfied in a less computationally demanding fashion with population-averaged models, which ultimately yields better convergence rates, reduced need for atheoretical model constraints, and better statistical properties of model estimates.

To outline the structure of this manuscript, we first overview the generic latent-growth model and demonstrate how it naturally extends to GMMs. We discuss how the random-effect approach makes estimation more demanding, which can augment computational difficulties. We then provide evidence from the post-traumatic stress literature—in which mixture models frequently appear—to demonstrate that research questions rarely make use of the information provided by within-class random effects featured in GMMs. Population-averaged models are then overviewed with specific focus on covariance pattern models and the advantages they provide in the context of mixture models for longitudinal data. We provide a Monte Carlo simulation study to highlight how covariance pattern mixture models can address issues that tend to plague applications of GMMs. Specifically, we explore convergence rate, class trajectory bias, classification accuracy, and class enumeration. We then provide an empirical example to compare and contrast the traditional GMM with our proposed population-averaged approach. A detailed appendix of annotated Mplus code is also provided to facilitate the use of these models by empirical researchers.

Overview of latent-growth models and growth mixture models

The latent-growth model

First, consider a traditional latent-growth model, which can be thought of as a special case of a GMM with only one class. The general linear latent-growth model with q time-invariant covariates can be written as a restricted confirmatory factor analysis model with a structured mean vector of the observed variables such that

$$ {\mathbf{y}}_i={\boldsymbol{\Lambda}}_i{\boldsymbol{\upeta}}_i+{\boldsymbol{\upvarepsilon}}_i $$

(1)

and

$$ {\boldsymbol{\upeta}}_i=\boldsymbol{\upalpha} +{\boldsymbol{\Gamma} \mathbf{x}}_i+{\boldsymbol{\upzeta}}_i. $$

(2)

In Eq. 1, y_i is an n_i × 1 vector of responses, where n_i is the number of observations for individual i; Λ_i is an n_i × q matrix of loadings for q the number of growth factors where the loadings are commonly, but not always, prespecified to fit a specific type of growth trajectory;¹η_i is a q × 1 vector of individual-specific growth factor scores for individual i, and ε_i is an n_i × 1 vector of time-specific residuals where ε_i~MVN(0, Θ_i) and Θ_i depends on i only through its dimension, although this assumption can be relaxed (Davidian & Giltinan, 1995). In Eq. 2, the individual-specific growth factor scores are equal to a q × 1 vector of factor means α, a q × p matrix of time-invariant coefficients in Γ for p the number of time-invariant covariates, a p × 1 vector of time-invariant covariate values x_i, and a q × 1 vector of random effects, ζ_i~MVN(0, Ψ).

The model-implied mean and covariance structures of the repeated measures are thus,

$$ E\left[{\mathbf{y}}_i\right]={\boldsymbol{\upmu}}_i={\boldsymbol{\Lambda}}_i\left(\boldsymbol{\upalpha} +\boldsymbol{\Gamma} \boldsymbol{\upkappa} \right) $$

(3)

and

$$ \operatorname{var}\left({\mathbf{y}}_i\right)={\boldsymbol{\Sigma}}_i={\boldsymbol{\Lambda}}_i\left(\boldsymbol{\Gamma}\;\boldsymbol{\Phi}\;{\boldsymbol{\Gamma}}^{\mathrm{T}}+\kern0.5em \boldsymbol{\Psi} \right){\boldsymbol{\Lambda}}_i^{\mathrm{T}}+{\boldsymbol{\Theta}}_i $$

(4)

where κ is the vector of covariate means and Φ is the covariance matrix of the time-invariant covariates.

Multiple group growth models

Populations are often heterogeneous and different segments of the population may follow different growth trajectories. If the heterogeneity is the result of known group membership, parameters can be estimated separately for each group with what is referred to as a multiple-group model (e.g., Muthén & Curran, 1997). Notationally, the vectors and matrices of Eqs. 1–4 would take a g subscript (where g = 1, . . . , G) to denote to which observed group the parameters belong.

Although the conceptual idea is alluring, multiple group models require that the grouping variable be an observed variable in the data, which is not frequently the case with heterogeneous populations (e.g., it is hard to objectively assign “fast” learner or “slow” learner labels to individuals). Group membership is more often latent and not known a priori (Nylund-Gibson, Grimm, Quirk, & Furlong, 2014), leading to the use of mixture models to sort individuals via latent classes.

Growth mixture model

GMMs are a generalization of the multiple group framework in which group membership is unobserved (Muthén, 2001; Muthén & Shedden, 1999; Nagin, 1999; Verbeke & Lesaffre, 1996). Instead of a known value for group membership, each observation receives a probability of membership in each of the estimated latent classes. Assuming multivariate normality, the composite density of a vector of continuous outcome variables for the ith individual, y_i, can be written as

$$ f\left({\mathbf{y}}_i|\boldsymbol{\upvarphi}, {\boldsymbol{\upmu}}_i,{\boldsymbol{\Sigma}}_i\right)=\sum \limits_{k=1}^K{\varphi}_k{f}_k\left({\mathbf{y}}_i|\;{\boldsymbol{\upmu}}_{ik},{\boldsymbol{\Sigma}}_{ik}\right), $$

(5)

where K is the number of latent classes that the researcher specifies, f_k is the component density for the kth class, μ_ik is the model-implied mean vector for the kth class, Σ_ik is the model-implied covariance matrix for the kth class, and φ_k is the mixing proportion for the kth class where 0 ≤ φ_k ≤ 1 and ${\varphi}_K=1-\sum \limits_{k=1}^{K-1}{\varphi}_k$. Given class k, Eqs. 1 and 2 can be extended to accommodate the inclusion of latent classes as

$$ {\mathbf{y}}_i={\boldsymbol{\Lambda}}_i{\boldsymbol{\upeta}}_i+{\boldsymbol{\upvarepsilon}}_i $$

(6)

$$ {\boldsymbol{\upeta}}_i={\boldsymbol{\upalpha}}_k+{\boldsymbol{\Gamma}}_k{\mathbf{x}}_i+{\boldsymbol{\upzeta}}_i $$

(7)

with the assumption that the residuals and random effects for the ith individual follow separate multivariate distributions, ε_i ∣ k~MVN(0, Θ_ik), and  ζ_i ∣ k~MVN(0, Ψ_k). Following the notation from Eqs. 3 and 4, the model-implied mean vector and model-implied covariance matrix from Eqs. 6 and 7 can be written as

$$ {\boldsymbol{\upmu}}_i\mid k={\boldsymbol{\Lambda}}_i\left({\boldsymbol{\upalpha}}_k+{\boldsymbol{\Gamma}}_k\boldsymbol{\upkappa} \right) $$

(8)

$$ {\boldsymbol{\Sigma}}_i\mid k={\boldsymbol{\Lambda}}_i\left({\boldsymbol{\Gamma}}_k\;\boldsymbol{\Phi}\;{\boldsymbol{\Gamma}}_k^{\mathrm{T}}+\kern0.5em {\boldsymbol{\Psi}}_k\right){\boldsymbol{\Lambda}}_i^{\mathrm{T}}+{\boldsymbol{\Theta}}_{ik}. $$

(9)

More conceptually, GMMs add a discrete latent variable with a specific number of categories to a traditional latent-growth model. This discrete latent variable then serves as a moderator for the whole model, allowing parameter estimates to differ for the different categories of the discrete latent variable.

Within-class variation

Though GMMs have the advantage that they summarize the covariances among the repeated measures in a more realistic manner (based on Eq. 9) than LCGMs do, this richer model specification containing (latent) within-class random effects can be difficult to estimate on top of the latent classes. That is, variances of growth factor random effects are difficult to estimate in any growth model, so a model that requires unique growth factor variances and time-specific residual variances within each class quickly becomes challenging. Indeed, the frequency of inadmissible or non-converging solutions is notable when the variance parameters are uniquely estimated for each class and the frequency rapidly increases as the complexity of the model increases (Diallo et al., 2016; M. Liu & Hancock, 2014).

A common method by which to work around estimation issues encountered with estimating unique covariance parameters in each class is to constrain covariance parameters to be equal across classes (i.e., Θ_ik = Θ_i; and Ψ_k = Ψ for all k in Eq. 9; see, e.g., Petras & Masyn, 2010). In fact, this constraint is applied by default in Mplus and must be actively overridden (Diallo, Morin, & Lu, 2016). This simplifies Eq. 9 by removing the k subscript on Σ, Ψ, and/or Θ.

More conceptually, if the growth factor variances and covariances are difficult to estimate, applying constraints so that the model features fewer of these parameters will simplify the estimation. The rationale for this decision is often rooted in a desire to reduce the complexity of the estimation rather than for substantive reasons (Bauer & Curran, 2003; Enders & Tofighi, 2008; Gilthorope, Dahly, Tu, Kubzansky, & Goodman, 2014; Harring & Hodis, 2016, Infurna & Grimm, 2017; Infurna & Luthar, 2016; van de Schoot et al., 2017).

Though commonly implemented in empirical settings (Infurna & Grimm, 2017), the approach of constraining variance terms across classes has been widely criticized in the methodological literature. The main reason being that the rationale behind this modeling decision is to aid estimation rather than because theory posits that each latent class actually has equal variance(s). Bauer and Curran (2003) explicitly questioned the choice to apply constraints across classes by stating,

Although [covariance equality constraints] are statistically expedient, we do not regard these equality constraints as optimal from a theoretical standpoint, and in our experience, they are rarely found to be tenable in practice. Indeed, implementing these constraints is in some ways inconsistent with the spirit of the analysis, because one is forcing the majority of the parameter estimates to be the same over classes (permitting only mean differences in the within-class trajectories). (p. 346)

Furthermore, recent methodological studies by Diallo et al. (2016) and Morin et al. (2011) have demonstrated that implementing covariance equality constraints directly impacts class enumeration because the estimation attempts to classify individuals who best mirror the within-class growth characteristics defined by the model. Thus, individuals must necessarily vary around the within-class mean trajectories in equal amounts while holding the amount of variability within individuals across time to be equal as well. This has the effect of adding an additional homogeneity of variance assumption into the model that is questionably tenable and likely false in many applications.

The critical take-home message is that the individuals assigned to each latent class, the number of enumerated classes, and the trajectories of the classes are all impacted by constraining covariance parameters across classes. However, this choice is frequently based on whether the model converges rather than on criteria related to the theory being tested. With such rampant frequency of convergence issues and the current solution of cross-class constraints being known to cause so many issues, a natural question that emerges is whether the complexity of GMMs is necessary in order to answer the questions being asked by researchers or whether a simpler model may suffice. The next section reviews a segment of the psychological literature that frequently uses GMMs to explore whether researchers’ questions necessitate a model as complex as GMMs.

Do mixture model research questions require random effects?

Despite GMMs often being described as a person-oriented or person-centered modeling approach (Bergman & Magnusson, 1997; Laursen & Hoff, 2006; Muthén & Muthén, 2000), the most common interest in empirical studies applying GMMs pertains to classes, not individuals (Cole & Bauer, 2016; Sterba & Bauer, 2010, 2014). To provide evidence that researchers are employing GMMs with random effects when the research questions of interest do not require them, we reviewed research questions, modeling practices, and reporting practices in empirical articles using mixture models in post-traumatic stress disorder (PTSD) research. We use the literature review of van de Schoot et al. (2018), the results of which are available on the original author’s Open Science Framework page. Van de Schoot et al. conducted a thorough review of all studies employing any type of mixture model within the field of PTSD research up to October 2016; ultimately locating 34 articles from 11,395 initially identified articles that satisfied keywords (full details are available in Appendix A of van de Schoot et al., 2018).

Our interest in these articles deviated from the original authors’ interests, so we reviewed each of these 34 studies to identify (a) which type of mixture model was used in the study, (b) whether the model constrained covariance parameters across classes, (c) whether the growth factor covariance estimates were reported, and (d) whether any subject-specific information was reported or required to answer the research questions.

The results of our review showed that 18 studies (53%) used GMMs (the other 47% used LCGMs). A surprising minority of these GMM studies reported any information related to the within-class random effects: 83% did not report any covariance parameter estimates. Furthermore, 39% reported applying cross-class covariance constraints to aid convergence, and another 44% did not provide enough information to determine if covariance constraints were present or not (i.e., only 17% definitively did not constrain covariance estimates across classes). None of the studies that applied cross-class constraints reported doing so for a theoretical reason (i.e., it is highly probable that constraints were uniformly applied to address convergence issues or as a default software option).

Most importantly, and similar to points made in Cole and Bauer (2016), zero studies reported or had asked any research questions about subject-specific curves. Studies invariably had the same three basic interests: (a) how many classes exist, (b) what the class trajectories look like, and (c) which covariates predict class membership. Notably, none of these three interests requires within-class random effects. Although the individual is the central focus of latent-growth models, the latent class is the central focus of GMMs. From this evidence, it seems that the within-class random effects are not providing answers to substantively motivated questions and do not appear to be a factor that researchers are seriously considering when modeling their data (e.g., perhaps GMMs are used because researchers have been exposed to them rather than for their correspondence with the research question).

This is extremely relevant because researchers regularly encounter rampant convergence issues because of overly complex models, which ultimately leads them to atheoretically constrain any parameters they can across classes with the sole purpose of achieving model convergence. Poignantly, this process is undertaken to obtain quantities (partitioned variance components and subject-specific curves) that are irrelevant to the research questions.

Instead, we argue that a more advantageous modeling strategy is to bypass within-class random effects and adopt a population-average approach, a class of models that specifically focuses on the broader mean trajectory while accounting for the variances and correlations among the repeated measures. As we outline in detail in the next section, these methods can similarly account for complex covariance structures but do so without relying on random effects.

Modeling change without random effects

As an extension of latent-growth models, GMMs explicitly model between-individual variability and within-individual variability. However, the random-effect framework is not necessarily required in order to properly model repeated measures data in all circumstances, especially when subject-specific curves are not needed. Although the random-effect framework is omnipresent for growth models in psychology, the subject-specific focus concomitant with these models has largely been forgotten (e.g., Cudeck & Codd, 2012; Liu, Rovine, and Molenaar, 2012a, b; McNeish, Stapleton, & Silverman, 2017; Molenaar, 2004; Molenaar & Campbell, 2009). Cudeck and Codd (2012) aptly summarize the disconnect between the widespread use of random-effect models and their ensuing model interpretation by noting, “the current curious state of practice is to sing the praises of the model as an ideal method for the study of individual change, but then ignore the individuals and resort to an analysis of the mean change profile” (p. 5).

If the research questions can be sufficiently addressed without needing to inspect subject-specific curves or if the interest is in the mean trajectories within each class while properly accounting for within-class variation, the high computational demands of GMMs are needlessly taken on. In such cases, researchers (perhaps unknowingly) are augmenting the complexity of an already complex model with random effects and making an already difficult estimation problem more difficult, all for the purpose of obtaining information that is not central to the primary goals of a mixture model analysis and whose estimates are often not reported.

A different perspective: Population-averaged models

The population-averaged approach in non-mixture contexts has been written about extensively in the biostatistics literature (e.g., Diggle, Heagerty, Liang, & Zeger, 2002; Vonesh, 2013). In the context of continuous outcomes measured longitudinally, the goal is to obtain the average growth trajectory in the sample (conditional on any relevant covariates like sex or treatment group) while accommodating the covariance that arises due to the dependent nature of the repeated measures without partitioning the variance or estimating subject-specific random effects (Fitzmaurice, Laird, & Ware, 2011; Jennrich & Schluchter, 1986; Verbeke & Molenberghs, 2000). Put another way, the goal of population-averaged models is to describe the covariance between repeated measures rather than try to explain the covariance between repeated measures with random effects, as is the goal in latent-growth models.

As an advantage, the estimation of population-averaged models, even in the non-mixture context, is much easier due to the simplified form of the covariance structure. This approach to summarizing the underlying change process has received very little attention in the behavioral sciences, especially in mixture contexts where the appeal of simplified estimation would seem to be very attractive given widespread convergence issues encountered with GMMs. We review a specific type of population-averaged model—the covariance pattern model—in the next section and compare it to the latent-growth model.

Differentiating between covariance pattern and latent-growth models

Consider the role of the marginal covariance in growth models. Because data within an individual are dependent, the off-diagonal terms representing the covariance between pairs of repeated measures within a person are likely nonzero. For some arbitrary design in which time t = 1, . . . , T, the covariance of the raw repeated measures of the outcome Y takes the general form

$$ \left[\begin{array}{cccc} Var\left({Y}_1\right)& & & \\ {} Cov\left({Y}_1,{Y}_2\right)& Var\left({Y}_2\right)& & \\ {}\vdots & \ddots & \ddots & \\ {} Cov\left({Y}_1,{Y}_T\right)& \cdots & Cov\left({Y}_{T-1},{Y}_T\right)& Var\left({Y}_T\right)\end{array}\right]. $$

In latent-growth models, the marginal covariance structure is computed by partitioning the variance in between-individual (Ψ) and within-individual (Θ_i) components with random effects and then combining the between-individual and within-individual covariance matrices together by adhering to distributional assumptions and following standard methods of deriving the model-implied second moment: ${\boldsymbol{\Sigma}}_i={\boldsymbol{\Lambda}}_i\left(\boldsymbol{\Gamma}\;\boldsymbol{\Phi}\;{\boldsymbol{\Gamma}}^{\mathrm{T}}+\kern0.5em \boldsymbol{\Psi} \right){\boldsymbol{\Lambda}}_i^{\mathrm{T}}+{\boldsymbol{\Theta}}_i$.

In covariance pattern models, the variance is not partitioned and the marginal covariance is directly modeled. That is, a standard single-level regression model is fit to the data but assumptions about the residuals are relaxed. Rather than assuming constant variance and that the residuals are independent (e.g., $\varepsilon \overset{i.i.d.}{\sim }N\left(0,{\sigma}^2\right)$ as in ordinary least squares), maximum likelihood allows the residuals from the same individual to be related to each another: ε_i~MVN(0, Σ_i), where Σ is a residual covariance structure specified by the researcher. The model is called a “covariance pattern model” because the researcher selects a covariance structure that patterns how the residuals are related to each other. The elements of the structure that is selected for Σ are then directly estimated as parameters with maximum likelihood. For instance, Cov(Y₁, T₂)from the matrix above would be directly estimated with a covariance pattern model, whereas in a latent-growth model it be an indirect combination of Ψ (the between-individual covariance matrix) and elements of Θ_i (the within-individual covariance matrix). The word “pattern” is used because a parsimonious structure is typically applied (e.g., all repeated measures that are one occasion apart have the same correlation) rather than uniquely estimating each individual element of the matrix (though simply estimating all unique elements is also possible). The covariance pattern model has fallen out of favor in recent years within psychology as computational advances have removed the computational barrier that once existed for the estimation of random-effect models. However, the model continues to receives attention for its generality and flexibility in the quantitative psychology literature (e.g., Azevedo, Fox, & Andrade, 2016; S. Liu, Rovine, & Molenaar, 2012a, 2012b; Lix & Sajobi, 2010).

Though the mechanism adopted by latent-growth models and covariance pattern models differs, each model essentially has the same goal: to provide estimates that reproduce the observed covariances as closely as possible. The next subsection discusses some of the common structures used in covariance pattern models and when different structures may be best applied.

Common covariance pattern covariance structures

Similar to the requirement that researchers select the structure of the within- and between-individual covariance matrices in latent-growth models, researchers must similarly select the covariance pattern structure in covariance pattern models. This is often accomplished through an exploration of the repeated measures data taking into account longitudinal design features (e.g., spacing of the measurements and whether the measurement occasions are fixed across subjects).

We discuss four possible structures in the following subsections. Note that these structures are not exclusive to covariance pattern models and are sometimes used to describe the within-individual covariance matrix in latent-growth models (though less complicated structures with all off-diagonal elements constrained to be zero remain the most popular choices; Grimm & Widaman, 2010). The difference in covariance pattern models is that the structure captures all residual covariance—not just within-person residual covariance, as in latent-growth models—so structures with nonzero off-diagonal terms are typically required with covariance pattern models.

Compound symmetry

One common patterned structure is a compound symmetric (i.e., exchangeable) structure, where ${\boldsymbol{\Sigma}}_i={\sigma}_c{\mathbf{J}}_{n_i}+{\sigma}^2{\mathbf{I}}_{n_i}$for ${\mathbf{J}}_{n_i}$ a matrix of ones of dimension n_i and ${\mathbf{I}}_{n_i}$ is an identity matrix of dimension, n_i. This results in a correlation matrix with equal off-diagonal elements. The variance terms on the diagonal can also be heterogeneous if the variance of the repeated measures changes over time. In a hypothetical case of five repeated measures, the compound symmetric correlation matrix would be

$$ \left[\begin{array}{ccccc}1& & & & \\ {}\rho & 1& & & \\ {}\rho & \rho & 1& & \\ {}\rho & \rho & \rho & 1& \\ {}\rho & \rho & \rho & \rho & 1\end{array}\right]. $$

First-order autoregressive

Another popular structure features residuals that follow a first-order autoregressive process such that the (j, j′)th element is Σ_{i (j, j')} = σ²ρ^{|j − j'|}. In this first-order autoregressive structure, pairs of repeated measures separated by the one measurement occasion (i.e., that are lagged by one) are correlated equally. Repeated measures with larger lags are correlated to a lesser degree based on an exponential function of the one-lag correlation. For instance, with this structure, repeated measures that are one lag apart (e.g., Time 1 and Time 2) are correlated at some estimated value ρ, and repeated measures that are two lags apart (e.g., Time 1 and Time 3) would be correlated at ρ². The structure increases flexibility without sacrificing parsimony because it allows for correlations to vary across lags (i.e., measurements that are further apart are less related) but does not require additional parameters to be estimated because each lag is a function of a single estimate, ρ. This structure could be embellished to allow for heterogeneous variances across time. In a hypothetical case of five repeated measures, the autoregressive correlation matrix would be

$$ \left[\begin{array}{ccccc}1& & & & \\ {}\rho & 1& & & \\ {}{\rho}^2& \rho & 1& & \\ {}{\rho}^3& {\rho}^2& \rho & 1& \\ {}{\rho}^4& {\rho}^3& {\rho}^2& \rho & 1\end{array}\right]. $$

Toeplitz

A structure that is similar to the first-order autoregressive structure that maintains more flexibility is the Toeplitz structure. In a Toeplitz structure, the autocorrelation process for the (j, j′)th element is Σ_{i (j, j')} = σ^{|j − j'| + 1}. Similar to the first-order autoregressive structure, all measures separated by one measurement occasion are equally correlated. However, for measures lagged by two, the Toeplitz structure estimates a separate correlation rather than simply squaring the lag 1 correlation. Each subsequent lag also receives a unique estimate, so the number of off-diagonal parameters to be estimated is equal to the number of measurement occasions minus one. Like the first-order autoregressive structure, this allows the correlation between measures to change as the measures become more distant in time. Unlike the first-order autoregressive structure, a Toeplitz structure does not require that the change in correlation follow a specific function of the lag 1 correlation. In a hypothetical case of five repeated measures, the Toeplitz correlation matrix would be

$$ \left[\begin{array}{ccccc}1& & & & \\ {}{\rho}_1& 1& & & \\ {}{\rho}_2& {\rho}_1& 1& & \\ {}{\rho}_3& {\rho}_2& {\rho}_1& 1& \\ {}{\rho}_4& {\rho}_3& {\rho}_2& {\rho}_1& 1\end{array}\right]. $$

Unstructured

The most flexible of all within-class covariance structures is one that is completely unstructured, so that every element is uniquely estimated. In a hypothetical case of five repeated measures, the unstructured correlation matrix would be

$$ \left[\begin{array}{ccccc}1& & & & \\ {}{\rho}_{21}& 1& & & \\ {}{\rho}_{31}& {\rho}_{32}& 1& & \\ {}{\rho}_{41}& {\rho}_{42}& {\rho}_{43}& 1& \\ {}{\rho}_{51}& {\rho}_{52}& {\rho}_{53}& {\rho}_{54}& 1\end{array}\right]. $$

This structure is reminiscent of the covariance structure in multivariate analysis of variance within a general linear modeling framework (S. Liu et al., 2012a).

Selecting a covariance structure

The selection of which type of structure to use in a covariance pattern model can be a challenge to researchers not well-versed in this framework. Many options exist and readers looking for a good summary of possible options may wish to consult the treatment provided in the SAS 9.2 manual under the Repeated Statement section of the PROC MIXED chapter (PROC MIXED is the SAS procedure used to fit covariance pattern models even though they are not technically mixed-effects models). Chapter 7 of Fitzmaurice et al. (2011) is also dedicated to discussing covariance pattern models. As general guidance,

• Compound symmetry tends to be most useful when there are few repeated measures or when repeated measures are spaced very closely together. Compound symmetry in a covariance pattern model produces an identical marginal covariance matrix as a latent-growth model with random intercepts but no random slopes.

• First-order autoregressive structures are most useful when there are many repeated measures and the spacing between measurement occasions is equal or nearly equal.

• Toeplitz is best suited to a moderate number of repeated measures but correlations are not expected to decrease exponentially over time.

• Unstructured modeling is typically reserved for very few measurement occasions or when the measurement occasions have an unorthodox structure.

Ultimately, the goal is to strive for parsimony, such that the covariance pattern structure reflects the dependency among repeated measures with as few parameters as possible.

Equivalency of mean structures

Though latent-growth models and covariance pattern models differ with respect to the formation of the covariance structure and whether subject-specific curves are available, either model will produce the same mean trajectory with identical interpretations with continuous outcomes. Covariance pattern models estimate the growth trajectory for the typical individual in a sample but does not include random effect to capture individual deviation from the mean trajectory. Therefore, the means structure is written very similarly to the latent-growth mean structure in Eq. 1 except that the growth factors have no i subscript because they do not vary by individual. This can be written as

$$ {\mathbf{y}}_i={\boldsymbol{\Lambda}}_i\boldsymbol{\upeta} +{\boldsymbol{\upvarepsilon}}_i $$

(10)

The mean growth trajectory of the covariance pattern model can be obtained by taking the expectation of y_i:

$$ E\left({\mathbf{y}}_i\right)=E\left({\boldsymbol{\Lambda}}_i\boldsymbol{\upeta} \right)+E\left({\boldsymbol{\upvarepsilon}}_i\right) $$

(11a)

$$ ={\boldsymbol{\Lambda}}_i\boldsymbol{\upalpha}, $$

(11b)

The mean growth trajectory of the latent-growth model can similarly be obtained by taking the expectation of Eq. 3, which yields a quantity identical to that in Eq. 11b:

$$ E\left({\mathbf{y}}_i\right)=E\left({\boldsymbol{\Lambda}}_i{\boldsymbol{\upeta}}_i\right)+E\left({\boldsymbol{\Lambda}}_i{\boldsymbol{\upzeta}}_i\right)+E\left({\boldsymbol{\upvarepsilon}}_i\right) $$

(12a)

$$ ={\boldsymbol{\Lambda}}_i\boldsymbol{\upalpha}, $$

(12b)

given that the random effects and residuals have a zero mean vector [i.e.,E(ζ_i) = E(ε_i) = 0] and are uncorrelated [i.e.,Cov(ζ_i, ε_i) = 0].

Extending covariance pattern models to the mixture context

To place the covariance pattern mixture model (CPMM) on the present continuum of mixture models for repeated measures data, CPMMs fall between the LCGM from Nagin (2005) and the GMM from Muthén and Shedden (1999). Like LCGMs, CPMMs acknowledge that the latent classes are already a discretization of the random-effect distribution and the discrete classes are the focus of the interpretation, so random effects within classes are not necessarily required. CPMMs address possible issues in LCGMs by expanding the marginal covariance structure so that extra classes are not extracted because of a covariance structure misspecification. Like GMMs, CPMMs fully model all variation by including a patterned marginal covariance structure that reflects between- and within-individual variation. Unlike GMMs, the marginal covariance in CPMMs is directly estimated rather than a combination of partitioned variance components.

If researchers are primarily interested in enumerating classes and interpreting the mean trajectory for each class while satisfactorily summarizing the pattern of variances and covariances among the repeated measures, a CPMM accomplishes these tasks in a more parsimonious and more efficient manner than GMMs. Concurrently, the CPMM has a simpler specification than does a GMM, which should theoretically make convergence, inadmissible solutions, atheoretical parameter constraints, and other estimation-related issues less frequent. These claims are explicitly assessed and demonstrated via simulation evidence in the next section.

Simulation design

Data generation

The data generation model is based on the so-called “cat’s cradle” pattern that emerges in substance use (Sher, Jackson, & Steinley, 2011) and post-traumatic stress research (Bonanno, 2004). In these research domains, four classes typically emerge: one class that starts at higher values and maintains high values (the “chronic” class), a second class that starts low and maintains low values (the “unaffected” class), a third class that starts high but decreases over time (the “recovery” class), and a fourth class that starts low and increases over time (the “delayed-onset” class). In both research domains in which such solutions are found, the chronic and unaffected classes typically comprise a majority of the data (approximately 65% to 80%; Bonanno, 2004; Sher et al., 2011). Of the remaining data, the recovery class tends to be about twice as big as the delayed-onset class.

Figure 1 shows a plot of the trajectories in each of the four classes, and Fig. 2 shows the general path diagram of the model. Table 1 shows the model equations and covariance structures that were used to generate data from these trajectories within Mplus version 8; the population-generating model is a GMM.

Fig. 1

Plots of the mean trajectories in each of the four simulated classes in Model 2. Using the class proportions in a study by Depaoli, van de Schoot, van Loey, and Sijbrandij (2015), we assigned 63% of the sample to Class 1, 12% to Class 2, 19% to Class 3, and 6% to Class 4

Fig. 2

Path diagram of the data generation model. C is a discrete latent variable representing each of the different classes. The α parameters represent the latent variable means; the η₀ latent variable represents the intercept, η₁ represents the linear slope, and η₂ represents the quadratic slope. The intercept latent variable varies across people within a class (with variance Ψ₀₀), as does the linear slope latent variable (with variance Ψ₁₁). The quadratic slope latent variable does not vary across people within a class. The latent-variable loadings are fixed because the data are time-structured, such that all people have the same occasions of observations. The residual variances are constrained to be equal across time

Table 1 Data generation equations for our population model

The growth trajectory in each class has both linear and quadratic components, to achieve nonlinear trajectories. The linear slope varies across individuals within classes but the quadratic slope variance was constrained to zero in the population. The unaffected group comprised 63% of the population, the recovery class 12%, the chronic class 19%, and the delayed-onset class 6%, in an attempt to mirror empirical applications of mixture models in which class proportions are disparate. The data feature five time points that represent either months after baseline in the substance use context or weeks in the post-traumatic stress context. The loadings from the linear slope factor to the observed variable are 0 (baseline), 1, 10, 18, and 26. The loadings from the quadratic slope factor to the observed variables are the squares of these loadings. The growth factor variances are rather large relative to the growth factor means for the intercept and linear slope, which was intentional, in order to generate data that were not well separated, as are typically encountered in empirical examples.

Simulation conditions

The simulation features sample sizes of 500 and 1,500. Our assessment of the van de Schoot et al. (2018) literature review on mixture models in PTSD research resulted in a median sample size of 509, which informed our smaller sample size condition. We then selected 1,500 to represent a study that is far above average, because 1,500 corresponded to about the 85th percentile of sample sizes in the van de Schoot et al. review.

Three different models were fit to the data: a CPMM with a compound symmetric structure with homogeneous variances that was unconstrained across classes (CPMM; two covariance parameters per class: one residual variance, one covariance), a GMM with all variances unconstrained across classes (GMM; four covariance parameters per class: one residual variance, intercept variance, slope variance, and a covariance between intercepts and slopes), and a GMM with all covariance parameters constrained across classes (GMMC; four covariance parameters total: one residual variance, intercept variance, slope variance, and a covariance between intercepts and slopes). The residual variance was constrained to be equal within classes across all models, to match the data generation process. The path diagram for the GMM was identical to that in Fig. 2. The path diagram for the GMMC was similar to that in Fig. 2, with the exception that the Ψ and θ parameters were constrained to be equal across all classes. The CPMM path diagram is shown in Fig. 3.

Fig. 3

Path diagram of the covariance pattern mixture model. The parameter definitions are the same as in Fig. 2. The newly added ρ is a residual covariance; with the compound symmetric structure, all residual covariances are constrained to be equal. The residual variances are not shown, to avoid overcrowding, but each residual variance is constrained to be θ, as in Fig. 2. Also note that the latent-variable variances are all constrained to be 0, which forces all the residual variance to the observed repeated measures, rather than partitioning it into within-person and between-person components. A covariance pattern is then applied directly to the residuals of the repeated measures

As an important note, the four-class GMM is identical to the data generation model. Also of note, because the data generation included nontrivial random slopes, the CPMM covariance structure will be moderately misspecified. This was done intentionally. Using a misspecified CPMM would paint a more realistic picture of performance and would avoid artificially inflating the performance of CPMMs by unrealistically modeling the true covariance structure. Instead, the results reflect the results that would be obtained if someone were to use CPMMs somewhat naively and to select an unfavorable covariance structure. So, keep in mind that the results we present compare a perfect GMM with a misspecified CPMM. As a secondary consideration, we hope that this will alleviate potential fears that researchers may have about switching model types and not specifying the model perfectly—our results already have built in some possible user error that might be encountered if using an unfamiliar modeling framework.

Simulation outcomes

Our discussion will follow the four outcomes in the simulation: class enumeration, percentage of convergent models, relative bias in the class-specific growth trajectories, and classification accuracy. For the last three outcomes (convergence, bias, and classification), the results can be easily automated within Mplus version 8 using the MonteCarlo module. These results are based on 500 replications for each sample size condition. In each of these 500 replications, the results will be based on the assumption that the correct four-class solution has been fit to the data. For these three outcomes measures, the population values for the class trajectories were used as starting values for the mean structure in each class. The default Mplus starting values were used for all covariance structure parameters. To study the class enumeration, a separate simulation using a different setup was required, which will be outlined next.

Details of the separate class enumeration simulation

To study the class enumeration behavior of each of the three fitted models, we generated 100 datasets for each sample size condition and then fit three-, four-, and five-class models to each generated dataset. Fewer replications were used than for other simulation outcomes because class enumeration requires fitting multiple models per replication. We then compared the sample-size-adjusted Bayesian information criterion (SA-BIC; Sclove, 1987) across the three different class solutions for each replication, for each model. The solution with the lowest SA-BIC was then selected for each replication. SA-BIC was chosen because Yang (2006) and Tofighi and Enders (2007) found that it tends to perform better than other information criteria for class enumeration. Tofighi and Enders, in particular, noted that SA-BIC is the clear choice for enumeration with moderate sample sizes (p. 332) or poorly separated classes (p. 333), or when there is a large disparity in the class proportions (p. 334), all of which exist in some or all conditions of our simulation design.

The goal of the simulation was to track the number of times each model type selected the correct four-class solution. The class enumeration simulation used Mplus default starting values rather than using the population values as starting values. Default starting values were used because (a) it was unclear which starting values should be used for the incorrect three-class and five-class solutions, as there would not be any population values for these classes; (b) default starting values are more representative of how classes are enumerated in empirical studies in the initial stages of analyses (i.e., researchers do not have a good idea of the class trajectories before they know how many classes there are); and (c) it may be helpful to present simulation results for how starting values may impact convergence. We also tracked the percentage of non-convergent replications for each of the fitted models. Replications in which the best likelihood was not replicated from multiple random sets of random starting values were not treated as nonconverging for this simulation.

These models were run by calling Mplus version 8 via SAS PROC IML to facilitate aggregating the results because this type of simulation cannot be performed entirely within the Mplus MonteCarlo module (to our knowledge). We used 100 random starts and 10 final stage optimizations based on recommendations in M. Liu and Hancock (2014) and Li, Harring, and Macready (2014) so that the full likelihood surface could be explored. All code for the simulation from SAS and Mplus are included on the first author’s Open Science Framework webpage (https://osf.io/yh6kf/).

Simulation results: Unknown number of classes

Class enumeration

The initial step of a mixture model analysis is typically to determine the number of latent classes that are present, so we begin with the enumeration and convergence results. Table 2 shows the numbers of replications that converged for each class solution and the numbers of replications selecting each class solution, by model type and sample size. The numbers of replications selecting each class solution might not add up to 100, because in some of the replications none of the competing class solutions converged (and therefore, none of the competing options was selected). We did include cases in which some but not all class solutions converged. For example, if only the three-class solution converged, but the four- and five-class solutions did not, the replication was recorded as selecting the three-class solution. We followed this criterion because it most closely mirrors how we felt the situation would be handled with empirical data.

Table 2 Numbers of replications selecting a three-, four-, or five-class solution, based on the SA-BIC and the convergence rate by the number of classes

N = 500 condition

In the N = 500 condition, the CPMM narrowly had the highest number of replications in which the true four-class solution was selected (33 out of 100). This vastly exceeds the GMM that only selected the four-class solution in two replications (poor performance was largely driven by convergence issues) but only narrowly eclipses the number of times the GMMC selected the correct four-class solution (32 out of 100).

Regarding convergence, using Mplus default starting values, the convergence issues encountered by the GMM are readily apparent: Only 5% of the four-class models converged, even though this was the exact model from which data were generated. Constraining all the covariance structure parameters to be equal across classes is clearly effective for convergence, in that convergence rates of the GMMC were in the high 60s to low 80s. Do note that the CPMM convergence was in the high 80s to high 90s without requiring the assumptions implied by constraints, however. Constrained variances in the GMMC were not warranted on some parameters (i.e., intercept variance, residual variances). This may explain why the GMMC seemed to prefer the five-class solution because the misspecified covariance structure may be emerging as a separate class, especially when considering that BIC-based measures tend to be conservative and underextract the number of classes (e.g., Diallo, Morin, & Lu, 2017; Dziak, Lanza, & Tan, 2014). Despite the improved convergence of the GMMC over the GMM, the CPMM uniformly had the highest convergence rates, especially for the correct four-class solution.

N = 1,500 condition

In the N = 1,500 condition, the frequency with which the CPMM selected the correct four-class solution increased to 74 out of 100, and convergence issues were essentially negligible across conditions. For the GMM, even though the model was identical to the data generation model and the sample size was in the 85th percentile of empirical studies in this area, convergence issues remained immensely problematic, with only 16 out of 100 replications converging for the four-class solution. As a result, the GMM most often selected the three-class solution (66 out of 100 replications) and only selected the correct four-class solution in two replications. As expected, the GMMC vastly improved convergence rates as compared to the GMM. However, the GMMC overwhelmingly favored the five-class solution, which is an unconventional finding, given the conservative nature of the BIC-based metrics and their tendency to underextract. The spurious class is likely attributable to the covariance structure misspecification, such that additional classes represent assumption violations rather than a substantively interesting group of people (e.g., Bauer & Curran, 2003). Across all conditions, the convergence rate of the CPMM was, at worst, within 1% of the GMMC, and CPMM convergence rates exceeded the GMMC rates by a wide margin in other conditions, particularly in the true four-class solution condition.

Although the CPMM is not perfect (or even necessarily good in the N = 500 condition, in an absolute sense), the CPMM gives the best relative chance to select the correct number of classes. Part of this improved performance is related to improved convergence rates—in the GMM (and GMMC, to a lesser extent), the four-class solution could not converge due to the augmented complexity of the model, so there was no chance that the correct solution could be selected. Though the GMMC certainly improves convergence when good starting values are not known a priori, convergence is worse than the CPMM, it requires more assumptions about constraints across classes, and it selects the proper number of classes less often than the CPMM. The behavior as sample size increases is also telling—the GMMC performed much more poorly in the larger sample size, possibly suggesting that the four-class solutions in the smaller sample size conditions may be attributable to uncertainty or the conservative nature of BIC-based measures. On the other hand, the CPMM dramatically improved at the larger sample size.

Simulation results: Known number of classes

The results in the previous section approached the analysis as an empirical study, in that the number of classes was unknown a priori. Even though there were discrepancies in the ability of each approach to correctly identify the number of classes, the results presented in this section are fit as if the enumeration yielded the correct four-class solution. This was done with an interest in gauging the quality of the model estimates independent of each approach’s ability to detect the correct number of classes. These analyses also used the population values from the data generation for the mean structure in each class, as it would be more reasonable that a researcher would have a better idea about the different trajectories that exist in the data once the number of classes was determined.

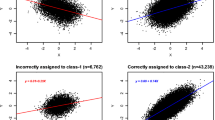
Convergence rates, population starting values

The results previously reported in Table 2 contained information about convergence when the Mplus default starting values were used. Figure 4 shows the percentages of the 500 replications with a four-class solution that successfully converged with the population values used as starting values for each class. As we noted previously, convergence is a major obstacle to fitting GMMs in empirical studies—even with good starting values—which is reflected in Fig. 4. Only 26% of GMMs converged when N = 500, and only 33% converged when N = 1,500. Good starting values made an improvement over the four-class values in Table 2, but the results still are troubling, considering that this is true model with the population values for the starting value of each class. The GMMC was again effective for convergence, as evidenced by the 68% and 100% convergence rates for GMMC in the N = 500 and N = 1,500 conditions, respectively. However, the covariance pattern approach led to the best convergence rates in Fig. 4, with 99% and 100% convergence in the N = 500 and N = 1,500 conditions, respectively. Coinciding with the argument that CPMMs reduce model complexity, the starting values made the smallest difference in convergence for the CPMMs, as compared to the GMMs or GMMCs.

Fig. 4

Plot of the convergence rates from 500 replications of the four-class solution by model type and sample size condition. CPMM = covariance pattern mixture model, GMMC = growth mixture model with covariance parameters constrained to equality across classes, GMM = unconstrained growth mixture model

Though a helpful starting point, simply achieving convergence and obtaining estimated values in software output is not indicative of improved performance. The next subsection investigates the estimated trajectories of the classes to assess the quality of the estimates that are obtained from each model type once convergence is achieved.

Trajectory bias

Figure 5 shows the class trajectories from each model type with a four-class solution, averaged over replications that converged for the N = 500 condition. We only present the N = 500 results in text for brevity, due to similarities across the conditions, but the bias for the N = 1,500 condition is available from the supplementary material, for interested readers.

Fig. 5

Comparison of the true population average class trajectories (upper left) to the covariance pattern mixture model (CPMM, upper right), the unconstrained growth mixture model (GMM, lower left), and the constrained growth mixture model (GMMC, lower right) for the N = 500 condition

The generated population trajectories are shown in the upper left as a reference. The CPMM model, in the upper right, does not perfectly match the population trajectories—the recovery class slope, in solid gray, is noticeably steeper, and the delayed-onset class slope, in dashed gray, is noticeably flatter. In fact, the relative biases of these slopes and the unaffected-class slope, in solid black, exceed the 10% threshold typically used in simulation studies (Flora & Curran, 2004), though the intercept bias was negligible for all classes. Despite this bias, the four classes from the generating model are still rather clear: The “cat’s cradle” pattern is quite apparent, and the basic substantive interpretation of the classes is discernible.

The GMM and GMMC trajectories shown in the bottom panels, on the other hand, do not reflect the population trajectories very accurately. With both the GMM and the GMMC, the recovery class slope in solid grey goes in the wrong direction and increases over time whereas the delayed-onset class slope in dashed grey is essentially flat. The relative bias for the slopes in the recovery and delayed-onset classes in these model types ranged from – 120% to – 334%. Of ultimate importance, the class trajectories from either the GMM or the GMMC do not show the “cat’s cradle” pattern, and instead show four nearly horizontal lines. Though the GMMC helped improve convergence, as is noted in Fig. 4, the class trajectories produced by this model have the highest relative bias for all but one parameter (slope of the unaffected class, in solid black; the CPMM has the highest relative bias for this parameter).

So far, the CPMM shows better enumeration, convergence rates, and improved (but not perfect) estimates of class trajectories, even as compared to the true GMM. However, a typical substantive interest of mixture models for longitudinal data is the ability to assign individuals to the proper class. The performance of classification accuracy is covered in the next subsection to address this property of each model type.

Classification accuracy

Table 3 shows the classification percentages for each model type and sample size condition for converged replications for the four-class solution. This outcome measure shows the percentage of simulated individuals who were assigned to the appropriate class by the model (this is possible in a simulation because the true class is known). For example, the 96% value in the CPMM column for N = 500 means that 96% of the simulated individuals who were generated to be in the unaffected class were assigned to the unaffected class by the CPMM. The total number of correctly classified individuals is included at the bottom of the table (because the class sizes are very different, this value is not equal to the unweighted average in each column).

Table 3 Classification accuracy for simulated data for each sample size and model type, showing the percentages of simulated people who were assigned to the correct class

In Table 3, the classification accuracy was the lowest for the recovery and delayed-onset classes (the two middle classes whose trajectories cross in Fig. 1). This makes sense from the data generation because the intercepts of these classes are very similar to those of the other classes, and the slope variances were rather large relative to the magnitude of the growth factor means. Additionally, the recovery and delayed-onset classes were the smallest classes (12% and 6%, respectively).

In both sample size conditions, the CPMM had the highest overall classification rate, but the CPMM was not always the best at classifying individuals for each class. Classification percentages for the unaffected and chronic classes differed slightly across model type and sample size, but the percentages were roughly the same. However, the CPMM tended to be worse than the GMM and GMMC models for the recovery class, whereas the GMM and GMMC performed noticeably worse for the delayed-onset class. The classification rates for the delayed-onset class also decreased with sample size for both the CPMM and GMM.

Of particular note is that the GMMC did not accurately assign any individuals in the delayed-onset class. GMMC did assign some individuals who were generated to be members of other classes into the delayed-onset class, so the class was not empty; however, these individuals truthfully belonged to a different class. Nearly all (97% in both sample size conditions) of the individuals generated to be in the delayed-onset class were assigned to the unaffected class in the GMMC. This somewhat odd finding may be attributable to the large trajectory bias seen in Fig. 5. That is, given the values for the intercept and slope variances and the fact that the GMMC class trajectories were essentially four horizontal lines, it is questionable whether the delayed-onset class has the same meaning in the GMM or GMMC that it does in the data generation model. Conversely, the CPMM has some difficulty accurately assigning individuals to the small, overlapping classes, but the classes at least appear to have the same general meaning as is intended in the data generation model.

In the next section, we show how the general findings from the simulation study apply to an empirical dataset.

Empirical example

Consider a subset of 405 children and mothers from the National Longitudinal Survey of Youth (NLSY), which can be found in Hox (2010). Each child’s reading recognition was measured at four different time points, when the children were between 6 and 8 years old at baseline. To these data, we fit a CPMM and GMM/GMMC to outline the difference in approaches with a single empirical dataset. Mixture models were estimated in Mplus 8 with 100 random starts and ten final stage optimizations. Complete files containing the Mplus code and results for models used in the example as well as the data are provided on the first author’s Open Science Framework webpage. Mplus code for each of the common covariance structures we discussed previous for CPMMs is provided in the Appendix.

Determining the mean structure

To this data, we first fit an unconditional growth model to the reading recognition variable without extracting any latent classes (means at the four time points are 2.52, 4.08, 5.00, and 5.77). When looking at the empirical means as well as exploratory plots, it seemed plausible that the growth trajectory may be nonlinear because the difference between successive time points decreases for larger values of time. When fitting the latent-growth model without multiple latent classes, we fit a linear growth model and a quadratic growth model. The quadratic model resulted in a significant likelihood ratio test [χ²(1) = 146.99, p < .01], and this mean structure was retained.

Adding mixture components

Then we subsequently fit a CPMM and a GMM. The CPMM was fit with a homogeneous Toeplitz structure because the measures are equally spaced and the raw variances at each point are rather close (0.86, 1.17, 1.35, 1.56 for Time 1 through Time 4, respectively). Raw correlations between time points were also high (range: .45 to .80) and decreased over time but in a not consistent fashion. The GMM was fit with a homogeneous diagonal residual structure; the quadratic growth factor variance was set to 0 but the intercept and slope variance were estimated and allowed to covary. We did consider heterogeneous variances for both models as well, but the SA-BIC was worse with heterogeneous variances in all instances.

For growth in academic measures like reading, it is typical to find three latent classes generally corresponding to “fast” learners, “on-time” learners, and “slow” learners (e.g., Musu-Gillette et al., 2015). Along with this theory, we compared the two-, three-, and four-class models for both the CPMM and the GMM using the SA-BIC and the bootstrapped likelihood ratio tests with 100 replications (BLRT; McLachlan, 1987). Though the BLRT was not included in the simulation because of its heavy computational demand, its use has been advocated for along with BIC-based measures in previous studies (Nylund, Asparouhov, & Muthén, 2007; Nylund-Gibson & Masyn, 2016).

Enumerating classes

CPMM enumeration

With the CPMM, the SA-BIC of the three-class solution was smaller than the two-class solution (three-class SA-BIC = 3,107 vs. two-class SA-BIC = 3,154) and the BLRT was significant in the three-class model (∆-2LL = 69.81, p_BLRT < .01), suggesting that the three-class solution fit better. The four-class solution best likelihood could not be replicated with different starting values. The issue likely stemmed from the fact that the fourth class was very small (only 2% of the sample, which is ten individuals for this data). Furthermore, the estimates that were output (along with the warning message) had a nearly identical class trajectory to another class, suggesting that the four classes was an over-extraction. We therefore continued with the three-class solution for the CPMM.

GMM enumeration

When fitting an unconstrained GMM, the two-class solution converged without issue (SA-BIC = 3,097). When allowing all parameters to be class-specific, the three-class GMM did not converge due to a non-positive definite growth factor covariance matrix. Constraining the growth factor covariance matrices to be equal across classes did not lead to convergence, but constraining the growth factor covariance matrices and residual covariance matrices across classes did allow the model to converge (i.e., a GMMC was required in order to achieve convergence; three-class SA-BIC = 3,180). The BLRT was significant for the three-class solution (∆–2LL = 32.93, p_BLRT < .01), suggesting that three classes fit better than two classes. As with the CPMM, the four-class GMM solution could not converge with all covariances freely estimated across classes. Constraining growth factor covariance matrices did not help, but constraining all covariance parameters did converge (four-class SA-BIC = 3,166). The BLRT was significant for the four-class solution (∆–2LL = 25.62, p_BLRT < .01), suggesting that the four-class solution fit better than the three-class solution. Although the two-class SA-BIC was lower, the BLRT was significant, so we proceed with the four-class solution because both the SA-BIC and BLRT support four classes over three classes and the BLRT also supported three classes over two classes. We acknowledge that the two-class solution could also be used, depending on which metrics researchers choose to weigh most heavily.

Class trajectories and proportions

A plot of the class trajectories and the percentages of the sample assigned to each class for the CPMM is shown in the top panel of Fig. 6. The classes were well-separated, with average latent-class probabilities of .877 for Class 1, .806 for Class 2, and .870 for Class 3. The bottom panel of Fig. 6 shows the results from the four-class GMMC (with all covariance parameters constrained across classes). The classes were also well-separated, with average latent-class probabilities of .839 for Class 1, .806 for Class 2, .858 for Class 3, and .851 for Class 4.

Fig. 6

Growth trajectories of three extracted classes using a covariance pattern mixture model (top), as compared to the growth trajectories of four extracted classes using a growth mixture model with all covariance parameters constrained across classes (bottom)

When comparing the class trajectories between the CPMM and the GMMC in Fig. 6, the GMMC has more classes, and the assignment of participants to the classes is quite different. Class 1 contains about the same proportion of the sample in both the CPMM (22%) and the GMMC (23%). In the GMMC, Class 2 makes up a majority of the sample, at 60%. In the CPMM, Class 2 contains only 26% of the sample. A majority of the sample in the CPMM were assigned to Class 3 (52%), whereas Class 3 (13%) and Class 4 (4%) together amounted to only 17% of the sample in the GMMC.

Differences in this empirical example mirror the findings from the simulation study. Namely, the more theoretically desirable GMM showed notable convergence problems, necessitating a switch to a GMMC for the sake of achieving convergence. Also as we saw in the simulation, the likely misspecification present in the GMMC resulted in additional extracted classes, which reflect the misspecification to the covariance structure rather than a substantively motivated class. In the CPMM, the class-specific marginal covariances (e.g., Class 1 lag 1 = .076, Class 2 lag 1 = .205, Class 3 lag 1 = .520) and class-specific residual variances (Class 1 = .186, Class 2 = .308, Class 3 = .943) were quite different, suggesting that the constraints applied in the GMM were an inappropriate methodological shortcut required in order to reach convergence. The CPMM was fit and converged without issues, allowing the desired model (without undesirable constraints) to be fit and interpreted as intended.

Discussion

Though random-effect modeling is thoroughly engrained in psychology, a growing body of literature is questioning its status as the default method when considering the types of questions being asked. In the context of mixture models for longitudinal data, the random effects can make an already complex estimation process more complex, leading to higher rates of convergence issues and poor statistical properties of estimates, even if the model is the exact true model and sample size is large. Moreover, as we found in our review of PTSD mixture model studies, the most concerning aspect of the universal random-effect usage is that researchers are not using these quantities that are responsible for making the estimation so demanding.

If the goal is to obtain the average growth trajectory in each latent class, population-averaged models are the simplest type of model that is capable of addressing these questions while still accounting for the variances and covariances among the repeated measures in a sensible manner. The CPMM presented in this article is one such approach, and our results unambiguously support that CPMMs vastly improve convergence, class enumeration, and class trajectories as compared to GMMs. In this way, CPMMs align with the recommendations in Wilkinson and the Task Force on Statistical Inference (1999), which call for psychological researchers to choose a minimally sufficient analysis (p. 598). The simpler, population-averaged approach is just as capable as random-effect models for answering research questions asked in the empirical literature. Though GMMs (and the GMMC variation used to combat convergence issues) are currently being used to address these questions, the model tends to be overly complex for the intended purpose, which leads to convergence issues, poor performance, and, commonly, the need for questionable cross-class constraints. Though convergence issues can arise for a variety of reasons, a mismatch in model complexity and data quality can be a primary culprit, and the oft-noted convergence issues with GMMs are a strong indicator that less complex alternatives are a fruitful avenue to explore.

One concern concomitant with the CPMM approach is that the researcher must select the covariance structure, and might not choose the optimal structure. However, the results from the present investigation suggest that this may not be overly important. In our simulation studies, we purposefully chose the most misaligned covariance structure given the data generation, and even a noticeably misspecified CPMM was clearly superior to a GMM that was identical to the data generation model and that used the population values as starting values, as well as to the GMMC version of the model often used in practice. In a relative sense, the more adverse issue is that GMMs are too complex to be reasonably applied in most contexts, rather than whether the CPMM covariance structure is misspecified.

Furthermore, we want to emphasize that the GMM-implied covariance structure is not necessarily correct in empirical data in all cases, either. As we noted earlier (Eq. 9), GMMs pose a specific functional form to the model-implied covariance, which may or may not adequately summarize the variability among the repeated measures. This could possibly lead to some misspecification, especially given that the model-implied covariance similarly requires the researcher to select the appropriate structures of Ψ and Θ, similar to CPMMs. The most general, parsimonious form of the covariance structure is Σ = D^1/2PD^1/2, where the variance matrix, D, can have its own structure uncoupled from the correlational (off-diagonal) structure in P (see Harring & Blozis, 2014). Covariance structures in either CPMMs and GMMs can be seen as restricted versions of this most general structure. CPMMs are not necessarily more misspecified than GMMs—both are at risk of misspecification based on researchers’ modeling decisions. CPMMs happened to be (intentionally) more misspecified in our simulation study, because the generating model was a GMM, so GMM or GMMC could degrade even further if the covariance structure were not properly specified.

Nonetheless, if researchers continue to be concerned about possible covariance structure misspecification in CPMMs, such traditional choices as compound symmetry, Toeplitz, or autoregressive can be sidestepped if they are deemed insufficient. An alternative method would be to inspect the observed covariance or correlation matrix of the repeated measures for guidance about the appropriate structure. If the structure does not appear to follow one of the traditional structures, the flexibility of the structural equation modeling framework under which CPMMs fall makes custom covariance structures easy to specify (Grimm & Widaman, 2010). For example, the observed marginal correlation matrix from the NLSY data has a form that could deviate from traditional structures:

$$ \left[\begin{array}{cccc}1& & & \\ {}.66& 1& & \\ {}.54& .78& 1& \\ {}.45& .76& .80& 1\end{array}\right]. $$

One could customize a marginal structure in which the (3, 2), (4, 2), and (4, 3) elements (.78, .76, and .80, respectively) are captured by one parameter, while the (2, 1), (3, 1), and (4, 1) elements (.66, .54, and .45, respectively) are each captured by unique parameters, so the marginal correlation structure would be

$$ \left[\begin{array}{cccc}1& & & \\ {}{\rho}_1& 1& & \\ {}{\rho}_3& {\rho}_2& 1& \\ {}{\rho}_4& {\rho}_2& {\rho}_2& 1\end{array}\right]. $$

This does not adhere to one of the traditional forms, but in terms of implementation, it is no more difficult to fit in software than the traditional forms, and it could help further reduce the risk of misspecification (example Mplus code for this structure is provided in the Appendix).

Concluding remarks for empirical researchers

Random-effect models are the default method for longitudinal data analysis in psychology. Though the reasons for this preference are defensible in the context of data without latent classes (e.g., Grimm & Stegmann, 2019), the role of within-class random effects is much reduced in latent-class models. The classes provide the primary latent information for the research questions, by qualitatively grouping would-be continuous random effects, thereby reducing the dimensionality of the solution. This makes the extra latent information provided by the within-class random effects of little utility in many cases, beyond properly specifying the marginal covariance. Though not incorrect, using random effects solely to pattern the marginal covariance is inefficient as compared to approaches taken by population-averaged models.

In naturally complex models such as mixture models for longitudinal data, unnecessarily employing within-class random effects leads to exceedingly high levels of nonconvergence and inadmissible solutions. The present method to circumvent these issues is to apply cross-class constraints; however, though this does improve convergence, it also raises additional issues, and typically results in highly biased class trajectories and poor class enumeration. Much of the computational complexity of GMMs can be avoided with more theoretically aligned CPMMs, which avoid the within-class random effects but retain the flexibility to properly model the covariance structure.

Model choice in mixture modeling should operate in the same way as in any other model: The simplest model that can answer the question at hand should be preferred. We encourage researchers to consider which questions they wish to answer and to think critically about which is the simplest model capable of answering these questions. In our view, GMMs are rarely the answer to this question if CPMMs are simultaneously considered.

Open Sciences Practices Statement

All simulated data sets, simulation code, and simulation data management code are provided and are publically available on the Open Science Framework (OSF). The anonymized link to access this information is https://osf.io/yh6kf/?view_only=d2ed0cc33d0c423a9a9193c718109c7c. The data used for the empirical example, as well as all software code used to analyze the empirical-example data, are also accessible via the same OSF link. No aspects of this simulation study were preregistered.

Appendix: Mplus code for fitting covariance pattern mixture models

To specify a covariance pattern matrix in general structural equation modeling software such as Mplus, the general strategy is to set the factor variances of the growth factors (e.g., intercept, slope) to 0 and then to apply the covariance pattern to the residual variances at each time point. Growth models in this framework are treated in a multivariate manner, such that each repeated measure is treated as a unique dependent variable. This can make the covariance pattern a little tricky to apply, because each element of the matrix must be programmed with a separate statement.

The challenge of specifying the covariance pattern depends on whether the residual variances at each time point are homogeneous (i.e., variances are equal for each repeated measure) or heterogeneous (i.e., the variances are uniquely estimated for each repeated measure). The covariance pattern is easier to specify with homogeneous variances; with heterogeneous variances, model constraints are necessary, to ensure that the correlations follow the desired pattern.

The following pages show the Mplus code for fitting covariance pattern mixture models with compound symmetry, first-order autoregressive, Toeplitz, unstructured covariance matrices, and a custom structure, as mentioned in the Discussion section. All code will assume that two classes are being extracted, but the number of classes can be changed without affecting the general idea of the code. To provide some context, we will use the NLSY data; these data can be downloaded from http://www.joophox.net/mlbook2/MLbook.htm or from the first author’s Open Science Framework page for this project (https://osf.io/yh6kf/). These data have four repeated measures, but the code can be extended to accommodate any number of repeated measures. We start with the homogeneous variance structures first, and then proceed to the heterogeneous variance structures.

Mplus code for covariance pattern mixture models is not appreciably different from standard growth mixture models. The primary difference stems from how the covariance matrices are modeled. Other options are not changed in Mplus when using a covariance pattern mixture model than for a standard growth mixture model.

Homogeneous variances, exchangeable structure

The exchangeable structure models all covariances as being equal, regardless of how far apart the measures are in time. It is also referred to as an exchangeable or equicorrelated structure. A covariance pattern model with an exchangeable structure is equivalent to a random-intercept model. Though parsimonious, in that all covariances are modeled with a single parameter, it can be too simplistic for some types of data in which the repeated measures are less related as they become further apart in time.

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}^2& & & \\ {}{\sigma}^2\rho & {\sigma}^2& & \\ {}{\sigma}^2\rho & {\sigma}^2\rho & {\sigma}^2& \\ {}{\sigma}^2\rho & {\sigma}^2\rho & {\sigma}^2\rho & {\sigma}^2\end{array}\right]. $$

Homogeneous variances, autoregressive structure

The autoregressive structure allows for observations to be less related as the observations grow further apart. To maintain parsimony, the autoregressive structure only estimates a single covariance parameter ρ. The covariance at lag 1 is equal to ρ, lag 2’s is equal to ρ², lag 3’s is equal to ρ³, and so forth. This structure requires model constraints to ensure that only the single ρ is estimated.

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}^2& & & \\ {}{\sigma}^2\rho & {\sigma}^2& & \\ {}{\sigma}^2{\rho}^2& {\sigma}^2\rho & {\sigma}^2& \\ {}{\sigma}^2{\rho}^3& {\sigma}^2{\rho}^2& {\sigma}^2\rho & {\sigma}^2\end{array}\right]. $$

Homogenous variances, Toeplitz structure

The main idea of a Toeplitz structure is that the covariances at equivalent lags are equal but that unequal lags are freely estimated. So, the covariances for time points that are one lag apart are constrained to be the same; the same is true for covariances of time points that are two lags apart. However, unlike in an autoregressive structure, the lag 1 covariance is completely unrelated to the lag 2 covariance (e.g., the lag 2 covariance is not the square of the lag 1 covariance, as with the autoregressive structure).

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}^2& & & \\ {}{\sigma}^2{\rho}_1& {\sigma}^2& & \\ {}{\sigma}^2{\rho}_2& {\sigma}^2{\rho}_1& {\sigma}^2& \\ {}{\sigma}^2{\rho}_3& {\sigma}^2{\rho}_2& {\sigma}^2{\rho}_1& {\sigma}^2\end{array}\right]. $$

Homogeneous variances, unstructured structure

An unstructured matrix is the most flexible but the least parsimonious option. Every element of the covariance matrix is uniquely estimated, so if there are many repeated measures or many latent classes, this can quickly lead to a large number of parameters. Reaching convergence with an unstructured matrix can be difficult and often requires a very large sample. If the model converges, it can sometimes provide a good initial idea for alternative structures that could be more parsimonious (e.g., if the estimates look approximately equal down the diagonals, perhaps an autoregressive or Toeplitz structure could provide a similar fit with fewer parameters).

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}^2& & & \\ {}{\sigma}_{21}& {\sigma}^2& & \\ {}{\sigma}_{31}& {\sigma}_{32}& {\sigma}^2& \\ {}{\sigma}_{41}& {\sigma}_{42}& {\sigma}_{43}& {\sigma}^2\end{array}\right]. $$

Homogeneous variances, custom structure

As we mentioned in the Discussion section, the flexibility of the structural equation modeling framework means that essentially any marginal structure can be specified. The observed correlation matrix of the four repeated measures is

$$ \left[\begin{array}{cccc}1& & & \\ {}.66& 1& & \\ {}.54& .78& 1& \\ {}.45& .76& .80& 1\end{array}\right]. $$

So let’s imagine that the (3, 2), (4, 2), and (4, 3) elements look close enough to constrain to be equal but the (2, 1), (3, 1), and (4, 1) elements should be uniquely estimated. The marginal covariance to be estimated would then be

$$ \left[\begin{array}{cccc}{\sigma}^2& & & \\ {}{\rho}_1& {\sigma}^2& & \\ {}{\rho}_3& {\rho}_2& {\sigma}^2& \\ {}{\rho}_4& {\rho}_2& {\rho}_2& {\sigma}^2\end{array}\right]. $$

This structure has only one additional parameter relative to the Toeplitz structure, but one could argue that the structure makes more efficient use of the parameters that are estimated (provided that the structure is roughly equal in each class).

General difference with heterogeneous variances

When the variances are uniquely estimated at each time point, the structure gets a little more complicated to ensure that the correlation for constrained off diagonals are in fact equal. If the same structures as the homogeneous case were used, the correlation could vary for constrained elements depending on the magnitude of the variance at the two time points of interest (this can be seen visual by allowing the variances to be uniquely estimated and requesting the STDXY standardized output in Mplus—the off-diagonal terms will be constrained but the correlations will be different to the extent that the variances differ). Therefore, the square root of the variances at each time point must be included in the off diagonal elements to appropriately scale these elements and ensure that all elements have equal correlations. Heterogeneous variances require a model constraint is nearly all cases so that elements are appropriately scaled.

Heterogeneous variances, compound symmetry

For the NLSY data, the marginal covariance matrix for this structure would be

Heterogeneous variances, autoregressive structure

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}_1^2& & & \\ {}{\rho \sigma}_2{\sigma}_1& {\sigma}_2^2& & \\ {}{\rho}^2{\sigma}_3{\sigma}_1& {\rho \sigma}_3{\sigma}_2& {\sigma}_3^2& \\ {}{\rho}^3\sigma 4{\sigma}_1& {\rho}^2{\sigma}_4{\sigma}_2& {\rho \sigma}_4{\sigma}_3& {\sigma}_4^2\end{array}\right]. $$

Heterogeneous variances, Toeplitz structure

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}_1^2& & & \\ {}{\rho}_1{\sigma}_2{\sigma}_1& {\sigma}_2^2& & \\ {}{\rho}_2{\sigma}_3{\sigma}_1& {\rho}_1{\sigma}_3{\sigma}_2& {\sigma}_3^2& \\ {}{\rho}_3\sigma 4{\sigma}_1& {\rho}_2{\sigma}_4{\sigma}_2& {\rho}_1{\sigma}_4{\sigma}_3& {\sigma}_4^2\end{array}\right]. $$

Heterogeneous variances, unstructured structure

For the NLSY data, the marginal covariance matrix for this structure would be

$$ \left[\begin{array}{cccc}{\sigma}_1^2& & & \\ {}{\sigma}_{21}& {\sigma}_2^2& & \\ {}{\sigma}_{31}& {\sigma}_{32}& {\sigma}_3^2& \\ {}{\sigma}_{41}& {\sigma}_{42}& {\sigma}_{43}& {\sigma}_4^2\end{array}\right]. $$

Because the unstructured structure does not set constraints in the off-diagonal, transitioning from homogeneous variances to heterogeneous variances does not have an effect on how the model is specified. That is, the heterogeneous variances do not affect the correlation of constrained elements because there are no constrained elements. The only difference to the above code for the homogeneous structure is that the parameter constraint labels (i.e., var1 and var2) need to be removed from the residual variances. Because there is no other difference, we will not write out all of the code again with this one minor alteration.

Heterogeneous variances, custom structure

Again using the observed correlation matrix of the four repeated measures, which is

$$ \left[\begin{array}{cccc}1& & & \\ {}.66& 1& & \\ {}.54& .78& 1& \\ {}.45& .76& .80& 1\end{array}\right]. $$

If we still wanted to constrain the (3, 2), (4, 2), and (4, 3) elements but freely estimate the (2, 1), (3, 1), and (4, 1) elements, while allowing the variances to be heterogeneous, the marginal covariance to be estimated would then be

$$ \left[\begin{array}{cccc}{\sigma}_1^2& & & \\ {}{\rho}_1{\sigma}_2{\sigma}_1& {\sigma}_2^2& & \\ {}{\rho}_3{\sigma}_3{\sigma}_1& {\rho}_2{\sigma}_3{\sigma}_2& {\sigma}_3^2& \\ {}{\rho}_4{\sigma}_4{\sigma}_1& {\rho}_2{\sigma}_4{\sigma}_2& {\rho}_2{\sigma}_4{\sigma}_3& {\sigma}_4^2\end{array}\right]. $$