Fluid intelligence refers to the ability to solve problems without relying on explicit knowledge derived from previous experience (Cattell, 1963). Raven’s Advanced Progressive Matrices (APM) is one of the most widely used standardized tests that is used as a proxy for higher-order cognitive ability (Arthur & Day, 1994), and as such, it is often administered to undergraduate university students. One of the drawbacks of APM is its protracted test time, which ranges from 40 to 60 min. Although this may be appropriate for a single testing session, researchers often choose to administer multiple cognitive tests, extending the testing time to several hours, which can lead to fatigue and decreased participant engagement (Ackerman & Kanfer, 2009). Moreover, the lack of parallel forms of APM has led researchers to split the test, but due to the limited set of items, this approach only results in two versions, which does not allow for a third assessment—for example, in a longitudinal design. It is also not always evident that the resulting versions are similar in difficulty (Jaeggi, Buschkuehl, Shah, & Jonides, 2014), and most importantly, the reduced amount of items diminishes the test’s reliability (Sefcek, Miller, & Figueredo, 2016). Matzen et al. (2010) addressed those issues by creating software for systematically generating large numbers of matrix problems, which were validated against Raven’s Standard Progressive Matrices (SPM). Even though this presents a solution in terms of the quantity of test items, the quality of the drawings presents certain limitations, especially if the items are presented on a small screen.

In general, online tests of reasoning ability can be expensive for researchers and offer little control over the content of the tasks. Recently, there has been a shift toward developing products that are in the public domain, such as the International Cognitive Ability Resource (ICAR), which includes 11 matrix reasoning problems (Condon & Revelle, 2014), as well as 27 progressive matrices. ICAR collaborators have contributed more items that could allow for repeated testing, but no psychometric data are available for these item sets (ICAR Catalogue, 2017). A growing number of researchers and healthcare services are adopting cognitive testing through touch screen devices, yet, to our knowledge, a validated tablet-based measure of analytical intelligence with multiple versions does not exist. To address the limitations of current approaches in the field, we developed a modified matrix reasoning test (the University of California Matrix Reasoning Task [UCMRT]) based largely on matrix problems generated by Sandia Laboratories (Matzen et al., 2010), which (1) only takes 12–15 min to complete, (2) has three parallel forms, (3) can be administered on tablets and mobile devices, (4) does not require the presence of an administrator, and (5) is designed for people of above-average aptitude.

The goals of the present study were to evaluate the psychometric properties of UCMRT and to examine whether the difficulty level is appropriate for healthy young adults. Specifically, we tested whether the parallel forms are comparable, and we also examined convergent and external validity by comparing performance on the new test with that on Raven’s APM, as well as math scores, and furthermore, we examined the relationship between UCMRT performance and both scores from standardized proficiency tests and GPA.

Method

Participants

A total of 713 participants (mean age = 20.02 years, SD = 2.74; NFemale = 494, NMale = 201, NOther = 18) took part in at least one session of UCMRT over a period of 6 months. The participants were a sample of ethnically diverse university students (see Table S1 of the supplemental materials) recruited at the University of California, Riverside (UCR; N = 353), or the University of California, Irvine (UCI; N = 360), with normal or corrected-to-normal vision. All participants provided informed consent and received either course credit or monetary compensation for their participation. Most participants (N = 676) were asked for permission to obtain their educational records, which was granted by 416 of the students. A subset of the participants also completed a newly developed, tablet-based Math Test (N = 483), and some of these (N = 238) also completed Raven’s APM, allowing for analyses of convergent and external validity (see the Convergent Validity Tasks section for more information). Another subset of the participants (N = 213) performed alternate versions of the UCMRT on two occasions, which allowed us to calculate test–retest reliability. All study procedures were approved by the UCR and UCI institutional review boards.

University of California Matrix Reasoning Task (UCMRT)

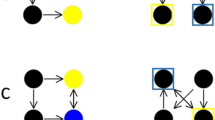
The UCMRT consists of Raven-like matrix problems, most of which are based on the matrices produced by Sandia National Laboratories.Footnote 1 The software developed by this laboratory can systematically generate a large number of matrices, which provide a good match to Raven’s SPM (Matzen et al., 2010). However, we believe that the Sandia matrix problems are limited in terms of their graphics: Overlapping items are difficult to discern, and some of the details are very small, making it difficult to judge shape and shading properties that are crucial to solving the problem (see Fig. 1). Hence, we redesigned the three versions of the task using larger, nonoverlapping stimuli that are not limited to grayscale, while keeping the same number and types of rules and the basic structure of the task (3×3 matrix with eight answer alternatives). Because our target population was healthy young adults, we excluded the easy, one-relation Sandia matrix problems, in which only one rule governs the patterns of changes in the matrix, and focused instead on problems that contain at least two relations or are logic-based. Whereas the answer options are presented horizontally in the Sandia matrices (two rows, four columns), the answer options in UCMRT are presented vertically, to maximize the space available on mobile devices (four rows, two columns; see Fig. 2).

Fig. 1
figure 1

Example of a logic problem generated by the Sandia software. The 3×3 matrix on the left represents the problem, with the lower right cell missing, and the eight answer options are presented on the right

Full size image
Fig. 2
figure 2

Examples of UCMRT problems using the same structure as Sandia matrices, apart from the answer options, which are presented vertically. All types of problems are shown in the practice section: (1) one-relation problem, (2) two-relation problem, (3) logic, (4) three-relation with one transformation, (5) three-relation with two transformations, and (6) three-relation with three transformations

Full size image

Each alternate form of UCMRT consists of two example problems, six practice problems, and 23 test problems. During practice, participants receive feedback (correct/incorrect) along with an explicit explanation of the rules that must be combined to solve the problem (Hossiep, Turck, & Hasella, 1999). If a participant fails to pass the practice criteria (at least four out of six correct), the practice is repeated once with a different set of problems. The test portion begins with 2 two-relation problems, followed by a mixed order of 15 three-relation problems and 6 logic problems, with a time limit of 10 min. No feedback is provided, but participants can change their answer, skip problems, and navigate back and forth between the problems,Footnote 2 akin to paper-and-pencil versions of Raven’s matrices (Raven, Raven, & Court, 1998). The problem number (e.g., 5/23) is shown in the top right corner of the screen, and a countdown timer is presented in the upper left corner. The task ends when the participants submits the answers or when the 10-min limit is reached.

Matrix reasoning problems can be broken down by type, as defined by Matzen et al. (2010). The UCMRT contains two types of object transformation problems: two-relation problems (i.e., two rules govern the pattern of changes within a matrix; cf. Fig. 2.2) and three-relation problems (i.e., three rules make up the pattern of changes; cf. Figs. 2.4–2.6). The rules featured in these problems relate to shape, orientation, size, and number, as well as shading/color.Footnote 3 The three-relation problems can be further distinguished on the basis of the number of diagonal or outward transformations (1–3) in the matrix. UCMRT also contains three types of logic problems (see Fig. 2.3): addition/conjunction (AND), disjunction (OR), and exclusive disjunction (XOR). Each alternate version consists of 2 two-relation problems, 3 three-relation problems with one transformation, 6 three-relation problems with two transformations, 6 three-relation problems with three transformations, and 6 logic problems. To control for context effects, the problems are not ordered by problem type (with the exception of the two-relation problems), nor are they specifically ordered in terms of difficulty—apart from the overall structure, in which two-relation and three-relation problems with fewer transformations are distributed at the beginning, whereas those that require more transformations are distributed toward the end. In all three versions, the order is the same with respect to problem type; however, the rules that govern the problem type can differ.Footnote 4

Implementation

UCMRT runs on Unity, which supports multiple platforms and can be utilized to make the test more available over time. Presently, UCRMT is supported by iOS and Android, and it can be released on other platforms per request. The app supports the creation of usernames that can be used to hide the identity of the participant. Researchers who wish to use UCMRT are encouraged to contact one of the authors. Data files are logged locally (i.e., text files are stored on the device itself), and in addition, they are logged on an Amazon-housed server as long as a wireless Internet connection is maintained. The server-stored data can be made available to researchers upon request.

Convergent validity tasks

Two tasks were used to assess the convergent validity of UCMRT. The first task was Raven’s APM Set II (Raven et al., 1998), a valid and widely used measure of fluid intelligence (Arthur & Woehr, 1993). APM Set II consists of 36 problems in ascending difficulty. Each problem comprises a 3×3 matrix with the lower right cell missing, and the participant has to select one out of eight answer options that best completes the matrix. The participants solved a paper-and-pencil version of the task, using Set I as practice (12 problems) and Set II as the test, with a time limit of 25 min. This time restriction was applied in order to approximate the conditions for the UCMRT and to avoid the ceiling performance often observed in our lab with longer or no time restrictions.Footnote 5 The second task was a tablet-based Math Test consisting of 21 word-based math problems with a time limit of 15 min (see Math Test in the supplemental materials), administered via Qualtrics software (Qualtrics, Provo, UT, https://www.qualtrics.com).

Educational data

For those participants who gave consent, college grade point average (GPA), high school GPA, and SAT and ACT scores were obtained from university records. GPA reflects overall performance during the academic year and is on a 4.0 scale. The SAT and ACT are standardized tests used for college admission in the United States. The tests are somewhat different but are universally accepted by colleges and universities; thus, students can decide which test they want to take. Since it was unclear which scores would be affected by recent major changes in the SAT sections, particularly for verbal measures (and furthermore, some scores were not scaled), and also given that the maximum SAT score changed from of 2,400 to 1,600 in 2016, we decided to exclude the SAT Verbal/Evidence-Based Reading and Writing and SAT Total measures from the analyses. Although certain changes were implemented on the SAT Math measure, its scale has remained the same (200–800), and therefore it was not excluded. For ACT, scores on the Reading, Math, Writing, and Science sections were obtained, all of which were included in the analyses.

Procedure

Performance on UCMRT was obtained in the context of three studies. In one study, participants completed a battery of tablet-based cognitive tests, including the Math Test and UCMRT, which were presented together at the beginning of a session (in that order). In another study, we aimed to estimate improvement on the battery of cognitive tests (excluding the Math Test) and to assess test–retest reliability; thus, the participants were asked to attend a second session 10–14 days later. Both sessions took place at the same time of day, and UCMRT was completed at the beginning of each session. These participants were divided randomly into three groups: One group completed Version A in Session 1 and Version B in Session 2; another completed Version B in Session 1 and Version C in Session 2; and the third completed Version C in Session 1 and Version A in Session 2. In a third study, participants were randomly assigned to complete one of the three versions of UCMRT (A, B, or C), one of the two versions of the Math Test (I or II), as well as the APM. The order of the two matrix reasoning tests (APM and UCMRT) was counterbalanced, and they were always separated by the Math Test.

Statistical analyses

SPSS Version 24 and JASP Version 0.9.0.1 (JASP Team, 2018) were used to analyze the data. Along with conventional null-hypothesis statistical testing, Bayes factors (BFs) were calculated using the default priors in JASP. BFs calculate the probability of the null (H0) or alternative (H1) hypothesis being true, given the present data. Thus, the results of our frequentist analyses were supplemented with BFs—specifically, BF10, which grades the intensity of the evidence that the data provide for H1 versus H0. A BF10 value between 1 and 3 is considered to be only anecdotal evidence for H1; 3–10 indicate moderate evidence; 10–30, strong evidence; 30–100, very strong evidence; and > 100, extreme evidence (Lee & Wagenmakers, 2013; Wagenmakers et al., 2018).

Bonferroni correction was applied to post-hoc computed Student’s t tests; note that the reported effect size, Cohen’s d, does not correct for multiple comparisons.

Results

UCMRT performance and reliability

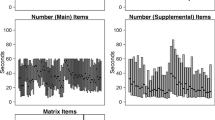
Ten outliers (1.4%) were removed from the sample: six individuals on the basis of number of responses (i.e., skipping at least 48% of the problems; z> = 4), and four on the basis of number of correctly solved problems (|z| ≥ 2.5). Descriptive statistics are presented in Table 1. There was no statistical difference in performance among the three versions of the UCMRT, as determined by a one-way analysis of variance (ANOVA) [F(2, 700) = 2.70, p = .07, η2 = .01], which was further confirmed by a JZS Bayes factor ANOVA with default prior scales (BF10 = 0.21). Although Bonferroni-corrected post-hoc tests showed no significant differences between the pairs of tests (A–B, p = .63; B–C, p = .82; and A–C, p = .06), Bayesian post-hoc tests revealed anecdotal evidence in favor of H1 for the A–C comparison (A–C: BF10,U = 1.78), but this was not observed for the A–B (BF10,U = 0.21) or B–C (BF10,U = 0.18) comparisons.

Table 1 Descriptive statistics for UCMRT scores (maximum = 23)
Full size table

The internal consistency of the 23 problems, based on Cronbach’s α, was .66, .76, and .72 in Versions A, B, and C, respectively (combined versions: α = .71; cf. Table 1). Similarly, Cronbach’s α for the sets of Sandia matrices, consisting of 42 problems each, was .76 (Matzen et al., 2010). For the 36 items of Raven’s APM, Cronbach’s α was .82 in our sample and .84 in other data sets (Arthur & Day, 1994; Bors & Stokes, 1998). For a short version consisting of 18 problems, αs of .64 (Unsworth, Redick, Lakey, & Young, 2010) and .79 (Sefcek et al., 2016) have been reported. Considering the relatively low number of problems and short testing time of the UCMRT, the internal consistency of the three versions seems adequate.

We also report descriptive statistics for a subsample that was subject to more rigorous selection criteria (Table 1). Only participants who correctly solved the first two problems of UCMRT (i.e., the easy, two-relation problems) were included in the analysis. Performance on the three versions of UCMRT was not statistically different, as determined by a one-way ANOVA [F(2, 384) = 0.22, p = .80, η2 = .001, BF10 = 0.04]. Bonferroni-corrected post-hoc tests showed no significant differences between the pairs of tests (A–B: p = 1, BF10,U = 0.16; B–C: p = 1, BF10,U = 0.13; and A–C: p = 1, BF10,U = 0.17). Because they demonstrated an understanding of the rules that apply to the two-relation problems, this subsample may have been particularly suited to UCMRT testing. Nevertheless, as we demonstrated above, the entire sample also showed adequate performance.

Problem type

Overall, accuracy decreased as the number of relations/transformations increased (M2-REL = 73.47%, SE2-REL = 1.21%; M3-REL-1 = 68.94%, SE3-REL-1 = 1.08%; M3-REL-2 = 61.93%, SE3-REL-2 = 0.89%; M3-REL-3 = 38.48%, SE3-REL-3 = 0.88%),Footnote 6 which is consistent with the findings reported by Matzen et al. (2010) in a sample of undergraduate university students. For logic-based problems, the average accuracy across all versions was 50.88% (SE = 1.00%), which is higher than that reported for the Sandia logic problems (M = 37.9%, SE = 3%). Some reasons for this may have been the improved visibility of details and shapes, which are nonoverlapping in UCMRT (see Fig. 2), as well as the inclusion of practice problems in our version. Figure 3 shows average accuracy based on problem type, presented separately for participants who completed the different versions of UCRMT and correctly solved the first two problems (whole-sample data are presented in Fig. S1, supplemental materials). One-way ANOVAs were used to determine whether performance on the three versions differed for each problem type. For three-relation problems with one transformation, performance on the three versions of the test was not statistically different [F(2, 384) = 2.21, p = .11, BF10 = 0.23]. For three-relation problems with two transformations, both types of analyses indicated a statistically significant difference in performance between the three versions [F(2, 384) = 7.32, p < .05, BF10 = 19.48]. Bonferroni-corrected post-hoc tests showed that performance on Version A was significantly lower than performance on Version B (p = .02, BF10,U = 10.31) and on Version C (p < .001, BF10,U = 142.92), but there was no significant difference between Versions B and C (p = 1, BF10,U = 0.15). For three-relation problems with three transformations [F(2, 384) = 1.23, p = .29, BF10,U = 0.09] and for logic problems [F(2, 384) = 0.16, p = .85, BF10,U = 0.03], no significant difference in performance was observed (see Fig. 3). Overall, performance on the subtypes of problems was well matched, with the exception of the three-relation problems with two transformations. This may not be problematic, since, as we demonstrated in the previous section, the final scores on the three versions were adequately balanced, and the participants using Version A also scored worse on the APM (see below).

Fig. 3
figure 3

Mean accuracy based on problem type for the A, B, and C versions of UCMRT, in participants who correctly solved two-relation problems. 3-REL-1 = three-relation with one transformation, 3-REL-2 = three-relation with two transformations, 3-REL-3 = three-relation with three transformations

Full size image

Test–retest

Eight outliers (3.8%) were removed (zNoResp ≥ 4 and zHits ≥ 2.5) from the data set, in which participants completed two sessions (N = 213). Descriptive statistics for the performance on different versions of UCMRT at two time points are presented in Table 2. Test–retest reliability as measured by Pearson’s correlation coefficient was .62 (p < .001, BF10 > 100). A paired-samples t test collapsed across versions showed that performance was not significantly different in the two sessions [t(204) = – 1.82, p = .07, Cohen’s dFootnote 7 = 0.13, BF10 = 0.40]. These results may be of use to future intervention studies trying to estimate improvements on the alternate versions of UCMRT in the absence of an intervention. Repeated testing on APM divided into parallel forms (18 items per test) in no-contact control groups has shown similar results, with Cohen’s d effect sizes ranging from 0.10 (Jaeggi et al., 2010) to 0.38 (Hogrefe, Studer-Luethi, Kodzhabashev, & Perrig, 2017), and some even reporting worse performance in the second session than in the first (Clark, Lawlor-Savage, & Goghari, 2017; Colom et al., 2013; Redick et al., 2013; Stough et al., 2011).

Table 2 Descriptive statistics for repeated testing on different versions of UCMRT
Full size table

On the other hand, significant changes in performance in the two sessions were observed as a function of group (Table 2). Paired-samples t tests showed that in Group 1, accuracy increased in the second session relative to the first [t(67) = 3.91, p < .001, Cohen’s d = 0.47, BF10 = 102.3], and a similar trend was observed for Group 2 [t(67) = 1.83, p = .07, Cohen’s d = 0.22, BF10 = 0.64]. In contrast, Group 3 showed a decrease in performance in the second session relative to the first [t(68) = – 2.54, p = .01, Cohen’s d = – 0.31, BF10 = 2.57].

Although we were not able to test all possible pairs of alternate forms, the results shown in Fig. 4 suggest that different groups of participants showed similar performance on the same version of the test in different sessions. Independent-samples t tests showed no significant differences in performance on the three versions of UCMRT at different points in time [Version A: t(135) = – 0.45, p = .66, Cohen’s d = – 0.08, BF10 = 0.20; Version B: t(134) = – 1.77, p = .08, Cohen’s d = – 0.30, BF10 = 0.76; Version C: t(135) = 0.21, p = .83, Cohen’s d = 0.04, BF10 = 0.19].

Fig. 4
figure 4

Average numbers of correctly solved problems on the alternate versions of UCMRT at two time points. Each participant completed two out of three alternate versions. Error bars = SEMs

Full size image

Convergent and external validity

Raven’s APM

Two additional outliers were removed on the basis of performance on Raven’s APM Set II (z ≥ 2.5). Performance on UCMRT was significantly correlated with performance on APM, both in the total sample (N = 233, r = .58, p < .001, BF10 > 100) and in the three subgroups of participants (Group A: N = 79, r = .44, p < .001, BF10 > 100; Group B: N = 80, r = .67, p < .001, BF10 > 100; Group C: N = 74, r = .58, p < .001, BF10 > 100) (see Fig. 5). Matzen et al. (2010) reported a correlation of .69 between accuracy for the Sandia matrices and Raven’s SPM. However, the authors only included in the analysis a subset of the SPMs that had structures that were comparable to those of the Sandia problems. Instead, we report correlations with all problems in APM Set II, many of which are governed by noncomparable rules and transformations.

Fig. 5
figure 5

Scatterplots illustrating the correlations between UCMRT and APM accuracy for the three groups of participants who solved the A, B, and C versions of UCMRT

Full size image

The difficulty levels of the two matrix reasoning tests are comparable; in the sample of 233 participants, average accuracy was 51.9% (SD = 17.2) on UCMRT and 53.5% (SD = 14.9) on APM. A paired-samples t test showed that performance on the two tests was not significantly different [t(232) = – 1.59, p = .11, Cohen’s d = 0.10, BF10 = 0.25]. As can be seen in Fig. 6, the APM accuracy for the three groups follows a pattern similar to that of UCMRT accuracy, with Group A performing slightly worse than Groups B and C, which may indicate inherent group differences in reasoning ability, suggesting that the small differences between the versions may reflect cohort effects rather than differences in difficulty between the A, B, and C measures.

Fig. 6
figure 6

Mean accuracy on the UCMRT and APM in the three groups of participants who solved the alternate versions of UCMRT. Error bars = SEMs

Full size image

Math test

We developed two alternate versions of the Math Test (see the supplemental materials): 255 participants completed Version I (M = 8.47, SD = 2.86), and 232 participants completed Version II (M = 8.06, SD = 3.23). Performance on the two versions was not statistically different, as was determined by an independent-samples t test [t(485) = – 1.49, p = .14, BF10 = 0.29]; hence, the data were collapsed. As expected, performance on the Math Test showed strong correlations with SAT Math (r = .55, p < .001, BF10 > 100) and ACT Math (r = .61, p < .001, BF10 > 100). Furthermore, performance on the Math Test correlated significantly with performance on both UCMRT (r = .36, p < .001, BF10 > 100) and APM (r = .34, p < .001, BF10 > 100), providing further evidence for the validity of UCMRT (see Table 3).

Table 3 Pearson correlation coefficients for performance on UCMRT (all versions), APM, educational records, and math
Full size table

Tests of academic proficiency

We correlated accuracy on UCMRT and APM with academic proficiency, where those data were available (see Table 3). Performance on both UCMRT and APM showed small but significant correlations with current college GPA (rUCMRT = .13, p = .007, BF10 = 2.19; rAPM = .16, p = .045, BF10 = 0.75). This is line with previous research in which performance on APM was somewhat weakly related to both first-term (r = .19, p < .05) and second-term (r = .18, p < .05) college GPA (Coyle & Pillow, 2008). As a side note, the only measure that correlated significantly with high school GPA was college GPA (r = .16, p = .003, BF10 = 5.03).Footnote 8 Although high school GPA and performance on college admission tests is typically highly correlated (Koretz et al., 2016; Westrick, Le, Robbins, Radunzel, & Schmidt, 2015), this was not observed in the present sample, at least not in the ACT and SAT subtests included in the analysis.

Performance on both UCMRT and APM also correlated with SAT Math (rUCMRT = .45, p < .001, BF10 > 100; rAPM = .44, p < .001, BF10 > 100) and ACT Math (rUCMRT = .35, p < .001, BF10 > 100; rAPM = .35, p = .02, BF10 = 3.26), which is consistent with the literature (Koenig, Frey, & Detterman, 2008; Rohde & Thompson, 2007). On the other hand, we did find differential correlations as a function of matrix reasoning test in various academic measures: Performance on UCMRT, but not on APM, predicted ACT Reading (rUCMRT = .27, p < .001, BF10 = 52.53; rAPM = .04, p = .790, BF10 = 0.19), ACT Writing (rUCMRT = .29, p < .001, BF10 > 100; rAPM = .03, p = .862, BF10 = 0.18), and ACT Science (rUCMRT = .35, p < .001, BF10 > 100; rAPM = .07, p = .639, BF10 = 0.20), suggesting that UCMRT is predictive of global cognitive function. It should be noted that the sample size for APM was smaller; however, on the basis of the correlation coefficients (.03–.07) and visual inspection of scatterplots (cf. Fig. S2, supplemental materials), a stronger relation with ACT subtests would not be expected even if the sample size were larger. There is limited research indicating that SAT and ACT composite scores predict performance on tests of general ability (Coyle & Pillow, 2008; Koenig et al., 2008), and furthermore, ACT subtests show significant correlations with reasoning ability (Goff & Ackerman, 1992); hence, the validity of UCMRT is in line with previous work.

Individual versions of UCMRT showed similar relations, albeit the evidence was limited by a smaller sample size in certain cases (cf. Tables S4–S6, supplemental materials). Version A showed significant correlations with SAT Math (r = .48, p < .001, BF10 > 100 ), ACT Writing (r = .30, p = .028, BF10 = 1.80), and ACT Science (r = .40, p = .003, BF10 = 12.51). Version B significantly correlated with SAT Math (r = .46, p < .001, BF10 > 100), ACT Math (r = .40, p = .003, BF10 = 13.18), and ACT Science (r = .28, p = .044, BF10 = 1.22). Version C was related to SAT Math (r = .40, p < .001, BF10 > 100), ACT Reading (r = .37, p = .002, BF10 = 14.46), ACT Math (r = .40, p < .001, BF10 = 31.03), ACT Writing (r = .33, p = .007, BF10 = 5.37), and ACT Science (r = .34, p = .006, BF10 = 6.17). In summary, all three versions correlated with APM (Fig. 5), the Math Test, and SAT Math and ACT Science, and all but Version A correlated with ACT Math.

Discussion

UCMRT is a tablet-based matrix reasoning test with three parallel versions that can serve as a proxy for fluid intelligence. The A, B, and C versions of the test were validated in a large sample of college students at two different sites. Overall, performance was similar across the three versions and showed adequate internal consistency. Alternate-form reliability was comparable to that in the literature (Colom et al., 2010; Freund & Holling, 2011; Unsworth, Heitz, Schrock, & Engle, 2005), suggesting that the participants did not show significant increases in performance over time and that the versions were comparable. Convergent validity was established by comparing UCMRT to Raven’s APM. In addition, performance on UCMRT correlated with a newly developed Math Test, college GPA, and scores obtained on college admission tests, showing correlations similar to those for APM, thereby demonstrating external validity. In fact, performance on UCMRT correlated significantly with all ACT subtest scores (Math, Science, Reading, and Writing), whereas performance on APM showed significant correlations only with ACT Math.

Matrix reasoning problems have been the hallmark of tests estimating nonverbal fluid intelligence for over eight decades (Raven, 1938). Matrices adapted to different ability levels have been developed over time, yet the Raven matrices have remained remarkably unchanged in the past two decades (Raven et al., 1998). The core aspects of these types of problems, such as ease of administration and relative independence from language, are worth retaining; however, when researchers are faced with a limited set of test items, many of which can be found online, it is time to expand the set and adapt it for modern technology. Although there have been certain efforts in this direction,Footnote 9 UCMRT is unique in that it consists of multiple validated versions that will be freely available to researchers. By making these available, we hope to be able to collect large data sets and to unify studies using a wide variety of fluid intelligence tasks. The parallel forms of UCMRT are especially appropriate for longitudinal studies—for example, those investigating the effects of an intervention at multiple time points. Although alternate versions may show small differences in terms of accuracy, in our case such differences could have been driven by inherent group differences, such issues can be addressed with counterbalancing when test repetition is needed.

Perhaps the greatest advantages of UCMRT are its short administration time and the fact that it is self-administrable, which allows for remote testing. Log files instantly provide the numbers of problems that were solved correctly, solved incorrectly, or skipped, data that will be easily understandable for researchers, clinicians, and users alike. More detailed log files are also available that provide insight into problem-solving patterns and reaction times, functionality that is not available with standard paper-and-pencil tests.

Since the rules that make up the problems are clearly defined, there is no limit to the number of items that can be produced. In the future we plan to develop the items procedurally, leading to even more parallel versions of UCMRT. In addition, we plan to release sets of items that are better customized for different age and ability groups.

Conclusions

Overall, our data suggest that UCMRT is a reliable and valid measure of nonverbal problem solving that is predictive of academic proficiency and could serve as a proxy for fluid intelligence. Moreover, it can be used to differentiate among people at the high end of intellectual ability, akin to Raven’s APM. As compared to APM, the UCMRT is shorter (10 min, excluding practice), offers three parallel test versions, and can be used on iOS and Android devices.

Author note

This work has been supported by the National Institute of Mental Health (Grant No. 1R01MH111742) to A.R.S. and S.M.J; in addition, S.M.J. is supported by the National Institute on Aging (Grant No. 1K02AG054665). S.M.J. has an indirect financial interest with the MIND Research Institute, whose interest is related to this work. We thank David Arellano, Austin Moon, and research assistants at UCR and UCI for data collection. We also thank Laura E. Matzen for providing access to the matrices generated by Sandia National Laboratories and Gabriella Del Greco for helping with the design of the interface.