Mediation analysis is often used in social and behavioral sciences to explain the mechanism for how and why an effect occurs (MacKinnon, 2008). Mediation is said to occur when the effect of an independent variable (X) on a dependent variable (Y) is transmitted by a third variable (M; Baron & Kenny, 1986). The third variable M is termed a mediator. When mediation occurs, the total effect of X on Y is partitioned into two components: the indirect effect of X on Y through M and the direct effect of X on Y that cannot be explained by the indirect effect (denoted by c'). The indirect effect is denoted by ab because it is often quantified by the product of two effects: the effect of X on M (a effect) and the effect of M on Y controlling for X (b effect; MacKinnon, 2008). Given a nonzero ab, if c' is zero in the population, M is said to completely mediate the X and Y relationship. Otherwise, M partially mediates the effect of X on Y.

In practice, it is strongly recommended to establish mediation with longitudinal data (Cole & Maxwell, 2003; Maxwell & Cole, 2007) for at least two reasons: (1) the effects (e.g., a, b, ab, and c') involved in a mediation analysis are causal effects that need time to unfold. Temporally, X precedes M, and M precedes Y. (2) Prior levels of M or Y are confounding variables that should be controlled when testing the indirect effect and direct effect. Failure to do so can lead to substantial bias in parameter estimates in mediation analysis (Cole & Maxwell, 2003; Gollob & Reichardt, 1991).

Note that there are two types of longitudinal designs: longitudinal panel designs and intensive longitudinal designs. For the former designs, individuals are repeatedly measured for a limited number of time points, each separated by several months or more, whereas for the latter designs, individuals are measured for a large number of time points, with relatively brief intervals between occasions (Collins, 2006; Wu, Selig, & Little, 2013). The models suitable for data collected from the two designs may be different. The present study is focused on mediation models designed for the data resulted from longitudinal panel designs.

With longitudinal panel designs, the most popular model for mediation analysis is the cross-lagged panel model (CLPM; Preacher, 2015). As was pointed out by Selig and Preacher (2009), “the CLPM allows time for causes to have their effects, supports stronger inference about the direction of causation in comparison to models using cross-sectional data, and reduces the probable parameter bias that arises when using cross-sectional data.” However, the CLPM has a limitation that has been overlooked in previous research: The effects (e.g., direct and indirect) in the CLPM are assumed to be fixed (i.e., constant) across individuals. As a result, researchers can neither account for potential individual variability on the effects nor evaluate covarying relationships that may have arisen out of this variability. If any of the effects is random (i.e., variant) across individuals, the CLPM may yield biased parameter estimates and misleading statistical inferences.

An alternative model for longitudinal mediation analysis can accommodate individual-specific direct and indirect effects. This is a multilevel model (MLM), which is proposed on the basis of the fact that longitudinal data are clustered in nature: The repeated measures are nested within individuals (Kenny, Korchmaros, & Bolger, 2003; Bauer, Preacher, & Gil, 2006). However, the MLM itself has several limitations. First, the relationships among X, M, and Y are examined concurrently in the MLM proposed in the previous literature. This is only appropriate when the causal effects occur in a very short time frame. Second, the previous measures on M and Y are not controlled in the model. Third, although effects are allowed to be random across individuals in the MLM, these effects are constrained to be equal over time. Thus, it cannot capture possible changes of these effects over time. These limitations make MLM a less desirable method for longitudinal mediation analysis than the CLPM.

In this article, we propose a new model to incorporate random effects in longitudinal mediation analysis. This model is a direct extension of the CLPM by allowing random effects in the model. Unlike the MLM, the proposed model is a single-level model, thus we refer to the model a single level random effects cross-lagged panel model (RE-CLPM). Through the model, we emphasize that it is possible to accommodate random effects even when the model is a single level model. The proposed model can be implemented in Mplus (B. Muthén, Muthén, & Asparouhov, 2015), thus is readily available to applied researchers.

The rest of the article is organized as follows. We first review the traditional CLPM for longitudinal mediation analysis followed by an introduction of the proposed method. We then present three simulation studies conducted to evaluate the performance of the proposed model under a variety of conditions, in comparison to the traditional CLPM. We conclude this article by discussing limitation and implications of the simulation studies, as well as potential directions for future research.

Traditional cross-lagged panel model (CLPM)

Fitting a cross-lagged panel model for longitudinal mediation typically requires at least three waves of data, although it is possible to run the analysis with two waves of data, with additional assumptions imposed (Cole & Maxwell, 2003). Three waves of data are also most common in practice. Thus, we illustrate the traditional CLPM using a longitudinal study with three waves of data on the variables X, M, and Y.

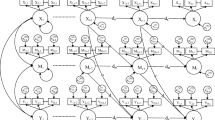
To fit a CLPM, the longitudinal data must be organized in such a way that the repeated measures at each of the three time points are represented by separate variables, such as X 1 . . . X 3, M 1 . . . M 3, and Y 1 . . . Y 3, respectively. This method of organizing the data is called wide-format. Although the longitudinal data are multilevel in nature, with data organized in wide format, the CLPM is a single-level model. This is analogous to the comparison between the MLM and latent curve model approaches for growth curve modeling, where the latter is viewed as a single-level model. Figure 1 shows a typical CLPM that can be fit to wide-format data to test longitudinal mediation. With only manifest variables, this model is simply a path analysis model in structural equation modeling.

Fig. 1
figure 1

A fixed-effect cross-lagged panel model with three waves of measurement

Full size image

The relationships among the variables in the CLPM can be described using the following equations (see also Selig & Preacher, 2009):

$$ {\displaystyle \begin{array}{l}{X}_{it}={d}_{xt}+{s}_{x\left(t-1\right)}{X}_{i\left(t-1\right)}+{e}_{xit}\\ {}{M}_{it}={d}_{mt}+{a}_{\left(t-1\right)}{X}_{i\left(t-1\right)}+{s}_{m\left(t-1\right)}{M}_{i\left(t-1\right)}+{e}_{mit}\\ {}{Y}_{it}={d}_{yt}+{s}_{y\left(t-1\right)}{Y}_{i\left(t-1\right)}+{c}_{\left(t-2\right)}^{\hbox{'}}{X}_{i\left(t-2\right)}+{b}_{\left(t-1\right)}{M}_{i\left(t-1\right)}+{e}_{yit}\end{array}} $$
(1)

where i represents the individual and t represents the time point; the s coefficients represent autoregressive effects that capture the stability of the constructs over time in terms of the rank orders of the scores; the a, b, and c' coefficients represent the cross-lagged effects that are the focus of a mediation analysis. The d coefficients are intercepts, and the es are residuals. Let e i t  = (e xit , e mit , e yit )′ be the vector of residuals for individual i. The residuals are assumed to follow a multivariate normal distribution with

$$ \boldsymbol{\upmu} \left({\mathbf{e}}_{\mathbf{i}t}\right)={\left(0,0,0\right)}^{\prime}\mathrm{and}\kern0.5em \sum \left({\mathbf{e}}_{\mathbf{i}t}\right)\left(\begin{array}{lll}{\sigma}_{ext}^2& & \\ {}{\sigma}_{emt,\mathit{\operatorname{ext}}}& {\sigma}_{emt}^2& \\ {}{\sigma}_{eyt,\mathit{\operatorname{ext}}}& {\sigma}_{eyt, emt}& {\sigma}_{eyt}^2\end{array}\right) $$

where μ(e i t ) is the mean vector and Σ(e i t ) is the covariance matrix of the residuals. Note that following common practice, we also assume that the residuals are not correlated over time although this assumption may be relaxed.

The model shown in Fig. 1 allows researchers to examine the indirect effect of X 1 on Y 3 through M 2 (i.e., a 1 b 2) and the leftover direct effect of X 1 on Y 3 (i.e., c'). As was mentioned above, the indirect and direct effects, although they may vary across time, are assumed to be constant across individuals in this model. In this article, we show that this assumption can be relaxed using random-effects cross-lagged panel models (RE-CLPM).

Random-effects cross-lagged panel models

The RE-CLPM is an extension of the CLPM that allows the effects in a model to be random. Using the same example shown in Eq. 1, if all of the effects are random, then Eq. 1 should be modified as follows.

$$ {\displaystyle \begin{array}{l}{X}_{it}={d}_{xt}+{s}_{xi\left(t-1\right)}{X}_{i\left(t-1\right)}+{e}_{xi t}\\ {}{M}_{it}={d}_{mt}+{a}_{i\left(t-1\right)}{X}_{i\left(t-1\right)}+{s}_{mi\left(t-1\right)}{M}_{i\left(t-1\right)}+{e}_{mi t}\\ {}{Y}_{it}={d}_{yt}+{s}_{yi\left(t-1\right)}{Y}_{i\left(t-1\right)}+{c}_{i\left(t-1\right)}^{\hbox{'}}{X}_{i\left(t-2\right)}+{b}_{i\left(t-1\right)}{M}_{i\left(t-1\right)}+{e}_{yi t}\end{array}} $$
(2)

Comparing Eq. 2 to Eq. 1, an i subscript is attached to each of the effects that are allowed to be random (i.e., s, a, b, and c' effects), indicating that they are individual specific. The RE-CLPM allow more parameters to be estimated than the CLPM. For each random effect, mean and variance will be estimated in addition to possible covariances with any of the other random effects. For simplicity, let’s assume that all of the random effects are constant across time and that u i  = (s xi , s mi , s yi , a i , b i , c i )′ represents the vector of random effects for individual i. The mean vector of the random effects [E(u i )] can be then written as

$$ E\left({\mathbf{u}}_{\mathbf{i}}\right)={\left({s}_{x,}{s}_{m,}{s}_{y,}a,b,c\right)}^{\prime } $$

where a, b, and c represent the means of the a, b, and c effects across individuals. The covariance matrix of the random effects [Σ(u i )] can be written as

$$ \sum \left({\mathbf{u}}_{\mathbf{i}}\right)=\left(\begin{array}{llllll}{\sigma}_{sx}^2& & & & & \\ {}{\sigma}_{sm, sx}^2& {\sigma}_{sm}^2& & & & \\ {}{\sigma}_{sy, sx}& {\sigma}_{sy, sm}& {\sigma}_{sy}^2& & & \\ {}{\sigma}_{a, sx}& {\sigma}_{a, sm}& {\sigma}_{a, sy}& {\sigma}_a^2& & \\ {}{\sigma}_{b, sx}& {\sigma}_{b, sm}& {\sigma}_{b, sy}& {\sigma}_{b,a}& {\sigma}_b^2& \\ {}{\sigma}_{c, sx}& {\sigma}_{c, sm}& {\sigma}_{c, sy}& {\sigma}_{c,a}& {\sigma}_{c,b}& {\sigma}_c^2\end{array}\right) $$

where \( {\sigma}_a^2 \) and \( {\sigma}_b^2 \) are the variances of the a and b effects, respectively, and σ b, a is the covariance between the a and b effects. On the basis of these parameter estimates, the mean and variance of the indirect effect (ab i ) can be computed using the following formula (Kendall & Stuart, 1969):

$$ E\left({ab}_i\right)=a\times b+{\sigma}_{b,a} $$
(3)
$$ \operatorname{var}\left({a}_i{b}_i\right)={b}^2{\sigma}_a^2+{a}^2{\sigma}_b^2+{\sigma}_a^2{\sigma}_b^2+2 ab{\sigma}_{b,a}+{\left({\sigma}_{b,a}\right)}^2 $$
(4)

Note that for Eq. 4 to be valid, the random effects are assumed to be normally distributed. However, this assumption does not need to be true for Eq. 3 to be valid (Kendall & Stuart, 1969).

One limitation of the RE-CLPM is that with random effects, popular model fit indices that are available to the CLPM, such as the chi-square test statistic, root mean square error of approximation (RMSEA), and comparative fit index (CFI), cannot be computed. However, researchers can use information criteria such as the Akaike information criterion (AIC; Akaike, 1973) and the Bayesian information criterion (BIC; Raftery, 1995) to compare the RE-CLPM to the CLPM. Note that both the BIC and AIC also have sample-size-adjusted versions. The adjusted BIC and AIC are referred to as ABIC and AICC, respectively. Past research has shown that ABIC can outperform BIC with a small sample size or a large number of parameters (Yang, 2006), and AICC can outperform AIC with a small sample size (Burnham & Anderson, 2004; Hurvich & Tsai, 1989). The performance of these information criteria in selecting the right model between the traditional and RE-CLPM is examined in the simulation studies. Note that for any of the criteria, a smaller value indicates a better model.

$$ {\displaystyle \begin{array}{l} AIC=-2 LL+2k\kern1.00em \\ {} BIC=-2 LL+k\ln (n)\kern1.00em \\ {} ABIC=-2 LL+k\ln \left(\frac{n+2}{24}\right)\kern1.00em \\ {} AIC C= AIC+\frac{2k\left(k+1\right)}{n-k-1}\kern1.00em \end{array}} $$

where LL stands for log likelihood, n is the sample size,Footnote 1 and k is the number of parameters.

As we mentioned above, the RE-CLPM is a single-level model, which is different from the multilevel cross-lagged panel models for mediation analysis (Fall, 2011; Preacher, Zhang, & Zyphur, 2011; Preacher, Zyphur, & Zhang, 2010), designed for cases in which individuals are nested within higher-level units (e.g., classrooms). With only a single level, why should random effects be modeled, and how are the parameters related to the random effects estimated?

Why should random effects be modeled?

If effects are random but treated as fixed in the CLPM, there are two potential consequences. First, the covariance between the a and b effects that comprise an indirect effect cannot be estimated (i.e., it is treated as 0). Since the covariance should be taken into account when computing the mean indirect effect (see Eq. 3), this will result in a biased estimate for the mean indirect effect. Second, random effects will cause heteroscedasticity in the residuals. Failure to take into account this heteroscedasticity can bias the standard error estimates, leading to misleading statistical inferences. The second point is further illustrated below using simple regression analysis and path analysis as examples.

Simple regression model

Let Y be the dependent variable and X be the independent variable in a simple regression analysis. The regression equation is written as follows when the X effect is fixed across individuals:

$$ {Y}_i={\beta}_0+{\beta}_1{X}_i+{\varepsilon}_i $$
(5)

where β 0 and β 1 represent the fixed intercept and the regression coefficient, respectively, and ε i represents the residual from the fixed effect for individual i. Here ε i is assumed to be independent of X and to have a constant variance over X (homoscedasticity assumption).

If the regression coefficient β 1 is random, then Eq. 5 should be modified to

$$ {Y}_1={\beta}_0+\left({\beta}_1+{\delta}_1\right){X}_i+{e}_i=\left({\beta}_0+{\beta}_1{X}_i\right)+\left({\delta}_i{X}_i+{e}_i\right) $$
(6)

where the effect of X on Y for individual i contains two components: β 1 (the mean effect of X on Y across individuals) and δ i (the deviation of the effect for individual i from the mean effect). The residual from the random effect is denoted by e i, which is assumed to be normally distributed and independent of X. On the basis of Eqs. 5 and 6, it is clear that if a fixed-effect model is fit to the data generated from a random-effect model, the homoscedasticity assumption will be automatically violated (i.e., the residuals will be heteroscedastic). Specifically, ε i will be dependent on X (ε i  = δ i X i  + e i ), and the variance of ε i will no longer be constant over X, but a quadratic function of X. The quadratic function is presented in Eq. 7 and displayed in Fig. 2. As is shown in Eq. 7, the quadratic effect of X on the residual variance is determined by the variance of the variance of the random coefficient [i.e., var(δ i )]. As the latter increases, the severity of the heteroscedasticity also increases.

Fig. 2
figure 2

Plot of the residuals on Y against X when a fixed-effect regression model is fit to data from a random-effect regression model

Full size image
$$ \operatorname{var}\left({\delta}_i{X}_i+{e}_i\right)={\sigma}_{\delta}^2{X}_i^2+2{\sigma}_{\delta, e}{X}_i+{\sigma}_e^2 $$
(7)

Path analysis model

Since the CLPM is a path analysis model, we extend the illustration to a path analysis model in which two or more regression equations are estimated simultaneously. Considering a simple path analysis model with two regression equations, in which Y 1 is regressed on X 1, and Y 2 is regressed on X 2. The two equations with random effects can be written as follows:

$$ {\displaystyle \begin{array}{c}{Y}_{1_i=}\left({\beta}_1+{\beta}_2{X}_{1_i}\right)+\left({\delta}_{1i}{X}_{1i}+{e}_{1i}\right)\\ {}{Y}_{2i}=\left({\beta}_3+{\beta}_4{X}_{2i}\right)+\left({\delta}_{2i}{X}_{2i}+{e}_{2i}\right)\end{array}} $$

With two regression equations, in addition to residual variances (see Eqs. 8 and 9), the residual covariance may also be heterogeneous over Xs (see Eq. 10). Specifically, if there was covariance between the random effects (\( {\sigma}_{\delta_1,{\delta}_2} \)), X 1 and X 2 will interact with each other to influence the residual covariance. The larger the covariance, the bigger the interaction effect is.

$$ \operatorname{var}\left({\delta}_{1i}+{e}_{1i}\right)={\sigma}_{\delta_1}^2{X}_{1i}^2+2{\sigma}_{\delta_1,{e}_1}{X}_{1i}+{\sigma}_{e_1}^2 $$
(8)
$$ \operatorname{var}\left({\delta}_{2i}+{e}_{2i}\right)={\sigma}_{\delta_2}^2{X}_{2i}^2+2{\sigma}_{\delta_2,{e}_2}{X}_{2i}+{\sigma}_e^2 $$
(9)
$$ \operatorname{cov}\left({\delta}_{1i}{X}_{1i}+{e}_{1i}{\delta}_{2i}{X}_{1i}+{e}_{2i}\right)={\sigma}_{\delta_1,{\delta}_2}{X}_{2i}{X}_{1i}+{\sigma}_{\delta_1,{e}_1}{X}_{1i}+{\sigma}_{\delta_2,{e}_1}{X}_{2i}+{\sigma}_{e_1,{e}_2} $$
(10)

How to estimate a single-level random-coefficient model?

Two approaches have been developed to estimate a single-level random-coefficient model. The first is to model the heteroscedasticity directly based on the pattern of the heteroscedasticity. This approach was initially developed in economics to model random effects in a single-level linear regression analysis (Goldstein, 2003; Hildreth & Houck, 1968; Johnston, 1984; Swamy, 1971; Weisberg, 2014). Taking the example shown in Eq. 7, this approach will explicitly specify the residual variance of Y on X to be a quadratic function of X, and it uses the estimated quadratic effect as the estimate for the variance of the random effect of X on Y [i.e., var(δ i )]. Following the same logic, the covariance between the two random effects shown in Eq. 10 can be estimated as the interaction effect between X 1 and X 2 on the residual covariance. As one can imagine, this approach can soon become cumbersome when the number of random effects increases.

The second approach is to model the random effects directly, which indirectly accounts for the heteroscedasticity. This is the approach implemented in Mplus (B. Muthén et al., 2015). This approach treats random effects as unobserved or latent variables, which is essentially no different from how random effects are handled in a multilevel structural equation model. Because it is computationally challenging to estimate models with random effects, an iterative algorithm called an EM algorithm is used to obtain the maximum likelihood estimates of model parameters. EM stands for expectation and maximization, which are the two steps involved in each iteration of the EM algorithm. Simply speaking, the expectation step predicts the values of the random effects from the observed data. The maximization step then treats the predicted values for the random effects as if they were known and uses them to estimate the model parameters through the maximum likelihood estimation method. The EM algorithm iterates between the two steps until the parameter estimates stop changing meaningfully from one iteration to the next. To mitigate some of the computational intensity of the EM algorithm and hasten convergence, an accelerated version of the EM algorithm is used in Mplus. Readers can refer to Jamshidian and Jennrich (1997) or Lee and Poon (1998) for information on the ways to accelerate an EM algorithm.

Simulation studies

In this section, three simulation studies are described that we conducted to assess the performance of the RE-CLPM. The first study was designed to examine whether the RE-CLPM performs suboptimally when the model effects are in fact fixed in the population. The second study aimed to examine whether RE-CLPM performs as expected when the effects are random in the population, and to what extent using the traditional CLPM can lead to a biased result. The third study was a preliminary investigation into whether the RE-CLPM is robust to the violation of the normality assumption of random effects. All of the simulation studies were conducted using SAS 9.4 and Mplus 7.4 (L. K. Muthén & Muthén, 2015).

Study 1

Recall that the purpose of Study 1 was to examine how the random-effects models would perform if the effects were actually fixed (i.e., no heteroscedasticity) in the population. Two models are compared in this study: RE-CLPM and CLPM.

Data generation model

The data generation model in this study was similar to the CLPM shown in Fig. 1, with three waves of data. The variables at the first time point (i.e., X 1, M 1, and Y 1) were all in standardized metric and had correlations of .3 with one another. For simplicity, all of the path coefficients were constrained to be equal over time; hereinafter, we use a, b, c', and ab to represent the constant coefficients over time. Following an example provided in Maxwell and Cole (2007, Fig. 4), the autoregressive effects were set at .8, .3, and .7 for X, M, and Y, respectively, representing a wide range of stability coefficients. The effect size for a or b (note that the sizes of a and b were kept equal) was varied at two levels (explained below). The direct effect (i.e., c') was fixed at zero, representing a complete-mediation scenario. The residual variances on X, M, and Y (at the second, third, and fourth time points) were constant over time. They were set up in such a way that the outcome variables were in a standardized metric at any of the time points (see the population values for the residual variances below). The data generation model, with population values for the parameters, is presented in Fig. 3.

Fig. 3
figure 3

Data generation model in Simulation Study 1

Full size image

Design factors

Two design factors were manipulated in this study: sample size and the effect size of a and b. Sample size was varied at three levels (100, 200, or 500), reflecting small, moderate, and large sample sizes in the social and behavior sciences. The effect size of a and b was varied at two levels: 0.3 (ab = 0.09), or 0.6 (ab = 0.36), representing small and large effects, respectively. Correspondingly, the residual variances on X, M, and Y were set at 0.36, 0.82, and 0.42, respectively, when a and b = 0.3, and at 0.36, 0.55, and 0.15, respectively, when a and b = 0.6, to make the total variances of the variables to be 1. In total, there were 3 × 2 = 6 conditions. One thousand replications were generated for each condition, and the two models were fit to each replication. The CLPM was the same as the population-generating model. The RE-CLPM was specified to be the same as that used in Simulation Study 2. Specifically, all of the effects (both autoregressive and cross-lagged effects) in the RE-CLPM were freed to be random across individuals but equated across time. In addition, the correlation between a i and b i was freely estimated. Note that the RE-CLPM is an overspecification of the population model, in this case. The Mplus syntaxes for fitting the two models can be found in the Appendices.

Evaluation criteria

The following criteria were used to evaluate the models we examined. We focus on the extent to which the models recovered the mean effects a, b, c', and ab, given that they are often of most interest to applied researchers.

Convergence rate

The convergence rate was calculated as the proportion of replications that successfully converged. With more parameters to be estimated, we would expect it to be more challenging for RE-CLPM to converge than the CLPM, especially under small sample sizes.

Percentage relative bias

The percentage relative bias for a specific parameter θ is computed as follows if the population value for the parameter (θ 0) is not zero or close to zero.

$$ \%\mathrm{bias}=100\times \left(\overline{\theta}-{\theta}_0\right)/{\theta}_0 $$

where \( \overline{\theta} \) is the average effect over replications. If θ 0 is zero or close to zero (<.01), the percentage of relative bias is computed by \( 100\times \left(\overline{\theta}-{\theta}_0\right) \). Following B. Muthén, Kaplan, and Hollis (1987), a relative bias less than 10% is considered acceptable.

Confidence interval coverage

The 95% confidence interval (CI) coverage rates are reported for the target effects. For each parameter, the 95% CI coverage is calculated as the proportion of the 95% CIs that cover the population value across replications. Upper and lower limits of the CIs were computed on the basis of the corresponding standard error estimates. Note that the standard error for ab is computed using the delta method, which is a popular method for obtaining the standard errors of nonlinear combinations of estimated coefficients (Sobel, 1982). The CI for ab computed in this way is not optimal because it cannot reflect the nonnormality of ab. Given this practical concession as it relates to simulation design, it sufficed for the purpose of this study to differentiate the performances of the examined methods. On the basis of the acceptable range for the Type I error rate, a coverage rate between 92.5% and 97.5% was considered acceptable.

Power or Type I error rate

The power for any nonzero effect or Type I error rate for any zero effect was calculated as the proportion of replications that yielded a significant effect under each condition. Following Bradley (1978), a Type I error rate within the range of .025 to .075 was considered acceptable for a .05 nominal rate.

Model selection

In addition to the parameter estimates, we also examined the extent to which the true model (i.e., the CLPM in this study) could be correctly selected using the AIC, BIC, ABIC, and AICc. Specifically, the success rate of model selection (i.e., the proportion of replications for which an information criterion led to the correct model selection) was used to quantify the accuracy of model selection.

Results

The results from the first study are summarized in Table 1. Since the same result pattern was observed for different effect sizes and sample sizes, we only report the results for effect size = 0.3 and n = 200 in Table 1. In addition, the results for the a effect was consistent with that for the b effect; thus, we do not report the results for the b effect in Table 1. As is shown in the table, the RE-CLPM and CLPM were comparable regarding parameter estimates, CI coverage, and Type I error rates, indicating that allowing random effects when the effects were in fact fixed in the population was not particularly harmful. However, the CLPM was more efficient, since it yielded higher power to detect the target effects.

Table 1 Results from Simulation Study 1 (n = 200, effect size of a/b = 0.3)
Full size table

Convergence rate

The convergence rate for the CLPM was 100% under all conditions. The estimation for the RE-CLPM reached saddle points for some of the replications, at which the negative of the matrix of the second derivatives with respect to the model parameters was not positive definite, especially when the sample size was small. For the RE-CLPM, saddle points occurred in 53.0%, 15.6%, and 0.4% of the replications for n = 100, 200, and 500, respectively. When saddle points occur, Mplus uses an ad-hoc estimator to compute the standard error estimates. A detail explanation of saddle points and possible causes for saddle points is provided in Asparouhov and Muthén (2012). Since we were not sure about the accuracy of the ad-hoc estimator, the replications with saddle points were not included in the final result.

Model selection

For all of the conditions examined in the study, all information criteria led to above a 98% success rate of selecting the right model, indicating that the information criteria all performed very well in differentiating the traditional and random-effects models when the misspecified model was an overspecification of the true model.

Study 2

As we mentioned above, the purpose of Study 2 was to compare the performance of the RE-CLPM and CLPM when random effects exist in the population.

Data generation model

Using the CLPM shown in Fig. 3 as the baseline model, we freed the autoregressive (i.e., s) and cross-lagged (i.e., a, b, and c') effects to be random and used the modified model to generate the data in this study. For simplicity, the random effects were normally distributed and equated across time, and only the a and b effects were allowed to correlate. The variance of c' was fixed at 0.04. The variances of the s effects were all fixed at 0.01. The variances of a and b were varied at two levels, as is shown below.

Design factors

Besides the two factors (sample size and the effect size of a and b) varied at Study 1, we manipulated two additional factors in this study. The population values for the design factors were selected on the basis of the study conducted by Bauer, Preacher, and Gil (2006).

  1. 1.

    The variance of a or b (\( {\sigma}_a^2 \) or \( {\sigma}_b^2 \)) was varied at two levels: 0.04 and 0.16. These values were chosen to represent low and high levels of heterogeneity in the data. Since the RE-CLPM is not currently used by researchers, no conventions or individual cases exist that could aid in determining “low” and “high” heterogeneity in this context. To this end, the values for the variances were simply motivated to induce differences in results by method, such that one could infer general themes in the performance of the CLPM versus RE-CLPM for data of this type.

  2. 2.

    The correlation between the a and b effects (r a,b ) was varied at five levels: – .6, – .3, 0, .3, and .6, representing large negative, small negative, zero, small positive, and large positive correlations between the two effects.

In sum, there were 3 (sample size) × 2 (effect size) × 2 (variance) × 5 (correlation) = 60 conditions. One thousand replications were generated for each condition, and the same two models as in Study 1 were fit to each replication. The same set of information criteria was also used to compare the models. Similar to Study 1, the performance of the AIC, BIC, ABIC, and AICC in recovering the true model (RE-CLPM, in this case) was examined.

Results

The results from the second simulation study are summarized in Table 2. Similar to Study 1, because the result patterns were the same across effect sizes and sample sizes, only the results for effect size = 0.3 and n = 200 are reported. As is shown in Table 2, it is evident that the RE-CLPM performed well under all examined conditions. In contrast, the CLPM, because it failed to account for random effects, did not yield satisfactory results in most of the conditions. We describe the result in detail below.

Table 2 Results from Simulation Study 2 (effect size of a/b = 0.3, n = 200)
Full size table

Convergence rate

Again, the CLPM converged 100% of the time under all conditions. The estimation for the RE-CLPM reached saddle points in about 19%, 1.9%, and 0% of the replications on average for n = 100, 200, and 500, respectively. Thus, considering saddle points, n ≥ 200 seems preferred for the RE-CLPM.

Bias

The relative biases from RE-CLPM were generally within 5% (see Table 2). In comparison, although the estimates of a, b, and c' from the CLPM were accurate, the estimates for ab were biased when the covariance between a and b was nonzero. This is not surprising, because the CLPM could not account for the covariance between a and b in the computation of ab (see Eq. 3). Consequently, it underestimated ab when the covariance was positive (relative bias ranging from – 2.84% to – 55.55%), and overestimated ab when the covariance was negative (relative bias ranging from 8.41% to 1,401.67%). The bias was larger as the variance increased and the size of the correlation increased.

CI coverage

The CI coverage rates from the RE-CLPM all fell in the acceptable range (see Table 2). In contrast, the CI coverage rates from the CLPM were below the acceptable range under most conditions. The CI coverage rate from the CLPM tended to decrease as the variance of a or b increased for the focal effects. In the most extreme case, the CI coverage rate for ab was about 25% when the variance of a or b was large and the covariance between a i and b i was positive. This low CI coverage was attributable to both the bias in the parameter estimate and an underestimated sampling variability, due to the failure to account for random effects. Even under the conditions in which the parameter estimates from the CLPM were accurate, the CI coverage from the CLPM could drop way below 90%. For example, the CI coverage rates for c' could be as low as 65% when the variance of a or b was large, although the relative biases for c' were very small (see Table 2).

Power/Type I error rate

On average, the power to detect ab was higher for CLPM (see Table 2); however, this gain in power was not really meaningful, considering the poor CI coverage rates from the CLPM. For the direct effect (c'), the CLPM resulted in inflated Type I error rates, particularly for the conditions in which the correlation between a i and b i was nonzero. When the variance of a or b was large, the Type I error rate for c' could be as high as .35. In comparison, the Type I error rates for c' from RE-CLPM were all close to 5%.

Model selection

As we mentioned above, we examined the extent to which information criteria can lead to selection of the correct model (i.e., RE-CLPM in this study). Table 3 shows the success rates of model selection with the four indices. The correlation between a and b did not have a strong influence on the success rates. Thus, the results were collapsed over the different levels of correlations in Table 3. As expected, the accuracy of model selection by all four indices improved as the sample size increased, given that there was less sampling error with a larger sample size (Preacher & Merkle, 2012). It also improved as the variance of a or b increased, because as the variance of a or b increased, the level of heteroscedasticity also increased, which led to a greater degree of discrepancy between the RE-CLPM and CLPM. In addition, the accuracy of model selection by all four indices increased as the effect size increased, because a larger effect size was associated with smaller measurement errors, due to how the data were generated in the study. In general, with a small sample size (n = 100), ABIC had the highest success rates, making it the best index to use among the four indices examined. With a moderate or large sample size (n = 200 or 500), AIC performed much better than BIC, and slightly better than ABIC and AICC, making it the most desirable index to use.

Table 3 Success rates of model selection in Study 2
Full size table

Study 3

The purpose of Study 3 was to examine whether the RE-CLPM is robust to the violation of the normality assumption of random effects. We used the same data generation model as in Study 2, except that the a and b effects were generated from nonnormal distributions. Similar to Study 2, the sample size was varied at three levels (100, 200, 500), and the variance of a or b was varied at two levels (0.04, 0.16). Since the effect size of a or b did not influence the results in the first two studies, we fixed the effect size of a or b at 0.3. As a preliminary investigation, we considered only two levels of correlation between a and b: 0 and .3. The same set of criteria were used to evaluate the performance of the RE-CLPM.

The nonnormal distributions for a and b were generated in such a way that the skewness and excess kurtosis of the distributions were 2.25 and 7, respectively. This degree of nonnormality was considered moderate in Finch, West, and MacKinnon (1997) or West, Finch, and Curran (1995). Specifically, the nonnormal distributions were generated using Fleishman’s (1978) power transformation approach. To ensure that the correlations between a and b were comparable between the nonnormal distribution conditions in this study and the normal distribution conditions examined in Study 2, we computed intermediate correlation effects following Vale and Maurelli (1983) and imposed Fleishman’s (1978) power transformation on the data generated from the intermediate correlation effects.

Results

The results from Study 3 are presented in Table 4. For comparison purposes, we also include in Table 4 the results for the corresponding normal-distribution conditions obtained in Study 2. Given that the sample size did not affect the results, we only report the results for n = 200.

Table 4 Results from Simulation Study 3 (effect size of a/b = 0.3, n = 200)
Full size table

As is shown in Table 4, the RE-CLPM was robust to moderate deviations from normality for the a and b effects. The parameter estimates were unbiased. The CI coverage rates were slightly decreased, the power rates for the indirect effect were slightly overestimated, and the Type I error rates for the direct effect were slightly inflated by nonnormality; however, they were all very close to those obtained under the normality assumption.

Empirical example

In this section, an empirical example is provided to demonstrate the proposed method. The original dataset was from Little (2013, p. 303), used there to test the hypothesis that substance use (M) mediated the effect of family conflict (X) on victimization (Y). Specifically, family conflict is expected to increase substance use, which in turn increases victimization. In this illustration, we used three waves of data collected 6 months apart from 1,132 middle school students. Note that family conflict, substance use, and victimization were latent constructs in the original analysis. Given that the RE-CLPM cannot yet be applied to latent variables (discussed below), we created scale scores for the constructs. The scale scores were the weighted sums of the manifest indicators, using the factor loadings reported in the book chapter as the weights.

We first fit the traditional CLPM, which is similar to that shown in Fig. 1, to the data. We then freed the autoregressive and cross-lagged effects to be random. Note that the autoregressive effects associated with the mediator were fixed in the model, because freeing them to be random caused convergence problems. In addition, we specified a less restricted model than the RE-CLPM used in the simulation studies, by allowing all of the random effects to vary across time. We also explored the covariance structure of the random effects by allowing any significant covariances to be freely estimated.

The results from the RE-CLPM and CLPM are summarized in Table 5. Consistent with the simulation studies, we focus on reporting the result for the mean indirect and direct effects. The complete outputs for the fitted models are available upon request. As is shown in Table 5, the estimated effects from the CLPM and RE-CLPM were consistent in terms of their directions. However, there were two noteworthy differences between the results from CLPM and RE-CLPM. The mean effect M 2➔Y 3 was significant in the CLPM but not in the RE-CLPM. Consequently, the indirect effect X 1➔M 2➔Y 3 was also significant in the CLPM but not in the RE-CLPM. Given that all information criteria were smaller for the RE-CLPM (see Table 5) and that the variances of several random effects [e.g., a 1 (X 1➔ M 2) and the autoregressive effects associated with the X and Y variables] were significant, we believe that the result from the RE-CLPM is more trustworthy.

Table 5 Results for the empirical example
Full size table

Conclusions and discussions

The present article tackles an overlooked limitation of the CLPM for longitudinal mediation analysis: the CLPM does not accommodate random or individually varying direct and indirect effects. It showed that random effects would give rise to heteroscedasticity in the data. Ignoring this heteroscedasticity can potentially result in biased estimates for the indirect effects, unacceptably low CI coverage rates, and highly inflated Type I error rates for the target effects.

We proposed the RE-CLPM to solve the problem. Our simulation studies showed that the RE-CLPM exhibited desirable properties. It yielded accurate parameter estimates and reliable statistical inferences for both mean indirect and direct effects when random effects exist in the population. When random effects do not exist, the RE-CLPM did not produce harmful results. It also showed robustness to moderate deviation from the normality assumption of random effects. However, these desirable properties do not necessarily mean that the RE-CLPM is categorically superior to the CLPM. With only fixed effects, one gains in statistical efficiency and power by using the CLPM. In addition, researchers can assess the data model fit via model fit indices for the CLPM. Furthermore, even with random effects, if the degree of heteroscedasticity introduced by the random effects is low, there may not be meaningful differences in the results between the CLPM and RE-CLPM.

So, when the RE-CLPM should be adopted? In practice, it is usually difficult to know a priori whether there are true random effects and the degree of heteroscedasticity introduced by those effects. One may examine the residual plot for each outcome variable at each time point. However, these residual plots cannot reflect heteroscedasticity in the residual covariance structure for multiple outcome variables jointly. A practical strategy is to fit both the RE-CLPM and the CLPM to the data, and then compare the results from the two models. One should start with the CLPM, to ensure that the CLPM fits the data first, and then free the effects in the model to be random. Two things should be examined when selecting between the models. First are the information criteria. The present study suggests that if the sample size is small, ABIC is the best choice. Otherwise, AIC should be used. Researchers should also examine whether there are meaningful differences between the two sets of results—for example, whether there is significant variance or covariance for any of the random effects specified in the model, and whether the two models lead to diverse conclusions regarding the key effects. If there is no meaningful difference, it is reasonable to report the CLPM result.

A few limitations of the simulation studies are worth mentioning. First, the present study only examined RE-CLPMs with three waves of data in the simulation studies. We cannot extrapolate in an informed manner whether the results would apply to datasets with more waves of data. For example, the simulation studies showed that it is desirable to have n ≥ 200 for the RE-CLPM with three waves of data. The sample size requirement would be presumably larger with more than three waves of data.

Second, the CI for the indirect effect ab was computed using the delta method, but there are better ways to establish the CI. For example, the CI may be established using a Monte Carlo simulation approach (Preacher & Selig, 2012) or a bootstrapping approach (MacKinnon, Lockwood, & Williams, 2004). Kenny, Korchmaros, and Bolger (2003) did not find meaningful differences between the Monte Carlo approach and the delta method for the multilevel model. It will be interesting to investigate whether the Monte Carlo simulation and bootstrapping approaches provide better CIs for the RE-CLPM, especially in the case in which a or b does not follow a normal distribution.

The proposed RE-CLPM is also limited in several ways. First, it can only be applied to manifest variables, so far. As a result, the presence of measurement errors can potentially bias the results. To correctly account for measurement errors, methods to accommodate latent variables in the RE-CLPM need to be developed. A possible direction toward solving the problem would be to use Bayesian structural equation modeling given the computational advantages of Bayesian estimation methods in handling complex models (Zhang, Wang, & Bergeman, 2016). Second, the RE-CLPM also has limited applicability to categorical variables. B. Muthén, Muthén, and Asparouhov (2015) noted that random-coefficient models may not be identified with categorical data.

Third, like the traditional CLPM, the RE-CLPM assumes that the lags between observations are constant across individuals, and the effects detected using the RE-CLPM are limited to the lags. Deboeck and Preacher (2016) have termed the traditional CLPM a discrete-time model, and proposed a so-called continuous-time model (CTM) to overcome the limitations of the CLPM. The CTM allows random lags (i.e., individually varying lags) and produces autoregressive and cross-lagged effect estimates that are independent of the lags. Although the autoregressive and cross-lagged effects obtained from the CTM have different interpretations than those obtained from the CLPM, they are mathematically related. On the basis of the effects estimated in the CTM model, one might compute the corresponding effects in the discrete-time model of any given lag through nonlinear transformations. Deboeck and Preacher only considered the CTM with fixed effects; however, they pointed out that it is also possible to accommodate random effects in the CTM. It would be interesting to compare continuous-time and discrete-time models when random effects are included in both models. The only downside of the CTM is that it is less flexible than the CLPM in modeling time-varying effects.

A few other extensions of the RE-CLPM deserve future investigation. First, the RE-CLPM can be extended to incorporate potential covariates for any of the random effects (e.g., indirect effects). If a covariate effect is significant, the random coefficient will vary as a function of the covariate, and the covariate is said to moderate the effect (e.g., moderated indirect effects). This is analogous to a moderated mediation analysis with the traditional CLPM (Hayes, 2013). However, the RE-CLPM may be able to produce more accurate standard error estimates for covariate effects than the CLPM can. In addition, with the RE-CLPM, researchers can examine the proportions of variance in the random effect explained by the covariate, which may serve as an effect size measure for the moderation effect. Future research will need to be conducted to examine to what extent the RE-CLPM can correctly recover moderation effects.

Second, given that missing data are ubiquitous in longitudinal studies, it is worth noting that the RE-CLPM may be fitted when missing data are present by using the full-information maximum-likelihood estimation method (Asparouhov & Muthén, 2003; Yuan & Bentler, 2000; Yuan, Yang-Wallentin, & Bentler, 2012). Future research will be warranted to examine whether the RE-CLPM will perform as well with missing data. Another principal missing data method is multiple imputation (MI). However, researchers should be cautious about using MI in this case, because the commonly used imputation models (e.g., regression models) do not take random effects or heteroscedasticity into account, which can potentially introduce bias into the analysis result.

Third, the article only addresses heteroscedastic residuals induced by random effects; thus, heteroscedasticity will disappear after accounting for the random effects. It is possible that different causes of heteroscedastic residuals may coexist in one model (e.g., nonnormality of the outcome variables), with random effects being only one of the causes. In this case, we suspect that modeling random effects may mitigate but not completely solve the heteroscedasticity problem. To account for heteroscedastic residuals that are not due to random effects while modeling the random effects at the same time in a single-level model would be an interesting yet challenging venue for future research. It is also likely that the heteroscedastic residuals, if they exist, are not induced by random effects at all. In this scenario, it would be interesting to examine whether the presence of heteroscedastic residuals would lead to wrong detection of random effects.

Finally, the present study only incorporated random effects in the cross-lagged panel model. A recent study conducted by Hamaker, Kuiper, and Grasman (2015) pointed out that it is also necessary to account for random intercepts in CLPMs if the constructs under study contain trait-like or time-invariant components. Failure to do so may result in spurious effects or misleading conclusions regarding the size and direction of a cross-lagged effect. They suggested that random intercepts can be included as latent factors underlying corresponding repeated measures with loadings fixed at 1. The random intercepts would extract the time-invariant components for each individual out of the repeated measures. The autoregressive and cross-lagged effects could be then tested for the disturbances on the repeated measures after accounting for the random intercepts. The cross-lagged effects detected in this way would reflect the mediation process, controlling for the time-invariant components. Given that the disturbances are modeled as latent variables in the random-intercept model proposed by Hamaker et al., there is no good way yet to allow random autoregressive and cross-lagged effects in the random-intercept model. Future research will be warranted to develop ways to accommodate both random intercepts and random effects in the longitudinal mediation model.