In natural tasks, humans direct their eyes toward objects of interest to make the best use of the high acuity vision in the fovea. Many factors influence eye movements. However, it is possible to get consistent scan patterns and, therefore, to separate signal from noise if the stimuli are presented repeatedly. However, repetition introduces the risk that the participants will recognize the repeated scenes and alter their gaze behavior. In many tasks, repeated presentation of the same scene is undesirable, because some subjects will recognize the scene and examine previously unexplored areas, encode additional details, and/or find targets more efficiently on the basis of their previous experience. Dorr, Martinetz, Gegenfurtner, and Barth (2010) compared the variability of eye movements during free viewing of dynamic natural scenes and found that whereas between-subjects coherence was maximal at the first presentation of the movie, it decreased during later presentations throughout the day. Dorr et al. suggested that this decrease in the between-subjects coherence was caused by a rising influence of individual viewing strategies. Gaze patterns are even affected when the stimulus is not explicitly recognized. In studies on contextual cueing, Chun and Jiang (1998) showed that people implicitly learn the positions of targets over time, which then results in shorter response times.

One way to decrease the chance that participants will recognize the repetition is to increase the number of filler trials. The disadvantage of this approach is an increase of the experiment’s duration, which can have a negative impact on the performance of the participants. Another possibility is to modify the stimuli in a way that will keep scan patterns similar to the unmodified version. Geometrical transformations of the stimuli are one way to achieve this goal. The use of geometrical transformations is limited with structured scenes such as movie clips, in which the orientation is meaningful; however, scenes without an inherent structure offer a wider range of possibilities.

In this study, we utilized Multiple Object Tracking (MOT; Pylyshyn & Storm, 1988). MOT is an experimental paradigm in which subjects must track several moving target objects among other moving distractor objects. It has been found that when MOT trials are presented repeatedly, participants fail to notice the repetition (Lukavský, 2013; Ogawa, Watanabe, & Yagi, 2009). This task is convenient for two reasons: First, because the stimuli in MOT are simple displays with moving objects/dots, they can be easily transformed without any change in meaning. Second, MOT is a dynamic task, and people need to sustain their attention over the course of the whole trial. Thus, their eye movements are likely to be connected to the scene properties or object positions rather than to other factors (e.g., guidance or search strategies). Additionally, examining human eye movement strategies in a situation of distributed attention can be useful for understanding behavior in many other everyday tasks.

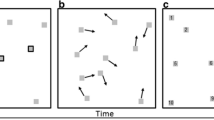
In a dynamic task like MOT, eye movement data can be easily represented as scan patterns (see Fig. 1 below). Examining scan patterns instead of saccades or fixations on areas of interest is useful, since it can account for similarities in smooth pursuit or cases in which people fixate empty space between objects. Similarly, scan pattern coherence has been used to examine human eye movements while viewing movies (Dorr et al., 2010).

Fig. 1
figure 1

Calculating correlation distance. Two scan patterns (A1, A2) are convolved with a Gaussian filter into two spatio-temporal fixation maps (B1, B2). The correlation distance is 1 – corr(B1, B2)

Full size image

Here, we asked whether human observers would transform spatio-temporal scan patterns in a way that corresponds to geometric transformations that were applied to MOT trials by the experimenter. If the two transformations are similar, then the data from both the transformed and the original MOT trials could be pooled. One of the possible transformations would be to flip the stimuli around axes. This operation should be plausible if the eye movements were symmetrical with respect to the left and right hemifields (or the upper and lower hemifields, depending on the axis of a transformation).

Behaviorally, the existence of a left–right asymmetry is unclear. Unlike the upper–lower asymmetry (Levine & McAnany, 2005), a left–right asymmetry is rarely reported in healthy subjects (Greene, Brown, & Dauphin, 2014; Petrov & Meleshkevich, 2011; cf. Corballis, Funnell, & Gazzaniga, 2002). In the case of MOT, if people track a group of targets as a single object (Yantis, 1992), we should expect no left–right difference, since the optimal viewing position is found at the center of the perceived object, with no lateral bias (Foulsham & Kingstone, 2010). Conversely, others have reported a preference for early fixations to the left part of the scene (Dickinson & Intraub, 2009; Foulsham, Gray, Nasiopoulos, & Kingstone; 2013; Nuthmann & Matthias, 2014; Ossandón, Onat, & König, 2014). This bias is often discussed with respect to “pseudoneglect”: a leftward bias in the line-bisection task in healthy humans (Bowers & Heilman, 1980; Jewell & McCourt; 2000).

When viewing natural scenes, people make more horizontal than vertical saccades and show no left–right asymmetry in these saccades (Foulsham, Kingstone, & Underwood, 2008). Performance in an antisaccade task has shown that people are better prepared to make rightward saccades, which are performed faster and with fewer errors (Evdokimidis et al., 2002; Tatler & Hutton, 2007). This asymmetry may be a result of a learned behavior, since it is consistent with the findings of Abed (1991) comparing the directions of saccades when looking at simple dot patterns in Western, Middle Eastern, and East Asian participants.

All of the abovementioned studies used static stimuli. The left–right asymmetries in fixation patterns happen within a few fixations at the beginning of a trial and later disappear (Nuthmann & Matthias, 2014; Ossandón et al., 2014). In a dynamic task like MOT, it is an open question whether a left–right asymmetry would be observed. To our knowledge, there are currently no studies regarding the symmetry of scan patterns using dynamic stimuli.

To summarize the aims of our study: We wanted to test whether we could flip stimuli around the axes as a way of masking the repetition of trials. We chose the MOT paradigm because it has suitable properties for this goal. During preparation of the experiment, we found that few methods have been developed to test the statistical differences between groups of scan patterns. Any two scan patterns are almost certainly different from each other; the important question is how large that difference is, given the noise. Thus, for testing differences between two groups of scan patterns, the within-group coherence has to be computed first. The usual approach is to compute the average distance between all possible pairs of scan patterns. There are several pairwise comparison methods, such as the Levenshtein distance (Levenshtein, 1966), ScanMatch (Cristino, Mathôt, Theeuwes, & Gilchrist, 2010), and Multimatch (Dewhurst et al., 2012; Jarodzka, Holmqvist, & Nyström, 2010), that work with scan patterns represented using an event-based approach (Le Meur & Baccino, 2013). This representation is complicated in MOT, however, because of the prevalence of smooth pursuit, which is difficult to detect in eyetracking data. The alternative approach is to use the raw data, as in Dorr et al. (2010), and compute the distance using Normalized Scanpath Saliency (Peters, Iyer, Koch, & Itti, 2010), which works with a spatio-temporal fixation map (or three-dimensional saliency map).

Usually, a saliency map is computed for scan patterns collapsed over time and represents areas in the scene that participants fixated during the trial. There are two sets of methods for using saliency maps to compare scan patterns. First, both scan patterns can be expressed in the form of saliency maps and then compared to one another. Second, we can compute how well a scan pattern can be explained by a given saliency map. Both approaches are similar, and most of the methods can be used for both representations. When both scan patterns are represented as saliency maps, there are several methods for computing similarity, such as ROC analysis (Tatler, Baddeley, & Gilchrist, 2005), Kullback–Leibler distance (Rajashekar, Cormack, & Bovik, 2004; Tatler et al., 2005), and correlation-based metrics (Jost, Ouerhani, von Wartburg, Müri, & Hügli, 2005; Toet, 2011). When only one scan pattern is represented as a saliency map, researchers can use Percentile metric (Peters & Itti, 2008) or Normalized Scanpath Saliency. ROC analysis and the Kullback–Leibler distance can be used in this case. For dynamic tasks, using the spatio-temporal fixation map is an interesting extension, because it keeps the time dimension in the analysis. Correlation-based metrics and Percentile metric can still be used for the spatio-temporal fixation maps. Metrics that work with the saliency map can compute within-group coherence by using the leave-one-out method, in which all of the scan patterns except one are summed into one saliency map, and then the distance is computed using one of the available metrics. Because a saliency map can be created from a single scan pattern, these methods can be also used for pairwise comparison.

With within-group coherence computed for each group, it is an open question how to test correctly whether the between-group variability is larger than the within-group variability—in other words, whether the scan patterns from one group are significantly different from the scan patterns in other group. Currently, only one method, that of Feusner and Lukoff (2008), addresses this situation, and it is only applicable using the pairwise comparison approach. Their method computes the distance for all pairs within each group and between groups using one metric selected a priori. It then tests the significance of the differences between the overall within-group distance and the overall between-group distance using permutation tests. The choice for the distance metric is dependent on the researcher’s task. Tang, Topczewski, Topczewski, and Pienta (2012) extended this method for scan patterns of unequal lengths.

In this study, we tested whether the scan patterns from MOT trials are similar to the scan patterns from the same trials flipped around the y-axis (Exp. 2) and around the x-axis (Exp. 3). Prior to this, we developed two additional strategies for comparing groups of scan patterns and tested their discrimination capabilities on simulated data (Simulation Experiment 1).

Experiment 1 (Simulation)

To determine which method for statistical group comparison could most accurately determine differences between groups, we conducted a simulation experiment with artificial scan patterns. The scan patterns were divided into two groups to achieve a ground truth classification. We manipulated the variability within groups relative to the intergroup distance and used three methods to determine their classification sensitivity. To summarize, the purpose of this experiment was to determine the relationship between methods for measuring statistical differences between groups of scan patterns.

Method

In this experiment, we used artificial trajectories similar to the scan patterns from behavioral data. Those artificial trajectories were then divided into two groups, and similarity between the groups was tested using three comparison strategies. In following subsections, we first describe the metric for evaluating the similarity of individual scan patterns (or groups of scan patterns). Then we describe three comparison strategies using this metric to evaluate the statistical significance of the differences. Finally, we describe the process of creating artificial scan patterns and using those patterns to evaluate the three analysis strategies.

In the following experiments, we will be working with scan patterns (vectors x, y, t). For both the artificial and behavioral scan patterns, the data were first binned into a 3-D spatio-temporal matrix with a bin size of 0.25° × 0.25° × 20 ms, in which the number in each bin represented how many gaze samples fell into that bin. The data were analyzed using the statistical program R (R Development Core Team, 2014).

Metrics for comparisons

In this study, we distinguished between comparison metrics (to determine the distance between scan patterns) and comparison strategies (to test the significance of a difference, described later). To evaluate the similarity of scan patterns or a group of scan patterns, we employed the correlation distance (CD) metric.

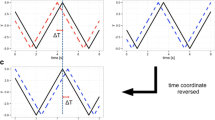
The CD (Jost et al., 2005; Le Meur, Le Callet, Barba, & Thoreau, 2006; Rajashekar, van der Linde, Bovik, & Cormack, 2008) can be used to evaluate the similarity of two saliency maps or to compare the similarity of a set of fixation points with a saliency map. The saliency map represents areas in the scene where participant fixated during the task. Those fixation points are usually smoothed by an isotropic bidimensional Gaussian function (Le Meur & Baccino, 2013). Due to smoothing, two scan patterns slightly shifted in one of the spatial coordinates are treated as similar. Because this approach does not take the temporal order of fixations into account, we extended the saliency maps into the 3-D variant, denoted as spatio-temporal fixation maps. Convolving scan patterns with a spatio-temporal Gaussian filter preserves identity for the time scale, as well. Therefore, identical scan patterns shifted in space or in time would be treated as very similar up to some degree, defined by the properties of the Gaussian filter. In our case, the Gaussian filter had the parameters σ x = 1.2°, σ y = 1.2°, σ t = 26.25 ms, but as was shown by Lukavský (2013), similar results were obtained for filters with different parameters. We then computed the correlation between the scan patterns, preserving the temporal order of the fixations.

Since spatio-temporal fixation maps can consist of several scan patterns, we compared the distance between two groups of scan patterns. In that case, the parts of the spatio-temporal fixation map in which several scan patterns were similar would have higher values. The computation of the similarity of two scan patterns is shown in Fig. 1. More specifically, the CD metric is computed as follows: Each of two groups of scan patterns (if we calculate the distance between two individual scan patterns, each group can contain only one scan pattern) is convolved with a spatio-temporal Gaussian. Thus, we obtain two spatio-temporal fixation maps. The similarity between two scan patterns is preserved even if they are slightly shifted in the time coordinate. Using the Pearson correlation coefficient, the correlation between those two maps is computed, and the CD metric is 1 – r. Due to the nature of fixation maps, the correlation coefficient can occasionally be less than 0. Therefore, for negative correlation coefficients, we set the CD metric as 1. As a consequence, the values of the CD metric can range from 0 (absolute correspondence) to 1 (completely different trajectories). Lukavský (2013) showed that the most similar scan patterns are two patterns from the same subject and same trial; followed by scan patterns from different subjects and the same trial, and from the same subject on different trials; and the least similar were scan patterns from different subjects on different trials. On the scale of the CD metric, two random scan patterns would have CD values around .95, and two scan patterns from the same subject and repeated presentation of the same trial would have a CD value around .47. The main advantages of the CD metric are the limited range [0, +1] and intuitive evaluation of the results in comparison to other metrics, such as Normalized Scanpath Salience (Dorr et al., 2010) and Kullback–Leibler divergence (Rajashekar et al., 2004).

Comparison strategies

The CD was used to measure the distance between scan patterns or between groups of scan patterns. However, given the observed variability of the scan patterns, the statistical significance of a measured difference was uncertain. In the context of repeated presentation, we must discriminate whether the variability introduced by repeated presentation differs from variability from the experimental manipulation (e.g., flipping around the y-axis). For the following text, we will work with two groups of scan patterns, G1 and G2, each consisting of six scan patterns. We proposed three strategies for comparing groups of trajectories to achieve this goal.

The first strategy (subset comparison) compared the within-group variabilities for random subsets of the merged G1 and G2 groups. If the scan patterns from each group were similar, we should get the same within-group distance for subsets of scan patterns, irrespective of whether they were all selected from one group or were instead selected from both groups. Therefore, using this strategy, we randomly sampled a subset of scan patterns and measured their overall distance. Then we compared whether these distances differed when the scan patterns were selected from a single group or from both groups. The number of scan patterns forming each subset was preselected to allow for multiple possible samples within each group. Thus, we chose four out of six trials. Next, we defined a method to measure the mutual similarity within a group by computing the CD of each scan pattern with others. Finally, we compared these mutual similarities for all quadruples sampled solely from one category with mixed quadruples having half of the elements from each category. Specifically, we compared \( 2*\left(\begin{array}{c}6\\ {}4\end{array}\right)=30 \) quadruples for each of the G1 and G2 groups (G values), and \( \left(\begin{array}{c}6\\ {}2\end{array}\right)*\left(\begin{array}{c}6\\ {}2\end{array}\right)=225 \) mixed quadruples (M values). The difference between the G and M values was tested using a two-sample t-test.

The second strategy (pairwise comparison) computed the differences between the G1 and G2 groups using the permutation test introduced by Feusner and Lukoff (2008). This method computed differences between two groups of trajectories using pairwise comparisons and compared the distances of pairs from the same and from different categories. Note that we could have used an arbitrary distance metric for the comparison of two trajectories. For each possible assignment into one of two groups of equal sizes, the overall distance is defined as d* = d betw – d ingrp, where d betw and d ingrp denote the grand mean distances of pairs selected from different groups or from the same group, respectively. The value d* expressed the overall distance between two groups. Finally, we compared the d* values for the experimental condition assignment (G1 and G2 groups) with the distribution of d* for all other possible groupings. Because we had six scan patterns in both the G1 and G2 groups, we had a distribution of \( \left(\begin{array}{c}12\\ {}6\end{array}\right)=924 \) d* values. The gaze patterns from each groups were significantly different (i.e., the G1 and G2 groups were nonrandomly grouped), if the corresponding d* exceeded the 95 % quantile of the distribution.

The third strategy (groupwise comparison) combined both previous strategies. First, we computed summed spatio-temporal fixation maps for groups G1 and G2 and expressed the similarity of those two maps using the CD metric. We then applied a permutation test and computed the similarity for all assignments of all trajectories in the two groups, and again compared the similarity of groups G1 and G2 with the 95 % quantile of this distribution.

All three strategies are schematically captured in Fig. 2.

Fig. 2
figure 2

Schemas of three strategies for comparing groups of scan patterns: (a) subset comparison, (b) pairwise comparison, and (c) groupwise comparison

Full size image

Artificial trajectories

We created artificial scan patterns to match parts of the gaze trajectories without the saccades from an MOT experiment (here reported as Exp. 2). To obtain such parts, we first identified the saccades from the recorded eye movement data using an algorithm from Nyström and Holmqvist (2010). We then selected only intersaccadic segments, which consisted of both fixations and smooth pursuit eye movements with a varying number of samples. For those samples, we computed the average distances between subsequent points in the scan patterns and the total scan pattern lengths. Next, we created artificial trajectories similar to smooth pursuit eye movements (similar with respect to those two respective measures) and used artificial data for evaluating the methods for testing significance. Although we wanted the trajectories to be similar to the observed trajectories, we believe that the exact algorithm and parameters are not crucial for our argument, given that the main purpose was to introduce trajectories with the amount of variability observed in the task. Accordingly, using trajectories of low variability might inflate the similarity measure over time. Artificial trajectories were created as random walks, in which each subsequent position was sampled from a bivariate normal distribution centered at the last position with covariance matrix α·I, in which α varied from .0005 to .005 (step size .0005) and I denoted the identity matrix. The initial position of an artificial scan pattern was varied as described in the Design section. We also varied the number of samples between each two generated values and interpolated the positions between them. The interpolation factor varied from 1 (no subsequent samples) to 5 (four interpolated samples between two generated samples), with step size .5. From all of the possible artificial trajectories, we selected those with high similarity to the segments of behavioral data previously identified. More specifically, we attempted to match the subsequent distances between the samples and the total scan pattern lengths. Values for α and the interpolation factor from the most similar artificial trajectories were used for generating the trajectories for the experiment. To obtain more robust results, we also used parameters for α and the interpolation factor, which resulted in more variable scan patterns, measured in the subsequent distances and scan pattern lengths.

A comparison of the artificial trajectories with the human gaze trajectories from Experiment 2 is presented in Table 1. To compute two descriptive measures of the behavioral scan patterns, we selected from the behavioral data only parts with 500 to 600 subsequent samples (corresponding to 2.0–2.4 s recorded with an EyeLink II at 250 Hz). We found 457 smooth pursuit parts of the desired length. Correspondingly, we modeled the artificial trajectories consisting of 500 gaze samples.

Table 1 Mean and standard deviations (SD in brackets) of two characteristics of generated data
Full size table

For the present experiment, we generated two types of trajectories with the parameters α = .001, interp = 1.5 (scan patterns with low variability) and α = .003, interp = 1 (scan patterns with high variability).

Design

For evaluating the discrimination properties of our strategies, we created the following setting. There were two groups of trajectories (G1 and G2), each of which consisted of six trajectories. The trajectories started on a separate circle with a 1° diameter, and the distance of the centers of both groups was kept constant (10°). The first sample in each trajectory from the G1 group started on odd multiples of π/6, and the trajectories for the G2 group started on even multiples of π/6, as depicted in Fig. 3. Then we created additional identical copies of the trajectories from both the G1 and G2 groups and moved all of the spatial coordinates of the trajectories in the direction of the arrows from 0° to 5° by a step size of 0.5° (therefore, the radii varied from 1° to 6°). Therefore, with the increasing radii in both the G1 and G2 groups, otherwise identical trajectories were becoming more distant from the trajectories in the starting group, and the distinction between groups G1 and G2 would become less evident. This setting was generated randomly 50 times. Similarity between the groups was evaluated using the three strategies. We report the distance for which strategies reached chance level for rejecting the null hypothesis as the ratio of the group diameter over the distance of the centers of the groups.

Fig. 3
figure 3

Starting positions of artificial G1 and G2 groups. The dots are the initial positions of the generated trajectories. The radii for both groups were varied from 1° to 6°, and the distance between the centers was kept constant

Full size image

Results

As expected, the classification accuracy decreased with the increasing diameter of each group for all strategies. In general, the subset strategy exhibited the best precision, followed by the groupwise strategy, and finally the pairwise strategy. When circles on which the scan patterns were generated were separated by more than 3°, all three strategies discriminated two groups in 100 % of the cases. Similarly, for distances lower than 1°, all of the strategies failed to discriminate two groups in all cases. If we define the group variability as the maximum initial distance, the distances reported above mean that all strategies discriminated the groups at the distance of 143 % or more of the group variability, and failed at distances lower than 111 %.

For all three strategies, the data were fit with a cumulative Gaussian to obtain threshold values. For the less variable trajectories (α = .001), the subset strategy reached chance level when the ratio of the group radius over the distance between the centers reached .41; the groupwise strategy reached chance level when the ratio reached .40; and the pairwise strategy reached chance level at the .39 threshold (Fig. 4). For the more variable trajectories, the values were similar: .43 for subset, .41 for groupwise, and .38 for pairwise.

Fig. 4
figure 4

Percentages of correct responses for artificial trajectories with low (a) and high (b) variability. The results are fitted with a cumulative Gaussian function

Full size image

Discussion

All three strategies showed similar capabilities to discriminate between the scan patterns from two groups. The subset strategy nonetheless had better precision than the other two, and was selected for the following experiments. Similar results were found for more variable scan patterns, but the fitted function was less steep. Here we only checked the situation in which two groups differed in their initial positions. In general, scan patterns could differ in other properties, such as the general shape of a scan pattern, but for the basic assessment of the comparison strategies, we assumed that manipulating the initial positions would be sufficient.

Experiment 2

In Experiment 2, we presented participants with MOT in original and flipped trials (mirrored around the y-axis), and we evaluated the effect of symmetry on the eye movements. Each trial was repeatedly presented several times in both the original and flipped versions, and we used the CD metric to evaluate the scan pattern distances and the subset strategy to evaluate the statistical significance, on the basis of the results of Experiment 1. This experiment would determine whether flipping trials around the y-axis can provide comparable scan patterns, and therefore we could use this technique for masking trial repetition.

Method

Participants

Thirty-one students (27 female, four male; ages 19–28 years, mean 20.8) participated in the experiment. All had normal or corrected-to-normal vision, and none had previously participated in this type of experiment. We originally collected data from 32 participants, but had to exclude one participant due to a technical error.

Apparatus and stimuli

The experiment was presented on a 19-in. CRT monitor with a resolution of 1,024 × 768 and an 85-Hz refresh rate, using MATLAB with the Psychophysics Toolbox extension (Brainard, 1997; Kleiner, Brainard, & Pelli, 2007; Pelli, 1997). Participants viewed the screen from a distance of 50 cm, and their head movements were restrained with a chinrest. Gaze position was recorded at 250 Hz using an EyeLink II (SR Research, Canada). The eyetracker was calibrated using a 9-point calibration procedure at the beginning of each block, and drift correction was performed before each trial.

The stimuli used in this experiment included eight gray 1°-diameter circles on a black background. Each of them moved with a constant speed of 5°/s. All objects moved in a 30°-diameter circular arena. The direction of the objects was sampled from a von Mises distribution with a concentration parameter of κ = 40 for each frame, which resulted in an impression of Brownian motion. The objects bounced off an invisible envelope surrounding the other objects, allowing at least a 0.1° space between objects. The objects also bounced off the circular border back to the central area, with a random change of direction of 45° left and right from the center. The bouncing did not follow the laws of reflection, because this would result in predictable direction changes (e.g., they would copy the shape of an n-gon).

Procedure

The experiment consisted of 90 experimental trials divided into six blocks, each of which consisted of 15 trials. Five extra training trials were presented at the beginning of the experiment. In each trial, eight objects were presented at random positions on the screen. Four of the objects were highlighted with green (targets), whereas the other four were gray (distractors). After 2 s the targets turned gray, and all objects moved for 8 s. Finally, all objects stopped, and the participant was asked to select all objects that were originally in the highlighted set using the mouse. During response collection, the selected dots changed to yellow. When four dots were selected, the feedback was presented; the screen turned black with the message “OK” in green if all of the targets were identified correctly, or with the number of incorrectly selected targets in red.

'Each block consisted of 15 trials: five experimental trials (L trials), five trials in which the L trials were flipped around the y-axis (R trials), and five unique trials. The last group—the five unique trials—was presented to mask the repetition of the trials throughout the experiment. To reduce the possibility that the participants would notice the repetition, we generated a 10-s period of motion for each trial and randomly manipulated the starting time of each trial (between 0 and 2 s). Because the trials lasted for 8 s, all repeated trials shared a common time segment of 6 s.

Data analysis

Blink detection

Participants usually blink during tracking. In the recorded data, the blinks manifest as fast vertical movement with a decreasing pupil size. For each trial, we computed the maximum pupil size and discarded all data with a pupil size lower than 75 % of this maximum.

Data preparation

We kept only eye gaze data in the range of −15° to +15° for both the horizontal and vertical directions. Because the display area was circular, this method could miss some eye gaze data between of the display area and the rectangular border, but since such data constituted only 0.07 % of the samples, we retained those data for analysis. All eye gaze data from the R trials were flipped back around the y-axis to ensure comparable coordinates. Similarly, as in Experiment 1, we binned the data for each scan pattern into a 3-D spatio-temporal matrix for computation of spatio-temporal fixation map.

Comparison metric and strategy

Between-group distances were computed using the CD metric, and on the basis of our results from Experiment 1, we used the subset strategy for testing significance. In this experiment, the groups of scan patterns were denoted as L and R trials, and each group represented scan patterns from repeated presentation of the same trial.

Results

Overall, participants’ accuracy was high. On 91 % of all trials, all targets were correctly selected. The per-subject accuracy ranged from 76 % to 99 %. Only trials on which all four targets were correctly identified were included in the analysis.

Differences between L trials and R trials were tested using linear mixed models with Subject ID and Trajectory ID as random factors (the same trajectory was presented for each L and R trial), where the distance between individual groups was measured using CD distance. On the basis of the subset strategy, we had three similarity conditions: L (similarity within repetitions of the original stimulus); R (similarity within repetitions of a flipped stimulus); and M values (similarity within mixed trials). We expected the L and R values to be equal, where the potential difference would represent a difference in scan pattern variability after a flip. Such a difference would be possible at the trial level, but since the L and R assignment was arbitrary (we could perceive L as a mirrored version of an R trial, and vice versa), the effect should cancel out across trials. The L and R values provide a baseline for later comparison with the M values. For our manipulation, the crucial comparison was between L and R versus the M values. The potential difference showed that scan patterns in flipped trials differed significantly from the gaze patterns in the original trial (when flipped back to ensure consistency of the coordinates). The mean value from both L and R trials was denoted LR (in Exp. 1, this value was denoted as G).

As expected, we found no differences between the CDs of L trials (mean = .47, SD = .12) and R trials (mean = .47, SD = .12) when using mixed models [χ 2(1) = 0.01, p = .920]. However, the CD between groups with mixed L and R trials (M values) was significantly higher (mean = .53, SD = .11) [χ 2(1) = 89.4, p < .001], albeit the increase in overall distance was only 13 % relative to the LR values. Although we found a significant difference between LR and M values, the means of those values per trajectory strongly correlated (r = .83, p < .001).

The differences between flipped and nonflipped were significant. We did not know whether the difference was due to the different shapes of the scan patterns or whether the difference appeared because the scan patterns were biased to a specific side. To rule out the latter possibility, we systematically varied the overall position of scan patterns in the R trials on the x-axis and compared their similarity with the L trials. Each scan pattern in the R trials was moved −0.5° to 0.5° on the x-axis (step size 0.25°) relative to the original R trial. All of the changes to the R trials had no effect, and the differences remained significant (p < .001). Therefore, the scan patterns from each group were not systematically shifted to either the left or right. This ensured us that the differences between the L and R trials were not caused by a noncentered viewing point. Because EyeLink II is a head-mounted eyetracker, we also tested moving the R trials in each block separately, but the difference between the LR and M values remained significant (p < .001 for all cases).

Discussion

Comparing L and R trials using the subset comparison strategy revealed differences between the trials, which means that the scan patterns during MOT were not symmetric about the y-axis. However, this difference was not big (only 13 % relatively to the baseline from the nonflipped trials), and the overall distance for groups consisting of scan patterns only from one condition strongly correlated to the overall distance for groups consisting of scan patterns from both conditions. Therefore, our results have one important application. If trials are repeatedly presented to participants, there is a chance that they will notice the repetition and consciously learn the trials. If we flip some of the repeatedly presented trials and then flip them back again to the original coordinates before the analysis, the observed scan patterns will be slightly noisier (more variable, relative to nonflipped trials), but they will still be highly correlated on a per-trajectory level. This means that we could use flipping to conceal repetition, use a smaller number of repetitions per trial, and test over a larger number of different stimuli.

Experiment 3

Following on Experiment 2, we were also interested in identifying differences when trials were flipped around the x-axis. We remind readers that the purpose of this experiment was to answer the question of whether trials can be flipped around the x-axis while keeping scan patterns similar to the scan patterns from nonflipped trials.

Method

Participants

Thirty-two students (27 female, five male; ages 19–28 years, mean 21.8) participated in the experiment. All had normal or corrected-to-normal vision, and none had previously participated in this type of experiment.

Apparatus and stimuli

The apparatus and stimuli were the same as in Experiment 2.

Procedure

The structure of the experiment was the same as in Experiment 2. The only difference between Experiments 2 and 3 was in the experimental trials. Each block consisted of five experimental trials, each of which was presented in two variants: once in the normal condition (U trial, upward), and once flipped around the x-axis (D trial, downward).

Data analysis

The same metric and strategy as in Experiment 2 were used in this experiment. Here, we denote the average value for the U and D trials used for subset strategy as the UD value.

Results

As in Experiment 2, the overall accuracy was high. On 96 % of trials, the participants correctly selected all four targets, and the per-subject accuracy ranged from 86 % to 100 %. Only trials during which all four targets were correctly identified were included in the analysis.

Differences between the U trials and D trials were tested using linear mixed models with Subject ID and Trajectory ID as random factors (the same trajectory was presented for each U and D trial). As expected, the results showed no differences in CDs between U trials (mean = 0.49, SD = 0.14) and D trials (mean = .48, SD = .14) using mixed models [χ 2(1) = 0.68, p = .409]. As in Experiment 2, the CD for mixed UD trials was significantly higher (mean = .59, SD = .14) [χ 2(1) = 139.93, p < .001]. Again, on the trajectory level, the UD and M values strongly correlated (r = .82, p < .001). The increase in the overall distance of M values was 22 % relative to the UD values.

Discussion

We found significant differences between the U and D trials, and the observed differences were greater than those in Experiment 2, thus confirming that there is a greater asymmetry between the upper and lower visual fields than between the left and right visual fields, as has been reported in previous studies. As the horizontal and vertical planes differ in many ways, including visual acuity for letter recognition (Freeman, 1980), mental imagery (Finke & Kosslyn, 1980), and the extent of crowding (Toet & Levi, 1992), we could expect similar differences in the extent of dissimilarity in the horizontal and vertical planes, as well.

General discussion

Our study has several implications. In Experiments 2 and 3, we measured the differences between dynamical stimuli flipped around the y- and x-axes. In both cases we found significant differences, indicating that the scan patterns were not symmetrical. However, the difference was small—the overall distance for groups containing scan patterns from both flipped and nonflipped trials increased only by 13 % relative to the groups containing scan patterns from one condition only when trajectories were flipped around the y-axis (and 22 % for flipping around the x-axis). Moreover, the coherence values within the repetitions of the identical stimuli and within the mixed groups containing flipped and nonflipped trials were highly correlated (r = .83 for flipping around the y-axis, and r = .82 for the x-axis). Therefore, the technique of flipping trials can still be used for masking repetition.

Our finding that scan patterns were not symmetric contrasts with the idea that people track a group as a single object and fixate the centroid of the group (Fehd & Seiffert, 2008; Foulsham & Kingstone, 2010; Yantis, 1992). The differences between the scan patterns could be caused by a combination of several sources. First, human visual perception may not be symmetrical across the visual field (Bradley, Abrams, & Geisler, 2014; Najemnik & Geisler, 2009), and thus, to compensate for the asymmetries, both tracking strategies and eye movements have to be slightly different, a factor that current models do not reflect (Fehd & Seiffert, 2008, 2010; Lukavský, 2013). Second, as previous results showed (Ke, Lam, Pai, & Spering, 2013), there are asymmetries in smooth pursuit movements, which is the main part of the scan patterns in MOT. Finally, learned biases (such as reading direction) may affect the scan pattern shapes.

Compared with other studies documenting asymmetries in left–right fixation distribution (Nuthmann & Matthias, 2014; Ossandón et al., 2014), we used a dynamic task in which the repeated presentation was concealed. Therefore, participants had to sustain their attention and adjust their eye movements accordingly over the course of the trial, and they had smaller freedom to look at the remaining parts of the display, which were not relevant for the task. Due to the easier concealment of repetition in MOT, we could use a within-subjects design to compare the effects of symmetry.

In accordance with the studies showing a lower–upper asymmetry in the visual field (Green et al., 2014; Hagenbeek & Van Strien, 2002; Pitzalis & Di Russo, 2001), we found greater differences in gaze patterns when the trajectories were flipped vertically. The differences between flipped scan patterns were complex, such that a simple overall shift of the flip axis did not reduce differences between groups of scan patterns. In the context of studying the perception of geometrically transformed dynamical stimuli, MOT is a very convenient task: Geometric transformations of the scene do not change its meaning, and participants fail to notice the transformations.

Another important conclusion from our study is methodological. In studies in which scan patterns are of interest, only one strategy can be used for comparing between-group coherences. Because this complicates possible experimental designs, simpler forms of analysis are often employed—for example, reducing scan patterns to the distribution of fixations and saccades and comparing only the distributions rather than the entire scan patterns. We believe that the two new methods presented here can help other researchers to use scan patterns more extensively in their analyses. It is important to note that our strategies can be used only with comparison methods capable of computing the coherence of a group of scan patterns. Nevertheless, in applicable scenarios, our two novel strategies scored slightly higher than the original strategy of Feusner and Lukoff (2008), and the difference seemed to be even greater when the scan patterns were more variable.