PsiMLE: A maximum-likelihood estimation approach to estimating psychophysical scaling and variability more reliably, efficiently, and flexibly

Abstract

A simple and popular psychophysical model—usually described as overlapping Gaussian tuning curves arranged along an ordered internal scale—is capable of accurately describing both human and nonhuman behavioral performance and neural coding in magnitude estimation, production, and reproduction tasks for most psychological dimensions (e.g., time, space, number, or brightness). This model traditionally includes two parameters that determine how a physical stimulus is transformed into a psychological magnitude: (1) an exponent that describes the compression or expansion of the physical signal into the relevant psychological scale (β), and (2) an estimate of the amount of inherent variability (often called internal noise) in the Gaussian activations along the psychological scale (σ). To date, linear slopes on log–log plots have traditionally been used to estimate β, and a completely separate method of averaging coefficients of variance has been used to estimate σ. We provide a respectful, yet critical, review of these traditional methods, and offer a tutorial on a maximum-likelihood estimation (MLE) and a Bayesian estimation method for estimating both β and σ [PsiMLE(β,σ)], coupled with free software that researchers can use to implement it without a background in MLE or Bayesian statistics (R-PsiMLE). We demonstrate the validity, reliability, efficiency, and flexibility of this method through a series of simulations and behavioral experiments, and find the new method to be superior to the traditional methods in all respects.

One of the foundational challenges for psychology is to determine how the mind represents physical dimensions. After more than a century of research, psychophysics—the study of the relationship between external stimuli and internal sensation—has converged on a simple model of internal representations for most psychological dimensions (Cantlon, Platt, & Brannon, 2009; Dehaene, 2003; Gescheider, 1997; Gibbon, 1991; Laming, 1986, 1997; Lu & Dosher, 2014; S. S. Stevens, 1964; Whalen, Gallistel, & Gelman, 1999). Under this model, various dimensions (e.g., distance, time, number) across various senses (e.g., vision, taste, touch) are represented internally on continuous ratio scales, with regions of these scales being activated in response to the intensity of a physical stimulus. Sensory organs and early sensory processing can expand or compress the signals from the world, and these signals are often subjected to some corruption—typically described as Gaussian internal noise. Though this classic model is by no means complete (e.g., Luce, Steingrimsson, & Narens, 2010; Steingrimsson & Luce, 2012), it remains highly influential and is widely used in cognitive, comparative, and developmental psychology, as well as neuroscience and computational modeling.

This classic psychophysical model traditionally has two parameters: (1) the degree of psychophysical scaling (e.g., the power law exponent β, variously named in the literature as β, a, n, r, and slope; Laming, 1997; Stevens, 1964), which is thought to reflect the underlying compression or expansion of the external signal onto the internal scale (e.g., how the means of the Gaussian activations change with increasing stimulus intensity), and (2) the inherent variability, or noise, in the Gaussian activations along the scale, which linearly scales with the mean (σ, also discussed in the literature as CV, the Weber fraction, JND, or k; Laming, 1997).¹ Intuitively, β maps to the central tendency of an experienced Gaussian distribution (e.g., “that tone lasted around 3 s”), and σ to the observer’s internal noise and confidence in this estimate. As we discuss below, evidence for the underlying representations being coded as Gaussian distributions has come from a variety of sources, including single-unit recording and fMRI (Jacob & Nieder, 2009; Nieder & Miller, 2004; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004; Tudusciuc & Nieder, 2007).

Consistent with these two primary parameters, behavioral performance across many different tasks obeys two key signatures: Observers typically either under- or overestimate the stimulus intensity (subject to β; Fig. 1) and show increasing variability in responses to stimuli of higher intensities (subject to σ; Fig. 1). For example, if observers are asked to estimate the duration of a briefly presented tone, they typically slightly underestimate the duration of each tone (e.g., say by 40 ms for a 100-ms tone; β ≈ 0.8), and show linearly increasing response variability as the target duration increases (e.g., a standard deviation of 2.8 for 100 ms; σ ≈ 0.07; Grondin, 2012). The observed values for signal compression/expansion (β) and response variability (σ) are different for different psychological dimensions. For example, if observers are asked to estimate felt pressure on the skin, they will typically overestimate the intensity of tactile stimulation (e.g., 251 for 100 pounds of pressure; β ≈ 1.2) and show less rapidly increasing response variability as the target stimulation increases (e.g., standard deviation of 7.53 for 100 pounds; σ ≈ 0.03; J. C. Stevens & Mack, 1959). Thus, internal representations for a wide variety of psychological dimensions can be described by simply varying the fitted values for β and σ.

Fig. 1

Simulated behavioral responses, based on norms from the empirical literature for six examples, demonstrating the range of β (vertical) and σ (horizontal) values for various dimensions: finger spread (Gaydos, 1958; S. S. Stevens & Stone, 1959), pressure on skin (J. C. Stevens & Mack, 1959), auditory duration (Grondin, 2012), visual number (Krueger, 1984), felt vibration (J. C. Stevens & Mack, 1959), and the odor of n-amyl alcohol (Cain, 1977).

Though it is not completely without criticism (Lockhead, 2004; Luce et al., 2010; Steingrimsson & Luce, 2012), this psychophysical model has been productively used to describe representations of most psychological dimensions (e.g., finger spread, pressure on skin, auditory duration, visual number, felt vibration, odor concentration, brightness, loudness, etc.; see Fig. 1 and the citations therein). The values for β and σ across different dimensions (e.g., pain, brightness, or time) have been thoroughly explored, and these results have informed theories of behavior and the underlying neural coding of these dimensions (Dehaene, Izard, Spelke, & Pica, 2008; Gescheider, 1988, 1997; Lu & Dosher, 2014; Shepard, 1981). This simple Gaussian model also successfully captures several psychophysical “laws”—for instance, Weber’s law (Dehaene, 2003; Dehaene & Changeux, 1993; Laming, 1997; Meck & Church, 1983; Stoianov & Zorzi, 2012) and scalar variability (Cordes, Gelman, Gallistel, & Whalen, 2001; Gibbon, 1991; Whalen et al., 1999). The model’s predictions have been explored computationally (Dehaene & Changeux, 1993; Stoianov & Zorzi, 2012; Verguts & Fias, 2004), developmentally (Droit-Volet, Clément, & Fayol, 2008; Odic, Libertus, Feigenson, & Halberda, 2013; Xu & Spelke, 2000), comparatively (Brannon, Wusthoff, Gallistel, & Gibbon, 2001; Cheng, Srinivasan, & Zhang, 1999; Piffer, Agrillo, & Hyde, 2011; Platt & Johnson, 1971), and neurally (Nieder, 2005; Nieder & Miller, 2004; Pinel, Piazza, Le Bihan, & Dehaene, 2004; Roitman, Brannon, & Platt, 2007).

In recent decades, research in this area has increasingly focused on individual differences in humans’ representations of physical dimensions and the possible relationships between such differences and broader cognitive abilities. For example, expertise in racquet sports and golf modulates β (i.e., the amount of underestimation) in distance perception (Chang, Wade, Stoffregen, & Ho, 2008), whereas music expertise decreases σ in time perception (Grondin & Killeen, 2009; Madison, 2014). Developmentally, the σ of approximate number estimation improves with age (Halberda & Feigenson, 2008; Halberda, Ly, Wilmer, Naiman, & Germine, 2012; Halberda, Mazzocco, & Feigenson, 2008; Odic et al., 2013), and individual differences in σ correlate with math performance prior to and after schooling, even when other cognitive and perceptual abilities are controlled for (Halberda et al., 2008; Libertus, Feigenson, & Halberda, 2011; Libertus, Odic, & Halberda, 2012). Work in developmental psychology has mapped changes in β and σ across development for several dimensions, including number and surface area (Odic et al., 2013), and has shown that the precision of some dimensions continues to improve even into adulthood (Halberda et al., 2012). Finally, comparative psychologists have shown that nonhuman animals—including pigeons, guppies, monkeys, rats, and apes—are able to approximate a variety of dimensions with β and σ values quite similar to those of humans (Beran & Rumbaugh, 2001; Cantlon & Brannon, 2006; Meck & Church, 1983).

With the increased interest in measuring psychophysical scaling (i.e., β) and internal variability (i.e., σ), along with their relevance to research questions across many subdisciplines in psychology and neuroscience, there is also an increased need for appropriate measurement tools. The most common and extremely popular task used to measure either β or σ is the magnitude estimation (ME) task. In this task, the observer is presented with a physical stimulus of a particular intensity (e.g., a 1,500-ms flash) and is asked to estimate its value along a numeric scale. A closely related method has the observer first see a numeric target value and then adjust the stimulus intensity until the subjective experience matches this value; this method is called magnitude production (MP). Following either of these methods, the experimenter has access to the relationship between the stimulus intensity physically present on each trial and the numeric value assigned to it by the observer. By using this type of data, the experimenter can estimate β or σ.

The most common analysis for estimating β is to plot the target values on the x-axis and the observer’s reported values on the y-axis, and then, typically via ordinary least squares, estimate which power function fits the data best—that is, response = intensity^β. The best-fitting power function is almost always found by converting the axes into log–log values, because a power function is linear in a log–log space, with the linear slope being equivalent to β. This traditional log–log method—which we call TradLog(β), for short—has been prevalent in psychophysics since at least S. S. Stevens (1957), and is widely used to estimate β even today (e.g., Crollen, Castronovo, & Seron, 2011; Huang & Griffin, 2014).

An entirely separate analysis method is typically used to estimate σ. In both the ME and MP tasks, σ is estimated through the coefficient of variation (CV): the standard deviation of the observer’s responses, divided by the mean of their responses. To calculate the CV, researchers measure both the mean response and the standard deviation of responses at a subset of the possible target values along a dimension. As a result, the observer is asked to estimate or produce the same target value many times over the course of the experiment (a “restricted-sampling” design) in order to generate sufficient data for measuring both the standard deviation and the mean response for each target value. An estimate of the CV is calculated separately for each target value, and these CVs are then averaged into a single, global CV (e.g., Cordes, Gelman, Gallistel, & Whalen, 2001; Crollen et al., 2011; Frank, Everett, Fedorenko, & Gibson, 2008; Grondin, 2012; Le Corre & Carey, 2007). To date, this restricted-sampling method—repeatedly presenting the same target values many times throughout the experiment—and computing an average CV has been the only method for estimating σ in ME and MP tasks. We term this method the traditional CV averaging method for estimating σ—or TradCV(σ), for short.

Although the two available analysis methods for estimating β and σ have been productive and widely used, they are not optimally designed. As we demonstrate in detail below, because these methods use separate analyses to estimate β and σ, they fail to account for one parameter when measuring the other, resulting in less reliable estimates that require many trials to converge (see “PsiMLE(β,σ) is reliable across and within subjects (simulated and behavioral data)” and “PsiMLE(β,σ) requires fewer trials to converge (simulated data)” sections). These two existing methods also limit the kinds of experimental designs that researchers can use e.g., only restricted-sampling designs, in which target values are repeated many times, can be used for TradCV(σ); see “PsiMLE(β,σ) is flexible across experimental designs (simulated and behavioral data)” section. The traditional methods also violate several statistical assumptions, including forcing researchers to use log-normal residuals and not accounting for the heteroscedasticity inherent in participants’ responses, both of which violate the assumptions of standard linear regression. As a result, they are not as reliable, sensitive, or flexible as modern parameter estimation methods.

Here, we propose a different method for estimating β and σ within a single analysis—the maximum-likelihood method—or PsiMLE(β,σ), for short. This method simultaneously estimates both β and σ and allows for freedom in the experimental design, including designs in which each target value is presented only once (i.e., “unrestricted-sampling” designs). In comparing the PsiMLE(β,σ) method to the two traditional methods [i.e., TradLog(β) and TradCV(σ)], we find that the parameter estimates from PsiMLE(β,σ) are more precise and more reliable, require fewer trials to converge, and do not violate the assumptions for statistical tests. PsiMLE(β,σ) can also be used to probe issues currently of interest in several literatures, including determining whether the observers in number and time estimation tasks rely on counting, and whether scalar variability is violated for very low or very high stimulus intensity ranges. For advanced users, we also provide a Bayesian version of our method, allowing the incorporation of priors and capitalizing on the many further advantages of Bayesian data analysis, as compared to traditional frequentist statistics.

In the “Implementing PsiMLE(β,σ)” section, we provide a basic outline of the PsiMLE(β,σ) method and its advantages relative to the two traditional methods. Online, we also provide a guide to how the method can be used with freely available software (R-PsiMLE, which can be downloaded from www.panamath.org/psimle/) and without any prior understanding of maximum-likelihood estimation (MLE) or R. This first section and the online guide are sufficient to allow researchers to understand how the method works, how to implement it in their own paradigms, and the basics of its advantages. We also provide additional R and JAGS code—both online and in the Appendix—for users familiar with these software packages.

In the “Extending PsiMLE(β,σ) to test model violations” section, we demonstrate an important extension of PsiMLE(β,σ)—the ability for researchers to detect violations of the typical model, including cases in which participants counted number or time or in which scalar variability has been violated. PsiMLE(β,σ) allows researchers to robustly compare the standard model to these model violations, using methods including Akaike information criteria (AICs), deviance information criteria (DICs), likelihood ratios, Bayes factors, and so forth.

In “Empirical demonstration of PsiMLE(β,σ)’s advantages” section, we provide extensive data—both simulated and behavioral—supporting the validity, reliability, efficiency, and flexibility of PsiMLE(β,σ).

Finally, in the Appendix, we demonstrate how the PsiMLE(β,σ) method can be integrated into a Bayesian approach to data analysis. We also provide additional code for using the PsiMLE(β,σ) method in R, in JAGS, and through the free R-PsiMLE software. Although the Bayesian approach holds several further advantages relative to the pure maximum-likelihood approach, it also requires a greater degree of mathematical and statistical sophistication than we cannot expect of most readers. Thus, although we anticipate that researchers in psychophysics, psychology, and neuroscience will continue to turn to Bayesian data analysis over the next 10 years, here we primarily focus on the maximum-likelihood approach to measuring psychophysical scaling, as this is an important first step beyond the currently dominant traditional methods. We refer readers interested in the Bayesian approach to the Appendix and to our guide online.

Implementing PsiMLE(β,σ)

Using the PsiMLE(β,σ) method is simple and can be done with data from new designs as well as from traditional ME, MP, and reproduction tasks—even those that were collected prior to reading this. For most researchers, the only challenge to using the method may stem from unfamiliarity with parameter estimation software and model selection. To alleviate these issues, we first describe how researchers can intuitively understand PsiMLE(β,σ). Additionally, we have provided R-PsiMLE, a free, user-friendly application that automatically implements the method and requires no prior knowledge of R, MLE, or Bayesian methods. R-PsiMLE is implemented in Java and works on the Windows, MacOS, and UNIX platforms. Interested researchers can download R-PsiMLE and a step-by-step guide to using it from our website (www.panamath.org/psimle/).

Basic overview of PsiMLE(β,σ)

The PsiMLE(β,σ) method is an implementation of a more general MLE approach and, as such, relies on the idea of probability/likelihood. If we assume—as the psychophysical model described above does—that the observer makes a response by taking a random sample from their internal Gaussian activation generated by the experimentally presented physical signal, then the set of behavioral or neural responses across trials will be a reflection of these internal distributions (i.e., subject to the observer’s personal β and σ). Hence, we can ask: What is the most likely internal distribution that generated the participant’s observed samples?

To determine the most likely parameters of the internal distribution given the observed responses, we require three things: a parameterized model of the internal representations (e.g., the psychophysical model with parameters β and σ), the observer’s actual responses, and an optimization method that estimates the most likely parameters from the responses.

As we reviewed above, the internal representations of most psychological dimensions are modeled as a series of Gaussian distributions that are defined by the amount of scale compression or expansion (β) and internal variability (σ). A third parameter—the scaling factor α—can be added to the model to account for the units used in the task (e.g., seconds vs. minutes vs. hours, in time estimation). PsiMLE(β,σ) includes this parameter, though most psychophysicists largely ignore it. Now, if we assume that each response is a random draw from these internal representations, we can use the participant’s observed responses to determine the most likely values for β and σ. Specifically, we can calculate the probability of each response, given particular values for β and σ, and find the values of β and σ that maximize the probability of observing these responses.

As an example, let’s assume that the target values (e.g., length of lines, pounds of weights) presented to the observer were {10, 10, 20, 20, 30, 30, 40, 40} and that the observer’s responses were {6, 7, 11, 13, 15, 14, 17, 22}; this example, of course, is for illustration only, and real data sets would have many more trials and could be from any psychological dimension of interest. The psychophysical model states that each of these responses is a random draw from a Gaussian distribution with a mean of intensity^β and a standard deviation of intensity^β × σ. If, for example, β = 0.80 and σ = 0.12, the Gaussian distribution for the target value 10 would be N(10^0.8, 10^0.8 × 0.12), or N(6.3, 0.75); responses around 6 would, therefore, be highly likely, with responses farther away from 6 gradually becoming less and less so. Hence, we can use the mathematics of normal distributions to calculate the probability of each response given particular values of β and σ. For example, if we try β = 1.0 and σ = 0.2, the probabilities of responses across these trials would be {.31, .27, .18, .12, .13, .12, .09, .08}; but if we try parameter values that are closer to the distribution that generated these samples (β = 0.8 and σ = 0.12), we get much higher probabilities for these responses: {.48, .35, .30, .09, .22, .18, .11, .08}.

Formally, given the standard statistical i.i.d. assumption, the likelihood function for the set of responses (e.g., 30 responses) would simply be the product of the probabilities of the different responses (e.g., the probability of the first response times the probability of the second times . . .). Since the underlying model is Gaussian, we take the Gaussian probability density function and apply the mean α × I ^β and the standard deviation (α × I ^β) × σ. The resulting likelihood function of the observer’s responses (Obs) across n trials is thus:

$$ \mathrm{\mathcal{L}}\left(\left.\beta, \sigma, \alpha \right|\mathrm{O}\mathrm{b}\mathrm{s},I\right)={\displaystyle {\prod}_{i=1}^n\frac{1}{\sqrt{2\pi {\left(\alpha \ast {I}_i^{\beta}\ast \sigma \right)}^2}} \exp \left(-\frac{1}{2{\left(\alpha \ast {I}_i^{\beta}\ast \sigma \right)}^2}\ast {\left({\mathrm{Obs}}_i-\alpha \ast {I}_i^{\beta}\right)}^2\right).} $$

Note that this description assumes the typical and convenient (if unlikely) assumption that the internal signal directly maps to a response without any intervening and distorting process (Gescheider, 1988; Shepard, 1981). Finally, note that the assumption of Gaussian error is not just the standard assumption in the field, but has been empirically validated in terms of both behavior (Cordes et al., 2001; Platt & Johnson, 1971; Whalen et al., 1999) and patterns of neural firing (Nieder & Miller, 2004; Piazza et al., 2004; Tudusciuc & Nieder, 2007).

Given that we can generate a combined probability for any given values of β and σ, we can use an optimization algorithm to find the most likely values (i.e., the maximum-likelihood estimate). This is done by finding the values of β and σ that produce the highest likelihood of the observed data (i.e., that make the observed data most probable). Note that, to simplify computations of products into sums and to work with most modern optimization software, statisticians typically take the negative log of the function above; this log transformation only changes the likelihood function into a negative log-likelihood function, permitting the summing of log probabilities, and does not transform the data (Myung, 2003). Finding the most probable parameters in this model (i.e., the ones that minimize the negative log-likelihood) is usually done through an optimization procedure that simultaneously estimates all parameters. Our preferred software for this is R (through the nlminb optimizer), because it is free and efficient, though alternative software, such as MATLAB, can perform this task as well.

Notice that, unlike the TradLog(β) and TradCV(σ) methods, the MLE approach outlined here uses all available participant responses to simultaneously estimate both β and σ. As we discuss below, this gives PsiMLE(β,σ) a higher degree of efficiency, reliability, and precision, because the estimates of one parameter (e.g., σ) can significantly impact the estimation of the other (e.g., β). Furthermore, because PsiMLE(β,σ) combines likelihoods across different target values, this method also allows us to estimate the parameters without repeating target values (e.g., we could choose to present each target value only once). This is in strong contrast to TradCV(σ), which requires multiple trials at a single target value in order to calculate a mean and SD at each target value.

In the Bayesian approach, we further add information about our prior expectations about how β and σ should be distributed in our population of study. For example, on the basis of prior research with over 10,000 participants, we can expect the σ values of typical college-aged students performing an approximate-number task to be normally (or log-normally) distributed with a mean of 0.26 and a standard deviation of 0.04 (Halberda et al., 2012). By specifying this additional information, estimating β and σ is further enhanced—allowing for a more accurate estimate with fewer data points. The Bayesian approach holds a number of other advantages, since it allows us to specify true credibility intervals, allows us to predict future values, and provides for more robust model comparisons (Kruschke, 2011). Further details on the Bayesian approach are provided in the Appendix.

Advantages of PsiMLE(β,σ) over traditional methods

The advantages of the PsiMLE(β,σ) method come from two sources: the general advantages of MLE over ordinary least-squares regression, and the specific advantages of simultaneously estimating β and σ without having to repeat target values. These advantages are further enhanced when PsiMLE(β,σ) is combined with a Bayesian approach, especially in situations in which we have good information on the prior distributions.

There is an increased interest in using MLE methods for parameter estimation in cognitive psychology and psychophysics (for reviews and basic tutorials on MLE, see Kruschke, 2011; Kuss, Jäkel, & Wichmann, 2005; Myung, 2003; Wichmann & Hill, 2001). A cursory look at other scientific and engineering disciplines—in which the phenomena of interest often comply with power laws and also display linearly increasing variability with time or value (e.g., economics, physics)—reveals that MLE has for decades been the estimator of choice (Clauset, Shalizi, & Newman, 2009; Donkin & Van Maanen, 2014; Gabaix, 2008; Myung, 2003), with most of these fields continuing to expand into Bayesian methods. MLE provides several advantages over ordinary least-squares estimation: (1) Unlike ordinary least squares, MLE is a general-purpose estimation that can be straightforwardly applied to nonlinear regression (e.g., S. S. Stevens’s power law); (2) unlike ordinary least squares, MLE can easily accommodate nonconstant variance (e.g., heteroscedasticity, scalar variability); (3) MLE provides a straightforward and principled way of constructing confidence intervals; (4) MLE can be used for excellent model comparison and model selection through the AIC or Bayesian information criterion (BIC), a point we will discuss in “Extending PsiMLE(β,σ) to test model violations” section; (5) MLE can be easily implemented in a variety of free software packages, including R; and (6) MLE provides several highly desirable statistical properties, including maximal efficiency for nonlinear regression² (for discussion on all of these points, see Myung, 2003).

PsiMLE(β,σ) also provides additional practical advantages over the TradLog(β) and TradCV(σ) methods. We will empirically demonstrate these advantages with simulated and real data in “Empirical demonstration of PsiMLE(β,σ)’s advantages” section:

PsiMLE(β,σ) can be flexibly applied to a range of experimental designs (“PsiMLE(β,σ) is flexible across experimental designs (simulated and behavioral data)” section)

Because the method does not require the repetition of the same target values (i.e., restricted sampling), it can be used both in experiments in which each target value is unique or repeated (i.e., unrestricted sampling) and in designs in which the presented target values are optimally adjusted during the experiment to maximize the parameter estimation procedure (i.e., adaptive sampling, such as in QUEST and PEST; Lesmes, Jeon, Lu, & Dosher, 2006; Treutwein, 1995; Watson & Pelli, 1983). The method also generates an entire probability distribution modeling the participant’s internal representations, thus allowing for predicting responses to target values not presented. Although PsiMLE(β,σ) can also be applied to a restricted-sampling design, there are numerous disadvantages to this design, including that observers form anchoring and adjustment strategies from experiencing the same target values repeatedly (see “PsiMLE(β,σ) is flexible across experimental designs (simulated and behavioral data)” section).

PsiMLE(β,σ) provides more reliable estimates with fewer trials (“PsiMLE(β,σ) is reliable across and within subjects (simulated and behavioral data)” and “PsiMLE(β,σ) requires fewer trials to converge (simulated data)” sections)

Because each data point contributes to the global estimate of the parameters, PsiMLE(β,σ) can simultaneously and more reliably estimate the parameter values with fewer trials (in some simulations, we need only a third of the trials needed for the traditional methods). This is especially important when testing special populations who cannot sit through long experiments (e.g., children or elderly adults) and when testing populations with highly variable responses (e.g., observers suffering from dyscalculia or Williams’s Syndrome; Libertus, Feigenson, Halberda, & Landau, 2014; Mazzocco, Feigenson, & Halberda, 2011; Piazza et al., 2010).

PsiMLE(β,σ) can be used to test for violations of the standard psychophysical model (“Extending PsiMLE(β,σ) to test model violations” and “PsiMLE(β,σ) can detect violations of the standard psychophysical model (simulated data)” sections)

Researchers are often interested in examining whether behavioral data are fit better by the standard psychophysical model or by a different model (e.g., one in which observers counted or in which σ discontinuously changes in low or high intensity ranges). The PsiMLE(β,σ) method can test for this by comparing the likelihood of the standard psychophysical model to the likelihood of a nonstandard model. Importantly, by using a variety of modern model comparison tools—including the AIC, DIC, Bayes factor, and so forth—researchers using the PsiMLE(β,σ) method can determine the more probable model while controlling for the higher number of free parameters in many nonstandard models.

Extending PsiMLE(β,σ) to test model violations

Recently, interest has increased in examining and measuring violations of the standard psychophysical model. Two violations have been of especially high interest: whether the participants counted, rather than estimated, the stimulus presented (Cordes et al., 2001; Frank et al., 2008; Grondin, Meilleur-Wells, & Lachance, 1999; Odic, Le Corre, & Halberda, 2015) and whether the σ value changes with high or low intensities (Bizo, Chu, Sanabria, & Killeen, 2006; Grondin, 2012; Lejeune & Wearden, 2006; Wearden & Lejeune, 2008). For example, in the time literature, evidence for changes in the σ value have been used as evidence for multiple independent clock mechanisms, each for a different scale of duration (Gibbon, Malapani, Dale, & Gallistel, 1997; Grondin, 2012; Lewis & Miall, 2009).

In this section, we demonstrate how PsiMLE(β,σ) can be easily extended to test whether a participant’s responses showed either of these violations and how modern model comparison methods can be used to test for each participant whether the standard or the violation model is more likely to have generated the responses. Advanced model comparison is especially important in this literature, because many nonstandard models have more free parameters than the standard model. As a concrete example, we also empirically demonstrate that PsiMLE(β,σ) is a more sensitive measure for deciding whether or not each individual participant counted instead of estimated (“PsiMLE(β,σ) can detect violations of the standard psychophysical model (simulated data)” section).

Checking whether observers counted

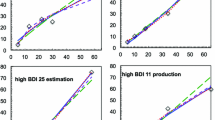
A prominent problem in both the time and number estimation literatures is the possibility that observers subvocally counted during the task. Cordes and colleagues (2001) have demonstrated that σ values, as estimated by the CV, can differentiate counting from noncounting responses: If the observer is counting, the variability is not scalar, but binomial, and the response variability does not increase linearly with target value, but as a square root of target value. As a result, CV estimates decrease linearly with increasing target value whenever observers count (ideally, they decrease with a slope of –0.5 in log–log plots), whereas they remain constant when observers do not count (cf. Figs. 2A and C for a visual example of noncounting vs. counting data). This finding has been confirmed for both time (Grondin et al., 1999) and number (Cordes et al., 2001), and may explain several deviations from Weber’s law in the time literature for the longer durations at which counting is possible and advantageous (Lewis & Miall, 2009). Hence, when using the traditional methods, researchers have checked for counting by testing whether the slope of CV values across target values is significantly below 0 (Cordes et al., 2001; Le Corre & Carey, 2007).

Fig. 2

Four patterns of responses that researchers should be wary of and use nonstandard models for. (A) Expected pattern of responses given the standard model (notice the increasing spread, consistent with scalar variability). (B) Expected pattern of responses if observers are purely guessing around a response; in these situations, β will be 0 and σ is not interpretable. (C) Expected pattern of responses if the observer is counting; notice that there is too much variability in low target values and too little variability in the high target values, consistent with binomial variability. (D) Expected pattern of responses if σ changes at low versus high target values; notice the “pinch” around target value 30, indicating a suddenly changing σ

An improved method for identifying counting-dependent responding becomes possible within PsiMLE(β,σ)—that is, determining (via the AIC, DIC, or Bayes factor) whether the data are fit better by the standard (noncounting) psychophysical model or by the counting model, or whether there is insufficient evidence to adjudicate between them. The likelihood function of the counting model alters the standard deviation of the Gaussian model to increase by the root of target value (α × I^β)^1/σ. Once fit, the model can be compared via AIC/DIC/Bayes factor to the standard psychophysical model. This approach holds numerous advantages over the traditional one, including that it is more sensitive to catching counters and can be applied to individual observers, instead of only to entire groups of participants (“PsiMLE(β,σ) can detect violations of the standard psychophysical model (simulated data)” section).

In the R-PsiMLE software, researchers can select whether they want to test the counting model against the standard model, and the output will include, for each observer, the parameter estimates for the standard and counting models, along with the AIC/DIC difference. If specified, the output will also include a graph of the data and the counting model so that visual inspection can further help researchers decide whether the counting model was appropriate. We stress, however, that to prevent false alarms, this analysis should be theoretically motivated (e.g., there should be independent reasons to suspect that a counting strategy may have been likely) and should not be applied blindly.

Checking whether σ is different for high or low intensities

The standard psychophysical model requires that the standard deviation of the Gaussian distributions increase linearly with target intensity. However, this assumption has occasionally been challenged in the literature—for instance, with different σ values being observed in extremely low and extremely high intensity ranges (see, e.g., Fig. 2D for a visual example of a change in σ). For example, in time perception research, it has often been shown that subsecond time perception is subject to a different σ than is time perception for durations over 1 s (Bizo et al., 2006; Grondin, 2012; Grondin et al., 1999). Such results suggest that different mechanisms of time perception may apply at different duration ranges, which remains an empirical question of great interest. Similar arguments have been made in the number literature for values above and below 20 (Durgin, 1995).

To test for this possibility, we can specify a model that takes a “point of discontinuity” (e.g., 1 s, 20 dots) and estimates a separate σ for target values and responses on each side of this point. Subsequently, this discontinuous model can be compared to the standard one, which assumes an identical σ throughout the range, via an AIC or DIC difference. The AIC/DIC method is especially apt for this research question, because the discontinuous model has more free parameters and, hence, should require more evidence in its favor for it to be likely.

R-PsiMLE allows researchers to test for violations of scalar variability by specifying the point of discontinuity (the point should be chosen in light of theory or previous work or by visually inspecting the outputted graphs). The output file will then provide the estimated parameters for the standard model and the discontinuous model, the AIC/DIC difference, and whether either of the models is more likely. If specified, the output will also include graphs of the data and of the model with changing σ, so that visual inspection can further help researchers decide whether the model was appropriate and what the possible point of discontinuity could be.

Empirical demonstration of PsiMLE(β,σ)’s advantages

In this section, we empirically quantify five major advantages: (1) PsiMLE(β,σ) is a valid estimate of the two psychophysical parameters; (2) PsiMLE(β,σ) is more flexible—it can be used in both restricted- and unrestricted-sampling as well as adaptive-sampling procedures; (3) PsiMLE(β,σ) produces a more reliable measure than the traditional methods given a wide range of actual β and σ values; (4) PsiMLE(β,σ) is more efficient, allowing researchers to get reliable estimates with fewer trials; and (5) PsiMLE(β,σ) can be used to adjudicate between competing models, including identifying observers who counted.

We empirically demonstrate these advantages with both simulated and real data. Simulations allow us to validate PsiMLE(β,σ) in ideal circumstances, and to examine the method’s performance in contexts that are not experimentally or practically testable (e.g., upward to 2,000 trials, or across very wide ranges of true β and σ values). Additionally, because the true parameter values are known in the simulations, we can estimate error rates of both the maximum-likelihood method and traditional methods. We provide simulations for both restricted- and unrestricted-sampling designs to demonstrate the flexibility of PsiMLE(β,σ). The technical details of the simulations are presented in “Simulation and behavioral methods” section, but can be skipped without loss of readability.

We also assessed the performance of PsiMLE(β,σ) in real-world settings. This is done in three experimental tasks: a number magnitude estimation task, a number magnitude production task, and a time reproduction task. In all three, we directly compare parameter estimates generated by PsiMLE(β,σ) to estimates generated by the traditional analysis methods, TradCV(σ), TradLog(β). The similarities in parameter estimates from real behavioral data demonstrate the validity of PsiMLE(β,σ) and its ability to replace traditional methods, and split-half tests reveal that PsiMLE(β,σ) is more reliable than the traditional analysis methods. All of these results would also hold true in the Bayesian approach to PsiMLE(β,σ).

Simulation and behavioral methods

In simulations, we programmed observers whose internal representations are generated from the standard psychophysical model described above. We systematically varied the β and σ for every simulated observer in order to determine how both PsiMLE(β,σ) and traditional methods perform across a variety of values. In each simulation, 500 simulated observers were made for every combination of β and σ, which generated responses to a series of trials on which target values were shown. To remain dimension-neutral, we will refer to the simulated target values as “units”; the reader is welcome to assume that these units refer to any specific unit, including seconds, concentration of liquid, finger span, number of objects, and so forth. The simulated observer had to generate a response on each trial by drawing a random sample from a normal distribution with μ = α × I ^β, and σ = μ × σ. Once all of the responses were generated, we applied both the traditional methods—that is, TradCV(σ) and TradLog(β), and PsiMLE(β,σ) to estimate both β and σ.

Because measurement error will naturally be higher as data variability increases (i.e., with higher σ), we calculated estimation error in two ways. Because σ is bound at 0, our primary measure of error in estimating σ was the percent error from true value (i.e., |estimated – true|/true); this gives us an additional advantage of quantifying error independent of the growing variability (σ). But, because β is both positively and negatively unbounded, our primary measure of error in estimating β was the absolute error from true value (i.e., |estimated – true|).

We ran two types of experimental designs. In the restricted-sampling design, the simulated observers were presented with a set of four target values (10, 20, 30, and 40 units). This design is the most popular design for both ME and MP tasks throughout the literature, and is the only design that the TradCV(σ) method can be applied to. Hence, the restricted-sampling design simulated the traditional experimental paradigm for estimating β and σ, and had observers repeatedly respond to the identical four target values (note that in these simulations, we did not simulate any response biases that may arise in human and animal observers in response to repeated sampling).

In the unrestricted-sampling design, the simulated observers were presented with values drawn from a uniform distribution between 20 and 40 units. The unrestricted-sampling procedure is an experimental design that should reduce real human observer bias and improve parameter estimation. But, the TradCV(σ) method cannot be applied to this method without binning responses into ad hoc categories (e.g., target values between 20 and 30).

In the simulations, β was set to 0.6, 0.8, 1.0, 1.2, or 1.4, and σ was set to 0.01, 0.05, 0.10, 0.15, 0.20, 0.30, 0.40, or 0.50. We also ran simulations with different numbers of trials: 20, 40, 60, 120, 240, 320, 400, or 800 trials. For each combination of β, σ, and number of trials, we ran 500 simulated observers.

Note that due to the very high number of simulations (n = 160,000 for each design), the reported differences between mean errors were always significantly different at p < .05; hence, we do not report significance statistics and, instead, report the means and SD values.

To assess the validity of PsiMLE(β,σ) in estimating parameters for real human observers in magnitude estimation (ME) and magnitude production (MP) tasks, we gave 40 naïve observers a number ME task (Human Exp. 1) and a separate group of 40 naive observers a number MP task (Human Exp. 2). In the ME task, observers saw a briefly flashed set of dots on the screen and had to estimate their number. Similar methods have been used extensively to assess human abilities to estimate numerosity (Cordes et al., 2001; Crollen et al., 2011; Izard & Dehaene, 2008; Krueger, 1984; Whalen et al., 1999). In the MP task, observers were shown an Arabic digit on the screen and had to tap the “L” button that number of times while rapidly repeating the word “the” to prevent verbal counting. Similar methods have been used extensively to assess human abilities to produce approximate numerosities (e.g., Cordes et al., 2001). For each task (i.e., ME, MP), half of the participants took part in a restricted-sampling design (i.e., the target values 9, 13, 17, and 21 were repeated multiple times), and half took part in an unrestricted-sampling design (i.e., the target values were freely sampled from a uniform distribution between 5 and 25). Each participant performed 60 trials.

To demonstrate the validity of the PsiMLE(β,σ) method in magnitude reproduction tasks, we also presented ten naive observers with a time reproduction task (Human Exp. 3). On each trial, the observer heard three equally spaced tones that each gave an example of the target duration, which was drawn from a uniform distribution ranging between 500 and 1,300 ms. After hearing the three tones, the observer pressed the spacebar to begin the reproduction and the spacebar again to end it in an attempt to match as closely as possible the duration they had heard during the first three tones. The task consisted of 60 trials. Grondin (2012) administered this same task using the restricted sampling design and found σ values [as estimated by TradCV(σ)] to be around 0.07 for the range of 1,000–1,900 ms. Although β values were not reported, they could be estimated from Fig. 3 in Grondin (2012) to be around 0.80. In the present experiment, we gave observers the same task as in Grondin (2012), but extended this approach to estimate both β and σ values using PsiMLE(β,σ) in an unrestricted-sampling design.

Fig. 3

Estimation errors as the true σ increases in both restricted-sampling (top) and unrestricted-sampling (bottom) designs. PsiMLE(β,σ) is superior to the traditional methods (i.e., produces lower error) in all four plots

PsiMLE(β,σ) generates valid estimates of β and σ (simulated and behavioral data)

The validity of the PsiMLE(β,σ) method, can be demonstrated in two ways: theoretical face validity (i.e., the method directly reflects the underlying psychophysical model) and practical construct validity (i.e., the method’s error in estimating parameters is convergent with but smaller than traditional methods).

PsiMLE(β,σ) transparently follows from the underlying psychophysical model; in effect, given the model’s assumption that the observer draws samples from their continuous internal Gaussian distribution specified by both β and σ, the method does the inverse and estimates the most likely continuous internal Gaussian distribution given the samples. Relatedly, unlike the two traditional methods, TradCV(σ) and TradLog(β), PsiMLE(β,σ) simultaneously estimates both β and σ and uses the one parameter’s value to aid in estimating the other; in this way, it is more true to the underlying psychophysical model, which always requires both parameters.

Practically speaking, PsiMLE(β,σ) shows validity in both simulated and real data. Because the TradCV(σ) method requires a restricted sampling design, we first report data from simulations and experiments that implemented this design; data from the unrestricted-sampling design is presented in “PsiMLE(β,σ) is flexible across experimental designs (simulated and behavioral data)” section to demonstrate the flexibility of PsiMLE(β,σ).

Simulated data

Averaged across all simulations, the absolute error in estimating β with PsiMLE(β,σ) was 0.029 (SD = 0.045), demonstrating that the method can successfully estimate β. This error was significantly lower than that for estimates derived from the TradLog(β) method (M = 0.046, SD = 0.083). This advantage is due to the superior estimates that can be made on β once information about σ is considered within the MLE framework of PsiMLE(β,σ). There was no difference in absolute errors as the true β changed (although, as we demonstrate in “PsiMLE(β,σ) is reliable across and within subjects (simulated and behavioral data)” section, there was as σ changed).

Averaged across all simulations, the percent error in estimating σ with PsiMLE(β,σ) was 6.3 % (SD = 10.7 %) of true σ, demonstrating that PsiMLE(β,σ) can successfully estimate σ. This error was significantly lower than that for estimates derived from the TradCV(σ) method (M = 8.1 %, SD = 11.7 %). The percent error for estimating σ with PsiMLE(β,σ) remained at a constant 6 %–7 % throughout the range of true σ values.

Together, the results from the simulations suggest that PsiMLE(β,σ) shows valid and more precise estimates than those from the traditional methods.

Behavioral data

Next, we turn to the data from real observers; because we did not know their true parameter values, we used correlations between the parameter estimates derived from PsiMLE(β,σ) and the traditional methods, TradLog(β) and TradCV(σ), to assess the convergent validity of the estimates derived from PsiMLE(β,σ)—that is, PsiMLE(β,σ) measures the same things that the traditional methods were designed to measure. Once again, we only compared estimates from the restricted-sampling design. In the number ME task (Human Exp. 1), the average estimated βs were near identical for PsiMLE(β,σ) (M = 0.84, SE = 0.07) and the TradLog(β) method (M = 0.83, SE = 0.06), and the average estimated σs were identical for PsiMLE(β,σ) (M = 0.18, SE = 0.02) and the TradCV(σ) method (M = 0.18, SE = 0.02). The convergent validity between these estimates was very high (rs = .98 for both β and σ). These results were replicated in the number MP task (Human Exp. 2) for both the estimated β [PsiMLE(β,σ): M = 1.10, SE = 0.03; TradLog(β): M = 1.09, SE = 0.03] and the estimated σ [PsiMLE(β,σ): M = 0.12, SE = 0.01; TradCV(σ): M = 0.12, SE = 0.01]; again the convergent validity was high (r = .97 for β and .99 for σ). All of these estimates, including the difference in under- versus overestimation in ME and MP tasks (i.e., β < 1 in the ME task, and β > 1 in the MP task), are consistent with previous estimates in the literature (Crollen et al., 2011; Krueger, 1984).

PsiMLE(β,σ) is flexible across experimental designs (simulated and behavioral data)

Thus far, we have only shown data from the restricted-sampling design; this choice was made because the TradCV(σ) method can only be applied to this design. But one of the major advantages of PsiMLE(β,σ) is that it can also be applied to the unrestricted-sampling designs. This experimental design has numerous advantages, including reducing the response biases, such as anchoring and adjustment, that may come from a repetition of identical target values throughout the course of the experiment. Here, we demonstrate the flexibility of the PsiMLE(β,σ) method both in simulations (i.e., the average estimation error in unrestricted sampling is small) and in real data (i.e., the estimates from unrestricted sampling match those from restricted sampling). Finally, we demonstrate that, in the real data, there is a significantly higher amount of response bias in the restricted-sampling method.

Simulated data

Averaged across all unrestricted-sampling design simulations, we found that the PsiMLE(β,σ) absolute error in estimating β was small (M = 0.042, SD = 0.065) and lower than the absolute error of the TradLog(β) method (M = 0.063, SD = 0.12). Because the TradCV(σ) method cannot be applied to an unrestricted-sampling design, we attempted to find best estimates by binning the randomly chosen values; we attempted several binning methods, and found that the best performance was achieved by binning target values into five equivalently sized bins. Averaged across all simulations, the PsiMLE(β,σ) percent error in estimating σ was 6.5 % (SD = 10.7 %) and was significantly lower than the error for TradCV(σ) applied over the binned data (M = 24 %, SD = 34.6 %). These extremely high error rates in the TradCV(σ) method came about because the optimal number of bins strongly depends on the true σ value (e.g., when the true σ is low, having few bins makes it appear that response variability is much greater than it really is). Practically speaking, this implies that the binning method cannot be reliably implemented in actual experiments, because the optimal number of bins will strongly depend on the parameter one is trying to estimate.

Behavioral data

In the number ME task, the average values estimated in the unrestricted-sampling design by the PsiMLE(β,σ) method were near identical to those from the restricted-sampling design, with an average σ of 0.17 (SE = 0.01) and an average β of 0.87 (SE = 0.04), with a high convergence between the PsiMLE(β,σ) and TradLog(β) estimates for β (r = .99). The identical pattern of results was found in the number MP task, with an average σ of 0.13 (SE = 0.007), an average β of 0.98 (SE = 0.019), and high convergent validity (r = .99).

In the unrestricted-sampling time reproduction task, the average β estimated by the PsiMLE(β,σ) method was 0.71 (SE = 0.02), a value slightly, though nonsignificantly, lower than the 0.80 seen in Grondin’s (2012) figure. The σ values estimated by the PsiMLE(β,σ) method ranged between 0.06 and 0.14, with an average of 0.089 (SE = 0.008). These values are extremely similar to those found in Grondin (2012), and demonstrate the validity of the PsiMLE(β,σ) method in unrestricted-sampling designs for time reproduction.

Bias in restricted sampling

To examine whether observers really produce higher bias in the restricted-sampling design, we reexamined the number MP and ME data for which we had both restricted- and unrestricted-sampling data sets. We defined bias via the Kolmogorov–Smirnov method as any deviation from the expected distribution of responses, given the underlying psychophysical model. Previous work has suggested that restricted-sampling designs are prone to bias, in that participants show sequential and anchoring effects (for reviews, see Podsakoff, MacKenzie, Lee, & Podsakoff, 2003). Thus, given each person’s σ and the trials presented during the experiment, we can estimate the expected distribution of responses (which should be normal and use all available numbers) and compare it to the actual distribution given by the participant. We measured bias as the absolute difference between the expected and response distributions (i.e., the closer to 0, the less biased individual participants were, since their responses conformed to the expected normal distribution). We chose this metric because it allows us to collapse across a variety of biases into a single metric. This bias metric reflects, for example, response skew, kurtosis, avoidance of or affinity for specific response bins (e.g., a preference to report round numbers—e.g., “ten”), and so forth. We operationalized the question of whether restricted sampling led to increased bias in answers by asking whether bias was significantly higher in the restricted-sampling than in the unrestricted-sampling designs.

In the ME task, observers responding in the restricted-sampling design produced significantly higher bias (M = 1.42, SE = 0.10) than in the unrestricted-sampling design (M = 1.16, SE = 0.07), t(19) = 2.13, p < .05. The main source of bias in the ME task was participants using too many round numbers (e.g., 10, 15, and 20).

In the MP task, observers responding in the restricted-sampling design produced a significantly higher bias (M = 1.23, SE = 0.09) than in the unrestricted-sampling design (M = 0.89, SE = 0.03), t(19) = 5.01, p < .001. The main source of bias in the MP task appears to be an overproduction of similar values (perhaps as a result of rhythmically tapping the same values multiple times), though the values that participants converged on varied widely from individual to individual.

Together, these results demonstrate that restricted sampling produces higher levels of bias and confirms previous suggestions in the literature regarding the effect of repeating target values on the observer’s responses (Tune, 1964). Given that the PsiMLE(β,σ) method is the only one that can estimate σ in an unrestricted-sampling design, this is another reason to prefer it over the TradCV(σ) method.

PsiMLE(β,σ) is reliable across and within subjects (simulated and behavioral data)

Because PsiMLE(β,σ) simultaneously estimates both β and σ, and because each trial contributes to a global estimate of both parameters, we should expect that its estimates would be more reliable and accurate than those based on the traditional methods. Here we demonstrate the method’s reliability in two ways. In simulated data, we show that the method has high reliability across a wide range of true β and σ values; this is especially important given that many populations of interest (e.g., children, lesioned animals, or dyscalculics) show high σ values, with higher variability in σ across time and contexts (Mazzocco et al., 2011; Piazza et al., 2010). In actual data, we demonstrate that the PsiMLE(β,σ) method shows high within-subjects reliability.

Simulated data

Error in estimating β and σ did not vary with the true β values for both the TradLog(β) method and the PsiMLE(β,σ) methods.

Behavioral data

To assess the reliability of parameter estimates in real data, we examined Spearman–Brown-corrected random split-half reliabilities; if the methods were perfectly reliable and the participants were stable in their behavior, we should find correlations of around 1.0 between the estimates computed independently from randomly split halves of trials. Because the identical split-half data were used for all methods, any differences in reliability could only be attributed to the methods themselves. Finally, because the TradCV(σ) method can only estimate σ in the restricted-sampling procedure, we only report the reliabilities from this design.

In the ME task, the Spearman–Brown-corrected split-half reliability of the PsiMLE(β,σ) method for estimating σ was high (r = .93) and was equivalent to the reliability of the TradCV(σ) method (r = .94); the reliability of the PsiMLE(β,σ) method for estimating β was also high (r = .95) and was higher than the reliability of the TradLog(β) method (r = .89).

In the MP task, the Spearman–Brown-corrected split-half reliability of the PsiMLE(β,σ) method for estimating σ was moderately high (r = .83) and was higher than the reliability of the TradCV(σ) method (r = .68); the reliability of the PsiMLE(β,σ) method for estimating β was also moderately high (r = .83) and was identical to the reliability of the TradLog(β) method (r = .82). Together, these results demonstrate that the PsiMLE(β,σ) method is reliable.

PsiMLE(β,σ) requires fewer trials to converge (simulated data)

Because PsiMLE(β,σ) uses every trial to estimate global β and σ values, one benefit is its increased efficiency: PsiMLE(β,σ) should require fewer trials to make better estimates. To empirically test this, we computed the errors across the various numbers of trials in our simulated data. Rapid improvement in estimation accuracy should be seen as a decrease in estimation error with increasing numbers of trials. We compared these rates of improvement across PsiMLE(β,σ), TradCV(σ), and TradLog(β).

The decrease in error with an increasing number of trials was captured best by a power function, with a more negative exponent corresponding to fewer trials being required for PsiMLE(β,σ) than for TradCV(σ) and TradLog(β) (see Fig. 4). In the restricted-sampling design simulations, the PsiMLE(β,σ) method showed more rapid decreases in estimation error for both β [PsiMLE(β,σ), –0.51; TradCV(σ), –0.48] and σ [PsiMLE(β,σ), –0.52; TradLog(β), –0.35]. These results were replicated in the unrestricted-sampling design for both β [PsiMLE(β,σ), –0.52; TradLog(β), –0.16] and σ [PsiMLE(β,σ), –0.52; binned TradCV(σ), –0.49]. Put in terms of the number of trials required to reach a particular level of error, the traditional methods required more than twice as many trials as PsiMLE(β,σ) to attain a similar level of performance. For example, to achieve a percent error of 5 % of true σ, the TradCV(σ) method required around 400 trials, whereas PsiMLE(β,σ) required only 150 trials; similarly, to achieve an absolute error of 0.02, the TradLog(β) method required 542 trials, whereas PsiMLE(β,σ) required 214 trials. The simulations therefore demonstrate that the PsiMLE(β,σ) method is more efficient than the traditional methods.

Fig. 4

Estimation errors as the number of trials increases in both restricted-sampling (top) and unrestricted-sampling (bottom) designs. PsiMLE(β,σ) is more efficient than the traditional methods (i.e., requires fewer trials for lower errors) in all four plots

PsiMLE(β,σ) can detect violations of the standard psychophysical model (simulated data)

As we reviewed in “Extending PsiMLE(β,σ) to test model violations” section, researchers are often interested in determining whether a pattern of responses is consistent with the standard psychophysical model or whether this model was violated. Two especially pertinent violations are counting (which results in binomial, rather than scalar, variability) and nonconstant scalar variability (i.e., a different σ in low or high intensities). Counting is most likely to happen with number and time estimation tasks. In “Extending PsiMLE(β,σ) to test model violations” section, we described how PsiMLE(β,σ) can be used to detect these violations. In this section, we empirically demonstrate its ability and sensitivity to catch violations of the standard model, namely by identifying simulated observers who “counted.”

The traditional method of catching counters relies on the fact that—given the binomial variability of counting—CVs tend to decrease with target values on a log–log plot [i.e., since counting variability increases as a square root of the target number, the slope of log(CV) over log(number) should be –0.5]. Thus, a counter is classified as such if the slope of the log–log plot of CVs over target numbers is significantly different from 0 (in practice, however, most researchers simply check whether the slopes are negative; e.g., Cordes et al., 2001; Crollen et al., 2011). But—as we demonstrate below—this method is not as accurate as the maximum-likelihood alternative, cannot be applied to unrestricted-sampling designs, and requires many more trials to achieve equivalent power.

The PsiMLE(β,σ) method, instead, compares the likelihood of the standard model (i.e., scalar variability) to the likelihood of the counting model (i.e., binomial variability) via their AICs; if the AIC value of the counting model is lower by at least 3.0 than that of the standard model, we have evidence that the observer likely counted. As we demonstrate below, this method holds numerous advantages over the traditional one—it is more accurate than the traditional method, can be applied to any design, and is more efficient.

To test the sensitivity of the PsiMLE(β,σ) method for catching counters, we implemented simulated observers in a restricted-sampling design who imperfectly “counted” over 200 trials and made both double-counting errors (i.e., counted one item as two) and skipping errors (i.e., did not count an item). The target values were 20, 30, 40, and 50. We varied the probabilities of these two errors from 5 %/item to 20 %/item. These simulated observers showed the mathematical characteristics of counting: Their errors were binomially distributed, and—consistent with variability increasing with the square root of numerosity—had an average slope of –0.49 on a log–log plot (e.g., see Fig. 2C). To directly compare PsiMLE(β,σ) against the traditional method, we randomly generated 8,000 observers that either counted (i.e., had binomial variability) or did not count (i.e., had scalar variability with σ between 0.05 and 0.20). We then used the traditional and PsiMLE(β,σ) methods to decide, for every simulated observer, whether they were likely to have counted or not counted.

The traditional method correctly classified simulated observers as counters or noncounters in 84.3 % of cases (SE = 0.59), whereas the PsiMLE(β,σ) method correctly classified in 96.1 % of cases (SE = 0.39), showing superior performance. Both methods performed better when simulated observers had higher percentages of counting errors. The traditional method also showed a significantly lower hit rate [TradCV(σ), 71.2 %, PsiMLE(β,σ), 93.4 %] and a significantly higher false-alarm rate [TradCV(σ), 2.7 %; PsiMLE(β,σ), 1.2 %], resulting in a poorer d' value for the traditional method than for PsiMLE(β,σ) [TradCV(σ) d', 2.48; PsiMLE(β,σ) d', 3.73].

Next, we redid the simulations in an unrestricted-sampling design (i.e., target values randomly varied between 20 and 50) with 200 trials and counting error rates between 5 % and 20 %. As before, we could not get reliable estimates of CV from the TradCV(σ) method and, hence, could not apply the traditional method of catching counters. On the other hand, the PsiMLE(β,σ) method performed well in the unrestricted-sampling design and correctly classified simulated observers as counters or noncounters in 91.23 % of cases (SE = 0.45).

Finally, we tested the efficiencies of the two methods at catching counters. We simulated both counters and noncounters in an unrestricted-sampling design with 40, 100, 200, and 400 trials, and with the error rate at a constant 15 %. Unsurprisingly, the number of trials had an effect on both methods; however, the PsiMLE(β,σ) showed much better performance across the different numbers of trials (M ₄₀ = 77.5 %, M ₁₀₀ = 90.53 %, M ₂₀₀ = 97.0 %, M ₄₀₀ = 99.5 %) than did the traditional method (M ₄₀ = 59.6 %, M ₁₀₀ = 72.21 %, M ₂₀₀ = 84.96 %, M ₄₀₀ = 94.82 %). This advantage was primarily due to the traditional method requiring many more trials for the negative slope to be statistically significant (removing this criterion produced an extremely high number of false alarms, however); the PsiMLE(β,σ) approach, on the other hand, requires substantially fewer trials by using the AIC method.

Overall, the results of the counting simulation suggest that the PsiMLE(β,σ) method can catch counters more accurately, more flexibly, and more efficiently than the traditional method.

General discussion

Over a century of work in psychophysics has shown a surprising degree of commonality in how our cognitive system represents quantity—the vast majority of psychological dimensions, across every modality, are best described by a simple model of Gaussian tuning curves (whose variability is captured by σ) along an ordered ratio scale (whose expansion/compression is captured by β). This model can capture most known behavioral signatures, including scalar variability, S. S. Stevens’s power law, and Weber’s law, and as a result, has unified findings across psychophysics, cognition, development, neuroscience, comparative psychology, and computational modeling.

But, although this model is defined by two inherently related variables, existing methods have focused on measuring them in isolation. Additionally, the existing methods have numerous shortcomings, including lower reliability, a lack of design flexibility (i.e., requiring restricted sampling), and reduced efficiency.

Here, we proposed a novel, maximum-likelihood-based method—PsiMLE(β,σ)—that follows directly from the standard psychophysical model. This new method retains the underlying continuous representations, allows for great flexibility in research designs (including designs that randomly sample the continuous distributions), and as a result of using each trial to estimate the global parameters, is more reliable and efficient than the traditional methods. Furthermore, we have demonstrated how this model can be used to test possible nonstandard models, including those in which observers may have counted or in which σ may change in the high or low stimulus ranges. The method can also be easily extended to a Bayesian approach to data analysis (see the Appendix).

The PsiMLE(β,σ) method, in virtue of following maximum-likelihood principles, can easily be extended and refined to further cases. For example, should psychophysics discover the presence of a third parameter, or that the expansion or compression of target values is not governed by power laws, the PsiMLE(β,σ) equations can easily be adapted. Additionally, this method allows for excellent comparisons across a variety of different nonstandard models, allowing researchers to continue discovering where the standard model may hold and where it may break.

We hope that this new method and the freely available R-PsiMLE software will be adopted by other researchers and used to infer the structure of the underlying representations of quantity across dimensions, individuals, and response strategies.

Appendix: A Bayesian extension to PsiMLE(β,σ)

In this appendix, we demonstrate how PsiMLE(β,σ) can be extended into a Bayesian framework and provide code that can be implemented in JAGS. Our R-PsiMLE GUI interface also has (a simplified) method of running this code through R; further information on R-PsiMLE is available online. For a general introduction to Bayesian data analysis, see Kruschke (2010).

The Bayesian approach to parameter estimation inherits all of the advantages of PsiMLE(β,σ), but it also has further advantages in virtue of Bayesian parameter estimation. A full overview of the Bayesian approach is outside the scope of this article, and here we assume some familiarity with Bayesian parameter estimation and with JAGS.

A Bayesian version of PsiMLE(β,σ) requires two things: a regression model that specifies linearly increasing scalar variability, and a set of priors over α, β, and σ (see below). To help us specify the priors, we examined a wealth of research on psychophysical scaling, all reviewed in the introduction. Our best guess for priors over α and β was that they are normally distributed, with the mean and standard deviation depending on both the dimension in question and whether the task is based on a form of estimation or production (values for most dimensions can be found in standard textbooks on psychophysics, including Gescheider, 1997). Similarly, the empirically measured prior distribution for σ is either a normal or log-normal distribution, with specific values depending on the dimension in hand (e.g., specific values for number can be found at Halberda et al., 2012). Of course, the exact nature of the priors remains an empirical question, and readers are welcome to alter these as they see fit.

Here we provide the JAGS model for standard power-distributed regression with scalar variability modeled as a log-normal distribution, given target values x, participant responses y, and number of trials n (the priors here are purposefully weak):

#psimle_jagspower model

model{

#priors

alpha ~ dnorm(1,0.001)

beta ~ dnorm(1,0.001)

sigma ~ dlnorm(1,0.001)

for(i in 1:n){

mu[i] <- alpha*pow(x[i],beta)

prec[i] <- 1/pow(mu[i]*sigma,2)

y[i] ~ dnorm(mu[i],prec[i])

}

}

The R code implementing this model through rjags, given some participant data, is

library('rjags')

#INITIALIZE DATA

inits <- list('alpha'=1,'beta'=1,'sigma'=0.5)

#SET UP MODEL

parameters = c('alpha','beta','sigma')

n.adapt = 100

n.burn = 1000

n.chains = 4

n.saved = 4000

n.thin = 1

n.iter = ceiling((n.saved * n.thin) / n.chains)

jags.power <- jags.model('psimle_jagspower.bug',

data = list('x' = target_values,

'y' = responses,

'n' = length(responses)),

inits = inits,

n.chains = n.chains,

n.adapt = n.adapt)

#BURN IN

update(jags.power, n.burn)

#GET VALUES AND CREDIBILITY INTERVALS

codaSamples <- coda.samples(jags.power,

parameters,

n.iter = n.iter,

thin = n.thin)

summary(codaSamples)

#PLOT

plot(codaSamples)

In our simulations, we found that three or four chains with anywhere between 800 and 2,000 iterations per chain was more than sufficient for reliable estimation.

Altering the JAGS code to accommodate other models discussed above is straightforward. For example, for the counting model: Alter precision so that σ is raised to the power of the linearly distributed mean. In the case of counting, we should also expect σ to be reliably normally distributed around 0.5, and thus the prior should also be adjusted (see, e.g., Cordes, Gelman, Gallistel, & Whalen, 2001):

#psimle_jagscounting model

model{

#priors

alpha ~ dnorm(1,0.001)

beta ~ dnorm(1,0.001)

sigma ~ dnorm(0.5,0.001)

for(i in 1:n){

mu[i] <- alpha+x[i]*beta

prec[i] <- 1/pow(mu[i]^sigma,2)

y[i] ~ dnorm(mu[i],prec[i])

}

}

Model comparison can then be done by means of either the DIC or the Bayes factor. For example, the R function dic.samples() can be used to provide DIC values. These can then be compared against an alternative model. For a guide to using the DIC, see Berg, Meyer, and Yu (2004).