Structural equation modeling with small sample sizes using two-stage ridge least-squares estimation

Abstract

In covariance structure analysis, two-stage least-squares (2SLS) estimation has been recommended for use over maximum likelihood estimation when model misspecification is suspected. However, 2SLS often fails to provide stable and accurate solutions, particularly for structural equation models with small samples. To address this issue, a regularized extension of 2SLS is proposed that integrates a ridge type of regularization into 2SLS, thereby enabling the method to effectively handle the small-sample-size problem. Results are then reported of a Monte Carlo study conducted to evaluate the performance of the proposed method, as compared to its nonregularized counterpart. Finally, an application is presented that demonstrates the empirical usefulness of the proposed method.

Structural equation modeling or path analysis with latent variables is a basic tool in a variety of disciplines. The attraction of structural equation models is their ability to provide a flexible measurement and testing framework for investigating the interrelationships among observed and latent variables (Kaplan, 2009). Covariance structure analysis, or CSA (Jöreskog, 1973), has been routinely employed for structural equation modeling in social and behavioral research. The maximum likelihood estimation, MLE, method is by far the dominant estimation procedure for CSA (Bollen, 1989). MLE is a full-information estimation procedure, and accordingly, all else being equal, MLE is less robust against model misspecification, because specification errors in some equations can contaminate the estimation of parameters appearing in other equations, since all parameters are estimated simultaneously. The misspecification issue led to the development of a two-stage least-squares (2SLS) method for CSA (Bollen, 1996). 2SLS is a limited-information estimation method in which a single equation is estimated at a time from multiple structural equations. This helps reduce the spread of specification errors from one equation to the other equations.

The utility of an estimation procedure for CSA depends heavily on the procedure’s ability to produce stable and accurate estimates of parameters in structural equation models. Parameter recovery is arguably the most important requirement for good interpretation and inference. With the introduction of 2SLS, there has been some interest in evaluating MLE and 2SLS in terms of their parameter recovery capabilities. Bollen, Kirby, Curran, Paxton, and Chen (2007) conducted a Monte Carlo simulation study to investigate the ability of these two estimation methods to recover parameters under conditions commonly encountered in the use of structural equation modeling in social and behavioral research: small and moderate sample sizes (such as 50, 75, 100, 200, or more samples) and model specification. The results of this simulation study demonstrated that when models are incorrectly specified, 2SLS is preferable to MLE, because the former outperforms the latter in terms of bias. More specifically, MLE spread bias to other, correctly specified equations, whereas 2SLS was better at isolating the impact of specification errors in models. Under model misspecification, MLE has higher bias than does 2SLS across sample sizes. The ability of 2SLS to perform well under model misspecification is an important result, since researchers rarely, if ever, know that their models are correctly specified, and fit indices often lead them to claim that a misspecified model is not a bad model (see Bollen et al., 2007; Hayduk, Cummings, Boadu, Pazderka-Robinson, & Boulianne, 2007). However, the results of the study do not strongly favor either of the two methods in terms of efficiency, regardless of model specification.

In their comparative study, Bollen et al. (2007) also introduced a variant of 2SLS with a reduced set of instrumental variables (IVs) in an attempt to yield less bias in small samples. 2SLS requires model-implied IVs for parameter estimation, which are the observed variables available in the specified model that can serve as IVs in a given equation (see Bollen & Bauer, 2004). In practice, 2SLS commonly encounters the problem of many IVs, which generally represent more IVs than are required to identify the equation. In small samples, using all available IVs can lower the variance of 2SLS but can increase bias to some extent (e.g., Johnston, 1984). Bollen et al. recommended using 2SLS with one additional IV (2SLS-OVERID1), which has one more IV than is needed for identification, because 2SLS-OVERID1 performed better with less bias. However, a consequence of using a subset of IVs is the danger of obtaining unstable estimates of parameters in structural equation models with small samples. Moreover, Buse (1992) suggested that the relation to bias is more complicated than just the degree of overidentification.

The small-sample-size problem has received a lot of attention from researchers because a failure to produce good-quality solutions is often observed in small samples. Popular recommendations regarding the minimum necessary sample size in CSA range from 100 (e.g., Kline, 2005) to 200 (e.g., Boomsma & Hoogland, 2001), so as to yield good-quality results. However, data sets with small samples and many observed variables are common in a wide variety of research areas. Examples of such data are not limited to psychological data, but also abound in medical research, neuroimaging research, behavioral genetics research, animal behavior research, and so on. For instance, the potential application of structural equation modeling in animal behavior studies even involves those cases in which the number of observed variables exceeds the number of observations (e.g., Budaev, 2010).

In statistics, a large body of literature emphasizes the importance of regularization when analyzing high-dimensional data with small samples (e.g., Hastie, Tibshirani, & Friedman, 2001). In particular, a ridge type of regularization has been extensively incorporated into a wide range of multivariate data analysis techniques (e.g., Friedman, 1989; Jung & Lee, 2011; Le Cessi & Van Houwelingen, 1992; Tenenhaus & Tenenhaus, 2011). The present article proposes a new method named two-stage ridge least squares (2SRLS) for estimating structural equation models with small samples. This regularized estimation procedure technically corresponds to ridge regression (Hoerl & Kennard, 1970). As in ridge regression, a small positive value called the ridge parameter is added to the 2SLS estimation procedure. This value typically introduces a little bias but dramatically reduces the variance of the estimates. In other words, the ridge estimator is usually biased (albeit often only slightly), but it provides more accurate estimates of parameters than does the ordinary least-squares estimator because it has a much smaller variance. It is well known that the ridge estimates of parameters are on average closer to the true population values than are the (nonregularized) least-squares counterparts (see Groß, 2003, pp. 118–120). This effect of regularization is more prominent in small samples (e.g., Takane & Jung, 2008).

The structure of this article is as follows. In the next section, the proposed 2SRLS is discussed in detail. Following that, a Monte Carlo study is described that investigated the performance of the proposed regularized method in terms of parameter recovery under different experimental conditions. Then, a real example is presented to demonstrate the empirical usefulness of the proposed method. The final section briefly summarizes the previous sections and discusses further prospects for 2SRLS.

Method

Linear structural equation models with latent variables consist of two distinct models: a structural model and a measurement model. The estimation procedure of 2SLS is the same in both models (see Bollen, 1996). To conserve space, the present article discusses a regularized extension of 2SLS under the structural model. (This extension is equally applicable to the measurement model.) The structural model establishes relationships among the latent variables:

$$ \eta = {{\bf B}}\eta + \Gamma \xi + \zeta, $$

(1)

where η is the vector of latent endogenous variables, ξ is the vector of latent exogenous variables, and ζ is the vector of disturbances. The B matrix gives the effect of the endogenous latent variables on each other, and Γ is the matrix of path coefficients for the effects of the latent exogenous variables on the latent endogenous variables.

To apply 2SLS to Eq. 1, each latent variable must have a single observed variable to scale it, such that

$$ \matrix{ {{{{\bf y}}_1} = \eta + {\varepsilon_1},} \\ {{{{\bf x}}_1} = \xi + {\delta_1},} \\ }<!end array> $$

(2)

where y ₁ and x ₁ are the vectors of scaling indicators. Substituting η = y ₁ – ε ₁ and ξ = x ₁ – δ ₁ from Eq. 2 into Eq. 1 gives

$$ {{{\bf y}}_1} = {{\bf B}}{{{\bf y}}_1} + \Gamma {{{\bf x}}_1} + {{\bf u}}, $$

(3)

where u = ε ₁ – Bε ₁ – Γδ ₁  + ζ is the composite disturbance terms. To simplify the presentation of 2SLS estimation, we consider the following single equation from the structural model in Eq. 3.

$$ {y_i} = {{{\bf B}}_i}{{{\bf y}}_1} + {\Gamma_i}{{{\bf x}}_1} + {u_i}, $$

(4)

where y _i is the ith element of y ₁, B _i is the ith row from B, Γ _i is the ith row from Γ, and u _i is the ith element from u. For the full sample specification, the above structural equation is rewritten as

$$ {{{\bf w}}_i} = {{{\bf Z}}_i}{{{\bf a}}_i} + {{{\bf u}}_i}, $$

(5)

where w _i is an N × 1 vector of observations on the criterion variable y _i ; a _i is a column vector consisting of r free elements in B _i and Γ _i ; Z _i is an N × r matrix of predictor variables consisting of a subset of y ₁ and x ₁, corresponding to the free coefficients in B _i and Γ _i ; and u _i is an N × 1 vector of error terms containing elements of u _i . The ordinary least-squares (OLS) estimator of a _i fails to provide consistent estimates of path coefficients because the predictor variables in the Eq. 5 are correlated with the errors (e.g., Bound, Jaeger, & Baker, 1995). A popular strategy for overcoming this problem is to use the 2SLS estimation method. This estimation requires the existence of IVs that satisfy the following conditions: These variables are correlated with the predictor variables in an equation, but they are uncorrelated with errors. While the choice of valid IVs is often challenging, Bollen and Bauer (2004) proposed a method to automate the selection of model-implied IVs for an equation in the specified model. Let V _i denote an N × c matrix of instrumental variables. Then, the 2SLS estimator (Bollen, 1996) is

$$ {\widehat{{{\bf a}}}_i} = {\left( {\widehat{{{\bf Z}}}_i^{\prime }\;\widehat{{{\bf Z}}}_i^{\prime }} \right)^{{ - 1}}}\widehat{{{\bf Z}}}_i^{\prime }\;{{{\bf w}}_i}, $$

(6)

where

$$ {{{\bf \hat{Z}}}_i} = {{{\bf V}}_i}{\left( {{{\bf V}}_i^{\prime }\;{{{\bf V}}_i}} \right)^{{ - 1}}}{{\bf V}}_i^{\prime }\;{{{\bf Z}}_i}. $$

(7)

This shows that 2SLS stems from two OLS regressions. In the first stage, the predictors Z _i are regressed on the instrumental variables V _i . In the second stage, the 2SLS estimator is obtained by regressing the criterion variable w _i on the first-stage fitted values ${{{\bf \hat{Z}}}_i}$.

As stated earlier, the 2SLS estimator can have poor small-sample properties. The proposed regularized 2SLS aims to deal with the adverse effects of small samples on path coefficients by minimizing the following regularized least-squares optimization criterion:

$$ {f_{\rm{R}}} = {\hbox{SS}}{\left( {{{{\bf w}}_i} - {{{\bf Z}}_i}{{{\bf a}}_i}} \right)_{{{{{\bf P}}_{{{{{\bf V}}_i}}}}}}} + \lambda {\hbox{SS}}\left( {{{{\bf a}}_i}} \right), $$

(8)

where ${{{\bf P}}_{{{{{\bf V}}_{{_{{{\bf i}}}}}}}}} = {{{\bf V}}_i}{\left( {{{\bf V}}_i^{\prime }{{{\bf V}}_i}} \right)^{ - }}{{\bf V}}_i^{\prime }$ is the orthogonal projector on Sp(V _i ), and superscript “–” indicates a generalized inverse (g-inverse). Sp(V _i ) indicates the range of V _i . For the regularized 2SLS, we do not assume that V _i is always columnwise nonsingular. In other words, the number of instruments is not limited and may be smaller or larger than the sample size. A ridge term λSS(a _i ) is added to penalize the size of 2SLS estimates, where λ denotes the ridge parameter. A two-stage ridge least-squares (2SRLS) estimator of a _i that minimizes the ridge least-squares criterion (Eq. 8) is given by

$$ {\widehat{{{\bf a}}}_i}\left( \lambda \right) = {\left( {\widehat{{{\bf Z}}}_i^{\prime }\;{{\widehat{{{\bf Z}}}}_i} + \lambda {{\bf I}}} \right)^{{ - 1}}}\widehat{{{\bf Z}}}_i^{\prime }\;{{{\bf w}}_i}, $$

(9)

where ${\widehat{{{\bf Z}}}_i} = {{{\bf P}}_{{{{{\bf V}}_{{{\bf i}}}}}}}{{\bf Z}}$. The 2SRLS estimator in structural equation models is analogous to the ridge least-squares estimator (Hoerl & Kennard, 1970) in multiple regression models. Thus, the 2SRLS can improve the small-sample performance of the 2SLS.

The proposed 2SRLS uses the bootstrap method (Efron, 1982) to estimate the standard errors of the parameter estimates. More specifically, the standard errors are estimated nonparametrically on the basis of the bootstrap method with 200 bootstrap samples. Furthermore, the bootstrap may be used to test the significance of the ridge parameter estimate (e.g., Takane & Jung, 2008). Suppose, for instance, that an estimate with the original data turns out to be positive. The number of times that the estimate of the same parameter comes out to be negative is then counted in the bootstrap samples. If the relative frequency of the bootstrap estimates crossing over zero is less than a prescribed significance level, the parameter estimate may be considered positively significant.

The method proposed here employs the K-fold cross-validation method to select the value of λ (e.g., Hastie et al., 2001). In K-fold cross validation, the entire data set is randomly divided into K subsets. One of the K subsets is set aside, while the remaining K–1 subsets are used for fitting a single structural equation, and the estimates of the path coefficients are obtained. These estimates are then used to predict values for the one omitted group. This is repeated k times with the one group set aside changed systematically, and the prediction error is accumulated. The K-fold cross-validation procedure systematically varies the values of the regularization parameter, and the value that gives the smallest prediction error is chosen. When K is equal to N (the sample size in the original data), the cross-validation procedure is also known as the leaving-one-out cross-validation (LOOCV). Molinaro, Simon, and Pfeiffer (2005) recently conducted a simulation study to evaluate the performance of LOOCV for estimating the true prediction error under small samples. The results of their study demonstrated that LOOCV generally performs very well with small samples.

A Monte Carlo simulation

A Monte Carlo simulation study was conducted to evaluate the relative performance of 2SRLS, (nonregularized) 2SLS (with all valid IVs), and 2SLS with one additional IV (2SLS-OVERID1) in terms of parameter recovery under different experimental conditions. All computations for this study were carried out using MATLAB R2009a (The MathWorks, Inc.). In the 2SLS-OVERID1 simulation, we selected IVs from the full set of valid IVs, which yields the highest R ² value from the first-stage regression.

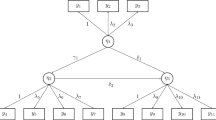
We specified a structural equation model that consisted of three latent variables (η) and three observed variables (Y) per latent variable. The model specification is identical to that given in Bollen et al. (2007). Figure 1 displays the correct specification and a misspecification of the model, along with their parameter values. In the misspecified model, three cross-loadings are omitted and an additional path coefficient is specified, indicated by the dashed lines in Fig. 1.

Fig. 1

The specified model for the simulation study. The model misspecification indicates omission of the dashed loadings and inclusion of the dashed path coefficient.

The simulation study involved manipulating three experimental conditions as follows: approach (2SLS, 2SLS-OVERID1, and 2SRLS), small sample sizes (5–50), and model specification (correct vs. incorrect). In the study, the parameter values of the cross-loadings, loadings, and path coefficients were chosen as 0.3, 1, and 0.6, respectively. The population covariance matrix was derived from a covariance structure analysis formulation (i.e., the reticular action model; McArdle & McDonald, 1984). A total of 200 samples were generated from a multivariate normal distribution with zero means and the covariance matrix at each level of the experimental conditions, resulting in 2,400 samples for each estimation method (6 sample sizes × 2 model specifications × 200 replications). For each sample, the path coefficients were estimated by means of the three estimation methods being compared. In 2SRLS, the value of the ridge parameter was automatically selected in each sample on the basis of the cross-validation procedure.

One way of assessing the quality of estimators is in terms of mean squared error (MSE). MSE is the average squared distance between a parameter and its estimate (i.e., the smaller the MSE, the closer the estimate is to the parameter). Specifically, the mean-square error (MSE) is given by

$$ MSE\left( {{{\hat{\theta }}_j}} \right) = E\left[ {{{\left( {{{\hat{\theta }}_j}-{ }{\theta_j}} \right)}^2}} \right] = E\left[ {{{\left( {{{\hat{\theta }}_j}-E\left( {{{\hat{\theta }}_j}} \right)} \right)}^2}} \right] + {\left[ {E\left( {{{\hat{\theta }}_j}} \right) - {\theta_j}} \right]^2}, $$

where θ^ _j and θ _j are an estimate and its parameter, respectively. This relation indicates that the mean-square error of an estimate is the sum of its variance and squared bias. Thus, the mean-square error takes account of both the bias and variability of the estimate (Mood, Graybill, & Boes, 1974). The estimators would be compared on the following criteria: bias, standard error (SE), and mean-square error (MSE).

Table 1 presents the biases, SEs, and MSEs of the estimates of path coefficients obtained from three competing methods under different conditions. 2SRLS provided more stable and accurate estimates than did 2SLS and 2SLS-OVERID1. 2SRLS was also consistently associated with larger values of bias. A similar pattern of MSE, bias, and SE has been observed in a vast body of literature on regularization (e.g., Takane & Jung, 2008).

Table 1 Overall finite-sample properties of the estimates of path coefficients obtained from the two-stage least-squares (2SLS), 2SLS with one additional parameter (2SLS-OVERID1), and two-stage ridge least-squares (2SRLS) methods under different conditions

In the study, absolute relative-bias values greater than 10 % may be singled out as unacceptable (Bollen et al., 2007). All of these competing approaches led to biased path coefficient estimates for a very small sample size. As sample size increased, 2SLS and 2SLS-OVERID1 yielded unbiased estimates of the path coefficients, whereas 2SRLS showed positively (albeit marginally) biased estimates. Nonetheless, in practice, some degree of bias is often permitted in order to reduce the variance of an estimate and, in turn, the MSE (Hastie et al., 2001).

In general, MSEs of the estimates of path coefficients decreased with increasing sample sizes, regardless of model specification. On average, the 2SRLS method tended to result in parameter estimates having smaller MSEs than those from 2SLS and 2SLS-OVERID1 across sample sizes in both the correct and incorrect models. In particular, this tendency of parameter recovery became more apparent in the two smallest sample sizes for the misspecified model. However, the discrepancies in parameter recovery among the three estimation methods seemed to diminish as sample size increased under the correct model.

The present simulation study showed that small samples indeed posed problems in the estimation accuracy of 2SLS. These problems became more serious in small samples in combination with model misspecification. The proposed 2SRLS was generally shown to result in more stable and accurate parameter estimates than either 2SLS or 2SLS-OVERID1, which shows the usefulness of regularization in estimating structural equation models.

An empirical application

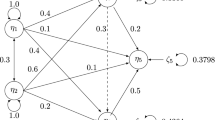
The present example is based on product-level data used in the sensory analysis of food (Pagès & Tenenhaus, 2001). The sample was six orange juices described by 39 observed variables: the physicochemical properties and the ratings of a set of experts on an overall hedonic judgment and on sensorial attributes (e.g., sweetness). Despite the fairly small population of orange juice products, we would not consider the data to be insufficient, because the sample adequately represents the intended population. Figure 2 displays the structural model for the three latent variables, presented in M. Tenenhaus (2008). (All observed variables and disturbance terms are omitted from this figure to avoid clutter.) This structural model included paths from an exogenous latent variable, named Physicochemical, to two endogenous latent variables, named Sensorial and Hedonic, and from Sensorial to Hedonic. In the model, Sensorial functions as a mediator linking Physicochemical to Hedonic. In this application, we applied nonregularized and regularized 2SLS (i.e., 2SLS and 2SRLS) to fit the structural model to the data. In both approaches, the standard errors were estimated nonparametrically using the bootstrap method described earlier. The 2SLS-OVERID1 method was not used because the simulation study reported earlier showed the worst performance of this model on the recovery of population parameter values at the smallest sample size (i.e., N = 5).

Fig. 2

The structural model for the orange juice data.

Table 2 provides the path coefficient estimates obtained from 2SLS and 2SRLS. For 2SLS, the interpretations of the path coefficient estimates appeared to be generally inconsistent with the relationships among the latent variables displayed in Fig. 2. The 2SLS produced unstable estimates of path coefficients due to its poor performance in small samples. Only the path from Physicochemical to Sensorial was significant. To deal with this problem, regularized 2SLS (i.e., 2SRLS) was applied to the data. The structural model in Fig. 2 has two structural equations because it contains two endogenous latent variables. The leaving-one-out cross-validation indicated that λ ₁ = 1.5 and λ ₂ = 0.2 should be chosen for the first and second equations, respectively, since each of these values yielded the smallest cross-validation estimate of predictor error among the values of the ridge parameter ranging from 0 to 10. Table 3 provides the prediction error values estimated under different values of the regularization parameter. As expected, the standard errors from 2SRLS were consistently smaller than those from 2SLS. All parameter estimates were considered highly significant. These seemed to support the specified relationships among the three latent variables in the sensory food analysis.

Table 2 Estimates of path coefficients and their standard errors (in parentheses) obtained from non-regularized and regularized 2SLS for the orange juice data

Table 3 Cross-validation estimates of prediction error (CV) under different values of the regularization parameter (λ) for the orange juice data

Concluding remarks

In this article, a regularized extension of two-stage least-squares estimation was proposed to deal with potential small-sample problems, by optimizing with respect to the ridge parameter. An optimal value of the regularization parameter was chosen in such a way that a cross-validated estimate of prediction errors was minimized. The relative performance of the proposed method was then compared to nonregularized 2SLS on the basis of simulated and empirical data. Specifically, in the simulation, regularized 2SLS tended to produce more accurate parameter estimates than did either nonregularized 2SLS or 2SLS with a reduced subset of instruments under the conditions of model misspecification and/or small samples. In the empirical application, the path coefficients from regularized 2SLS were all significant and provided strong support for the relationships among latent variables in the hypothesized model.

2SLS has been shown to be a viable alternative to MLE under model misspecification (Bollen et al., 2007). 2SRLS is favored over 2SLS for estimation in structural equation modeling with small sample sizes. In practice, however, MLE is by far the dominant estimation procedure. It may be important for the researcher to be aware of any disadvantage of using 2SLS estimation methods. As discussed earlier, MLE is a full-information estimator that integrates both measurement and structural models into a unified algebraic formulation (i.e., a single equation). 2SLS, on the other hand, is a limited-information estimation procedure that uses one equation at a time for estimating parameters, and consequently, 2SLS involves minimizing separate least-squares optimization functions. Due to the absence of a global optimization function, 2SLS offers no measures of overall model fit. Instead, nonnested tests can be implemented for testing alternative models (Oczkowski, 2002). 2SLS also provides local fit measures (such as R ²). Despite the importance of measures of local fit in evaluating the suitability of models (Bollen, 1989), an overall model fit index gives more information on how well a model fits the data as a whole.

As a future extension, we will consider the development of a regularized estimation method for structural equation models involving nonlinear relations among the latent variables (i.e., quadratic and/or interaction terms of latent variables). Testing moderator (interaction) effects is popular in a wide range of behavioral research, and such effects are typically formulated into nonlinear interaction terms. A variety of estimation methods have been developed for modeling the interactive relationships among latent variables. In particular, Bollen (1995) provided two-stage least-squares estimation procedures for latent moderator models. However, evaluating interaction effects in structural equation modeling is generally hampered by some critical challenges, such as small sample sizes and nonnormality (e.g., Dimitruk, Schermelleh-Engel, Kelava, & Moosbrugger, 2007). To address this issue, we may adapt a ridge type of regularization to the two-stage least-squares method for modeling interaction effects.

Finally, although the present simulation study took into account various experimental conditions that are frequently used in Monte Carlo simulation studies in the domain of structural equation modeling, it may be necessary to investigate the relative performance of regularized 2SLS under a larger variety of experimental conditions and with varying model complexity. Moreover, it would be desirable to apply the proposed method to a broad range of applications in various fields of research (such as animal behavior research, behavioral genetics, etc.).